Редуктор волновой характеристики: Редуктор волновой с эвольвентным профилем зубьев.

принцип работы, устройство, применение, типы

Волновая передача

Как работает волновая передача?

Волновая зубчатая передача состоит из трёх основных деталей: генератора волны, гибкого кольца и жёсткого кольца. Генератор волны представляет собой тонкостенный шарикоподшипник напрессованный на эллиптическую втулку. Гибкое кольцо — это тонкостенное зубчатое колесо с внешним зубом. При сборке редуктора генератор волны устанавливается внутрь гибкого кольца. Диаметр гибкого кольца несколько меньше чем диаметр генератора волны, и при сборке гибкое кольцо принимает форму генератора волны. Жёсткое кольцо представляет собой прочное жёсткое зубчатое кольцо с внутренним зубом. Количество зубьев жёсткого кольца обычно на 2 зуба (реже – на 4) меньше чем у гибкого кольца. Гибкое кольцо, установленное на генератор волны, помещается внутрь жёсткого кольца и входит в зацепление с ним в двух зонах, расположенных по большой полуоси эллипса генератора волны. Вне этих зон зацепления зубья жёсткого и гибкого кольца не находятся в контакте.

Strain Wave Gear Principle — Harmonic Drive AG

А можно ли по-другому?

Описанный способ использования – неподвижное жёсткое кольцо, вход на генератор волны и выход с гибкого кольца — не единственный способ использования волнового редуктора. В качестве входа и выхода можно использовать любые из трёх указанных деталей волнового редуктора в любых сочетаниях. При этом редуктор может становиться понижающим или повышающим, изменяться передаточное число и направление вращение выхода относительно входа.

Описанная выше классическая схема волнового редуктора, в которой подшипник генератора волны принимает свою форму благодаря эллиптической втулке, не является единственной. Вместо втулки может применяться коромысло с роликами (Harmonic Drive Polimer) или планетарная ступень (Micromotion). В последнем случае речь, строго говоря, идёт уже о двухступенчатом планетарно-волновом редукторе. Также возможны варианты конструкции волнового редуктора с тремя зонами зацепления вместо двух и генератором волны более сложной формы, но они применяются редко.Чем отличается волновая передача?

• Высокое передаточное отношение на одну ступень (для большинства серийных изделий Harmonic Drive от 50:1 до 160:1, для отдельных серий и специальных разработок – от 30:1 до 320:1)
• Передаточное отношение ограничено снизу: не менее 30:1
• Высокий удельный момент в расчёте на единицу объёма и массы
• Короткая осевая длина
• Возможность легко реализовать передачу вращения в другую среду
• Возможность легко реализовать большой полый вал
• Высокая точность (HDAG)
• Отсутствие люфта (HDAG)
• Стабильность точностных характеристик в течение срока службы
• Ограниченная жёсткость на скручивание
• Несамостопорящяяся (подвержена обратному прокручиванию)
• Высокая надёжность вследствие простоты конструкции

Основные отличительные свойства волновой передачи — высокая точность, низкая масса и малая осевая длина – однозначно указывают на те случаи, когда применение волновой передачи является наиболее оправданным. По этой причине волновая передача часто применяется в применениях, требующих высокой точности, таких как высокоточные станки, роботы и промышленные манипуляторы самого разного назначения, приводы ориентации антенн связи и радаров, или требующих хороших массо-габаритных показателей: авиационная и космическая техника, оборудование для мобильных платформ. Кроме того, возможность реализации редукторов с полым валом позволяет создавать компактные конструкции многоосевых систем за счёт расположения внутри полого вала вращающихся контактных устройств (токосъёмников) для передачи электрических, оптических или гидравлических цепей на следующую ступень подвижности. Похожим образом можно размещать внутри полого вала другой вал, передающий вращение на следующую ступень подвижности, получая определённый выигрыш за счёт размещения двигателей в неподвижной части системы.

Классификация редукторов

На сегодняшний день типы редукторов классифицируются на основе:

• типа механической передачи;
• расположения элементов в пространстве;
• конструктивных особенностей.

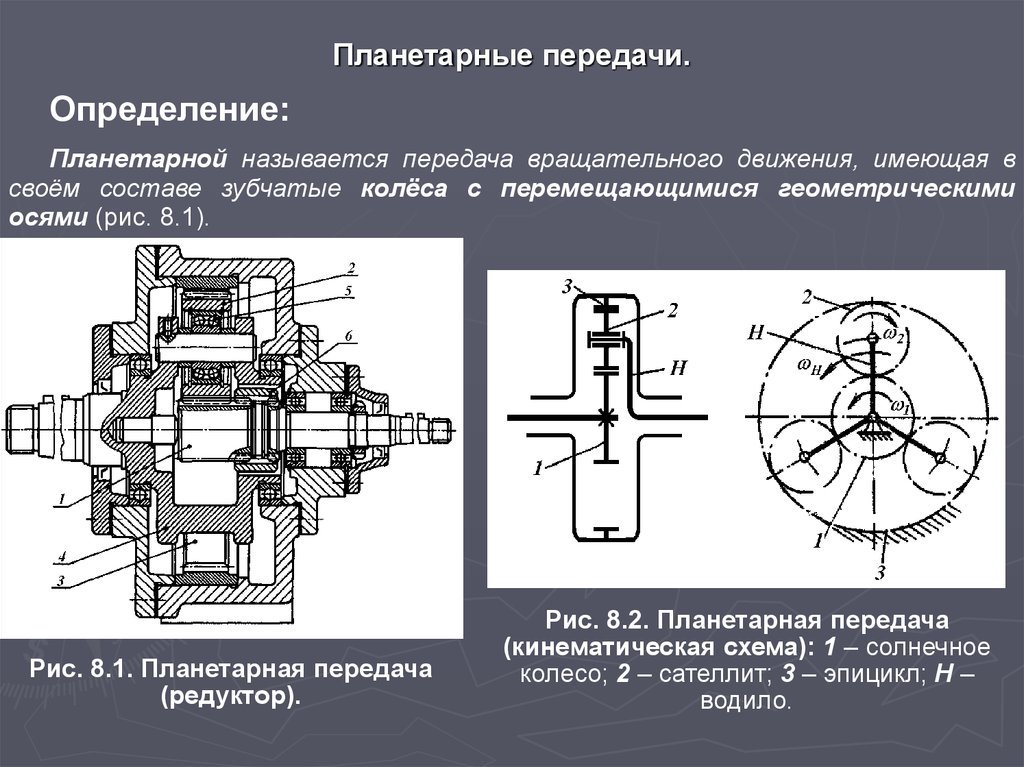
В зависимости от расположения элементов они бывают вертикального и горизонтального исполнения. Среди различных типов можно выделить традиционные механические и мотор-редукторы (с дополнительно установленной двигательной установкой).

Основная, общепринятая классификация редукторов разработана в зависимости от типа передачи и по форме шестерен:

Цилиндрический и конический редуктор

В основе таких моделей используются конические и цилиндрические передачи. Данный тип прямого редуктора характеризируется высоким уровнем КПД (более 80%, в зависимости от количества зубьев). Еще одним преимуществом является практически полное отсутствие нагрева из-за отсутствия нагревающихся элементов. Это позволяет добиться простоты механизма, отсутствия необходимости в дополнительных мерах охлаждения. Данный тип получил высокую популярность благодаря надежности и долговечности.

Планетарный

Отличается от большинства других видов схемой расположения элементов. В его основе лежит планетарная передача. Основной ее функцией можно назвать преобразование поступающего момента. Подобные модели отличаются компактностью благодаря тому, что рабочие элементы находятся в одной геометрической оси, чего нельзя встретить в стандартных механизмах. Широко распространены в сфере приборостроения и машиностроения. Они позволяют комбинировать преимущества цилиндрических и червячных.

Позволяют также добиться оптимального соотношения производительности, компактности, надежности и долговечности.

Червячный

В основе этого вида лежит червячная передача, которая позволяет использовать его для различных целей. Использование этой модели помогает преобразовывать как прямой, так и угловой крутящий момент. В основе конструкции лежит спиралевидный винт, который формой напоминает червяка, из-за чего он получил свое название. Используется довольно редко, так как не отличается надежностью и высокой производительностью. В некоторых случаях при повышении нагрузки может выйти из строя. Несмотря на свои недостатки, он прочно занял свое место в машиностроении, так как является незаменимым при передаче усилия между перпендикулярно расположенными валами.

Волновой

Имеет особенный характеристический размер и тип конструкции, в основе которой лежит неподвижный корпус с нарезанными зубьями. Внутри корпуса расположен гибкий элемент, усилие на которые передается ведущим валом, соединенным с ним. Гибкий элемент изготовлен в виде овала, благодаря чему при движении внутри корпуса создает волнообразные движения.

Данный тип отличается высокой производительностью, имея высокое передаточное отношение, достичь которое невозможно с помощью других моделей

Отличается компактными размерами, что особо важно для использования в точном машиностроении

Следует отметить, что современные тенденции машиностроения требуют особых характеристик от редукторов.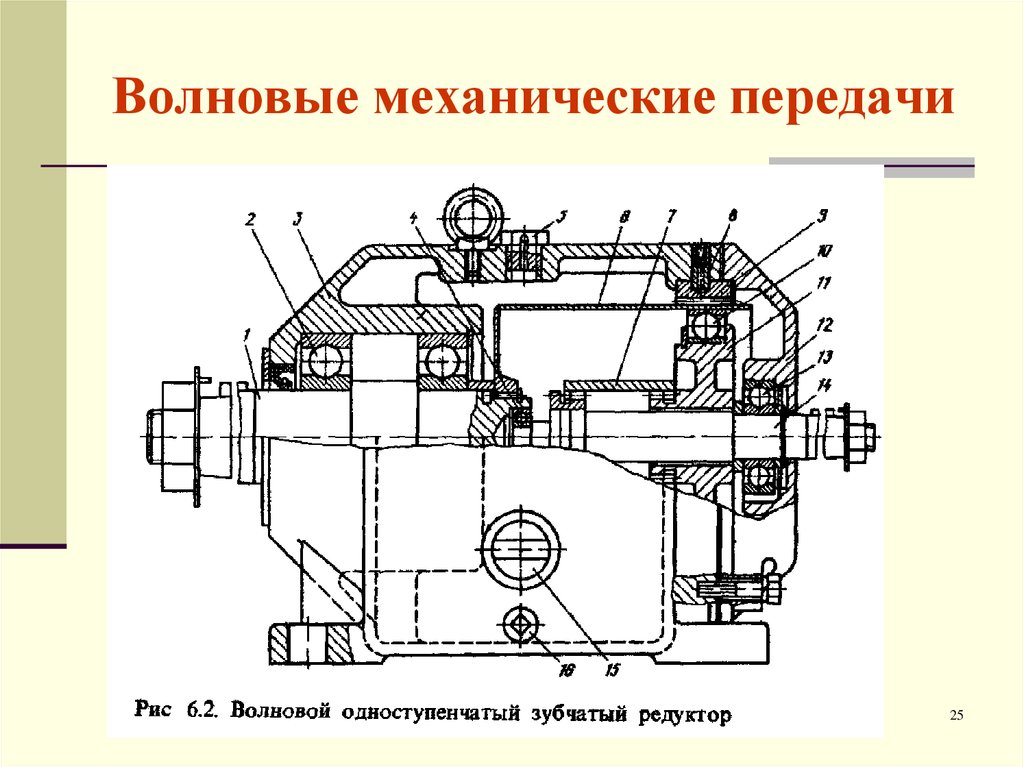 Из-за этого все большего распространения получают комбинированные модели. Цилиндрические модели дополняют коническими горизонтальными передачами. Червячные дополняются дополнительными валами, а также некоторые модели оснащаются дополнительными моторами.

Различные виды мотор-редукторов получили широкое распространение благодаря тому, что в одном механизме объединяют еще и электродвигатель и все необходимые дополнительные элементы.

Волновой редуктор: принцип работы, устройство, применение, типы

Появление и дальнейший процесс развития волновой передачи был осуществлен в далеком 1959 году. Изобретателем, а также человеком, который запатентовал эту технологию, стал американский инженер Массер.

Волновой редуктор состоит из нескольких основных элементов:

• Неподвижное колесо, имеющее внутренние зубья.
• Вращающееся колесо, имеющее наружные зубья.
• Водило.

Среди преимуществ, которые можно выделить у этого способа передачи движения, – меньшая масса и размеры устройства, более высокая точность с кинематической точки зрения, а также меньший мертвый ход.

Если есть необходимость, то использовать такой тип передачи движения можно и в герметичном пространстве, не используя при этом уплотняющие сальники. Данный показатель наиболее важен для такой техники, как авиационная, космическая, подводная.

Кроме того, волновой редуктор применяется и в некоторых машинах, использующихся в отрасли химической промышленности.

Принцип работы редуктора

С кинематической точки зрения, волновые передачи – это разновидность планетарных передач, которая имеет одно гибкое и зубачатое колесо.

Принцип работы волнового редуктора заключается в следующем. Неподвижное колесо устройства крепится в нужном корпусе, а выполняется оно в виде простого зубчатого колеса, имеющего внутреннее зацепление.

Гибкое же зубчатое колесо выполняется в форме стакана, обладающего тонкой стенкой, легко поддающейся деформации. В более толстой части этого же колеса, то есть левой, нарезают зубья, в то время как правая часть выполняется в форме вала.

Само же движение осуществляется за счет того, что происходит деформация зубчатого венца гибкого колеса.

Принцип работы устройства

Принцип работы волнового редуктора основывается на деформации гибкого элемента, которая обеспечивает движение зубчатого колеса внутри втулки. Деформация происходит под действием специального эксцентричного механизма, который растягивает гибкую деталь до образования двух точек соприкосновения внутренней шестеренки с зубцами внешней втулки.

Благодаря зацеплению зубьев между собой появляется возможность продолжить вращение внутренней части. При этом количество зубьев у гибкого элемента меньше, чем это число у неподвижного элемента.

Благодаря этому факту и получается обеспечивать требуемую плавность и точность движений.

Волновой мотор редуктор представляет собой волновую передачу, объединенную с электрическим двигателем. Они имеют очень широкую сферу применения во многих отраслях промышленности. Этим обусловлено большое количество различных вариантов исполнения. Двигатели отличаются размерами, максимально возможной нагрузкой, мощностью и коэффициентом полезного действия.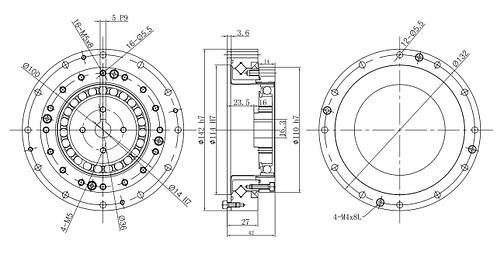

Из преимуществ силовых агрегатов данного типа можно отметить более компактные габариты, чем у других моторов при одинаковой мощности. Также они способны длительное время работать на предельных нагрузках без видимого износа основных механизмов. Волновые моторы характеризуются низким уровнем шума при работе и практически отсутствующей вибрацией.

Конструкции редукторов

В настоящее время науке известно множество разнообразных конструкций для волнового редуктора. Чаще всего предназначение всех этих устройств – это преобразование входного вращательного движения в выходное вращательное или же выходное поступательное.

Также стоит отметить, что волновую передачу можно рассматривать, как разновидность многопоточного планетарного механизма. Это вполне возможно, так как эти механизмы обладают многозонным, а если брать в расчет зубчатый механизм, то еще и многопарным контактом между выходным звеном и гибким колесом механизма.

Также можно добавить, что в зависимости от числа зон или же волн в устройстве они подразделяются на одноволновые, двухволновые и т. д.

Волновой мотор-редуктор

Описание данного типа волновой передачи можно сделать на основе мотора редуктора модели МВз2-160-5,5. Данная модель обладает сдвоенной волновой зубчатой передачей.

Конструкция данного редуктора состоит из гибкого колеса, которое выполнено в виде кольца с тонкими стенками и двумя зубчатыми венцами.

Кроме того, в конструкции имеется и общий для этих деталей кулачковый генератор волн, обладающий гибким подшипником.

Также у этой модели есть несколько особенностей, касающихся конструкции редуктора:

1. Размер вдоль оси вала невелик.
2. Генератор волн плавающего типа, а соединение с валом электродвигателя шарнирное.
3. На конце выходного вала этого устройства располагаются прямобочные шлицы.

Этот тип мотора-редуктора может использоваться, как индивидуальный приводной модуль.

Классификация в зависимости от сферы применения

В зависимости от сферы применения редукторы под газовый баллон разделяются на несколько видов:

• Бытовые нерегулируемые.
• Универсальные регулируемые
• Профессиональные.

Бытовые нерегулируемые

К этому виду относятся самые простые редукторы, применяемые в бытовом газоснабжении домовладений и в походных условиях. Вместе с бытовыми газовыми баллонами устанавливают редукторы РДСГ. Они имеют простейшую конструкцию, позволяющую использовать газ только в бытовых плитах и отличаются дешевизной и надежностью. Редуктор лягушка для газового баллона, или РДСГ-1 используется вместе с емкостями от 12 до -50 литров.

Для пятилитровых газовых баллонов, популярных у дачников, туристов и охотников, используют модель РДСГ-2 Балтика. Редуктор Балтика надевается на ниппель газового баллона сверху и фиксируется в резиновом уплотнении специальным зажимом. Редукторы настроены на рабочее давление 0,3 МПа и пропускную способность 1,2 м 3 /час

Универсальные регулируемые

Этот класс редукторов отличается более сложной конструкцией и более широкими возможностями. Их уже можно применять как для бытового газоснабжения, так и для производства работ в домашней мастерской. Эти редукторы имеют обязательно резьбовое присоединение к газовому баллону, надежно фиксирующее устройство.

Универсальный регулируемый для пропана с манометром

Они также снабжены манометром и регулировочным винтом, позволяющим менять рабочее давление от 0 до 0,3 МПа, в зависимости от потребностей подключенного к ним устройства–потребителя газа. Эти устройства также имеют большую, чем у бытовых, пропускную способность — до 5 м 3 /час

Профессиональные

Этот класс характеризуется применением более износостойких материалов и лучшее качество сборки и регулировки. Также шире и параметры регулировок рабочего давления – от 0,4 до 1,6 МПа.

Профессиональный редуктор с двумя манометрами

Некоторые модели снабжены двумя манометрами — для входного и рабочего давления соответственно.

Газовые

Эти агрегаты являются устройствами, которые способны понижать давление на выходе из какой-либо емкости (например, в баллоне).

Существуют следующие виды газовых редукторов:

• Кислородные, применяющиеся на многих машиностроительных предприятиях. С помощью таких редукторов можно выполнять любые автогенные работы. Например, сваривать или паять детали.
• Ацетиленовые, которые часто применяются в коммунальном хозяйстве для резки трубопроводов.
• Воздушные редукторы. Такие агрегаты используют многие предприятия. С их помощью можно непрерывно поддерживать необходимое давление воздуха в сетях и коммуникациях. Кроме того, подобные виды редукторов используют в дайвинге как устройства, которые способны снижать давление дыхательной смеси.
• Пропановые, использующиеся в металлургии. Они помогают рабочим проводить различные автогенные работы, наподобие резки или пайки. Кроме того, эти редукторы можно встретить и в быту. Ярким примером являются плиты, в которых встроены подобные регуляторы давления газа.

Обслуживание и ремонт

Сложность рассматриваемого механизма определяет то, что возникает необходимость в своевременном обслуживании и проведении ремонта

Для начала уделим внимание тому, каким образом проводится расчет планетарного редуктора. Среди особенностей этого процесса отметим следующие моменты:. Определяется требуемое число передаточных ступеней

Для этого применяются специальные формулы. Определяется число зубьев и расчет сателлитов. Зубчатые колеса могут иметь самое различное число зубьев

Определяется требуемое число передаточных ступеней. Для этого применяются специальные формулы. Определяется число зубьев и расчет сателлитов. Зубчатые колеса могут иметь самое различное число зубьев

В рассматриваемом случае их число довольно много, что является определяющим фактором

Уделяется внимание выбору наиболее подходящего материала, так как от его свойств зависят и основные эксплуатационные характеристики устройства. Определяется показатель межосевого расстояния

Делается проверочный расчет. Он позволяет исключить вероятность допущения ошибок на первоначальном этапе проектирования. Выбираются подшипники

Они предназначены для обеспечения плавного вращения основных элементов

При выборе подшипника уделяется внимание тому, на какую нагрузку они рассчитаны. Кроме этого, не рекомендуется использовать этот элемент без смазки, так как это приводит к существенному износу

Определяется оптимальная толщина колеса. Слишком большой показатель становится причиной увеличения веса конструкции, а также расходов. Проводится вычисление того, где именно должны быть расположены оси шестерен. Это проводится с учетом размеров зубчатых колес и некоторых других моментов. Как правило, в качестве основы применяется чертеж, который можно скачать из интернета. Самостоятельно разработать проект по изготовления планетарного редуктора достаточно сложно, так как нужно обладать навыками инженера для проведения соответствующих расчетов и проектирования.

Изготовить самостоятельно рассматриваемую конструкцию достаточно сложно, как и провести ремонт планетарных редукторов. Среди особенностей этой процедуры отметим следующее:

1. Процедура достаточно сложна, так как механизм состоит из большого количества различных элементов. Примером можно назвать то, что сразу после разбора все иголки могут высыпаться практически моментально.
2. Многие специалисты рекомендуют доверять рассматриваемую работу исключительно профессионалам, так как допущенные ошибки становятся причиной быстрого износа и выхода из строя механизма.
3. Ремонт зачастую предусматривает замену шестерен, которые со временем изнашиваются. Примером можно истирание зубьев, изменение размеров посадочного гнезда и многие другие дефекты. Самостоятельно изготовить подобные изделия практически невозможно, так как для этого требуется специальное оборудование.

Чаще всего обслуживание предусматривает добавление масла. Смазка планетарного редуктора позволяет существенно продлить срок службы конструкции, так как соприкосновение и трение металла становится причиной его истирания. Рекомендуется смазывать механизм периодически, так как масло выступает еще в качестве охлаждения. В продаже встречаются специальные смазывающие вещества, которые характеризуются определенными эксплуатационными качествами.

Сегодня ремонтом редукторов занимаются компании, которые специализируются на предоставлении соответствующих услуг. Признаком того, что механизм начинает выходить из строя становится появление сильного шума, вибрации, рывков, нагрев и многое другое. Со временем процесс износа существенно ускоряется, так как металл, находящийся в масле попадает в зацепление шестерен. В большинстве случаев ремонт предусматривает замену всех элементов на новые.

В заключение отметим, что планетарный редуктор характеризуется весьма привлекательными свойствами. Примером можно назвать отсутствие большого количества крепежных элементов, а также равномерное распространение нагрузки. Как ранее было отмечено, редуктор применяется при создании различных узлов транспортных средств.

Обслуживание колесного редуктора

Для повышения надёжности агрегата и продления срока его безопасного функционирования, необходимо с определённой периодичностью проводить его техосмотр и соответствующее обслуживание, используя для этого специальную контролирующую и измерительную аппаратуру. Перед началом ремонтных работ следует предварительно отсоединить коробку передач от корпуса сцепления, под который, впрочем, как и под передний мост, устанавливают подвижные подставки. Под коробку передач ставится подставка неподвижного типа. Далее следует отключить гидросистему и разъединить тракторный остов, раскатать его и отсоединить от корпуса сцепления полураму.

После того как разборка завершена, можно переходить к диагностике агрегата, в первую очередь обратив внимание на следующие моменты:

• Показатели уровня масла в гидравлическом баке;
• Функционирует ли двигатель на полной мощности;
• В каком состоянии находится ходовая;
• Имеет ли место утечка масла;
• Есть ли давление в сливной линии гидромотора и на входе в него;
• В каком состоянии находятся крепёжные соединения;
• Исправны ли подшипники роликового типа;
• Не нуждается ли в замене система зубчатого сцепления на верхних и нижних конических парах.

Если в процессе осмотра колёсного редуктора будет обнаружено существенное уменьшение уровня масла в верхней конической паре, значит это верный признак того, что в системе имеется утечка. Нужно обязательно выявить причины её возникновения и максимально оперативно устранить неисправность. Вполне возможно, что для этого может потребоваться даже частичная разборка этого узла, хотя, по сути, это единственный способ устранения проблемы.

Классификация по основным признакам

Современные инженерно-технические стандарты предусматривают классификацию редукторов по следующим признакам:

• конструкция используемой передачи;
• пространственное расположение элементов;
• конструктивное исполнение.

По пространственному расположению ключевых элементов эти устройства подразделяются на редукторы вертикального исполнения и традиционные горизонтальные. Конструктивное исполнение предусматривает два дополнительных вида: чистый механический редуктор, и редуктор с двигательной установкой (мотор-редуктор). Однако общепринятой классификацией редукторов считается таковая по типу используемого передаточного узла (передачи).

Принцип работы устройства

Редуктор понижает давление газа при выходе из баллона

Различают приборы прямого и обратного действия. Принцип работы газового редуктора определяется конструкцией.

В варианте прямого действия газ из резервуара через штуцер давит на клапан, газовая смесь проникает в камеру высокого давления. Теперь пропан давит изнутри – прижимает клапан пружиной и перекрывает доступ следующей порции газа. Рабочая мембрана медленно возвращает клапан, давление газа уменьшается до рабочего – той величины, с которой работает плита.

При снижении напора пружина расслабляется и освобождает клапан. Последний открывается под напором газа, поступающего из резервуара, и весь цикл повторяется.

Такого типа регуляторы делятся на 2 вида:

• Одноступенчатый – с 1 камерой, где снижается давление. Минус – показатель газа на выходе зависит от величины на входе.
• Двухступенчатый – включает 2 камеры. Газ последовательно проходит камеру высокого и рабочего давления и лишь затем подается к плите. Такая конструкция позволяет установить любое значение на выходе, вне зависимости от напора в баллоне и более точно регулировать показатели. Скачки давления исключаются.

Регуляторы могут оборудоваться подводом дополнительной энергии за счет установки пневматических и гидравлических датчиков или электронных автоматических устройств.

Принцип работы редуктора давления газа обратного действия другой. При поступлении газа клапан сжимается, перекрывая доступ следующей порции смеси. Регулятивный винт заставляет сжиматься базовую пружину. При этом мембрана между камерами изгибается, а передаточный диск давит на обратную пружину. Клапан поднимается и пропускает газ из баллона.

В рабочей камере редуктора давление растет вместе с показателем в баллоне или трубе, по которой подается смесь из газгольдера. Основная пружина распрямляет мембрану, передаточный диск двигается вниз и давит на обратную пружину. Последняя вновь сдавливает пропускающий клапан и перекрывает подачу.

Волновые редукторы российского производства компании Сервосила

Компания Сервосила наладила производство миниатюрных волновых редукторов, — впервые в современной России. Можно сказать, что с распадом Советского Союза технология производства волновых редукторов была утеряна. Усилиями конструкторов и технологов компании Сервосила, российского производителя и экспортера робототехники, был восстановлен этот пробел. Уже третий год компания Сервосила обеспечивает себя и своих партнеров миниатюрными волновыми редукторами .

Волновой редуктор — загадочная штука. Даже просто понять принцип его работы большинству людей удается не сразу. А в технологии его изготовления и методиках расчета скрыто множество подводных камней.

Компания Сервосила — это отечественный производитель мобильных роботов и сервоприводов. Волновые редукторы широко применяются в робототехнике , так как обеспечивают минимальную массу и минимальный люфт при заданном коэффициенте редукции. Изначально Сервосила закупала волновые редукторы за рубежом, что негативно сказывалось на себестоимости продукции. Благодаря освоению производства волновых редукторов, удалось не только снизить себестоимость, но и значительно улучшить компоновку и технологичность выпускаемой продукции, в том числе сервоприводов . Также волновые редукторы применяются в станкостроении и авиации.

Волновые редукторы отличает малая масса при заданном коэффициенте редукции, а также малый люфт. По сравнению с планетарными редукторами, выигрыш по массе может составлять 1.5-2 раза. Также волновые редукторы отличает компактность формы и малые размеры.

Малая масса и компактная форма важны во многих областях, таких как робототехника и авиация

У волновых редукторов также малый люфт, что очень важно в точных электромеханических системах, таких как сервоприводы манипуляторов роботов или систем позиционирования

Достоинства и недостатки планетарных передач

Планетарная передача выигрывает у простых зубчатых механизмов аналогичной мощности компактным размером и массой меньшей в 2 — 3 раза. Используя нескольких планетных шестерней, достигается зацепление зубьев на 80%. Нагрузочная способность механизма повышается, а давление на каждый зубец уменьшается.

Кинематическая характеристика планетарного механизма доходит до 1000 с малым числом зубчатых колёс без применения многорядных конструкций. Помимо передачи планетарная схема способна работать как дифференциал.

За счёт соосности валов планетарного механизма, компоновать машины проще, чем с другими редукторами.

Применение планетарного ряда в АКПП снижает уровень шума в салоне автомобиля. Сбалансированная система имеет высокую вибропрочность за счет демпфирования колебаний. Соответственно снижается вибрация кузова.

Недостатки планетарного механизма:

• сложное производство и высокая точность сборки;
• в сателлиты устанавливают подшипники, которые выходят из строят быстрее, чем шестерня;
• при повышении передаточных отношений КПД падает, поэтому приходится усложнять конструкцию.

Читать

Переключение селектора передач АКПП на ходу

Мотор-редукторы волновые

компания ТЕХПРОМ Адрес: Самара, Камышинская ул., 21, Самара.: (846243-72-22,264-10-40 Факс.:  (846)264-10-40 Саратов .: (8452) 92-44-38 сот. 89093383218 E-mail: &nbsp [email protected] E-mail:  [email protected] http:       www.proizwodim.ru

Спецпредложение Цепи 4ПР-19,05 по 500р. мотор-редуктор 3МП31,5-280 по цене 14900р. Главная » Мотор-редукторы » Мотор-редукторы волновые (МВЗ-80,мвз-160) Мотор-редукторы волновые. Тип МВз ОСНОВНЫЕ ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ МОТОР-РЕДУКТОРОВ МВз Частота вращения выходного вала, об/мин: 7,1; 9; 12,5; 16; 18 Обозначение мотор-редуктора Номинальный крутящий момент на выходном валу, Н.м Допускаемая консольная нагрузка на выходном валу, Н КПД редукторной части Масса мотор-редуктора, кг Мощность эл/дв, кВт МВз-80 100 3000 0,87 13 0,25 МВз-160 900 8000 0,87 66 1,5     ГАБАРИТНЫЕ И ПРИСОЕДИНИТЕЛЬНЫЕ РАЗМЕРЫ МОТОР-РЕДУКТОРОВ МВз Обозначение мотор-редуктора А А 1 B D D 1 D 2 H H 1 L L 1 d d 1 h l b t МВз-80 130 155 190 100 130 160 180 80 430 85 28 13 15 60 8 31 МВз-160 220 220 270 180 215 250 285 125 705 145 55 19 25 110 16 59   Пример условного обозначения мотор-редуктора при заказе: МВЗ-160-16-G110-Ц-У3, ТУУ 29. 1-24587406.003-2003 где МВз — тип мотор-редуктора; 160 — внутренний диаметр гибкого колеса, мм; 16 — частота вращения выходного вала, об/мин; G110 — конструктивное исполнение по способу монтажа; Ц — вариант исполнения выходного вала; У3 — климатическое исполнение и категория размещения. ВОЛНОВЫЕ ПЕРЕДАЧИ Волновые передачи кинематически пред­ставляют собой планетарные передачи с одним из колес в виде гибкого венца. Гиб­кий венец 1 (рис. 10.44) деформируется генератором волн 3 и входит в зацепление с центральным колесом 2 в двух зонах. Принцип волновых передач заключается в многопарности зацепления зубьев, кото­рая определяет все положительные каче­ства этих передач по сравнению с другими. Волновые передачи в сравнении с обыч­ными зубчатыми имеют меньшую массу и меньшие габариты, обеспечивают более высокую кинематическую точность, имеют меньший мертвый ход, обладают высокой демпфирующей способностью (в 4-5 раз большей, чем у ~бычных), работают с мень­шим шумом. При необходимости. волновые передачи позволяют передавать движение в гермети­зированное пространство без применения сальников. Волновые передачи позволяют осущест­влять большие передаточные отношения в одной ступени; .при зубчатых колесах из стали umin =60 (ограничивается проч­ностью при изгибе гибкого колеса) и Итах = 300 (ограничивается минимально допустимой величиной модуля, равной           0,2                0,15 мм). При этом КПД равен»          80   90 %, как и в планетарных передачах с тем же передаточным отношением. К недостаткам .волновых передач можно отнести ограниченные частоты вращения ведущего вала генератора волн при боль­ших диаметрах колес (во избежание боль­ших окружных скоростей генератора), мелкие модули зубчатых колес (0,15 … 2 мм). При серийном изготовлении в специализированном производстве вол­новые передачи дешевле планетарных. Крутильная жесткость волновых передач несколько меньше простых зубчатых, но обычно является достаточной. На рис. 10.44 гибкий венец 1 нарезан на деформируемом конце тонкой цилинд­рической оболочки 5, другой конец которой через тонкое дно соединяется с выходным валом 4. Генератор волн 3 состоит из овальногО кулачка соответствующего профиля и спе­циального шарикоподшипника 6 с гибкими кольцами. Иногда выполняют генератор волн в виде двух дисков (роликов), распо­ложенных на валу или в виде четырех ро­ликов. Сборку зацепления можно осуще­ствить только после деформации гибкого колеса. На концах большой оси вала зубья зацепляютсЯ по всей высоте, на малЬй оси зубья не зацепляютСЯ. Между этими участ­ками зубья гибкого колеса погружены во впадины жесткого колеса на разную глу­бину. Зацепление напоминает шлицевое соединение. При вращении генератора волн гибкий зубчатый венец обкатывается по непо­движному колесу, вращая оболочку и вал. Принцип работы волновой передачи ана­логичен планетарной передаче с парал­лельными кривошипами.

принцип работы, устройство, применение, типы

Волновые передачи

Появление и дальнейший процесс развития волновой передачи был осуществлен в далеком 1959 году. Изобретателем, а также человеком, который запатентовал эту технологию, стал американский инженер Массер.

Волновой редуктор состоит из нескольких основных элементов:

• Неподвижное колесо, имеющее внутренние зубья.
• Вращающееся колесо, имеющее наружные зубья.
• Водило.

Среди преимуществ, которые можно выделить у этого способа передачи движения, — меньшая масса и размеры устройства, более высокая точность с кинематической точки зрения, а также меньший мертвый ход. Если есть необходимость, то использовать такой тип передачи движения можно и в герметичном пространстве, не используя при этом уплотняющие сальники. Данный показатель наиболее важен для такой техники, как авиационная, космическая, подводная.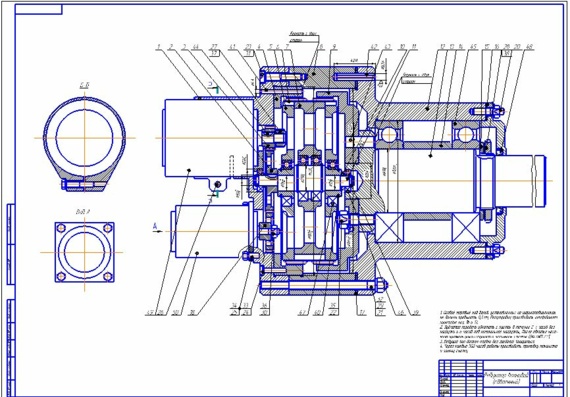 Кроме того, волновой редуктор применяется и в некоторых машинах, использующихся в отрасли химической промышленности.

Основные серии установочных комплектов

В каталоге Harmonic Drive в настоящее время представлено шесть серий редукторов в исполнении установочный комплект. Все эти серии отличаются по параметрам и в частности по производительности. Можно выделить группу серий с базовой производительностью: HFUC-2A, HFUS-2A и CPL-2A. Серия HFUC представлена в самом широком диапазоне габаритов (типоразмеров): от 8 до 100, в части прочих параметров она занимает среднее положение. Гибкое кольцо выполнено в классической форме «кастрюля». Серия HFUS имеет несколько иную конструкцию: гибкое кольцо выполнено в форме «шляпа», что даёт больше пространства внутри редуктора. С другой стороны, по этой причине наружный диаметр и масса редукторов HFUS-2A несколько увеличились по сравнению с аналогичными редукторами HFUC-2A. Серия установочных комплектов CPL-2A была разработана для применения в авиационных и космических системах, где требуется минимальные размеры и масса. При разработке была проведена оптимизация конструкции, благодаря чему масса и длина редуктора были уменьшены, и при этом удалось сохранить на прежнем уровне номинальный момент.

Ещё одна группа серий характеризуется увеличенной производительностью: номинальный момент у них выше, чем у серий с базовой производительностью. К таким сериям относятся CSG-2A и CobaltLine-2A. Обе серии кроме увеличенного номинального момента (примерно на 30%) имеют также значительно (на 40%) увеличенный срок службы по сравнению с сериями базовой производительности. По остальным параметрам и по конструкции эти две серии одинаковы, различие состоит в месте производства: CSG-2A на заводе в Японии, CobaltLine-2A — на заводе в Германии.

Рис. 6 CobaltLine Double

Кроме двух перечисленных выше, есть ещё одна группа редукторов, отличающихся пониженной производительностью для тех же типоразмеров. В настоящее время к этой группе относится только одна серия: CSD-2A. Эта серия имеет пониженную массу (на 40% по сравнению с HFUC) и значительно сниженную осевую длину (на 50%). Легко видеть, что по длине эта серия даже более компактна, чем CPL-2A (у последней длина короче, чем у HFUC, всего на 10%), однако за это приходится расплачиваться более низкой производительностью.

Поскольку установочные комплекты содержат в себе необходимый минимум компонентов с тем, чтобы все остальные детали добавлялись при интеграции редуктора в конструкцию конечного изделия, то полый вал как элемент конструкции также отсутствует. Он может быть установлен непосредственно в конечном изделии, если это необходимо. Кроме того, необходимо отметить что установочные комплекты поставляются.

Принцип работы редуктора

С кинематической точки зрения, волновые передачи — это разновидность планетарных передач, которая имеет одно гибкое и зубачатое колесо.

Принцип работы волнового редуктора заключается в следующем. Неподвижное колесо устройства крепится в нужном корпусе, а выполняется оно в виде простого зубчатого колеса, имеющего внутреннее зацепление. Гибкое же зубчатое колесо выполняется в форме стакана, обладающего тонкой стенкой, легко поддающейся деформации. В более толстой части этого же колеса, то есть левой, нарезают зубья, в то время как правая часть выполняется в форме вала. Самый простой элемент — это водило, которое состоит из овального кулачка и подшипника.

Само же движение осуществляется за счет того, что происходит деформация зубчатого венца гибкого колеса.

Принцип работы

Волновые редукторы имеют следующий принцип работы:

1. Недеформируемое колесо с внутренними зубьями крепится в корпусе.
2. Гибкое зубчатое колесо с тонкими стенками устанавливается на генератор волн.
3. При вращении генератор волн деформирует гибкое колесо, тем самым перемещает точки соприкосновения наружной и внутренней шестерней.

Плавность хода обеспечивается тем, что на гибком колесе меньшее количество зубьев.

Конструкции редукторов

В настоящее время науке известно множество разнообразных конструкций для волнового редуктора. Чаще всего предназначение всех этих устройств — это преобразование входного вращательного движения в выходное вращательное или же выходное поступательное. Также стоит отметить, что волновую передачу можно рассматривать, как разновидность многопоточного планетарного механизма. Это вполне возможно, так как эти механизмы обладают многозонным, а если брать в расчет зубчатый механизм, то еще и многопарным контактом между выходным звеном и гибким колесом механизма. Можно отметить, что при номинальной нагрузке на волновой редуктор лишь от 15 до 20% всех зубьев устройства находится в зацеплении. Именно по этой причине во всех волновых передачах используют мелкомодульные механизмы, число зубьев на которых находится в переделах от 100 до 600. Также можно добавить, что в зависимости от числа зон или же волн в устройстве они подразделяются на одноволновые, двухволновые и т.д.

Особенности конструкции

Устройство волнового редуктора зависит от сферы его применения. Основная цель, для которой используется этот механизм – преобразование входного вращательного движения двигателей в:

• выходное поступательное;
• выходное вращательное.

По своей конструкции они схожи с планетарными механизмами так как имеется несколько зон соприкосновения с гибким колесом. Обеспечивает одновременное соприкосновение кулачок. Он имеет несколько выступов, которые образуют волны при вращении. При этом нагрузка распределена по всем зацепляемым зубьям равномерно. При производстве волновых редукторов количество зубьев на колесах варьируется в пределах от 100 до 600.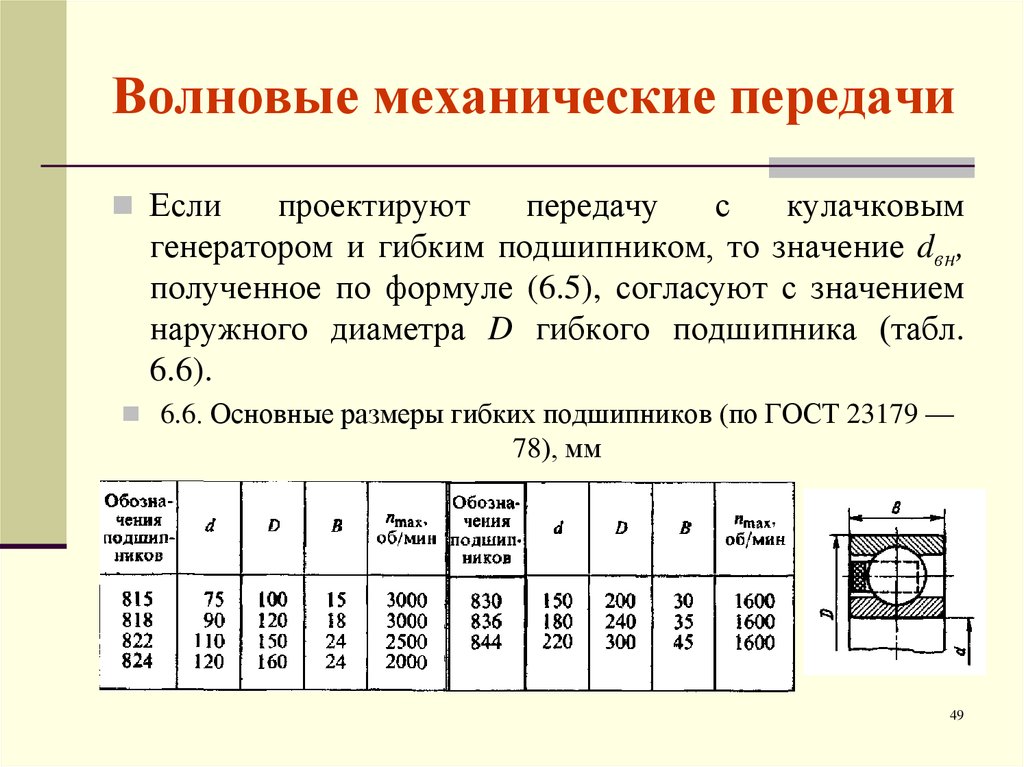

Место, где вершина волны деформируемого элемента соприкасаются с другой шестерней, называется зоной зацепления.

По количеству таких зон редуктор с гибким элементом может быть:

Большее количество волн встречается крайне редко.

Волновой мотор-редуктор

Описание данного типа волновой передачи можно сделать на основе мотора редуктора модели МВз2-160-5,5. Данная модель обладает сдвоенной волновой зубчатой передачей. Конструкция данного редуктора состоит из гибкого колеса, которое выполнено в виде кольца с тонкими стенками и двумя зубчатыми венцами. Кроме того, в конструкции имеется и общий для этих деталей кулачковый генератор волн, обладающий гибким подшипником.

Также у этой модели есть несколько особенностей, касающихся конструкции редуктора:

1. Размер вдоль оси вала невелик.
2. Генератор волн плавающего типа, а соединение с валом электродвигателя шарнирное.
3. На конце выходного вала этого устройства располагаются прямобочные шлицы.

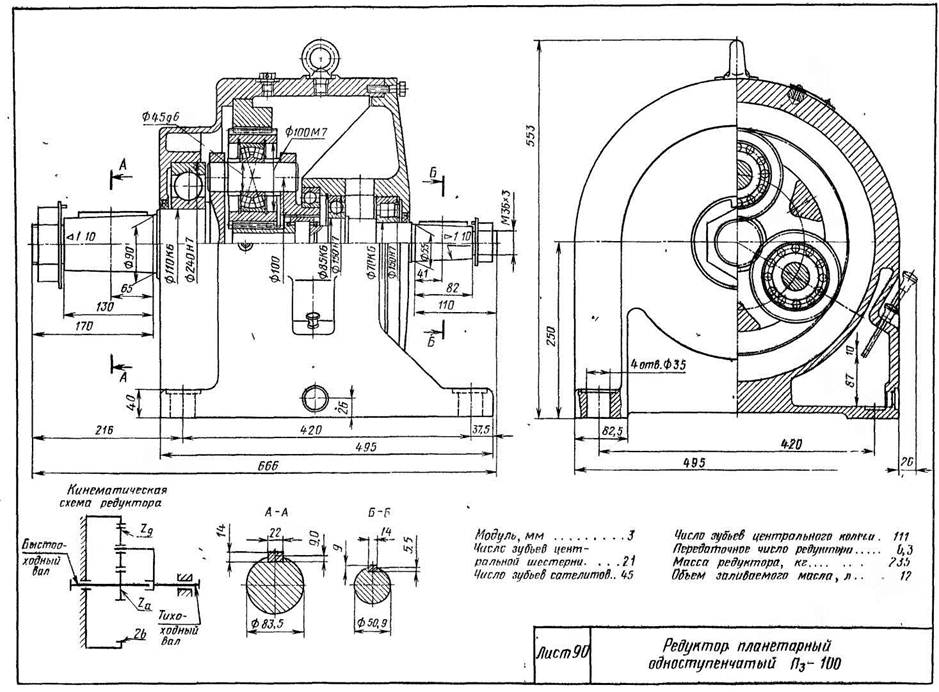
Этот тип мотора-редуктора может использоваться, как индивидуальный приводной модуль.

Редуктор волновой с эвольвентным профилем зубьев.

Описание конструкции волнового редуктора.

Редуктор волновой с эвольвентным профилем зубьев — это одноступенчатый редуктор с двумя зубчатыми колесами: одно — жесткое с внутренними зубьями, второе — гибкое — в виде цилиндра с зубчатым венцом. Гибкий зубчатый венец деформируется генератором волн. Генератор состоит из кулачка, насаженного на быстроходный вал, и шарикоподшипника с тонкими кольцами. Недеформируемый конец гибкого цилиндра шлицевый. Шлицы нарезаны обычным зуборезным инструментом. От осевого смещения цилиндр удерживается проволочным кольцом, расположенным на шлицах.

Тихоходный вал вращается в противоположном направлении относительно быстроходного вала.

Сборка жесткого колеса с гибким осуществляется после деформации гибкого зубчатого венца генератором. Зацепление и подшипники смазываются маслом, разбрызгиваемым генератором. Охлаждается редуктор вентилятором, установленным на быстроходном валу.

Редуктор предназначен для непрерывной длительной работы. КПД редуктора 0,85…0,9. Возможна передача вращения от тихоходного вала к быстроходному, КПД мультипликатора на 15…30% ниже КПД редуктора.

Схема взаимодействия звеньев.

Технические характеристики волнового редуктора.

1. Крутящий момент на тихоходном валу: 1000 Н⋅м;
2. Частота вращения тихоходного вала: 14,2 мин -1 ;
3. Мощность на тихоходном валу: 1,5 кВт;
4. Передаточное число: 100;
5. КПД редуктора: 0,85…0,9;
6. Материал зубчатых колес: сталь 30ХГС, твердость: 30…35HRCэ.

Технические параметры мотора-редуктора

Технические параметры для волнового мотора-редуктора — это несколько основных критериев:

• Первый параметр, которому должен соответствовать редуктор — это крутящийся момент на выходном валу. Он должен составлять — 250 Н⋅м.
• Второй параметр — это частота вращения вала редуктора. 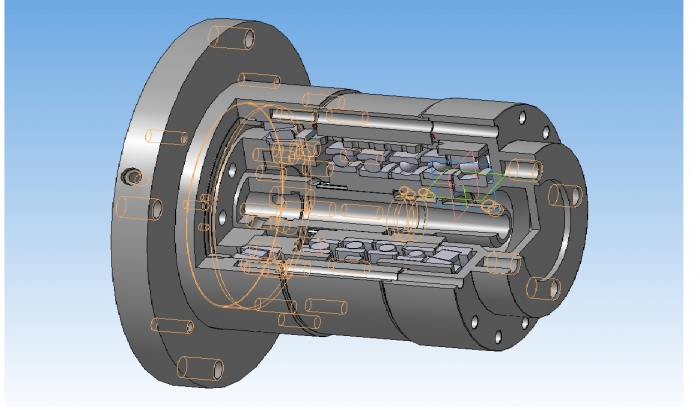Показатель этого параметра должен быть — 5,5 мин-1.
• Третий параметр для этого устройства — передаточное отношение. Показатель данного параметра — 264.
• Коэффициент полезного действия волнового мотора-редуктора должен быть 0,7.
• Параметры электродвигателя для этой модели следующие: 0,31 кВт мощности, Частота вращения 1450 мин-1, рабочее напряжение для этого механизма 220 В или 380 В.
• Полный вес устройства составляет 20 кг.

Это основные параметры, которые предъявляются к волновому мотору-редуктору.

Зубчатая передача

Не так давно инженерами был создан новый вид зубчатой передачи, которая по своим параметрам, а также конструкции схожа с планетарной передачей, однако при этом обладает принципиально новой передачей вращения. Эти новые изобретения — волновые зубчатые редукторы. Для того чтобы передавать вращательное движение в этих устройствах, была достигнута волновая бегущая деформация, которой поддается одно из зубчатых колес редуктора. Данное изобретение отлично зарекомендовало себя в некоторого вида следящих системах, а также в системах автоматического управления с высоким требованием к точности. Такое специфическое предназначение эти редукторы получили из-за своих характеристик: небольшой физический вес, а также малые размеры всего устройства в целом, которое при этом обладает большим показателем передаточного отношения, характеризуется более высоким коэффициентом полезного действия, то есть КПД, небольшими люфтами, а также малым износом деталей редуктора. Именно эти параметры и стали решающими в определении цели работы для волновых зубчатых редукторов.

Лебедка с волновым редуктором

Волновые редукторы могут быть двух типов — зубчатые и червячные. Применение лебедки в данном устройстве нашло себя лишь при использовании редуктора червячного типа. Также в волновых редукторах червячного типа с использованием лебедки существует два способа расположения червяка. Нижняя установка, когда он находится под червячным колесом, а также верхняя, когда червяк располагается над этим же колесом.

Кроме того, привод с лебедкой может использоваться для установки на космическом корабле. Привод с лебедкой для космического корабля представляет собой двухступенчатый волновой редуктор. Предназначение этого устройства на таких кораблях — это передача вращения в полностью герметичное пространство. Так как редуктор является двухступенчатым, то первая ступень — планетарная, а вторая — волновая передача. Также стоит отметить, что есть возможность сделать устройство самотормозящим. Для этого необходимо заменить планетарную передачу в редукторе на червячную.

Применение редукторов волнового типа

Волновой редуктор РВП 240-21 используется в качестве привода для шнекового конвейера КШ25/12,5. Механизм изготовлен с применением самых передовых конструкторских решений отечественных и мировых инженеров. Он обладает высоким запасом прочности и рассчитан на длительный период эксплуатации. Все электронное оборудование изготовлено в полностью взрывобезопасном варианте, так что механизм может быть использован и на опасных производствах.

Конвейеры были разработаны отечественным «Опытно-механическим заводом» и введены в эксплуатацию на некоторых предприятиях лишь в 2014 году. Их использование позволило повысить безопасность производства. Волновые редукторы для ЧПУ пользуются достаточно высоким спросом. Причем многие заводы предлагают изготовление механизмов по индивидуальным запросам клиента. Для станков с числовым управлением очень важна точность и плавность движений, которую могут обеспечить волновые передачи. Подобные элементы используются в медицине, ювелирном деле, точном машиностроении и робототехнике.

Стоимость индивидуально изготовленного прибора будет не маленькой, зато он идеально подойдет для выполнения отведенных функций. Кроме того изготовитель выедет на место и поможет осуществить правильную настройку механизма по желанию клиента. Также заказчик может рассчитывать и на гарантийное обслуживание в случае возникновения каких-либо проблем.

Расчеты редуктора

Как и для любой другой детали, для создания редуктора необходимо проводить определенные расчеты, которые будут показывать, способно ли устройство выполнять свои функции, а также из какого материала должно выполняться устройство и т. д. Основным критерием для расчета волнового редуктора, его работоспособности, является прочность гибкого колеса. Оценить данный параметр можно при помощи сопротивления усталости зубчатого венца. Основной габаритный размер передачи — это внутренний диаметр гибкого колеса. Определяется он по приближенной зависимости сопротивления усталости с учетом нормальных напряжений.

Ультразвуковая физика и приборы — StatPearls

Основные принципы физики ультразвука

Важнейшие физические принципы, необходимые для понимания и оптимизации клинического ультразвука, включают частоту, скорость распространения, импульсный ультразвук, взаимодействие волн с тканью, угол падения и затухание[3]. Звук — это механическая энергия, которая движется через чередующиеся волны высокого и низкого давления в среде. Источник звука производит колебания продольных волн, позволяя распространять энергию и критические формы волны для клинического ультразвука. Фаза высокого давления звуковой волны — это фаза сжатия, а фаза низкого давления — фаза разрежения.

В клиническом УЗИ задействованными средами являются воздух, вода, жидкости организма, мягкие ткани, кровь и кости.

Частота относится к количеству циклов в секунду, излучаемых зондом в течение одной секунды, и выражается в герцах (Гц). Период — это время, в течение которого происходит полный цикл волны (разрежение и сжатие), и он обратно пропорционален частоте. Точно так же описанная длина волны представляет собой расстояние между двумя соседними волновыми пиками. Важно различать разницу между периодом и длиной волны; первое — это расстояние, а второе — продолжительность времени.[4] Ультразвуковые волны передаются с частотой более 20 МГц, что выше верхнего предела человеческого слуха. Частота зависит от источника излучения и совершенно не зависит от ткани, с которой взаимодействуют волны.[3] Частоты, используемые в клиническом УЗИ, находятся в диапазоне от 1 МГц до 20 МГц, в зависимости от используемого датчика и желаемого применения. Частота имеет соответствующую связь с разрешением и обратную зависимость с глубиной.

Чем выше используемая частота, тем ниже проникновение, но выше разрешение изображения.[5]

Амплитуда — это высота или сила волны, определяемая расстоянием между пиком и средним значением самой высокой и самой низкой точек волны. Мощность в ультразвуке относится к квадрату амплитуды волны или разнице между максимальным и средним значениями распространяющихся волн.[6] И мощность, и амплитуда могут контролироваться сонографистом и регулироваться с помощью регулировки усиления. Мощность измеряется в ваттах или милливаттах, но может отображаться на ультразвуковом аппарате либо в децибелах (дБ), либо в процентах от общей акустической мощности.[4]

Интенсивность относится к мощности, подаваемой на определенную площадь, выраженной в ваттах/см2 или милливаттах/см2.[4] Пространственный пик — это место, где интенсивность максимальна (наибольшая мощность на наименьшей площади), и представляет фокус ультразвуковых лучей.

Децибелы (дБ) представляют собой логарифмическое выражение отношения двух интенсивностей звука. дБ можно определить, рассчитав соотношение интенсивности источника звука и наименьшей слышимой интенсивности, рассчитав LOG и умножив его на 10. Существует упрощенное правило 3 дБ, которое утверждает усиление на каждые 3 дБ. Должно быть дополнительное удвоение подаваемой мощности. Таким образом, для усиления 3 дБ требуется удвоенная мощность, для усиления 6 дБ требуется четырехкратная мощность, а для усиления 9Для усиления дБ требуется восьмикратная мощность.

Скорость распространения — это скорость, с которой волны проходят через среду. Скорость ультразвуковых волн принята равной 1540 м/с в мягких тканях, известной как акустический импеданс. Скорость распространения зависит от характеристик среды, через которую распространяются волны, и не зависит от частоты. По мере увеличения плотности ткани скорость распространения уменьшается. Напротив, чем жестче ткань, тем выше скорость распространения.[4]

Для достижения желаемой глубины и разрешения для клинического ультразвука датчик излучает волны в виде импульсов, обычно длительностью в миллисекунды и повторяющихся до нескольких тысяч раз в секунду. Этот принцип называется импульсным ультразвуком.

Ультразвуковые волны проникают в ткань и отражаются обратно к датчику со скоростью, определяемой консистенцией ткани-мишени. Отражения звука, которые возвращаются к зонду, называются эхом и определяются поверхностью раздела двух разных материалов.[3] Изображения, полученные на основе эхосигналов, придают структурам и средам разную плотность на экране, называемую эхогенностью. Чем значительнее разница в плотности двух материалов (тканей), тем сильнее будет создаваемое эхо.[3] Структуры с более высокой плотностью отражают больше звука и считаются более эхогенными (белыми). Таким образом, кости и плотные инородные тела полностью отражают звук и кажутся яркими на экране, тогда как жидкости, такие как вода или моча, не отражают звук на датчик и кажутся анэхогенными (черными).[6] Слабые эхо-сигналы выглядят серыми. Когда волны возвращаются к датчику от таких материалов, как кость и воздух, которые не могут распространять звук, звуковые волны не могут проходить в более глубокие ткани, и возникает тень за границей раздела.

Угол, под которым ультразвуковые волны воздействуют на любую структуру, называется углом падения. Структуры идеально отображаются с углом падения, перпендикулярным излучаемым волнам, потому что отраженные волны возвращаются к зонду в наибольшей концентрации. Когда волны взаимодействуют со структурой под углом, меньшее количество волн отражается обратно к зонду, что снижает как яркость структуры, так и разрешение. Волны, падающие на структуру, возвращаются к зонду под углом, равным углу, первоначально падающему на границу конструкции.[3] Если угол не перпендикулярен углу падения, волна будет отражаться от источника.[4]

Точно так же волны отклоняются от прямой линии, когда скорость волн различается между двумя структурами, что приводит к преломлению.[3] Исходный угол падения и разница в скорости распространения двух сред определяют конечный угол преломления. Преломление является источником артефактов в ультразвуке, учитывая, что все ультразвуковые аппараты работают исходя из предположения, что волны всегда будут распространяться и возвращаться по прямой линии. [3]

Различные поверхности раздела тканей отражают по-разному и влияют на качество изображения. Гладкие границы раздела считаются зеркальными отражателями и возвращают большую часть волн к преобразователю. Зеркальные отражатели контрастируют с нерегулярными границами раздела, называемыми диффузными отражателями, которые заставляют звуковые волны отражаться от преобразователя и снижать качество изображения. Важный тип рассеяния, называемый рассеянием Рэлея, возникает, когда объект меньше длины волны ультразвукового луча. Красные кровяные тельца демонстрируют этот тип рассеяния, в результате чего волны рассеиваются во всех направлениях.[4]

Учитывая, что ультразвуковые волны не могут распространяться по воздуху, для взаимодействия с тканями датчики должны контактировать с кожей пациента через связующую среду. Сцепление происходит за счет использования ультразвукового геля или водяных бань. Поскольку ультразвуковые волны взаимодействуют с тканью и отражают датчик, энергия, связанная с любыми оставшимися лучами, уменьшается с увеличением глубины. Сила проникающих волн снижается за счет преломления, рассеяния и поглощения.[5] Когда волны рассеиваются и энергия поглощается, это приводит к энергии вибрации и теплу. Все процессы, которые способствуют уменьшению энергии, в совокупности называются затуханием.

Затухание волны, или снижение интенсивности на заданном расстоянии, также измеряется в децибелах (дБ) и происходит со скоростью на сантиметр, примерно равной исходной частоте излучения. Таким образом, волна 5 МГц будет затухать примерно на 5 дБ в первом сантиметре и еще на 5 дБ в следующем сантиметре. Предельное проникновение волн определяется глубиной, на которой интенсивность волн уменьшается на 50%, в обратном порядке, используемом для определения усиления в дБ, описанного выше. Таким образом, глубина, на которой ослабляется 50% интенсивности, эквивалентна потере 3 дБ. Волны более высокой частоты и волны для глубокой визуализации затухают быстрее, чем низкочастотные волны или волны, используемые для поверхностной визуализации. [4]

Усиление (мощность) можно регулировать по всему изображению или, в зависимости от используемого аппарата, на разных глубинах, чтобы лучше визуализировать структуры на этих глубинах. Кроме того, более глубокие структуры должны использовать более низкие частоты, чтобы стать видимыми. Такая видимость достигается за счет разрешения, которое улучшается с более высокими частотами. Специалисты по УЗИ должны управлять используемой частотой, чтобы сбалансировать потребность как в глубине, так и в разрешении в зависимости от применения ультразвука для любой конкретной целевой структуры.

Датчики

Преобразователи представляют собой приборы, излучающие и принимающие ультразвуковые волны путем преобразования электрического сигнала в звуковые волны. Ультразвуковые преобразователи содержат пьезоэлектрические кристаллы, которые при подаче электрических импульсов производят волны с частотами, определяемыми скоростью распространения кристалла, деленной на удвоенную толщину кристаллического слоя. Типичная толщина кристаллических слоев составляет от 0,2 мм до 2 мм. Полоса пропускания конкретного пробника — это диапазон частот, в котором пробник будет работать.

Преобразователи могут как посылать, так и принимать ультразвуковые волны, применяя энергию и, в конечном счете, звуковые волны в импульсах. Пульсирующий характер создаваемых ультразвуковых волн облегчает излучение и прием звуковых волн. Когда падающие импульсы отражаются от тканей, создавая эхо, устройство может определять силу, направление и время прихода эхо.[3] Количество импульсов, производимых за одну секунду, представляет собой частоту повторения импульсов (PRF), а период повторения импульсов (PRP) — это время между началом двух импульсов. PRF и PRP, как и период и частота, описанные выше, обратно пропорциональны друг другу. Более высокий PRF будет соответствовать большему разрешению изображения, но меньшей глубине, в то время как более высокий PRP и увеличенное время «прослушивания» датчика позволят увеличить глубину. [4]

Типичные датчики, используемые в клиническом ультразвуковом исследовании, включают линейную решетку, фазированную решетку и криволинейную решетку, которые имеют несколько конфигураций и частот в зависимости от необходимого применения. Кристаллы поверхности преобразователя и расположение структуры определяют площадь и форму создаваемого изображения. Линейные массивы имеют плоские грани, которые создают прямоугольное изображение. Фазированные решетки имеют конфигурации кристаллов и последовательности мощности, которые направляют лучи из одной точки для создания секторного изображения, идеального для сканирования между ребрами. Криволинейные массивы имеют изогнутые поверхности различных радиусов, которые также могут использоваться в разных полосах пропускания в зависимости от желаемого приложения. Например, низкочастотные криволинейные датчики часто используются для исследований органов брюшной полости из-за их глубокого проникновения и широкого поля зрения. Напротив, высокочастотные внутриполостные криволинейные датчики используются для обследования женского таза из-за их высокого разрешения и небольших размеров.

Управление изображениями

Частота

Выбор датчика с соответствующей полосой пропускания является важным фактором для получения идеального изображения. Для общих предустановок сканирования машины часто устанавливаются на «GEN» или «общий», как правило, средний диапазон для полосы пропускания зонда. Если для оценки структуры требуется более высокое разрешение, частоту можно увеличить непосредственно на машине или с помощью доступного «RES» для разрешения. Повышенная частота пожертвует глубиной проникновения. Обратное верно, если требуется большее проникновение. Частота уменьшается напрямую или с помощью настройки «PEN» или проникновения.

Усиление

Когда необходимо управлять затуханием из-за того, что цель слишком яркая или слишком темная, мощность можно увеличить или уменьшить либо по всему изображению, либо на заданной глубине. Увеличение усиления добавит мощности для борьбы с затуханием за счет увеличения яркости. [5] Усиление уменьшается при снижении мощности и общей яркости. Когда изображения имеют чрезмерное или недостаточное усиление, разрешение ухудшается.

Компенсация выигрыша по времени

Компенсация усиления по времени относится к элементам управления мощностью на определенной глубине изображения для борьбы с затуханием с глубиной. Это помогает улучшить визуализацию глубоких структур, в основном, если глубокая ткань подвергается заднему акустическому усилению. Эту функцию часто можно увидеть с помощью «ползунков» на ультразвуковой консоли.

Глубина резкости

Глубина резкости — это глубина, на которую передаются и принимаются звуковые лучи. Глубина изменяется на дисплее, чтобы оптимизировать мощность и временное разрешение машины для просмотра целевых структур. Глубина должна быть достаточно значительной, чтобы при необходимости можно было увидеть глубокие структуры, и достаточно мелкой, чтобы видеть мелкие структуры с адекватным разрешением. Когда глубина слишком велика для поверхностных исследований, качество изображения целевой структуры ухудшается.

Фокус и Резолюция

Ультразвуковые лучи выходят из датчика на той же ширине, что и лицо. Они проходят через ближнюю зону, затем сужаются в фокальной зоне и расширяются в дальней зоне. Разрешение, или способность различать два близко расположенных объекта, и боковое разрешение лучше всего в фокальной зоне. Пространственное разрешение также может быть улучшено за счет более высоких частот, меньшей частоты повторения импульсов и короткой длительности импульса. Осевое разрешение, или способность различать две структуры на пути луча, как правило, лучше, чем боковое разрешение, или способность различать две расположенные рядом структуры из-за того, что ультразвуковые лучи короче, чем их ширина. Боковое разрешение наибольшее в фокусе, где ширина луча самая узкая. Временное разрешение, или время, необходимое машине для создания изображения, обратно пропорционально частоте кадров.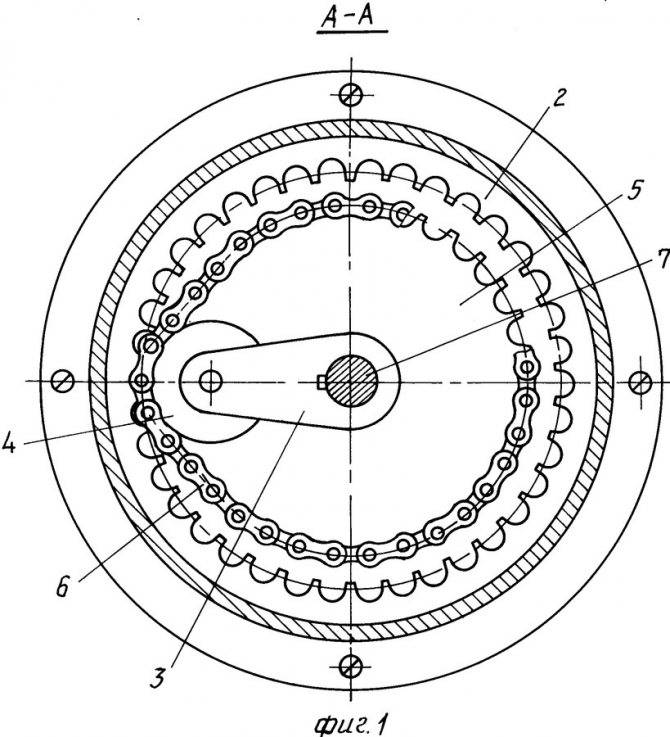 При более высокой частоте кадров получаются изображения с более низким разрешением, а при более низкой частоте кадров — изображения с более высоким разрешением. Частота кадров не менее 15 кадров в секунду позволяет получать изображения в реальном времени.[6] Временное разрешение наиболее важно для движущихся объектов, и если частота кадров слишком низкая, поддерживающая высокое временное разрешение, способность обнаруживать движение снижается. Дополнительные инструменты увеличения, такие как микропузырьки, повышают разрешающую способность за счет сильного отражения ультразвуковых лучей, особенно в сосудистой системе.[8]

Многолучевой

Современные ультразвуковые датчики предназначены для отправки ультразвуковых сигналов под разными углами по поверхности датчика. Они создают несколько углов падения, которые имеют несколько углов отражения обратно к приемнику зонда. Это помогает улучшить качество изображения, особенно вокруг структур, которые в противном случае были бы склонны к артефактам рефракции.

Тканевые гармоники

Гармоники ткани относятся к тенденции ткани резонировать на частотах, кратных падающей частоте, передаваемой датчиком. Например, когда к ткани передаются волны частотой 3 МГц, ткань будет резонировать на частотах 3 МГц, 6 МГц и 9 МГц.МГц. Преобразователи можно настроить на получение частоты падения и частот гармоник, комбинируя их для создания изображения с более высоким разрешением. Использование настроек тканевых гармоник также помогает уменьшить артефакты.

М-режим

М-режим, или отображение движения во времени, позволяет одному лучу излучаться датчиком вдоль определенной дорожки в сочетании с записывающим устройством, которое фиксирует все движения, происходящие на пути. Этот режим обеспечивает высокое временное разрешение, тем самым предоставляя исследователю превосходный обзор тонких движений.[5] Клинически этот режим идеально подходит для регистрации изменений диаметра сосудов, движения сердечных клапанов и определения сердцебиения плода.

Артефакты

Артефакты — это ошибки изображения, которые интерпретируются ультразвуковым аппаратом в связи с ранее обсуждавшимися физическими принципами. Они часто являются результатом предположения, что ультразвуковые волны всегда распространяются прямолинейно, что все ткани передают звук со скоростью 1540 м/с и что волны всегда отражаются непосредственно в преобразователе.[9] Понимание природы артефактов жизненно важно для сонографистов и тех, кто интерпретирует изображения, потому что артефакты часто используются в качестве подсказок для обнаружения конкретных патологических изменений.

Реверберации

Артефакты реверберации возникают в результате отражения звуковых волн между гладким отражателем и поверхностью преобразователя.[10] Они выглядят как регулярно расположенные линии с интервалами, равными расстоянию между датчиком и конструкцией. Обычными нормальными находками, возникающими в результате артефакта реверберации, являются «линии А» в легочных полях.

Заднее акустическое усиление

Жидкость имеет более высокую скорость распространения и меньшее затухание, чем мягкие ткани. В результате звуковые волны распространяются и возвращаются из глубоких тканей в структуры, заполненные жидкостью, быстрее, чем звуковые волны в соседних, не заполненных жидкостью структурах.[10] Когда датчики принимают звук быстрее и с большей интенсивностью, изображение, создаваемое позади заполненной жидкостью структуры, будет казаться более ярким по сравнению с окружающей тканью. Гиперэхогенный сигнал может скрывать детали ткани. Обычным применением для иллюстрации заднего акустического усиления является ультразвуковое исследование мочевого пузыря, при котором компенсация выигрыша во времени часто должна быть уменьшена для наилучшей оценки тканей глубоко в мочевом пузыре. Неожиданное акустическое усиление сзади также может быть диагностическим признаком того, что жидкость присутствует в местах, представляющих патологические процессы, например, в брюшной полости или плевральной полости.

Тени

Структуры с высокой плотностью обладают высокой отражательной способностью, возвращая большую часть звуковых волн к преобразователю и почти не позволяя волнам проникать в глубокие ткани.[3] Полученное изображение структуры показывает яркую гиперэхогенную линию или плотность с темной гипоэхогенной тенью позади нее. Кость, металл, пластик, дерево, стекло и кальциевые камни имеют достаточную плотность, чтобы быть настолько отражающими и создавать «чистые» глубокие тени. С другой стороны, хотя воздух и не плотный, он также не передает ультразвуковые волны в глубокие структуры. Воздушные интерфейсы также обладают высокой отражающей способностью, но обычно создают менее различимые тени. Воздушные интерфейсы с затенением обычно отмечаются в легких и кишечнике и могут называться «грязными» тенями.

Зеркало

Когда звук отражается от сильного гладкого отражателя, преобразователь может отражать пульсирующую волну, из-за чего аппарат считает, что граница раздела тканей глубокая и такая же, как граница раздела тканей с поверхностными структурами. [3][10] Это обычно видно при просмотре диафрагмы через печень, когда машины будут отображать печень ниже и выше диафрагмы.

Звонок вниз

Артефакты затухания возникают, когда крошечные пузырьки или кристаллы резонируют на той же частоте, что и излучаемый ультразвук, который излучает собственные волны. Звук, полученный от них, приходит после исходного эха и интерпретируется машиной как глубинные структуры. Образующийся в результате артефакт выглядит как гиперэхогенная линия в глубине повреждающей структуры, которую часто называют хвостом кометы. Артефакты кольца вниз являются диагностически полезными в случаях аденомиоматоза желчного пузыря, когда стенки желчного пузыря инфильтрированы кристаллами холестерина.[10]

Преломление

Артефакты преломления, часто называемые краевыми артефактами, возникают, когда падающие ультразвуковые волны взаимодействуют с поверхностями структур под углами, отличными от 90 градусов. Разница в плотности структуры способствует преломлению или отклонению звуковых волн от поверхности.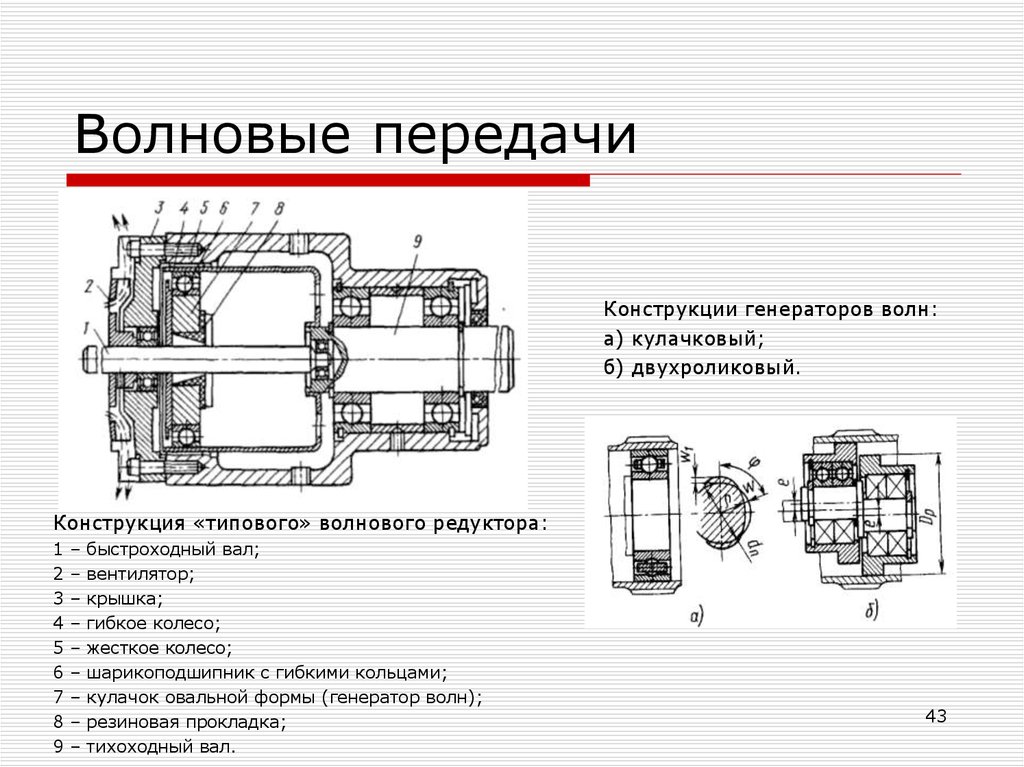 В результате эхо-сигналы не возвращаются к преобразователю из области, которая, как ожидается, будет отражать эхо-сигналы, и, таким образом, создается тень.[9] Этот артефакт обычно наблюдается при просмотре круглых структур, таких как желчный пузырь, где тени будут следовать за краями, соответствующими стенам, когда через них происходит веер.

Анализ контактно-механических характеристик гибких деталей в гармоническом редукторе

Гармонический редуктор широко используется в промышленных роботах, аэрокосмической, оптике и других высокотехнологичных областях. Отказ гармонического редуктора в основном вызван повреждением гибкого подшипника и гибкого шлица тонкостенных уязвимых компонентов. Для изучения контактных механических характеристик гибких компонентов, таких как гибкий подшипник и гибкая рейка в гармоническом редукторе, были созданы контактно-механическая модель гибкого подшипника, дифференциальное уравнение вибрации гибкой шлицы и конечно-элементная модель каждого компонента в гармоническом редукторе. На основе созданной модели гармонического зубчатого редуктора обсуждается влияние длины цилиндра гибкого шлица и толщины дна цилиндра на напряжение гибкого вала, соответственно, и исследуются характеристики движения гибкого подшипника. В то же время изучается пространственное распределение смещения гибкого вала и осевая вибрационная реакция гибкого вала. Корректность модели, установленной в данной работе, проверена экспериментально. Результаты показывают, что увеличение длины цилиндра может улучшить нагрузку на гибкие шлицы в редукторе с гармонической передачей; толщина стенки дна цилиндра в основном влияет на напряжение в нижней части гибкого шлица, но мало влияет на напряжение зубчатого венца и гладкого цилиндра. Вдоль направления оси гибкого шлица радиальное смещение, смещение по окружности и угловое смещение увеличиваются линейно с увеличением осевого расстояния между цилиндром и днищем. Когда частота возбуждения высока, режим вибрации оболочки flexspline представляет собой в основном осевую вибрацию. Результаты исследования послужат теоретической базой для оптимальной конструкции гармонического редуктора и увеличения срока службы гибких частей.

1. Введение

Зубчатая передача имеет преимущества высокой точности передачи и компактной конструкции, которая широко используется в области механической передачи [1, 2]. Редуктор Harmonic обладает такими преимуществами, как большое передаточное число, малый вес, малый объем и т. д. Он может нормально работать в условиях вакуума, сильного излучения и большой разницы температур. Благодаря своим уникальным преимуществам, гармонический редуктор нашел широкое применение в робототехнике [3] и в аэрокосмической промышленности [4]. В процессе передачи гармонического зубчатого редуктора гибкий подшипник и гибкий шлиц относятся к тонкостенным деталям и в течение длительного времени выдерживают переменную циклическую нагрузку.

Будзик и др. [5] объединили метод конечных элементов с контактным элементом для анализа влияния различных значений крутящего момента на напряжение гибкого шлица. Реом и др. [6] выполнили анализ методом конечных элементов жесткости на кручение гармонической зубчатой ​​передачи и изучили жесткость зацепления между круговым шлицем и гибким зубом шестерни. Фолега [7] использовал метод граничных элементов для расчета прочности зубьев гибкого зубчатого венца в процессе гармонической передачи и проанализировал конструктивные характеристики гибкого колеса и влияние различных форм зубьев на величину напряжения нижняя поверхность зубчатого венца. Ли и др. В работе [8] была создана оптимизационная модель профиля генератора волн и определена целевая функция для минимизации максимального окружного напряжения гибкого вала в сборе с генератором волн гармонического зубчатого редуктора. Ли [9] соответственно выполнили анализ моделирования методом конечных элементов на цилиндрическом гибком шлице, гибком шлице в форме чашки и гибком шлице в форме шляпы, изучили механические характеристики различных гибких колес и проверили результаты моделирования со ссылкой на эксперимент. Пакана и др. [10] установил четыре типа моделей волновых генераторов: двухроликовый, четырехроликовый, кулачковый и дисковый. В двух режимах работы без нагрузки и под нагрузкой численно рассчитана величина напряжения на зубе гибкого шлица гармонического привода и изучен закон влияния типа генератора волн на распределение напряжения в зубе гибкой шестерни. Хуанфу и др. В работе [11] создана динамическая модель для отколовшихся зубчатых пар, а характеристики зацепления проанализированы с использованием метода контактного анализа нагруженной поверхности зуба. Раус и др. [12] установили уравнение гидродинамической смазки между коническим зазором кулачка и поверхностью узла гибкого шлица и проанализировали явление конуса и механизм смазки в гармоническом приводе. Мо и др. В работах [13, 14] изучалось влияние жесткости гибкой опоры и фазы ошибки сборки на характеристики распределения нагрузки в системе зубчатой ​​передачи. Ши и др. [15] предложили модель, учитывающую температурный зазор, для анализа динамических характеристик керамической подшипниковой системы. Ван и др. [16] разработали автоматизированную систему изготовления косинусных зубчатых колес на основе сопряженной теории цифровых поверхностей и зубчатых колес. Адамс и др. [17] создали модель гибкой опоры и изучили частоту вибрации гибкой опоры. Валха и др. [18] изучали напряжение и деформацию гибкого подшипника в гармоническом редукторе с использованием конечно-элементного программного обеспечения. Шах и др. [19] спрогнозирована усталостная долговечность подшипника при динамическом нагружении и получен закон влияния структурного размерного изменения внутреннего и наружного колец подшипника на контактное напряжение и усталостную долговечность. Чен и др. [20] создали аналитическую конечно-элементную модель жесткости зубчатого зацепления с учетом пути распространения трещины и проанализировали влияние пути распространения трещины на жесткость зацепления. Остапский [21] проанализировал распределение напряжения гибкого подшипника при симметричной радиальной нагрузке и влияние погрешности сборки на его усталостное повреждение. Леон и др. В работе [22] проанализировано влияние геометрического строения зубьев гибкой шестерни на характеристики гармонического привода. Граваньо и др. В работе [23] исследовано влияние формы генератора волн на погрешность движения в процессе гармонического привода и проведена его количественная оценка.

Из приведенных выше ссылок следует, что многие модели гармонического редуктора созданы и проанализированы, но всесторонний анализ контактных механических свойств гибкого подшипника и гибкого шлица с тонкостенными уязвимыми компонентами проводится редко. На основе установленной модели контактной механики и модели конечных элементов анализируются характеристики движения гибкого подшипника и динамическая реакция гибкого шлица. Документ изложен следующим образом. После этого введения в Разделе 2 представлена ​​математическая модель гибкого подшипника и гибкого шлица в гармоническом редукторе. Конечно-элементная модель гибкого шлица, кругового шлица и генератора волн в гармоническом редукторе представлена ​​в разделе 3. Для проверки правильности модели в разделе 4 проведены соответствующие эксперименты. В разделе 5 приведены контактные механические характеристики проанализированы гибкие детали в гармоническом редукторе. Выводы настоящего исследования обобщены в последнем разделе.

2. Математические модели

Редуктор Harmonic имеет простую структуру и высокое передаточное отношение. Структура гармонического редуктора B ₃ -80 показана на рис. 1.

На рис. 1 гармонический редуктор состоит из трех основных компонентов, а именно генератора волн, гибкого шлица и кругового шлица. Редуктор с гармонической передачей передает мощность или движение через волну деформации, создаваемую гибкими частями с контролируемой деформацией.

2.1. Модель контактной механики гибкого подшипника

При изменении возбуждения периодического смещения изменяется состояние контакта между шариком и внутренней и внешней дорожками качения, а также контактная жесткость и контактное усилие. Для анализа контактных механических характеристик гибкой опоры рассчитывается контактная жесткость гибкой опоры, показанной на рисунке 2.

Конструктивные параметры гибкого подшипника приведены в таблице 1.

Согласно теории контакта Герца, шарик определяется как контакт I, а внутреннее и внешнее кольца подшипника являются контактным телом II. Плоскость, параллельная радиальной плоскости подшипника и проходящая через нормаль поверхности контакта шарика с дорожкой качения, определяется как главная плоскость 1, а плоскость, параллельная осевой плоскости подшипника и проходящая через геометрический центр шарика является главной плоскостью 2. Главную кривизну шарика, находящегося в контакте с внутренним кольцом подшипника, можно выразить следующим образом: где — диаметр шарика, d _i — внутренний диаметр внутреннего кольца, r _i — радиус кривизны канавки внутреннего кольца, ρ ij — кривизна контакта ij поверхность каждого предмета.

Главную кривизну шарика, находящегося в контакте с наружным кольцом подшипника, можно выразить следующим образом: где d _o — наружный диаметр наружного кольца и r _o — радиус кривизны канавки наружного кольца.

Сумма кривизны контактных пар может быть выражена как

Разность кривизны контактных пар может быть выражена следующим образом:

Эквивалентный модуль упругости определяется следующим образом: где E ₁ и E ₂ — модуль упругости материала шарика и кольца подшипника соответственно, а μ 1 и μ ₂ — коэффициент Пуассона материала шарика и кольца подшипника соответственно.

Согласно теории контакта Герца контактная упругая деформация между шариком и дорожкой качения подшипника подчиняется теореме Гука. По сравнению с радиусом кривизны контактной поверхности размер контактной поверхности очень мал. Выражения для размера площади контактного эллипса и контактной деформации могут быть выражены следующим образом: где k — параметр контактного эллипса, Γ — полный эллиптический интеграл первого рода, ε — второй тип полного эллиптического интеграла, а Q — значение нагрузки.

Используя метод наименьших квадратов, расчетные формулы k , Γ и ε можно выразить следующим образом [24]: где

Контактная жесткость между шариком и внутренней и внешней дорожками качения подшипника может быть выражена следующим образом:

Когда нагрузка равна Q  = 1500 Н, из уравнений (6)–(9) можно рассчитать, что a _i  = 1.427, b _i  = 0.165 and a _o  = 1.189, b _o  = 0.200 when the rolling element contacts with the outer ring .

Радиус кривизны в любом положении может быть выражен следующим образом:

Путем подстановки геометрических параметров дорожек качения внутренней и внешней качения гибкого подшипника в уравнение (12) радиусы кривизны дорожек качения внутренней и внешней качения при различных полярных углы можно получить следующим образом:где R _i — радиус кривизны дорожки качения внутреннего кольца, а r _o — радиус кривизны дорожки качения наружного кольца.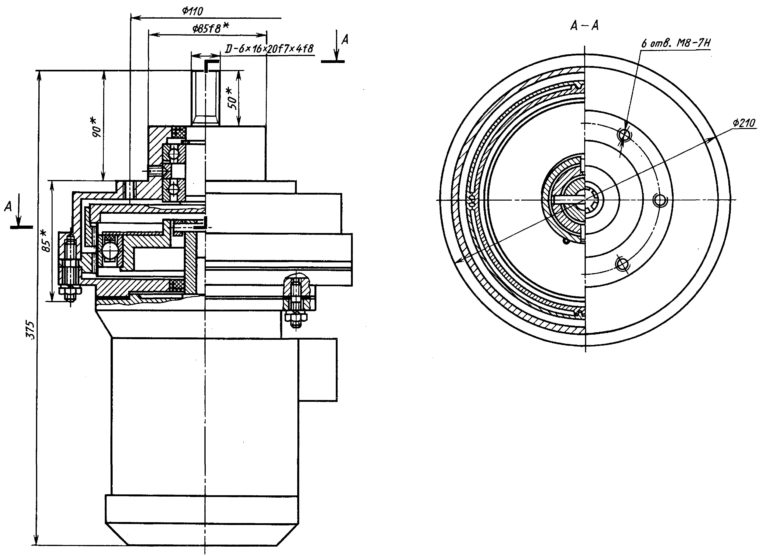

2.2. Дифференциальное уравнение вибрации гибких шлицов

Динамические характеристики гибких шлицов оказывают большое влияние на всю систему передачи. Цилиндрический чашеобразный гибкий шлиец можно рассматривать как вращающуюся конструкцию, состоящую из гладкой цилиндрической оболочки и зубчатого венца, а размер зуба части зубчатого венца очень мал, что может быть преобразовано в цилиндрическую оболочку по принципу инерции. эквивалентность [25]. Микроэлемент перехватывается на криволинейной поверхности оболочки гибкого шлица гармонического зубчатого редуктора, как показано на рисунке 3.

На рис. 3 направление системы координат x — это направление диаметра оболочки гибкого шлица, направление y системы координат — это направление касательной окружности оболочки гибкого шлица, а направление z система координат – направление оси оболочки гибкого шлица, , , , – мембранные силы на единицу длины, – поперечные сдвигающие силы на единицу длины, – изгибающие моменты на единицу длины, – крутящий момент на единицу длины, – внешние компоненты нагрузки на единицу площади вдоль x , y и z направлений, а , , и – компоненты силы инерции на единицу площади вдоль x , y и z направлений.

При совместном действии пленочной силы, поперечной поперечной силы, изгибающего момента, крутящего момента, внешней составляющей нагрузки и инерционной составляющей сила микроэлемента оболочки сгибателя гармонического зубчатого редуктора должна сохраняться в равновесии. Путем вывода формулы математической модели условие силового равновесия сегмента микроэлемента может быть получено следующим образом: где R — радиус кривизны нейтральной поверхности.

Компоненты силы инерции единицы площади в направлениях x , y, и z в любой точке на криволинейной поверхности кожуха гибкого шлица гармонического зубчатого редуктора удовлетворяют следующей формуле: где , , и — осевые, тангенциальные и нормальные дислокации любой точки на нейтральной поверхности микроэлемента – плотность 30 CrMnSi легированной конструкционной стали, – толщина гладкой стенки цилиндра гибкого колеса.

Подставляя уравнение (15) в уравнение (14), можно получить следующее уравнение: модуль и коэффициент Пуассона легированной конструкционной стали 30 CrMnSi материала гибких шлицов соответственно.

Дифференциальные уравнения колебаний без оболочки, показанные в уравнении (18), могут быть установлены совместными уравнениями (16) и (17).

При свободных вертикальных свободно опертых граничных условиях на обоих концах гибкой оболочки длиной L соответствующие формы колебаний трех составляющих перемещений u , , и могут быть выражены следующим образом [26]:где m и n представляют осевое полуволновое число и окружное полное волновое число соответствующих мод вибрации трех компонентов смещения оболочки соответственно.

Комбинируя уравнения (18) и (19) однородные линейные уравнения составляющей смещения, соответствующей свободным колебаниям оболочки гибкого вала, можно записать в виде

. Матрица коэффициентов A может быть выражена в виде , j  = 1, 2, 3) в матрице коэффициентов A имеют следующий вид: где – безразмерный частотный коэффициент, а его связь с круговой частотой можно выразить следующим образом:

Вектор x может быть выражен следующим образом:

Вектор-столбец b может быть выражен следующим образом:

Чтобы получить ненулевое решение уравнения (20), определитель матрицы коэффициентов A должен быть нуль. После перебора унарное кубическое уравнение безразмерного частотного коэффициента можно записать в виде

. Коэффициенты a , b, и c уравнения можно выразить следующим образом: где a _i ( i  = 1, 2, 3), b _i ( i  = 1, 2, 3, 4), and c _i ( i  = 1, 2, 3, 4, 5), определенные в уравнении (27), выражены в «Приложении A».

Согласно уравнению (19), соответствующие формы смещения трех корней уравнения (26) могут быть получены следующим образом: где B , C, и D , определенные в уравнении (28), выражаются в «Приложении Б».

3. Модели конечных элементов

Сначала разрабатывается полная структура гибкого шлица, кругового шлица и генератора волн, а затем создается модель конечных элементов в соответствии с их конструктивными размерами.

3.1. Flexspline Модель

Внутренний диаметр flexspline 80 мм, номинальное передаточное отношение 85, модуль 0,5 мм, допустимый крутящий момент тихоходного вала 90 Н·м, допустимая радиальная нагрузка тихоходного вала 3000 Н, а вес 90,2 кг. Выбран эвольвентный профиль зуба со стабильным движением, равномерным усилием и зрелой технологией обработки. Угол давления α  = 20°, коэффициент высоты надстройки  = 1,0, коэффициент зазора вершины  = 0,35 и коэффициент радиальной деформации  = 1,0. Диаметр индексной окружности гибкого шлица составляет 84 мм, диаметр корневой окружности составляет 83 мм, а диаметр вспомогательной окружности составляет 84,6 мм. Длина гибкого цилиндра составляет 70 мм, ширина зубчатого венца 12 мм, толщина стенки зубчатого венца 1 мм, толщина стенки гладкого цилиндра 0,8 мм, толщина стенки дна цилиндра 0,8 мм. Конечно-элементная модель гибкого сплайна, показанная на рисунке 4, создается восходящим методом.

На рис. 4 в качестве материала гибкого шлица выбрана конструкционная сталь из сплава 30 CrMnSi. Его модуль упругости составляет 204 ГПа, коэффициент Пуассона – 0,29, а плотность – 6691 кг/м ³ .

3.2. Модель круглого шлица

В процессе передачи гармонического зубчатого редуктора гибкие шлицы и зубья кругового шлица зацепляются для завершения передачи движения и силы. Следовательно, модуль, угол давления, дополнительный коэффициент и коэффициент зазора круглого шлица такие же, как и у гибкого шлица. Диаметр индексной окружности кругового шлица составляет 85 мм, диаметр корневой окружности – 86,7 мм, а диаметр вспомогательной окружности – 84,35 мм. Толщина стенки зубчатого венца 14 мм, толщина кольцевого шлица 7 мм. Конечно-элементная модель кругового сплайна, созданная восходящим методом, показана на рис. 5.9.0005

На рисунке 5 материал кругового шлица представляет собой сталь 45 с коэффициентом Пуассона 0,3, модулем упругости 210 ГПа и плотностью 7850 кг/м ³ .

3.3. Генератор волн Модель

Генератор волн состоит из кулачка и гибкого подшипника. Это компонент, который создает волну деформации в процессе передачи гармонического редуктора. Структура механического генератора косинусоидальных колебаний показана на рисунке 6.

Уравнение профиля кулачка в полярных координатах выглядит следующим образом: где θ — полярный угол, а ρ ( θ ) — полярный диаметр.

В соответствии с уравнением кулачка в полярных координатах создается плоский профиль, а затем посредством растяжения формируется косинусная 3D-модель кулачка. Наконец, модель делится на левый и правый полукулачки вдоль направления короткой оси, и два полукулачка объединяются в сетку с помощью метода создания сетки отображения. По расчетам максимальный полярный диаметр косинусного кулачка составляет 30,5 мм, а минимальный полярный диаметр — 29 мм.0,5 мм. Конечно-элементная модель косинусного кулачка показана на рисунке 7.

На рисунке 7 материал кулачка представляет собой сталь 45 с коэффициентом Пуассона 0,3, модулем упругости 210 ГПа и плотностью 7850 кг/м ³ .

Гибкий подшипник является еще одной частью генератора волн. Как и обычный подшипник, он состоит из внутреннего и наружного колец, сепаратора и шарика. Однако толщина внутреннего и наружного колец намного меньше, чем у обычного подшипника, который относится к тонкостенным подшипникам. Конечно-элементная модель гибкой опоры показана на рис. 8.9.0005

На рис. 8 в качестве материала внутреннего и наружного колец гибкого подшипника выбран ZGCr15 с коэффициентом Пуассона 0,3, модулем упругости 207 ГПа и плотностью 7800 кг/м ³ . В качестве материала каркаса был выбран нейлон 66 с коэффициентом Пуассона 0,28, модулем упругости 8,3 ГПа и плотностью 1150 кг/м ³ . В качестве материала шара выбран GCr1 с коэффициентом Пуассона 0,29, модулем упругости 217 ГПа и плотностью 7850 кг/м ³ .

4. Экспериментальная проверка

Для проверки правильности конечно-элементной модели гармонического редуктора, установленной в этой статье, тензометрический тестер используется в качестве сборщика данных для изучения характеристик деформации гибкого шлица гармонического редуктора. В эксперименте двигатель, входной вал, муфта, соединительный вал, гармонический редуктор, выходной вал, радиальный шарикоподшипник, шайба и гайка соединяются по очереди. Тензорезистор BFh2K-1.5EB, двигатель постоянного тока XD-37GB555 и B ₃ -80 Коробка передач гармонического редуктора выбрана. Скорость двигателя была установлена ​​на 6 об/мин. Деформация измеряется тензодатчиком сопротивления, а сигнал извлекается тензометрическим тестером. В середину окружной наружной поверхности гибкого шлица гармонического зубчатого редуктора вклеен тензорезистор. Экспериментальная платформа характеристик деформации гибкого шлица в гармоническом редукторе показана на рисунке 9.

На рисунке 9 нагрузка создается шайбой, гайкой и динамометрическим ключом с заданным крутящим моментом типа TLA. Гайка предварительно затягивается динамометрическим ключом, а нагрузка создается за счет трения между круглой поверхностью шайбы и боковой стороной кронштейна подшипника. Нагрузку можно регулировать, изменяя значение предустановленного динамометрического ключа; когда шайба и гайка удалены, выходной вал работает на холостом ходу, имитируя состояние холостого хода.

Значение деформации, соответствующее вращению гибкого шлица в гармоническом редукторе, извлекается, и экспериментальные данные сравниваются с теоретическим значением, полученным с помощью моделирования контактной механики методом конечных элементов. Результаты сравнения показаны на рисунке 10.

На рисунке 10 результаты моделирования конечно-элементной модели контактной механики, установленной в этой статье, согласуются с экспериментальными результатами, а относительная ошибка невелика. Таким образом, правильность модели контактной механики конечных элементов гармонического редуктора, установленной в этой статье, проверена, и модель может быть использована для прогнозирования деформации гибкого шлица гармонического зубчатого редуктора.

5. Результат и обсуждение

5.1. Анализ чувствительности характеристик напряжения гибкого шлица

Для анализа чувствительности гибкого шлица к напряжению в гармоническом редукторе обсуждается влияние длины цилиндра и толщины нижней стенки цилиндра на напряжение гибкого шлица.

5.1.1. Влияние длины цилиндра на напряжение гибкого шлица

Длина L цилиндра определяет геометрическую структуру гибкого шлица в осевом направлении. Это один из ключевых конструктивных параметров гибкого шлица с цилиндрической чашкой, который оказывает значительное влияние на характеристики напряжения гибкого шлица. Поэтому нагрузочные характеристики гибкого шлица анализируются в диапазоне L  = 50∼85 мм. Нефограмма напряжения гибкого шлица при различной длине цилиндра показана на рисунке 11.

На рисунке 11 при увеличении длины L гибкого вала с 50 мм до 85 мм максимальное эквивалентное напряжение уменьшается на 34,3%. Следовательно, увеличение длины цилиндра L может эффективно улучшить напряженное состояние гибкого шлица.

Гибкая шлицовка разделена на три части: зубчатое колесо, цилиндр и нижняя часть гибкой шлицовки. Можно получить кривую влияния напряжения на длину трубки гибкой шлицевой части, как показано на рисунке 12.

На рис. 12 по сравнению с нижней частью зубчатого венца напряжение зубчатого венца выше. В диапазоне L  = 50∼70 мм максимальное эквивалентное напряжение кольца, цилиндра и днища гибкого вала явно уменьшается с 683 МПа до 514 МПа, с 682 МПа до 365 МПа и со 142 МПа до 98,1 МПа. . В диапазоне L  = 70∼85 мм тенденция снижения максимального эквивалентного напряжения имеет пологий характер: от 514 МПа до 488 МПа, от 406 МПа до 303 МПа и от 98,1 МПа до 79 МПа. 0,2 МПа. Это показывает, что концентрация напряжений в гибком шлице уменьшается с увеличением длины цилиндра.

5.1.2. Влияние толщины нижней стенки на напряжение гибкого шлица

Для анализа влияния толщины нижней стенки на напряжение гибкого шлица были проанализированы характеристики напряжения гибкого шлица в диапазоне толщины стенки = 0,80~1,15 мм. Нефограмма напряжения гибкого шлица при разной толщине стенки днища цилиндра показана на рис. 13.

На рис. 13 при увеличении толщины стенки в нижней части цилиндра максимальное эквивалентное напряжение гибкого шлица составляет около 506 МПа. Он показывает, что изменение толщины стенки в нижней части цилиндра мало влияет на напряжение гибкого шлица.

Гибкий шлиц разделен на три части: зубчатое колесо, цилиндр и дно гибкого шлица, и можно получить кривую напряжения толщины нижней стенки гибкого шлица, как показано на рис. 14.

На рис. 14 максимальное эквивалентное значение напряжения часть зубчатого кольца колеблется около 506  МПа, максимальное значение эквивалентного напряжения цилиндрической части колеблется около 403  МПа, а максимальное значение эквивалентного напряжения нижней части гибкого вала составляет около 103  МПа в диапазоне   =   0,8 ~ 0,95 мм и имеет значительное увеличение в диапазоне  = 0,95~1,15 мм, от 105 МПа до 181 МПа, увеличение на 72%. Видно, что толщина нижней стенки гильзы гибкого вала в основном влияет на напряженное состояние дна гибкого вала, в то время как на максимальное значение эквивалентного напряжения зубчатого кольца и цилиндрической части практически не влияет. Поэтому толщина нижней стенки бочки флекссплайна должна быть менее 1,0 мм, если позволяет технология обработки.

5.2. Анализ контактных характеристик гибкого подшипника

5.2.1. Влияние гибкого кольца на контактную жесткость подшипника

Для изучения влияния гибкого кольца на контактную жесткость подшипника в гармоническом редукторе было проанализировано влияние характеристик жесткости и гибкости кольца на контактную жесткость с обычным жестким подшипником в качестве объекта сравнения. Разница контактной жесткости между шариком и внутренним и наружным кольцами жесткого подшипника и гибкого подшипника при разных полярных углах показана на рисунке 15.9.0005

На рис. 15 вблизи углов 0°, 90°, 180° и 270° разница жесткости контакта между шарикоподшипником с жестким кольцом и гибким кольцом и каналом невелика. The difference values ​​of the inner ring contact stiffness △ K _i were 2.39 × 10 ⁸  N/m, 2.16 × 10 ⁸  N/m, 2.39 × 10 ⁸  N/m, and 2,16 × 10 ⁸  Н/м соответственно. Разница значений контактной жесткости наружного кольца △ K _O составляли 2,04 × 10 ⁸ Н/м, 1,73 × 10 ⁸ Н/м, 2,04 × 10 ⁸ н/м и 1,73 × 10 ⁸ N/M. Поскольку полярные углы 0°, 90°, 180° и 270° являются положениями большой и малой осей генератора косинусных кулачковых волн, значение контактной жесткости между шариком и внутренним и внешним кольцами ближе .

5.2.2. Анализ характеристик движения гибкой опоры

Шарик в сферических координатах (35, 0) был определен как шар №. 1, а затем были выделены узел N52521 в центре сферы и узел N53753 в области контакта между сферой и дорожкой качения соответственно. Кривая скорости центра тела качения и поверхностных узлов узлов N52521 и N53753 показаны на рисунке 16.

На рисунке 16 кривая скорости узла N52521 в центре шара представляет собой закон синусов и косинусов вдоль направления оси x и оси y . Явление флуктуации возникало в небольшом диапазоне кривой скорости. Колебания были вызваны зазором 0,1 мм между шариком и отверстием кармана клетки, а также небольшим столкновением между шариком и клеткой во время движения шарика. Суставная скорость узла N53753 на поверхности шара изменяется в пределах 0∼13,57 м/с, а пик и впадина суставной скорости чередуются через 0,006 с. Соответствующее время пика скорости представляет контакт между узлом и дорожкой качения внутреннего кольца подшипника, а соответствующее время впадины скорости представляет собой контакт между узлом и дорожкой качения наружного кольца подшипника. Период движения узла равен 0,003 с, то есть период вращения шара равен 0,003 с.

5.3. Анализ состояния пространственного распределения смещения гибкого шлица

В трех различных поперечных сечениях корпуса гибкого шлица пространственное распределение радиального смещения, смещения по окружности, осевого смещения и углового смещения гибкого шлица вместе с изменением полярного угла а осевое расстояние между гильзой с гибким шлицем и дном гильзы показано на рис. 17.

На рис. 17 вдоль направления полюсного угла θ радиальное смещение, окружное смещение, осевое смещение и угловое смещение гибкого шлица подчиняются закону синусов и косинусов. Вдоль направления центральной оси гибкого цилиндра с увеличением осевого расстояния Z от дна цилиндра значения радиального смещения, окружного смещения и углового смещения постепенно увеличиваются, демонстрируя тенденцию к линейному увеличению. По сравнению с радиальным и окружным смещениями величина осевого смещения на порядок меньше, и его величина не меняется с размером осевого расстояния З .

5.4. Анализ отклика на осевую вибрацию гибкого шлица

Окружное полное волновое число n остается неизменным. Когда осевое число полуволн м принимается за разные значения, получается отклик вибрации аксиального смещения гибкого шлица, и анализируется влияние осевого числа полуволн м на осевой вибрационный отклик гибкого шлица. Контурная карта осевого смещения гибкого шлица показана на рисунке 18.

Из рисунков 18(a)–18(c) видно, что при м  = 1 вдоль оси цилиндра на контурной карте есть пиковое значение и значение впадины. По окружности цилиндра есть два пиковых значения, одно значение впадины или одно пиковое значение и два значения впадины. Когда i принимает 1, 2 и 3 соответственно, пропорциональное отношение амплитуды осевого смещения составляет 1 : −0,416 : 0,017. Из рисунков 18(d)–18(f) видно, что при м  = 2 имеются две вершины, одна впадина или одна вершина, две впадины вдоль оси и окружности цилиндра. Когда i равно 1, 2 и 3 соответственно, пропорциональная зависимость амплитуды осевого смещения составляет 1 : −0,101 : −0,006. Таким образом, увеличение осевого числа полуволн м улучшит вибрационную характеристику гибкого шлица при осевом смещении.

6. Выводы

В этой статье создана модель контактной механики гибких частей в гармоническом редукторе. Проанализировано влияние длины гибкого шлицевого цилиндра и толщины нижней стенки гибкого шлицевого цилиндра на напряжение гибкого шлица. Исследованы характеристики движения гибкой опоры в контактном процессе и проанализирована вибрационная характеристика гибкого шлица. Выводы можно резюмировать следующим образом: (1) Концентрация напряжения гибкого шлица уменьшается с увеличением длины цилиндра, а увеличение длины цилиндра может эффективно улучшить напряженное состояние гибкого шлица гармонического редуктора. (2) Изменение Толщина стенки в нижней части цилиндра мало влияет на напряжение гибких шлицев, а толщина нижней стенки корпуса гибких шлицов должна быть менее 1,0  мм, если позволяет технология обработки. (3) При разных полярных углах разница контактной жесткости между шариком и внутренним кольцом и наружным кольцом жесткого подшипника и гибкого подшипника различна. На длинной и короткой оси генератора косинусных кулачков состояние контакта гибкого кольцевого шарика больше похоже на состояние жесткого кольцевого шарика. (4) По сравнению с радиальным и окружным смещениями значение осевого смещения на один порядок меньше. , и его значение не меняется с размером осевого расстояния между цилиндрами. (5) При осевом полуволновом числе м принимается как разные значения, получается виброотклик гибкого шлица при осевом смещении, а увеличение осевого числа полуволн м усиливает виброотклик гибкого шлица при осевом смещении.

Приложение

A. Коэффициенты уравнения

The A _I ( I = 1,2,3), B = 1,2,3). ,3,4), и с _i ( i  = 1,2,3,4,5) определяются уравнением (27).

B. Матрица B, C и D

B , C, и D определяются уравнением (28).

Доступность данных

Данные, использованные для подтверждения результатов этого исследования, включены в статью. Обработанные данные доступны у соответствующего автора по запросу.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Благодарности

Проект был поддержан Национальной ключевой программой исследований и разработок Китая (2020YFB2007802) и Национальным фондом естественных наук Китая (грант № 51875092).

Copyright © 2021 Fanjie Li et al. Эта статья находится в открытом доступе и распространяется в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.

[PDF] Структурные характеристики редуктора с вектором вращения Свободная вибрация

• DOI: 10.1155/2017/4214370
• Идентификатор корпуса: 54556861

 @article{Chen2017StructuralCO,
  title={Структурные характеристики свободной вибрации редуктора вращения вектора},
  автор = {Чуан-Чан Чен и Юху Ян},
  журнал={Удар и вибрация},
  год = {2017},
  объем = {2017},
  страницы={1-14}
} 

• Chuan-Chiang Chen, Yuhu Yang
• Опубликовано в 2017 г.
• Инженерное дело
• Удары и вибрация

Для редуктора RV, широко используемого в роботах, вибрация значительно влияет на его производительность. Модель с сосредоточенными параметрами разработана для исследования характеристик свободных колебаний без учета и с учетом гироскопических эффектов. Динамическая модель учитывает ключевые факторы, влияющие на вибрацию, такие как жесткость зацепления эвольвентных и циклоидальных зубчатых колес, жесткость коленчатого вала на изгиб и жесткость подшипников. Как для негироскопических, так и для гироскопических систем исследуются свободные колебания и сравниваются друг с другом. Результаты показывают… 

Анализ жесткости при кручении на основе метода Лагранжа для прецизионного поворотно-векторного редуктора с эвольвентным редуктором переменной толщины

• L. Chang, Yucheng Huang, Najeeb Ullah, Ling Zhu, Zhenyu Lv, Yu Jing

• Engineering

  8 9002 Прикладные науки 5 9002
• 2022

Прецизионный векторный редуктор с эвольвентным зубом переменной толщины (PRVT) представляет собой высокопроизводительное прецизионное передаточное устройство, которое очень подходит для аэрокосмической, медицинской техники,…

Анализ нелинейных характеристик поступательно-крутильной динамической модели редуктора RV

• Чжэн Юйсинь, Ван Сян, Си Ин, Лю Цзяншань

• Инженерия, физика

  )

• 2019

Для исследования динамических характеристик редуктора ГС упрощена и построена поступательно-крутильная динамическая модель редуктора ГС с привязкой к методу моделирования 2К-Н…

Конструкция оптимизации RV Редоусорное подшипник Коленчатого вала

• Цзянь Хуанг, Чаоян Ли, Bingkui Chen

• Инженерия

  Applied Sciences

• 202020648

  Applied Sciences

• 202020648

  . . Однако из-за тяжелых рабочих нагрузок и ограниченного доступного пространства подшипник часто выходит из строя из-за усталости…

  Жесткие прецизионные редукторы для обработки промышленных роботов

  Обзор жестких прецизионных редукторов для обрабатывающих роботов показывает, что циклоидный редуктор является лучшим кандидатом среди прецизионных редукторов, учитывая как структурное соответствие, так и кинематическую точность обрабатываемых роботов.

  Прогнозирование частоты отказов и оценка надежности редуктора RV

  • B. Bai, Ze Li, Junyi Zhang

  • Инженерное дело

    Международная конференция по качеству, надежности, рискам, техническому обслуживанию и технике безопасности (QR2MSE), 2019 г.

  • 2019

  Для прогнозирования надежности редуктора RV в шести- осевые промышленные роботы.

  Метод прогнозирования точности собираемого редуктора RV с учетом функции взвешивания дендритов

  • Шоу-Сун Джин, Яньси Чен, Ипин Шао, Ялян Ван

  • Информатика

    Энергии

  • 2022

  Предлагаемый метод может помочь в выборе деталей в процессе сборки редуктора RV и может реализовать регрессионное прогнозирование массы редуктора и имеет хорошую точность прогнозирования и возможность обобщения.

  Диагностика неисправности коленчатого вала редуктора с вектором вращения с использованием методов акустической эмиссии

  • Haibo An, Wei Liang, Yinlong Zhang, Yang Li, Ye Liang, Jindong Tan

  • Engineering, Materials Science

    2017 5-я Международная конференция по корпоративным системам (ES)

  • 2017

  Этот документ специально разработан для диагностики износа коленчатого вала редуктора RV с использованием методов акустической эмиссии (АЭ), и результаты экспериментов доказывают, что этот метод способен эффективно обнаруживать неисправности коленчатого вала редукторов RV.

  ПОКАЗАНЫ 1–10 ИЗ 30 ССЫЛОК

  СОРТИРОВАТЬ ПОРелевантность Наиболее влиятельные документыНедавность

  Свойства свободной вибрации векторного редуктора вращения

  • Chuan-Chiang Chen, Yuhu Yang

  • Engineering

  • 2016

  Для редуктора RV, широко используемого в робототехнике, в этой работе разработана модель с сосредоточенными параметрами для исследования свойств свободной вибрации общего описания. 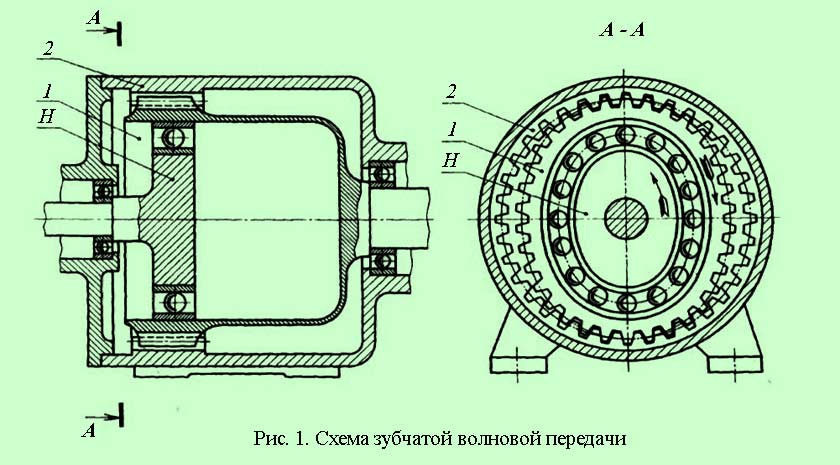Динамическая модель допускает три плоских степени…

  Динамическая модель редуктора РВ и ключевое влияние жесткости на характер природы влияние жесткости опорного подшипника и углового периодического…

  Аналитическая характеристика уникальных свойств свободных колебаний планетарных передач

  • Цзянь Линь, Р. Паркер

  • Физика

  • 1999

  В этой работе разработана аналитическая модель планетарных передач и используется их аналитическая модель для исследования их собственных частот. и режимы вибрации. Модель допускает три плоские степени свободы для каждой из…

  Свободная вибрация и устойчивость вращающейся системы «диск-шпиндель»

  • R. Parker, P. Sathe

  • Материаловедение

  • 1999

  В этой работе исследуется свободная вибрация и устойчивость вращающейся упругой системы диск-шпиндель. Расширенная формулировка оператора используется для дискретизации системы с использованием метода Галеркина…

  Динамический анализ циклоидальных редукторов скорости с вертлюжным и не вертлюжным колесами

  • C. Hsieh

  • Инженерное дело

  • 2014

  Циклоидные редукторы состоят в основном из скоростных2

  • эксцентрикового вала, выходных частей и комплекта, состоящего из циклоидальной шестерни и вертушки со штифтами или циклоидной шестерни и циклоидной внутренней шестерни. Это…

    Free torsional vibration characteristics of compound planetary gear sets

    • A. Kahraman

    • Engineering, Physics

    • 2001

    SENSITIVITY OF PLANETARY GEAR NATURAL FREQUENCIES AND VIBRATION MODES TO MODEL PARAMETERS

    • J. Lin, R Parker

    • Инженерия, физика

    • 1999

    Чувствительность собственных частот и режимов вибрации к системным параметрам тщательно исследована как для настроенных (циклически симметричных), так и для расстроенных планетарных передач. Параметры под…

    Влияние динамического несовершенства на вибрацию вращающихся дисков

    • С. А.