Запас насаждения по стандартной таблице — КиберПедия
Для выполнения расчётов надо знать высоту и полноту насаждения. В стандартной таблице (Лесотаксационный справочник, 2006; и многие др.), независимо от возраста и класса бонитета, каждой средней высоте соответствует определённый запас нормального насаждения. Чтобы найти запас, необходимо табличный запас нормального насаждения (с относительной полнотой 1,0) умножить на относительную полноту таксируемого насаждения. Все расчеты на практике обычно выполняются по элементам леса, в данном случае запас определяем только для главной породы – главного элемента леса.
Запас насаждения по основной формуле
Основная формула определения запаса имеет следующий вид:
М = G H F , (4.5)
где М — сумма площадей сечения в м2;
Н— средняя высота насаждения в м;
F — среднее видовое число
Среднее видовое число главного элемента леса определяется как средне-арифметическое из видовых чисел всех учётных деревьев главной породы. Видовое число (
Запас насаждения по таблице видовых высот
Запас определяется с использованием основной формулы:
М = G (hf) . (4.6)
Абсолютная полнота или сумма площадей сечения (G) приведена в таблице 4.1. Произведение высоты на видовое число (hf — видовая высота) находится по специальной таблице (Лесотаксационный справочник, 2006; и т.п.) в зависимости от средней высоты соответствующей древесной породы.
После определения запаса насаждения всеми способами рассчитывается процент отклонения установленных запасов от истинного (табл. 4.3). За истинный принимается запас, найденный по учётным деревьям.
Таблица 4.3
Точность различных способов определения запаса насаждения
| №№ | Способы определения запаса насаждения | Запас, м3 | Отклонения, | |
| пп | на пробн. площ. | на 1 га | % | |
| 1. | По средней модели | 176,50 | — 6,0 | |
| 2. | По объёмным таблицам | 198,70 | + 6,0 | |
| 3. | По кривой объёмов | 188,00 | ||
| 4. | По прямой объёмов | 183,00 | — 2,2 | |
| 5. | По учётным деревьям | 188,00 | ||
| 6. | По стандартной таблице | 204,00 | + 8,6 | |
| 7. | По основной формуле | 198,00 | + 5,2 | |
| 8. | По таблице видовых высот | 183,00 | — 2,2 |
4.2.5. Определение других таксационных показателей насаждения
Средний коэффициент формы
Определяется для преобладающей породы как среднеарифметическое из коэффициентов формы (ср.q2) всех учётных деревьев. Для сопутствующих пород средний коэффициент формы будет равен второму коэффициенту формы среднего модельного дерева данной породы.
Товарная структура запаса
Определяется по выходу деловой древесины, дров и отходов из учётных деревьев. Чем выше доля деловой древесины в общем запасе насаждения, тем выше класс товарности. В расчётах используются следующие формулы:
а) для преобладающей породы
М дел = Σvдел .G ,
Σg (4.7)
б) для сопутствующих пород
М дел = Vдел .G , (4.8)
g
гдеМ дел.– запас деловой древесины;
ΣVдел.— объём деловой части без коры в м3 всех учётных деревьев;
G — сумма площадей сечения всех деревьев данной породы;
Σg — сумма площадей сечения учётных деревьев;
g —площадь сечения среднего учётного дерева.
Таким же способом определяются запасы дров. Объём отходов рассчитывается по разности между общим запасом и запасом деловой древесины и дров. Запас деловой древесины, дров и отходов яруса равен сумме этих показателей у всех пород слагающих ярус.
Класс товарности
Класс товарности насаждений устанавливается в лесной таксации по выходу деловой древесины. Выход деловой древесины определяется в %. Для расчёта класса товарности используется специальная шкала (табл. 4.4), в которой класс товарности устанавливается по выходу деловой древесины от общего запаса древостоя.
Таблица 4.4
Определение класса товарности по выходу деловой древесины (%)
| Класс товарности | I | II | III | IV |
| Хвойные породы (кроме лиственницы) | 81 и более | 61-80 | до 60 | - |
| Лиственные породы ( и лиственница) | 71 и более | 51-70 | 31-50 | до 30 |
В отдельных случаях класс товарности может быть установлен по выходу (%) деловых деревьев от их общего количества.
Прирост насаждения
Прирост необходимо вначале рассчитать по элементам леса.
Средний прирост по запасу (ΔМ) определяется путём деления запаса на 1га древесной породы(Мср.)на её средний возраст(Аср):
ΔМ = Мср. / Аср. (4.9)
Средний прирост яруса находится суммированием прироста отдельных пород, входящих в этот ярус.
Текущий прирост по запасу (ΖМ) определяется по следующим формулам:
а) для преобладающей породы ΖМ = ΣZV . G ; (4.10)
Σg
б) для сопутствующей породы ΖМ = ZV . G ,
g (4.11)
где
G — сумма площадей сечения на 1 га данной древесной породы;
Σg – сумма площадей сечения учётных деревьев;
ZV и g — текущий прирост и площадь сечения среднего модельного дерева
Текущий годичный прирост по запасу яруса равен сумме приростов всех древесных пород, слагающих таксируемый ярус.
Состав древостоя
Определяется отдельно для каждого яруса. Он записывается формулой, в которую входят сокращенное название породы и числовые показатели — коэффициенты состава в целых числах, показывающие долю участия каждой породы в образовании общего запаса яруса. Для определения коэффициентов состава надо подсчитать, какая часть общего запаса яруса приходится на каждую породу.
В рассматриваемом примере в I ярус входит только одна порода — ель, поэтому и состав этого яруса будет 10 Е. Во II ярус входит липа и клён, общий запас которых равен 157 м 3. Из этого запаса 82 м3 или примерно 5/10 приходится на липу, а остальные 5/10 запаса — на клён. Следовательно, состав II яруса будет выражен формулой 5Лп 5Кл.
Древесные породы, на долю которых приходится 2-5% общего запаса, записываются в формуле состава со знаком плюс (+). Если запас породы составляет менее 2%, она в формуле состава обозначается приставкой «ед.» – то есть единично.
Для основных древесных пород устанавливаются следующие сокращенные обозначения: сосна – С, ель — Е, пихта — П, кедр — К, дуб — Д, Клён — Кл, ясень — Я, Ильм — И, ива – Ив, осина — Ос, липа — Лп, и т.д. На первое место в формуле состава ставится главная порода, а при равном запасе у нескольких пород — та, которая имеет в данных природно-климатических и экономических условиях наибольшее хозяйственное значение.
Насаждение по происхождению может быть искусственным или естественным, семенным или порослевым. В рассматриваемом примере насаждение по происхождению естественное.
По форме насаждения делятся на простые (одноярусные, состоящие из одного полога) и сложные (двух- или трёхъярусные). В нашем примере, древостой сложный, двухъярусный.
По составу насаждения могут быть чистыми, образованными одной древесной породой, или смешанными состоящими из двух или нескольких пород. Чистым считается древостой, в котором доля участия других пород не превышает 15%. Древесная порода, имеющая наибольший коэффициент состава в основном ярусе, называется преобладающей, а остальные породы — сопутствующими. Главная порода (целевая, имеет наибольшее хозяйственное значение, оказывает наибольшее влияние на развитие лесонасаждения).
По среднему возрасту главной породы устанавливаются класс возраста и группа возраста всего насаждения. В большинстве случаев продолжительность класса возраста установлена для хвойных и твердолиственных семенных насаждений в 20 лет, для мягколиственных семенных насаждений — 10 лет. Группы возраста у хвойных можно условно принять следующие: молодняки — насаждения I и IIклассов возраста, средневозрастные — III класс возраста, приспевающие — IVкласс, спелые — Vкласс возраста, перестойные — насаждения – VI, VII, VIII и выше классы возраста.
В зависимости от колебания возраста отдельных стволов различают насаждения четырёх видов: I) одновозрастные — возраст у всех деревьев одинаковый; 2) условно одновозрастные — состоят из деревьев с разностью в возрасте до 20 лет; 3) условно разновозрастные — с разностью в возрасте у деревьев до 40-50 лет; 4) разновозрастные -состоят из деревьев с разностью в возрасте 60 и более лет. Вид насаждения можно установить по разности в возрасте у срубленных учётных деревьев.
О производительности насаждения принято судить по классу бонитета. Насаждения
Полнота насаждения характеризует степень использования лесом занимаемого пространства. Насаждения с полнотой 0,6-1,0 считаются высокополнотными, с полнотой 0,5-0,7 – среднеполнотными, 0,3-0,4 -низкополнотными, с полнотой менее 0,3 — рединами.
Класс товарности позволяет судить о качественном состоянии насаждения. При первом классе древостой считается высокого качества, при втором – среднего, а при третьем или четвёртом классе товарности — древостой низкого качества, имеет небольшой выход деловой древесины.
По завершении всех расчётов необходимо полученное таксационное описание насаждения охарактеризовать. Характеристика таксируемого насаждения приводится в отчёте как в виде расчётов, таблиц, рисунков, графиков, так и в виде текста. Текстовая часть отчёта должна содержать краткие пояснения расчётов и описание полученных результатов.
ГЛУШКО СЕРГЕЙ ГЕННАДЬЕВИЧ
ЛЕСНАЯ ТАКСАЦИЯ
Программа, методические указания и контрольные задания для студентов – заочников Факультета лесного хозяйства и экологии
(направление обучения – лесное дело)
Казанский государственный аграрный университет.
420015, г. Казань, ул. Карла Маркса, 65
Лицензия на издательскую деятельность код 221 ИД № 06342 от 28.11.2001г.
cyberpedia.su
7.2. Определение запаса древостоя методом модельных деревьев
Наиболее трудоемкий по сбору и обработке материалов метод. Он редко используется для определения запасов в парках и лесопарках, так как основан на детальном измерении значительного количества вырубленных модельных деревьев.
Таблица 18
Определение запаса по объемным таблицам
Ступени толщины | Порода – сосна | |||||
Число стволов, шт | Высоты, м | Запас по таблицам, м3 | ||||
по разрядным таблицам | по диаметру и высоте | |||||
объем ствола | запас ступени | объем ствола | запас ступени | |||
12 16 20 24 28 32 36 40 | 3 31 71 96 54 38 29 7 | 17,9 21,2 23,1 23,9 26,3 27,4 28,1 28,3 | 0,09 0,19 0,33 0,51 0,73 0,90 1,28 1,62 | 0,27 5,89 23,43 48,96 39,42 37,62 37,12 11,34 | 0,10 0,20 0,33 0,49 0,71 0,94 1,26 1,51 | 0,30 6,20 23,43 47,04 38,34 35,72 36,54 10,57 |
Всего | 329 | 204 | 198 | |||
Однако такие методы находят применение при таксации лесов других групп как наиболее точные. В связи с вышеизложенным определение запаса методом модельных деревьев может быть, по усмотрению преподавателя, вынесено на индивидуальные занятия.
При использовании данной методики в таксируемом древостое подбираются модельные деревья. Модельными (или моделями) называют деревья, взятые в качестве типичных образцов, характеризующих в среднем некоторые совокупности деревьев (древостой, ступень толщины) по диаметру, высоте, форме, объему ствола и т.д.
Существуют следующие методы определения запаса по модельным деревьям:
а) по моделям, представленным для каждой ступени толщины. В древостое проводят перечет деревьев по ступеням толщины, замеряют высоты и по полученным данным строят график высот. Каждая ступень толщины рассматривается как отдельный древостой со средним диаметром, равным значению ступени, средняя высота которой равна сглаженной высоте ступени.
Для каждой ступени толщины в древостое подбирают средние модели. Модельные деревья срубают, производят их обмер и определяют объем по сложной формуле срединных сечений (Губера). Запас древостоя определяют по формуле
. (54)
где G1, G2, G3, …, Gn – суммы площади сечений ступеней толщины, м2; g1, g2,…, gn – площади сечений модельных деревьев по ступеням толщины, м2; V1, V2, …, Vn – объемы моделей по ступеням толщины, м3.
б) по методу средней модели для древостоя. Средний диаметр и средняя высота древостоя являются показателями теоретической модели и служат основными придержками для подбора фактической модели в древостое. Отыскать дерево в древостое, размеры и форма которого точно совпали бы с размерами и формой теоретической расчетной модели, практически невозможно. Ввиду трудности точного подбора диаметра модели, отвечающего средним величинам, в древостое подбирают средние модели, близкие к средним таксационным показателям древостоя. Дерево, отобранное в качестве средней модели, срубают и объем его определяют по сложной формуле срединных сечений (Губера). Запас древостоя М в этом случае вычисляется по формуле
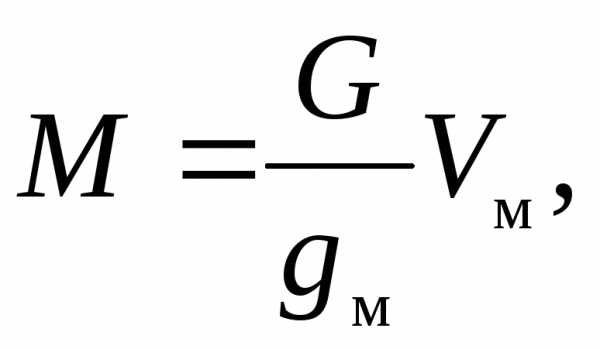 (55)
(55)
где G – сумма площадей сечений древостоя м2; gм – площадь сечения модельного дерева, м2; Vм – объем модельного дерева, м3.
Ввиду трудности точного подбора диаметра модели, отвечающего средним величинам, в древостое подбирают средние модели, близкие к средним таксационным показателям древостоя. Число моделей устанавливается на основе коэффициента вариации объемов стволов средних моделей в древостое. Обычно берут 3–5 моделей.
Запас древостоя М, м3,в этом случае вычисляется по формуле
 (56)
(56)
где G – сумма площадей сечений древостоя м2; 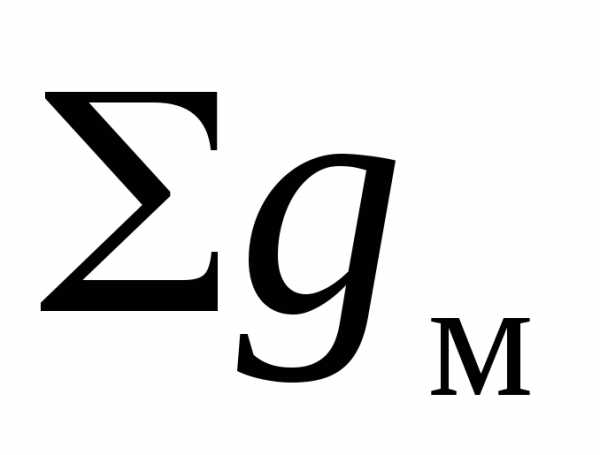 – суммы площадей сечений модельных
деревьев на высоте 1,3 м, м2;
– суммы площадей сечений модельных
деревьев на высоте 1,3 м, м2;  – суммы объемов модельный деревьев,
м3.
– суммы объемов модельный деревьев,
м3.
Для определения запаса древостоя методом модельных деревьев исходные данные выдаются преподавателем.
Пример 17. Для определения запаса древостоя методом модельных деревьев по вариантам (табл. 18) с использованием таблицы П.1.4 по каждой ступени толщины подбираются модельные деревья по средней высоте ступени. Параметры модельных деревьев выписываются в бланки задания (табл. 19). Далее по ф. 54 вычисляется запас древостоя:
Таблица 19.
studfiles.net
60. Варьирование таксационных показателей древостоя и его влияние на
точность таксации.
61. Запас насаждения. Эксплуатационный и товарный запас
насаждения. Запас насаждения (древостоя) – это сумма объемов составляющих его деревьев, он обозначается буквой М. В то же время термин «запас насаждения» еще не в полной мере характеризует ценность древостоя. Различают запас общий, эксплуатационный и товарный.
Общий запас – это запас всего древостоя. Он складывается из запаса стволовой древесины, сучьев и фитомассы.
Таксация имеет дело в основном с запасом стволовой древесины, хотя в последние годы все большее внимание уделяется всей надземной фитомассе.
Эксплуатационный запас – это запас древостоя, который может быть вырублен в ближайшие 10 – 20 лет. Его составляют приспевающие, спелые и перестойные древостои.
Товарный запас – это запас той части древостоя, которая имеет сбыт, т.е. будет использована в народном хозяйстве. Его еще называют ликвидным запасом или ликвидом. Последнее выражение употребляется чаще, хотя правильнее говорить «товарный». В лесхозах обычно употребляют слово «ликвид».
Товарный запас представляет собой общий запас минус отходы, т.е. деловую и дрова. Все расчеты лесопользования обычно ведут в ликвиде (товарном запасе), т.к. для потребителя важен именно этот запас.
62. Товарные таблицы и область их применения. Товарные таблицы содержат учетные данные о сортиметном составе для совокупности древостоев.Эти величины приведены в процентах от общего запаса древостоев в зависимости от породы, среднего диаметра, высоты и качественного состояния насаждений, определяемого классами товарности.
В связи с тем, что спелые мягколиственные древостои, особенно осина, могут иметь очень низкий выход деловой древесины, то в Беларуси для этой категории древостоев введен 4 класс товарности.
Классы товарности устанавливают по проценту выхода деловой древесины. Делает это таксатор в полевых условиях. Глазомерное нахождение процента выхода деловой древесины затруднено. Поэтому в натуре таксатор обычно ориентируется на процент деловых деревьев в древостое, руководствуясь специальной таблицей
Класс товарности | Выход деловой древесины (%) и количество деловых стволов (%) | |||
Хвойные | Лиственные | |||
Запас деловой древесины | Количество деловых стволов | Запас деловой древесины | Количество деловых стволов | |
1 | ≥81 | ≥91 | ≥71 | ≥91 |
2 | 61-80 | 71-90 | 51-70 | 66-90 |
3 | <60 | <70 | 31-50 | 41-65 |
4 | — | — | <50 | <40 |
Товарными таблицами пользуются лесоустроители при товаризации эксплуатационного фонда. К эксплуатационному фонду относятся перестойные, спелые и приспевающие древостои, Для товарных таблиц первичная единица учета – выдел
63. Точность таксации лесосек
Особое внимание должно быть уделено правильной таксации насаждений, находящихся на грани приспевающей и спелой возрастных групп для обоснованного их отнесения к указанным группам. Предельно допустимой величиной систематической ошибки определения любого из таксационных показателей устанавливается ±5%.
При таксации леса к недопустимым ошибкам относятся неправильное определение класса товарности древесины, класса бонитета, типов леса, отсутствие или неправильное назначение вида мероприятия, главной породы лесовос-становления, назначения процента выборки древесины выше или ниже пределов, указанных в наставлениях и правилах.
При таксации древостоев необходимо придерживаться градаций определения таксационных показателей насаждений, которые приведены в таблице 13.4. При этом применяют единицы измерений , которые общеприняты в лесной таксации и использованы в таблице 13.4.
В настоящее время данные лесоинвентаризации являются основой для планирования и проведения всех хозяйственных мероприятий. Отступления от них, как правило, не допускаются. Это накладывает повышенную ответственность на специалистов, которые делают инвентаризацию леса и повышает требования к её точности.
Поэтому органы лесного хозяйства в последнее время усилили требования к качеству работ по лесоинвентаризации. Новая лесоустроительная инструкция, которая будет принята в ближайшие годы, предполагает повысить точность таксации лесных насаждений. В то же время повышение точности таксации должно повлечь за собой изменения в технологии ее проведения в сторону усложнения. Должны применяться более трудоёмкие методы учёта леса. Это с неизбежностью потребует увеличения затрат на проведение лесоустройства.
Учитывая, что возможность увеличения затрат на лесоустройство в настоящее время проблематична, то учёным и практикам необходимо разработать новые, более совершенные методы таксации на основе последних достижений научно—технического прогресса.
Таблица 13.3. Нормативы точности таксации лесных насаждений
Категории насаждений | Допустимые случайные ошибки таксационных показателей насаждений | ||||
Срелнее для яруса, % | Среднее для основных элементов леса | Количество подроста на 1га, % | |||
Запаса на 1 га | Высоты | Коэфф. состава, единиц | Диаметра, % | ||
1.Все насаждения, назначенные в предстоящем ревизионном периоде в главного пользования и обновления | 10 | 7 | 1 | 10 | 20 |
2. Все остальные насаждения | 15 | 7 | 1 | 10 | 20 |
Таблица 13.4 Градации определения таксационных показателей насаждений
Таксационные показатели насаждений | Единица измерения и градация определения таксационных показателей насаждений | |
При производственной таксации | При исследовательских и обследовательских работах | |
Средняя высота древостоя | 1м | 0,1м |
Средний диаметр древостоя а) При среднем лиаметре до 32см б) при среднем диамнтре более 32см | 2см 4см | |
Запас сырорастузего древостоя | 10и3 | 1м3 |
Запас для кустарников | 1м3 | |
Запас единичных деревьев, сухостоя и захламленночти | 5м3 | 1м3 |
Сумма площадей сечений на высотк 1,3м на 1га | 1м2 | 0,1м2 |
Доля участия (коэффициент состава) элементов леса (пород) в составе древостоя | 10% | 1% |
Возраст: а) Молодняков хвойных до 10 лет, диственных до 5 лет, культур ревизионного периода и остальных возрастов | 1год | 1год |
б) Насаждений до 100 лет | 5 лет | |
в) Насаждений свыше 100лет | 10лет | |
Бонитет | 1 класс | 1 класс |
Класс товарности | 1 класс | 1% выхода деловой древесины |
Средняя высота древостоя: | ||
а) При высоте до 0,5м | 0,1м | 0,1м |
б) При высоте более 0,5м | 0,5м | 0,1м |
Средний возраст подроста | 5 лет | 1 год |
Количество пней на вырубке | 100щт. | |
Год вырубки, пожара, производства лесных культур, закладки плантаций | 1 год | 1год |
Процент проективного покрытия ягодниками, напочвенного покрова | 5% | 1% |
studfiles.net
Запас лесных насаждений
содержание .. 60 61 62 63 64 65 66 67 68 69 70 ..
Запас лесных насаждений
После того как установлены состав, возраст, средняя высота, бонитет и полнота таксируемого насаждения, переходят к определению общего количества древесины на единице площади насаждения, обычно на 1га,т. е. к установлению запаса древостоя. Запас насаждения можно определить разными способами.
При точных таксационных изысканиях запас определяют по модельным деревьям. В широкой практике, особенно при отводах лесосек, для нахождения запаса насаждения обычно применяют способ перечислительной таксации с его оценкой по объёмным и сортиментнымх таблицам. В этих таблицах приведены объемы деревьев разных ступеней толщины. Умножив объем на число деревьев соответствующей ступени, установленное при перечете, и сложив все произведения, получают общий запас насаждений.
Можно также определить запас древостоя по методу пробных площадей, применяемому при частичном перечете деревьев. Вычисленный по пробной площади запас насаждения умножают на отношение площади таксируемого участка к площади пробы и получают общий запас.
При таксации обширных лесных пространств частичный перечет деревьев с последующим использованием объемных и сортиментных таблиц часто бывает затруднительным. В этом случае применяют способы глазомерной таксации, позволяющие находить запас без перечета деревьев.
Умение определять запас насаждений без перечета деревьев требует большого навыка и опыта. У таксатора, заложившего много пробных площадей и устанавливавшего запас по моделям и массовым таблицам, запечатлеваются в памяти типичные насаждения, с которыми он и сравнивает таксируемые участки леса. Поэтому он может глазомерно определить запас, полноту и прочие таксационные признаки осматриваемых насаждений. Однако точность результатов при глазомерной таксации даже у самых опытных таксаторов колеблется в пределах ±10-15%.
При глазомерной таксации для определения запаса насаждения пользуются как подсобным материалом выдержками из таблиц хода роста, которые называются стандартными таблицами сумм площадей сечений и запасов при полноте 1,0.
Зная среднюю высоту дерева и полноту насаждения, можно достаточно просто найти его запас.Формулы для ориентировочного определения запаса базируются на основной формуле запаса насаждения:
М = å GHF.
Произведение суммы площадей сечений деревьев (в квадратных метрах) на видовое число åGF есть величина почти постоянная, для сосны и бука изменяющаяся в пределах от 14 до 18, а в среднем равная 16, для ели и пихты — от 16 до 22, в среднем же равная 18. Соответственно этому запас нормального насаждения М будет равен для сосны и бука 16 Н, для ели и пихты 18 Н. Включив в эти формулы дополнительный показатель, полноту насаждения Р, можно найти запас насаждений, имеющих разную полноту. Если произведение å GF заменить буквой О, получим формулу для определения запаса всех пород:
М = OHP.
Однако опытная проверка показала, что величина О в насаждениях разных бонитетов неодинакова: в высших бонитетах она больше указанных цифр. Поэтому в насаждениях высших бонитетов приведенная формула приуменьшает запас, а низших — преувеличивает. Лучший результат получается для насаждений средних бонитетов.
Таким образом, рассмотренные формулы дают весьма приближенные запасы таксируемых насаждений.
Проф. Н.В. Третьяков (1952) более детально изучил зависимость запасов древостоя от суммы площадей сечений, видовых чисел и высоты åGhf. Математически обработав числовые величины многих таблиц хода роста насаждений, он предложил для определения запаса насаждений следующие формулу:
Где K и a – коэффициенты, выведенные опытным путем,
P – относительная полнота.
Постоянный поправочный коэффициент а, корректирующий высоту h, уменьшающуюся от высших бонитетов к низшим, более существенно влияет на величину запаса в насаждениях низших классов бонитета. Поэтому при пользовании формулами Третьякова устраняется ошибка при определении запасов, которую давала формула M= OHP.
Недостатком этих формул является их громоздкость и трудность вычислений.
На основе анализа обширных экспериментальных Н.П. Анучину удалось вывести довольно простые формулы, позволяющие определять запасы насаждений с достаточной точностью. При выводе этих формул главнейшие древесные породы были разделены на две группы. В первую из них вошли сосна, лиственница, береза, осина и ольха. Вторую группу древесных пород образуют ель, пихта, кедр, бук, дуб, ильм и ясень.
У древесных пород первой группы видовое число оказалось равным f=0,40+1,20/H, а во второй группе f=0,42+1,26/H.
Соответственно этим уравнениям получены следующие две формулы, определяющие запасы насаждений двух указанных выше групп древесных пород:
MI = (0,40+1,20/H) H åg = (1,20+0,40H) åg;
MII = (0,42+1,26/H) H åg = (1,26+0,42H) åg.
Числовой коэффициент при H обозначим через К, тогда нашим формулам можно придать следующий вид:
М = (ЗК + KH) åg.
Выражение, заключенное в скобки (ЗК+KH), является видовой высотой насаждения. У древесных пород первой группы, когда средняя высота насаждения равна 22 м, видовая высота (ЗК+KH) оказывается равной (3х0,40+0,40×22)=10 м. В этом случае определение запаса предельно упрощается. Запас насаждения, имеющего среднюю высоту 22 м, оказывается равным
M = 10 åg.
Сумму площадей поперечных сечений åg находим с помощью углового шаблона Биттерлиха или призмы Анучина. Увеличив найденный результат в 10 раз, получаем запас насаждения.
Исследования показали, что видовая высота имеет линейную связь со средней высотой насаждения, при этом на каждый метр средней высоты она увеличивается на 0,40 м. В связи с этим высоту таксируемого древостоя обозначим через Hd, а разницу ее с высотой равной 22м — через Dh = Hd -22.
Соответственно этим условиям получаем следующую формулу, определяющую запас насаждений первой группы древесных пород:
МI = 10 åg ± 0,4 Dh åg.
Этой же формуле может быть придан следующий вид:
МI = 10 åg ± 0,4 åg (Hd -22).
В насаждениях, имеющих среднюю высоту, меньшую 22 м, второе слагаемое формулы обращается в минусовую величину. Прибавляя последнюю к запасу, указываемому первым слагаемым, получаем запас, приведенный в соответствие с уменьшенной средней высотой.
Применение этой формулы иллюстрируем примерами. Допустим, что высота таксируемого насаждения Hd оказалась равной 25 м, а сумма площадей сечений åg =30 м2. В этом случае запас насаждения равняется
МI = 10 . 30 +0,4 . 30 (25-22) =336 м3.
Предположим, что средняя высота таксируемого насаждения равна 20 м, а сумма площадей сечений — 25 м2. В этом случае запас насаждения будет равен
МI = 10 . 25 + 0,4 . 25 (20-22) = 230 м3.
У древесных пород, относящихся ко второй группе, видовая высота, близкая к 10 м, оказывается в том случае, когда насаждение имеет среднюю высоту, округленно равную 21 м. В этом случае запас будет близок к
М= 10 åg.
Эта вторая формула применяется так же, как первая. Разница заключается лишь в том, что базовой высотой, не требующей в расчетах соответствующей поправки, является средняя высота насаждений
21 м.
Для расчета запаса обеих групп древесных пород нашей формуле может быть придан следующий общий вид:
M = 10 åg + 0,4 å g (Hd — Hb).
В этой формуле Hb означает базовую высоту насаждения, для первой группы пород равную 22 м, а для второй группы пород — 21 м. Все остальные величины известны из предыдущего изложения.
Приведенные формулы просты, но они отражают общий недостаток уравнений, где используются коэффициенты, выведенные эмпирически. Поэтому применять их можно лишь для приближенного установления запаса.
В общий древесный запас входят объемы не только крупных деревьев, представляющих с эксплуатационной точки зрения наибольшую производственную ценность, но и мелких деревьев.
Та часть запасов древесины, которая по своим размерам и качеству пригодна для выработки продукции для народного хозяйства, называется эксплуатационным запасом.
В процессе заготовки и последующей разделки срубленных деревьев неизбежны отходы в виде пней, вершин и частей ствола, пораженных гнилью, кроме того, для последующего восстановления леса на вырубках оставляют крупные деревья — семенники, а иногда и семенные куртины. На крутых склонах и вершинах гор часть леса недоступна для эксплуатации. Поэтому при расчетах и определении выхода готовой лесопродукции необходимо из эксплуатационного запаса вычитать объем, приходящийся на отходы, остающиеся семенники, семенные куртины.
Не включаются в эксплуатационный запас, особенно в лесах Севера и Сибири, насаждения, имеющие на 1 га менее 30 м3, а также те древесные породы, рубка которых запрещена ввиду их особой ценности (кедр, орех, бархатное дерево и др.). Оставшаяся после их вычета часть эксплуатационного запаса называется ликвидным запасом. А.Г. Мошкалев рекомендует называть его «товарным запасом». Это предложение широкого распространения не получило. Запас реализуемой древесины в практике называют ликвидным запасом или просто ликвидом.
Для каждого таксационного участка, как мы уже говорили, устанавливается преобладающая порода. Суммируя по преобладающей породе запасы отдельных таксационных участков, получают данные для массива в целом. При подсчете запаса преобладающей древесной породы в него включают кубатуру примесей. Так, в общий запас насаждений с преобладанием сосны обязательно включают примесь ели, березы и других пород, а в запас насаждений с преобладанием ели — примесь сосны.
Поскольку эти примеси должны взаимно компенсироваться, казалось бы, общий запас насаждений с преобладанием определенной породы можно приравнять к запасу данной породы во всем массиве. Однако такой вывод был бы неверным, так как в лесном массиве различные древесные породы могут занимать неодинаковые площади. Поэтому примеси отдельных пород могут взаимно компенсироваться лишь частично. Следует также иметь в виду, что биологические свойства пород, так же как условия местопроизрастания и возраст насаждений, не одинаковы.
Из сказанного следует, что суммарный запас насаждений с преобладанием определенной древесной породы нельзя считать близким к запасу данной породы во всем массиве. В таксационной практике проводится дифференциация древесных запасов по породам, называемая учетом по составляющим, или чистым, породам. В тех участках, где чистая порода преобладает, надо исключать из общего запаса примеси и к полученному результату прибавлять запас этой же породы тех участков, где она встречается как примесь.
Таким образом, дифференциация запасов по составляющим, или чистым, породам сводится к следующему. Просматривая таксационное описание, отбирают все участки, в составе которых встречается данная порода. Общие запасы участков перемножают на коэффициенты состава насаждения, который берут в десятых долях единицы. Полученные произведения дают общий запас древесины данной древесной породы. Подобные расчеты производят для всех пород. В конечном итоге весь запас массива окажется расчлененным по отдельным породам. Если какая-нибудь порода встречается в составе насаждения единично или отмечена знаком плюс, запас этой породы в расчет не принимается.
Разделение запасов по чистым породам особенно необходимо в связи с тем, что для правильного планирования отпуска леса требуется уточненная сортиментация леса, основанная в первую очередь на учете отдельных древесных пород.
При расчленении общего запаса по чистым породам рекомендуется шире использовать данные перечислительной таксации, полученные при закладке пробных площадей, отводе лесосек в рубку и других видах работ. В этом случае можно учесть запасы древесных пород с долей участия в составе насаждения менее 0,1.
содержание .. 60 61 62 63 64 65 66 67 68 69 70 ..
zinref.ru
§ 52. ЗАПАС НАСАЖДЕНИЙ : ЛЕСНАЯ ТАКСАЦИЯ ИЗДАНИЕ 5-Е, ДОПОЛНЕННОЕ Часть 3 : Юридическая библиотека
Можно также определить запас древостоя по методу пробных площадей, применяемому при частичном перечете деревьев. Вычисленный по пробной площади запас насаждения умножают па отношение площади таксируемого участка к площади пробы и получают общий запас.
При таксации обширных лесных пространств частичный перечет деревьев с последующим использованием объемных и сор- тиментных таблиц часто бывает затруднительным. В этом случае применяют способы глазомерной таксации, позволяющие находить запас без перечета деревьев.
Умение определять запас насаждений без перечета деревьев требует большого навыка и опыта. У таксатора, заложившего много пробных площадей и устанавливавшего запас по моделям и массовым таблицам, запечатлеваются в памяти типичные насаждения, с которыми он и сравнивает таксируемые участки леса. Поэтому он может глазомерно определить запас, полноту и прочие таксационные признаки осматриваемых насаждений. Однако точность результатов при глазомерной таксации даже у самых опытных таксаторов колеблется в пределах ±10%.
При глазомерной таксации для определения запаса насаждения пользуются как подсобным материалом таблицами хода роста насаждений.
Зная среднюю высоту дерева и полноту насаждения, можно при помощи формул найти его запас.
Формулы для ориентировочного определения запаса базируются на основной формуле запаса насаждения:
M=Yj Ghf- (222)
Произведение суммы площадей сечений деревьев (в квадратных метрах) на видовое число 2G/ есть величина почти постоянная, для сосны и бука изменяющаяся в пределах от 14 до 18, а в среднем равная 16, для ели и пихты — от 16 до 22, в среднем же равная 18. Соответственно этому запас нормального насаждения М будет равен для сосны и бука 16 Н, для ели и пихты 18 Н. Включив в эти формулы дополнительный показатель, полноту насаждения Р, можно найти запас насаждений, имеющих разную полноту. Если произведение EGf заменить буквой О, получим формулу для определения запаса всех пород
М = OhP. (223)
Однако опытная проверка показала, что величина О в насаждениях разных бонитетов неодинакова: в высших бонитетах она больше указанных цифр. Поэтому в насаждениях высших бонитетов приведенная формула приуменьшает запас, а низших — преувеличивает. Лучший результат получается для насаждений средних бонитетов.
Таким образом, рассмотренные формулы дают весьма приближенные запасы таксируемых насаждений.
Проф. II. 13. Третьяков (1952) более детально изучил зависимость запасов древостоя от суммы площадей сечений, видовых чисел и высоты 2G/i/. Математически обработав числовые величины многих таблиц хода роста насаждений, он предложил для определения запаса насаждений следующие формулы:
для сосны М — 17,5 (h — 2) Р; (224)
для ели М = 23,3 (/1 — 6) Р; (225)
для березы Л1 — 17,5 (Л — 6) Р; (226)
для осины М =-. 22,5 (h — 7) Р; (227)
для дуба, клена, ильма М — 20 (h — 6) Р; (228)
для липы М — 30 (h — 8) Р. (229) Все эти формулы он обобщил и одну
М — О (h — а) Р. (230)
Постоянный поправочный коэффициент а, корректирующий высоту h, уменьшающуюся от высших бонитетов к низшим, более существенно влияет на величину запаса в насаждениях низших классов бонитета. Поэтому при пользовании формулами Третьякова устраняется ошибка при определении запасов, которую давала формула M = OhP.
Недостатком этих формул является их громоздкость и трудность вычислений. Например, для определения запаса еловых насаждений, имеющих высоту 27 м и полноту 0,7, надо из 27 вычесть 6, полученное число 21 умножить на 23,3 и произведение 490 умножить на 0,7. Всс эти действия произвести в уме почти невозможно, поэтому таксатор обычно не пользуется этими формулами.
На основе анализа обширных экспериментальных данных автору учебника удалось вывести довольно простые формулы, позволяющие определять запасы насаждений с достаточной точностью. При выводе этих формул главнейшие древесные породы были разделены на две группы. В первую из них вошли сосна, лиственница, береза, осина и ольха. Вторую группу древесных пород образуют ель, пихта, кедр, бук, дуб, ильм и ясень.
У древесных пород первой группы видовое число оказалось 1,20 „ 1,26 равным / = 0,40-| —, а во второй группе f = 0,42+-—— •
Соответственно этим уравнениям получены следующие две формулы, определяющие запасы насаждений двух указанных выше групп древесных пород:
УИ, = ^0,40+-^-^ h 2 g= (1,20 + 0,40Л) 2 g; (231)
Ми = (0,42 + А 2 g = (l,26+0,42h) 2 g ■ (232)
Числовой коэффициент при h обозначим через К, тогда нашим формулам можно придать следующий вид:
Л/ (Л К (233)
Выражение, заключенное в скобки (3K+Kh), является видовой высотой насаждения. У древесных пород первой группы, когда средняя высота насаждения равна 22 м, видовая высота (3K + Kh) оказывается равной (3×0,40 + 0,40×22) = 10 м. В этом случае определение запаса предельно упрощается. Запас насаждения, имеющего среднюю высоту 22 м, оказывается равным
(234)
Сумму площадей поперечных сечений Eg находим с помощью таксационного прицела (призмы). Увеличив найденный результат в 10 раз, получаем запас насаждения.
Исследования показали, что видовая высота имеет линейную связь со средней высотой насаждения, при этом на каждый метр средней высоты насаждения она увеличивается на 0,40 м. В связи с этим высоту таксируемого насаждения обозначим через hd, а разницу ее с высотой равной 22 м — через Ah = hd—22.
Соответственно этим условиям получаем следующую простую формулу, определяющую запас насаждений первой группы древесных пород:
М\ =— Ю y\g ± 0,4А/г \ g. (235)
Этой же формуле может быть придан следующий вид:
м,10 2g-1-0,4^^(^-22). (236)
В насаждениях, имеющих среднюю высоту, меньшую 22 м, второе слагаемое формулы обращается в минусовую величину. Прибавляя последнюю к запасу, указываемому первым слагаемым, получаем запас, приведенный в соответствие с уменьшенной средней высотой.
Применение этой формулы иллюстрируем примерами. Допустим, что высота таксируемого насаждения hd оказалась равной 25 м, а сумма площадей сечений Eg = 30 м2. В этом случае запас насаждения равняется
М, — 10-30 : 0,4-30(25 22) 336 м3.
Предположим, что средняя высота таксируемого насаждения равна 20 м, а сумма площадей сечений — 25 м2. В этом случае запас насаждения будет равен
Mi = 10-25 + 0,4.25(20— 22) = 230 м3.
У древесных пород, относящихся ко второй группе, видовая высота, близкая к 10 м, оказывается в том случае, когда наса
ждение имеет среднюю высоту, округленно равную 21 м. В этом случае запас будет близок к
м\\ = Ю5>
Эта вторая формула применяется так же, как первая. Разница заключается лишь в том, что базовой высотой, не требующей в расчетах соответствующей поправки, является средняя высота насаждений 21 м.
Для расчета запаса обеих групп древесных пород нашей формуле может быть придан следующий общий вид:
M = 0A^g{hd-hb) . (237)
В этой формуле hb означает базовую высоту насаждения, для первой группы пород равную 22 м, а для второй группы пород — 21 м. Все остальные величины известны из предыдущего изложения.
Рассмотренные примеры дают основание заключить, что определение запаса по предлагаемым формулам предельно просто, не требует громоздких вычислений и может быть выполнено при устном счете.
В целях дальнейшего упрощения решения задачи по определению запаса насаждения применительно к рассмотренным формулам автором учебника разработана специальная номограмма. При ее составлении исходим из следующих расчетов:
M = (Kh + 3K)Y,g ■ (238)
Прологарифмировав это уравнение и разделив пополам обе его половины, получим следующее логарифмическое уравнение:
0,5 lg Af = te<*» + 3*> + ‘gSg . (239)
Выражение 0,51gAl обозначим через U lg{Kh + 3K) — через а и lgSg через Ь.
Введение этих вспомогательных переменных наше уравнение предельно упрощает. Оно будет следующим:
2
Величины а и b принимаем за параллельные линии трапеции. В этом случае I определяет ее среднюю линию.
Применительно к свойствам параллельных сторон трапеции строим номограмму. Задаваясь различными значениями вспомогательных переменных, наносим их на параллельные стороны трапеции и на ее срединную линию. В конечном счете создаем систему логарифмических шкал. Поскольку главнейшие древесные породы мы разделили на две группы, то соответственно этому на параллельных линиях трапеции получили по две шкалы. Построенная таким путем номограмма дана на рис. 79.
Определение запаса на 1 га насаждения по полученной номограмме предельно просто.
|
Высота, п |
|
|
породы |
|
|
Сосна, |
Ель, |
|
листвен |
пиша, |
|
ница, |
кедр, |
|
береза, |
бук, |
|
осина, |
дуб, |
|
ольха |
ильм, |
|
|
ясень |
40 — 36 — 32 —
28 —
26 — 24 —
22 — 20- 18 — 16 —
14 — 12-
10-
-40 -36 -32
-28 -26 -24 -22
-20 -18
-16 -14 -12 -10
1200 _ 1000 — 900 — 800 — 700 — 600-
500- 400- 300-
200- 150-
100 — 90 80 70 60
50
UO
30
20 200
10
. 1200
: woo
-900
-800
-700
-SOO
-500
-400
-300 — 250
-WO -150
-1000 900 ■ 800 700 ■ 600
■ 500 ■400
■ 300
-100
Число деревьев на круговой пробе, равное сумме площадей. сечений, всех деревьев на 1га,и2
60.
40- 35- 30.
25-
Запас
по породщ м3
тщщ,
600-^ 500- 400- 300-
20
15′
-Г 10-
201
100-
60 50
40 + 30
-60
-40 -35 -30
-25 20
Коэффициенты состава
15
Jf
Щв
7
7} 77.
-10
У,
а<£
V/
Рис. 79. Номограмма для определения состава и запаса древостоя по высоте и сумме площадей поперечных сечений на 1 га
Допустим, что мы таксируем насаждение, в составе которого преобладает сосна. Средняя высота таксируемого насаждения оказалась равной 22 м, а сумма площадей сечений, найденная с помощью таксационного прицела, 25 м2. Поперек номограммы кладем линейку с таким расчетом, чтобы ее левый конец на шкале высот отсекал деление 22, а правый конец линейки — деление 25. В этом случае срединная часть линейки пересечет на срединной шкале деление 250. Оно указывает, что в таксируемом насаждении запас на 1 га равен 250 м3.
В нижнем правом углу номограмма имеет дополнительные шкалы, служащие для определения коэффициентов состава насаждения. Пользование ими иллюстрируется примером.
Допустим, что общий запас насаждения на 1 га равен 250 м3 и из этого запаса на долю основной породы падает 200 м3. Линейку накладываем на нижние шкалы с таким расчетом, чтобы ее край па центральной шкале внизу отсекал деление 250, а на правой шкале, имеющей вверху надпись «Запас по породам, м3»,— деление 200. При соблюдении этих условий на крайней правой шкале с надписью наверху «Коэффициенты состава» правый конец линейки отсечет заштрихованный участок шкалы, обозначенный цифрой 8. Эта цифра указывает на то, что в данном насаждении на долю основной природы приходится 0,8 от общего запаса.
Запасы насаждений по рассматриваемой номограмме можно определить с высокой точностью, поэтому она рекомендуется для широкого применения на практике при определении древесных запасов.
В общий древесный запас входят объемы не только крупных деревьев, представляющих с эксплуатационной точки зрения наибольшую производственную ценность, но и мелких деревьев, которые в рубку не идут. При определении запасов товарной древесины обычно; учитывают массу древесины в спелых и приспевающих насаждениях. Запас древесины в молодняках чаще всего товарной ценности не имеет.
Та часть запасов древесины, которая по своим размерам и качеству пригодна для выработки продукции для народного хозяйства, называется эксплуатационным запасом.
В процессе заготовки и последующей разделки срубленных деревьев неизбежны отходы в виде пней, вершин и частей ствола, пораженных гнилью, кроме того, для последующего восстановления леса на вырубках оставляют крупные деревья — семенники, а иногда и семенные куртины. На крутых склонах и вершинах гор часть леса недоступна для эксплуатации. Поэтому при расчетах и определении выхода готовой лесопродукции необходимо из эксплуатационного запаса вычитать объем,приходящийся на отходы, остающиеся семенники, семенные куртины.
Не включаются в эксплуатационный запас, особенно в лесах Севера и Сибири, насаждения, имеющие на 1 га менее 30 м3, а также те древесные породы, рубка которых запрещена ввиду их особой ценности (кедр, орех, бархатное дерево и др.). Оставшаяся после их вычета часть эксплуатационного запаса называется ликвидным запасом.
Для каждого таксационного участка, как мы уже говорили, устанавливается преобладающая порода. Суммируя по преобладающей породе запасы отдельных таксационных участков, получают данные для массива в целом. При подсчете запаса преобладающей древесной породы в него включают кубатуру примесей. Так, в общий запас насаждений с преобладанием сосны обязательно включают примесь ели, березы и других пород, а в запас насаждений с преобладанием ели — примесь сосны.
Поскольку эти примеси должны взаимно компенсироваться, казалось бы, общий запас насаждений с преобладанием определенной породы можно приравнять к запасу данной породы во всем массиве. Однако такой вывод был бы неверным, так как
в лесном массиве различные древесные породы могут занимать неодинаковые площади. Поэтому примеси отдельных пород могут взаимно компенсироваться лишь частично. Следует также иметь в виду, что биологические свойства пород, так же как условия местопроизрастания и возраст насаждений, не одинаковы.
В малоосвоенных лесах таежной зоны, состоящих из спелых и перестойных насаждений, в большей части массива обычно преобладают хвойные породы, а лиственные (береза, осина) встречаются в виде примесей. Поэтому запас таксационных участков с преобладанием лиственных пород будет относительно небольшим, в то время как суммарный учет примесей лиственных пород по всему массиву может дать сравнительно большую величину. В зоне смешанных лесов ясень, клен, граб и др. обычно встречаются как сопутствующие породы. Насаждений с ясно выраженным преобладанием этих пород здесь почти не бывает.
Из сказанного следует, что суммарный запас насаждений с преобладанием определенной древесной породы нельзя считать близким к запасу данной породы во всем массиве. В таксационной практике проводится дифференциация древесных запасов по породам, называемая учетом по составляющим, или чистым, породам. В тех участках, где чистая порода преобладает, надо исключать из общего запаса примеси и к полученному результату прибавлять запас этой же породы тех участков, где она встречается как примесь.
Таким образом, дифференциация запасов по составляющим, или чистым, породам сводится к следующему. Просматривая таксационное описание, отбирают все участки, в составе которых встречается данная порода. Общие запасы участков перемножают на коэффициенты состава насаждения, который берут в десятых долях единицы. Полученные произведения дают общий запас древесины данной древесной породы. Подобные расчеты производят для всех пород. В конечном итоге весь запас массива окажется расчлененным по отдельным породам. Если какая-нибудь порода встречается в составе насаждения единично или отмечена знаком плюс, запас этой породы в расчет не принимается.
Разделение запасов по чистым породам особенно необходимо в связи с тем, что для правильного планирования лесной промышленности требуется уточненная сортиментация леса, основанная в первую очередь па учете отдельных древесных пород.
При расчленении общего запаса по чистым породам рекомендуется шире использовать данные перечислительной таксации, полученные при закладке пробных площадей, отводе лесосек в рубку и других видах работ. В этом случае возможно учесть запасы древесных пород с долей участия в составе насаждения менее 0,1. Разделение запаса по чистым породам необходимо в массивах, имеющих ценные твердолиственные породы.
bookzie.com
Определение запаса древостоя методом модельных деревьев
Ступени толщины | Число стволов, шт. | Сумма площадей сечений, м2 | Показатели моделей | Запас ступени, м3 | ||
№ | g, м2 | V, м3 | ||||
12 16 20 24 28 32 36 40 | 3 31 71 96 54 38 29 7 | 0,034 0,623 2,229 4,339 3,326 3,055 2,952 0,880 | 3 7 10 14 24 31 34 37 | 0,0119 0,0209 0,0327 0,0475 0,0594 0,0819 0,1034 0,1281 | 0,081 0,179 0,311 0,502 0,667 0,946 1,248 1,561 | 0,23 5,34 21,20 45,86 37,35 35,29 35,63 10,72 |
Всего | 329 | 17,438 | 192 | |||
По средней высоте и среднему диаметру древостоя подбирают среднюю модель. Ее параметры также заносятся в бланк (табл. 20) и по ф. 55 вычисляется запас древостоя:
Таблица 20.
Определение запаса древостоя методом модельных деревьев
Показатели древостоя | Показатели моделей | Запас древостоя, м3 | ||||||
d, см | h, м | g, м2 | № | d, см | h, м | g, м2 | V, м3 | |
25,9 | 25,8 | 17,43 | 20 | 26,5 | 24,9 | 0,606 | 191,7 | |
7.3. Графический способ кривой и прямой объемов древесных стволов.
В древостое производится перечет стволов на пробной площади. Устанавливаются соотношения между диаметрами и высотами данного древостоя. Затем выбирают и срубают модельные деревьев по ступеням толщины.
На основании экспериментальных данных строят графики. По оси абсцисс откладываются ступени толщины, по оси ординат – объемы взятых моделей по ступеням толщины (рис. 4). Вершины ординат соединяют сглаживается плавной вогнутой кривой, характеризующей объемы стволов для всех ступеней толщины.
Общий запас вычисляется на основании объемов стволов по графику и числу стволов по перечету, используя формулу (ф. 53)
M = V1n1+ V2n2 + V3n3+ … + Vnnn,
где V1,V2, …, Vm – объемы стволов определенные по графику; n1,n2, …, nm– число деревьев по ступеням толщины.
V, м3
2,0
1,0
0,0
8 12 16 20 24 28 32 36 40 D, см
Рис. 4. Кривая объемов Шпейделя
Дополнительно строится вторая кривая объемов на основании установленных соотношений d и Н, при этом объемы стволов берутся из массовых таблиц.
Второй способ Р. Копецкого основан на линейной зависимости между объемами стволов и площадями сечения gm на высоте 1,3 м. В данном случае по оси абсцисс откладываются не диаметры стволов по ступеням толщины, а площади их сечений, по оси ординат – объемы моделей (рис. 5). В этом случае вершины ординат в основном располагаются по слаболоманой линии, которую легко сгладить в прямую. Определение запаса древостоя производится по формуле 53.
V, м3
2,0
1,0
0,0
0,0050 0,0113 0,0201 0,0314 0,0452 0,0616 0,0804 0,1018 0,1257 G, м2
Рис. .5. Прямая объемов Капецкого
При выполнении задания студенты на миллиметровой бумаге выстраивают соответствующие графики, снимают с них показания, заносят в таблицы бланков и высчитывают по ф. 52 запас древостоя.
studfiles.net
§ 52. ЗАПАС НАСАЖДЕНИЙ : ЛЕСНАЯ ТАКСАЦИЯ ИЗДАНИЕ 5-Е, ДОПОЛНЕННОЕ Часть 3 : Экономико-правовая библиотека
Можно также определить запас древостоя по методу пробных площадей, применяемому при частичном перечете деревьев. Вычисленный по пробной площади запас насаждения умножают па отношение площади таксируемого участка к площади пробы и получают общий запас.
При таксации обширных лесных пространств частичный перечет деревьев с последующим использованием объемных и сор- тиментных таблиц часто бывает затруднительным. В этом случае применяют способы глазомерной таксации, позволяющие находить запас без перечета деревьев.
Умение определять запас насаждений без перечета деревьев требует большого навыка и опыта. У таксатора, заложившего много пробных площадей и устанавливавшего запас по моделям и массовым таблицам, запечатлеваются в памяти типичные насаждения, с которыми он и сравнивает таксируемые участки леса. Поэтому он может глазомерно определить запас, полноту и прочие таксационные признаки осматриваемых насаждений. Однако точность результатов при глазомерной таксации даже у самых опытных таксаторов колеблется в пределах ±10%.
При глазомерной таксации для определения запаса насаждения пользуются как подсобным материалом таблицами хода роста насаждений.
Зная среднюю высоту дерева и полноту насаждения, можно при помощи формул найти его запас.
Формулы для ориентировочного определения запаса базируются на основной формуле запаса насаждения:
M=Yj Ghf- (222)
Произведение суммы площадей сечений деревьев (в квадратных метрах) на видовое число 2G/ есть величина почти постоянная, для сосны и бука изменяющаяся в пределах от 14 до 18, а в среднем равная 16, для ели и пихты — от 16 до 22, в среднем же равная 18. Соответственно этому запас нормального насаждения М будет равен для сосны и бука 16 Н, для ели и пихты 18 Н. Включив в эти формулы дополнительный показатель, полноту насаждения Р, можно найти запас насаждений, имеющих разную полноту. Если произведение EGf заменить буквой О, получим формулу для определения запаса всех пород
М = OhP. (223)
Однако опытная проверка показала, что величина О в насаждениях разных бонитетов неодинакова: в высших бонитетах она больше указанных цифр. Поэтому в насаждениях высших бонитетов приведенная формула приуменьшает запас, а низших — преувеличивает. Лучший результат получается для насаждений средних бонитетов.
Таким образом, рассмотренные формулы дают весьма приближенные запасы таксируемых насаждений.
Проф. II. 13. Третьяков (1952) более детально изучил зависимость запасов древостоя от суммы площадей сечений, видовых чисел и высоты 2G/i/. Математически обработав числовые величины многих таблиц хода роста насаждений, он предложил для определения запаса насаждений следующие формулы:
для сосны М — 17,5 (h — 2) Р; (224)
для ели М = 23,3 (/1 — 6) Р; (225)
для березы Л1 — 17,5 (Л — 6) Р; (226)
для осины М =-. 22,5 (h — 7) Р; (227)
для дуба, клена, ильма М — 20 (h — 6) Р; (228)
для липы М — 30 (h — 8) Р. (229) Все эти формулы он обобщил и одну
М — О (h — а) Р. (230)
Постоянный поправочный коэффициент а, корректирующий высоту h, уменьшающуюся от высших бонитетов к низшим, более существенно влияет на величину запаса в насаждениях низших классов бонитета. Поэтому при пользовании формулами Третьякова устраняется ошибка при определении запасов, которую давала формула M = OhP.
Недостатком этих формул является их громоздкость и трудность вычислений. Например, для определения запаса еловых насаждений, имеющих высоту 27 м и полноту 0,7, надо из 27 вычесть 6, полученное число 21 умножить на 23,3 и произведение 490 умножить на 0,7. Всс эти действия произвести в уме почти невозможно, поэтому таксатор обычно не пользуется этими формулами.
На основе анализа обширных экспериментальных данных автору учебника удалось вывести довольно простые формулы, позволяющие определять запасы насаждений с достаточной точностью. При выводе этих формул главнейшие древесные породы были разделены на две группы. В первую из них вошли сосна, лиственница, береза, осина и ольха. Вторую группу древесных пород образуют ель, пихта, кедр, бук, дуб, ильм и ясень.
У древесных пород первой группы видовое число оказалось 1,20 „ 1,26 равным / = 0,40-| —, а во второй группе f = 0,42+-—— •
Соответственно этим уравнениям получены следующие две формулы, определяющие запасы насаждений двух указанных выше групп древесных пород:
УИ, = ^0,40+-^-^ h 2 g= (1,20 + 0,40Л) 2 g; (231)
Ми = (0,42 + А 2 g = (l,26+0,42h) 2 g ■ (232)
Числовой коэффициент при h обозначим через К, тогда нашим формулам можно придать следующий вид:
Л/ (Л К (233)
Выражение, заключенное в скобки (3K+Kh), является видовой высотой насаждения. У древесных пород первой группы, когда средняя высота насаждения равна 22 м, видовая высота (3K + Kh) оказывается равной (3×0,40 + 0,40×22) = 10 м. В этом случае определение запаса предельно упрощается. Запас насаждения, имеющего среднюю высоту 22 м, оказывается равным
(234)
Сумму площадей поперечных сечений Eg находим с помощью таксационного прицела (призмы). Увеличив найденный результат в 10 раз, получаем запас насаждения.
Исследования показали, что видовая высота имеет линейную связь со средней высотой насаждения, при этом на каждый метр средней высоты насаждения она увеличивается на 0,40 м. В связи с этим высоту таксируемого насаждения обозначим через hd, а разницу ее с высотой равной 22 м — через Ah = hd—22.
Соответственно этим условиям получаем следующую простую формулу, определяющую запас насаждений первой группы древесных пород:
М\ =— Ю y\g ± 0,4А/г \ g. (235)
Этой же формуле может быть придан следующий вид:
м,10 2g-1-0,4^^(^-22). (236)
В насаждениях, имеющих среднюю высоту, меньшую 22 м, второе слагаемое формулы обращается в минусовую величину. Прибавляя последнюю к запасу, указываемому первым слагаемым, получаем запас, приведенный в соответствие с уменьшенной средней высотой.
Применение этой формулы иллюстрируем примерами. Допустим, что высота таксируемого насаждения hd оказалась равной 25 м, а сумма площадей сечений Eg = 30 м2. В этом случае запас насаждения равняется
М, — 10-30 : 0,4-30(25 22) 336 м3.
Предположим, что средняя высота таксируемого насаждения равна 20 м, а сумма площадей сечений — 25 м2. В этом случае запас насаждения будет равен
Mi = 10-25 + 0,4.25(20— 22) = 230 м3.
У древесных пород, относящихся ко второй группе, видовая высота, близкая к 10 м, оказывается в том случае, когда наса
ждение имеет среднюю высоту, округленно равную 21 м. В этом случае запас будет близок к
м\\ = Ю5>
Эта вторая формула применяется так же, как первая. Разница заключается лишь в том, что базовой высотой, не требующей в расчетах соответствующей поправки, является средняя высота насаждений 21 м.
Для расчета запаса обеих групп древесных пород нашей формуле может быть придан следующий общий вид:
M = 0A^g{hd-hb) . (237)
В этой формуле hb означает базовую высоту насаждения, для первой группы пород равную 22 м, а для второй группы пород — 21 м. Все остальные величины известны из предыдущего изложения.
Рассмотренные примеры дают основание заключить, что определение запаса по предлагаемым формулам предельно просто, не требует громоздких вычислений и может быть выполнено при устном счете.
В целях дальнейшего упрощения решения задачи по определению запаса насаждения применительно к рассмотренным формулам автором учебника разработана специальная номограмма. При ее составлении исходим из следующих расчетов:
M = (Kh + 3K)Y,g ■ (238)
Прологарифмировав это уравнение и разделив пополам обе его половины, получим следующее логарифмическое уравнение:
0,5 lg Af = te<*» + 3*> + ‘gSg . (239)
Выражение 0,51gAl обозначим через U lg{Kh + 3K) — через а и lgSg через Ь.
Введение этих вспомогательных переменных наше уравнение предельно упрощает. Оно будет следующим:
2
Величины а и b принимаем за параллельные линии трапеции. В этом случае I определяет ее среднюю линию.
Применительно к свойствам параллельных сторон трапеции строим номограмму. Задаваясь различными значениями вспомогательных переменных, наносим их на параллельные стороны трапеции и на ее срединную линию. В конечном счете создаем систему логарифмических шкал. Поскольку главнейшие древесные породы мы разделили на две группы, то соответственно этому на параллельных линиях трапеции получили по две шкалы. Построенная таким путем номограмма дана на рис. 79.
Определение запаса на 1 га насаждения по полученной номограмме предельно просто.
|
Высота, п |
|
|
породы |
|
|
Сосна, |
Ель, |
|
листвен |
пиша, |
|
ница, |
кедр, |
|
береза, |
бук, |
|
осина, |
дуб, |
|
ольха |
ильм, |
|
|
ясень |
40 — 36 — 32 —
28 —
26 — 24 —
22 — 20- 18 — 16 —
14 — 12-
10-
-40 -36 -32
-28 -26 -24 -22
-20 -18
-16 -14 -12 -10
1200 _ 1000 — 900 — 800 — 700 — 600-
500- 400- 300-
200- 150-
100 — 90 80 70 60
50
UO
30
20 200
10
. 1200
: woo
-900
-800
-700
-SOO
-500
-400
-300 — 250
-WO -150
-1000 900 ■ 800 700 ■ 600
■ 500 ■400
■ 300
-100
Число деревьев на круговой пробе, равное сумме площадей. сечений, всех деревьев на 1га,и2
60.
40- 35- 30.
25-
Запас
по породщ м3
тщщ,
600-^ 500- 400- 300-
20
15′
-Г 10-
201
100-
60 50
40 + 30
-60
-40 -35 -30
-25 20
Коэффициенты состава
15
Jf
Щв
7
7} 77.
-10
У,
а<£
V/
Рис. 79. Номограмма для определения состава и запаса древостоя по высоте и сумме площадей поперечных сечений на 1 га
Допустим, что мы таксируем насаждение, в составе которого преобладает сосна. Средняя высота таксируемого насаждения оказалась равной 22 м, а сумма площадей сечений, найденная с помощью таксационного прицела, 25 м2. Поперек номограммы кладем линейку с таким расчетом, чтобы ее левый конец на шкале высот отсекал деление 22, а правый конец линейки — деление 25. В этом случае срединная часть линейки пересечет на срединной шкале деление 250. Оно указывает, что в таксируемом насаждении запас на 1 га равен 250 м3.
В нижнем правом углу номограмма имеет дополнительные шкалы, служащие для определения коэффициентов состава насаждения. Пользование ими иллюстрируется примером.
Допустим, что общий запас насаждения на 1 га равен 250 м3 и из этого запаса на долю основной породы падает 200 м3. Линейку накладываем на нижние шкалы с таким расчетом, чтобы ее край па центральной шкале внизу отсекал деление 250, а на правой шкале, имеющей вверху надпись «Запас по породам, м3»,— деление 200. При соблюдении этих условий на крайней правой шкале с надписью наверху «Коэффициенты состава» правый конец линейки отсечет заштрихованный участок шкалы, обозначенный цифрой 8. Эта цифра указывает на то, что в данном насаждении на долю основной природы приходится 0,8 от общего запаса.
Запасы насаждений по рассматриваемой номограмме можно определить с высокой точностью, поэтому она рекомендуется для широкого применения на практике при определении древесных запасов.
В общий древесный запас входят объемы не только крупных деревьев, представляющих с эксплуатационной точки зрения наибольшую производственную ценность, но и мелких деревьев, которые в рубку не идут. При определении запасов товарной древесины обычно; учитывают массу древесины в спелых и приспевающих насаждениях. Запас древесины в молодняках чаще всего товарной ценности не имеет.
Та часть запасов древесины, которая по своим размерам и качеству пригодна для выработки продукции для народного хозяйства, называется эксплуатационным запасом.
В процессе заготовки и последующей разделки срубленных деревьев неизбежны отходы в виде пней, вершин и частей ствола, пораженных гнилью, кроме того, для последующего восстановления леса на вырубках оставляют крупные деревья — семенники, а иногда и семенные куртины. На крутых склонах и вершинах гор часть леса недоступна для эксплуатации. Поэтому при расчетах и определении выхода готовой лесопродукции необходимо из эксплуатационного запаса вычитать объем,приходящийся на отходы, остающиеся семенники, семенные куртины.
Не включаются в эксплуатационный запас, особенно в лесах Севера и Сибири, насаждения, имеющие на 1 га менее 30 м3, а также те древесные породы, рубка которых запрещена ввиду их особой ценности (кедр, орех, бархатное дерево и др.). Оставшаяся после их вычета часть эксплуатационного запаса называется ликвидным запасом.
Для каждого таксационного участка, как мы уже говорили, устанавливается преобладающая порода. Суммируя по преобладающей породе запасы отдельных таксационных участков, получают данные для массива в целом. При подсчете запаса преобладающей древесной породы в него включают кубатуру примесей. Так, в общий запас насаждений с преобладанием сосны обязательно включают примесь ели, березы и других пород, а в запас насаждений с преобладанием ели — примесь сосны.
Поскольку эти примеси должны взаимно компенсироваться, казалось бы, общий запас насаждений с преобладанием определенной породы можно приравнять к запасу данной породы во всем массиве. Однако такой вывод был бы неверным, так как
в лесном массиве различные древесные породы могут занимать неодинаковые площади. Поэтому примеси отдельных пород могут взаимно компенсироваться лишь частично. Следует также иметь в виду, что биологические свойства пород, так же как условия местопроизрастания и возраст насаждений, не одинаковы.
В малоосвоенных лесах таежной зоны, состоящих из спелых и перестойных насаждений, в большей части массива обычно преобладают хвойные породы, а лиственные (береза, осина) встречаются в виде примесей. Поэтому запас таксационных участков с преобладанием лиственных пород будет относительно небольшим, в то время как суммарный учет примесей лиственных пород по всему массиву может дать сравнительно большую величину. В зоне смешанных лесов ясень, клен, граб и др. обычно встречаются как сопутствующие породы. Насаждений с ясно выраженным преобладанием этих пород здесь почти не бывает.
Из сказанного следует, что суммарный запас насаждений с преобладанием определенной древесной породы нельзя считать близким к запасу данной породы во всем массиве. В таксационной практике проводится дифференциация древесных запасов по породам, называемая учетом по составляющим, или чистым, породам. В тех участках, где чистая порода преобладает, надо исключать из общего запаса примеси и к полученному результату прибавлять запас этой же породы тех участков, где она встречается как примесь.
Таким образом, дифференциация запасов по составляющим, или чистым, породам сводится к следующему. Просматривая таксационное описание, отбирают все участки, в составе которых встречается данная порода. Общие запасы участков перемножают на коэффициенты состава насаждения, который берут в десятых долях единицы. Полученные произведения дают общий запас древесины данной древесной породы. Подобные расчеты производят для всех пород. В конечном итоге весь запас массива окажется расчлененным по отдельным породам. Если какая-нибудь порода встречается в составе насаждения единично или отмечена знаком плюс, запас этой породы в расчет не принимается.
Разделение запасов по чистым породам особенно необходимо в связи с тем, что для правильного планирования лесной промышленности требуется уточненная сортиментация леса, основанная в первую очередь па учете отдельных древесных пород.
При расчленении общего запаса по чистым породам рекомендуется шире использовать данные перечислительной таксации, полученные при закладке пробных площадей, отводе лесосек в рубку и других видах работ. В этом случае возможно учесть запасы древесных пород с долей участия в составе насаждения менее 0,1. Разделение запаса по чистым породам необходимо в массивах, имеющих ценные твердолиственные породы.
www.vuzllib.su
