Тепло и электропроводность металлов: От чего зависит тепло и электропроводность металлов

Вопрос 1 Сравнение механизма электропроводности металлов с механизмов проводимости в полупроводниках

Теплопроводностью называется процесс переноса тепла от более нагретых частей тела к менее нагретым, приводящий к выравниванию температуры тела. В твердых телах, в отличие от жидкостей и газов, невозможна конвекция (передача тепла потоками нагретого вещества), поэтому перенос тепла осуществляется только за счет колебаний кристаллической решетки или с точки зрения квантовой теории за счет движения фононов. Если при данной температуре T один из узлов колеблется с амплитудой u, большей среднего значения  , то он, будучи связан с соседями силой межатомного взаимодействия, будет действовать на них, вызывая рост амплитуды колебаний соседних частиц. Таким образом, энергия передается от одного узла решетки к другому. Если концы твердого тела (например, стержня) поддерживаются при разных температурах, то в образце возникает непрерывный поток тепла. Каждый узел колеблется с меньшей амплитудой, чем соседний с ним со стороны более нагретого конца, и с большей амплитудой, чем соседний с ним со стороны менее нагретого конца.

Количественно тепловой поток  через поперечное сечение стержня   за время   пропорционален градиенту температуры   (закон Фурье):

,

(6.53)

где   коэффициент теплопроводности, который численно равен количеству тепла, прошедшего через единицу площади за единицу времени при градиенте температуры, равном единице (площадка   перпендикулярна оси x). В системе СИ размерность коэффициента теплопроводности составляет Вт/(мК), но часто используют размерности Вт/(смК) и кал/(смсК). Знак минус в формуле (6.63) показывает, что распространение тепла идет в сторону выравнивания градиента температуры (от более нагретой части тела к менее нагретой).

При низких температурах следует учитывать квантовый характер тепловых волн. Если  , то при теплообмене возбуждаются любые колебания в кристалле, все квантовые переходы возможны, и поэтому квантовый характер явления теплообмена не заметен. При низких температурах, когда  , в кристалле возбуждены лишь колебания с малыми частотами, и большие энергетические ступеньки не могут быть преодолены возникающими тепловыми «толчками». Рассмотрим процесс передачи тепла на основе представлений о фононах.

Из теории Дебая следует, что возбужденное состояние решетки можно представить как идеальный газ фононов, свободно движущийся в объеме кристалла. Фононный газ в определенном интервале температур ведет себя подобно идеальному газу, а поскольку фононы являются основными переносчиками тепла в твердом теле (это утверждение справедливо только для диэлектриков), то коэффициент теплопроводности твердого тела можно выразить такой же зависимостью, как коэффициент теплопроводности идеального газа

,

(6. 54)

где   − теплоемкость единицы объема фононного газа,   − средняя длина свободного пробега фонона,   − скорость распространения звука в данном теле.

Вычисление средней длины свободного пробега фонона представляет собой сложную задачу, поскольку она зависит от того, на чем происходит рассеяние фононов: на других фононах, на дефектах структуры или на внешних гранях образца. Однако теоретический анализ приводит к тому, что при достаточно высоких температурах средняя длина свободного пробега фонона обратно пропорциональна абсолютной температуре. Поэтому коэффициент теплопроводности твердых тел при температурах выше характеристической ( ) обратно пропорционален абсолютной температуре.

В достаточно чистых и бездефектных кристаллах при температуре, близкой к абсолютному нулю, возникает зависимость средней длины свободного пробега фононов от размеров образца. Это объясняется тем, что при низких температурах концентрация фононов мала, а следовательно, мала вероятность рассеяния фононов на других фононах. Пример зависимости коэффициента теплопроводности от температуры при различных сечениях образца монокристалла LiF показан на рис. 6.10 [98]. Видно, что различие в теплопроводности для образцов разного сечения проявляется только в области низких температур.

 

Рис. 6.10. Решеточная (фононная) теплопроводность как функция от температуры для монокристалла LiF при его различных сечениях: а  1,33  0,91 мм; б  7,55  6,97 мм

 

Полагая среднюю длину свободного пробега фононов приблизительно равной линейным размерам кристалла ( , где L − линейный размер кристалла), можно уравнение (6.54) переписать в виде

.

(6.55)

В правой части уравнения (6.55) от температуры зависит только теплоемкость единицы объема фононного газа . При температурах, близких к абсолютному нулю, теплоемкость пропорциональна   (закон   Дебая), поэтому и коэффициент теплопроводности 

 пропорционален кубу абсолютной температуры. Такой вывод подтверждается экспериментальными данными.

Анизотропия сил связи в кристаллах приводит к анизотропии коэффициента теплопроводности. Это можно проиллюстрировать на примере монокристалла кварца (рис. 6.11). В табл. 6.5 [52] представлены данные о коэффициенте теплопроводности по направлению, параллельному оси с, и по перпендикулярному к этой оси направлению.

 

 

Коэффициент теплопроводности вдоль гексагональной оси с кварца приблизительно вдвое выше соответствующих значений в направлениях перпендикулярных оси с, т.

е. в направленииях, лежащих в базисной плоскости кристалла. С понижением температуры коэффициент теплопроводности возрастает, как и предсказывает квантовая теория.

Все вышесказанное относится к решеточной (фононной) части теплоемкости твердого тела, свойственной неметаллическим кристаллам. В металлах в переносе тепла, кроме атомов кристаллической решетки, участвуют еще и свободные электроны, которые одновременно являются и носителями электрического заряда, обеспечивая высокую электропроводность металлов. Более того, в чистых металлах основными носителями тепла являются именно свободные электроны, а не фононы. При достаточно высоких температурах металлов решеточная составляющая теплопроводности составляет всего 1−2 % от электронной теплопроводности. Этим объясняется высокая теплопроводность чистых металлов по сравнению с диэлектриками. Например, у алюминия при комнатной температуре коэффициент теплопроводности  = 2,26 10

6 Вт/(смК), что приблизительно на два порядка больше, чем у кварца (см. табл. 6.5). Однако при очень низких температурах в металлах электронная часть теплопроводности меньше, чем решеточная. Это объясняется эффектами электрон-фононного рассеяния.

На рис. 6.12 приведен вид зависимости теплопроводности от температуры для диэлектриков и металлов.

 

Рис. 6.12. Сравнительные температурные зависимости коэффициента теплопроводности : а  для диэлектриков; б  для металлов [52]

 

В диэлектриках, практически не имеющих свободных электронов, перенос тепла осуществляется только фононами. Выше было сказано, что средняя длина свободного пробега   зависит от процессов рассеяния фононов на различных объектах. Все это приводит к тому, что температурная зависимость коэффициента теплопроводности 

 для диэлектриков имеет вид кривой с максимумом (рис. 6.12, а). Левая восходящая ветвь зависимости обусловлена увеличением числа фононов с ростом температуры, а правая нисходящая связана с ослабляющими фонон-фононным и другими видами рассеяния. Вид зависимости (T) для металлов (рис. 6.12, б) качественно похож на кривую для диэлектриков. Это связано с преобладанием при очень низких температурах фононного механизма теплопередачи. Однако с ростом температуры вклад фононной составляющей в этот процесс становится пренебрежимо мал и теплопередача осуществляется в основном свободными электронами. При относительно высоких температурах в металлах коэффициент теплопроводности 

 практически перестает изменяться с увеличением Т.

Билет 12.

Зависимость электропроводности металлов от температуры. Зависимость теплопроводности диэлектриков от температуры

Другие предметы \ Физические основы микроэлектроники

Страницы работы

3 страницы (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

29. Зависимость электропроводности металлов от температуры.

Неупорядоченные сплавы металлов не имеют четкого че­редования ионов различных видов, образующих сплав. Бла­годаря этому, средняя длина свободного пробега электрона очень невелика, так как он рассеивается на часто встречаю­щихся нарушениях дальнего порядка кристаллической решет­ки сплава. В этом смысле можно говорить об аналогии про­цессов рассеяния электронов в неупорядоченных сплавах и фононов в аморфных телах. На рис. 18.1,

а показана зависи­мость от температуры параметров, определяющих тепло- и электропроводность металла.Теплопроводность таких материалов невелика и монотон­но растет с температурой вплоть до значений , а элек­тропроводность остается практически постоянной в широком интервале температур. Сплавы широко используются как ма­териалы с весьма малым ТКС (температурный коэффициент сопротивления). Стабильность сопротивления объясняется тем, что основным процессом рассеяния является рассеяние на дефектах, параметры которого практически не зависят от температуры.

б)  Моно- и поликристаллические металлы

На рис. 18.1,6 показана температурная зависимость ос­новных параметров, определяющих тепло- и электропроводность металлов. Основные механизмы рассеяния, участвующие в формировании сопротивления переносу тепла и заряда,— это электрон-фононное рассеяние и рассеяние электронов на дефектах. Электрон-фононное рассеяние,. то есть рассеяние электронов на тепловых флюктуациях кристаллической решетки, играет решающую роль при достаточно высоких тем­пературах. Эта область значений Т соответствует области I (рис. 18.1,6). В низкотемпературной области решающую роль играет рассеяние на дефектах. Заметим, что теплопроводность металла в низкотемпературной области пропорциональна Т, а не , как в случае диэлектриков.

Электропроводность металла монотонно растет с уменьшением температуры, достигая в некоторых случаях (чистые ме­таллы, монокристаллы) огромных значений. Теплопровод­ность металла имеет максимум при  и также может иметь большую величину.
30. Зависимость теплопроводности диэлектриков от температуры.

В   аморфных  телах  длина   свободного  пробега   фононов очень мала и имеет величину порядка 10—15 Ангстрем. Это связано с сильным рассеянием волн в решетке вещества на неоднородностях структуры самой решетки аморфного тела. Рассеяние на неоднородностях структуры оказывается преобладающим в широком интервале температур от единиц градусов Кельвина до температуры размягчения аморфного тела. При очень низких температурах в спектре тепловых ко­лебаний исчезают высокочастотные фононы; низкочастотные длинноволновые фононы не испытывают сильного рассеяния на неоднородностях, размер которых меньше длины волны, и поэтому при очень низких температурах среднее время сво­бодного пробега несколько возрастает. В соответствии с кине­тической формулой  зависимость коэффициента тепло­проводности от температуры определяется в основном тем­пературным ходом теплоемкости. На рис. 17.1, а показан тем­пературный ход , Сvи х для аморфных диэлектриков.

Теплопроводность диэлектрических монокристаллов не мо­жет быть рассмотрена только с позиций рассеяния фононов на дефектах кристаллической решетки. В этом случае ре­шающую роль играют процессы взаимодействия фононов между собой. Говоря о вкладе фонон-фононного взаимодейст­вия в процессах теплопереноса, нужно четко различать роль нормальных процессов (N-процессов) и процессов переброса (U-процессов).

При N-процессах фонон, возникший в результате акта взаимодействия, сохраняет квазиимпульс двух фононов, его породивших: . То же происходит и при N-процессах распада одного фонона на два. Таким образом, при N -про­цессах происходит перераспределение энергии между фононами, но сохраняется их квазиимпульс, т. е. сохраняется на­правленность движения и сохраняется общая сумма энергии, переносимой в данном направлении. Перераспределение энергии между фононами не влияет на перенос тепла, так как тепловая энергия не связана с фононами определенной частоты. Таким образом, N-процессы не создают сопротивления тепловому потоку. Они только выравнивают распределение энергии между фононами разной частоты, если такое распределение может быть нару­шено другими взаимодействиями.

Иначе обстоит дело с U-процессами, при которых в ре­зультате взаимодействия двух фононов рождается третий, на­правление распространения которого может оказаться проти­воположным направлению распространения исходных фоно­нов. Другими словами, в результате U-процессов могут воз­никать элементарные тепловые потоки, направленные в об­ратную сторону по отношению к основному потоку. В силу этого U-процессы создают тепловое сопротивление, которое при не очень низкой температуре может оказаться решающим.

При достаточно большой температуре средняя длина сво­бодного пробега фононов, определяемая U-процессами, обрат­но пропорциональна температуре, При уменьшении темпера­туры величины  и растут по закону   .

U-процессы возникают тогда, когда суммарный волновой вектор  выходит за пределы зоны Бриллюэна.

При  начинает сказываться уменьшение возбуждения высококачественных фононов, для которых  Бла­годаря этому начинает резко падать число фононов, способ­ных участвовать в процессах переброса. Поэтому  и начи­нают   расти   с  уменьшением   Т   гораздо   быстрее,   чем  .С уменьшением температуры средняя длина свободного про­бега растет вплоть до тех значений, при которых заметно сказывается рассеяние на дефектах или границах образца. На рис. 17.1,6 показан ход зависимостей , Сvи х от темпе­ратуры. Температурную зависимость коэффициента теплопро­водности х можно разделить на три участка: I – высокотемпературная область, , решающую роль в об­разовании теплового сопротивления играют U-процессы. II- область максимума теплопроводности, эта область обычно ле­жит при Т . III — низкотемпературная область, в этой области тепловое сопротивление определяется рассеянием на дефектах, , что задается температурным ходом емкости.

Похожие материалы

Информация о работе

Скачать файл

Выбери свой ВУЗ

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 267
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 603
• БГУ 155
• БГУИР 391
• БелГУТ 4908
• БГЭУ 963
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 120
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1966
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 299
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 408
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 498
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 131
• ИжГТУ 145
• КемГППК 171
• КемГУ 508
• КГМТУ 270
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2910
• КрасГАУ 345
• КрасГМУ 629
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 138
• КубГУ 109
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 369
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 331
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 637
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 455
• НИУ МЭИ 640
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 213
• НУК им. Макарова 543
• НВ 1001
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1993
• НГУЭУ 499
• НИИ 201
• ОмГТУ 302
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 120
• РАНХиГС 190
• РОАТ МИИТ 608
• РТА 245
• РГГМУ 117
• РГПУ им. Герцена 123
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 123
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 131
• СПбГАСУ 315
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 146
• СПбГПУ 1599
• СПбГТИ (ТУ) 293
• СПбГТУРП 236
• СПбГУ 578
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 194
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 379
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1654
• СибГТУ 946
• СГУПС 1473
• СибГУТИ 2083
• СибУПК 377
• СФУ 2424
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 325
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 309

Полный список ВУЗов

Физическое объяснение теплопроводности металлов

Обычно известно, что металлы являются высокоэффективными теплопроводниками.

В этой статье будут рассмотрены механизмы теплопередачи, что делает металлы идеальными проводниками тепла, а также использование обычных металлов и сплавов.

Важность теплопроводности в повседневной жизни

Изображение 1. A

Изображение 1. B

Изображение 1. A и B показывают наглядные иллюстрации людей на кухне, использующих кухонные принадлежности.

Кулинария является частью повседневной жизни большинства людей. Следовательно, кухонные приборы разработаны с целью обеспечения максимальной безопасности и эффективности. Это требует понимания теплофизики. Есть причина, по которой нагревательный элемент тостера обычно изготавливается из нихромовой проволоки, ложки для смешивания, как правило, деревянные, а материал, из которого изготовлены прихватки, и никогда не включает в себя соединение металла.

Определение температуры и теплопроводности

Необходимо вспомнить определение температуры , чтобы понять теплопроводность математически.

Рабочее определение T:

Рабочее определение температуры – это значение, измеренное термометром, который просто измеряет расширение объема Ртути.

Изображение 2. Иллюстрация двух термометров в градусах Цельсия и Фаренгейта

Физическое определение T:

В теплофизике температура и теплопроводность понимаются через изучение движения молекул.

Шредер, автор « Введение в теплофизику », математически описывает температуру как:

\[ \frac{1}{T} = \Bigg( \frac{dS}{dU} \Bigg) \scriptscriptstyle N ,V \]

где:
S=энтропия,
U=энергия,
N=количество частиц,
V=объем системы (Schroeder, 2007).

Следовательно, температура системы зависит от энтропии и энергии , когда количество частиц и объем системы остаются постоянными.

Шредер формулирует словами: «Температура есть мера склонности объекта самопроизвольно отдавать энергию своему окружению. Когда два объекта находятся в тепловом контакте, тот, который склонен спонтанно терять энергию, имеет более высокую температуру» (Schroeder, 2007). Это связано с тем, что два контактирующих объекта будут пытаться достичь теплового равновесия ; становятся одной температуры.

Для визуализации температуры и теплопроводности на микроскопическом уровне Рис. 1 A и B показаны ниже. Представьте, что неизвестные объекты А и В находятся в физическом контакте друг с другом. Объект A имеет более высокую температуру, чем объект B. Что произойдет с температурой с течением времени?

Рисунок 1. A

Рисунок 1.B

На рисунке 1.A показаны два неизвестных объекта, находящихся в физическом контакте друг с другом, а на рисунке 1. B показаны молекулы объектов.

At _0, T _A > T _B

At _1, T _A > T _B

3 90.

.

At t _n, T _A = T _B

At t _0, Ø _A > Ø _B

At t _1, ŝ _A > ŝ _B

.

.

At t _n, ŝ _A > ŝ _B

Учитывая, что t _n : момент времени, T _A : температура объекта 3 B 9007 , ŝ _A : средняя скорость частицы A, ŝ _B : средняя скорость частицы B.

В t ₀ атомы объекта A движутся с большей скоростью, а атомы объекта B движутся с меньшей скоростью (T _А > Т _В ). Со временем объект A отдает энергию, а объект B получает энергию, пока они не достигнут одинаковой температуры (T _A = T _B ) и не достигнут теплового равновесия. Это теплопроводность описанная на молекулярном уровне. Ближайшие атомы объекта A сталкиваются с атомами объекта B. Атомы объекта B, которые первоначально взаимодействовали с атомами объекта A, сталкиваются с другими атомами объекта B, пока энергия не будет передана через все атомы объекта B.

Шредер определяет теплопроводность как «перенос тепла посредством молекулярного контакта: быстро движущиеся молекулы сталкиваются с медленно движущимися, отдавая при этом часть своей энергии» (Schroeder, 2007).

Способы теплопередачи для металлов

Важно напомнить три режима теплопередачи; конвекция для газов/жидкостей, излучение для объектов, разделенных пустым пространством и проводимость для объектов, находящихся в непосредственном контакте.

Теплопроводность также подразделяется на три категории: молекулярные столкновения для газовых/жидких форм, колебания решетки для твердых тел и электроны проводимости для металлов, как показано на рисунке 2 ниже.

Рис. 2. Способы теплообмена.

Теплопроводность металлов будет включать в себя столкновения молекул + электронов проводимости для металлов в газообразном состоянии и колебания решетки + электроны проводимости для металлов в твердом состоянии. Электроны проводимости, по сути, делают металл невероятным проводником . Прежде чем объяснить, что такое электрон проводимости, необходимо вспомнить определение металла.

Определение металлов

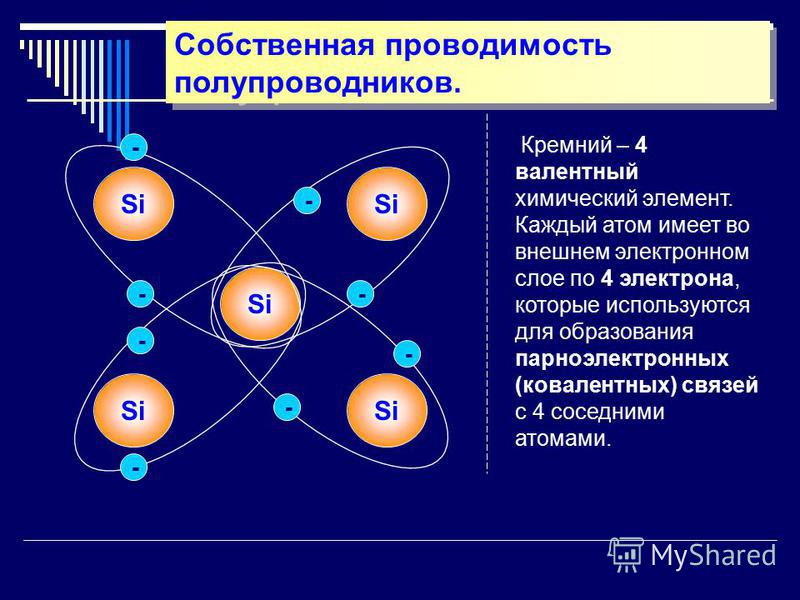
Все элементы можно найти в периодической таблице, включая металлы, неметаллы и металлоиды. Металлы определяются как «элементы, которые образуют положительные ионы, теряя электроны во время химических реакций» (Blaber, 2015).

Рисунок 3. Периодическая таблица, показывающая все элементы, разделенные на металлы, неметаллы и металлоиды.

Таблица 1. Список типичных физических свойств металлов.

Физические свойства большинства металлов
Твердый при комнатной температуре
Жесткий
Высокая плотность
Высокая температура плавления
Высокая точка кипения
Податливый
Ковкий
Блестящий

Что делает металлы хорошими теплопроводниками?

Что делает металл хорошим проводником тепла, так это свободно движущиеся электроны проводимости .

Рис. 4. Нагретый металлический блок, демонстрирующий атомы и свободно текущие электроны.

Атомы металлов теряют валентные электроны при химической реакции с атомами неметаллов, т.е. образуя оксиды и соли. Таким образом, ионы металлов являются катионами в водном растворе. Что делает металлы и металлические сплавы хорошими проводниками, так это особое металлическое соединение. В металлических твердых телах связанные атомы разделяют свои валентные электроны, образуя море свободно движущихся электронов проводимости, которые несут как тепло, так и электрический заряд. Таким образом, в отличие от, например, электронов в ковалентных связях, валентные электроны в металле могут свободно течь через металлические решетки, эффективно перенося тепло, не привязываясь к отдельному атомному ядру.

Математическое моделирование значения теплопроводности (k)

Теплопроводность (k) измеряет способность объекта проводить тепло (Q).

Высокое значение k: высокая теплопроводность

Рис. 4. Лист материала с уравнением теплопроводности.

Дано:

k = теплопроводность (Вт/м•K),

ΔQ = передача энергии (Джоули/сек),

Δt = изменение во времени (секунды),

ΔT = температурный градиент (K),

A = площадь теплопроводности (м ² ),

Δx = толщина материала.

Таблица 2. Список типичных физических свойств металлов.

Металлы	Теплопроводность при комнатной температуре (Вт/м•К)
Алюминий	226
Углеродистая сталь	71
Магний	151
Латунь (желтая)	117
Бронза (алюминий)	71
Медь	397
Железо	72
Нержавеющая сталь (446)	23
Вольфрам	197
Свинец	34
Никель	88
Сталь углеродистая 1020 (0,2 – 0,6 c)	71
Цинк	112
Титан	21
Олово	62

Примечание.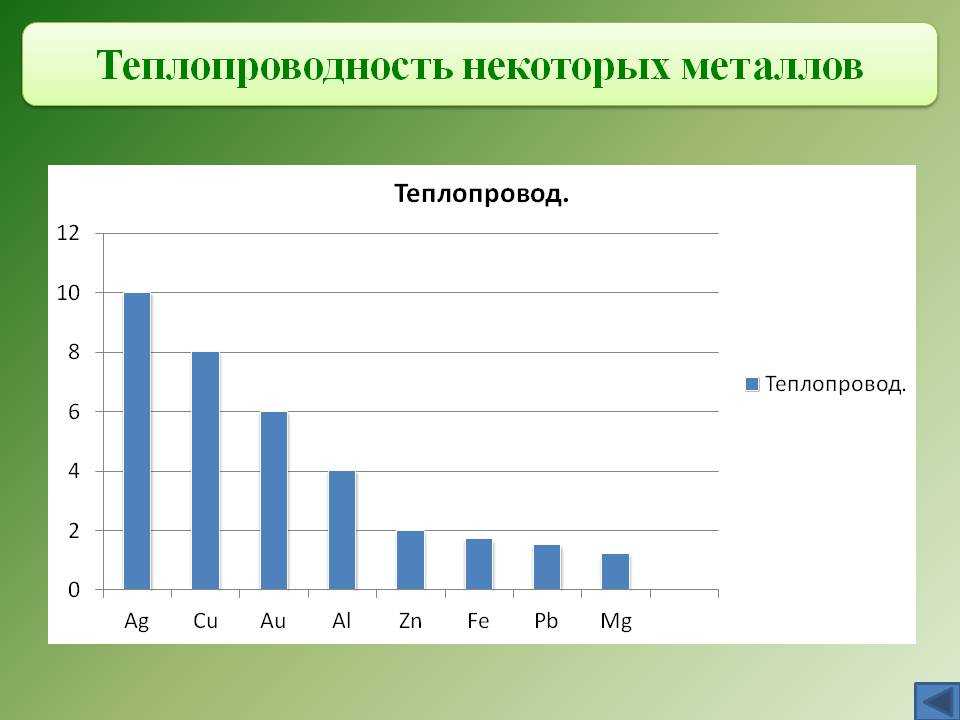 Медь и алюминий имеют самое высокое значение теплопроводности (k). Проверьте нашу базу данных материалов.

Использование обычных металлов и сплавов в таблице выше

Металлы и сплавы (материалы, изготовленные из комбинации металлов) используются в качестве строительных материалов в различных отраслях промышленности, таких как электроника, машиностроение, лабораторное оборудование, медицинские приборы, товары для дома и строительство.

Самые высокие значения теплопроводности для металлов имеют Серебро (-429 Вт/м•К), Медь (-398 Вт/м•К) и Золото (-315 Вт/м•К).

Металлы очень важны для изготовления электроники, поскольку они являются хорошими проводниками электричества. Медь, алюминий, олово, свинец, магний и пластик часто используются для изготовления деталей телефонов, ноутбуков, компьютеров и автомобильной электроники. Медь экономична и используется для электропроводки. Свинец используется для оболочки кабелей и изготовления аккумуляторов. Олово используется для изготовления припоев. Магниевые сплавы используются в производстве новой техники, так как они легкие. Пластик используется для изготовления деталей электроники, которые не должны проводить электричество, а титан используется для производства пластика.

Металлы также играют важную роль в машиностроении. Алюминий часто используется при изготовлении деталей автомобилей и самолетов, а также в виде сплава, так как его чистая форма слаба. Автомобильное литье изготовлено из цинка. Железо, сталь и никель являются распространенными металлами, используемыми в строительстве и инфраструктуре. Сталь представляет собой сплав железа и углерода (а часто и других элементов). Увеличение содержания углерода в стали создает углеродистую сталь, которая делает материал более прочным, но менее пластичным. Углеродистая сталь часто используется в строительных материалах. Латунь и бронза (медь в сплаве с цинком и оловом соответственно) обладают благоприятными свойствами поверхностного трения и используются для замков и петель, а также рам дверей и окон соответственно.

Наконец, нити накаливания для люминесцентных ламп традиционно изготавливаются из вольфрама. Однако от них постепенно отказываются, поскольку в таком источнике света только около 5% мощности преобразуется в свет, остальная часть мощности преобразуется в тепло. Современные источники света часто основаны на светодиодной технологии и полупроводниках.

В заключение, теплопроводность металлов очень важна для проектирования любой конструкции. Это неотъемлемая часть безопасности, эффективности и инноваций в промышленности. Электроны проводника являются механизмом высокой проводимости металлов по сравнению с неметаллическими материалами. Однако значение теплопроводности (k) также может сильно различаться среди металлов.

Ссылки

Schroeder, DV (2018). Введение в теплофизику. Индия: Образовательные услуги Pearson India.

База данных материалов – Термические свойства. (н.д.). Получено с https://thermtest.com/materials-database

Алюминиевые сплавы 101. (9 марта 2020 г.). Получено с https://www.aluminum.org/resources/industry-standards/aluminum-alloys-101

Elert, G. (nd). Проводка. Получено с https://physics.info/conduction/

Blaber, M. (2019, 3 июня). 9.2: Металлы и неметаллы и их ионы. Получено с https://chem.libretexts.org/Bookshelves/General_Chemistry/Map:_General_Chemistry_(Petrucci_et_al.)/09:_The_Periodic_Table_and_Some_Atomic_Properties/9.2:_Metals_and_Nonmetals_and_their_Ions

Теплопроводность. (н.д.). Получено с http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/thercond.html

Диоксид титана для пластмасс. (н.д.). Получено с https://polymer-additives.specialchem.com/centers/titanium-dioxide-for-plastics-center

Сандхана Л. и Джозеф А. (2020, 6 марта). Что такое углеродистая сталь? Получено с https://www.wisegeek.com/what-is-carbon-steel.html

(nd). Получено с http://www.elementalmatter.info/element-aluminium.html

Images

Image 1.A: Mohamed, M. (2019). Кулинария Леди [Иллюстрация]. Получено с https://pxhere.com/en/photo/1584957.

Изображение 1.B: Мохамед, М. (2019). Шеф-повар готовит [иллюстрация]. Получено с https://pxhere.com/en/photo/1587003.

Изображение 2: Википедия. Термометр [Иллюстрация]. Получено с https://upload.wikimedia.org/wikipedia/commons/7/70/Thermometer_CF.svg

Автор: Selen Yildir | Младший технический писатель | Thermtest

Теплопроводность и закон Видемана-Франца

Теплопередача путем теплопроводности включает передачу энергии внутри материала без какого-либо движения материала в целом. Скорость теплопередачи зависит от градиента температуры и теплопроводности материала. Теплопроводность — это довольно простое понятие, когда вы обсуждаете потери тепла через стены вашего дома, и вы можете найти таблицы, характеризующие строительные материалы и позволяющие сделать разумные расчеты.

Более фундаментальные вопросы возникают, когда вы исследуете причины больших изменений теплопроводности. Газы передают тепло за счет прямых столкновений между молекулами, и, как и следовало ожидать, их теплопроводность низка по сравнению с большинством твердых тел, поскольку они являются разбавленными средами. Неметаллические твердые тела передают тепло за счет колебаний решетки, так что нет чистого движения среды при распространении энергии. Такой теплообмен часто описывают в терминах «фононов», квантов колебаний решетки. Металлы являются гораздо лучшими теплопроводниками, чем неметаллы, потому что те же самые подвижные электроны, которые участвуют в электропроводности, участвуют и в передаче тепла.

Концептуально теплопроводность можно рассматривать как контейнер для свойств, зависящих от среды, которые связывают скорость потери тепла на единицу площади со скоростью изменения температуры.

Более формальный режим

Для идеального газа скорость теплопередачи пропорциональна средней молекулярной скорости, длине свободного пробега и молярной теплоемкости газа.

Для неметаллических твердых тел передача тепла рассматривается как передача через колебания решетки, поскольку атомы, вибрирующие более энергично в одной части твердого тела, передают эту энергию соседним атомам с меньшей энергией. Это может быть усилено кооперативным движением в виде распространяющихся волн решетки, которые в квантовом пределе квантуются как фононы. На практике для неметаллических твердых тел существует такая большая изменчивость, что мы обычно просто характеризуем вещество с помощью измеренной теплопроводности при выполнении обычных расчетов.

Для металлов теплопроводность довольно высока, и те металлы, которые являются лучшими проводниками электричества, также являются лучшими проводниками тепла. При заданной температуре тепло- и электропроводность металлов пропорциональны, но повышение температуры увеличивает теплопроводность при уменьшении электропроводности. Это поведение количественно определяется законом Видемана-Франца:

, где константа пропорциональности L называется числом Лоренца. Качественно это соотношение основано на том факте, что перенос тепла и электричества связан со свободными электронами в металле. Теплопроводность увеличивается со средней скоростью частиц, поскольку это увеличивает прямой перенос энергии.