| Популярные металлы | Медь |
|    Вопросы и ответы |
Часто во время осуществления сварки или пайки металлов и их сплавов возникают неожиданные проблемы. О многих из них мы и поговорим в разделе «вопросы и ответы» О многих из них мы и поговорим в разделе «вопросы и ответы» |
Перейти в раздел >>
|    Технологии работ |
| Как производится закалка и отпуск стали |
Способы резки металла под водой
Сварка угловых и тавровых соединений
| Обслуживание и уход за сварочным оборудованием |
Сварочные генераторы постоянного тока
Характеристики источников питания
Электрошлаковая сварка углеродистых сталей
| Эмалирование металлов – технология, которая позволяет наносить на поверхность изделий из стали специальный защитный слой, отличающийся великолепными эстетическими свойствами. |
Узнать подробности >>
| Технология производства покрытых электродов |
Электроды для дуговой сварки, наплавки, резки
Газоэлектрическая сварка в среде углекислого газа
Самоходные однодуговые сварочные головки
Электрическая сварочная дуга и ее свойства
Сплавы для проводников и элементов сопротивления :: Технология металлов
Проводниковые материалы должны изготовляться из возможно чистых металлов, а материалы высокого сопротивления — из сплавов, структура которых представляет твердый раствор.
Основными проводниковыми материалами являются медь и алюминий. Понятие «чистого» металла условно, так как чистота получаемых металлов повышается из года в год по мере роста технических средств в производстве и в лабораториях. С другой стороны, электрическое сопротивление чистых металлов резко возрастает при наличии малых количеств растворенных примесей. Из рис. видно, как значительно падает проводимость меди при введении в ее состав таких примесей, как кремний, железо, мышьяк, бериллий в количествах <0,2%. Для проводниковой техники разработан интернациональный стандарт технически чистой отожженной меди (1913 г.), удельное сопротивление которой при 20° С равно 1,7241 мкОм-см. С тех пор добились дальнейшего очищения меди и повышения ее проводимости.
Для повышения прочности медного провода в его состав вводят примеси Cd, Sn, Αl, Ρ, Cr, Be. Электропроводность при этом, естественно, понижается.
Рис. 1. Влияние примесей на электропроводность меди
Наиболее распространенной является так называемая кадмиевая бронза (0,9% Cd, остальное медь), которая в твердотянутом состоянии обладает проводимостью до 90% от проводимости меди при временном сопротивлении при растяжении, в 2—2,5 раза большем, чем у меди. В табл. 25 приведены составы и свойства медных проводниковых материалов.
В табл. 25 приведены составы и свойства медных проводниковых материалов.
Проводниковый алюминий имеет электропроводность, равную 65% от проводимости меди. Однако ввиду малой плотности алюминия его проводимость, рассчитанная на 1 кг проводника, составляет 214% от таковой для меди. Это позволяет облегчить конструкцию опор на линиях передач с алюминиевыми проводами. Для повышения прочности алюминиевых проводов в их состав вводят магний и кремний (совместно), которые образуют соединение Mg 2Si, очень мало растворимое в алюминии при комнатной температуре (меньше 0,25%). Путем закалки и старения удается повысить временное сопротивление такого сплава в 2 раза при электропроводности 90% от проводимости чистого алюминия. Сплавы такого типа (альдрей и альмелек) содержат 0,4 и 0,7% Mg, 0,5—0,6% Si и до 0,3% Fe. Альдрей (0,4% Mg, 0,6% Si и 0,3% Fe) имеет температурный коэффициент электрического спротивления, равный 3,6 * 10-4, т. е. весьма близкий к температурному коэффициенту чистого алюминия (4,0 * 10-4).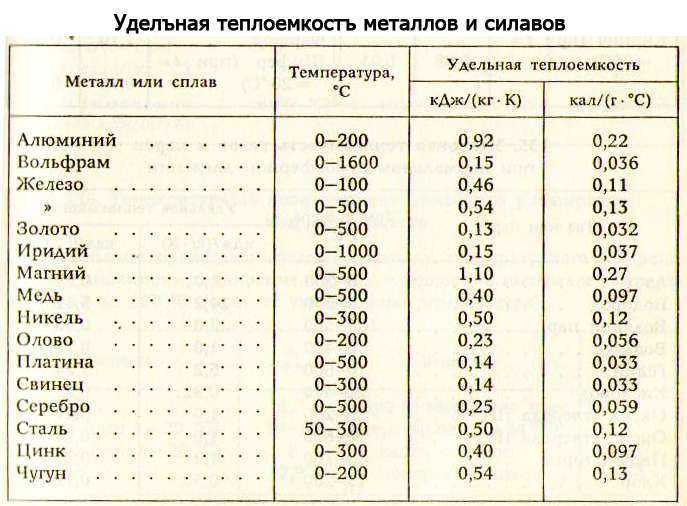 Это еще раз свидетельствует о том, что при обработке путем дисперсионного твердения Mg2Si выделяется из раствора почти нацело.
Это еще раз свидетельствует о том, что при обработке путем дисперсионного твердения Mg2Si выделяется из раствора почти нацело.
Для реостатов в нагревательных приборах, а также там, где необходимо высокое электрическое сопротивление и малый температурный коэффициент, применяют сплавы железа с примесями, образующими твердые растворы. В табл. 2 приводятся типичные железные сплавы, а также для сравнения сплавы на никелевой основе.
Эти сплавы являются не только сплавами высокого сопротивления, но и жаростойкими. Для придания жаростойкости в железные сплавы вводятся хром и алюминий. Железные сплавы дешевле никелевых, однако они не только не являются заменителями, но имеют также и более высокую рабочую температуру.
В качестве элементов сопротивления применяются медноникелевые сплавы— константан и никелин. Рабочая температура константана до 400° С, никелина — до 200° С.
Таблица 1
Медные проводниковые сплавы
Сплав | Состояние | Электропроводность, % | Временное сопротивление при растяжении, МПа | Удлинение, % |
Чистая медь | Отожженная | 101 | 220—270 | 50 |
Твердотянутая | 98 | До 480 | 4 | |
Кадмиевая бронза (0,9% Cd) | Отожженная | 95 | 310—380 | 50 |
Твердотянутая | 83—90 | До 730 | 4 | |
Бронза (0,75% Sn или 0,8% Cd и 0,6% Sn) | Отожженная | 55—60 | 290 . | 55 |
Твердотянутая | 50—55 | До 730 | 4 | |
Бронза (2,5% А1, 2% Sn) | Отожженная | 15—18 | 370 | 45 |
Твердотянутая | 15—18 | До 970 | 4 | |
Фосфористая бронза (7% Sn, 0,1% Ρ) | Отожженная | 10—15 | 400 | 60 |
Твердотянутая | 10—15 | 1050 | 3 |
Таблица 2
Сплавы для реостатов и нагревательных приборов
Сплав | Состав (средний), % | Удельное электросопротивление, мкОм · см | Температурный коэффициент α | Наивысшая рабочая температура, °С |
Х13Ю4 (фехраль) | 13,5 Сr; 4,5 Аl; остальное Fe | 126 | 0,00005 | 1000 |
0Х23Ю5 | 23 Сr; 5 Аl; остальное Fe | 137 | — | 1200 |
0Х27Ю5А | 27 Сr; 5,5 Аl; остальное Fe | 142 | 0,00002 | 1300 |
Сверхмегапир | 37 Сr; 7,5 Аl; остальное Fe | 180 | 0,00012 | 1350 |
Х15Н60 (нихром) | 16,5 Сr: 58 Ni: остальное Fe | 110 | 0,00017 | 1000 |
Х20Н80 | 21,5 Сr; остальное Ni | 100 | — | 1100 |
Таблица 3.
Влияние различных элементов на удельное электросопротивление железа
Элемент
| Пределы концентрации и температуры | Средние значения возрастания удельного сопротивления, мкОм.см | ||
% (по массе) | °с | на 1 % (по массе) | на 1 % (ат.) | |
Аl | 0—2,0 | 18—23 | 11,1—14,4 | 6,0—7,7 |
As | 0—2,6 | — | 6,8 | 9,10 |
Au | — | — | 1. | 5,80 |
В | 0—0,45 | — | 6,2 | 1,25 |
С | 0—0,9 | 20 | 34,0 | 7,6 |
Со | 0,5 | 18—30 | 1,0—3,0 | 1,1—3,2 |
Сг | 0,3 | 12 | 2,5—5,4 | 2,3—5,0 |
Сu | 0—1 | — | 3,0—4,0 | 3,4—4,6 |
Μn | 0—2 | 18—30 | 5,0—10,5 | 4,9—10,3 |
Mo | 0—1 | 17 | 3,4 | 5,8 |
Ν | 0—0,1 | 20 | 14,6 | 3,8 |
Ni | 0—5 | 18—30 | 1,55—4,45 | 1,7-4,7 |
Ρ | 0—0,3 | — | 11,4 | 6,1 |
S | 0—0,1 | 20 | 12,0 | 6,9 |
Si | 0—1 | 20 | 13—15,8 | 6,5—8,0 |
Ti | — | — | 1,0 | 0,9 |
V | 0—1 | — | 6,7 | 6,1 |
W | 0—2 | 15—20 | 2,0—3,6 | 6,5—11,8 |
Источник:
Лившиц Б.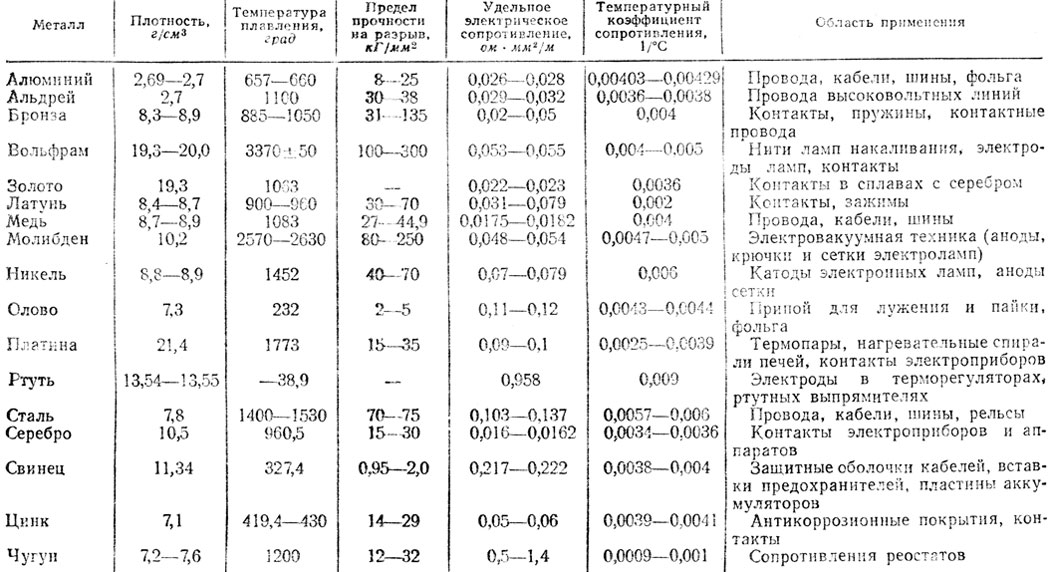 Г., Крапошин В.С, Липецкий Я.Л. «Физические свойства металлов и сплавов». М. «Металлургия», 1980.
Г., Крапошин В.С, Липецкий Я.Л. «Физические свойства металлов и сплавов». М. «Металлургия», 1980.
Объемное удельное сопротивление и проводимость металлов
Выпуск 020, 9 ноября 2021 г.
Меган К. Пуглиа, доктор философии, старший химик-исследователь
Удельное сопротивление (ρ) определяет способность материала препятствовать электрическому току (уравнение 1) . Уравнение 1 определяет удельное сопротивление математически, где R — сопротивление, A — площадь поперечного сечения материала, а l — длина материала.[1] Единицей СИ, используемой для выражения удельного сопротивления, является омметр (Ом∙м).
Уравнение 1:
Удельное сопротивление — это величина, обратная проводимости (σ), которая определяет способность материала пропускать через себя электроны на определенную единицу размера (уравнение 2).[1] Единицей проводимости в системе СИ является сименс на метр (См/м).
Уравнение 2:
Важно отметить, что удельное сопротивление и проводимость — это свойства материала, которые номинально не зависят от размера и формы. Сопротивление, с другой стороны, является характеристикой компонента и может быть изменено путем изменения размеров детали.
Сопротивление, с другой стороны, является характеристикой компонента и может быть изменено путем изменения размеров детали.
Удельное сопротивление в металле сильно зависит от длины свободного пробега свободно движущегося (валентного) электрона в его кристаллической решетке. Средняя длина свободного пробега — это среднее расстояние, которое электрон может пройти между событиями рассеяния или столкновениями, которые сбивают электрон с его первоначального маршрута через материал. События рассеяния увеличивают удельное сопротивление и вызываются неоднородностями в кристаллической структуре металлов. Примеры включают поля деформации вокруг атомов растворенных веществ, границ зерен и частиц и дислокаций. Обычно механизмы упрочнения материала увеличивают количество случаев рассеяния и, следовательно, снижают проводимость металла. Следовательно, проводимость металлов, подвергшихся холодной обработке с внесением дислокаций, ниже, чем у отожженных материалов того же состава.[2] Однако интересно то, что удельное сопротивление сплава обычно снижается при дисперсионном твердении; растворенные атомы изолируются в осадках, перестраиваются путем дальнего упорядочения и т. д., тем самым уменьшая их участие в рассеянии электронов.
д., тем самым уменьшая их участие в рассеянии электронов.
На удельное сопротивление и проводимость также влияет температура материала. Повышение температуры вызывает усиление колебаний решетки (фононов), что приводит к большему структурному беспорядку и точкам столкновения электронов, пытающихся двигаться через материал. Собственная проводимость чистых элементов связана со многими другими аспектами; среди них валентные электроны, кристаллическая структура и плотность электронов вблизи энергетического уровня Ферми.[2]
Удельное сопротивление металлов и других материалов, которые являются хорошими проводниками, часто указывается в единицах микроом∙см, тогда как у изоляционных материалов высокие значения удельного сопротивления указываются в ом∙см. Некоторые справочники и руководства ранжируют материалы по их процентной проводимости по отношению к международному стандарту отожженной меди (IACS), известному как %IACS. IACS представляет собой эталон отожженной меди, выдерживаемый при 20°C, с принятым значением проводимости 58×10⁶ См/м [1,72 мкОм-см]. Следовательно, сообщаемая проводимость 50% IACS означает, что материал имеет половину проводимости стандарта отожженной меди, или 27,5 x 10⁶ См/м [3,45 мкОм-см].
Следовательно, сообщаемая проводимость 50% IACS означает, что материал имеет половину проводимости стандарта отожженной меди, или 27,5 x 10⁶ См/м [3,45 мкОм-см].
Сообщается, что серебро, медь и золото обладают самой высокой электропроводностью среди всех металлов, отчасти благодаря тому, что каждый из их одиночных валентных электронов легко возбуждается, чтобы свободно двигаться через их кристаллическую решетку.[2] Обратите внимание, что чистое серебро и медь с большей вероятностью потускнеют по сравнению с золотом и другими благородными металлами в определенных условиях, что увеличивает контактное сопротивление.[3] Кроме того, более высокая проводимость обычно указывает на снижение прочности материала, как упоминалось ранее. По этим причинам важно выбирать контактные материалы, которые уравновешивают проводимость, прочность, благородство и стоимость, соответствующие предполагаемому применению, и избегать узкого внимания только к объемной проводимости.
Deringer-Ney, Inc. производит ряд сплавов с различными комбинациями удельного сопротивления, твердости, благородства и стоимости, чтобы соответствовать широкому спектру различных применений и сред, как показано в таблице 1.[1]
производит ряд сплавов с различными комбинациями удельного сопротивления, твердости, благородства и стоимости, чтобы соответствовать широкому спектру различных применений и сред, как показано в таблице 1.[1]
Таблица 1: Оценочные значения удельного сопротивления, проводимости и %IACS для различных металлических сплавов. Для получения информации о других сплавах DNI или альтернативных сплавах посетите сайт deringerney.com. Все значения являются оценочными. Значения удельного сопротивления и твердости чистого металла из ссылок 4 и 5 соответственно. Значения, соответствующие измерениям твердости по Кнупу, обозначены HK, а значения, соответствующие измерениям твердости по Виккерсу, обозначены HV.
Ссылки:
[1] Pitney, Kenneth E. Ney Contact Manual: Electric Contacts for Low Energy Uses. 1-е изд., The JM Ney Company, 1973.
[2] Картер, Джайлз Ф. Принципы физической и химической металлургии. ASM International, 1979
[3] Боуэн, П.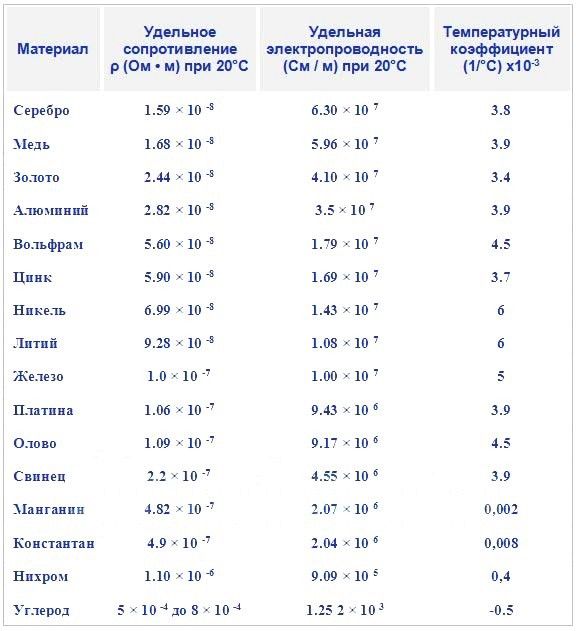 К. «Основы теории контактного сопротивления», технические сводки Дерингера-Ней, 2 декабря 2020 г. https://www.deringerney.com/resource-library/.
К. «Основы теории контактного сопротивления», технические сводки Дерингера-Ней, 2 декабря 2020 г. https://www.deringerney.com/resource-library/.
[4] Haynes, William M., et al. «Свойства твердых тел». Справочник CRC по химии и физике: готовый справочник химических и физических данных: 2012–2013 гг., CRC Press, Бока-Ратон, Флорида, 2012 г., стр. 12–41-12–42.
[5] Брандес, Эрик А. и Колин Джеймс Смителлс. Справочник Smithells Metals. 6-е изд., Butterworths, 1983.
Метод оценки решеточной теплопроводности металлических сплавов (Технический отчет)
Метод оценки решеточной теплопроводности металлических сплавов (Технический отчет) | ОСТИ.GOVперейти к основному содержанию
- Полная запись
- Другое связанное исследование
Описан метод расчета решеточной теплопроводности сплавов в зависимости от температуры и состава для температур выше тета/суб D//2 с использованием доступной информации об атомных частицах, присутствующих в сплаве. В расчете учитываются взаимодействия фононов с точечными дефектами, электронами и другими фононами. Обсуждаются сравнения экспериментальных теплопроводностей (удельных сопротивлений) с расчетными значениями для бинарных сплавов полупроводников, галогенидов щелочных металлов и металлов. За обсуждением теоретических основ следует достаточная численная работа, чтобы облегчить расчет решеточной теплопроводности сплава, для которого не существует данных по проводимости.
В расчете учитываются взаимодействия фононов с точечными дефектами, электронами и другими фононами. Обсуждаются сравнения экспериментальных теплопроводностей (удельных сопротивлений) с расчетными значениями для бинарных сплавов полупроводников, галогенидов щелочных металлов и металлов. За обсуждением теоретических основ следует достаточная численная работа, чтобы облегчить расчет решеточной теплопроводности сплава, для которого не существует данных по проводимости.
- Авторов:
- Ярбро, DW; Уильямс, Р. К.
- Дата публикации:
- Исследовательская организация:
- Национальная лаборатория Ок-Ридж.
 (ORNL), Ок-Ридж, Теннесси (США)
(ORNL), Ок-Ридж, Теннесси (США)
- Идентификатор ОСТИ:
- 6825949
- Номер(а) отчета:
- ОРНЛ-5434
РНН: 78-019870
- Номер контракта Министерства энергетики США:
- W-7405-ENG-26
- Тип ресурса:
- Технический отчет
- Страна публикации:
- США
- Язык:
- Английский
- Тема:
- 36 МАТЕРИАЛОВЕДЕНИЕ; СПЛАВЫ; ТЕПЛОПРОВОДНОСТЬ; БИНАРНЫЕ СПЛАВНЫЕ СИСТЕМЫ; КРИСТАЛЛИЧЕСКИЕ РЕШЕТКИ; МАТЕМАТИЧЕСКИЕ МОДЕЛИ; ФОНОНЫ; ПОЛУПРОВОДНИКОВЫЕ МАТЕРИАЛЫ; СПЛАВНЫЕ СИСТЕМЫ; КРИСТАЛЬНАЯ СТРУКТУРА; ФИЗИЧЕСКИЕ СВОЙСТВА; КВАЗИЧАСТИЦЫ; ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА; 360104* – Металлы и сплавы – Физические свойства
Форматы цитирования
- MLA
- АПА
- Чикаго
- БибТекс
Ярбро Д. В. и Уильямс Р.К. Метод оценки решеточной теплопроводности металлических сплавов . США: Н. П., 1978.
Веб. дои: 10.2172/6825949.
В. и Уильямс Р.К. Метод оценки решеточной теплопроводности металлических сплавов . США: Н. П., 1978.
Веб. дои: 10.2172/6825949.
Копировать в буфер обмена
Ярбро, Д. В., и Уильямс, Р. К. Метод оценки решеточной теплопроводности металлических сплавов . Соединенные Штаты. https://doi.org/10.2172/6825949
Копировать в буфер обмена
Ярбро, Д. В., и Уильямс, Р. К., 1978.
«Метод оценки решеточной теплопроводности металлических сплавов». Соединенные Штаты. https://doi.org/10.2172/6825949. https://www.osti.gov/servlets/purl/6825949.
Копировать в буфер обмена
@статья{osti_6825949,
title = {Метод оценки решеточной теплопроводности металлических сплавов},
автор = {Ярбро, Д. В. и Уильямс, Р.К.},
В. и Уильямс, Р.К.},
abstractNote = {Описан метод расчета решеточной теплопроводности сплавов в зависимости от температуры и состава для температур выше тета/суб D//2 с использованием доступной информации об атомных частицах, присутствующих в сплаве. В расчете учитываются взаимодействия фононов с точечными дефектами, электронами и другими фононами. Обсуждаются сравнения экспериментальных теплопроводностей (удельных сопротивлений) с расчетными значениями для бинарных сплавов полупроводников, галогенидов щелочных металлов и металлов. За обсуждением теоретических основ следует достаточная численная работа, чтобы облегчить расчет решеточной теплопроводности сплава, для которого нет данных по проводимости.},
дои = {10,2172/6825949},
URL = {https://www.osti.gov/biblio/6825949},
журнал = {},
номер =,
объем = ,
место = {США},
год = {1978},
месяц = {8}
}
Копировать в буфер обмена
Посмотреть технический отчет (0,94 МБ)
https://doi.

 с.) – так назвали этот коэффициент. Если взять два проводника с одинаковым сечением и длиной и поставить их в цепь по очереди, то, измеряя силу тока и сопротивление, можно увидеть, что в двух случаях эти показатели будут разными. Таким образом, удельное электрическое сопротивление – это характеристика материала, из которого сделан проводник, а если быть еще более точным, то вещества.
с.) – так назвали этот коэффициент. Если взять два проводника с одинаковым сечением и длиной и поставить их в цепь по очереди, то, измеряя силу тока и сопротивление, можно увидеть, что в двух случаях эти показатели будут разными. Таким образом, удельное электрическое сопротивление – это характеристика материала, из которого сделан проводник, а если быть еще более точным, то вещества.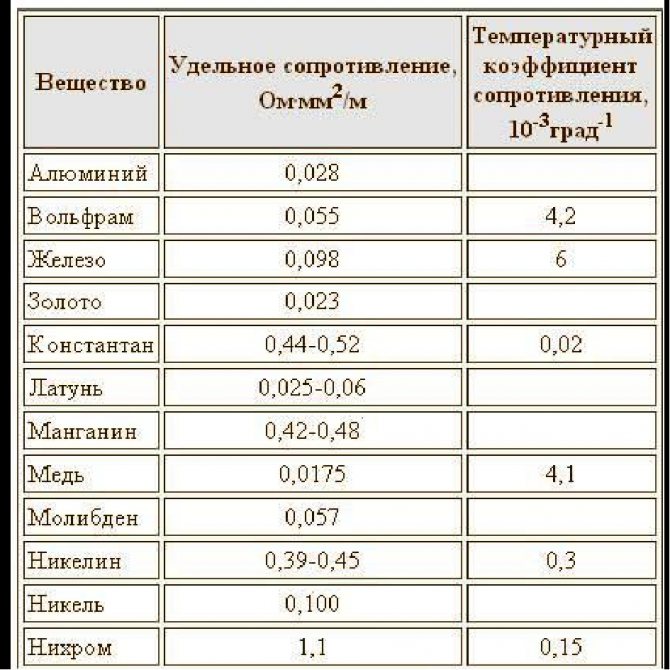 В ситуации же, когда мы располагаем чистым металлом, он имеет кристаллическую структуру, в которой эти наружные электроны общие. Они-то и переносят заряд, если приложить к металлу электрическое поле.
В ситуации же, когда мы располагаем чистым металлом, он имеет кристаллическую структуру, в которой эти наружные электроны общие. Они-то и переносят заряд, если приложить к металлу электрическое поле.


 С другой стороны, в точной электронике, это довольно нежелательный эффект.
С другой стороны, в точной электронике, это довольно нежелательный эффект. 

 (ORNL), Ок-Ридж, Теннесси (США)
(ORNL), Ок-Ридж, Теннесси (США)