Таблица кубатурник: Кубатурник круглого леса - скачать таблицу кубатурник леса от 1 до 12 метров

Содержание

Кубатурник пиломатериала таблица — Смоленские пиломатериалы

Таблица кубатурник доски, сколько доски в кубе
Наименование	Размер, мм	Кол-во штук в одном м3	Кол-во погонных метров в одном м3	Объём одной доски, м3	Площадь одной доски, кв.м.	Вес одной доски, кг (влажн. 20%)
Доска обрезная	20х100х6000	83,3	500	0,012	0,6	9
Доска обрезная	20х100х3000	167,6	500	0,006	0,3	4,5
Доска обрезная	20х150х6000	55,6	333,3	0,018	0,9	13,5
Доска обрезная	20х150х3000	111,1	333,3	0,009	0,45	6,75

Доска обрезная	22х100х6000	75,8	454,5	0,0132	0,6	9,9
Доска обрезная	22х100х3000	151,5	454,5	0,0066	0,3	4,95
Доска обрезная	22х125х6000	60,6	363,6	0,0165	0,75	12,375
Доска обрезная	22х125х3000	121,2	363,6	0,00825	0,0375	6,19
Доска обрезная	22х150х6000	50,5	303	0,0198	0,09	14,85
Доска обрезная	22х150х3000	101	303	0,0099	0,045	7,425
Доска обрезная	22х175х6000	43,3	259,7	0,0231	1,05	17,325
Доска обрезная	22х175х3000	86,6	259,7	0,01155	0,525	8,66
Доска обрезная	22х200х6000	37,9	227,3	0,0264	1,2	19,8
Доска обрезная	22х200х3000	75,8	227,3	0,0132	0,6	9,9
Доска обрезная	22х225х6000	33,7	202	0,0297	1,35	22,275
Доска обрезная	22х225х3000	37,3	202	0,01485	0,675	11,138
Доска обрезная	22х250х6000	30,3	181,8	0,033	1,5	24,75
Доска обрезная	22х250х3000	60,6	181,8	0,0165	0,75	12,375

Доска обрезная	25х100х6000	66,7	400	0,015	0,6	11,25
Доска обрезная	25х100х3000	133,3	400	0,0075	0,3	5,625
Доска обрезная	25х100х2000	200	400	0,005	0,2	3,75
Доска обрезная	25х125х6000	53,3	320	0,01875	0,75	14,06
Доска обрезная	25х125х3000	106,7	320	0,009375	0,0375	7,03
Доска обрезная	25х150х6000	44,4	266,7	0,0225	0,9	16,875
Доска обрезная	25х150х3000	88,9	266,7	0,01125	0,45	8,44
Доска обрезная	25х150х2000	133,3	266,7	0,0075	0,3	5,625
Доска обрезная	25х175х6000	38,1	228,6	0,02625	1,05	19,69
Доска обрезная	25х175х3000	76,2	228,6	0,012125	0,525	9,094
Доска обрезная	25х200х6000	33,3	200	0,03	1,2	22,5
Доска обрезная	25х200х3000	66,7	200	0,015	0,6	11,25
Доска обрезная	25х225х6000	29,6	177,8	0,03375	1,35	25,31
Доска обрезная	25х225х3000	59,3	177,8	0,016875	0,675	12,656
Доска обрезная	25х250х6000	26,7	160	0,0375	1,5	28,125
Доска обрезная	25х250х3000	53,3	160	0,01875	0,75	14,06

Доска обрезная	32х100х6000	52,1	312,5	0,0192	0,6	14,4
Доска обрезная	32х100х3000	104,2	312,5	0,0096	0,3	7,2
Доска обрезная	32х125х6000	41,7	250	0,024	0,75	18
Доска обрезная	32х125х3000	83,3	250	0,012	0,0375	9
Доска обрезная	32х150х6000	34,7	208,3	0,0288	0,9	21,6
Доска обрезная	32х150х3000	69,4	208,3	0,0144	0,45	10,8
Доска обрезная	32х175х6000	29,8	178,6	0,0336	1,05	25,2
Доска обрезная	32х175х3000	59,5	178,6	0,0168	0,525	12,6
Доска обрезная	32х200х6000	26	156,3	0,0384	1,2	28,8
Доска обрезная	32х200х3000	52,1	156,3	0,0192	0,6	14,4
Доска обрезная	32х225х6000	23,1	138,9	0,0432	1,35	32,4
Доска обрезная	32х225х3000	46,3	138,9	0,0216	0,675	16,2
Доска обрезная	32х250х6000	20,8	125	0,048	1,5	36
Доска обрезная	32х250х3000	41,7	125	0,024	0,75	18

Доска обрезная	40х100х6000	41,7	250	0,024	0,6	18
Доска обрезная	40х100х3000	83,3	250	0,012	0,3	9
Доска обрезная	40х125х6000	33,3	200	0,03	0,75	22,5
Доска обрезная	40х125х3000	66,7	200	0,015	0,0375	11,25
Доска обрезная	40х150х6000	27,8	166,7	0,036	0,9	27
Доска обрезная	40х150х3000	55,6	166,7	0,018	0,45	13,5
Доска обрезная	40х175х6000	23,8	142,9	0,042	1,05	31,5
Доска обрезная	40х175х3000	47,6	142,9	0,021	0,525	15,75
Доска обрезная	40х200х6000	20,8	125	0,048	1,2	36
Доска обрезная	40х200х3000	41,7	125	0,024	0,6	18
Доска обрезная	40х225х6000	18,5	111,1	0,054	1,35	40,5
Доска обрезная	40х225х3000	37	111,1	0,027	0,675	20,25
Доска обрезная	40х250х6000	16,7	100	0,06	1,5	45
Доска обрезная	40х250х3000	33,3	100	0,03	0,75	22,5

Доска обрезная	50х100х6000	33,3	200	0,03	0,6	22,5
Доска обрезная	50х100х3000	66,7	200	0,015	0,3	11,25
Доска обрезная	50х125х6000	26,7	160	0,0375	0,75	28,125
Доска обрезная	50х125х3000	53,3	160	0,01875	0,0375	14,06
Доска обрезная	50х150х6000	22,2	133,3	0,045	0,9	33,75
Доска обрезная	50х150х3000	44,4	133,3	0,0225	0,45	16,875
Доска обрезная	50х175х6000	19	114,3	0,0525	1,05	39,375
Доска обрезная	50х175х3000	38,1	114,3	0,02625	0,525	19,688
Доска обрезная	50х200х6000	16,7	100	0,06	1,2	45
Доска обрезная	50х200х3000	33,3	100	0,03	0,6	22,5
Доска обрезная	50х225х6000	14,8	88,9	0,0675	1,35	50,625
Доска обрезная	50х225х3000	29,6	88,9	0,03375	0,675	25,31
Доска обрезная	50х250х6000	13,3	80	0,075	1,5	56,25
Доска обрезная	50х250х3000	26,7	80	0,0375	0,75	28,125

Доска обрезная	60х125х6000	22,2	133,3	0,045	0,75	33,75
Доска обрезная	60х125х3000	44,4	133,3	0,0225	0,0375	28,125
Доска обрезная	60х150х6000	18,5	111,1	0,054	0,9	40,5
Доска обрезная	60х150х3000	37	111,1	0,027	0,45	20,25
Доска обрезная	60х175х6000	15,9	95,2	0,063	1,05	47,25
Доска обрезная	60х200х6000	13,9	83,3	0,072	1,2	54
Доска обрезная	60х225х6000	12,3	74,1	0,081	1,35	60,75
Доска обрезная	60х250х6000	11,1	66,7	0,09	1,5	67,5
Доска обрезная	60х250х3000	22,2	66,7	0,045	0,75	33,75

Доска обрезная	75х175х6000	12,7	76,2	0,07875	1,05	59,06
Доска обрезная	75х175х3000	25,4	76,2	0,0394	0,525	29,55
Доска обрезная	75х200х6000	11,1	66,7	0,09	1,2	67,5
Доска обрезная	75х200х3000	22,2	66,7	0,045	0,6	33,75
Доска обрезная	75х225х6000	9,9	59,3	0,101	1,35	75,75
Доска обрезная	75х225х3000	19,7	59,3	0,051	0,675	38,25
Доска обрезная	75х250х6000	8,9	53,3	0,1123	1,5	84,225
Таблица кубатурник бруса, сколько бруса в кубе
Наименование	Размер, мм	Кол-во штук в одном м3	Кол-во погонных метров в одном м3	Объём одной доски, м3	Площадь одной доски, кв. м.
Брусок	50х50х6000	66,67	400	0,015	11,25
Брусок	50х50х3000	133,33	400	0,0075	5,625
Брус	50х100х6000	33,33	200	0,03	22,5
Брус	50х100х3000	66,67	200	0,015	11,25
Брусок	60х60х6000	46,3	277,78	0,0216	16,2
Брусок	60х60х3000	92,6	277,78	0,0108	8,1
Брус	60х100х6000	27,78	166,67	0,036	27
Брус	60х100х3000	55,55	166,67	0,018	13,5
Брус	75х75х6000	29,63	177,78	0,03375	25,31
Брус	75х75х3000	59,26	177,78	0,0169	12,675
Брус	75х100х6000	22,22	133,33	0,045	33,75
Брус	75х100х3000	44,44	133,33	0,0225	16,875
Брус	75х150х6000	14,8	88,89	0,0675	50,625
Брус	100х100х6000	16,67	100	0,06	45
Брус	100х100х3000	33,33	100	0,03	22,5
Брус	100х150х6000	11,11	66,67	0,09	67,5
Брус	100х200х6000	8,33	50	0,12	90
Брус	100х250х6000	6,67	40	0,15	112,5
Брус	125х125х6000	10,67	64	0,09375	70,31
Брус	150х150х6000	7,41	44,44	0,135	101,25
Брус	200х200х6000	4,17	25	0,24	180
Брус	200х250х6000	3,33	20	0,3	225
Брус	250х250х6000	2,67	16	0,375	281,25

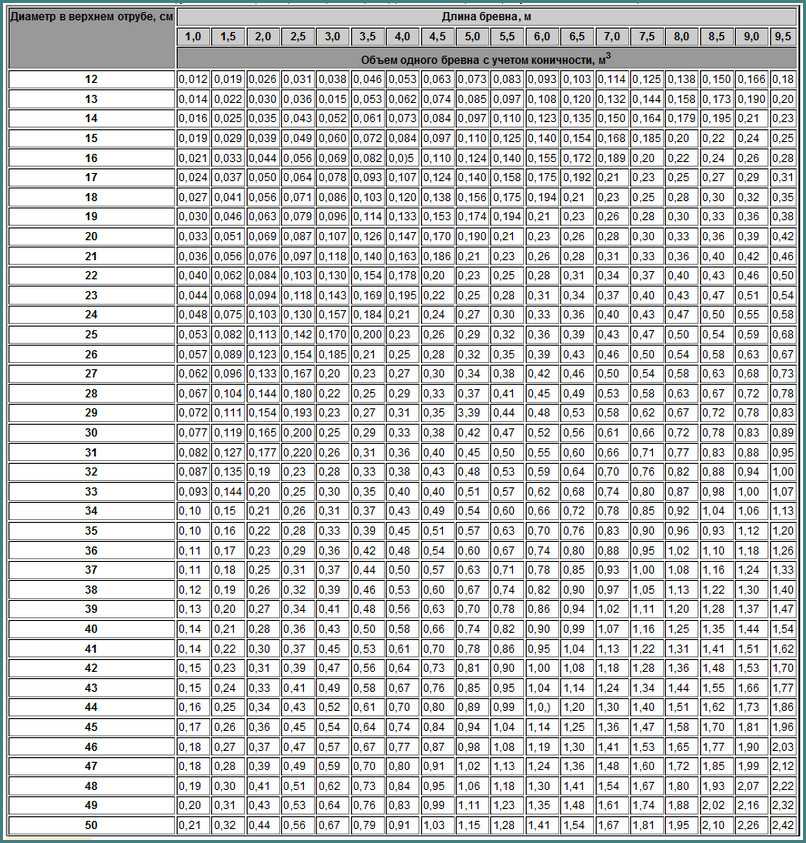
Кубатурник круглого леса.

Расчет объемов бревна в срубе

Диаметр бревна	Длина бревна, м
Диаметр бревна	3 м	3,5 м	4 м	4,5 м	5 м	5,5 м	6 м	6,5 м	7 м	7,5 м	8 м
D 10 см	0,026	0,031	0,037	0,044	0,051	0,058	0,065	0,075	0,082	0,09	0,1
D 11 cм	0,032	0,037	0,045	0,053	0,062	0,07	0,08	0,09	0,098	0,108	0,12
D 12 cм	0,038	0,046	0,053	0,063	0,073	0,083	0,093	0,103	0,114	0,125	0,138
D 13 cм	0,045	0,053	0,062	0,075	0,085	0,097	0,108	0,12	0,132	0,144	0,158
D 14 cм	0,052	0,061	0,073	0,084	0,097	0,11	0,123	0,135	0,15	0,164	0,179
D 15 cм	0,06	0,071	0,084	0,097	0,11	0,125	0,139	0,153	0,169	0,182	0,199
D 16 cм	0,069	0,082	0,095	0,11	0,124	0,14	0,155	0,172	0,189	0,2	0,22
D 17 cм	0,077	0,092	0,107	0,124	0,14	0,157	0,174	0,191	0,209	0,225	0,25
D 18 cм	0,086	0,103	0,12	0,138	0,156	0,175	0,194	0,21	0,23	0,25	0,28
D 19 cм	0,097	0,115	0,134	0,154	0,173	0,193	0,212	0,235	0,255	0,275	0,305
D 20 cм	0,107	0,126	0,147	0,17	0,19	0,21	0,23	0,26	0,28	0,3	0,33
D 21 см	0,119	0,14	0,163	0,185	0,21	0,23	0,255	0,285	0,31	0,335	0,365
D 22 cм	0,134	0,154	0,178	0,2	0,23	0,25	0,28	0,31	0,34	0,37	0,4
D 23 cм	0,114	0,169	0,194	0,22	0,25	0,275	0,305	0,335	0,37	0,4	0,435
D 24 cм	0,157	0,184	0,21	0,24	0,27	0,3	0,33	0,36	0,4	0,43	0,47
D 25 cм	0,171	0,197	0,23	0,26	0,295	0,325	0,36	0,395	0,43	0,465	0,505
D 26 cм	0,185	0,21	0,25	0,28	0,32	0,35	0,39	0,43	0,46	0,5	0,54
D 27 cм	0,203	0,23	0,27	0,305	0,345	0,38	0,42	0,46	0,495	0,54	0,585
D 28 cм	0,22	0,25	0,29	0,33	0,37	0,41	0,45	0,49	0,53	0,58	0,63
D 29 cм	0,235	0,27	0,31	0,355	0,395	0,44	0,485	0,525	0,57	0,62	0,675
D 30 cм	0,25	0,29	0,33	0,38	0,42	0,47	0,52	0,56	0,61	0,66	0,72
D 31 мм	0,265	0,31	0,355	0,405	0,45	0,5	0,555	0,6	0,655	0,72	0,77
D 32 cм	0,28	0,33	0,38	0,43	0,48	0,53	0,59	0,64	0,7	0,76	0,82
D 33 cм	0,3	0,35	0,405	0,46	0,51	0,565	0,625	0,68	0,74	0,805	0,87
D 34 cм	0,32	0,37	0,43	0,49	0,54	0,6	0,66	0,72	0,78	0,85	0,92
D 35 cм	0,34	0,395	0,455	0,515	0,57	0,635	0,7	0,76	0,83	0,9	0,97
D 36 cм	0,36	0,42	0,48	0,54	0,6	0,67	0,74	0,8	0,88	0,95	1,02
D 37 cм	0,375	0,44	0,505	0,57	0,635	0,705	0,78	0,85	0,925	1,0	1,075
D 38 cм	0,39	0,46	0,53	0,6	0,67	0,74	0,82	0,9	0,97	1,05	1,13
D 39 cм	0,41	0,48	0,555	0,63	0,705	0,78	0,86	0,945	1,02	1,105	1,19
D 40 cм	0,43	0,5	0,58	0,66	0,74	0,82	0,9	0,99	1,07	1,16	1,25
D 41 cм	0,45	0,53	0,61	0,695	0,775	0,86	0,95	1,035	1,125	1,22	1,315
D 42 cм	0,47	0,56	0,64	0,73	0,81	0,9	1,0	1,08	1,18	1,28	1,38
D 43 cм	0,495	0,585	0,67	0,765	0,85	0,945	1,045	1,14	1,24	1,34	1,34
D 44 cм	0,515	0,61	0,7	0,8	0,89	0,89	1,09	1,2	1,3	1,4	1,51
D 45 cм	0,543	0,64	0,735	0,835	0,935	1,035	1,14	1,25	1,355	1,465	1,48
D 46 cм	0,57	0,67	0,77	0,87	0,98	1,08	1,19	1,3	1,41	1,53	1,65
D 47 cм	0,595	0,7	0,805	0,91	1,02	1,13	1,245	1,355	1,475	1,6	1,725
D 48 cм	0,62	0,73	0,84	0,95	1,06	1,18	1,3	1,41	1,54	1,167	1,8
D 49 cм	0,645	0,76	0,875	0,99	1,105	1,23	1,355	1,475	1,605	1,74	1,875
D 50 cм	0,67	0,79	0,91	1,03	1,15	1,28	1,41	1,54	1,67	1,81	1,95
D 51 cм	0,7	0,825	0,95	1,075	1,2	1,335	1,47	1,605	1,74	1,89	2,035
D 52 cм	0,73	0,86	0,99	1,12	1,25	1,39	1,53	1,67	1,81	1,97	2,12

Описание таблиц

В нашей подборке мы приводим отдельные таблицы с информацией о Правила кабины для следующих регионов конкретного измерения, C _N , T _N , S _N , E _N ^-R , n = 2,3,4. Е _н ^{-р ²} , н = 2,3,4,5 и один дополнительный стол для C _n , T _N , S _N , E _N ^-R и E _N ^{-R ²} общего размера.

В большинстве случаев мы также добавляем отдельную таблицу встроенных последовательностей Кубатурные правила. Эти последовательности полностью или частично встроенный. В полностью встроенной последовательности каждое кубатурное правило высшего степень включает в число своих точек интегрирования каждую точку всех кубатурные правила более низкой степени в последовательности. В частично встроенном последовательность, некоторые точки в кубатурном правиле более низкой степени не появляются среди точек кубатурного правила более высокой степени. Хотя, в теории, любая последовательность кубатурных правил может рассматриваться как частично встроенная последовательность, на практике мы требуем, чтобы количество точки, не входящие в кубатурное правило более высокой степени, будут «маленькими». Если мы ослабим условие в (2), что все веса w _i 0 , то мы можем посмотреть на частично встроенная последовательность как полностью встроенная последовательность, в которой некоторые веса исчезают. В наших таблицах мы используем этот подход и указываем частичное встраивание буквой Р в столбец с маркировкой Н . Заметим, что иногда кубатурные правила, появляющиеся в встроенная последовательность также включена в число отдельных кубатурных правил когда они более эффективны, чем некоторые из включенных кубатурных правил в таблицах, где мы определяем одно кубатурное правило над регионом B _n , чтобы быть более эффективным, чем другое кубатурное правило над одной и той же областью, если оба имеют одинаковую степень и первый кубатурное правило использует меньше точек, чем второе.

В наших таблицах мы даем следующую информацию о кубатуре правила и встроенные последовательности в дополнение к степени, d и соответствующие количество точек интеграции, N , а именно качество и Рекомендации. Качество кубатурного правила определяется одной или двумя буквами, которые используйте небольшое расширение обозначений, введенных в [LJ75]. Первый буква дает информацию о весах ш _я . Если все w _i положительные, мы обозначаем это буквой P , если только они не все равны, и в этом случае мы используем букву E . Если некоторые w _i отрицательны, указываем это буквой N . Иногда только точки кубатурного правила публикуются, а не веса, так как они могут быть довольно легко вычислить, решив систему линейных уравнений. В В этом случае мы заменяем первую букву знаком вопроса. Второй буква появляется только для ограниченных областей B _n и дает информацию о расположении точек интеграции x _i . Если все х _i B , то обозначаем это буквой I если только некоторые из x _i не лежат на границе B _n в в этом случае мы используем букву B . Если некоторые x _i B , мы пишем О . В случае вложенной последовательности, состоящей из p кубатурные правила, p или p+1 буквы используются в зависимости от того, B _n все пространство или нет. В последнем случае последняя буква дать информацию о точках интегрирования в последнем кубатурном правиле последовательности, а именно высшей степени. Во всех случаях первые p буквы дают информацию о весе всех кубатурных правила в последовательность, начинающаяся с кубатурного правила низшей степени. В колонке качества мы также указываем количество кубатурных правил, которые имеют одинаковые значения д и Н и одинакового качества. Если существует однопараметрическое семейство кубатурных правил с одинаковыми характеристиками, обозначим это бесконечностью символ, .

Теперь мы даем рекомендации для записей в столбце ссылок. которые мы постарались сделать как можно короче, хотя мы стараемся предоставить все полезные ссылки. Как руководитель ссылка, мы даем первое появление кубатурного правила в журнале или книге даже если он ранее появлялся во внутреннем отчете или диссертации. Иногда эта ссылка дополняется второй ссылкой, которая исправляет некоторые недостатки в первой ссылке или которая выводит одно и то же кубатурное правило в другом контексте. Другой случай, когда дополнительные ссылки включены, происходит, когда более поздняя статья содержит все кубатурные правила в более ранней статье, а также множество дополнительных. В этом случае мы хотите избавить пользователя от необходимости обращаться к двум ссылкам когда вся информация, которую он требует, появляется в более поздней статье. Внутренние отчеты и тезисы упоминаются только в том случае, если кубатурное правило не появиться в журнале или книге. Изучив кубатурные правила в таблицах, читатель может заметить, что в во многих случаях менее эффективные кубатурные правила вычислялись уже после появления более эффективных либо в [Str71], либо в другом месте. Один из возможных объяснение этому в том, что было вычислено менее эффективное кубатурное правило в качестве примера для иллюстрации конкретной теории построения кубатурных правил. Читатель также может заметить, что мы включили некоторые кубатурные правила. из [Str71], хотя нашей явной целью было представить кубатурные правила, которые не появлялся в [Str71]. Одной из причин этого является то, что во многих случаях кубатурное правило в [Str71] минимально, и мы хотели, чтобы читатель информации, поскольку мы добавляем звездочку ко всем кубатурным правилам, которые, как известно, содержат теоретически минимальное количество баллов. Другая причина состоит в том, чтобы избегайте пробелов в таблицах, так как исходите из одного значения д к другое значение d ₁ > d + 2 . Наконец, кубатурное правило из [Str71] не может быть минимален среди всех кубатурных правил данной степени, но все же имеет некоторые дополнительная полезная функция, которой нет в других кубатурных правилах. Итак, если в [Str71] указана формула, которая является PI и ни одна из известных формулы с меньшим количеством узлов — это PI, мы включаем ссылку на [Стр71]. Мы не даем дополнительных ссылок на кубатурные правила, появившиеся в [Стр71].

Все кубатурные правила в наших таблицах являются кубатурными правилами, для которых либо числа, либо формулы даны в справочниках по пунктам х _и и, в большинстве случаев, для гирь w _i . Поэтому мы не включили кубатурные правила в [Hue73], которые даны как функции моментов, ни кубатурные правила в [CH86a,Kea79], которые представляют значительный интерес и могут генерироваться по алгоритму, указанному там.

Эта страница была последний раз изменена в понедельник, 17 июня 2002 г., 16:11:28 CEST.

[PDF] НАБОР ПРАВИЛ СИММЕТРИЧНОЙ КВАДРАТУРЫ НА ТРЕУГОЛЬНИКАХ И ТЕТРАЭДРАХ

Идентификатор корпуса: 18353875

 @inproceedings{Linbo2009ASO,
  title={НАБОР ПРАВИЛ СИММЕТРИЧНОЙ КВАДРАТУРЫ НА ТРЕУГОЛЬНИКАХ И ТЕТРАЭДРАХ},
  автор={Линьбо, и Чжан, и Тао, и Цуй, и Хуэй, и Лю},
  год = {2009}
}

Линьбо, Чжан, Лю
Опубликовано в 2009 г.
Информатика, математика

Мы представляем программу для вычисления симметричных квадратурных правил на треугольниках и тетраэдрах. Набор правил получается с помощью этой программы. Были получены квадратурные правила до 21-го порядка для треугольников и до 14-го порядка для тетраэдров, которые полезны для использования в вычислениях методом конечных элементов. Все представленные здесь правила имеют положительные веса с точками, лежащими в области интегрирования.

lsec.cc.ac.cn

Симметричные квадратурные правила для тетраэдров на основе кубической плотноупакованной решетки

Об идентификации симметричных квадратурных правил для методов конечных элементов

F. Witherden, P. Vincent
Математика
Вычисл. Мат. заявл.
2015

Кубатурные правила высокого порядка для тетраэдров

В этой статье мы строим новые схемы численного интегрирования высокого порядка для тетраэдров с положительными весами и точками интегрирования, которые находятся внутри области. Строительство…

Эффективное вычисление кубатурных правил с применением новых асимметричных правил на треугольнике

Симметричные кубатурные правила высокого порядка для тетраэдров и пирамид

В этой статье мы представляем алгоритм построения полностью симметричных кубатурных правил высокого порядка для тетраэдров и пирамид. пирамидальные элементы с положительными весами и точками интегрирования, которые находятся в…

Эффективные квадратурные правила для вычисления матриц жесткости тетраэдрических элементов с сосредоточенными массами для линейных волновых задач

Мы представляем новые и эффективные квадратурные правила для вычисления матриц жесткости тетраэдрических элементов с сосредоточенными массами для моделирования распространения волн. Эти квадратурные правила позволяют более эффективно…

Базисы с ограничениями, согласующиеся с дивергенцией высокого порядка, для треугольных ячеек

В этой статье представлен алгебраический метод для создания базисов, соответствующих дивергенции произвольного порядка, для криволинейных треугольных ячеек путем применения соответствующих ограничений на линейная комбинация общих функций и извлечение желаемых базисов с использованием разложения по сингулярным числам.

Численные квадратуры высокого порядка в тетраэдре с неявно заданным криволинейным интерфейсом

Универсальный, надежный и численный алгоритм высокого порядка, который разлагает трехмерные интегралы по объему или двумерные поверхностные интегралы на несколько одномерных интегралов и вычисляет одномерные интегралы с помощью Гаусса. квадратуры.

Семейство симметричных оптимизированных квадратурных правил для пентатопов

Дэвид М. Уильямс, К. Фронтин, Э. А. Миллер, Д. Дармофал
Математика, информатика
Вычисл. Мат. заявл.
2020

Вычисление полностью симметричных кубатурных правил умеренной степени на треугольнике с использованием симметричных многочленов и алгебраического решения

Стефанос-Альдо Папаниколопулос
Математика, Информатика 90.56 Мат. заявл.
2015

ПОКАЗАНЫ 1-10 ИЗ 13 ССЫЛОК

СОРТИРОВАТЬ ПОРелевантность Наиболее влиятельные документыНедавность

Симметричные квадратурные правила на треугольнике

S. Wandzurat, Hong Xiao
Математика
2003

Алгорит кардинальной функции.

SIAM J. Нумер. Анальный.

2007

Представлен новый алгоритм численного вычисления квадратурных формул для произвольных областей, точно интегрирующих заданное полиномиальное пространство, который основан на построении кардинальных функций и, таким образом, требует, чтобы число точек квадратур равнялось размерности заданного полинометрического пространства меньшей размерности.

Построение полностью симметричных кубатурных формул для сферы

Сангву Хео, Юань Сюй
Математика
Матем. вычисл.
2001

Построим симметричные кубатурные формулы степеней в диапазоне 13-39 для поверхностной меры на единичной сфере. Мы используем недавно опубликованное соответствие между кубатурными формулами на…

Дискретный анализ Фурье, кубатура и интерполяция на шестиугольнике и треугольнике

Изучены некоторые задачи тригонометрической аппроксимации на шестиугольнике и треугольнике с помощью дискретного преобразования Фурье и ортогональных полиномов двух переменных и кубатурных формул и интерполяции на этих областях.

Сборник формул интегрирования FEM для символьной работы

C. Felippa
Математика
2004

как есть» в поддержку работы с символическими МКЭ, что позволяет избежать загрязнения плавающей арифметикой, препятствующей упрощению.

Таблица кубатурник: Кубатурник круглого леса — скачать таблицу кубатурник леса от 1 до 12 метров