Кубатурник бруса и обрезной доски
Объем бруса и доски высчитывается по формуле: объем = A * B * L (длина)
Таблица кубатуры обрезного бруса, длина — 6м:
| Брус, мм | Кол-во брусьев в 1 м.куб. | Кол-во пог. метров в 1 м.куб. | Объём 1 бруса, м.куб |
| 50*50*6000мм | 66,67 | 400 | 0,015 |
| 50*100*6000мм | 33,33 | 200 | 0,03 |
| 60*60*6000мм | 46,3 | 277,78 | 0,0216 |
| 60*100*6000мм | 27,78 | 166,67 | 0,036 |
| 100*100*6000мм | 16,67 | 100 | 0,06 |
| 100*150*6000мм | 11,11 | 66,67 | 0,09 |
| 100*200*6000мм | 8,33 | 50 | 0,12 |
| 125*125*6000мм | 10,67 | 64 | 0,09375 |
| 150*150*6000мм | 7,41 | 44,44 | 0,135 |
| 150*200*6000мм | 5,56 | 33,36 | 0,18 |
| 180*180*6000мм | 5,1 | 30,6 | 0,19 |
| 180*200*6000мм | 4,6 | 27,6 | 0,21 |
| 200*200*6000мм | 4,17 | 25 | 0,24 |
| 200*250*6000мм | 3,33 | 20 | 0,3 |
| 250*250*6000мм | 2,67 | 16 | 0,375 |
Таблица кубатуры доски обрезной, длина — 6м:
|
Доска обрезная, мм |
Кол-во досок в 1 м. куб. куб. |
Кол-во пог. метров в 1 м.куб. |
Объём 1 доски, м.куб |
Площадь 1 доски, кв.м. |
| 20*150*6000мм | 55,6 | 333,3 | 0,018 | 0,9 |
| 25*100*6000мм | 66,7 | 400 | 0,015 | 0,6 |
| 25*175*6000мм | 38,1 | 228,6 | 0,02625 | 1,05 |
| 25*200*6000мм | 33,3 | 200 | 0,03 | 1,2 |
| 32*100*6000мм | 52,1 | 312,5 | 0,0192 | 0,6 |
| 32*125*6000мм | 41,7 | 250 | 0,024 | 0,75 |
| 32*150*6000мм | 34,7 | 208,3 | 0,0288 | 0,9 |
| 32*175*6000мм | 29,8 | 178,6 | 0,0336 | 1,05 |
| 32*200*6000мм | 26 | 156,3 | 0,0384 | 1,2 |
| 40*100*6000мм | 41,7 | 250 | 0,024 | 0,6 |
| 40*125*6000мм | 33,3 | 200 | 0,03 | 0,75 |
| 40*150*6000мм | 27,8 | 166,7 | 0,036 | 0,9 |
| 40*175*6000мм | 23,8 | 142,9 | 0,042 | 1,05 |
| 40*200*6000мм | 20,8 | 125 | 0,048 | 1,2 |
| 50*100*6000мм | 33,3 | 200 | 0,03 | 0,6 |
| 50*125*6000мм | 26,7 | 160 | 0,0375 | 0,75 |
| 50*150*6000мм | 22,2 | 133,3 | 0,045 | 0,9 |
| 50*175*6000мм | 19 | 114,3 | 0,0525 | 1,05 |
| 50*200*6000мм | 16,7 | 100 | 0,06 | 1,2 |
| 50*225*6000мм | 14,8 | 88,9 | 0,0675 | 1,35 |
| 50*250*6000мм | 13,3 | 80 | 0,075 | 1,5 |
Таблица кубатуры обрезного бруса, длина — 4м:
| Брус, мм | Кол-во брусьев в 1 м.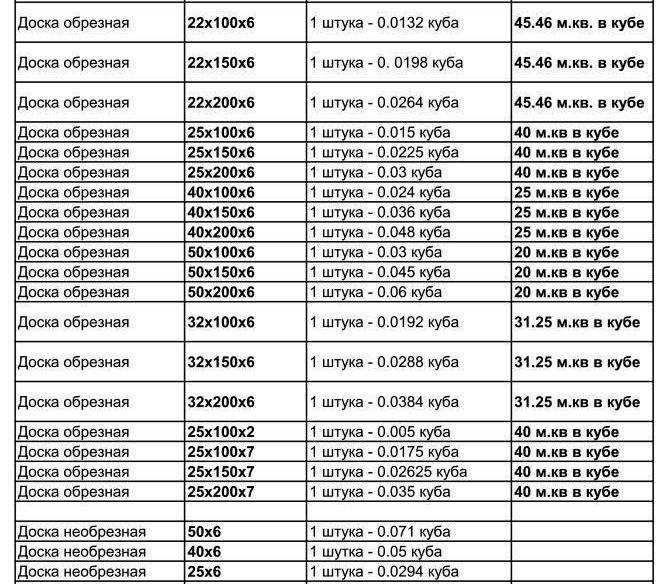 куб. куб. |
Кол-во пог. метров в 1 м.куб. | Объём 1 бруса, м.куб |
| 50*50*4000мм | 100 | 400 | 0,01 |
| 50*100*4000мм | 200 | 0,02 | |
| 60*60*4000мм | 69,4 | 277,7 | 0,0144 |
| 60*100*4000мм | 41,6 | 166,6 | 0,024 |
| 100*100*4000мм | 25 | 100 | 0,04 |
| 100*150*4000мм | 16,6 | 66,6 | 0,06 |
| 100*200*4000мм | 12,5 | 50 | 0,08 |
| 125*125*4000мм | 16 | 64 | 0,0625 |
| 150*150*4000мм | 11,1 | 44,44 | 0,09 |
| 150*200*4000мм | 8,3 | 33,33 | 0,12 |
| 180*180*4000мм | 7,7 | 30,7 | 0,1296 |
| 180*200*4000мм | 6,9 | 27,7 | 0,144 |
| 200*200*4000мм | 6,2 | 25 | 0,16 |
| 200*250*4000мм | 5 | 20 | 0,2 |
| 250*250*4000мм | 4 | 16 | 0,25 |
Таблица кубатуры доски обрезной, длина — 4м:
|
Доска обрезная, мм |
Кол-во досок в 1 м. куб. куб. |
Кол-во пог. метров в 1 м.куб. |
Объём 1 доски, м.куб |
Площадь 1 доски, кв.м. |
| 20*150*4000мм | 83,3 | 333,3 | 0,012 | 0,6 |
| 25*100*4000мм | 100 | 400 | 0,01 | 0,4 |
| 25*175*4000мм | 57,1 | 228,6 | 0,0175 | 0,7 |
| 25*200*4000мм | 50 | 200 | 0,02 | 0,8 |
| 32*100*4000мм | 78,1 | 312,5 | 0,0128 | 0,4 |
| 32*125*4000мм | 62,5 | 250 | 0,016 | 0,5 |
| 32*150*4000мм | 52 | 208 | 0,0192 | 0,6 |
| 32*175*4000мм | 44,6 | 178,6 | 0,0224 | 0,7 |
| 32*200*4000мм | 39 | 156 | 0,0256 | 0,8 |
| 40*100*4000мм | 62,5 | 250 | 0,016 | 0,4 |
| 40*125*4000мм | 50 | 200 | 0,02 | 0,5 |
| 40*150*4000мм | 41,6 | 166,6 | 0,024 | 0,6 |
| 40*175*4000мм | 35,7 | 142,8 | 0,028 | 0,7 |
| 40*200*4000мм | 31,25 | 125 | 0,032 | 0,8 |
| 50*100*4000мм | 50 | 200 | 0,02 | 0,4 |
| 50*125*4000мм | 40 | 160 | 0,025 | 0,5 |
| 50*150*4000мм | 33,3 | 133,3 | 0,03 | 0,6 |
| 50*175*4000мм | 28,5 | 114,3 | 0,035 | 0,7 |
| 50*200*4000мм | 25 | 100 | 0,04 | 0,8 |
| 50*225*4000мм | 22,2 | 88,8 | 0,045 | 0,9 |
| 50*250*4000мм | 20 | 80 | 0,05 | 1 |
Количество пиломатериалов в штуках/объем в кубических метрах:
| наименование | 1м.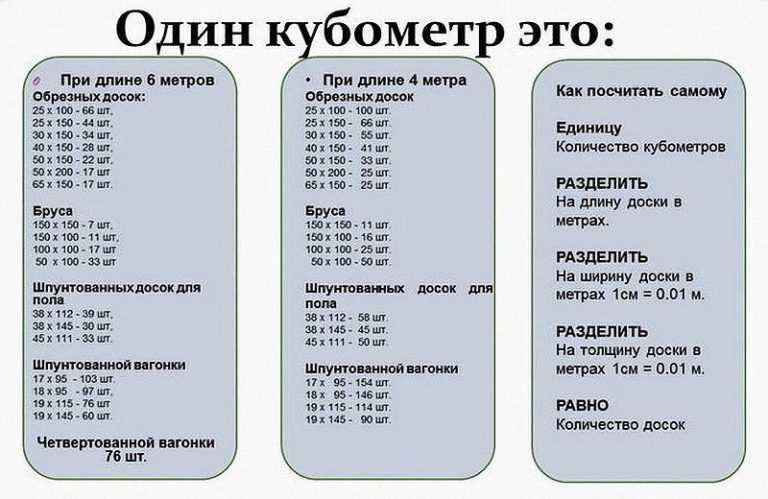 куб. куб. |
2м.куб. | 3м.куб. | 4м.куб. | 5м.куб. | 6м.куб. | 7м.куб. | 8м.куб. | 9м.куб. | 10м.куб. |
| доска обрезная 25*100*6000 | 67/1.005 | 134/2,01 | 200/3,00 | 267/4,005 | 334/5,01 | 400/6,00 | 467/7,005 | 534/8,01 | 600/9,00 | 67/10,005 |
| доска обрезная 25*150*6000 | 45/1,013 | 89/2,003 | 134/3,015 | 178/4,005 | 223/5,018 | 267/6,008 | 312/7,02 | 356/8,01 | 400/9,00 | 445/10,013 |
| доска обрезная 40*100*6000 | 42/1,008 | 84/2,016 | 125/3,00 | 167/4,008 | 209/5,016 | 250/6,00 | 292/7,008 | 334/8,016 | 375/9,00 | 417/10,008 |
| доска обрезная 40*150*6000 | 28/1,008 | 56/2,016 | 84/3,024 | 112/4,032 | 139/5,004 | 167/6,012 | 195/7,02 | 223/8,028 | 250/9,00 | 278/10,008 |
| доска обрезная 50*100*6000 | 34/1,02 | 67/2,01 | 100/3,00 | 134/4,02 | 167/5,01 | 200/6,00 | 234/7,02 | 300/9,00 | 334/10,02 | |
| доска обрезная 50*150*6000 | 23/1,035 | 45/2,025 | 67/3,05 | 89/4,005 | 112/5,04 | 134/6,03 | 156/7,02 | 178/8,01 | 200/9,00 | 223/10,035 |
| доска обрезная 50*200*6000 | 17/1,02 | 34/2,04 | 50/3,00 | 67/4,02 | 84/5,04 | 100/6,00 | 117/7,02 | 134/8,04 | 150/9,00 | 167/10,02 |
| брус 100*100*6000 | 17/1,02 | 34/2,04 | 50/3,00 | 67/4,02 | 84/5,04 | 100/6,00 | 117/7,02 | 134/8,04 | 150/9,00 | 167/10,02 |
| брус 100*150*6000 | 12/1,08 | 23/2,07 | 34/3,06 | 45/4,05 | 56/5,04 | 67/6,03 | 78/7,02 | 89/8,01 | 100/9,00 | 112/10,08 |
| брус 150*150*6000 | 8/1,08 | 15/2,025 | 23/3,105 | 30/4,05 | 38/5,13 | 45/6,075 | 52/7,02 | 60/8,10 | 67/9,045 | 75/10,125 |
| брус 150*200*6000 | 6/1,08 | 12/2,16 | 17/3,06 | 23/4,14 | 28/5,04 | 34/6,12 | 39/7,02 | 45/8,10 | 50/9,00 | 56/10,08 |
| брус 200*200*6000 | 5/1,2 | 9/2,16 | 13/3,12 | 17/4,08 | 21/5,04 | 25/6,00 | 30/7,20 | 34/8,16 | 38/9,12 | 42/10,08 |
Таблица кубатуры обрезной доски: система расчетов
Содержание
- Виды
- Обрезная
- Необрезная
- Показатели кубатуры
- Формулы для расчёта
- Сколько в 1 кубе досок: специальные таблицы
- Таблица количества обрезной доски в 1 кубометре
- Таблица количества бруса в 1 кубометре
- Таблица количества необрезной доски в 1 кубометре
- Калькуляторы кубатуры досок
- Калькулятор расчета количества досок в кубе
- Калькулятор расчета кубатуры досок по их количеству
- Что собой представляет кубатура
- Расчет кубатуры доски обрезной
- Что такое доска дюймовка и как высчитать её кубатуру
- Расчет кубатуры доски необрезной
- Что ещё нужно знать при подсчете необходимого количества пиломатериалов
- Кубатурник бруса
Виды
Обрезная
Обрезная доска больше подходит для чистовой отделки. Там, где нужна аккуратность и презентабельный внешний вид. Отличие от необрезной — ровный пропил не только по пластям, но и по кромкам. Материал используют для решения следующих задач:
Там, где нужна аккуратность и презентабельный внешний вид. Отличие от необрезной — ровный пропил не только по пластям, но и по кромкам. Материал используют для решения следующих задач:
Обрешётка кровельных систем.
Обивка стен каркасных построек.
Создание лестниц.
Производство мебели.
Необрезная
Как понятно из названия, необрезная доска отличается тем, что её кромки не спилены. Грубоватая «внешность» определяет сферу применения пиломатериала. Его используют в основном для строительства:
Складских помещений.
Кладовок и подсобок.
Заборов временного характера.
Навесных конструкций.
Не столь важно, какую доску использовать. Главная задача — провести предварительные расчёты
Это позволит сократить лишние расходы.
Показатели кубатуры
Чтобы читатели не занимались перемножением, мы подготовили таблицу со стандартными параметрами.
В списке не только кубатура, но и количество с метражом (площадью) хвойного пиломатериала:
| Размеры, мм | Объём штуки, м³ | Штук в 1 м³ | Площадь, м² |
| 25×75×6000 | 0,011 | 90 | 40,5 |
| 25×100×6000 | 0,015 | 67 | 40,2 |
| 25×125×6000 | 0,018 | 55 | 41,2 |
| 25×150×6000 | 0,0225 | 44 | 39,6 |
| 25×175×6000 | 0,026 | 38 | 39,9 |
| 25×200×6000 | 0,03 | 33 | 39,6 |
| 25×225×6000 | 0,033 | 30 | 40,5 |
| 25×250×6000 | 0,0375 | 26 | 39 |
| 25×275×6000 | 0,041 | 24 | 39,6 |
| 25×75×4000 | 0,0075 | 133 | 39,9 |
| 25×100×4000 | 0.01 | 100 | 40 |
| 25×125×4000 | 0,0125 | 80 | 40 |
| 25×150×4000 | 0,015 | 66 | 39,6 |
| 25×175×4000 | 0,0175 | 57 | 39,9 |
| 25×200×4000 | 0,02 | 50 | 40 |
| 25×225×4000 | 0,0225 | 44 | 39,6 |
| 25×250×4000 | 0,025 | 40 | 40 |
| 25×275×4000 | 0,0275 | 36 | 39,6 |
Аналогичные показатели для лиственного пиломатериала:
| Размеры, мм | Объём штуки, м³ | Штук в 1 м³ | Площадь, м² |
| 25×60×6000 | 0,009 | 111 | 39,96 |
| 25×70×6000 | 0,0105 | 95 | 39,9 |
| 25×80×6000 | 0,012 | 83 | 39,84 |
| 25×90×6000 | 0,0135 | 74 | 39,96 |
| 25×100×6000 | 0,015 | 66 | 39,6 |
| 25×110×6000 | 0,0165 | 60 | 39,6 |
| 25×130×6000 | 0,0195 | 51 | 39,78 |
| 25×150×6000 | 0,0225 | 44 | 39,6 |
| 25×180×6000 | 0,027 | 37 | 39,96 |
| 25×200×6000 | 0,03 | 33 | 39,6 |
| 25×60×4000 | 0,006 | 166 | 39,84 |
| 25×70×4000 | 0,007 | 142 | 39,76 |
| 25×80×4000 | 0,008 | 125 | 40 |
| 25×90×4000 | 0,009 | 111 | 39,96 |
| 25×100×4000 | 0,01 | 100 | 40 |
| 25×110×4000 | 0,011 | 90 | 39,6 |
| 25×130×4000 | 0,013 | 76 | 39,52 |
| 25×150×4000 | 0,015 | 66 | 39,6 |
| 25×180×4000 | 0,018 | 55 | 39,6 |
| 25×200×4000 | 0,02 | 50 | 40 |
Длина в 6 и 4 метра — это стандарт. Бывает меньше. Как раз на такой случай существуют формулы для расчётов.
Бывает меньше. Как раз на такой случай существуют формулы для расчётов.
Формулы для расчёта
В таблице может не хватать индивидуальных размеров, поэтому предлагаем ознакомиться с тремя формулами расчёта для объёма, кубатуры и площади. В качестве примера возьмём следующие характеристики:
Миллиметры нам не подходят, поэтому преобразуем их в метры, поделив на 1000:
Формула для получения объёма одной штуки будет такая (перемножаем стороны и толщину):
Чтобы посчитать количество штук в кубе, разделим 1 м³ на объём:
Осталось получить площадь материала в одном кубе. Для этого умножаем длину на ширину, а результат умножаем на количество штук:
Арифметика не слишком простая, но позволит заранее прикинуть, сколько нужно материала. А теперь разберёмся с вопросом о том, какую доску лучше использовать: обрезную или необрезную?
Сколько в 1 кубе досок: специальные таблицы
Чтобы вычислить, какое именно число досок определенной ширины, длины в 1 кубометре, применяются разнообразные таблицы. Далее указаны несколько таких специализированных таблиц, где указана кубатура распространенных и востребованных на сегодняшний день типов этого материала. Рассчитать объем различных досок, имеющих различные размеры, к примеру, материала для возведения забора на своем участке, имеется возможность самостоятельно, используя имеющуюся формулу, которая представлена выше.
Далее указаны несколько таких специализированных таблиц, где указана кубатура распространенных и востребованных на сегодняшний день типов этого материала. Рассчитать объем различных досок, имеющих различные размеры, к примеру, материала для возведения забора на своем участке, имеется возможность самостоятельно, используя имеющуюся формулу, которая представлена выше.
Таблица количества обрезной доски в 1 кубометре
| Размер доски | Объем 1-й доски (м3) | Количество досок в 1м3 (шт.) | Количество метров квадратных в 1м2 |
|---|---|---|---|
| Двадцатка | |||
| Доска 20х100х6000 | 0,012 м3 | 83 шт. | 50 м2 |
| Доска 20х120х6000 | 0,0144 м3 | 69 шт. | 50 м2 |
| Доска 20х150х6000 | 0,018 м3 | 55 шт. | 50 м2 |
| Доска 20х180х6000 | 0,0216 м3 | 46 шт. | 50 м2 |
| Доска 20х200х6000 | 0,024 м3 | 41 шт. | 50 м2 |
| Доска 20х250х6000 | 0,03 м3 | 33 шт. | 50 м2 |
| Двадцатьпятка | |||
| Доска 25х100х6000 | 0,015 м3 | 67 шт. | 40 м2 |
| Доска 25х120х6000 | 0,018 м3 | 55 шт. | 40 м2 |
| Доска 25х150х6000 | 0,0225 м3 | 44 шт. | 40 м2 |
| Доска 25х180х6000 | 0,027 м3 | 37 шт. | 40 м2 |
| Доска 25х200х6000 | 0,03 м3 | 33 шт. | 40 м2 |
| Доска 25х250х6000 | 0,0375 м3 | 26 шт. | 40 м2 |
| Тридцатка | |||
| Доска 30х100х6000 | 0,018 м3 | 55 шт. | 33 м2 |
| Доска 30х120х6000 | 0,0216 м3 | 46 шт. | 33 м2 |
| Доска 30х150х6000 | 0,027 м3 | 37 шт. | 33 м2 |
| Доска 30х180х6000 | 0,0324 м3 | 30 шт. | 33 м2 |
| Доска 30х200х6000 | 0,036 м3 | 27 шт. | 33 м2 |
| Доска 30х250х6000 | 0,045 м3 | 22 шт. | 33 м2 |
| Тридцатидвушка | |||
| Доска 32х100х6000 | 0,0192 м3 | 52 шт. | 31 м2 |
| Доска 32х120х6000 | 0,023 м3 | 43 шт. | 31 м2 |
| Доска 32х150х6000 | 0,0288 м3 | 34 шт. | 31 м2 |
| Доска 32х180х6000 | 0,0346 м3 | 28 шт. | 31 м2 |
| Доска 32х200х6000 | 0,0384 м3 | 26 шт. | 31 м2 |
| Доска 32х250х6000 | 0,048 м3 | 20 шт. | 31 м2 |
| Сороковка | |||
| Доска 40х100х6000 | 0,024 м3 | 41 шт. | 25 м2 |
| Доска 40х120х6000 | 0,0288 м3 | 34 шт. | 25 м2 |
| Доска 40х150х6000 | 0,036 м3 | 27 шт. | 25 м2 |
| Доска 40х180х6000 | 0,0432 м3 | 23 шт. | 25 м2 |
| Доска 40х200х6000 | 0,048 м3 | 20 шт. | 25 м2 |
| Доска 40х250х6000 | 0,06 м3 | 16 шт. | 25 м2 |
| Пятидесятка | |||
| Доска 50х100х6000 | 0,03 м3 | 33 шт. | 20 м2 |
| Доска 50х120х6000 | 0,036 м3 | 27 шт. | 20 м2 |
| Доска 50х150х6000 | 0,045 м3 | 22 шт. | 20 м2 |
| Доска 50х180х6000 | 0,054 м3 | 18 шт. | 20 м2 |
| Доска 50х200х6000 | 0,06 м3 | 16 шт. | 20 м2 |
| Доска 50х250х6000 | 0,075 м3 | 13 шт. | 20 м2 |
Таблица количества бруса в 1 кубометре
| Размер бруса | Объем 1-й штуки (м³) | Количество бруса в 1м³ (шт.) |
|---|---|---|
| 100×100×6000 | 0,06 м3 | 16 шт. |
| 100×150×6000 | 0,09 м3 | 11 шт. |
| 150×150×6000 | 0,135 м3 | 7 шт. |
| 100×180×6000 | 0,108 м3 | 9 шт. |
| 150×180×6000 | 0,162 м3 | 6 шт.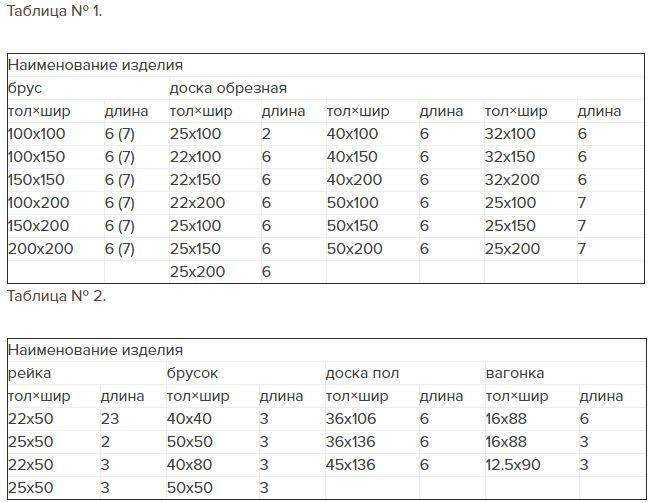 |
| 180×180×6000 | 0,1944 м3 | 5 шт. |
| 100×200×6000 | 0,12 м3 | 8 шт. |
| 150×200×6000 | 0,18 м3 | 5,5 шт. |
| 180×200×6000 | 0,216 м3 | 4,5 шт. |
| 200×200×6000 | 0,24 м3 | 4 шт. |
| 250×200×6000 | 0,3 м3 | 3 шт. |
Таблица количества необрезной доски в 1 кубометре
Размер доски | Объем 1-й доски (м3) | Количество досок в 1м3 (шт.) |
50х6 | 0,071 м3 | 14,08 шт. |
40х6 | 0,05 м3 | 20 шт. |
25х6 | 0,0294 м3 | 34,01 шт. |
Сколько кирпичей в поддоне: вычисления
Сколько в кубе тонн щебня
Памятка застройщику.» src=»https://www.youtube.com/embed/poA-uL9eWw8?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Калькуляторы кубатуры досок
Рассмотрев вышеприведенные формулы, в теории становится понятно, как посчитать кубатуру доски. Для повседневного использования и упрощения рутинного процесса на нашем сайте размещены калькуляторы, осуществляющие онлайн-расчет по различным критериям.
Калькулятор расчета количества досок в кубе
Данный калькулятор осуществляет расчет количества досок в штуках, содержащихся в заданном объеме пиломатериала в кубометрах. Чтобы рассчитать искомый показатель, необходимо ввести в соответствующие поля параметры одной доски (ширина, толщина, длина – в мм) и общий объем досок в м3.
Итоговый результат в штуках может иметь дробное значение, но продавцы пиломатериала, как правило, округляют расчетное количество досок в кубе до ближайшего меньшего целого числа, что также учитывает и наш онлайн-калькулятор.
Калькулятор расчета кубатуры досок по их количеству
Нижеприведенный калькулятор будет полезен, когда возникает задача перевести доски в кубы. В качестве исходных данных, как и для предыдущего онлайн-расчета, используется геометрические размеры одной доски в мм и общее количество досок в штуках, для которых нужно определить их кубатуру в м3.
Что собой представляет кубатура
Сразу стоит отметить, что обращать внимание на тип древесины при расчете кубатуры не стоит, так как показатель не влияет на значение объема, которое необходимо вычислить
Важно лишь понимание того, сколько досок или бревен получит покупатель в кубатуре. Для этого используется простейшая математическая формула, которая связывает габариты каждого отдельного предмета с общим объемом пиломатериала
Для этого используется простейшая математическая формула, которая связывает габариты каждого отдельного предмета с общим объемом пиломатериала.
Различают обработанные породы и необработанные.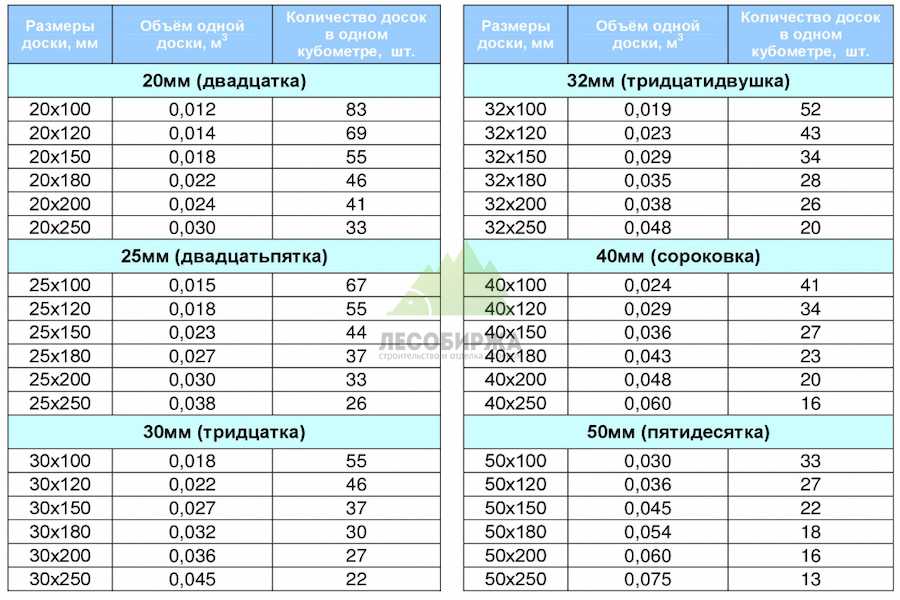
К первым относят шпунтованные виды древесины, которые имеют точные габариты каждого отдельного элемента, а также специальные пазы, служащие для удобства стыковки. Выгода использования подобных пиломатериалов состоит в высоком качестве, которое гарантирует надежное соединение без зазоров. Минусами использования шпунта является то, что при вычислении кубатуры пазы включаются в расчет, а при определении необходимого количество пиломатериала — нет. То есть по факту покупатель переплачивает за дополнительный объем, который не является полезным при работе.
Ко второму виду относят брус, обрезные и необрезанные доски. Причем если первые два вида имеют определенные габариты единицы, то последний вид строительного материала порой вызывает много вопросов из-за достаточно заметной разницы линейных размеров. В частности, чтобы перевести из штук в кубы необработанную древесину, необходимо подобрать размеры каждой определенным образом:
- средняя разница по толщине не должна превышать 2 см;
- средняя разница по ширине не должна превышать 10 см.

При этом уложить штабель из досок необходимо таким образом, чтобы величина зазоров была минимальна, а все более широкие концы находились в одной стороне. Лишь после этого производится замер высоты по центу стопки, а полученный результат умножается на специальный коэффициент, который учитывает воздушные пространства пустот в измеряемом пиломатериале. В результате получается определенная кубатура, которая и выкупается у продавца. Однако такой подсчет подходит только в случае приобретения достаточно большого объема. Если же покупается не более 10 досок, то размер кубатуры рассчитывается для каждой отдельно.
Расчет кубатуры доски обрезной
Как правило, большинство начинающих строителей не задумываются над вопросом «кубометр досок – это сколько, а просто пользуются таблицей, приведенной ниже. Однако мы настоятельно рекомендуем научиться высчитывать кубатуру самостоятельно, это значительно упростит работу, и только в таком случае вы сможете считать себя профессионалом.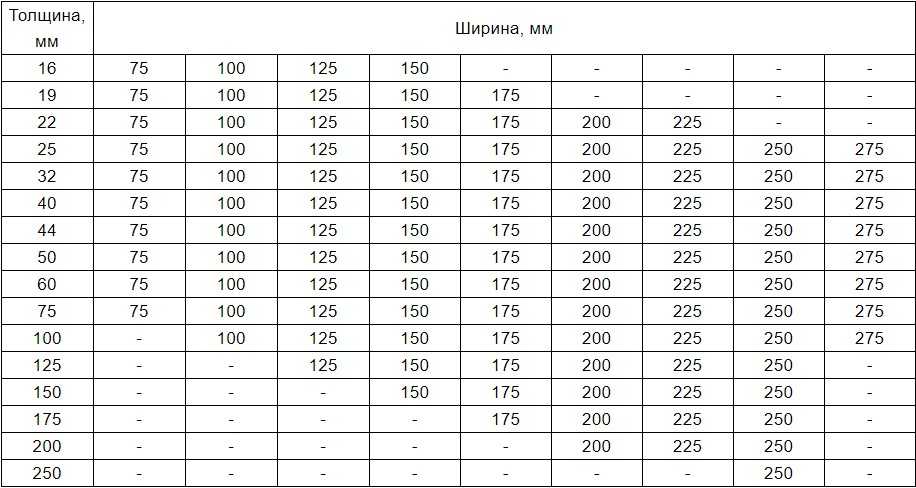
Если сравнивать обрезную доску с необрезной или односторонне-обрезной, на поверхности первой отсутствуют места, где раньше была кора, этот параметр называется обзолом. Небольшой обзол, как правило, допускается, но чем его меньше, тем лучше. Так что в плане геометрии такая доска в гарантировано представляет собой прямоугольный параллелепипед. Эта фигура обладает тремя параметрами: толщиной, шириной, длиной, которые принято выражать буквами a, b, l. Этих показателей достаточно чтобы знать как вычислить кубатуру доски за несколько секунд.
Важно знать, что существует официальный стандарт, по которому доски могут выпускаться только с параметром «a» равным 22, 25, 30, 40, 50, 100 мм. Существуют также другие пиломатериалы, которые изготавливаются из других методом продольного строгания или распила
Их ширина варьируется от 100 до 250 мм, шаг 50 мм. Длина таких досок может быть 3, 4, 6 м.
Формула расчета кубатуры
Толщина * Ширина * Длина
(a * b * l)
Как только вы узнали все величины, можно быстро ответить на вопрос как вычислить кубатуру доски. Перед расчетами вам нужно перевести все величины в метры. Например, у нас есть доска размером 25 мм х 10 см х 4 м, при переводе в метры получается 0. 025, 0.1, 4. Теперь перемножаем эти параметры:
Перед расчетами вам нужно перевести все величины в метры. Например, у нас есть доска размером 25 мм х 10 см х 4 м, при переводе в метры получается 0. 025, 0.1, 4. Теперь перемножаем эти параметры:
0.025 * 0.1 * 4 = 0.01
Теперь единицу делим на полученный результат и узнаем, как высчитать куб досок, а точнее количество досок в кубе древесины.
1 / 0.01 = 100
Таким образом, в кубическом метре будет содержаться 100 досок указанных размеров. Теперь вы можете легко ответить на вопрос как вычислить куб досок, однако вам нужно научиться считать количество необходимого для выполнения работ пиломатериала.
Что такое доска дюймовка и как высчитать её кубатуру
Дюймовка – это лишь название одного из размеров досок, также существуют сороковки, пятерки, брусы, это позволяет строителю быстро сориентироваться о какой доске идет речь. Чтобы узнать сколько в кубе доски дюймовки нужно произвести уже знакомые нам расчеты, в результате которых получится при ширине доски 10 см – 66 штук, при ширине доски 15 см – 44 штуки. Как правило, одного кубометра хватает на покрытие площади в 40 метров квадратных.
Как правило, одного кубометра хватает на покрытие площади в 40 метров квадратных.
Расчет кубатуры доски необрезной
Как уже было сказано, существует также необрезная доска, которая получается в результате продольного распиливания бревен без обработки по бокам. Так что это найти ответ на вопрос сколько досок в кубе необрезной доски обычно несколько сложнее, чем в первом случае. Дело в том, что у необрезных пиломатериалов точно указываются исключительно ширина и длина, а вот ширина может варьироваться. Многое зависит от того, из какой части дерева выпиливается определенная доска. Если вы задаетесь вопросом как считать кубатуру доски необрезной, нужно первым делом задуматься о поставленной задаче.
Например, вам может понадобиться обшить строение, в таком случае вы первым делом узнаете отделочную площадь и умножаете её на толщину обшивки, это позволит высчитать необходимый объем материала. Опишем данную ситуацию в цифрах:
Сколько может понадобиться необрезной доски толщиной 25 мм на обшивку прямоугольного строения 10*5 метров и высотой 3 метра?
Высчитываем всю площадь для отделки, для этого производим умножение периметра здания на его высоту: (10 + 10 + 5 + 5) * 3 = 90 квадратных метров.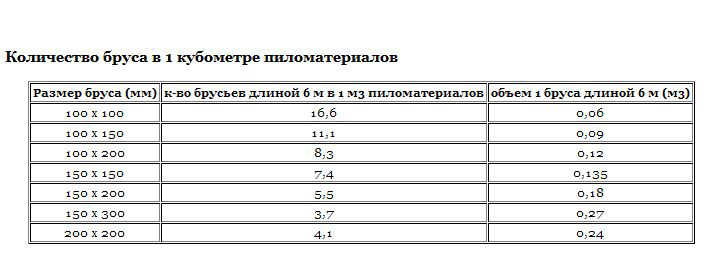 Теперь полученное значение умножаем на толщину материала: 90 * 0.025 (переводим миллиметры в метры) = 2.25 кубометров.
Теперь полученное значение умножаем на толщину материала: 90 * 0.025 (переводим миллиметры в метры) = 2.25 кубометров.
Как вы видите, в данном случае практически не имеет значения ширина отдельного обшивочного элемента, поскольку это не влияет на общую кубатуру. Впрочем, иногда вам все же может пригодиться знание усредненных габаритов доски, что позволит приблизительно узнать сколько необрезной доски в кубе. Эти приблизительные данные указаны в таблице:
Что ещё нужно знать при подсчете необходимого количества пиломатериалов
Всегда помните про погрешность расчетов. Дело в том, что любая фирма-производитель досок всегда округляет цифры в выгодную для себя сторону. Например, доска занимающая объем 0.045 по факту должна быть в кубометре древесины в количестве примерно 22 штуки, однако производитель округляет 0.045 до 0.05, в результате получается уже 20 досок на кубометр. Эта небольшая погрешность может казаться незначительной при объемах в несколько кубометров, однако когда дело идет о сотнях, разница в количестве досок кажется гораздо более существенной, не говоря уже о деньгах. Однако теперь вы определились, как узнать сколько досок в кубе, поэтому расчеты будет производить гораздо проще.
Однако теперь вы определились, как узнать сколько досок в кубе, поэтому расчеты будет производить гораздо проще.
Кубатурник бруса
В приведенных таблицах объемов пиломатериала указывается усредненное значение линейных размеров каждой единицы, например, 100 мм * 100 мм или 150 мм * 250 мм. В результате каждое сечение содержит два показателя — количество брусьев в кубическом метре и объем одного бруса. Поэтому при вычислении стоимости в смете расчет количества пиломатериалов легко определяется.
| Наименование | Размер, мм | Кол-во штук в одном м3 | Кол-во погонных метров в одном м3 | Объём одной штуки, м3 | Вес одной штуки, кг (влажн. 20%) |
|---|---|---|---|---|---|
| Брусок | 50х50х6000 | 66,67 | 400 | 0,015 | 11,25 |
| Брусок | 50х50х3000 | 133,33 | 400 | 0,0075 | 5,625 |
| Брус | 50х100х6000 | 33,33 | 200 | 0,03 | 22,5 |
| Брус | 50х100х3000 | 66,67 | 200 | 0,015 | 11,25 |
| Брусок | 60х60х6000 | 46,3 | 277,78 | 0,0216 | 16,2 |
| Брусок | 60х60х3000 | 92,6 | 277,78 | 0,0108 | 8,1 |
| Брус | 60х100х6000 | 27,78 | 166,67 | 0,036 | 27 |
| Брус | 60х100х3000 | 55,55 | 166,67 | 0,018 | 13,5 |
| Брус | 75х75х6000 | 29,63 | 177,78 | 0,03375 | 25,31 |
| Брус | 75х75х3000 | 59,26 | 177,78 | 0,0169 | 12,675 |
| Брус | 75х100х6000 | 22,22 | 133,33 | 0,045 | 33,75 |
| Брус | 75х100х3000 | 44,44 | 133,33 | 0,0225 | 16,875 |
| Брус | 75х150х6000 | 14,8 | 88,89 | 0,0675 | 50,625 |
| Брус | 100х100х6000 | 16,67 | 100 | 0,06 | 45 |
| Брус | 100х100х3000 | 33,33 | 100 | 0,03 | 22,5 |
| Брус | 100х150х6000 | 11,11 | 66,67 | 0,09 | 67,5 |
| Брус | 100х200х6000 | 8,33 | 50 | 0,12 | 90 |
| Брус | 100х250х6000 | 6,67 | 40 | 0,15 | 112,5 |
| Брус | 125х125х6000 | 10,67 | 64 | 0,09375 | 70,31 |
| Брус | 150х150х6000 | 7,41 | 44,44 | 0,135 | 101,25 |
| Брус | 200х200х6000 | 4,17 | 25 | 0,24 | 180 |
| Брус | 200х250х6000 | 3,33 | 20 | 0,3 | 225 |
| Брус | 250х250х6000 | 2,67 | 16 | 0,375 | 281,25 |
Однако стоит учитывать отклонение от стандартов у различных продавцов. В результате небольшой погрешности может получиться, что в рассчитанном количестве кубов не хватает брусьев, необходимых для строительства
В результате небольшой погрешности может получиться, что в рассчитанном количестве кубов не хватает брусьев, необходимых для строительства
Поэтому крайне важно пользоваться услугами проверенных строительных баз и магазинов
таблица, для разного размера, кубатура, пример
Любые строительные работы начинаются с составления проекта и сметы, которые подразумевают собой расчет количества стройматериала. Не являются исключением и доски, количество которых тоже необходимо правильно рассчитать. Это убережет от лишних денежных затрат в случае избытка или недостачи материала.
Виды пиломатериалов.
Особенности продажи пиломатериалов достаточно сложны, поэтому в некоторых случаях даже контролирующие органы не могут оценить точность отпуска такой продукции. В отличие от большинства других видов строительных материалов, доски продаются не на вес и не поштучно, а рассчитываются в м3. Поэтому нужно знать, как правильно рассчитать куб доски.
В некоторых случаях производители поставляют на рынок сбыта пиломатериал в готовых пакетах, прикрепляя к ним бирку с указанием точного объема и цены такой продукции. Если такая бирка имеется, это значительно упрощает весь процесс расчета. Но это бывает очень редко, так как обычно все измерения осуществляет кладовщик лесозаготовительного предприятия.
Если такая бирка имеется, это значительно упрощает весь процесс расчета. Но это бывает очень редко, так как обычно все измерения осуществляет кладовщик лесозаготовительного предприятия.
Расчет кубатуры напрямую будет зависеть от степени обработки древесины, ее сорта и вида.
Поэтому обрезная и необрезная доски будут рассчитываться по-разному. Также расчет будет зависеть и от породы древесины. Так, для лиственных и хвойных пород можно воспользоваться как замером и перемножением габаритов одного элемента с последующим умножением на их количество, так и стандартом – специальными таблицами (кубатурниками).
Вернуться к оглавлению
Как рассчитать куб обрезной доски
Таблица количества обрезных досок в 1 кубическом метре.
В ассортименте лесозаготовительных компаний обрезная доска – один из самых популярных видов продукции, основная особенность которой заключается в обработке пиломатериала со всех сторон. Сначала бревна распиливаются на доски, после чего они дополнительно опиливаются с боковых сторон. Удаление коры позволяет не только облегчить работу с данным материалом и улучшить его состыковку, но и обезопасить древесину от вредоносных микроорганизмов, которые со временем поражают кору.
Удаление коры позволяет не только облегчить работу с данным материалом и улучшить его состыковку, но и обезопасить древесину от вредоносных микроорганизмов, которые со временем поражают кору.
Чтобы увеличить эксплуатационные характеристики досок, они подвергаются многим операциям обработки, в результате их цена будет значительно выше необрезного варианта. Стоимость стройматериала будет зависеть от его сорта, который может быть отборным, первым, вторым, третьим и четвертым. Чем выше сортность, тем выше будет и стоимость материала.
В определении требуемого объема обрезной доски нет ничего сложного. Эта операция не займет у вас много времени и сил. Расчет будет производиться по формуле: V=l*h*a, где: V – объем пиломатериала, l – длина, h – высота, a – ширина. Например, требуется рассчитать объем одной доски размером 20х100х600 мм. Подставив эти значения в формулу, получим: V=20*100*600=0,02*0,1*6=0,012 м3. Имея данное значение, можно рассчитать количество таких элементов в 1 м3. Для этого нужно 1 м3 разделить на объем одного элемента. Для приведенного примера в 1 м3 будет находиться: 1/0,012=83,3 или 83 шт.
Для этого нужно 1 м3 разделить на объем одного элемента. Для приведенного примера в 1 м3 будет находиться: 1/0,012=83,3 или 83 шт.
Для упрощения расчетов можно воспользоваться кубатурником обрезной доски, представленной в таблице 1.
Таблица 1
| Размер обрезного пиломатериала, мм | Количество элементов длиной 6 м в 1 м3 | Объем одной доски, м3 |
| 25х100 | 66,67 | 0,015 |
| 25х150 | 44,44 | 0,0225 |
| 25х200 | 33,33 | 0,03 |
| 40х100 | 41,67 | 0,024 |
| 40х200 | 20,83 | 0,048 |
| 50х100 | 33,33 | 0,03 |
| 50х200 | 16,67 | 0,06 |
Вернуться к оглавлению
Как рассчитать куб необрезного материала
Схема устройства доски пола.
Необрезной пиломатериал получают посредством продольного распиливания бревен без дальнейшей их обработки по бокам. В связи с этим очень трудно или вовсе невозможно рассчитать кубатуру определенного количества пиломатериала через расчет объема одного элемента.
В отличие от обрезной доски, которая имеет стандартные габариты, у необрезного материала стандартная только толщина и длина, а ширина меняется, потому что она зависит от того, из какого участка бревна выпилен именно этот элемент.
Поэтому расчет кубатуры в этом случае будет производиться по другому принципу.
Например, если поставлена задача обшить здание, то следует просто узнать общую отделочную площадь, после чего умножить ее на толщину обшивки, что и будет требуемым объемом пиломатериала. В качестве примера будет приведена ситуация, когда нужно вычислить, сколько пойдет необрезной доски толщиной 25 мм на обшивку прямоугольного здания 7х4 м с высотой стен 3 м.
Сначала необходимо рассчитать общую отделочную площадь, для чего периметр здания следует умножить на высоту стен: (7+7+4+4)*3=66 м2. Затем данное значение умножается на толщину пиломатериала: 66*0,025=1,65 м3. Какой ширины будут отдельные обшивочные элементы, не играет роли, так как на кубатуру это не влияет.
Затем данное значение умножается на толщину пиломатериала: 66*0,025=1,65 м3. Какой ширины будут отдельные обшивочные элементы, не играет роли, так как на кубатуру это не влияет.
Однако средние габариты одной усредненной доски все же следует знать. В таблице 2 приведен кубатурник необрезного пиломатериала.
Таблица 2
| Толщина доски при длине 6 м, мм | 50 | 40 | 25 |
| Усредненный объем одного элемента, м3 | 0,071 | 0,05 | 0,0294 |
Из данных, приведенных в таблице, можно посчитать, что при толщине материала 50 мм средняя ширина будет равна 230 мм, при 40 мм – приблизительно 210 мм, а при 25 мм – 190 мм. Это логично, потому что более толстые доски изготавливаются из бревен большего сечения.
таблица и расчет количества досок в кубе, кубатуры пиломатериала 6 метров и других размеров
- Что это?
- Особенности расчета
- Сколько материала в 1 кубе?
- Балки
- Доски
Без пиломатериалов не обходится ни одна стройка, но самое главное – это правильный расчет необходимого количества бруса или досок. От этого зависит успех строительства и скорость выполнения работ. Чтобы не выполнять расчеты с нуля, рекомендуется использовать кубатурный ящик.
От этого зависит успех строительства и скорость выполнения работ. Чтобы не выполнять расчеты с нуля, рекомендуется использовать кубатурный ящик.
Что это?
Кабиной называют стол, позволяющий подсчитать количество пиломатериалов, обычно это кругляк. При этом размеры материала должны строго соответствовать всем требованиям ГОСТ для удобства транспортировки, хранения и обработки. Но даже при этом есть отходы, которые при обрезке и резке не идут в строительство.
Кубики и таблицы помогают определить точное количество материалов, необходимых для завершения проекта. Нетрудно догадаться, что для хозяйственного блока, сарая или бани, не говоря уже о малоэтажных частных домах и коттеджах, он будет другим. Таблицы также помогут вам сориентироваться в сочетании веса, объема и размера материалов.
При упрощении расчетов иногда используют специальный строительный калькулятор, где программируются и вводятся все необходимые данные. Но если вам нужно понять, как пользоваться таблицами, а данные, в отличие от калькулятора, есть под рукой, стоит обратить внимание на основную формулу и разобраться в особенностях расчетов.
Но если вам нужно понять, как пользоваться таблицами, а данные, в отличие от калькулятора, есть под рукой, стоит обратить внимание на основную формулу и разобраться в особенностях расчетов.
Особенности расчета
Для того чтобы воспользоваться калькулятором кубатуры, необходимо провести расчет по формуле определения объема: перемножить высоту, длину и ширину изделия между собой. Формула универсальна как для досок, так и для кругляка, поэтому правильно произвести расчет сможет даже новичок в строительстве. Кубическая таблица позволяет максимально быстро рассчитать еще несколько важных для строительства параметров:
- содержание строительного материала или изделия в кубическом метре;
- содержание погонных метров в одном кубическом метре на площадь;
- объем всего товара в целом;
- продуктовая зона.
Все эти параметры очень важны при составлении проекта строительства, независимо от типа сооружения и его сложности. Это дает достаточную точность для расчета необходимого количества ресурсов, а в результате разработчику не приходится тратиться на покупку дополнительных материалов. Также объем и размеры древесины влияют на ее цену. При выборе учитывается, нужен ли вам брус или доска, порода древесины, размер и уровень качества.
Это дает достаточную точность для расчета необходимого количества ресурсов, а в результате разработчику не приходится тратиться на покупку дополнительных материалов. Также объем и размеры древесины влияют на ее цену. При выборе учитывается, нужен ли вам брус или доска, порода древесины, размер и уровень качества.
При таком детальном подходе есть все шансы с первого раза успешно рассчитать требуемый материал, выполнить строительный проект.
Сколько материала в 1 кубе?
Кубатурная измерительная таблица позволяет легко определить точное количество досок или бруса в 1 м3. Таблицы дают возможность разработчику не только не ошибиться в габаритах изделий, но и учитывать вес. Для правильного выбора пиломатериала на пол исходя из этих параметров рекомендуется рассматривать древесину разных пород. Особенно популярны хвойные.
Виды пиломатериалов могут быть разными по своим свойствам и характеристикам. Размеры тоже меняются: есть не только стандартные обрезные доски 4 метра и 6 метров, расчеты по которым приведены в таблицах, но и по 3 или 5 метров включительно.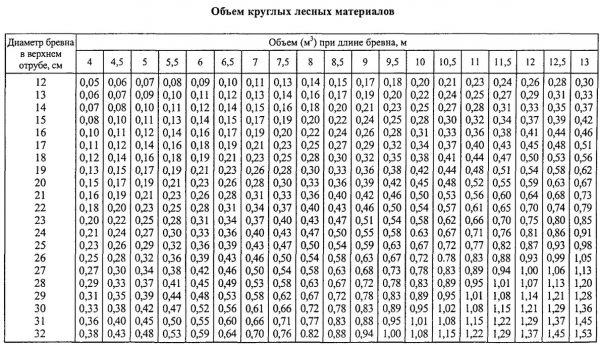 Подбирать пиломатериал можно индивидуально по требуемым размерам, но нужно учитывать, сколько он весит и сколько штук потребуется для строительства и реализации конкретного проекта. Помимо бруса и досок специалисты обращают внимание и на другое сырье.
Подбирать пиломатериал можно индивидуально по требуемым размерам, но нужно учитывать, сколько он весит и сколько штук потребуется для строительства и реализации конкретного проекта. Помимо бруса и досок специалисты обращают внимание и на другое сырье.
- Обапол — имеет частично распиленную внутреннюю поверхность, обычно используется для крепления в горах и при обустройстве участка. В отличие от стандартной обработки плиты, материал не имеет наружной пропиленной полости.
- Горбатый обапол — у него наоборот внешняя часть спилена примерно на половину его общей длины.
- Дощатый настил Обаполя спилен снаружи практически полностью, оставив нетронутой около трети площади.
- Горбыль — круглое бревно, распиленное либо с одной стороны, либо частично. Для таких изделий толщина и ширина обычно нормируются со стороны острых, тонких концов.
- Горбыль с частично распиленной наружной поверхностью.
Очень важно понимать разницу, так как в результате изменится и сфера применения этих материалов; некоторые считают, что они не отличаются друг от друга, что является грубой ошибкой. Но стоит учесть, что область применения того же обапола значительно уже плиты. Последний используется для нескольких целей:
Но стоит учесть, что область применения того же обапола значительно уже плиты. Последний используется для нескольких целей:
- при изготовлении чернового пола;
- при обрешетке крыши;
- при необходимости изготовление опалубки.
Но все же гораздо чаще в строительстве встречаются доски и брус, именно на них нужно обратить основное внимание, чтобы понять, сколько нужно пиломатериалов на кубический метр.
Брус
Брус — пиломатериалы, толщина которых начинается от 100 мм, также различаются высота сечения бруса и его ширина. Но обычно разница между параметрами не превышает значения вдвое. Брус чаще используют при строительстве каркасных или деревянных домов, а также при обустройстве лестниц и ограждений непосредственно внутри помещений. Иногда используется и брус меньшего диаметра сечения: ровно 75 мм. При расчете объема учитываются толщина, средняя ширина и высота стержня. После этого можно рассчитать количество бруса на единицу площади, разделив нужный параметр на единицу. Но гораздо проще воспользоваться специальными таблицами, чем самостоятельно рассчитывать данные или проверять расчеты по данным из таблиц непосредственно на финальном этапе.
После этого можно рассчитать количество бруса на единицу площади, разделив нужный параметр на единицу. Но гораздо проще воспользоваться специальными таблицами, чем самостоятельно рассчитывать данные или проверять расчеты по данным из таблиц непосредственно на финальном этапе.
Что касается цен на стройматериалы, исходя из полученных расчетов, то здесь ситуация интересная. При выборе материала очень важно обращать внимание на тип доски или бруса, так как от этого изменится стоимость сырья. И цена необходимого объема, соответственно, рассчитывается путем умножения на кубический метр. Стоит помнить, что при расчете кубатуры принято округлять числа до целых значений. Поэтому цена 1 доски из конкретного материала может отличаться от всей цены за кубометр. Кроме того, имеет значение и длина доски. Хорошо, если удастся приобрести доску или брус стандартной длины 6 или 4 м, но погрешность может быть разной, и она не учитывается при учете объема и формировании ценовой политики.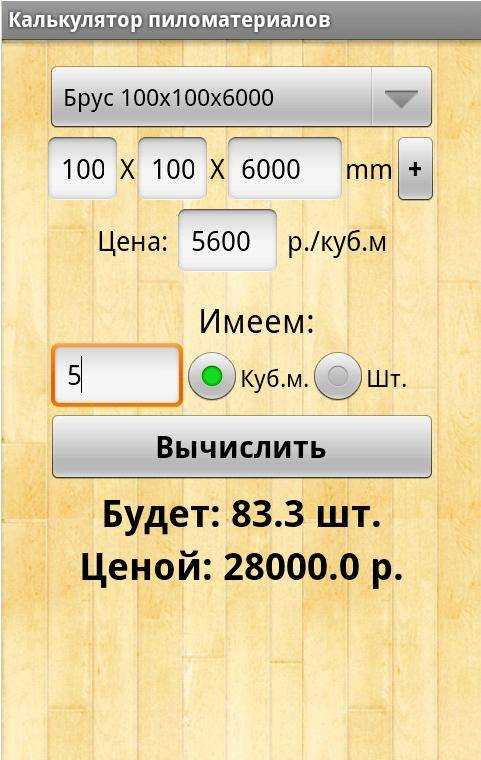 В конечном итоге цена на пиломатериал может вырасти на 1-2%. Эту ошибку необходимо учитывать при покупке большого количества досок или бруса для строительства.
В конечном итоге цена на пиломатериал может вырасти на 1-2%. Эту ошибку необходимо учитывать при покупке большого количества досок или бруса для строительства.
С брусом и необрезной доской ценовая политика формируется точно так же, значения округляются, а для расчета объема берется средняя ширина на концах. Предполагается, что длина материала будет примерно одинаковой. Все расчеты можно провести с помощью обычной рулетки, но при измерении бруса и разных видов досок всегда есть свои тонкости.
Доски
Что касается досок, то важно понимать следующее: доска обрезная и необрезная отличаются друг от друга. И каждый из этих типов имеет свои типоразмеры и свою область применения. Для необрезной доски толщина может быть от 25 до 50 мм при стандартной длине 6 метров. Такие доски хорошо подходят для временных заборов и подсобных помещений. Их используют как основу для облицовки другими отделочными материалами и дополнительно обрабатывают.
Доска обрезная пропилена на лицевой и кромочной и применяется более широко, даже для изготовления всевозможной дачной мебели корпусного типа. необходимое количество материалов. Для этого достаточно длину, ширину и толщину доски перемножить между собой, а чтобы получить точное количество досок, нужно разделить единицу на полученный объем. Например, при толщине 25 мм, ширине 150 и длине 6000 общий объем или кубатура пиломатериала будет равна 0,0225. И разделив единицу на полученное значение, получается, что нам нужно 44 целых доски для строительства без остатков и обрезков.
У необрезной доски расчеты ведутся точно так же, только нужно учитывать небольшую разницу в ширине, так как по швам она не обрезается одинаково. Для расчетов используется его среднее значение, ширина прибавляется с обеих сторон, затем полученное значение делится пополам. Результат обязательно округляется до четного числа, но чтобы не проводить расчеты вручную, всегда можно воспользоваться специальными таблицами.
Следуя такой простой технологии и конкретным цифрам, рассчитать количество необходимого материала совсем не сложно.
Кубатурный фильтр Калмана при минимальной энтропии ошибки с опорными точками для интеграции INS/GPS
| [1] | Б. Паркинсон, Дж. Спилкер, П. Аксельрад и П. Энге, Глобальная система позиционирования: теория и приложения . Норвуд, Массачусетс, США: Artech House, 2008. . |
| [2] | Л. Чанг, Дж. Ли и К. Ли, «Выравнивание на основе оптимизации для бесплатформенной инерциальной навигационной системы: сравнение и расширение», IEEE Trans. Аэросп. Электрон. Сист. , том. 52, нет. 4, стр. 1697–1713, август 2016 г. doi: 10.1109/TAES.2016.130824 |
| [3] | Д. Титтертон и Дж. Уэстон, Бесплатформенная инерциальная навигационная технология . Лондон, Великобритания: Инженерно-технологический институт, 2004 г. |
| [4] | П. Д. Гроувс, Принципы работы ГНСС, инерциальных и мультисенсорных интегрированных навигационных систем . Вашингтон, США: Американский институт аэронавтики и астронавтики, 1996. . |
| [5] | М. Гревал, Л. Вейл и А. Эндрюс, Системы глобального позиционирования, инерциальная навигация и интеграция . Хобокен, Нью-Джерси: John Wiley & Sons, 2007. . |
| [6] | Ф. Чжао, К. Чен, В. Хе и С. Сэм Ге, «Подход к фильтрации, основанный на MMAE для интегрированной навигационной системы БИНС / ЦНС», IEEE/CAA Journal of Automatica Sinica , vol. 5, нет. 6, стр. 1113–1120, ноябрь 2018 г. doi: 10.1109/JAS.2017.7510445 |
| [7] | Ю. Хуанг, Ю. Чжан и Л. Чан, «Новый быстрый метод грубой настройки в движении для недорогих БИНС с помощью GPS», IEEE/ASME Trans. |
| [8] | К. Б. Медейрос и М. М. Вандерли, «Многомодельный линейный фильтр Калмана для непредсказуемых сигналов», IEEE Sensors J. , vol. 14, нет. 4, стр. 979–991, апрель 2014 г. doi: 10.1109/JSEN.2013.2291683 |
| [9] | А. Сингх, «Основные разработки в области фильтрации Гаусса после использования фильтра Калмана без запаха», IEEE/CAA Journal of Automatica Sinica , vol. 7, нет. 5, стр. 1308–1325, сентябрь 2020 г. |
| [10] | С. Джулиер и Дж. Ульманн, «Новое расширение фильтра Калмана для нелинейных систем», в Proc. 11-й междунар. Симп. Аэрокосмическая/оборонная служба, Simul. Элементы управления , 1997, стр. 182–193. |
| [11] | К. Х. Ким, Дж. Г. Ли и К. Г. |
| [12] | Д. Сан, М. Г. Петовелло и М. Э. Кэннон, «Сверхплотная интеграция GPS/уменьшенный IMU для навигации наземных транспортных средств», IEEE Trans. Аэросп. Электрон. Сист. , том. 49, нет. 3, стр. 1781–1791, июль 2013 г. doi: 10.1109/TAES.2013.6558019 |
| [13] | Дж. Вендель, Дж. Мецгер, Р. Моэникес, А. Майер и Г. Ф. Троммер, «Сравнение производительности тесно связанных систем навигации GPS/ИНС на основе расширенных и сигма-точечных фильтров Калмана», Навигация , том. 53, нет. 1, стр. 21–31, август 2014 г. |
| [14] | J. Zhou, Y. Yang, J. Zhang, E. Edwan и O. Loffeld, «Сильная связь INS/GPS с использованием фильтра Калмана без запаха на основе кватернионов», в Proc. |
| [15] | Л. Чанг, К. Ли и Б. Ху, «Надежный фильтр погрешности процесса на основе оценки M компании Huber для интегрированной ИНС/GPS», IEEE Sensors J. , vol. 15, нет. 6, стр. 3367–3374, июнь 2015 г. doi: 10.1109/JSEN.2014.2384492 |
| [16] | И. Арасаратнам и С. Хайкин, «Кубатурные фильтры Калмана», IEEE Trans. автомат. Контроль , том. 54, стр. 1254–1269, июнь 2009 г. doi: 10.1109/TAC.2009.2019800 |
| [17] | B. Cui, X. Chen и X. Tang, «Улучшенный кубатурный фильтр Калмана для GNSS/INS на основе преобразования апостериорной ошибки сигма-точек», IEEE Trans. Сигнальный процесс. , том. 65, нет. 11, стр. 2975–2987, март 2017 г. doi: 10.1109/TSP.2017.2679685 |
| [18] | Ю. |
| [19] | B. Cui, X. Chen, Y. Xu, H. Huang и X. Liu, «Анализ производительности улучшенного повторяющегося кубатурного фильтра Калмана и его применение к GNSS/INS», ISA Trans. , том. 66, стр. 460–468, январь 2017 г. doi: 10.1016/j.isatra.2016.09.010 |
| [20] | М. Д. Фам, К. С. Лоу, С. Т. Гох и С. С. Чен, «Расширенный фильтр Калмана с планированием усиления для системы определения ориентации наноспутников», IEEE Trans. Аэросп. Электрон. Сист. , том. 51, нет. 2015. Т. 2. С. 1017–1028. doi: 10.1109/TAES.2014.130204 |
| [21] | С. В. Бордонаро, П. В., Ю. Бар-Шалом и Т. Лугинбул, «Сигма-точечный фильтр Калмана с преобразованными измерениями для бистатического гидролокатора и радиолокационного слежения», IEEE Trans. |
| [22] | K. Feng, J. Li, X. Zhang, X. Zhang, C. Shen, H. Cao, Y. Yang и J. Liu, «Улучшенный кубатурный фильтр Калмана с сильным отслеживанием для интегрированных навигационных систем GPS/INS, Датчики , об. 18, нет. 6, статья № 1919, июнь 2018 г. doi: 10.3390/s18061919 |
| [23] | X. Chen, C. Shen, WB Zhang, M. Tomizuka, Y. Xu и KL Chiu, «Новый гибрид сильного фильтра Калмана и вейвлетной нейронной сети для GPS/INS во время сбоев GPS», Measurement , vol. 46, нет. 10, стр. 3847–3854, декабрь 2013 г. doi: 10.1016/j.measurement.2013.07.016 |
| [24] | Арулампалам М. С., Маскелл С., Гордон Н. и Клапп Т. «Учебное пособие по фильтрам частиц для онлайн-нелинейного/негауссовского байесовского отслеживания», IEEE Trans. |
| [25] | X. Liu, H. Qu, J. Zhao и P. Yue, «Кубатурный фильтр Калмана с квадратным корнем максимальной коррентропии с применением к интегрированным системам SINS/GPS», ISA Trans. , том. 80, стр. 195–202, май 2018 г. doi: 10.1016/j.isatra.2018.05.001 |
| [26] | JC Príncipe, Информационно-теоретическое обучение: энтропия Реньи и перспективы ядра , Нью-Йорк, штат Нью-Йорк, США: Springer, 2010. |
| [27] | Д. Л. Алспах и Х. Соренсон, «Нелинейная байесовская оценка с использованием приближений суммы Гаусса», IEEE Trans. автомат. Контроль , том. 17, нет. 4, стр. 439–448, август 1972 г. doi: 10.1109/TAC.1972.1100034 |
| [28] | Y. Huang и Y. Zhang, «Новый устойчивый к неопределенности процесса фильтр Калмана на основе t Стьюдента для интеграции SINS/GPS», IEEE Access , vol. |
| [29] | О. Страка и Й. Дуник, «Стохастическая интеграция Студенческая − t filter», в Proc. 20-й междунар. конф. Инф. Fusion , стр. 1–8, июль 2017 г. |
| [30] | Ю. Хуанг и Ю. Чжан, «Надежный стохастический кубатурный фильтр на основе t Стьюдента для нелинейных систем с шумами процессов и измерений с тяжелыми хвостами», IEEE Access , vol. 5, нет. 5, стр. 7964–7974, май 2017 г. |
| [31] | F. Sun и L. Tang, «Кубатурный фильтр частиц», Syst. англ. Электрон. , том. 33, нет. 11, стр. 2554–2557, ноябрь 2011 г. |
| [32] | B. Cui, X. Chen, X. Tang, H. Huang и X. Liu, «Надежный кубатурный фильтр Калмана для GNSS/INS с отсутствующими наблюдениями и цветным шумом измерений», ISA Trans. |
| [33] | Мили Л., Стино Г., Добрака Ф. и Френч Д. Надежный метод оценки для выявления топологических ошибок // IEEE Trans. Система питания , том. 14, нет. 4, стр. 1469–1476, ноябрь 1999 г. doi: 10.1109/59.801932 |
| [34] | Л. Мили и К. В. Коукли, «Надежная оценка в структурированной линейной регрессии», 901:30 Энн. Статист. , том. 24, нет. 6, стр. 2593–2607, декабрь 1996 г. |
| [35] | Ю. С. Шмалий, «Итеративный алгоритм типа Калмана, игнорирующий шум и начальные условия», IEEE Trans. Сигнальный процесс. , том. 59, нет. 6, стр. 2465–2473, июнь 2011 г. doi: 10.1109/TSP.2011.2129516 |
| [36] | Т. Чиен-Хао, С. Ф. Лин и Дж. Дах-Цзин, «Надежный кубатурный фильтр Калмана на основе Губера для обработки GPS-навигации», J. |
| [37] | К. Ли, Б. Ху, Л. Чанг и Ю. Ли, «Надежный квадрат — кубатурный корневой фильтр Калмана на основе методологии оценки Хубера», Proc. Инст. мех. англ. Г-Дж. воздух , том. 229, нет. 7, стр. 1236–1245, июнь 2015 г. doi: 10.1177/0954410014548698 |
| [38] | А. Сингх и Дж. К. Принсипе, «Использование коррентропии как функции стоимости в линейных адаптивных фильтрах», в Proc. Междунар. Совместная конф. Нейронная сеть (IJCNN) , июль 2009 г., стр. 2950–2955. |
| [39] | Б. Чен, Дж. Ван, Х. Чжао, Н. Чжэн и Дж. К. Принсипи, «Сходимость алгоритма с фиксированной точкой по критерию максимальной коррентропии», IEEE Signal Process. лат. , том. 22, нет. 10, стр. 1723–1727, Otc. 2015. doi: 10.1109/LSP.2015.2428713 |
| [40] | B. |
| [41] | Х. Ван, Х. Ли, Дж. Цзо, В. Чжан и Х. Ван, «Надежный фильтр Калмана без производной максимальной коррентропии и сглаживатель», Доступ IEEE , том. 6, стр. 70794–70807, ноябрь 2018 г. doi: 10.1109/ACCESS.2018.2880618 |
| [42] | С. Ван, С. Инь, Г. Цянь, Ю. Фэн, С. Кай и Л. Ван, «Кубатурный фильтр Калмана с максимальной корретропией, основанный на статистической линейной регрессии», C.N. Патент, 106487358 A, 8 марта 2017 г. [Онлайн]. Доступно: https://ieeexplore.ieee.org/document/9546666. |
| [43] | Б. Чен, Л. Син, Б. Сюй, Х. Чжао и Дж. К. Принсипи, «Понимание надежности оценки энтропии с минимальной ошибкой», IEEE Trans. Нейронная сеть. |
| [44] | Д. Эрдогмус и Дж. К. Принсипи., «Минимизация энтропии ошибки для контролируемого обучения нелинейных адаптивных систем», IEEE Trans. Сигнальный процесс. , том. 50, нет. 7, стр. 1780–1786, июль 2002 г. doi: 10.1109/TSP.2002.1011217 |
| [45] | Y. Zhang, B. Chen, X. Liu, Z. Yuan, JC Príncipe, «Сходимость алгоритма энтропии минимальной ошибки с фиксированной точкой», Entropy , vol. 17, нет. 8, стр. 5549–5560, август 2015 г. |
| [46] | Чен Б., Данг Л., Гу Ю., Чжэн Н., Принцип Дж. К., «Энтропийный фильтр Калмана с минимальной ошибкой», IEEE Trans. Сист. , Человек , Киберн. , Сист. , том. 51, нет. 9, стр. 5819–5829, сентябрь 2021 г. |
| [47] | Лю В. |
| [48] | Дж. Чжао и Л. Мили, «Надежный фильтр Калмана с обобщенным максимальным правдоподобием для оценки динамического состояния энергосистемы», IEEE J. Sel. Темы Сигнальный процесс. , том. 12, нет. 4, стр. 578–592, август 2018 г. doi: 10.1109/JSTSP.2018.2827261 |
| [49] | К. Андреу и В. Каратанасси, «Оценка количества конечных элементов с использованием надежного метода обнаружения выбросов», IEEE J. Сел. Темы Наблюдение за Землей. Дистанционный датчик , том. 7, нет. 1, стр. 247–256, январь 2014 г. doi: 10.1109/JSTARS.2013.2260135 |
| [50] | B. Chen, X. Wang, Y. Li, and JC Príncipe, «Критерий максимальной корретропии с переменным центром», IEEE Signal Process. |
| [51] | Б. Чен, С. Ван, З. Юань, П. Рен и Дж. Цинь, «Многоядерная корретропия для надежного обучения», [онлайн]. Доступно: https://ieeexplore.ieee.org/document/9546666. Дата обращения: 15 октября 2021 г. |
| [52] | Б. Ристик, С. Арулампалам и Н. Гордон, Помимо фильтра Калмана: фильтры частиц для приложений отслеживания . Норвуд, Массачусетс, США: Artech House, 2003. |
Кубатурный фильтр Калмана с квадратным корнем без производной для нелинейных бесколлекторных двигателей постоянного тока Академическая исследовательская работа на тему «Электротехника, электроника, информационная инженерия»
IET Electric Power Applications Research Article
кубатурный фильтр Калмана для нелинейных бесколлекторных двигателей постоянного тока
ISSN 1751-8660 Получено 30 апреля 2015 г. Пересмотрено 7 декабря 2015 г. Принято 8 января 2016 г. doi: 10.1049/iet-epa.2015.0414 www.ietdl.org
Пересмотрено 7 декабря 2015 г. Принято 8 января 2016 г. doi: 10.1049/iet-epa.2015.0414 www.ietdl.org
Девендра Потнуру1, Кумар Пакки Бхарани Чандра2 e, Иенкаран Арасаратнам3, Да-Вей Гу4, Карлапуди Элис Мэри5, Сай Бабу Ч6
1Кафедра электротехники и электроники, Технологический институт GMR , Раджам, Андхра-Прадеш, Индия 2Колледж инженерии, математики и физических наук, Эксетерский университет, Великобритания, EX4 4QF 3Apple Inc., Купертино, Калифорния, США, 95051
4Технология управления, инженерный факультет, Лестерский университет, Великобритания , ЛЭ1 7РХ
5Электротехника и электроника, Институт информационных технологий Вигнана, Вишакхапатнам, Андхра-Прадеш, Индия 6Электротехника и электроника, Технологический университет им. Джавахарлала Неру, Какинада, Андхра-Прадеш, Индия ei В статье представлена нелинейная схема оценки квадратного корня для бесщеточных двигателей постоянного тока (BLDC). Кубатурный фильтр Калмана (CKF) является основным инструментом оценки для представленного подхода. CKF — это недавно предложенный метод оценки сильно нелинейных систем, и его эффективность была проверена в нескольких приложениях. Версия CKF с квадратным корнем предпочтительнее обычной CKF для приложений реального времени. Несмотря на наличие ряда преимуществ по сравнению с другими нелинейными фильтрами, CKF еще не исследовался для оценки состояния электроприводов в сообществе электроприводов. В этом исследовании авторы представляют CKF с квадратным корнем для оценки скорости и положения ротора сильно нелинейного и высокоточного двигателя BLDC, эти расчетные скорость и положение ротора затем возвращаются для управления скоростью двигателя BLDC. Эффективность представленного подхода для низких и высоких эталонных скоростей и при наличии параметрических неопределенностей демонстрируется экспериментами в реальном времени.
CKF — это недавно предложенный метод оценки сильно нелинейных систем, и его эффективность была проверена в нескольких приложениях. Версия CKF с квадратным корнем предпочтительнее обычной CKF для приложений реального времени. Несмотря на наличие ряда преимуществ по сравнению с другими нелинейными фильтрами, CKF еще не исследовался для оценки состояния электроприводов в сообществе электроприводов. В этом исследовании авторы представляют CKF с квадратным корнем для оценки скорости и положения ротора сильно нелинейного и высокоточного двигателя BLDC, эти расчетные скорость и положение ротора затем возвращаются для управления скоростью двигателя BLDC. Эффективность представленного подхода для низких и высоких эталонных скоростей и при наличии параметрических неопределенностей демонстрируется экспериментами в реальном времени.
1 Введение
Оценка состояния и управление бесщеточными двигателями постоянного тока с постоянными магнитами (BLDC) были важной областью исследований в течение последних нескольких десятилетий. BLDC двигатели и приводы широко используются в промышленности благодаря их высокому КПД и большой удельной мощности [1-7]. Было предложено и реализовано несколько стратегий управления приводами BLDC. Для большинства подходов к управлению BLDC важна информация о скорости и положении ротора. Можно либо использовать датчики для измерения скорости и положения, либо использовать некоторые методы оценки для получения скорости и положения. Более поздний подход весьма выгоден, поскольку позволяет избежать дополнительных затрат, пространства и веса и обычно известен как бессенсорные приводы BLDC.
BLDC двигатели и приводы широко используются в промышленности благодаря их высокому КПД и большой удельной мощности [1-7]. Было предложено и реализовано несколько стратегий управления приводами BLDC. Для большинства подходов к управлению BLDC важна информация о скорости и положении ротора. Можно либо использовать датчики для измерения скорости и положения, либо использовать некоторые методы оценки для получения скорости и положения. Более поздний подход весьма выгоден, поскольку позволяет избежать дополнительных затрат, пространства и веса и обычно известен как бессенсорные приводы BLDC.
Одну из известных исследовательских групп в области бессенсорных двигателей постоянного тока возглавляет Эхсани [1-4]. Схемы без датчиков для двигателей BLDC можно разделить на методы противо-ЭДС, методы запуска без датчиков, с использованием оценок состояния или наблюдателей и т. д. [1]. Поскольку одной из основных целей этой статьи является оценка скорости и положения ротора нелинейного двигателя BLDC, основное внимание уделяется бездатчиковому BLDC с использованием средств оценки состояния. Несколько исследователей исследовали методы управления и оценки для двигателей BLDC. Надежное управление положением на основе линейно-квадратичного регулятора и неизвестного наблюдателя крутящего момента входной нагрузки исследуется в [8], нелинейная модель объекта линеаризуется, а линейно-квадратичный регулятор разработан для BLDC. Неизвестный входной наблюдатель представлен для оценки момента нагрузки [8]. Аналогично, для цифрового управления положением BLDC предлагается адаптивный наблюдатель момента нагрузки [9].]. Оценка скорости и положения ротора с использованием расширенного фильтра Калмана (EKF) для BLDC двигателя разработана и реализована в [10]. Нелинейный объект линеаризуется для расчета EKF, и все переменные состояния двигателя BLDC оцениваются с использованием измерений линейного напряжения и тока статора. Недавно было разработано несколько наблюдателей для низкоскоростных приложений для синхронных двигателей с постоянными магнитами [11-13].
Несколько исследователей исследовали методы управления и оценки для двигателей BLDC. Надежное управление положением на основе линейно-квадратичного регулятора и неизвестного наблюдателя крутящего момента входной нагрузки исследуется в [8], нелинейная модель объекта линеаризуется, а линейно-квадратичный регулятор разработан для BLDC. Неизвестный входной наблюдатель представлен для оценки момента нагрузки [8]. Аналогично, для цифрового управления положением BLDC предлагается адаптивный наблюдатель момента нагрузки [9].]. Оценка скорости и положения ротора с использованием расширенного фильтра Калмана (EKF) для BLDC двигателя разработана и реализована в [10]. Нелинейный объект линеаризуется для расчета EKF, и все переменные состояния двигателя BLDC оцениваются с использованием измерений линейного напряжения и тока статора. Недавно было разработано несколько наблюдателей для низкоскоростных приложений для синхронных двигателей с постоянными магнитами [11-13].
Возможно, использование EKF будет ограничено для BLDC с серьезными нелинейностями, поскольку EKF нуждается в якобианах моделей процессов и измерений. Эти якобианы являются приближением первого порядка ряда Тейлора нелинейных функций. Чтобы обойти эти проблемы, для общих нелинейных систем несколько исследователей предложили методы оценки без производных, такие как неароматизированные фильтры Калмана [14, 15], фильтры частиц [16, 17] и т. д. Были исследованы EKF и фильтры частиц для BLDC. в [18]; где демонстрируется лучшая производительность фильтра частиц по сравнению с EKF за счет дополнительной вычислительной нагрузки. Недавно был представлен наблюдатель скользящего режима для приводов синхронных двигателей с постоянными магнитами [19].]. Использование UKF для оценки состояния двигателя BLDC еще предстоит изучить в сообществе электроприводов; однако он был исследован для асинхронных двигателей [20, 21]. Во многих реальных приложениях UKF может расходиться из-за отсутствия квадратного корня из ковариационной матрицы ошибок [22]. Совсем недавно кубатурный фильтр Калмана (CKF) был предложен для оценки состояния сильно нелинейных систем [22], который использует сферически-радиальное кубатурное правило для оценки численных многомерных интегралов для оценки момента.
Эти якобианы являются приближением первого порядка ряда Тейлора нелинейных функций. Чтобы обойти эти проблемы, для общих нелинейных систем несколько исследователей предложили методы оценки без производных, такие как неароматизированные фильтры Калмана [14, 15], фильтры частиц [16, 17] и т. д. Были исследованы EKF и фильтры частиц для BLDC. в [18]; где демонстрируется лучшая производительность фильтра частиц по сравнению с EKF за счет дополнительной вычислительной нагрузки. Недавно был представлен наблюдатель скользящего режима для приводов синхронных двигателей с постоянными магнитами [19].]. Использование UKF для оценки состояния двигателя BLDC еще предстоит изучить в сообществе электроприводов; однако он был исследован для асинхронных двигателей [20, 21]. Во многих реальных приложениях UKF может расходиться из-за отсутствия квадратного корня из ковариационной матрицы ошибок [22]. Совсем недавно кубатурный фильтр Калмана (CKF) был предложен для оценки состояния сильно нелинейных систем [22], который использует сферически-радиальное кубатурное правило для оценки численных многомерных интегралов для оценки момента. Показано, что CKF является наилучшей доступной нелинейной оценкой для нелинейных гауссовских систем. Для приложений реального времени фильтры квадратного корня предпочтительнее обычных фильтров [23-27].
Показано, что CKF является наилучшей доступной нелинейной оценкой для нелинейных гауссовских систем. Для приложений реального времени фильтры квадратного корня предпочтительнее обычных фильтров [23-27].
Несмотря на многочисленные преимущества фильтра CKF по сравнению с другими фильтрами, он еще не был изучен в сообществе электроприводов. В этой статье мы предлагаем использовать CKF с квадратным корнем для оценки состояния нелинейных двигателей BLDC; более конкретно, мы представляем CKF с квадратным корнем для оценки скорости и положения ротора сильно нелинейного и высокоточного двигателя BLDC. Расчетная скорость и положение ротора затем передаются на различные компоненты привода BLDC для управления скоростью. Ключевым вкладом этой статьи является предложение использовать CKF с квадратным корнем для двигателя BLDC. Выполнено сравнение EKF с квадратным корнем и CKF с квадратным корнем для оценки состояния реального BLDC двигателя. Некоторые преимущества использования квадратного корня CKF
по сравнению с другими оценщиками для двигателя BLDC, следующие: (i) CKF с квадратным корнем не содержит производных (ii) Он численно стабилен (iii) Что более важно, он более точен, чем любой другой существующий нелинейный алгоритм Калмана. оценщики фильтров.
оценщики фильтров.
Оставшаяся бумага организована следующим образом. В разделе 2 представлена теория двигателя BLDC, которая включает базовую модель пространства состояний, модель измерения, логику ЭДС, подход к управлению и т. д. В разделе 3 представлены подходы EKF и CKF и их реализация для двигателя BLDC. Экспериментальная установка и экспериментальные результаты приведены в разделе 4, и, наконец, раздел 5 завершает эту статью.
2 Модель привода BLDC
В этом разделе представлена подробная нелинейная модель двигателя BLDC [4]. Вектор состояния двигателя BLDC состоит из токов, скорости и положения ротора, а входными данными являются напряжения и крутящий момент нагрузки. Базовая блок-схема состоит из двигателя BLDC, блока ЭДС, инвертора и блока гистерезиса, а также ПИД-регулятора, показанного на рис. 1. Входными данными блока двигателя BLDC являются напряжения, противо-ЭДС и крутящий момент нагрузки, а выход состоит из полного вектора состояния. . Опорная скорость и фактическая скорость сравниваются, и ошибка между ними контролируется ПИД-регулятором, выходной сигнал ПИД-регулятора требуется для получения опорного тока Iref. Входные данные для двигателя BLDC и полученные от подсистемы инвертора, а также обратная ЭДС могут быть рассчитаны из блока ЭДС. Каждый из этих блоков подробно описан в следующих нескольких разделах. 9- pu + ioj
Входные данные для двигателя BLDC и полученные от подсистемы инвертора, а также обратная ЭДС могут быть рассчитаны из блока ЭДС. Каждый из этих блоков подробно описан в следующих нескольких разделах. 9- pu + ioj
— Keffl
— Kefil
•e-8]
Keffl Keffl
решение следующих динамических уравнений [4]
eab _j_ V ab
(L — M) M) L (L — M)L
(L — M)L (L — M) L (L — M)L
(L — M)l (L — M)L (L — M)L
2.1 BLDC двигатель
Вектор состояния BLDC двигателя, [ ia ib ic v U]T, состоит из фазных токов, скорости и положения ротора. Фазные токи можно получить как
ia = i1 — i3
ib = i2 — i1
ic = i3 — i2′
(1) (2) (3)
где межфазные токи, i2 и i3, можно получить с помощью
, где RL представляет собой линейный сопротивление линии, (L — M)L — разница между индуктивностью между линиями и взаимной индуктивностью, а Vab = Va — Vb, Vbc = Vb — Vc и Vca = Vc — Va — входные напряжения. В этой работе параметры двигателя BLDC: RL = 1,5 Ом, (L — M)L = 6,1 мГн.
В этой работе параметры двигателя BLDC: RL = 1,5 Ом, (L — M)L = 6,1 мГн.
Обратные ЭДС между линиями равны eab = ea — eb = Kemfab(0), ebc = eb — ec = Kefofbc(d) и eca = ec — ea = Kemfab(&), где постоянная противо-ЭДС равна Ke = 0,1074 В/(рад/с). Противо-ЭДС ea, eb и ec в зависимости от скорости и положения ротора приведены в таблице 1. Функции fab, fbc и fca приведены в таблице 2.
Когда обмотки статора распределены, обратная ЭДС также может иметь синусоидальную форму (как в случае синхронного двигателя с постоянными магнитами). Однако обратите внимание, что в этой статье мы использовали двигатель BLDC четырехугольного типа, чтобы продемонстрировать эффективность алгоритмов, и поэтому подробности в таблице 1 даны для трапециевидных форм волны. Скорость и ротор
Рис. 1 Блок-схема полной обратной связи по состоянию BLDC двигателя
положение
V = J [Te — Tl] 9i +
В первый момент приведенные выше уравнения кажутся линейными уравнениями состояния, но это не так. В основном это связано с обратными ЭДС, которые включают в себя несколько нелинейностей и будут обсуждаться в разделе 2.2. Далее может показаться, что электромагнитный момент (Te) будет равен бесконечности, если скорость w равна нулю. Однако после расширения членов противо-ЭДС (ea eb и ec), как указано в таблице 1, скорость в числителе и знаменателе Te аннулируется. Например, рассмотрим случай, когда 0 < 0 < n/6, ea = (6Kew/n0), eb = —KgW, ec = KgW. Как только эти противо-ЭДС подставляются в выражение Te, получается Te = (6Ke/n0)ia — Keib + Keic, и, следовательно, Te не зависит от w.
В основном это связано с обратными ЭДС, которые включают в себя несколько нелинейностей и будут обсуждаться в разделе 2.2. Далее может показаться, что электромагнитный момент (Te) будет равен бесконечности, если скорость w равна нулю. Однако после расширения членов противо-ЭДС (ea eb и ec), как указано в таблице 1, скорость в числителе и знаменателе Te аннулируется. Например, рассмотрим случай, когда 0 < 0 < n/6, ea = (6Kew/n0), eb = —KgW, ec = KgW. Как только эти противо-ЭДС подставляются в выражение Te, получается Te = (6Ke/n0)ia — Keib + Keic, и, следовательно, Te не зависит от w.
Обратите внимание, что в этой статье оценка выполняется на дискретных моделях. Непрерывная модель двигателя BLDC дискретизирована с использованием метода Эйлера с частотой дискретизации 10 000 Гц.
2.2 Противо-ЭДС и ПИД-регулятор
В этом разделе описывается конструкция противо-ЭДС и ПИД-регулятора.
2.2.1 Противо-ЭДС: Оценка противо-ЭДС играет ключевую роль в общей работе двигателя BLDC. Они в основном зависят от скорости и положения ротора [4] и могут быть рассчитаны по таблице 1.
Они в основном зависят от скорости и положения ротора [4] и могут быть рассчитаны по таблице 1.
2.2.2 ПИД-регулятор: Основная цель ПИД-регулятора — максимально приблизить фактическую скорость к заданной скорости. Невозможно достичь желаемой производительности, если коэффициенты ПИД-регулирования не настроены должным образом. В текущей работе желаемая производительность замкнутого контура с точки зрения характеристик временной области выбрана как время установления < 1 с и пиковое превышение < 20%. Для достижения желаемой производительности возможны различные комбинации усиления ПИД-регулятора. Предпринята попытка спроектировать и реализовать ПИД-регулятор. Однако в этой работе ПИ-регулятор (с усилением нулевой производной) оказался адекватным для достижения желаемой производительности. Метод Циглера-Николса используется для определения коэффициентов усиления ПИ-регулятора, которые затем настраиваются вручную для получения желаемого отклика. Настроенные коэффициенты усиления: Kp = 0,05 и K, - = 10. Выходной сигнал ПИ-регулятора масштабируется на Kt, чтобы получить опорный ток /ref, который затем требуется для подсистемы инвертора до
Выходной сигнал ПИ-регулятора масштабируется на Kt, чтобы получить опорный ток /ref, который затем требуется для подсистемы инвертора до
генерируют желаемое входное напряжение. В этой статье константа крутящего момента равна Kt = 0,21476 Нм.
2.3 Инвертор и блок гистерезиса
Подсистема инвертора отвечает за генерацию требуемых напряжений для двигателя BLDC на основе управления током гистерезиса. Управление током с гистерезисом обеспечивает функции переключения, необходимые для расчета фазных и линейных напряжений. Функции переключения можно получить с помощью таблицы 3, где /ad и Icd — фазные токи с задержкой [4], а T1 и T2 зависят от соответствующей последовательности токов.
Например, рассмотрим случай тока ia. При положительном ia
T1 = [(ia < 0,9/ref) - (ia > l.l/ref) + (ia
* (ia > iad) — (ia > °-94f) * (ia <
> 0-9/ref) * (ia < l-lIref)
1 — 11ref) * (ia < iad)]
Функционирование T1 основано на ia, /ref и текущем отсчете iad. Предположим, что если (ia < 0,9/ref), то есть первый член приведенного выше уравнения выполняется (и, следовательно, три других члена равны нулю), даст T1 = 1. Аналогично, если ia > 1,11ref, второй член будет равен активироваться, что даст T1 = —1. Если 0,9ref)
Предположим, что если (ia < 0,9/ref), то есть первый член приведенного выше уравнения выполняется (и, следовательно, три других члена равны нулю), даст T1 = 1. Аналогично, если ia > 1,11ref, второй член будет равен активироваться, что даст T1 = —1. Если 0,9ref)
(ia > -l-l1ref) * (ia < * (ia > l — l1ref) * (ia
¡’ad) + (ia < 0-91ref) > iad)]-
Нижний а верхние пределы гистерезисного регулятора тока равны 0,9/ref и 1,11ref соответственно. Аналогично для других токов и ic можно рассчитать соответствующие T1 и T2.
На основе этих функций переключения фазные напряжения могут быть рассчитаны как0016 Vai — Va — Vi
Vic — Vi — Vc
Функции fab, fbc и fca V ca — Vc — Va
fab fbc fca
0 с 0 < f 1 с 0 < f 60 „ — + 1 f 2 -2 60-5 60 --+ 1 f 3 - 60
f 5f 2 S 0 < IT 60 --+ 5 f 60-3 f -2
5f 7f H s 0 < 7B" 7f 9f 7F s 0 < 9T f 60 --+ 5 f - 2 f 2 60 --+ 9 60-7 f 60-7
9f 11 f s 0 < -a" 60 --11 f 60 --+ 9 f 2
iif — s 0 s 2f f 60 —11 f f -2 60 13— f
где – напряжение в звене постоянного тока, которое может быть получено либо путем предпроектного анализа, либо с помощью подходящего выпрямителя. Линейное напряжение инвертора теперь может быть получено как
Линейное напряжение инвертора теперь может быть получено как
Эти межфазные напряжения являются входами для двигателя BLDC.
Наконец, вектор состояния и выход модели двигателя BLDC могут быть выражены в форме пространства состояний как: (см. уравнение (14) внизу следующей страницы)
Таблица 3 Функции переключения для управления током с гистерезисом
Входы
Выходы
1a, 1ad
1c, 1cd
Fa = (0 >n/6)(0 <5n/6)7"1 + (0 >7n/6)(0 <11n/6) r2 Fb =(0 >O)(0
Рис. 2 Предлагаемая схема для BLDC двигателя
Выходное уравнение: y = Hx
1 0 0 0 0 0 10 0 0 0 0 10 0
Шумы процесса и измерения добавляются к уравнениям состояния и выхода соответственно. Уравнения в (14) и (15) находятся в непрерывной временной области, однако реализованные методы оценивания находятся в дискретной области. Следовательно, эти уравнения дискретизируются с использованием метода Эйлера [Модель непрерывного пространства состояний, x = Ax + Bu, может быть дискретизирована с использованием метода Эйлера как
Xn+i = (In + ADt)xn + DtBu,
, где At — время дискретизации, а In — единичная матрица n-го порядка] такая, что
xn+1 = (15 + F(xn)M) x„ + GDtd + V\tTh
, где I5 — единичная матрица пятого порядка, а At — время выборки. Выходное уравнение в дискретной временной области будет таким же, как и приведенное в (15)
Выходное уравнение в дискретной временной области будет таким же, как и приведенное в (15)
yn = Hxn-
Следующие предположения рассматриваются для математической модели двигателя BLDC и силовых преобразователей. Магнитный
поток в обмотке статора двигателя не насыщается, сопротивления статора всех трех фазных обмоток равны, собственная и взаимная индуктивности постоянны и не меняются при изменении нагрузки, устройства в инверторе идеальны, потери в стали незначительны [28] .
Обратите внимание, что, поскольку противо-ЭДС двигателя BLDC имеет трапециевидную форму, двигатель BLDC управляется возбуждением только двух фаз одновременно для каждых 60 градусов положения ротора. Кроме того, можно рассчитать все три тока, используя только два датчика тока в качестве 9.0019
ia + h + h = °
Из-за шума в датчиках тока не всегда возможно точно рассчитать все три тока от двух датчиков тока. В частности, при работе на низкой скорости датчики тока, используемые в этой статье, имеют низкое отношение сигнал/шум. Следовательно, для эффективного управления двигателем BLDC используются три датчика тока (тогда как одновременно возбуждаются только две фазы). Однако, используя только два датчика тока с высоким разрешением, можно эффективно управлять двигателем BLDC.
Следовательно, для эффективного управления двигателем BLDC используются три датчика тока (тогда как одновременно возбуждаются только две фазы). Однако, используя только два датчика тока с высоким разрешением, можно эффективно управлять двигателем BLDC.
3 EKF с квадратным корнем и CKF с квадратным корнем
В этом разделе представлены EKF с квадратным корнем [29, 30] и CKF [22].
3.1 Расширенный фильтр Калмана
Пусть модели нелинейных процессов и измерений в дискретной области будут
xn = f (xn-1, dn-1) + wn-1 yn = dn) + vn
(18) (19)
F(x)x + Gd + V TL
r Rl 0 0 -e
(L — M)l — (L — M )L
0 Rl 0 -e
(L — М) л — (Л — М )Л
0 0 Рл -е
(L — M)l — (L — M)l
k -J fab(U) — -J fbc(U) — y fca(U) B — J
0 0 0 P 2
fab (U) 0 fbc(ff) 0 fca(U) 0 0 0
(L — M) l 0
(L — M) l 0
(L — M) l 0
Vab 0
Vbc + 0 1 J 0 TL
где вектор состояния, управляющие входы и измерения представлены как xn [ , dn и yn соответственно. Шум процесса и шум измерений представлены как wn-1 и vn, а соответствующие им ковариационные матрицы — Qn-1 и Rn. В этой статье шум процесса и шум измерений предполагаются как гауссовский шум с нулевым средним значением.
Шум процесса и шум измерений представлены как wn-1 и vn, а соответствующие им ковариационные матрицы — Qn-1 и Rn. В этой статье шум процесса и шум измерений предполагаются как гауссовский шум с нулевым средним значением.
1) EKF с квадратным корнем: фильтры квадратного корня известны своей надежностью и стабильностью при реализации в реальном времени [31]. В отличие от обычных фильтров, в фильтрах квадратного корня распространяется коэффициент квадратного корня соответствующей ковариационной матрицы. Это распространение ковариационной матрицы квадратного корня является основной причиной создания стабильных и надежных фильтров квадратного корня. Кроме того, обратите внимание, что фильтры квадратного корня обеспечивают распространение симметричных положительно определенных ковариационных матриц [22, 27, 30-32].
Обратите внимание, что положительно определенная матрица M и ее обратная матрица могут быть факторизованы как
Таблица 4 Частные производные {dfab{0}}/d0, {dfbc{0}}/d0 и {dfca{0}}/d0
6 — 0 <2 P 5p
2 — 0 T — 0 <76 " T — 0 9P 11P T — 0 <11P — 0 — 2P d fab{0) a fbc {0) a fca{0) M = (M 1/2)(MT/2) M-1 = (M-r/2)(M-1/2) (20) (21) 2: Обновленное состояние EKF с квадратным корнем может быть получено как Матричная факторизация в (20) или (21) может быть получена несколькими способами. Два этапа для извлечения квадратного корня EKF представлены в алгоритме 1. Алгоритм 1: Инициализируйте вектор состояния и ковариацию как x0 и C0/2 (для индекса n = Предсказание: 1: Прогнозируемое состояние задается как •*»- = f (*n-1> dn-1) где xn- это прогнозируемое состояние, которое оценивается на основе предыдущего состояния выборки времени xn-1, а dn-1 является управляющим входом 2: Прогнозируемая ковариация CXJ2 может быть рассчитана по формуле Q/2] A = [Ci-2 0], где A — унитарная матрица [31], которая может быть вычислена с помощью qr-разложения, Vfx — якобиан функции f, оцененной при xn-1, а QJ2 — квадратный корень из ковариации шума процесса.Предсказанная ковариация C\J-2 оценивается на основе ковариации предыдущей временной выборки Cn1/21. en = R—n Wn — h*n-)]. EKF и EKF с квадратным корнем эквивалентны, но из-за специфической структуры ковариации для EKF с квадратным корнем она всегда обеспечивает положительную определенность ковариационной матрицы ошибок. Возводя в квадрат обе части (24) и выполняя некоторые прямые манипуляции с (25), можно показать, что ЭКФ и его версия с квадратным корнем эквивалентны [30]. Теперь обсудим квадратный корень EKF, заданный в Алгоритме 1 для реализации двигателя BLDC. Сначала инициализируйте вектор состояния (пять состояний) и соответствующую ему ковариационную матрицу, а затем выберите соответствующий процесс и ковариационные матрицы шума QJ2 и R/2. Вектор начального состояния x0 и C0/2 выбирается случайным образом из N([0 0 0 0,01 0,01]T, 10-5/5), где N представляет случайные величины с нормальным распределением. Ковариация шума процесса Q1J2 представляет собой диагональную матрицу пятого порядка со всеми диагональными элементами, равными 10-6, а ковариация шума измерения R]J2 представляет собой диагональную матрицу третьего порядка со всеми диагональными элементами, равными 0,1. (L — M)L 0 Kffab(0) 0 (L — M) L 0 K-ffb0 0 (L — M)l Kev f (0) J Jca(0) 0 L — Ml ; L — Ml L — Ml fab(0 — fbc(0) — fca(0) — КэВ 3fab(0)-L — ML 30 KeV L — ML 30 КэВ dfca(0) 0< 0 < p *n *n- + Gnen L — ML 30 требуются прогнозируемая ковариация CJ- (полученная на этапе прогнозирования), ковариация шума измерений RJ2 и якобиан матрицы измерений Vhx. Для двигателя BLDC три выхода считаются первыми тремя состояниями, и, следовательно, Vhx совпадает с матрицей измерений и определяется как 1: Оценка y « 1 0 0 0 0 0 10 0 0 0 0 10 0 Наконец, обновленный вектор состояния двигателя BLDC может быть получен из (25). Ti,»- = βi + Xn- ■ 2: Оценить предсказанное измерение 3.2 Кубатурный фильтр Калмана 3: Рассчитать промежуточные ковариационные матрицы Для линейных систем с гауссовым шумом фильтр Калмана является оптимальным фильтром . Для оценки состояния нелинейных систем исходный фильтр Калмана был расширен до EKF. В EKF отсутствует функция оптимальности фильтра Калмана. Это может быть не лучший выбор для некоторых реальных приложений, поскольку он основан на разложении в ряд Тейлора первого порядка и может не давать подходящих оценок для сильно нелинейных систем. CKF был недавно разработан фильтром для устранения некоторых недостатков EKF и является наиболее близким из известных приближенных фильтров для нелинейных систем с гауссовским шумом [22]. §n- = —= [X 1,n- — •*»- X2,n- •*»- X2n,n- •*»- (41) 3.2.1 CKF с квадратным корнем: CKF с квадратным корнем распространяет коэффициенты квадратного корня ковариационных матриц. CKF с квадратным корнем может быть выражен в два этапа: предсказание и обновление, для более подробной информации см. [22]. CKF с квадратным корнем подробно описан в Алгоритме 2 [22]. 4: Расчет усиления Калмана cT/2 \ i v’yy,n-‘ Алгоритм 2: Инициализация вектора состояния и ковариации как x0 и C0/2 (для индекса n = 1). Прогноз: 9. Обновление: где R]À2 — коэффициент квадратного корня из ковариации шума измерения. Теперь будет обсуждаться CKF с квадратным корнем, заданная в алгоритме 2 для реализации двигателя BLDC. Предложенная схема оценки состояния двигателя BLDC представлена на рис. 2. Сначала инициализируйте вектор состояния (пять состояний) и соответствующую ему ковариационную матрицу, а затем выберите подходящие ковариационные матрицы процесса и шума QJ2 и Rn2. Рис. 3 Экспериментa/установка для BLDC привода a Вид спереди экспериментальной установки для BLDC привода b Вид сбоку экспериментального BLDC привода Рис. [22] на основе моторных весов BLDC линейно с размерностью состояний двигателя BLDC (т.е. 5). 4 Эксперименты с асинхронным двигателем постоянного тока В этом разделе представлены экспериментальная установка асинхронного двигателя постоянного тока и экспериментальные результаты, полученные с использованием EKF и CKF с квадратным корнем. 4.1 Экспериментальная установка Экспериментальная установка, использованная для данной работы, представлена на рис. 3а и б. Экспериментальная установка состоит из асинхронного двигателя постоянного тока с инкрементным энкодером , интеллектуального силового модуля [33] (состоящего из выпрямителя, входного фильтра с использованием конденсаторов, модуля динамического торможения, инвертора источника напряжения, схемы драйвера затвора и оптопары), датчиков тока (LTS 25). датчики тока NP), плату контроллера dSPACE DS1103, соединительную панель dSPACE CLP1103 [34] и компьютер (пульт управления dSPACE). Рис. 5 Схема регулятора скорости с использованием квадратного корня CKF Рис. 6 Экспериментальные результаты для низкой эталонной скорости (30 об/мин) а Фактическая и расчетная скорости b Фактическое и расчетное положения ротора c Абсолютные ошибки оценки скорости d Нормированная скорость ошибки Рис. 7 Экспериментальные результаты для высокой эталонной скорости (2000 об/мин) a Фактическая и расчетная скорости b Фактическое и расчетное положения ротора c Абсолютные ошибки оценки скорости d Нормированные ошибки скорости Время(с) c Рис. a Без нагрузки b С крутящим моментом нагрузки 2 Н·м c С крутящим моментом нагрузки 4 Н·м Рис. 5 (что будет объяснено позже) моделируется с использованием различных совместимых с dSPACE наборов блоков RTI и Simulink на компьютере. Затем эта схема Simulink преобразуется во встроенный C-код с поддержкой цифровой обработки сигналов, который затем загружается в DSP-процессор TMS320F240 (на плате контроллера DS1103) для дальнейшей обработки для генерации импульсов широтно-импульсной модуляции (ШИМ) для инвертора. На основе этих ШИМ-импульсов инвертор генерирует необходимое напряжение для двигателя BLDC. Блок-схема на рис. 4 представляет собой часть привода BLDC, показанного на рис. 5. Основная цель — генерировать импульсы ШИМ для инвертора. Опорная скорость и скорость, полученная из блока CKF извлечения квадратного корня, сравниваются, и на основе ошибки оценки ПИД-блок генерирует опорный ток /ref. /ref вместе с предполагаемым положением ротора (из квадратного корня CKF) и измеренными токами генерирует импульсы PWM для инвертора [1]. 4.2 Результаты экспериментов Проведены три серии экспериментов; один с полной обратной связью по состоянию, а остальные два с механизмами на основе EKF и CKF с квадратным корнем. Эти эксперименты выполняются для низкой эталонной скорости 30 об/мин, высокой эталонной скорости 2000 об/мин и с параметрическими вариациями. Для эксперимента с обратной связью по полному состоянию все состояния измеряются с помощью преобразователей тока LTS 25 NP, а скорость и положение ротора измеряются с помощью инкрементного энкодера и датчиков Холла. Однако для привода BLDC используются только датчики тока, использующие версии EKF и CKF с квадратным корнем. 4.2.1 Результаты на низкой скорости: В этом эксперименте эталонная скорость двигателя BLDC выбрана равной 30 об/мин. Фактическая скорость и расчетная скорость с использованием квадратного корня EKF и CKF показаны на рис. 6a, а соответствующие положения ротора показаны на рис. близки друг к другу, тогда как расчетная скорость с использованием EKF с квадратным корнем имеет значительную погрешность. Ошибки между измеренной и расчетной скоростями приведены на рис. 6в. Максимальная ошибка оценки для EKF составляет около 20 об/мин, а для CKF — около 12 об/мин. Средняя абсолютная ошибка оценки скорости составляет 2,39.82 и 1,2525 об/мин для EKF и CKF соответственно. График нормализованной ошибки скорости показан на рис. 6d, нормированная скорость представляет собой отношение ошибки скорости к эталонной скорости. 4.2.2 Результаты для высокой скорости: В этом эксперименте эталонная скорость двигателя BLDC выбрана в качестве линейного сигнала (наклон 400 об/мин) с конечным значением 2000 об/мин. Фактическая скорость и расчетная скорость с использованием квадратного корня EKF и CKF показаны на рис. 7a, а соответствующие положения ротора показаны на рис. 7b. Как и в случае с низкой скоростью, измеренная скорость и расчетная скорость с использованием квадратного корня CKF близки друг к другу, тогда как расчетная скорость с использованием квадратного корня EKF имеет значительную ошибку. 4.2.3 Анализ устойчивости: В этом разделе рассмотрены характеристики оценок при наличии различных неопределенностей. Эти эксперименты проводятся при низкой эталонной скорости 30 об/мин и анализируются результаты установившегося состояния. (a) Изменение момента нагрузки: В этом эксперименте рассматривается момент нагрузки 2 Н·м и 4 Н·м. Эти механические нагрузки применяются с самого начала экспериментов. Номинальные результаты (без изменения момента нагрузки) приведены на рис. 8а, абсолютная погрешность средней скорости составляет 1,7327 об/мин и 0,7967 об/мин для EKF и CKF соответственно. Ошибки скорости при моменте нагрузки 2 Н·м приведены на рис. Рис. 9 Экспериментальные результаты с изменением сопротивления статора а При изменении сопротивления статора +30 % б При изменении сопротивления статора -30 % при моменте нагрузки 4 Н·м приведены на рис. 8в, где средняя ошибка для EKF и CKF составляет 2,4086 об/мин и 1,1743 об/мин соответственно. (b) Изменение сопротивления статора: В этом эксперименте сопротивление статора для оценщиков изменяется на ±30% от его номинального значения. Номинальные результаты (без изменения сопротивления статора) такие же, как на рис. 8а. Погрешности скорости при отклонении сопротивления статора на +30% от его номинального значения приведены на рис. 9а, где абсолютная средняя погрешность составляет 1,9144 об/мин и 0,9866 об/мин для EKF и CKF соответственно. Погрешности скорости при отклонении сопротивления статора от номинального значения -30% приведены на рис. (c) Расстройка индуктивности: В этом эксперименте индуктивность статора для оценщиков расстроена на 10% от ее номинального значения. Номинальные результаты (без изменения момента нагрузки) такие же, как на рис. 8а. Результаты с расстроенной индуктивностью приведены на рис. 10, где абсолютная средняя погрешность скорости составляет 3,5140 об/мин и 1,8106 об/мин соответственно. Экспериментальные результаты в этом разделе показывают, что можно оценить скорость и положение ротора как с EKF, так и с CKF. Эксперименты с различными параметрическими вариациями показывают надежность EKF и CKF. Однако во всех случаях производительность CKF лучше, чем EKF, это связано с тем, что EKF основан на приближении первого порядка нелинейной функции, тогда как для CKF это приближение не требуется. Время(с) Рис. 10 Ошибки оценки при расстроенной индуктивности статора В некоторых случаях существует вероятность того, что эти якобианы могут стать сингулярными, несмотря на использование квадратного корня EKF. Также замечено, что среди рассмотренных неопределенностей эффективность оценки чувствительна к расстроенной индуктивности. 5 Выводы Нелинейная оценка состояния электроприводов с использованием фильтров свободной производной и фильтра квадратного корня является важной темой исследований. Основная проблема с фильтрами на основе производных, такими как EKF, заключается в их применимости к жестким нелинейным системам. Более конкретно, в формулировке EKF нелинейные модели объектов и измерений аппроксимируются рядом Тейлорса первого порядка; из-за этого приближения трудно получить точную оценку вектора состояния. В этой статье была представлена оценка состояния без производной квадратного корня для двигателя BLDC. 6 Каталожные номера 1 Ким, Т., Ли, Х.В., Эхсани, М.: «Расположение бесщеточных двигателей/генераторов постоянного тока без датчиков: обзор и будущие тенденции. Электроэнергетические приложения», ИЭТ Электр. Power Appt., 2007, 1, (4), стр. 557-564 2 Johnson, J.P., Ehsani, M., Guzelgunler, Y.: «Обзор бессенсорных методов для бесщеточного постоянного тока. Конференция по отраслевым приложениям». 34-е ежегодное собрание IEEE IAS, Аризона, 1999 г., стр. 143-150 3 Ким, Т.Х., Эхсани, М.: «Бессенсорное управление бессенсорными двигателями постоянного тока от почти нуля до высоких скоростей», IEEE Trans. Электроэнергетика, 2004, 19, (6), стр. 1635-1645 4 Lee, B.K., Ehsani, M.: «Расширенная имитационная модель для бесколлекторных двигателей постоянного тока», Electr. Силовой комп. Syst., 2003, 31, (9), стр. 841-868 5 Wang, H.P., Liu, Y.T.: «Интегрированная конструкция бессенсорного и адаптивного регулятора скорости для бесщеточного двигателя постоянного тока», IEEE Trans. 6 Стирбан, А., Болдеа, А., Андрееску, Г.: «Бессенсорное управление двигателем BLDC-PM с автономной FEM-информацией. наблюдатель положения и скорости с помощью», IEEE Trans. Инд., 2012, 48, (6), с. 19.50-1958 7 Вадструп, П., Лоренц, Р.Д.: «Надежная схема оценки для приводов синхронных машин IPM на основе ввода сигналов». 39-е ежегодное собрание IAS, 2004 г., стр. 957-963 8 Ко, Дж.С., Ли, Дж.Х., Чанг, С.К. и др.: «Надежное цифровое управление положением бесщеточного двигателя постоянного тока с асинхронным наблюдателем крутящего момента», IEEE Транс. Ind. Electron., 1993, 40, (5), стр. 512-520 9 Ко, Дж. С., Ли, Дж. Х., Юн, М. Дж.: «Надежное цифровое управление положением бесщеточного двигателя постоянного тока с адаптивным наблюдателем момента нагрузки», 1994, IETElectr. Power Appl., 2007, 141, (2), стр. 63-70 10 Терзич, Б., Ядрик, М.: «Проектирование и реализация расширенного фильтра Калмана для оценки скорости и положения ротора бесщеточного двигателя постоянного тока. 19 Юань Л., Сяо Ф., Шэнь Дж. К. и др.: «Бессенсорное управление мощными внутренними синхронными двигателями с постоянными магнитами на очень низкой скорости», IET Electr. Power Appl., 2013, 7, (3), стр. 199-206 20 Джафарзаде, С., Ласку, К., Фадали, М.С.: «Оценка состояния приводов асинхронных двигателей с использованием фильтра Калмана без запаха», IEEE Trans . Ind. Electron., 2012, 59, (11), стр. 4207-4216 21 Ли, Дж., Чжун, Ю., Рен, Х.: «Оценка скорости индукционных машин с использованием фильтра Калмана без запаха с квадратным корнем». Конференция специалистов по силовой электронике IEEE, 2005 г., стр. 674–679.97 25 Verhaegen, M., Van Dooren, P.: «Численные аспекты различных реализаций фильтра Калмана», IEEE Trans. автомат. Control, 1986, 31, (10), стр. 907-917 26 Карлсон, Н.А.: «Федеративный фильтр квадратного корня для децентрализованных параллельных процессоров», IEEE Trans. Аэросп. Электрон. Syst., 1990, 26, (3), стр. 517-525 27 Чандра, К. 28 Кришнан, Р.: «Синхронные и бесщеточные двигатели постоянного тока с постоянными магнитами» (CRC Press, 2009).) 29 Мейбек, П.С.: «Стохастические модели, оценка и контроль» (Academic Press, 1979), vol. 1 30 Парк, П., Кайлат, Т.: «Новые алгоритмы извлечения квадратного корня для фильтрации Калмана», IEEE Trans. автомат. Control, 1995, 40, (5), стр. 895-899 31 Гревал, М.С., Эндрюс, А.П.: «Фильтрация Калмана: теория и практика с использованием MATLAB» (John Wiley & Sons, 2008), 3-е изд. 32 Саймон, Д.: «Оценка оптимального состояния: Калман и нелинейные подходы» (John Wiley & Sons, 2006) 33 Каталог интеллектуальных силовых модулей MITSUBISHI, 1998 г., последний доступ 3 апреля 2015 г. Доступен по адресу http://www.mitsubishielectric.com/semiconductors/files/ manuals/powermos6_0.pdf 34 DS1103 Каталог плат контроллеров PPC, Падерборн, Германия , 2008 г. Например, можно использовать qr-разложение, чтобы получить M1/2 или MsT/2, которые удовлетворяют (20). Эта факторизация является ключом к фильтрам квадратного корня для повышения численной надежности оцениваемого состояния.
Например, можно использовать qr-разложение, чтобы получить M1/2 или MsT/2, которые удовлетворяют (20). Эта факторизация является ключом к фильтрам квадратного корня для повышения численной надежности оцениваемого состояния. 92 представляет собой квадратный корень шума измерения.
92 представляет собой квадратный корень шума измерения. Прогнозируемое состояние может быть получено из (22), а предсказанная ковариация может быть получена из (23), где матрица Якоби Vfx (частная производная нелинейной функции f = F(x)x, заданной в (14) по к вектору состояния: (см. (27)) 9можно получить с помощью qr-факторизации. Для оценки этих параметров
Прогнозируемое состояние может быть получено из (22), а предсказанная ковариация может быть получена из (23), где матрица Якоби Vfx (частная производная нелинейной функции f = F(x)x, заданной в (14) по к вектору состояния: (см. (27)) 9можно получить с помощью qr-факторизации. Для оценки этих параметров На основе этих обновленных состояний и ковариационной матрицы оцениваются предсказанные состояния и ковариационная матрица для следующей временной выборки. Этот рекурсивный процесс продолжается до последней заданной временной выборки.
На основе этих обновленных состояний и ковариационной матрицы оцениваются предсказанные состояния и ковариационная матрица для следующей временной выборки. Этот рекурсивный процесс продолжается до последней заданной временной выборки. CKF — это фильтр без производных, который не требует якобианов и, как показано, превосходит центральные разностные фильтры или UKF [22]. 92»,»— ] (40)
CKF — это фильтр без производных, который не требует якобианов и, как показано, превосходит центральные разностные фильтры или UKF [22]. 92»,»— ] (40) Вектор начального состояния x0, C¿/2, ковариация шума процесса Q/2 и ковариация шума измерения R¡2 выбраны такими же, как и в разделе 3.1 (Квадратичный корень EKF). Поскольку двигатель BLDC имеет пять состояний, соответствующий $ in (29) равно ¡3¡ = 110 —110 ],-, где i изменяется от 1 до 10. Оценить y*H—, приведенную в (31), путем подстановки g,n-1 из (30) в модель нелинейного процесса /’, где ‘f такое же, как xn+1, заданное в (16). Прогнозируемое состояние и ковариация оцениваются по (32) и (33). Для этапа обновления оцените (35), подставив g,n_ из (36) в модель измерения «h», где «h» такое же, как yn, указанное в (17). После выполнения шагов 2-4 этапа обновления Алгоритма 2 состояние обновления и ковариация могут быть получены из (43) и (44) соответственно. Рекурсивный процесс предсказания и обновления продолжается до конца эксперимента. Для всех функциональных оценок вычислительная сложность квадратного корня CKF
Вектор начального состояния x0, C¿/2, ковариация шума процесса Q/2 и ковариация шума измерения R¡2 выбраны такими же, как и в разделе 3.1 (Квадратичный корень EKF). Поскольку двигатель BLDC имеет пять состояний, соответствующий $ in (29) равно ¡3¡ = 110 —110 ],-, где i изменяется от 1 до 10. Оценить y*H—, приведенную в (31), путем подстановки g,n-1 из (30) в модель нелинейного процесса /’, где ‘f такое же, как xn+1, заданное в (16). Прогнозируемое состояние и ковариация оцениваются по (32) и (33). Для этапа обновления оцените (35), подставив g,n_ из (36) в модель измерения «h», где «h» такое же, как yn, указанное в (17). После выполнения шагов 2-4 этапа обновления Алгоритма 2 состояние обновления и ковариация могут быть получены из (43) и (44) соответственно. Рекурсивный процесс предсказания и обновления продолжается до конца эксперимента. Для всех функциональных оценок вычислительная сложность квадратного корня CKF 4 Блок-схема для эксперимента BLDC
4 Блок-схема для эксперимента BLDC Эти устройства соединены между собой, как показано на рис. 4. Измеренные токи обрабатываются через соединительную панель dSPACE CLP1103, которая имеет аналого-цифровые и цифро-аналоговые порты, а также возможность подачи входных данных на плату dSPACE DS1103. Плата контроллера dSPACE DS1103 оснащена процессором DSP с аналого-цифровыми и цифро-аналоговыми преобразователями и другими компонентами, необходимыми для обработки данных. Несколько фильтров также включены для целей преобразования сигнала. Блок-схема, приведенная в
Эти устройства соединены между собой, как показано на рис. 4. Измеренные токи обрабатываются через соединительную панель dSPACE CLP1103, которая имеет аналого-цифровые и цифро-аналоговые порты, а также возможность подачи входных данных на плату dSPACE DS1103. Плата контроллера dSPACE DS1103 оснащена процессором DSP с аналого-цифровыми и цифро-аналоговыми преобразователями и другими компонентами, необходимыми для обработки данных. Несколько фильтров также включены для целей преобразования сигнала. Блок-схема, приведенная в 8 Экспериментальные результаты при изменении нагрузки
8 Экспериментальные результаты при изменении нагрузки Для получения более подробной информации см. Раздел 2.
Для получения более подробной информации см. Раздел 2. 6b. Измеренная скорость и расчетная скорость с использованием CKF с квадратным корнем
6b. Измеренная скорость и расчетная скорость с использованием CKF с квадратным корнем Ошибки между измеренной и расчетной скоростями приведены на рис. 7в. Максимальная ошибка оценки для EKF составляет около 115 об/мин, а для CKF — около 40 об/мин. Средняя абсолютная ошибка оценки скорости составляет 25,819.8 об/мин и 13,1036 об/мин для EKF и CKF соответственно. График нормализованной ошибки скорости показан на рис. 7d.
Ошибки между измеренной и расчетной скоростями приведены на рис. 7в. Максимальная ошибка оценки для EKF составляет около 115 об/мин, а для CKF — около 40 об/мин. Средняя абсолютная ошибка оценки скорости составляет 25,819.8 об/мин и 13,1036 об/мин для EKF и CKF соответственно. График нормализованной ошибки скорости показан на рис. 7d. 8б, где абсолютная средняя ошибка 1,1968 об/мин и 0,8336 об/мин для EKF и CKF соответственно. Ошибки скорости
8б, где абсолютная средняя ошибка 1,1968 об/мин и 0,8336 об/мин для EKF и CKF соответственно. Ошибки скорости 9.б, где абсолютная средняя ошибка 3,1422 об/мин и 0,8644 об/мин для EKF и CKF соответственно. Можно видеть, что ошибка скорости больше при отрицательном изменении сопротивления статора (-30%) по сравнению с +30% изменением сопротивления статора.
9.б, где абсолютная средняя ошибка 3,1422 об/мин и 0,8644 об/мин для EKF и CKF соответственно. Можно видеть, что ошибка скорости больше при отрицательном изменении сопротивления статора (-30%) по сравнению с +30% изменением сопротивления статора. Далее, вычисление якобианов для EKF довольно сложно и в
Далее, вычисление якобианов для EKF довольно сложно и в CKF с квадратным корнем использовался в качестве основного инструмента для оценки скорости и положения ротора сильно нелинейного двигателя BLDC. Для управления скоростью двигателя BLDC расчетная скорость и положение ротора возвращаются для расчета опорных токов. Эксперименты выполняются для низких и высоких эталонных скоростей и при наличии параметрических неопределенностей с использованием версий EKF и CKF с извлечением квадратного корня. Некоторые из преимуществ использования CKF с квадратным корнем по сравнению с другими оценщиками для двигателя BLDC заключаются в следующем: (i) CKF с квадратным корнем не содержит производных (ii) он численно стабилен (iii) что более важно, он более точнее, чем любые другие существующие нелинейные фильтры Калмана. Эти обнадеживающие результаты, полученные с использованием CKF с квадратным корнем для привода BLDC, могут быть дополнительно изучены для других электрических машин и приложений. Одной из будущих работ является исследование и реализация непрерывно-дискретной CKF [35] для двигателей BLDC.
CKF с квадратным корнем использовался в качестве основного инструмента для оценки скорости и положения ротора сильно нелинейного двигателя BLDC. Для управления скоростью двигателя BLDC расчетная скорость и положение ротора возвращаются для расчета опорных токов. Эксперименты выполняются для низких и высоких эталонных скоростей и при наличии параметрических неопределенностей с использованием версий EKF и CKF с извлечением квадратного корня. Некоторые из преимуществ использования CKF с квадратным корнем по сравнению с другими оценщиками для двигателя BLDC заключаются в следующем: (i) CKF с квадратным корнем не содержит производных (ii) он численно стабилен (iii) что более важно, он более точнее, чем любые другие существующие нелинейные фильтры Калмана. Эти обнадеживающие результаты, полученные с использованием CKF с квадратным корнем для привода BLDC, могут быть дополнительно изучены для других электрических машин и приложений. Одной из будущих работ является исследование и реализация непрерывно-дискретной CKF [35] для двигателей BLDC.
 Power Electron., 2006, 21, (2), стр. 518-523
Power Electron., 2006, 21, (2), стр. 518-523 10
10 П.Б., Гу, Д.-В., Постлетуэйт, И.: «Кубатурный информационный фильтр квадратного корня», IEEE Sens. J., 2013, 13, (2), стр. 750-758
П.Б., Гу, Д.-В., Постлетуэйт, И.: «Кубатурный информационный фильтр квадратного корня», IEEE Sens. J., 2013, 13, (2), стр. 750-758

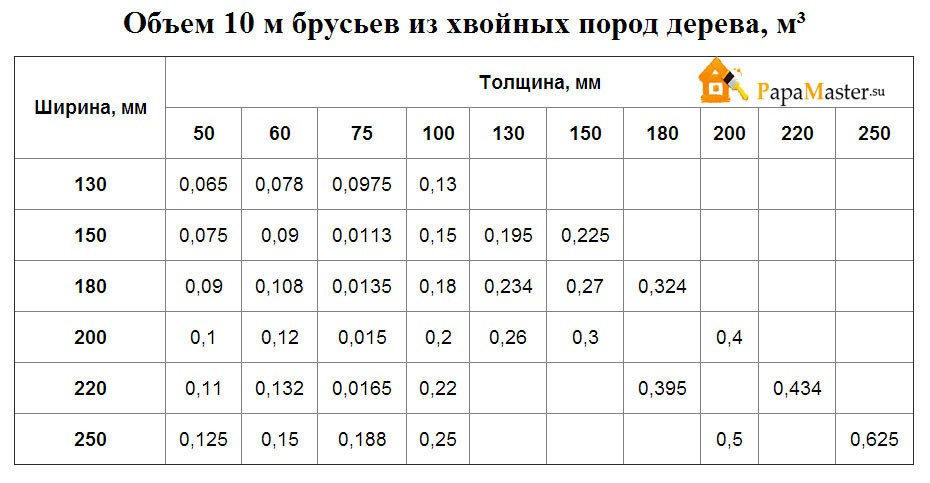
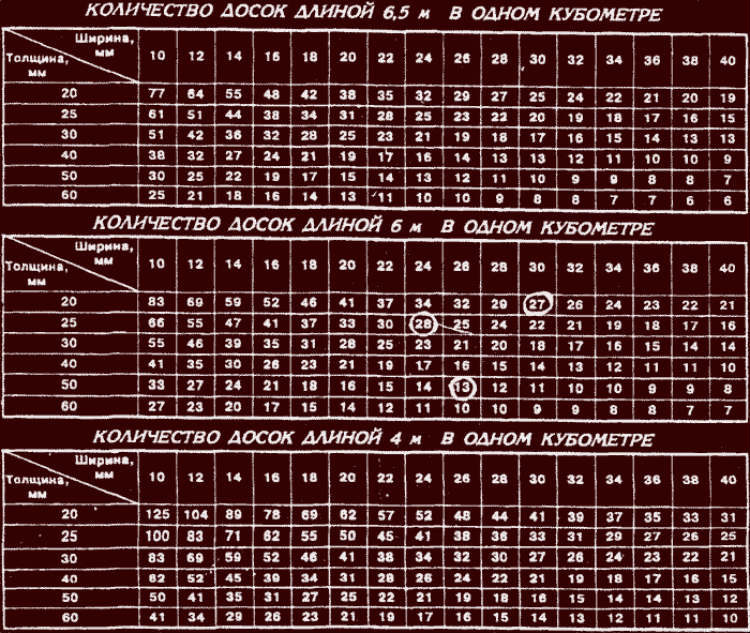
 Мехатроника , вып. 23, нет. 3, стр. 1303–1313, май 2018 г. doi: 10.1109/TMECH.2018.2835486
Мехатроника , вып. 23, нет. 3, стр. 1303–1313, май 2018 г. doi: 10.1109/TMECH.2018.2835486 Парк, «Адаптивный двухэтапный расширенный фильтр Калмана для отказоустойчивой слабосвязанной системы INS/GPS», IEEE Trans. Аэросп. Электрон. Сист. , том. 45, нет. 1, стр. 125–137, январь 2009 г. doi: 10.1109/TAES.2009.4805268
Парк, «Адаптивный двухэтапный расширенный фильтр Калмана для отказоустойчивой слабосвязанной системы INS/GPS», IEEE Trans. Аэросп. Электрон. Сист. , том. 45, нет. 1, стр. 125–137, январь 2009 г. doi: 10.1109/TAES.2009.4805268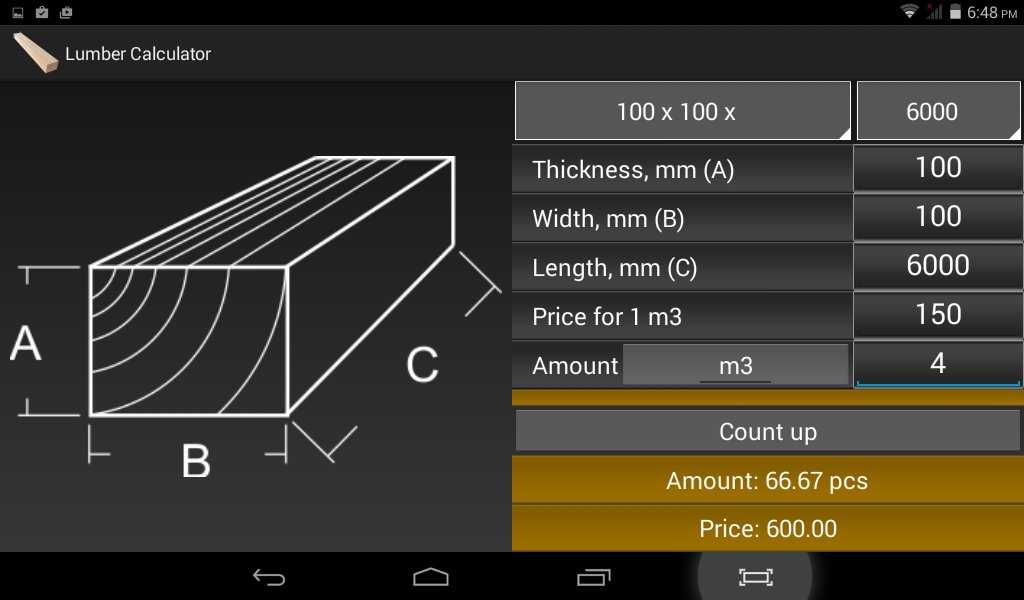 AIAA Guid., Navigat., Control Conf. , Портленд, штат Орегон, США, 2011 г., стр. 1–14.
AIAA Guid., Navigat., Control Conf. , Портленд, штат Орегон, США, 2011 г., стр. 1–14. Чжао, «Оценка эффективности кубатурного фильтра Калмана в тесно связанной навигационной системе GPS/IMU», Сигнальный процесс. , том. 119, стр. 67–79, февраль 2016 г. doi: 10.1016/j.sigpro.2015.07.014
Чжао, «Оценка эффективности кубатурного фильтра Калмана в тесно связанной навигационной системе GPS/IMU», Сигнальный процесс. , том. 119, стр. 67–79, февраль 2016 г. doi: 10.1016/j.sigpro.2015.07.014 Аэросп. Электрон. Сист. , том. 55, нет. 1, стр. 147–159, февраль 2019 г. doi: 10.1109/TAES.2018.2849179
Аэросп. Электрон. Сист. , том. 55, нет. 1, стр. 147–159, февраль 2019 г. doi: 10.1109/TAES.2018.2849179 Сигнальный процесс. , том. 50, нет. 2, стр. 174–188, февраль 2002 г. doi: 10.1109/78.978374
Сигнальный процесс. , том. 50, нет. 2, стр. 174–188, февраль 2002 г. doi: 10.1109/78.978374 5, стр. 14391–14404, июль 2017 г. doi: 10.1109/ACCESS.2017.2726519
5, стр. 14391–14404, июль 2017 г. doi: 10.1109/ACCESS.2017.2726519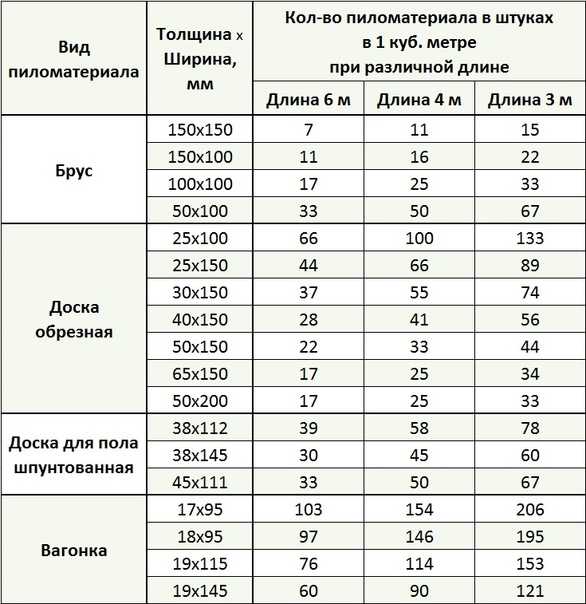 , том. 72, стр. 138–146, январь 2018 г. doi: 10.1016/j.isatra.2017.09.019
, том. 72, стр. 138–146, январь 2018 г. doi: 10.1016/j.isatra.2017.09.019