ᐉ Расчет пиломатериала • Таблица, кулькулятор, примеры
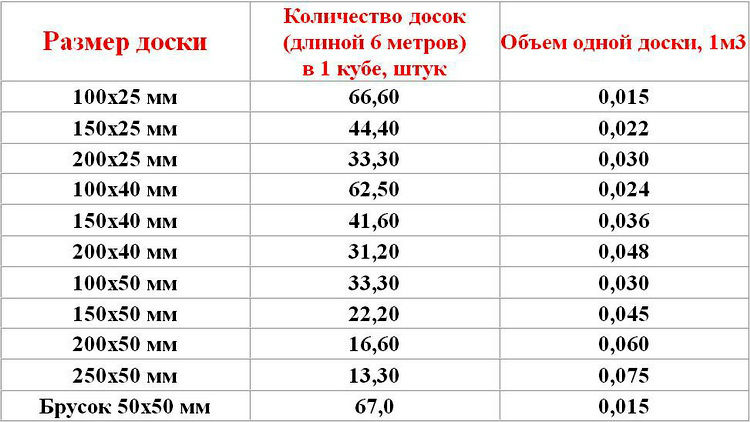
Для упрощения счета, мы подготовили для Вас сводную таблицу. Таблица позволяет сразу узнать, сколько досок в 1 кубе, количество погонных метров в 1 кубе, объем 1 доски и площадь 1 доски, не уделяя время лишним расчетам.
Формулы расчета доски
Кубатура
Примеры расчета доски размером 25х100х4000 мм
Формула расчета объема 1 доски:
0,025 м · 0,1 м · 4 м = 0,01 м3
Формула расчета количества досок в 1 кубе:
1 м3 / 0,01 м3 = 100 шт./м3
Квадратура
Примеры расчета доски размером 25х100х4000 мм
Формула расчета квадратуры 1 доски:
0,1 м · 4 м = 0,4 м2
Формула расчета количества квадратов в 1 кубе:
100 шт.(количество досок в кубе) · 0,4 м = 40 м2/ в 1 м3
Чтобы решить, сколько досок в 1 кубе, сначала нужно знать основные параметры приобретаемого материала – толщину, ширину и длину. Также можно делать расчет для досок любого сечения и длины.
Также можно делать расчет для досок любого сечения и длины.
Обрезная доска 25мм, 4000мм
| Обрезная доска, 25мм | Объем 1 доски, м3 | Количество досок в 1 м3 | Кол-во погонных метров в 1 м3 | Площадь 1 доски, м2 |
|---|---|---|---|---|
| 25х100х4000 | 0,01 м3 | 100 шт. | 400 метров. | 0,4 м2 |
| 25х120х4000 | 0,012 м3 | 83,3 шт. | 333,2 метра. | 0,48 м2 |
| 25х150х4000 | 0,015 м3 | 66,6 шт. | 266,4 метра. | 0,6 м2 |
| 25х200х4000 | 0,02 м3 | 50 шт. | 200 метров. | 0,8 м2 |
Обрезная доска 25мм, 4500мм
| Обрезная доска, 25мм | Объем 1 доски, м3 | Количество досок в 1 м3 | Кол-во погонных метров в 1 м3 | Площадь 1 доски, м2 |
|---|---|---|---|---|
| 25х100х4500 | 0,01125 м3 | 88,8 шт.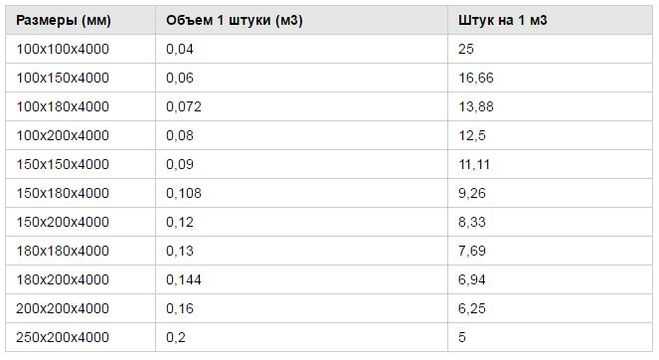 | 399,6 метра. | 0,45 м2 |
| 25х120х4500 | 0,0135 м3 | 74 шт. | 333 метра. | 0,54 м2 |
| 25х150х4500 | 0,0169 м3 | 59,2 шт. | 266,4 метра. | 0,675 м2 |
| 25х200х4500 | 0,0225 м3 | 44,4 шт. | 199,8 метров. | 0,9 м2 |
Обрезная доска 30мм, 4000мм
| Обрезная доска, 30мм | Объем 1 доски, м3 | Количество досок в 1 м3 | Кол-во погонных метров в 2 м3 | Площадь 1 доски, м2 |
|---|---|---|---|---|
| 30х100х4000 | 0,012 м3 | 83,3 шт. | 333,2 метра. | 0,4 м2 |
| 30х120х4000 | 0,0144 м3 | 69,4 шт. | 277,6 метра. | 0,48 м2 |
| 30х150х4000 | 0,018 м3 | 55,5 шт. | 222 метра. | 0,6 м2 |
| 30х200х4000 | 0,024 м3 | 41,6 шт. | 166,4 метра. | 0,8 м2 |
Обрезная доска 30мм, 4500мм
| Обрезная доска, 30мм | Объем 1 доски, м3 | Количество досок в 1 м3 | Кол-во погонных метров в 1 м3 | Площадь 1 доски, м2 |
|---|---|---|---|---|
| 30х100х4500 | 0,0135 м3 | 74 шт. | 333 метра. | 0,45 м2 |
| 30х120х4500 | 0,0162 м3 | 61,7 шт. | 377,65 метра. | 0,54 м2 |
| 30х150х4500 | 0,0203 м3 | 49,3 шт. | 221,85 метра. | 0,675 м2 |
| 30х200х4500 | 0,027 м3 | 37 шт. | 166,5 метра. | 0,9 м2 |
Страница содержит ответы на частые вопросы клиентов:
- Сколько досок
- Сколько кубов доски
- Сколько штук досок
- Досок в кубе
- Сколько кубов в досках
- Сколько штук в одном кубе
- Сколько в кубе обрезной доски
- Как подсчитать сколько досок в 1 кубе
- Количество досок в кубе
- Сколько квадратов в кубе
Зачем считать, сколько досок в 1 кубе?
Всего две причины для того, чтобы произвести расчеты:
- Вы узнаете общую цену всего объема бруса, нужного для вашего проекта. Достаточно знать цену за 1 доску и сколько всего штук (определяется расчетным путем или из нашей таблицы для стандартных размеров досок).

- Вы подсчитаете общее число досок, нужное для осуществления вашего проекта. И сделать расчет можно, зная, сколько нужно кубов материала для работы, и определив количество штук досок в 1 кубе.
Но если боитесь сделать неправильные расчеты, Вы всегда можете позвонить по нашим телефонам и наши специалисты помогут разобраться с правильным подсчетом!
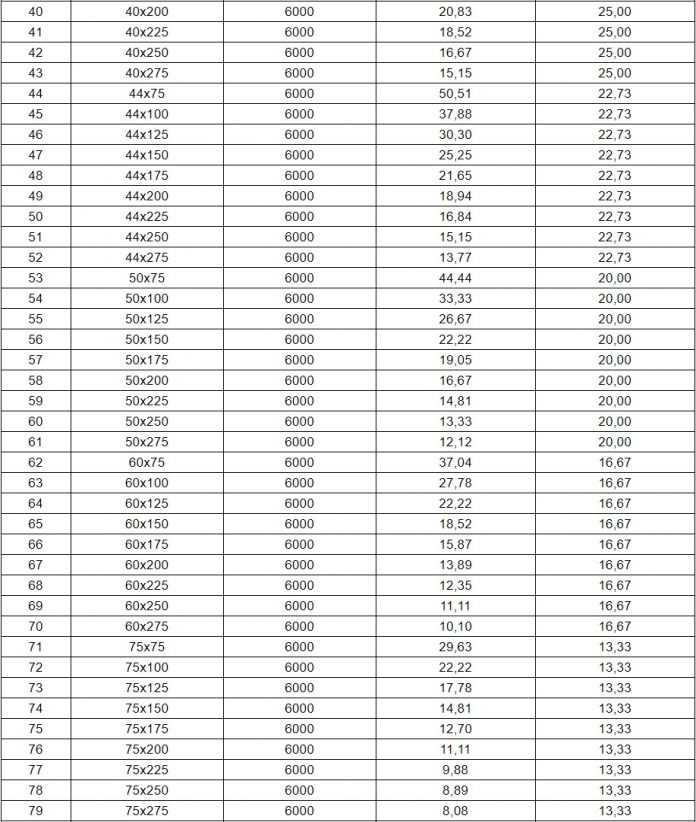
Таблица кубатуры пиломатериала — расчетная таблица
Главная / Статьи / Справочные данные /
| Брус | 100х100х6 | 1 штука — 0.06 куба | 16.67 штук в кубе |
| Брус | 100х150х6 | 1 штука — 0.09 куба | 11.11 штук в кубе |
| Брус | 150х150х6 | 1 штука — 0.135 куба | 7.41 штук в кубе |
| Брус | 100х200х6 | 1 штука — 0. 12 куба 12 куба |
8.33 штук в кубе |
| Брус | 150х200х6 | 1 штука — 0.18 куба | 5.56 штук в кубе |
| Брус | 200х200х6 | 1 штука — 0.24 куба | 4.17 штук в кубе |
| Брус | 100х100х7 | 1 штука — 0.07 куба | 14, 28 штук в кубе |
| Брус | 100х150х7 | 1 штука — 0.105 куба | 9.52 штук в кубе |
| Брус | 150х150х7 | 1 штука — 0.1575 куба | 6.35 штук в кубе |
| Брус | 100х200х7 | 1 штука — 0.14 куба | 7.14 штук в кубе |
| Брус | 150х200х7 | 1 штука — 0.21 куба | 4.76 штук в кубе |
| Брус | 200х200х7 | 1 штука — 0. 28 куба 28 куба |
3.57 штук в кубе |
| Доска обрезная | 22х100х6 | 1 штука — 0.0132 куба | 45.46 м.кв. в кубе |
| Доска обрезная | 22х150х6 | 1 штука — 0. 0198 куба | 45.46 м.кв. в кубе |
| Доска обрезная | 22х200х6 | 1 штука — 0.0264 куба | 45.46 м.кв. в кубе |
| Доска обрезная | 25х100х6 | 1 штука — 0.015 куба | 40 м.кв в кубе |
| Доска обрезная | 25х150х6 | 1 штука — 0.0225 куба | 40 м.кв в кубе |
| Доска обрезная | 25х200х6 | 1 штука — 0.03 куба | 40 м.кв в кубе |
| Доска обрезная | 1 штука — 0.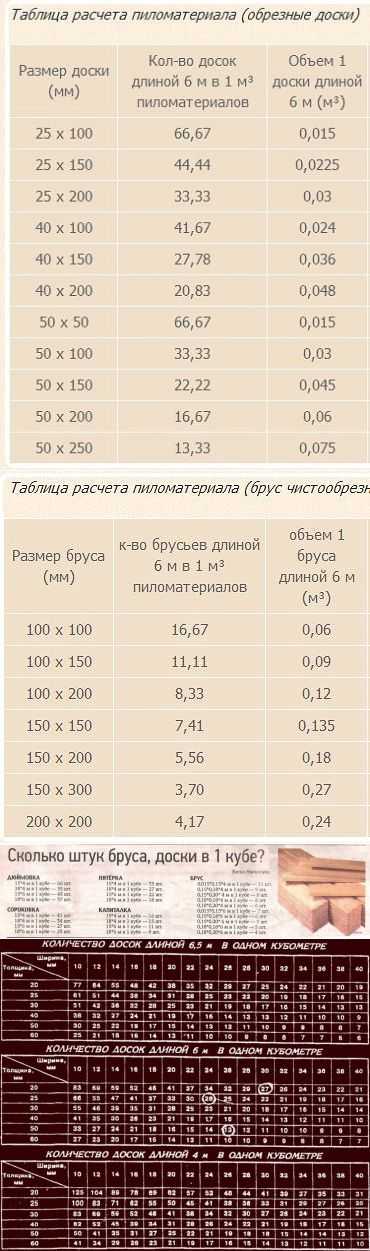 024 куба 024 куба |
25 м.кв в кубе | |
| Доска обрезная | 40х150х6 | 1 штука — 0.036 куба | 25 м.кв в кубе |
| Доска обрезная | 40х200х6 | 1 штука — 0.048 куба | 25 м.кв в кубе |
| Доска обрезная | 50х100х6 | 1 штука — 0.03 куба | 20 м.кв в кубе |
| Доска обрезная | 50х150х6 | 1 штука — 0.045 куба | 20 м.кв в кубе |
| Доска обрезная | 50х200х6 | 1 штука — 0.06 куба | 20 м.кв в кубе |
| Доска обрезная | 32х100х6 | 1 штука — 0.0192 куба | 31.25 м.кв в кубе |
| Доска обрезная | 32х150х6 | 1 штука — 0.0288 куба | 31. 25 м.кв в кубе 25 м.кв в кубе |
| Доска обрезная | 32х200х6 | 1 штука — 0.0384 куба | 31.25 м.кв в кубе |
| Доска обрезная | 25х100х2 | 1 штука — 0.005 куба | 40 м.кв в кубе |
| Доска обрезная | 25х100х7 | 1 штука — 0.0175 куба | 40 м.кв в кубе |
| Доска обрезная | 25х150х7 | 1 штука — 0.02625 куба | 40 м.кв в кубе |
| Доска обрезная | 25х200х7 | 1 штука — 0.035 куба | 40 м.кв в кубе |
| Доска необрезная | 50х6 | 1 штука — 0.071 куба | |
| Доска необрезная | 40х6 | 1 шутка — 0. 05 куба 05 куба |
|
| Доска необрезная | 25х6 | 1 штука — 0.0294 куба | |
| Рейка | 22х50х3 | 1 штука — 0.0033 куба | 909 м.п. в кубе |
| Рейка | 25х50х3 | 1 штука — 0.00375 куба | 800 м.п. в кубе |
| Рейка | 22х50х2 | 1 штука — 0.0022 куба | 909 м.п. в кубе |
| Рейка | 25х50х2 | 1 штука — 0.0025 куба | 800 м.п. в кубе |
| Брусок | 40х40х3 | 1 штука — 0.0048 куба | 624.99 м.п. в кубе |
| Брусок | 50х50х3 | 1 штука — 0. 006 куба 006 куба |
500.01 м.п. в кубе |
| Брусок | 40х80х3 | 1 штука — 0.0096 куба | 312.51 м.п. в кубе |
| Брусок | 50х50х3 | 1 штука — 0.0075 куба | 399.99 м.п. в кубе |
| Доска пола | 1 штука — 0.0229 куба | 27.77 м.кв. в кубе | |
| Доска пола | 36х136х6 | 1 штука — 0.0294 куба | 27.77 м.кв. в кубе |
| Доска пола | 45х136х6 | 1 штука — 0.0375 куба | 21.74 м.кв. в кубе |
| Вагонка | 16х88х6 | 1 штука — 0.0084 куба | 62.5 м.кв. в кубе в кубе |
| Вагонка | 16х88х3 | 1 штука — 0.0042 куба | 62.5 м.кв. в кубе |
| Вагонка | 12.5х90х3 | 1 штука — 0.0034 | 80 м.кв. в кубе |
Советуем почитать
Строганный пиломатериал
Всем известно, что пиломатериалы являются продуктами обработки древесины. Зачастую пиломатериал – это доска самых разнообразных сечений. Минимально доска имеет две параллельные грани. Строганные продукты получают при помощи продольной распиловки бревна, его специфической «очистки» от коры и оформления положенного вида исходя из заданных параметров.
17 февраля
Рынок пиломатериалов — тенденции и развитие
Пиломатериалы — это пиленая продукция, которая соответствует определенным параметрам качества и имеет две плоские поверхности, расположенные параллельно друг другу. Изделия из древесины изготавливают из цельного бревна, которое раскраивают и режут продольно или поперечно.
16 февраля
Методика дискретизации непрерывных данных для программирования адаптивных детерминированных кубатурных методов в умеренных размерах
Динь Ван Тьеп , Тран Тхи Хюэ
Факультет международного обучения, Технологический университет Тай Нгуен, ТНУ, Тай Нгуен, Вьетнам
Адрес для переписки: Динь Ван Тиеп, Факультет международного обучения, Технологический университет Тай Нгуен, ТНУ, Тай Нгуен, Вьетнам.
| Электронная почта: |
Copyright © 2020 Автор(ы). Опубликовано Scientific & Academic Publishing.
Эта работа находится под лицензией Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
Аннотация
Кубатурные методы использовались и хорошо развивались для аппроксимации интегралов большой размерности в течение длительного времени.
Ключевые слова: Адаптивная кубатурная программа, методы аппроксимации, дискретизация, непрерывные данные
Процитируйте эту статью: Динь Ван Тиеп, Тран Тхи Хью, Метод дискретизации непрерывных данных для программирования адаптивных детерминированных кубатурных методов в умеренных размерах, Applied Mathematics , Vol. 10 № 1, 2020. С. 1-6. doi: 10.5923/j.am.20201001.01.
10 № 1, 2020. С. 1-6. doi: 10.5923/j.am.20201001.01.
Описание статьи
- 1. Введение
- 1.1. История вопроса и описание проблемы
- 1.2. История вопроса и описание проблемы
- 1.3. Взнос
- 1.4. Организация статьи
- 2. Адаптивная кубатура
- 2.1. Аппроксимация кратных интегралов по непрямоугольным гиперблокам
- 2.2. Адаптивная кубатура в больших измерениях
- 3. Алгоритм адаптивной кубатуры
- 3.1. Псевдокод Matlab для реализации
- 3.2. Числовой пример
- 4. Выводы
- БЛАГОДАРНОСТИ
1. Введение
1110044- 9696969696
- .
.0004 1 . Регион B и его 4 субрегиона на первом шаге итерации (5), а затем теорему о среднем значении для второго члена (4), мы получаем для некоторых Аналогичным образом, применяя правило Симпсона последовательно к другим измерениям, мы завершаем доказательство. Составной Правило Симпсона правило с 3 n= Набор Подобно приведенному выше выводу правила Симпсона, для составного правила Симпсона получается следующий результат. Теорема 2 . (составное правило Симпсона) Позвольте быть коэффициентами составного правила Симпсона с We have,
(5), а затем теорему о среднем значении для второго члена (4), мы получаем для некоторых Аналогичным образом, применяя правило Симпсона последовательно к другим измерениям, мы завершаем доказательство. Составной Правило Симпсона правило с 3 n= Набор Подобно приведенному выше выводу правила Симпсона, для составного правила Симпсона получается следующий результат. Теорема 2 . (составное правило Симпсона) Позвольте быть коэффициентами составного правила Симпсона с We have,
для некоторых и некоторых(7) - 2,010. Адаптивная кубатура в больших измерениях
- Обозначим первый член в правой части (3), (7) соответственно. Предположим, что Итак, Поскольку имеем Следовательно,
Это означает, что мы можем использовать разницу между двумя оценками для аппроксимации ошибки аппроксимации, выявленной в (7).(8)  Следовательно, мы можем спроектировать размер ошибки так, чтобы он был меньше заданного допуска. Конкретно, если бы тогда мы могли полагать, что аппроксимируется с точностью до предела В противном случае, если мы в основном ошибаемся при использовании аппроксимации с ошибкой меньше, чем В последнем случае мы можно получить разумную аппроксимацию, повторно применив вышеупомянутую процедуру к меньшим областям (каждая из таких подобластей имеет размер, близкий к размеру исходной области, и ожидаемый допуск для аппроксимации интеграла по этой подобласти равен только Теперь в такой меньшей области мы ищемПоскольку размер таких подобластей становится все меньше и меньше, мы можем в конечном итоге достичь цели, если продолжим процедуру.Теоретически процедура всегда удается найти приближение лежащего в пределах заданного Однако компьютерная программа не может выполнять процедуру бесконечное число раз, поэтому мы устанавливаем ограничение на поиск, требуя, чтобы уровень субди видение (или количество повторений процедуры) не превышает предыдущего числа.
Следовательно, мы можем спроектировать размер ошибки так, чтобы он был меньше заданного допуска. Конкретно, если бы тогда мы могли полагать, что аппроксимируется с точностью до предела В противном случае, если мы в основном ошибаемся при использовании аппроксимации с ошибкой меньше, чем В последнем случае мы можно получить разумную аппроксимацию, повторно применив вышеупомянутую процедуру к меньшим областям (каждая из таких подобластей имеет размер, близкий к размеру исходной области, и ожидаемый допуск для аппроксимации интеграла по этой подобласти равен только Теперь в такой меньшей области мы ищемПоскольку размер таких подобластей становится все меньше и меньше, мы можем в конечном итоге достичь цели, если продолжим процедуру.Теоретически процедура всегда удается найти приближение лежащего в пределах заданного Однако компьютерная программа не может выполнять процедуру бесконечное число раз, поэтому мы устанавливаем ограничение на поиск, требуя, чтобы уровень субди видение (или количество повторений процедуры) не превышает предыдущего числа. Таким образом, программа покажет состояние отказа, если оно будет превышено. В противном случае получим желаемое приближение.
Таким образом, программа покажет состояние отказа, если оно будет превышено. В противном случае получим желаемое приближение.3. Алгоритм адаптивной кубатуры
3.1. Псевдокод Matlab для реализации
- Алгоритм вышеописанной процедуры опишем в виде псевдокода с использованием функций Matlab. Однако обозначения и структура повторяющихся циклов или условия if, оператора присваивания не такие, как в Matlab. Они изменены для того, чтобы программа познакомилась с математическими обозначениями, чтобы ее было проще анализировать. Входной область (включая и функциональные допуска с ограниченным уровнем Выход Приближение или сообщение объявляет, что уровень превышается (то есть процедура сбой!).
- Предыстория и постановка задачи
- Алгоритм адаптивной кубатуры, а также другие методы численного интегрирования в большой размерности разработаны и используются очень давно.
 Это определенно имеет преимущество в точности, но также имеет недостаток в стоимости вычислений, таких как затраты времени и памяти из-за возрастающей сложности вычислений. С помощью компьютеров необходимо скорректировать реализации такого алгоритма в большой размерности. Более того, в общем случае большой размерности программа для алгоритма еще не предоставлена. Основным препятствием для программирования алгоритма является тот факт, что интегрированная область большой размерности с гладкой границей описывается гиперповерхностями, которые создаются непрерывными данными точек. К сожалению, невозможно найти достаточно памяти аппаратного пространства для хранения данных. Это делает алгоритм несколько теоретическим и непрактичным с огромным объемом вычислений. Сам алгоритм исправляет это заданной ошибкой, называемой допуском, который требует, чтобы принятая ошибка оценки аппроксимации не превышала этого допуска. Это довольно сильно сокращает количество вычислений, но само по себе этого недостаточно, чтобы алгоритм можно было реализовать, потому что нам по-прежнему нужна стратегия для хранения необходимой нам в процессе вычислений информации о значениях подынтегрального выражения на границе области.
Это определенно имеет преимущество в точности, но также имеет недостаток в стоимости вычислений, таких как затраты времени и памяти из-за возрастающей сложности вычислений. С помощью компьютеров необходимо скорректировать реализации такого алгоритма в большой размерности. Более того, в общем случае большой размерности программа для алгоритма еще не предоставлена. Основным препятствием для программирования алгоритма является тот факт, что интегрированная область большой размерности с гладкой границей описывается гиперповерхностями, которые создаются непрерывными данными точек. К сожалению, невозможно найти достаточно памяти аппаратного пространства для хранения данных. Это делает алгоритм несколько теоретическим и непрактичным с огромным объемом вычислений. Сам алгоритм исправляет это заданной ошибкой, называемой допуском, который требует, чтобы принятая ошибка оценки аппроксимации не превышала этого допуска. Это довольно сильно сокращает количество вычислений, но само по себе этого недостаточно, чтобы алгоритм можно было реализовать, потому что нам по-прежнему нужна стратегия для хранения необходимой нам в процессе вычислений информации о значениях подынтегрального выражения на границе области. интегрированный домен.
интегрированный домен.1.2. Предыстория и постановка задачи
- Кубатура — это термин, введенный Кроммером и Уберхубером [1,2] для обозначения численного вычисления кратного интеграла. Он включает в себя множество методов, таких как кубатура Монте-Карло и квази-Монте-Карло, байесовская кубатура, адаптивная кубатура. Что касается адаптивной кубатуры, в 2003 году Genz и Cools опубликовали алгоритм адаптивной кубатуры для симплексов [3], а также CUBPACK на FORTRAN90. Мы знали, что в больших измерениях кубатура Монте-Карло является наиболее предпочтительным выбором для численного интегрирования из-за преимущества набора номера с проклятием размерности. Но этот метод, как правило, дает только скорость сходимости, которая довольно низка для количества точек выборки. Еще одним недостатком этого метода, особенно в случае отсутствия разрешения на использование вероятностной ошибки, является то, что порядок сходимости представлен только в рандомизированных терминах. То есть ошибка оценки, производимая методом Монте-Карло, не является детерминированной [4] и непригодна, если для кубатурной задачи требуется гарантированная ошибка.
 Это косвенная причина, по которой нам все еще необходимо обращаться к детерминированной кубатуре, особенно в умеренном числе измерений (скажем, меньше 7). Авторы Генц и Малик, Бернтсен и Эспелид и Генц, Доурен и Риддер представили в [5,6,7] свои работы по адаптивной кубатуре, однако они были разработаны на гиперкубе, который является простейшей областью в больших размерностях. . В этой статье обсуждается естественное развитие адаптивной кубатуры на более общей области больших размерностей.
Это косвенная причина, по которой нам все еще необходимо обращаться к детерминированной кубатуре, особенно в умеренном числе измерений (скажем, меньше 7). Авторы Генц и Малик, Бернтсен и Эспелид и Генц, Доурен и Риддер представили в [5,6,7] свои работы по адаптивной кубатуре, однако они были разработаны на гиперкубе, который является простейшей областью в больших размерностях. . В этой статье обсуждается естественное развитие адаптивной кубатуры на более общей области больших размерностей.1.3. Вклад
- В этой статье мы выводим алгоритм численного интегрирования по более общим областям, которые окружены измеримыми поверхностями. В некотором смысле хранение данных, описывающих регион, является еще одной проблемой. Мы не можем хранить все данные этой границы, потому что она составляет непрерывные поверхности. При необходимости стратегии хранения данных, необходимых для расчета на каждом итерированном шаге, мы устанавливаем сеть хранимых данных с более плотными точками сетки на области, по которой ошибка оценки не меньше, чем соответствующий допуск, распределенный по этому область, край.
 Этот метод представляет собой способ дискретизации непрерывных данных интегрированной области. Фаза извлечения для получения данных организована адаптивным образом, при котором вызываются только те значения, которые необходимы для расчета в следующей итерации. Введение этой техники для общей области размерности n является основным вкладом статьи. Кроме того, создание точек данных и хорошая организация их в виде сети, чтобы мы могли легко получить доступ к данным, также раскрывает еще одну проблему для программирования общего алгоритма. В статье мы предлагаем решение этой проблемы простым подходом, использующим деление пополам в не слишком больших размерностях. Такой подход в таких размерностях удобен для упрощения структуры программы и определенно способствует ускорению процесса вычислений.
Этот метод представляет собой способ дискретизации непрерывных данных интегрированной области. Фаза извлечения для получения данных организована адаптивным образом, при котором вызываются только те значения, которые необходимы для расчета в следующей итерации. Введение этой техники для общей области размерности n является основным вкладом статьи. Кроме того, создание точек данных и хорошая организация их в виде сети, чтобы мы могли легко получить доступ к данным, также раскрывает еще одну проблему для программирования общего алгоритма. В статье мы предлагаем решение этой проблемы простым подходом, использующим деление пополам в не слишком больших размерностях. Такой подход в таких размерностях удобен для упрощения структуры программы и определенно способствует ускорению процесса вычислений.1.4. Организация статьи
- Статья разделена на 4 раздела. Второй раздел предназначен для краткого описания основ адаптивной кубатуры для аппроксимации кратных интегралов по довольно общей области, так называемым непрямоугольным гипербоксам.
 Идея основана на двух указанных методах, правиле Симпсона и составном правиле Симпсона с 4 подынтервалами, разработанными для кратных интегралов. Вызовы связаны не только с проклятием размерности, но и со сложностью интегрированной области. Для этой точки, как уже упоминалось выше, сложность изображения общей области может быть преодолена в несколько временно приемлемом подходе, в котором мы храним дискретно набор точек данных, которые устанавливают скелет области. Мы не собираемся использовать эти точки все сразу, но с учетом требований каждого контрольного времени. Это не позволяет памяти компьютера работать без перегрузки. Еще одно преимущество этого подхода такое же, как и у обычной адаптивной кубатуры с гибкостью в подразделении интегрированной области путем корректировки размера подобластей для следующей итерации с учетом оценки ошибки, полученной при использовании двух методы, применяемые на этом этапе. В третьем разделе представлен алгоритм метода, организованный и представленный в целом в стиле языка Matlab.
Идея основана на двух указанных методах, правиле Симпсона и составном правиле Симпсона с 4 подынтервалами, разработанными для кратных интегралов. Вызовы связаны не только с проклятием размерности, но и со сложностью интегрированной области. Для этой точки, как уже упоминалось выше, сложность изображения общей области может быть преодолена в несколько временно приемлемом подходе, в котором мы храним дискретно набор точек данных, которые устанавливают скелет области. Мы не собираемся использовать эти точки все сразу, но с учетом требований каждого контрольного времени. Это не позволяет памяти компьютера работать без перегрузки. Еще одно преимущество этого подхода такое же, как и у обычной адаптивной кубатуры с гибкостью в подразделении интегрированной области путем корректировки размера подобластей для следующей итерации с учетом оценки ошибки, полученной при использовании двух методы, применяемые на этом этапе. В третьем разделе представлен алгоритм метода, организованный и представленный в целом в стиле языка Matlab. Также представлена иллюстрация правильной работы алгоритма в случае размерности 2, аппроксимации двойных интегралов. В последнем разделе мы кратко остановимся на характеристиках обсуждаемого алгоритма, включая его преимущества и недостатки.
Также представлена иллюстрация правильной работы алгоритма в случае размерности 2, аппроксимации двойных интегралов. В последнем разделе мы кратко остановимся на характеристиках обсуждаемого алгоритма, включая его преимущества и недостатки.2. Адаптивная кубатура
2.1. Аппроксимация кратных интегралов по непрямоугольным гиперблокам
- Рассмотрим задачу приближения кратного интеграла I функции, непрерывно дифференцируемой до порядка 4 в области непрямоугольного гиперблока — непрерывные функции в прямоугольном гиперблоке Наша цель теперь нужно сформулировать аппроксимацию для
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
3.
 2. Численный пример
2. Численный пример- Рассмотрим двойной интеграл, где непрямоугольная область Точный результат Реализация, использующая приведенный выше алгоритм, дает приближение в пределах заданного допуска Предельный уровень Вся процедура описана в Таблица 1.
|
4. Заключение
. метод, который позволяет оптимизировать реализацию научных компьютеров, даже когда установка множественного интегрирования является довольно общей, общие повторяющиеся области с непрерывной функцией многих переменных называются подынтегральной функцией.
В реализации представлены повторяющиеся циклы, которые являются вложенными циклами. Для реализации каждого такого цикла в программе необходимо произвести проверку на размерность кратного интеграла. Это означает, что каждое измерение имеет определенную программу для соответствующего алгоритма. Поэтому предпочтительнее использовать реализацию для не слишком высокой размерности, скажем, менее 7. Для этих размеров размерности алгоритм имеет гораздо больше преимуществ высокой скорости сходимости по сравнению с кубатурой Монте-Карло и квази-Монте-Карло, которые являются предпочтительным выбором в очень больших размерах.
Это означает, что каждое измерение имеет определенную программу для соответствующего алгоритма. Поэтому предпочтительнее использовать реализацию для не слишком высокой размерности, скажем, менее 7. Для этих размеров размерности алгоритм имеет гораздо больше преимуществ высокой скорости сходимости по сравнению с кубатурой Монте-Карло и квази-Монте-Карло, которые являются предпочтительным выбором в очень больших размерах.ПРИЗНАТЕЛЬНОСТЬ
- Авторы работают в Технологическом университете Тай Нгуен. Эта работа поддерживается университетом. Мы очень благодарны за эту помощь и другую помощь в получении ссылок, необходимых для завершения этой работы.
Каталожные номера
| [1] |  155-165. 155-165. |
| [2] | Ueberhuber, C.W. (1997). Численные вычисления 2: методы, программное обеспечение и анализ. Берлин: Springer-Verlag. |
| [3] | Genz, A.C., Cools, R. (2003), «Адаптивный кубатурный алгоритм для симплексов», ACM Trans. Мат. Софт., Том. 26, № 3, стр. 297-308. |
| [4] | Атанасов Э., Димов И.Т. (2008). «Что модели Монте-Карло могут и не могут делать эффективно?», Applied Mathematical Modeling, Vol. 32, стр. 1477-1500. |
| [5] | Genz, A.C. and Malik, A.A. (1980). «Адаптивный алгоритм численного интегрирования по N-мерной прямоугольной области», J. Comput. заявл. Матем., Том. 6, № 4, стр. 295-302. |
| [6] | Бернтсен, Дж., Эспелид, Т.О., Генц, А. (1991). «Адаптивный алгоритм приближенного вычисления кратных интегралов», ACM Trans. Мат. Софт., Том. 17, № 4, стр. 437-451. 437-451. |
| [7] | Доурен П., Риддер Л. (1976). «Адаптивный алгоритм численного интегрирования по n-мерному кубу», J. Comput. заявл. Матем., Том. 2, № 3, стр. 207-217. |
| [8] | Burden, R.L., Faires, JD (2000). Численный анализ. (9-е изд.). Брук/Коул, Cengage Learning, Бостон (2000). |
| [9] | Чапра, Южная Каролина (2012). Прикладные численные методы с MATLAB. (3-е изд.), McGraw-Hill, Нью-Йорк. |
| [10] | Радон, Дж. (1948). «Цур механиче Кубатур». Монац. Мат. Том. 42, стр. 286-300. |
| [11] | Кафлиш, Р. Э. (1998). Методы Монте-Карло и квази-Монте-Карло. Acta Numerica, Vol. 7, стр. 1-49. |
| [12] | Соболь И. М. (1990). «Методы квази-Монте-Карло». Прогресс в ядерной энергетике. Том. 24, вып.: 1-3, с. 55-61. |
| [13] | Пьер, Л’Э.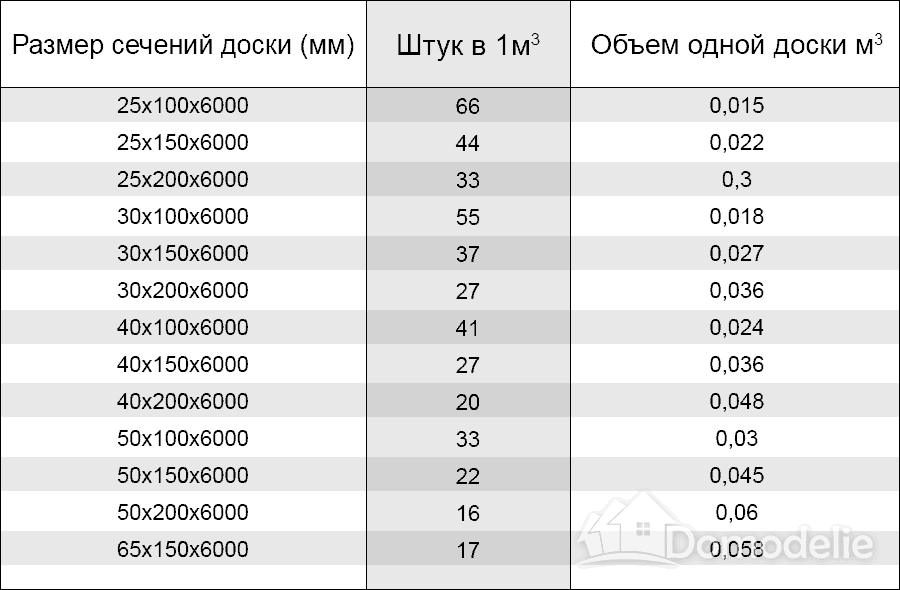 , Рандомизированный квази-Монте-Карло: введение для практиков. 12-я Международная конференция по методам Монте-Карло и квази-Монте-Карло в научных вычислениях (MCQMC 2016), Стэнфорд, США, hal-01561550. , Рандомизированный квази-Монте-Карло: введение для практиков. 12-я Международная конференция по методам Монте-Карло и квази-Монте-Карло в научных вычислениях (MCQMC 2016), Стэнфорд, США, hal-01561550. |
| [14] | Кулс, Р. (2003). «Энциклопедия кубатурных формул». J. Сложность, Vol. 19, стр. 445-453. |
Улучшенная стабилизация нелинейных микросетей постоянного тока: подход с кубатурным фильтром Калмана Улучшенная стабилизация нелинейных микросетей постоянного тока: подход с кубатурным фильтром Калмана
%PDF-1.4 % 1 0 объект > /Метаданные 2 0 R /Контуры 3 0 R /OutputIntents [4 0 R] /Страницы 5 0 Р /Сохранить потоки > /StructTreeRoot 8 0 R /Тип /Каталог >> эндообъект 90 объект /Subject (IEEE Transactions on Industry Applications; ;PP;99;10.1109/TIA.2018.2848959) /Title (Улучшенная стабилизация нелинейных микросетей постоянного тока: подход с кубатурным фильтром Калмана) >> эндообъект 2 0 объект > транслировать приложение/pdf
 1109/TIA.2018.2848959
1109/TIA.2018.2848959

 (5), а затем теорему о среднем значении для второго члена (4), мы получаем для некоторых Аналогичным образом, применяя правило Симпсона последовательно к другим измерениям, мы завершаем доказательство. Составной Правило Симпсона правило с 3 n= Набор Подобно приведенному выше выводу правила Симпсона, для составного правила Симпсона получается следующий результат. Теорема 2 . (составное правило Симпсона) Позвольте быть коэффициентами составного правила Симпсона с We have,
(5), а затем теорему о среднем значении для второго члена (4), мы получаем для некоторых Аналогичным образом, применяя правило Симпсона последовательно к другим измерениям, мы завершаем доказательство. Составной Правило Симпсона правило с 3 n= Набор Подобно приведенному выше выводу правила Симпсона, для составного правила Симпсона получается следующий результат. Теорема 2 . (составное правило Симпсона) Позвольте быть коэффициентами составного правила Симпсона с We have, Следовательно, мы можем спроектировать размер ошибки так, чтобы он был меньше заданного допуска. Конкретно, если бы тогда мы могли полагать, что аппроксимируется с точностью до предела В противном случае, если мы в основном ошибаемся при использовании аппроксимации с ошибкой меньше, чем В последнем случае мы можно получить разумную аппроксимацию, повторно применив вышеупомянутую процедуру к меньшим областям (каждая из таких подобластей имеет размер, близкий к размеру исходной области, и ожидаемый допуск для аппроксимации интеграла по этой подобласти равен только Теперь в такой меньшей области мы ищемПоскольку размер таких подобластей становится все меньше и меньше, мы можем в конечном итоге достичь цели, если продолжим процедуру.Теоретически процедура всегда удается найти приближение лежащего в пределах заданного Однако компьютерная программа не может выполнять процедуру бесконечное число раз, поэтому мы устанавливаем ограничение на поиск, требуя, чтобы уровень субди видение (или количество повторений процедуры) не превышает предыдущего числа.
Следовательно, мы можем спроектировать размер ошибки так, чтобы он был меньше заданного допуска. Конкретно, если бы тогда мы могли полагать, что аппроксимируется с точностью до предела В противном случае, если мы в основном ошибаемся при использовании аппроксимации с ошибкой меньше, чем В последнем случае мы можно получить разумную аппроксимацию, повторно применив вышеупомянутую процедуру к меньшим областям (каждая из таких подобластей имеет размер, близкий к размеру исходной области, и ожидаемый допуск для аппроксимации интеграла по этой подобласти равен только Теперь в такой меньшей области мы ищемПоскольку размер таких подобластей становится все меньше и меньше, мы можем в конечном итоге достичь цели, если продолжим процедуру.Теоретически процедура всегда удается найти приближение лежащего в пределах заданного Однако компьютерная программа не может выполнять процедуру бесконечное число раз, поэтому мы устанавливаем ограничение на поиск, требуя, чтобы уровень субди видение (или количество повторений процедуры) не превышает предыдущего числа. Таким образом, программа покажет состояние отказа, если оно будет превышено. В противном случае получим желаемое приближение.
Таким образом, программа покажет состояние отказа, если оно будет превышено. В противном случае получим желаемое приближение.