Катушка — сопротивление — Большая Энциклопедия Нефти и Газа, статья, страница 1
Катушка — сопротивление
Cтраница 1
Катушки сопротивления изготовляются по ТУ-П № ОПП. Катушки применяются по назначению в лабораторной и цеховой практике. [2]
Катушка сопротивления, состоящая из тонкой проволоки, концы которой выведены на большие медные массы, приблизительно удовлетворяет этим условиям, потому что потенциал внутри массивного электрода является почти постоянным, и любые разности потенциалов в разных точках одного и того же электрода могут считаться пренебрежимо малыми в сравнении с разностью потенциалов двух электродов. [3]
Катушка сопротивления — это проводник, который легко можно включить в вольтову цепь, с тем чтобы ввести в эту цепь известное сопротивление. [4]
Катушки сопротивления изготовляются, как правило, из металлов, имеющих наибольшее сопротивление и мало меняющихся с температурой. Этому требованию очень хорошо удовлетворяет нейзильбер ( мельхиор), но оказалось, что некоторые образцы с годами меняют свои свойства. Поэтому для стандартных сопротивлений применяются некоторые ч истые металлы, а также сплав платины и серебра; относительное сопротивление таких катушек на протяжении нескольких лет найдено постоянным в пределах современной точности. [5]
Катушки сопротивления по 2 5 ом включают в провода, соединяющие поверяемый мост с магазином, для создания требуемой величины внешнего сопротивления. [7]
Катушки сопротивлений от 1 до 10000 ом и спирали в 0 1 ом наматываются бифилярно. [8]
Катушки сопротивления с номинальным значением 100 ом и выше выполняются двухзажимными, а катушки ниже 100 ом имеют четыре зажима: два зажима токовые и два — потенциальные. С помощью токовых зажимов катушка включается в цепь тока, а сопротивление катушки определяется по падению напряжения между потенциальными зажимами. [9]
Катушки сопротивлений, размещенные на панели, позволяют обес лечить постоянную нагрузку на телескоп при отключении одного из приборов и привести сопротивление проводов к определенной величине. Три подгоночные ( уравнительные) катушки служат: Ry — для подгонки сопротивления соединительных проводов от телескопа до панели; Ry — для подгонки сопротивления линии от панели к самопишущему милливольтметру; Зу — для подгонки сопротивления линии от панели к показывающему милливольтметру. Две эквивалентные катушки R3, сопротивления которых соответственно равны сопротивлениям самопишущего и показывающего милливольтметров, служат для замещения этих приборов. Сопротивление линии соединительных проводов от панели к каждому из милливольтметров и от панели к радиационному пирометру должно составлять 5 0 1 ома. Сопротивление каждой уравнительной катушки составляет 5 ом, эквивалентной катушки 175 ом. [10]
Катушки сопротивлений, размещенные на панели, позволяют обес лечить постоянную нагрузку на телескоп при отключении одного из приборов и привести сопротивление проводов к определенной величине. Три подгоночные ( уравнительные) катушки служат: Ку — для подгонки сопротивления соединительных проводов от телескопа до панели; Ry — для подгонки сопротивления линии от панели к самопишущему милливольтметру; 1у — для подгонки сопротивления линии от панели к показывающему милливольтметру. Две эквивалентные катушки Ra, сопротивления которых соответственно равны сопротивлениям самопишущего и показывающего милливольтметров, служат для замещения этих приборов. Сопротивление линии соединительных проводов от панели к каждому из милливольтметров и от панели к радиационному пирометру должно составлять 5 0 1 ома. Сопротивление каждой уравнительной катушки составляет 5 ом, эквивалентной катушки 175 ом. [11]
Катушки сопротивлений рассчитаны иа ток порядка сотых долей ампера, поэтому сильные токи через магазин сопротивлений проходить не должны. На рис. 10 представлен общий вид магазина сопротивлений на 1110 ом. Такие штепсельные реостаты изготовляют на НПО ом и на другие сопротивления. [13]
Катушки сопротивления выполняют на номинальное значение сопротивления 10 л Ом, где п — целое число. Они имеют четыре зажима, два из которых называют токовыми, а два — потенциальными. Между потенциальными зажимами сопротивление катушки соответствует номинальному значению при включении катушки в цепь с помощью токовых зажимов. Обмотку катушки сопротивления выполняют из манганина, имеющего большое удельное электрическое сопротивление при малом температурном коэффициенте сопротивления, малой термо — ЭДС в паре с медью и при высокой стабильности своих свойств. [14]
Страницы: 1 2 3 4 5
www.ngpedia.ru
Сопротивление обмоток – каким оно должно быть, как проверить, измерить.
Тема: что нужно знать про электрическое сопротивление намоток катушек, их проверка.
Достаточно большое количество электрических устройств имеет в своем составе катушки в виде намотки медной изолированной проволоки. Главным свойством, которым обладает электрическая катушка является взаимодействие с электромагнитным полем. Для одних устройств катушка выступает в роли электромагнита, притягивающая либо отталкивающая металлические части или другие катушки. В иных же устройствах электрическая катушка может служить генератором электрической энергии, по средствам электромагнитной индукции (если на катушку воздействовать внешним электромагнитным полем).
Любая электрическая катушка имеет свое внутреннее сопротивление. Причем, это сопротивление можно разделить на два типа, это активное и реактивное. Активным сопротивлением обладают катушки, через которые протекает только постоянный ток. Активное сопротивление катушки зависит от материала провода катушки, его сечения, длины. При протекании через катушку переменного тока мы уже будет иметь дело с реактивным сопротивлением, величина которого уже будет зависеть ещё и от частоты протекающего переменного тока (чем частота выше, тем больше реактивное сопротивление).
На практике, в большинстве случаев, приходится сталкиваться именно с активным электрическим сопротивлением катушек. Это сопротивление обусловлено внутренней структурой атомов, из которых состоит вещество проводника. У различных проводников внутреннее сопротивление имеет разные значения (при одной и той же длине и сечении). Это ещё называется удельным сопротивлением проводника (его обычно берут из справочников). Для нахождения сопротивления определенного проводника можно воспользоваться простой формулой: сопротивление равно удельное сопротивление материала проводника умноженное на его длину и это всё деленное на площадь поперечного сечения.
Более простым способом нахождения сопротивления обмоток, широко используемом на практике, является метод обычного измерения. Берём мультиметр, омметр, выставляем нужный диапазон измерения (Омы, килоОмы, мегаОмы) и прикасаемся щупами измерителя прямо к катушке, обмотке. Наш тестер с достаточно большой точность покажет имеющееся сопротивление. Как правило, обмотка катушек, рассчитанных на низкое напряжение имеет достаточно малое сопротивление (в районе единицы-сотни Ом). Обмотки под напряжение 220, 380 и выше уже имеют сопротивление в пределах от сотен Ом до десятков килоОм.
Зная сопротивление обмотки, как минимум можно судить о её работоспособности (если в ней нет короткозамкнутых витков), а как максимум её величину можно использовать в различных формулах. Наиболее известной и широко используемой является формула закона Ома, которая позволяет найти любую одну неизвестную величину (из трех – напряжение, ток, сопротивление) из двух известных. Учтите, в формулах нужно использовать основные единицы измерения физических величин. В законе Ома таковыми являются: для силы тока это ампер, для напряжения это вольт и для сопротивления это Ом.
Если при измерении сопротивления обмотки прибор ничего не показывает (пробник не реагирует), значит в этой катушке имеется обрыв. В этом случае катушку следует разобрать, хорошо визуально осмотреть (возможно обрыв произошел возле самих выводов катушки, что происходит достаточно часто), при необходимости её перемотать. Но бывают случаи, когда обрыва нет, тестер показывает какое-то сопротивление, сама же катушка не работает как надо. В этом случае, если вы уверены надёжности проводов и цепей, по которым подводится к обмотке напряжение, возможен вариант короткозамкнутых витков.
Короткозамкнутые витки – это витки обмоточного провода катушки, которые были накоротко замкнуты внутри самой обмотке между собой. Естественно, участок обмотки с короткозамкнутыми витками является нерабочим, более того, он является причиной возникновения дополнительного нагрева самой катушки (по причине самоиндукции, в цепях переменного тока). Причиной возникновения такого явления может послужить полое качество изоляции обмоточного провода, температурный удар (возникший сильный перегрев катушки), который был прежде, чрезмерное динамическое воздействие на катушку (удары, тряски и т.д.). Сопротивление обмотки, что имеет короткозамкнутые витки, будет меньше номинального значения, а это ведёт к ненормальной работе самой этой катушки.
Короткозамкнутые витки выявляются не просто. Для проверки обмотки якоря электродвигателя существует специальное устройство (можно сделать и самому, это трансформатор со специальным распилом на своем магнитопроводе, куда и ложится якорь для проверки). Если катушка до этого работала нормально, при этом особо не нагревалась, а потом вдруг начала, то скорее всего у неё появились эти самые бракованные витки. Хорошо если вы изначально знаете номинальное сопротивление своей катушки, будет с чем сравнить при измерении и выявлении неисправности обмотки. Либо же нужно сравнивать сопротивление с заведомо рабочей обмоткой другого устройства. Или же прибегнуть в вычислением сопротивления по формуле, если известны: мощность, сила тока, напряжение.
P.S. Далеко не во всех случаях при неисправности катушки виновата сама обмотка. Достаточно часто бывает так, что те провода, которые питают эту самую катушку находятся в плохом состоянии. Окисленные контакты соединяющие концы обмотки и питающие клеммы, провода, место спая значительно увеличивают сопротивление электрической цепи. Достаточно хорошо почистить подобные места, как тут же работоспособность катушки того или иного устройства полностью восстановится.
electrohobby.ru
Реальная катушка в цепи переменного тока
Реальная катушка в отличии от идеальной имеет не только индуктивность, но и активное сопротивление, поэтому при протекании переменного тока в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.
Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле — реактивной мощностью Q.
В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому одна реальная катушка в схеме замещения должна быть представлена активным и реактивным элементами.
Схема замещения катушки с последовательным соединением элементов
В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.
Активное сопротивление определяется величиной мощности потерь
R = P/I2
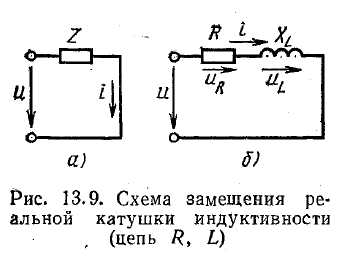
а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением i = Imsinωt. Требуется определить напряжение в цепи и мощность.
При переменном токе в катушке возникает э. д. с. самоиндукции eL поэтому ток зависит от действия приложенного напряжения и эдс eL. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид:
Приложенное к катушке напряжение состоит из двух слагаемых,одно из которых uR равно падению напряжения в активном сопротивлении, а другое uL уравновешивает эдс самоиндукции.
В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б).
Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам полученных в этих предыдущих двух (первая, вторая) статьях получим — uR совпадает по фазе с током, UL опережает ток на 90°.
Поэтому:
u = R*Imsinωt + ωLImsin(ωt+π/2).
Векторная диаграмма реальной катушки и полное её сопротивление
Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения
UmR = RIm; UmL = ωLIm ,
а действующие величины
UR = RI; UL = XLI .
Вектор общего напряжения
U = UR + UL
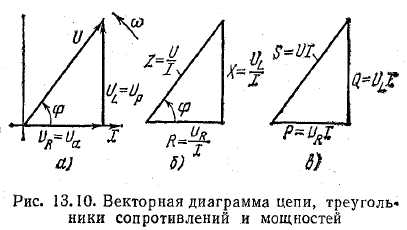
Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Mi и напряжения Мu.
За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока Ψi =0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.
Вектор UR по направлению совпадает с вектором тока I, а вектор UL направлен перпендикулярно вектору I с положительным углом.
Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ>0, но φ<90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях UR и UL :
UR = Ucosφ
Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается Ua. Для катушки по схеме рис. 13.9 при Ua = UR
U = Usinφ (13.14)
Проекция вектора напряжения U на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается Up. Для катушки Up = UL
При токе i = Imsinωt уравнение напряжения можно записать на основании векторной диаграммы в виде
U = Umsin(ωt+φ)
Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. 13.10, б), катетами которого являются активное R = UR/I и индуктивное XL = UL/I, сопротивления, а гипотенузой величина Z = U/I.
Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи.
Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени.
Из треугольника сопротивлений следует
Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими величинами напряжения и тока формулой, подобной формуле Ома:
Из треугольников сопротивления и напряжения определяются
cosφ = UR/U = R/Z; sinφ = UL/U = XL/Z; tgφ = UL/UR = XL/R. (13.18)
Мощность реальной катушки
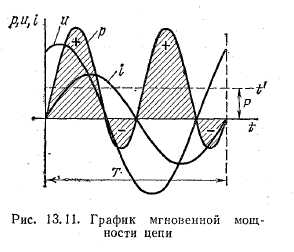
Мгновенная мощность катушки
p = ui = Umsin(ωt+φ) * Imsinωt
Из графика мгновенной мощности (рис. 13.11) видно, что в течение периода мощность четыре раза меняет знак; следовательно, направление потока энергии и в данном случае в течение периода меняется. Относительно некоторой оси t’, сдвинутой параллельно оси t на величину Р, график мгновенно мощности является синусоидальной функцией двойной частоты.
При положительном значении мощности энергия переходит от источника в приемник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, поступившей в приемник (положительная площадь), больше возвращенной обратно (отрицательная площадь).
Следовательно, в цепи с активным сопротивлением и индуктивностью часть энергии, поступающей от генератора, необратимо превращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).
Скорость необратимого процесса преобразования энергии оценивается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощностью Q.
Согласно выводам полученных в этих предыдущих (первая, вторая) статьях — в активном сопротивлении P = URI Q = 0; а в индуктивном Р = 0; Q = ULI.
Активная мощность всей цепи равна активной мощности в сопротивлении R, а реактивная — реактивной мощности в индуктивном сопротивлении XL. Подставляя значения UR = Ucosφ и UL = Usinφ, определяемые из треугольника напряжений по формулам (13.18), получим:
P = UIcosφ (13.19)
Q = UIsinφ (13.20)
Кроме активной и реактивной мощностей пользуются понятием полной мощности S, которая определяется произведением действующих величин напряжения и тока цепи;
S = UI = I2Z (13.21)
Величину полной мощности можно получить из выражения (13.22), которое легко доказать на основании формул (13.19) и (13.20):
(13.22)
Мощности S, Р, Q графически можно выразить сторонами прямоугольного треугольника (см. рис. 13.10, в). Треугольник мощностей получается из треугольника напряжений, если стороны последнего, выраженные в единицах напряжения, умножить на ток. Из треугольника мощностей можно определить
cosφ = P/S; sinφ = Q/S; tgφ = Q/P. (13.23)
Полная мощность имеет ту же размерность, что Р и Q, но для различия единицу полной мощности называют вольт-ампер (В · А).
Активная мощность Р меньше или равна полной мощности цепи.
Отношение активной мощности цепи к ее полной мощности P/S =
= cosφ называют коэффициентом мощности.
Назначение приемников электрической энергии — преобразование
ее в другие виды энергии. Поэтому колебания энергии в цепи не только
бесполезны, но и вредны, так как при этом в приемнике не совершается
полного преобразования электрической энергии в работу или тепло,
а в соединительных проводах она теряется.
Схема замещения реальной катушки в с параллельным соединением элементов
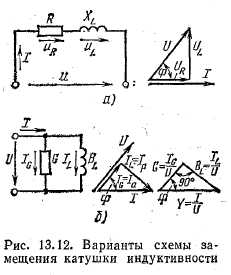
Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G и индуктивной BL проводимостями. На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее.
Покажем, что схемы рис. 13.12, а, б эквивалентны в том смысле, что при одинаковом напряжении сохраняются неизменными ток в неразветвленной части цепи, активная и реактивная мощности.
Вектор тока I можно разложить на две взаимно перпендикулярные составляющие и в соответствии со схемой и векторной диаграммой на рис. 13.12, б выразить векторным равенством
I = IG + IL (13.24)
Для схемы параллельного соединения активного и индуктивного элементов общим является приложенное напряжение, а токи разные: IG —ток в ветви с активной проводимостью, по фазе совпадает с напряжением; IL — ток в ветви с индуктивной проводимостью, по фазе отстает от напряжения на угол 90°.
Вектор тока I и его составляющие IG и IL образуют прямоугольный треугольник, поэтому
Составляющая тока в активном элементе
IG = Icosφ
Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается Iа. Для катушки по схеме на рис. 13.12, б Ia = IG.
Составляющая тока в реактивном элементе
IL = Isinφ
Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр. Для катушки Iр = IL .
Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U и получить подобный треугольник проводимостей, катетами которого являются активная G = IG/U и индуктивная ВL = IL/U проводимости, а гипотенузой — величина Y = I/U, называемая полной проводимостью цепи.
Из треугольника проводимостей и с учетом ранее полученных выражений из треугольника сопротивлений получим

electrikam.com
индуктивное сопротивление | Электрознайка. Домашний Электромастер.
Одним из самых распространенных элементов электрических схем является индуктивность. Это в общем случае катушка с проводом с вставленным в нее ферромагнитным сердечником или без него. Рассмотрим применения свойств катушки индуктивности в различных областях техники.
Индуктивность применяется в различных приборах в радиотехнике, электротехнике, технике связи, электронике, автоматике и многих других областях.
Это трансформаторы, различные электрические фильтры, электромагнитные реле, преобразователи электрической энергии и т.д.
Если конденсатор – это накопитель электрической энергии (заряда), то индуктивность – это накопитель электромагнитной энергии.
Самое простое применение катушки с проводом – это электромагнит.
При прохождении электрического тока по проводу, вокруг него образуется постоянное магнитное поле. Чем больше витков в катушке и чем больше электрический ток, проходящий через нее, тем больше магнитный поток пронизывающий витки катушки.
Для увеличения силы притяжения электромагнита в катушку вводят ферромагнитный (стальной) сердечник.
Свойство катушки с проводом образовывать магнитное поле, используется в мощных электромагнитах, во всевозможных электромеханических реле, электрических двигателях и генераторах и т.д.
Катушка индуктивности — фильтр
Катушка индуктивности имеет минимальное сопротивление для прохождения постоянного электрического тока, но для переменного тока имеет большое сопротивление.
Это свойство индуктивности используется для разделения цепей переменного и постоянного токов.
В технике электросвязи и радиосвязи используется множество различных фильтров нижних и верхних частот, схем дистанционного питания и т.д.
Катушка с ферромагнитным стальным сердечником используется в фильтрах блоков питания сетевых выпрямителей для сглаживания пульсаций переменного тока.
Катушка с проводом источник Э.Д.С.
При воздействии на катушку переменного магнитного поля в ней образуется переменный электрический ток.
Это свойство катушки индуктивности используется в электрических генераторах постоянного и переменного тока.
В них идет преобразование механической энергии в электрическую энергию.
Дизель-генераторные электростанции используют энергию сгорания дизельного топлива;
Тепловые электростанции – ТЭЦ используют энергию газа, угля, и др.;
Гидроэлектростанции – ГЭС используют энергию падающей воды;
Атомные электростанции — АЭС используют энергию деления атомного ядра.
Во всех циклах преобразования энергии конечным элементом является электрический генератор одно или трех — фазного переменного тока.
Катушка индуктивности — трансформатор.
При протекании переменного тока через катушку вокруг нее образуется переменное магнитное поле, которое в свою очередь воздействует на соседнюю катушку (обмотку) и создает в ней переменный электрический ток.
Трансформаторы тока – напряжения используются для преобразования переменного электрического напряжения и тока одной величины в напряжение и ток другой величины.
Трансформаторы служат также для согласования сопротивления нагрузки с внутренним сопротивлением источника (генератора) электрической энергии.
Трансформаторы используются во всех областях электротехники, радиотехники, электросвязи, автоматики и т.д.
Катушка индуктивности — элемент колебательного контура.
Если объединить свойства конденсатора и индуктивности, то можно создать электромагнитный контур для получения синусоидальных колебаний переменного тока. В этом контуре заряд, накопленный в конденсаторе, передается в катушку и преобразуется в магнитное поле. Магнитное поле в свою очередь, наводит ЭДС самоиндукции в катушке, которая и заряжает конденсатор. Процесс этот повторяется многократно, постепенно затухая из-за потерь в контуре.
Колебательные контуры бывают двух видов — параллельный и последовательный.
Колебательные контуры используются для получения незатухающих колебаний синусоидальной формы низкой – НЧ, высокой ВЧ и сверхвысокой СВЧ частот.
Электросвязь, радиотехника, автоматика, космическая связь – перечень применения колебательного контура в технике безграничен.
domasniyelektromaster.ru
чему равно индуктивное сопротивление катушки в цепи переменного тока?
катушка индуктивности оказывает сопротивление проходящему по ней переменному току. непрерывно возникающая в катушке ЭДС самоиндукции создает сопротивление переменному току. скорость изменения тока уменьшается по мере увеличения тока и увеличивается по мере его уменьшения, независимо от направления тока в цепи. ЭДС самоиндукции, вызываемая самим переменным током, препятствует его возрастанию и, наоборот, поддерживает его при убывании. в катушке индуктивности, включенной в цепь переменного тока, создается сопротивление прохождению тока. Но так как такое сопротивление вызывается в конечном счете индуктивностью катушки, то и называется оно индуктивным сопротивлением. Индуктивное сопротивление обозначается через XL и измеряется, как и активное сопротивление, в омах. Индуктивное сопротивление цепи тем больше, чем больше частота источника тока, питающего цепь, и чем больше индуктивность цепи. Следовательно, индуктивное сопротивление цепи прямо пропорционально частоте тока и индуктивности цепи; определяется оно по формуле XL = ωL, где ω — круговая частота, определяемая произведением 2πf. — индуктивность цепи в гн. Закон Ома для цепи переменного тока, содержащей индуктивное сопротивление, звучит так: величина тока прямо пропорциональна напряжению и обратно пропорциональна индуктивному сопротивлению цепи, т. е. I = U / XL, где I и U — действующие значения тока и напряжения, а XL— индуктивное сопротивление цепи. ри включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между током и напряжением, причем ток отстает по фазе от напряжения на четверть периода Таким образом, источник тока, отдав в течение первой четверти периода часть своей энергии в цепь, в течение второй четверти получает ее обратно от катушки, выполняющей приэтом роль своеобразного источника тока. Иначе говоря, цепь переменного тока, содержащая только индуктивное сопротивление, не потребляет энергии: в данном случае происходит колебание энергии между источником и цепью. Активное же сопротивление, наоборот, поглощает в себе всю энергию, сообщенную ему источником тока.
xL=w*L где xL — Индуктивное сопротивление (Ом) , w — циклическая частота (Рад/сек) , L — индуктивность (Гн) w=2*Pi*f Где f — частота (Гц)
touch.otvet.mail.ru
Активное сопротивление и катушка индуктивности в цепи переменного тока
Рассматривая цепь переменного тока, содержащую только индуктивное сопротивление (смотрите статью «Катушка индуктивности в цепи переменного тока»), мы подразумевали равным нулю активное сопротивление этой цепи.
Но в реальности как провод самой катушки, так и соединительные провода владеют хотя и маленьким, но активным сопротивлением, потому цепь безизбежно потребляет энергию источника тока.
Потому при определении общего сопротивления наружной цепи необходимо ложить ее реактивное и активное сопротивления. Но ложить эти два разных по собственному нраву сопротивления нельзя.
В данном случае полное сопротивление цепи переменному току находят методом геометрического сложения.
Строят прямоугольный треугольник (см. набросок 1) одной стороной которого служит величина индуктивного сопротивления, а другой — величина активного сопротивления. Разыскиваемое полное сопротивление цепи обусловится третьей стороной треугольника.
Набросок 1. Определение полного сопротивления цепи, содержащей индуктивное и активное сопротивление
Полное сопротивление цепи обозначается латинской буковкой Z и измеряется в омах. Из построения видно, что полное сопротивление всегда больше индуктивного и активного сопротивлений, раздельно взятых.
Алгебраическое выражение полного сопротивления цепи имеет вид:
где Z — общее сопротивление, R — активное сопротивление, XL — индуктивное сопротивление цепи.
Таким макаром, полное сопротивление цепи переменному току, состоящей из активного и индуктивною сопротивлений, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений этой цепи.
Закон Ома для таковой цепи выразится формулой I = U / Z,где Z — общее сопротивление цепи.
Разберем сейчас, какое будет напряжение, если цепь, не считая и и сдвиг фаз меж током и на индуктивности, обладает также сравнимо огромным активным сопротивлением. На практике таковой цепью может служить, к примеру, цепь, содержащая катушку индуктивности без стального сердечника, намотанную из узкой проволоки (дроссель высочайшей частоты).
В данном случае сдвиг фаз меж током и напряжением составит уже не четверть периода (как это было в цепи только с индуктивным сопротивлением), а существенно меньше; при этом чем больше будет активное сопротивление, тем наименьший получится сдвиг фаз.
Набросок 2. Ток и напряжение в цепи, содержащей R и L
Сейчас и сама ЭДС самоиндукции не находится в противофазе с напряжением источника тока, потому что сдвинута относительно напряжения уже не на одну вторую периода, а меньше. Не считая того, напряжение, создаваемое источником тока на зажимах катушки, не равно ЭДС самоиндукции, а больше нее на величину падения напряжения в активном сопротивлении провода катушки. По другому говоря, напряжение на катушке состоит вроде бы из 2-ух слагающих:
uL— реактивной слагающей напряжения, уравновешивающей действие ЭДС самоиндукции,
uR— активной слагающей напряжения, идущей на преодоление активного сопротивления цепи.
Если б мы включили в цепь поочередно с катушкой огромное активное сопротивление, то сдвиг фаз так бы уменьшился, что синусоида тока практически догнала бы синусоиду напряжения и разность фаз меж ними была бы чуть видна. В данном случае амплитуда слагающей и, была бы больше амплитуды слагающей.
Точно так же можно уменьшить сдвиг фаз и даже совершенно свести его к нулю, если уменьшить любым методом частоте генератора. Уменьшение частоты приведет к уменьшению ЭДС самоиндукции, а как следует, и к уменьшению вызываемого ею сдвига фаз меж током и напряжением в цепи.
Мощность цепи переменного тока, содержащей катушку индуктивности
Цепь переменного тока, содержащая катушку, не потребляет энергии источника тока и что в цепи происходит процесс обмена энергией меж генератором и цепью.
Разберем сейчас, как будет обстоять дело с мощностью, потребляемой таковой цепью.
Мощность, потребляемая в цепи переменного тока, равна произведению тока на напряжение, но потому что ток и напряжение есть переменные величины, то и мощность будет также переменной. При всем этом значение мощности для каждого момента времени мы сможем найти, если умножим величину тока на величину напряжения, подобающую данному моменту времени.
Чтоб получить график мощности, мы должны перемножить величины отрезков прямых линий, определяющие ток и напряжение в разные моменты времени. Такое построение и приведено на рис. 3, а. Пунктирная волнообразная кривая р указывает нам, как меняется мощность в цепи переменного тока, содержащей только индуктивное сопротивление.
При построении этой кривой использовалось последующее правило алгебраического умножения: при умножении положительной величины на отрицательную выходит отрицательная величина, а при перемножении 2-ух отрицательных либо 2-ух положительных — положительная величина.

Набросок 3. Графики мощности: а — в цепи содержащей индуктивное сопротивление, б — тоже, активное сопротивление
Набросок 4. График мощности для цепи, содержащей R и L
Кривая мощности в данном случае размещена выше оси времени. Это означает, что обмена энергией меж генератором и цепью не происходит, а как следует, мощность, отдаваемая генератором в цепь, стопроцентно потребляется цепью.
На рис. 4 изображен график мощности для цепи, содержащей внутри себя сразу индуктивное и активное сопротивления. В данном случае также происходит оборотный переход энергии из цепи к источнику тока, но в существенно наименьшей степени, чем в цепи с одним индуктивным сопротивлением.
Рассмотрев приведенные выше графики мощности, мы приходим к выводу, что только сдвиг фаз меж током и напряжением в цепи делает «отрицательную» мощность. При всем этом, чем больше будет сдвиг фаз меж током и напряжением в цепи тем потребляемая цепью мощность будет меньше, и, напротив, чем меньше сдвиг фаз, тем потребляемая цепью мощность будет больше.
elektrica.info
Измерительная катушка — сопротивление — Большая Энциклопедия Нефти и Газа, статья, страница 2
Измерительная катушка — сопротивление
Cтраница 2
На рис. 4.2 показано схематическое устройство герметизированной измерительной катушки сопротивления. [16]
Государственными эталонами ома и вольта служат соответственно набор особо точно изготовленных измерительных катушек сопротивления и группа нормальных насыщенных элементов. Устройство измерительных катушек сопротивления и нормальных элементов описано в следующей главе. [17]
Двойные мосты предназначаются для измерения малых сопротивлений, поэтому измеряемое сопротивление RX и сопротивление R0 ( обычно измерительная катушка сопротивления) должны быть четырех — зажимными. Соединяющие их провода входят в цепь питания и не влияют на условия равновесия. [18]
При комплектной поверке основная погрешность моста определяется путем измерения на нем точных сопротивлений ( например, измерительных катушек сопротивления) в соответствии с методикой, описанной ранее для измерения обычных сопротивлений. [19]
Если на катушке нет указания на величину тока, то надо исходить из того, что мощность, выделяемая в измерительной катушке сопротивления, не должна превышать 3 вт, а при точных измерениях-1 вт. [20]
Для поверочных целей и для таких измерений, когда требуется знать с высокой точностью значения воспроизводимой мерой величины, применяются так называемые измерительные катушки сопротивлений, индуктивности и взаимной индуктивности и конденсаторы как самостоятельные элементы. [21]
Точность измерения сопротивления в 0 01 %, достигаемая при помощи специально подогнанного моста, недостаточна при таких работах, как поверка и подгонка образцовых измерительных катушек сопротивления. В этих случаях прибегают к методам неполного или полного замещения. [22]
Государственными эталонами ома и вольта служат соответственно набор особо точно изготовленных измерительных катушек сопротивления и группа нормальных насыщенных элементов. Устройство измерительных катушек сопротивления и нормальных элементов описано в следующей главе. [23]
Измеряемое сопротивление Rx включается по четырехза-жимной схеме. В качестве сопротивления R0 используют образцовые измерительные катушки сопротивлений с сопротивлением, близким к измеряемому. [24]
Под компенсационным методом понимают метод поверки, основанный на принципе компенсации измеряемой величины известной величиной и осуществляемый с помощью потенциометра постоянного тока. Кроме потенциометра применяют нормальный элемент, измерительные катушки сопротивления, делитель напряжения, шунт. Класс точности образцовых средств измерений должен быть таким, чтобы относительная погрешность определения действительного значения измеряемой величины для конечного значения шкалы поверяемого прибора, выраженная в процентах, была в 5 раз меньше численного обозначения класса точности поверяемого прибора. [25]
Провода от потенциальных зажимов измеряемого сопротивления подключаются к зажимам Хт. К зажимам RH присоединяются провода от потенциальных зажимов образцовой измерительной катушки сопротивления. Через Ro и Rx, соединенные последовательно, пропускается ток необходимого значения от источника, не показанного на схеме. Вторая пара плеч моста образуется сопротивлениями Ri и R2, которые также будут всегда оставаться равными друг другу, так как щетки верхнего и нижнего комплектов катушек каждой декады механически соединены общей рукояткой. [26]
На рис. 2 — 3 приведена схема, эквивалентная измерительной катушке сопротивления. [27]
При использовании образцовых катушек сопротивления следует всегда иметь в виду, что пропускаемый через них ток не должен превосходить некоторого предельного значения, которое согласно ГОСТ 6864 — 54 должно обозначаться на катушке специальной надписью. При отсутствии такой надписи следует руководствоваться общим правилом: мощность, выделяемая в измерительной катушке сопротивления, никогда не должна превышать 3 вт, а при работах повышенной точности — 1 вт. [28]
Наличие систематических погрешностей может быть обнаружено путем анализа условий проведения эксперимента или повторными измерениями одного и того же значения измеряемой величины разными методами или приборами. Примером постоянной систематической погрешности может быть погрешность, обусловленная несоответствием истинного значения меры, например измерительной катушки сопротивления при косвенном измерении тока ( см. § 15 — 1), с помощью которой производится измерение, ее номинальному значению. [29]
Цифра класса точности указывает наибольшее допустимое отклонение ( в процентах) действительного значения сопротивления катушки от ее номинального при токе через катушку, не превышающем определенного значения. Если на катушке нет указания на величину тока, то следует исходить из того, что мощность, выделяемая в измерительной катушке сопротивления, не должна превышать 3 вт, а при точных измерениях 1 вт. [30]
Страницы: 1 2 3
www.ngpedia.ru
