Сколько кубов в одном дереве дуба
Автор Сфера закона На чтение 15 мин Просмотров 8 Опубликовано
Содержание
- Сколько бревен в кубе
- Онлайн-Калькулятор
- Для расчета потребуется следующая формула:
- Расчет кубометров дерева
- Сколько кубов древесины в одном дереве – сколько кубов в одном дереве — Как посчитать сколько кубов в дереве! — 22 ответа
- как подсчитать объем одного бруса или доски?
- Сколько бруса и досок в одном кубометре?
- Определение количества бревен в одном кубе
- Сколько досок в кубе | ЛЕСНОЙ КУПЕЧЕСКИЙ ДВОР
- 1 куб дерева это сколько.
- Количество древесины в кубе. Расчёт пиломатериала в одном кубе
- Особенности расчетов пиломатериалов в разных единицах
- не по теории а по практике
- Таблицы объемов круглого леса по ГОСТ 2708-75
Сколько бревен в кубе
Онлайн-Калькулятор
Но для неподготовленного человека это может показаться не только очень далеким, но и непонятным. И очень часто возникают разногласия между самими строителями, а также между строителями и заказчиком о том, сколько бревен в кубе должно быть.Для того, чтобы разобраться с этой проблемой, обычно используют математический метод, который в несколько минут может дать четкий ответ о том, сколько нужно бревен для определенного количества кубометров.
Как правило, в строительстве деревянных зданий используются оцилиндрованные бревна. Но этот материал может отличаться по размеру, то есть по длине и диаметру. За единицу измерения принято брать сантиметры. В одном кубометре находится один миллион сантиметров. Таким образом, вначале нужно определиться с размерами бревен.
Для того, чтобы измерить размер бревен, потребуется обычная сантиметровая рулетка. Все бревна, как правило, изначально должны быть одного размера, а в дальнейшем, в зависимости от проекта, они распиливаются на необходимые элементы.
Так, измерив с помощью рулетки размер бревна, мы получаем значения длины и диаметра в сантиметрах. Для примера, попробуем высчитать, сколько нужно бревен для одного кубометра, если бревна имеют длину шесть метров, а их диаметр восемнадцать сантиметров.
Для расчета потребуется следующая формула:
Объем = Пи * Радиус * Радиус * Длина.
Шесть метров в данном случае равняется шестистам сантиметрам. Число Пи всегда равняется 3,14. Радиус мы получаем путем деления диаметра на два. Таким образом, формула у нас приобретает следующий вид: Объем = 3,14 * (18:2) * (18:2) * 600 = 3,14 * 9 * 9 * 600 = 152604 сантиметров. Для перевода в кубометры делим получившееся число на один миллион: 152604 : 1000000 = 0,1526. Этот результат говорит нам о том, что одно бревно такого размера будет занимать всего лишь 0,15 с небольшим кубометра.
Теперь необходимо разобраться с тем, сколько бревен в метре. Это наша основная задача. Для этого мы разделим один кубометр на результат наших вычислений – 0,1526.
Получается: Количество = 1 : 0,1526 = 6,55 бревен. Получается, что для одного кубометра нам необходимо взять около семи бревен заданного размера.
Если рассматривать бревна большего диаметра, например, в двадцать четыре сантиметра, то результаты вычислений будут другими:
Объем = 3,14 * 12 * 12 * 600 = 271296 кубических сантиметров = 0,2713 кубометров.
Значит, в одном кубометре будет: 1 : 0,2713 = 3,69 бревен. В данном случае в одном кубометре будет меньше бревен.
Для расчета количества бревен в кубометре используется совсем простая формула, которая позволяет в считанные минуты высчитать результат. Для расчетов, конечно же, лучше вооружиться рулеткой и калькулятором.
Источник
Расчет кубометров дерева
Дополнения СИ №6 июнь 2004 г.
О замене Территориальных элементных сметных норм и единичных расценок по валке деревьев.
ТЕХНИЧЕСКАЯ ЧАСТЬ
1. Общие указания
1.
1. Настоящие территориальные элементные сметные нормы и единичные расценки распространяются на работы по валке деревьев диаметром от 10 до 150 см. без корчевки пней и предназначены для определения потребностей в ресурсах и сметной стоимости работ.
Валка деревьев с диаметром стволов более 150 см. должна производиться по фирменным сметным нормам (индивидуальным сметным нормативам), учитывающим реальные условия их произрастания, формы и размеры стволов и скелетных ветвей, объемы порубочных остатков, составы и количество машин и механизмов, применяемых при валке, погрузке и транспортировке.
1.2. Расценки разработаны в базисном уровне цен по состоянию на 1 января 2000 года.
1.3. В нормах и расценках предусмотрен полный комплекс основных, вспомогательных и сопутствующих работ по валке деревьев:
- пробег строительных машин и автотранспорта от авто предприятия до объекта производства работ и обратно;
- перемещение порубочных остатков на технологическую площадку;
- погрузка порубочных остатков на автомобиль и перевозка на городскую свалку (среднее расчетное расстояние 32 км.
).
).1.4. В нормах и расценках не учтены затраты по обработке порубочных остатков на городских свалках.
1.5. В табл. 1 справочно приведены усредненные объемы деревьев в плотных и складочных метрах в зависимости от диаметров ствола и высот деревьев, рассчитанных по данным Санкт-Петербургской государственной Лесотехнической академии.
1.6. Указанный в настоящем сборнике размер «до» включает в себя этот размер.
| Диаметр дерева, см. | Высота дерева, м. | Объем ствола, куб. м. | Объем коры, куб. м. | % коры | Расчетный складочный объем, скл. куб. м. | ||||
|---|---|---|---|---|---|---|---|---|---|
| ствола | сучьев | ветвей | крона | общий | |||||
| 10-30 | 11,2-13,3 | 0,304 | 0,022 | 7,4 | 0,45 | 0,15 | 0,89 | 1,04 | 1,49 |
| 30-50 | 13,39-18,9 | 1,079 | 0,109 | 10,1 | 1,59 | 0,47 | 2,63 | 3,1 | 4,69 |
| 50-70 | 18,91-24,2 | 2,481 | 0,283 | 11,4 | 3,65 | 0,99 | 5,29 | 6,28 | 9,93 |
| 70-90 | 24,27-28,1 | 4,567 | 0,571 | 12,5 | 6,71 | 1,98 | 8,78 | 10,76 | 17,47 |
| 90-110 | 28,15-30,6 | 7,510 | 0,999 | 13,3 | 11,04 | 2,89 | 13,25 | 16,14 | 21,18 |
| 110-130 | 30,67-33,2 | 11,253 | 1,587 | 14,1 | 16,54 | 3,7 | 18,56 | 22,26 | 38,8 |
| 130-150 | 33,28-35,3 | 13,8 | 2,029 | 14,7 | 20,29 | 4,44 | 23,15 | 27,59 | 47,88 |
2.
Правила исчисления объемов работ
2.1. В качестве единицы принято одно дерево.
2.2. При расчете норм времени и расценок были учтены объемы деревьев объемы надземной фитомассы деревьев (диаметры стволов, высоты деревьев, объем сучьев и ветвей).
Источник
Сколько кубов древесины в одном дереве – сколько кубов в одном дереве — Как посчитать сколько кубов в дереве! — 22 ответа
как подсчитать объем одного бруса или доски?
Дерево — один из лучших материалов, применяемых для строительства загородных домов, дач и коттеджей. При современном развитии технологий долговечность и прочность древесины не уступает другим стройматериалам, а по уровню комфорта деревянные строения не сравнимы с кирпичными или бетонными.
Расчет веса кубического метра древесины.
При определении необходимой потребности в пиломатериалах для того или иного строения зачастую приходится подсчитывать, сколько штук содержится в одном кубометре.
Цены на пиломатериалы чаще всего указываются за 1 куб, и объем в сметах на строительство также указывается в кубометрах.
Сколько бруса и досок в одном кубометре?
На российских просторах, богатых лесом, срубы ставят опытные мастера, для которых нет необходимости высчитывать точное количество бруса или доски. Но городскому жителю приходится за материалами идти на строительный рынок, и, чтобы не переплачивать, лучше заранее знать, сколько штук сортамента в одном кубическом метре.
Количество обрезных досок в 1 кубическом метре.
Привычное название единицы измерения «куб» означает не что иное, как один кубический м объема. Кубатуру поштучно любого вида дерева узнать не сложно, поскольку они представляют собой параллелепипед, она вычисляется умножением всех его сторон. При этом не важно, с пазами доска или без них или какова форма вагонки — достаточно указанных поставщиком характеристик. Пример: брус с сечением 100х150 мм длиной 6 м имеет объем, который можно подсчитать по формуле:
V = a x b x l= 0,1 х 0,15 х 6 = 0,09 м³.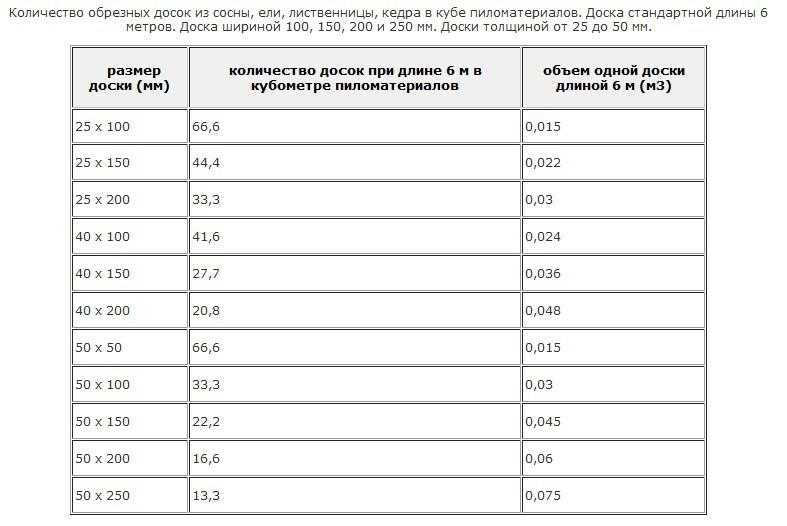
Если по проекту скалькулировать протяженность одинаковых балок, затем разделить это количество на 6 (стандарт для выпускаемых пиломатериалов), а затем получить частное от общей длины и числа брусьев в 1 кубе, то будет известно суммарное число кубов для выбранного строения. Зная этот алгоритм, вы всегда можете сосчитать количество пиломатериалов, независимо от их формы, будь то половые доски, рейка, брус или бревна.
Если вы покупаете грубый тес или другой нечистовой материал, то можно воспользоваться расчетными нормами, которые предлагает продавец.
Определение количества бревен в одном кубе
Бревенчатый дом — наиболее интересный и надежный вариант. Природа наделила натуральное дерево отличными свойствами.
Чтобы определить количество бревен в одном кубометре, нужно, как и в обсчете бруса и досок, вначале определить объем одного бревна.
Здесь нужно различать два вида пиломатериалов данного типа:
- оцилиндрованное бревно;
- бревно ручной рубки.
Схема расчета кубатуры бревна.
В первом случае размеры более точные, чем во втором, но все же некоторые предпочитают ставить срубы из обработанных вручную бревен.
3,14 — число «пи», постоянная величина;
Так, объем единицы оцилиндрованного материала диаметром 200 мм при длине 6 м будет равен:
Узнаем количество штук данного пиломатериала в одном кубометре, разделив единицу на полученный результат:
Подсчет кубатуры бревен аналогичен расчетам с деревом прямоугольного сечения. При обсчете изделий ручной рубки берут усредненный размер диаметра в партии.
Выполняя самостоятельно инженерно-экономические расчеты, нужно руководствоваться чертежами с как можно более точными параметрами всех элементов и нужно учитывать, что при строительстве неизбежны отходы, поэтому, определяя расход, нужно закладывать процент на них. В деревянном домостроении эта цифра может доходить до 20%. Чтобы не ошибиться в расчетах, нужно как можно точнее подсчитать количество бруса или другого дерева в одном кубе.
Сколько досок в кубе | ЛЕСНОЙ КУПЕЧЕСКИЙ ДВОР
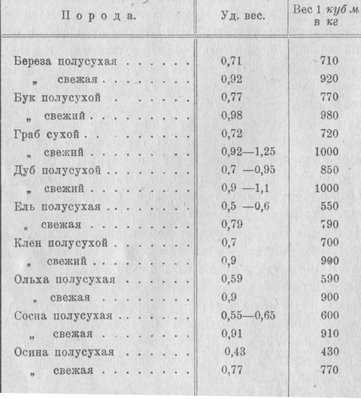
1 куб дерева это сколько.
Общеизвестен шуточный вопрос: что тяжелее – тонна дерева или тонна железа? Не подумавши, обыкновенно отвечают, что тонна железа тяжелее, вызывая дружный смех окружающих. Шутники, вероятно, еще громче рассмеются, если им ответят, что тонна дерева тяжелее, чем тонна железа. Такое утверждение кажется уж ни с чем не сообразным, – и однако, строго говоря, это ответ верный! Дело в том, что закон Архимеда применим не только к жидкостям, но и к газам. Каждое тело в воздухе “теряет” из своего веса столько, сколько весит вытесненный телом объем воздуха. Дерево и железо тоже, конечно, теряют в воздухе часть своего веса. Чтобы получить истинные их веса, нужно потерю прибавить. Следовательно, истинный вес дерева в нашем случае равен 1 тонне + вес воздуха в объеме дерева; истинный вес железа равен 1 тонне + вес воздуха в объеме железа.
Но тонна дерева занимает гораздо больший объем, нежели тонна железа (раз в 15), поэтому истинный вес тонны дерева больше истинного веса тонны железа! Выражаясь точнее, мы должны были бы сказать: истинный вес того дерева, которое в воздухе весит тонну, больше истинного веса того железа, которое весит в воздухе также одну тонну. Так как тонна железа занимает объем в 1/8 куб. м, а тонна дерева – около 2 куб. м, то разность в весе вытесняемого ими воздуха должна составлять около 2,5 кг. Вот насколько тонна дерева в действительности тяжелее тонны железа!
это по метру в длинну, высоту и в ширину.
метр на метр и еще раз на метр
Это 1000 куб дециметров дерева!! ! ))) — А если серьезно, то надо смотреть, какой толщины доска, или что там у вас, и тогда можно высчитать, сколько это будет КВАДРАТНЫХ МЕТРОВ. если именно это вас интересует….
Это 1 м. в длину, 1 м. в ширину, 1 м. в высоту.
это один кубик деревянный.)
Если Вы спрашиваете сколько весит 1 куб. метр древесины, то это зависит от породы древесины: 1куб весит, в тоннах: Бальса 0,12-0,20 Бамбук 0,4 Дуб 0,6-0,9 Бук 0,7-0,9 Железное дерево (бакаут) 1,1 -1,4 Кедр 0,5 — 0,6 Орех 0,6 — 0,7 Сосна, ель 0,4 — 0,5 Черное дерево 1,1 — 1,3 Тик 0,7 — 0,9 Ясень, красное дерево 0,6 — 0,8
Здравствуйте! Скажите пожалуйста сколько нужно будет кубов леса на дом 7*8.
Как сосчитать? Не могу сообразить)))
Количество древесины в кубе. Расчёт пиломатериала в одном кубе
При строительстве каркасного дома основной материал – деревянный брус. Он нужен не только для создания каркаса дома, но и для строительства крыши, при монтаже венцов сруба, обустройстве внутренних перегородок и других конструкций дома. Из-за широкого спектра применения древесины этот строительный материал имеет десятки и сотни позиций, регламентирующих размер изделия. Зная точные размеры одной единицы, можно, не вдаваясь в сложные расчеты, при помощи простых формул вычислить, сколько штук 6-метрового бруса умещается в 1 м 3 – для составления сметы и оптимизации логистических операций по доставке и хранению пиломатериалов на месте строительства.
Особенности расчетов пиломатериалов в разных единицах
Объем любого физического предмета прямоугольной формы – это результат перемножения длины, ширины и высоты прямоугольника, в нашем случае – деревянного бруса. Объем V = a х b х c, где обозначения: a — длина, b – ширина, и с – высота бруса.
Например, изделие длиной 6 метров, шириной 10 см и высотой 10 см будет иметь объем 0,06 м 3 .Но это идеальная математическая формула, а на практике изделия в одной партии могут иметь разные размеры, что допускается стандартами, но осложняет расчет объема пиломатериалов.
Обрезной или профилированный брус стоит намного дороже, чем обычный, поэтому точность расчетов имеет решающее значение – платить придется из своего кошелька. Традиционная система измерений при покупке пиломатериалов – кубический метр, но для бруса на стропила, стенового каркаса, балок перекрытий и древесины для набора пола удобнее пользоваться погонными метрами. Также особенности производства в деревообрабатывающей промышленности допускают некоторый разброс размеров, в частности — длины, которая может колебаться в пределах 3-6 метров с шагом в 50 см.
Разные единицы измерения и разные подходы при расчетах требуемого количества бруса могут порождать ошибки и неточности, а также вызывать общее непонимание ситуации – как пересчитать заданные единицы в другие.
- Например, требуется изделие сечением 100 х 50 мм, и известна общая длина партии – 100 п/м (погонных метров). Чтобы узнать объем бруса, необходимо вычислить площадь сечения одной единицы, а для этого мм преобразовать в м 2 , после чего перемножить площадь сечения «S S » и длину «a»: 0,1 х 0,05 х 100 = 0,50 м 3 . Стоимость партии рассчитать проще – нужно умножить объем партии на цену за 1 м 3 .
- Или как узнать, какое количество единиц бруса получится в определенном объеме пиломатериалов? Для этого нужно знать и сечение, и длину одной единицы. Например, есть данные об общей длине партии – 100 п/м, и требуется изделие длиной 4 м, то сколько штук будет в этой партии? Рассчитывается сначала объем одного изделия: 0,1 х 0,05 х 4 = 0,02 м 3 . При закупке 0,5 м 3 бруса получается 25 единиц, или 50 штук в 1 м 3 .
В индивидуальном строительстве на счету каждый рубль, поэтому заказывать, например, 4 м 3 бруса обрезного или профилированного, если нужно 3,8 м 3 , неэкономно.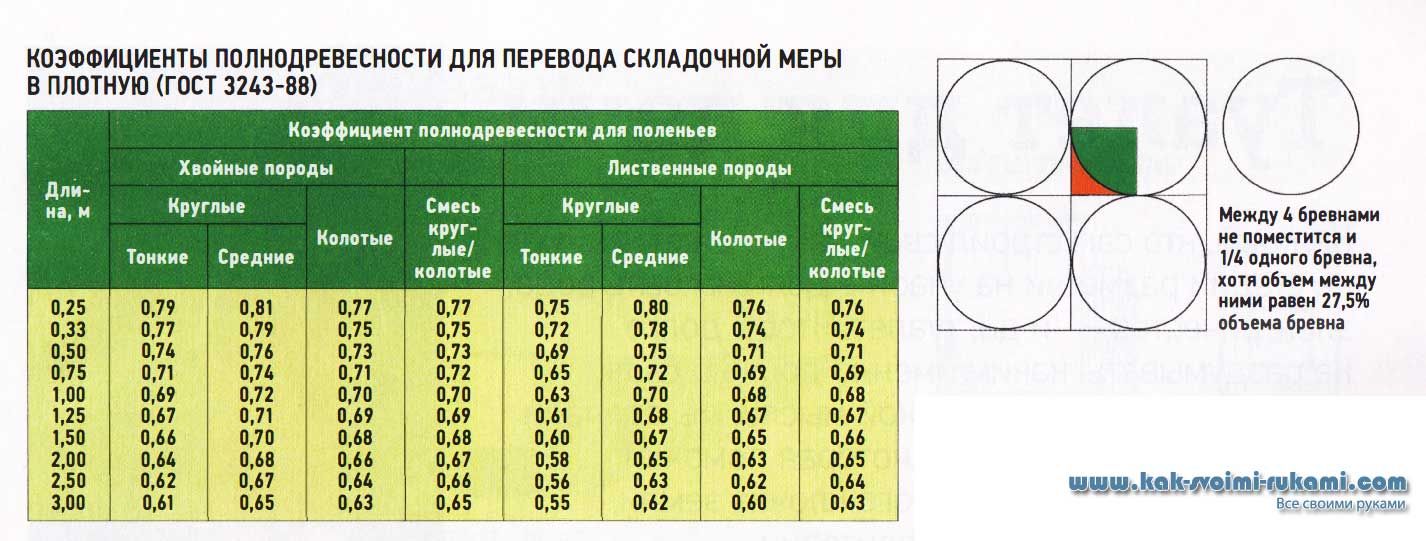
Пример: при покупке 52 п/м пиломатериалов сечением 100 х 180 мм и длиной 6 метров общий объем бруса будет равен: 52 х 0,1 х 0,18 = 0,936 м 3 . Узнать количество штук в этом объеме можно так: общий объем разделить на объем одной единицы. Узнаём объем одного изделия: 0,1 х 0,18 х 6 м/п = 0,108 м 3 . Последнее вычисление: 0,936 / 0,108 = 8,666 единиц. Так как в магазине пиломатериалы резать никто не будет, проще доплатить эту небольшую разницу за одну единицу, чем покупать всю партию с разницей в цене, умноженной на количество штук в партии.
Профилированный брус, хотя и более сложной формы, рассчитывают по тем же формулам. То есть, чтобы рассчитать площадь сечения профилированного изделия, высоту «c» нужно умножить на ширину «b». Высота профилированного бруса определяется, как расстояние от нижней поверхности, имеющей паз, до верхней точки шипа.
не по теории а по практике
Сама методика расчета объема круглого бревна, доски или бруса простая, сводится к математической задаче 5-6 класса.
Но в реальности все намного сложнее: бревна конические, доски часто измеряют в дюймах, брус имеет фаски, есть и другие тонкости и отличия реальных изделий из дерева. Поэтому так удобны таблицы, в которых сведены данные измерения кубатуры леса, учитывающие такие погрешности формы, как конусность бревен, наличие коры, сбег, сложность формы горбыля и пластины и другие нюансы.
Рисунок 1. Таблица расчета кубатуры обрезного пиломатериала.
Таблицы объемов круглого леса по ГОСТ 2708-75
Самая распространенная, точная и выверенная таблица для определения объемов круглого леса – это приведенная в официальном документе, ГОСТ 2708-75, без срока действия.
В ней приведены данные объема круглого леса, диаметра с 3 до 120 см, длины от 1 до 9,5 м, с шагом по диаметру в 1-2, а по длине – в 10 см. Дополнительно показаны специализированные типоразмеры круглого бревна: длиной в 0,5-0,9 м и 10-13,5 м, а толщиной в 6-15 см и 8-38 см соответственно. Также рассчитаны их объемы.
Есть еще более специфические размеры.
Табл. 1. Кубатура круглого леса толщиной в 6-60 см, длиной в 1-9 м
Источник
КУБОМЕТР ДРОВ-ЭТО СКОЛЬКО?
Если Вы решили купить дрова, то при оформлении заказа и получении дров можете столкнуться с таким вопросом: Как определить объём дров? И действительно, самый распространенный вопрос при покупке дров — вопрос измерения объёма.
Сколько кубов дров в машине? Как считать объём колотых дров? Как проверить продавца? Давайте разберёмся.
Кубический метр – это общепринятая единица мер для лесного хозяйства. Для круглого лесоматериала (кругляка) используется понятие плотный кубический метр (сплошной древесины без промежутков), а для дров — складочный кубический метр (считая промежутки).
Куб дров
Определить объем пиломатериала довольно просто, если он аккуратно сложен: умножаем длину на ширину и на высоту и готово. Сложнее вычислить объём колотых дров или дров в чурках. Для этого используют единицу меры – «складочный» кубометр, т.
е. кубометр дров с промежутками.
Для пересчета из складочных кубометров в кубометры древесины используют коэффициент пересчета, который зависит от вида древесины и от размера поленьев. В большинстве случаев для пересчета используют коэффициент, равный 0.7.
Например: Если вам привозят дрова, уложенные «в укладку», то замеряем длину, высоту и ширину этой укладки. Перемножаем параметры и умножаем полученный объем на коэффициент 0,7.
Объём = ширина * длина * высота* 0,7 — таким образом, мы получает реальный объем дров.
Насыпной куб дров
Однако, не все продавцы укладывают дрова, многие продают дрова наваломи (россыпью, без укладки). Для такой ситуации есть понятие – насыпной (навальный) кубометр.
Насыпной куб.м. (навальный куб.м.) — объём кузова, в который дрова накиданы, а не сложены.
Для точного подсчета дров используются коэффициенты пересчета «насыпных» кубов в «складочные» и наоборот. Для расчета используется коэффициент пересчета, который зависит от длины и толщины поленьев.
Например: Если вам привезли машину дров навалом, то сначала измеряем длину, высоту и ширину кузова машины, затем измеряем длину полена и рассчитываем складочный объем, используя коэффициент.
Если объём кузова (ширина * длина * высота) составляет 10 куб.м, а длина поленьев 50 см., то в машине – 10 * 0.75 = 7.5 «складочных» кубометров дров. Чтобы перевести складочные кубометры в реальные, умножаем объем на коэффициент 0,7 (см. выше). Т.о. объем сплошной древесины (реальных кубометров) составляет 7.5 * 0.7 = 5.25.
В каждом регионе сформировались свои правила по продаже дров. Дрова могут продавать навалом, с укладкой, в сетках, на поддонах, в коробках и т.д.
Мало кто из продавцов использует при расчетах объёма дров — 1 реальный кубометр древесины. Почти всегда говорят 1 кубометр дров подразумевая 1 складочный кубометр.
Если вам говорят, что дрова стоят «1400 грн за куб» – это значит что 1 складочный кубометр древесины стоит 1400 грн. Если вы попросите назвать цену за «реальный» кубометр древесины, то продавец просто разделит стоимость складочного метра на коэффициент 0.
7. В данном случае стоимость реального кубометра дров будет составлять 1400 / 0.7 = 2000 грн. за куб.
В сельской местности часто при продаже не используют расчеты объёма. Дрова продают телегами или машинами (газонами, зилами, камазами, газелями). Часто продавец телеги дров на вопрос «Какой объём дров в телеге?» — просто не знает ответа.
https://pelletronspb.ru/kubometr_drov
Комбинаторика
— Как найти количество остовных деревьев для куба?
спросил
Изменено 7 лет, 4 месяца назад
Просмотрено 924 раза
$\begingroup$
Не подскажете, как найти общее количество остовных деревьев в неориентированном размеченном графе $Q_d$ для $d = 3$.
Я знаю, что ответ — 384, но способ (я знаю, что их много) ускользает от меня.
- комбинаторика
- теория графов
- деревья
- теория размерности анализ
- графы Кэли
$\endgroup$
1
$\begingroup$
Расширение ответа Pegah. Собственные значения лапласиана $Q_d$ равны $(0,2,\ldots,2d)$ с соответствующими кратностями ${d \choose k}.$ 93 = 384,$, как подтвердил Хуан.
для ленивых можно также использовать Sage math
sage: G = graphs.CubeGraph(3) шалфей: G.spanning_trees_count() 384
$\endgroup$
$\begingroup$
Одной из самых интересных теорем о количестве остовных деревьев графа является теорема о матричном дереве.
Теорема о дереве матриц утверждает, что: Дан граф G без петель с множеством вершин $v_1,v_2,…,v_s$, пусть D — диагональная матрица, в которой $d_{ii}=deg_G(v_i)$, и пусть A — матрица смежности G..png)
*)$. 9{5}
$
Теперь количество остовных деревьев можно вычислить как $T(1,1)$, тогда мы получим
$T \left( 1,1 \right) =384$
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
геометрия — Как вырезать из пня куб, чтобы пара противоположных вершин находилась в центре?
спросил
Изменено 1 год, 9 месяцев назад
Просмотрено 5к раз
$\begingroup$
Я видел это изображение куба, вырезанного из пня.
Я пытался сделать то же самое из пня, но мне было трудно понять, как это сделать.
Одна из пар противоположных вершин находится в центре пня:
Я изо всех сил пытался найти числа и угол, необходимые для разрезов.
Будем признательны за любой совет. Спасибо, что нашли время, чтобы прочитать это, и я прошу прощения за мой плохой английский.
- геометрия
$\endgroup$
4
$\begingroup$
Сначала сформируйте из культи цилиндр высотой более $\frac{3}{\sqrt{2}}\приблизительно в 2,121$ раза больше его радиуса, чтобы куб поместился внутри цилиндра. Здесь мы предполагаем, что вы можете отметить заданные точки и линии на поверхности цилиндра, а также провести плоскость через $3$ точек.
Для первой вершины отметьте центр одной из круглых граней цилиндра. Далее отметьте из этой точки $3$ радиуса круглой грани на расстоянии $120$ градусов друг от друга (так, чтобы их концы образовывали равносторонний треугольник).
Теперь опуститесь от каждой из $3$ вершин треугольника на расстояние, равное $\frac{1}{\sqrt{2}}\приблизительно 0,707$ радиуса цилиндра, и отметьте там точки . Если ваш цилиндр имеет минимальное отношение высоты к радиусу, эти точки будут ровно на $\frac{1}{3}$ пути вниз.
Затем разрежьте $3$ плоскости через первую вершину и каждую пару следующих $3$ вершин, сформировав первый угол куба.
Теперь отметьте $3$ середины дуг, образованных вашими разрезами. Это следующие вершины куба. Еще раз, если ваш цилиндр имеет минимальное отношение высоты к радиусу, это будет $\frac{2}{3}$ пути вниз.
Наконец, вырежьте еще $3$ плоскостей, чтобы завершить форму куба. Вам не нужно отмечать последнюю вершину, так как она предопределена пересечением плоскостей. 9{\circ}$.
$\endgroup$
12
$\begingroup$
Метод
Вот подход, при котором вы имеете дело только с плоскими поверхностями.
- Вырежьте из пня (правильную) шестиугольную призму радиуса $r$ и высоты $\frac32r\sqrt2\приблизительно2,1213 r$.
Примечание: «Ширина» призмы от лицевой стороны к противоположной должна составлять $r\sqrt3\приблизительно1,732r$.
(Проверка работоспособности на правильность: края шестиугольной вершины и низа также должны быть $r$.)
На рисунке показан вид сверху и шесть «развернутых» боковых граней.
Каждое боковое ребро призмы разделить на три части и провести зигзаг поперек боковых граней, соединяя чередующиеся метки $\frac13$ и $\frac23$ на этих ребрах.
Каждый сегмент зигзага будет ребром конечного куба. (Его длина должна быть $e\примерно 1,2247r$.)
Каждая последовательная триада точек на зигзаге (вместе с верхней центральной или нижней центральной точкой призмы) определяет грань куба, поэтому «все, что вам нужно сделать», это удалить лишнюю древесину до тех пор, пока лица плоские.
Готово!
Математика
Для призмы с радиусом $r=2$ (во избежание дробей) пусть центр основания призмы будет началом координат $O=(0,0,0\sqrt2)$, а верхний центр равен $T=(0,0,3\sqrt2)$. 9\circ, (1\;\text{или}\;2)\sqrt{2} \right)$$
Конкретно,
$$A = (\phantom{-}2,0,2\sqrt{2}) \qquad B = (\phantom{-}1,\phantom{-}\sqrt{3},1\sqrt2) \qquad C = (-1,\фантом{-}\sqrt3,2\sqrt2)$$
$$D = (-2,0,1\sqrt2) \qquad E = (-1,-\sqrt3,2\sqrt2) \qquad F = (\phantom{-}1,-\sqrt3,1\sqrt2) $$
(где $A$, $C$, $E$ ближе к вершине призмы, а $B$, $D$, $F$ ближе к основанию). Отсюда мы можем убедиться, что
$$\begin{выравнивание}
T &= B+(A-B)+(C-B) &&\quad\to\quad T,A,B,C\;\text{копланарный} \\
&= D+(C-D)+(E-D) &&\quad\to\quad T,C,D,E\;\text{копланарный}\\
&= F+(E-F)+(A-F) &&\quad\to\quad T,E,F,A\;\text{компланарный}\\[4pt]
O &= A+(BA)+(FA) &&\quad\to\quad O,F,A,B\;\text{копланарный}\\
&=C+(B-C)+(D-C) &&\quad\to\quad O,B,C,D\;\text{копланарный}\\
&=E+(DE)+(FE) &&\quad\to\quad O,D,E,F\;\text{копланарный}
\end{выравнивание}$$
а также
$$\begin{align}2\,\sqrt{\frac32}=\sqrt{6}\;&=\;|AB|=|BC|=|CD|=|DE|=|EF|=|FA | \\
&=\;|TA|=|TC|=|TE| \\
&=\;|OB|=|OD|=|OE|\end{align}$$
так что все грани представляют собой четырехугольники с равными длинами ребер, что делает их 9\circ = \угол ATC = \угол CTE = \угол ETA =\угол BOD = \угол DOF = \угол FOB$$
То есть каждая грань ромба имеет по крайней мере один прямой угол, что делает его квадратом .
$\квадрат$
$\endgroup$
3
$\begingroup$
Поскольку вы сказали, что вам трудно найти числа, я, естественно, указал, как числа рассчитываются из трехмерной геометрии на этом математическом сайте..
Вершина V еще не обнаружена. Показан воображаемый конус.
Ось цилиндра проходит по OV =h. Линия OB проходит по оси x. A, B, C отмечены на базовой окружности на расстоянии 120 градусов друг от друга. OA=OB=OC=r и V является вершиной конуса, а VA,VB,VC взаимно перпендикулярны. OV=h и полувертикальный угол конуса равен OVB. Координаты A,B,V:
$$ (r,0,0),(-r/2, — r\sqrt 3/2 ),(0,0,h)$$
Векторы положения $ AV,BV$ соответственно $$(r\;i,0j,-h\;k),\;(-r\;i/2, — r\sqrt 3/2,-h\;k)$$ 9{\circ} $ двугранные вдоль VA,VB и VC с $V$ в качестве общей вершины.
Таким образом, три произвольных (по оси) разреза под $\угол OVM$ для каждой из трех пересекающихся плоскостей дают вершину/угол куба.
Три другие грани на другой стороне генерируются таким же образом при повороте цилиндра на 60, 180, 300 градусов.
Вышеизложенного достаточно, чтобы изготовить куб, показанный в вопросе. Его можно обобщить. Возможно, изменить соответствующим образом, чтобы даже огранить алмаз типа Кохи-нур (с помощью подходящих шлифовальных станков по камню / гранильному станку) для шлифования с получением нескольких многогранных граней.
$\endgroup$
$\begingroup$
Я надеюсь, что изображение поможет, иначе я не уверен, как это объяснить без визуальной поддержки.
В верхней части изображения у нас есть ромб ABCD, который, если смотреть сверху, выглядит как изображение внизу рисунка. Точка, соответствующая центру бревна, C.
Теперь сложная часть, требующая визуализации процесса. Представьте, что мы можем поднять точку А на прямой, ортогональной начальной плоскости ромба. Форма ABCD остается ромбом, если обе точки B и C также подняты соответственно.
Используя этот процесс, мы должны поднять точку A так, чтобы новая форма, описываемая сдвинутыми точками A’B’CD’ (C остается фиксированной), стала квадратной, что эквивалентно тому, что A’C=B’D’ (после сдвига точек!)
С помощью этой информации мы можем вычислить угол $\theta$ между текущим квадратом и исходной плоскостью, используя
$$\cos(\theta) = \frac{AC}{A ‘C} = \frac{AC}{BD}.$$
Эта формула применяется к полученному треугольнику ACA’.
Теперь нам нужно связать формулу этого угла с геометрией бревна. Вид бревна сверху с вставленным в него кубом будет выглядеть примерно так, как показано на следующем изображении, где точка C находится на верхней или нижней плоской поверхности бревна.
С этой точки зрения должно быть ясно, что при смещении упомянутого выше верно то, что BD=B’D’. Но BD — ребро равностороннего треугольника, а DC — радиус $r$ цилиндра. Таким образом, из этой точки вы можете вычислить радиус, зная ребро треугольника, что дает
$$r = DC = BD \frac{\sqrt{3}}{3}.