Доска обрезная в Прокопьевске — низкая цена за куб от производителя
Для изготовления мебели, отделки внутренних стен и пола, монтажа кровли, изготовления дверей и окон используется обрезная доска. Это распиленный на прямоугольные ламели кругляк, зачищенный по краям от обзола (коры). Для изготовления используется хвойная древесина камерной сушки с точным соблюдением государственных стандартов.
Завод пиломатериалов «ЛесПрофиль» изготавливает и продает доску обрезную стандартной толщины до 50 мм и обрезной брус сечением 100-200 мм. Производственные мощности находятся в Кирове, куда поставляется пиловочник с собственных делянок. Пиломатериал доставляется длинномерами во все регионы России.
Размеры и цены за куб обрезной доски в Прокопьевске
На весь ассортимент товара «ЛесПрофиль» держит самые низкие цены* в Прокопьевске – между нами и покупателями нет посредников и магазинов. Цены на перевозку у нас также минимальные – основная часть поставляется собственным транспортом, в удаленные регионы – транспортными компаниями.
|
Наименование |
Размеры, мм |
Ед. изм. |
Цена, нал/безнал. |
Примечание |
Сырье |
|
Обрезная доска |
20х100х6000 |
м3 |
7300/7800 |
допуск |
сосна, ель |
|
25х100х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
25х150х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
40х100х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
40х150х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
40х200х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
50х100х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
50х150х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
50х200х6000 |
7500/8000 |
допуск |
* — на первый заказ скидка 5%.
Оптовые цены на обрезную доску в Прокопьевске
Заказ сразу большой партии выгоден не только по стоимости – при покупке оптом вы экономите 20%, но и по визуальным характеристикам. Каждая партия заготавливается из кругляка одного повала, что гарантирует совпадение цвета и фактуры.
|
Наименование |
Размеры, мм |
Ед. изм. |
Цена, нал/безнал. |
Примечание |
Сырье |
|
Обрезная доска |
20х100х6000 |
м3 |
5840/6240 |
допуск |
сосна, ель |
|
25х100х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
25х150х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
40х100х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
40х150х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
40х200х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
50х100х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
50х150х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
50х200х6000 |
6000/6400 |
допуск |
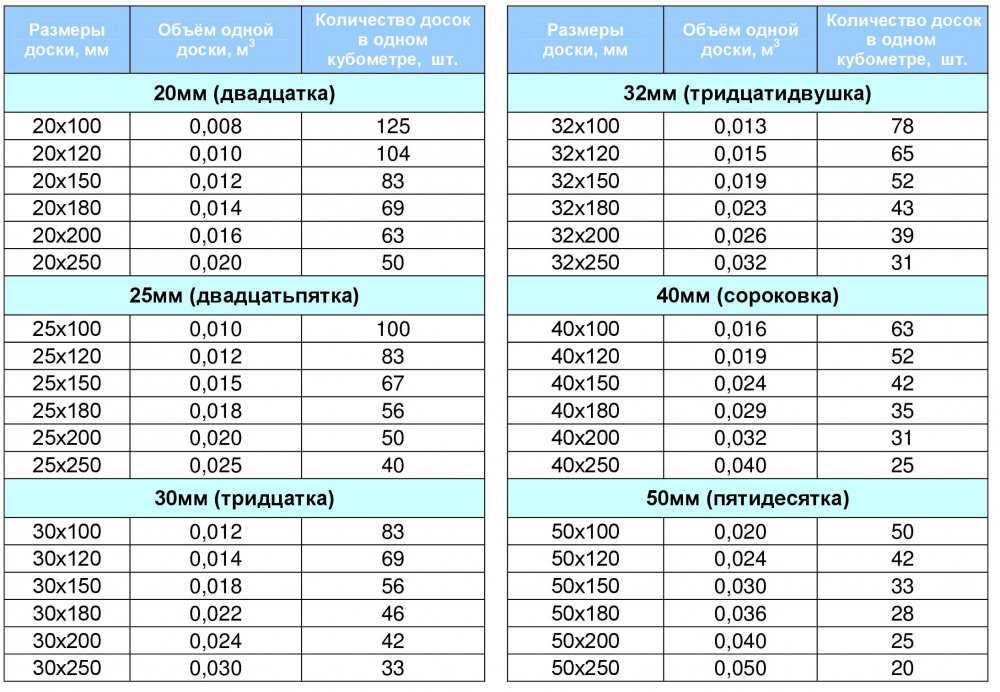
Сколько штук обрезной доски в 1 кубе
Для определения нужного объема необходимо знать кубатуру и количество планок в кубе с учетом линейных размеров.
|
Ширина, мм |
Высота, мм |
Длина, мм |
м3/шт |
шт/м3 |
|
100 |
20 |
6000 |
0,012 |
83,3 |
|
150 |
20 |
6000 |
0,018 |
55,6 |
|
200 |
20 |
6000 |
0,024 |
41,7 |
|
100 |
25 |
6000 |
0,015 |
|
|
150 |
25 |
6000 |
0,023 |
43,5 |
|
200 |
25 |
6000 |
0,03 |
33,3 |
|
100 |
40 |
6000 |
0,024 |
41,7 |
|
150 |
40 |
6000 |
0,036 |
27,8 |
|
200 |
40 |
6000 |
0,048 |
20,9 |
|
100 |
50 |
6000 |
0,03 |
33,3 |
|
150 |
50 |
6000 |
0,045 |
22,2 |
|
200 |
50 |
6000 |
0,06 |
16,7 |
Технология производства и сортировка
Для изготовления используются хвойные породы дерева – сосна и ель. За счет высокой концентрации смол обрезная строганная доска получается прочной плотной и долговечной. Ее можно использовать даже на открытом пространстве без риска коробления или биологических повреждений.
За счет высокой концентрации смол обрезная строганная доска получается прочной плотной и долговечной. Ее можно использовать даже на открытом пространстве без риска коробления или биологических повреждений.
После сортировки бревна отправляются в камеры для просушивания. Высыхание длится неделю, в результате чего влажность падает до 18%. Температура и продолжительность сушки зависят от диаметра кругляка и его вида. «ЛесПрофиль» не продает в Прокопьевске обрезную доску атмосферной сушки – этот материал не выдерживает проверку временем, в течение первых 3-х лет скручивается винтом.
После сушки пиловочник распускается на ламели, каждая из которых прогоняется через четырехсторонний станок. В результате по кромкам снимается обзол, а верхняя и нижняя пласти становятся ровными и гладкими.
Только после фрезеровки заготовок проводится сортировка по качеству. Что это означает? То, что обрезная доска 4 сорта (чернового) хорошего качества. Для определения сорта используются следующие квалифицирующие признаки (ГОСТ 8486–86):
|
Сорт |
Фото |
Характеристики |
|
I (высший, экстра) |
|
Идеальное состояние – равномерный цвет, минимальное количество сучков, до 5% обзола. |
|
II (В) |
|
Цвет может быть неравномерным. Допускаются здоровые сучки, обзол до 10%, невыпадающие карманы. |
|
III (С) |
|
Цвет неравномерный, встречаются здоровые и выпадающие сучки, незначительные потемнения, следы биологических повреждений, обзол до 25%, трещины, признаки старения древесины. |
|
IV (черновой) |
|
К качеству предъявляются минимальные требования – сучки, карманы, следы червоточин, жуков-короедов, заболони в виде пятен и полос, трещины, обзол долее 25%. |
Стандартная длина обрезной доски 6 метров. Возможна нарезка заготовок на длину от 1 метра с разным шагом. Высота 20-50 мм, ширина 100, 150 и 200 мм.
Возможна нарезка заготовок на длину от 1 метра с разным шагом. Высота 20-50 мм, ширина 100, 150 и 200 мм.
После сортировки весь пиломатериал проходит антисептическую и противопожарную защиту, после чего отправляется на склад для хранения. Из досок собираются штабеля, прокладываются брусьями для вентиляции. При подготовке заказа к отправке штабеля перемещаются на поддоны и упаковываются пленкой.
Стандартизация и сертификация
Каждый этап производства обрезной доски проводится в соответствии с регламентом конкретного государственного стандарта:
- заготовка сырья и сортировка по качеству – ГОСТ 8486-86 «Пиломатериалы хвойных пород»;
- камерная сушка и контроль влажности – ГОСТ 6782.1-75 «Пилопродукция из древесины хвойных пород».
- хранение на складе, упаковка и транспортировка – ГОСТ 3808.1-80 «Пиломатериалы хвойных пород. Атмосферная сушка и хранение».
К каждой партии выдается сертификат качества.
Где купить пиломатериал в Прокопьевске
География заказов «ЛесПрофиль» охватывает всю территорию России. Стабильно низкие цены, грамотная логистика и собственный автопарк ежедневно расширяют зону заказов – даже в самые удаленные регионы поставляются наши изделия. Для удобства клиентов мы обрабатываем комплексные заявки и можем отправить в одной партии разноплановый товар – евровагонка, обрезная доска, профилированный брус и т.д.
Сомневаетесь в выборе или затрудняетесь с подсчетом, обращайтесь к нам. Специалисты дадут вам исчерпывающую консультацию, помогут с выбором, дадут рекомендации по монтажу и уходу.
Доска обрезная в Междуреченске — низкая цена за куб от производителя
Для изготовления мебели, отделки внутренних стен и пола, монтажа кровли, изготовления дверей и окон используется обрезная доска. Это распиленный на прямоугольные ламели кругляк, зачищенный по краям от обзола (коры). Для изготовления используется хвойная древесина камерной сушки с точным соблюдением государственных стандартов.
Завод пиломатериалов «ЛесПрофиль» изготавливает и продает доску обрезную стандартной толщины до 50 мм и обрезной брус сечением 100-200 мм. Производственные мощности находятся в Кирове, куда поставляется пиловочник с собственных делянок. Пиломатериал доставляется длинномерами во все регионы России.
Размеры и цены за куб обрезной доски в Междуреченске
На весь ассортимент товара «ЛесПрофиль» держит самые низкие цены* в Междуреченске – между нами и покупателями нет посредников и магазинов. Цены на перевозку у нас также минимальные – основная часть поставляется собственным транспортом, в удаленные регионы – транспортными компаниями.
|
Наименование |
Размеры, мм |
Ед. изм. |
Цена, нал/безнал. |
Примечание |
Сырье |
|
Обрезная доска |
20х100х6000 |
м3 |
7300/7800 |
допуск |
сосна, ель |
|
25х100х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
25х150х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
40х100х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
40х150х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
40х200х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
50х100х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
50х150х6000 |
7500/8000 |
допуск |
|||
|
8500/9300 |
ГОСТ |
||||
|
50х200х6000 |
7500/8000 |
допуск |
* — на первый заказ скидка 5%.
Оптовые цены на обрезную доску в Междуреченске
Заказ сразу большой партии выгоден не только по стоимости – при покупке оптом вы экономите 20%, но и по визуальным характеристикам. Каждая партия заготавливается из кругляка одного повала, что гарантирует совпадение цвета и фактуры.
|
Наименование |
Размеры, мм |
Ед. изм. |
Цена, нал/безнал. |
Примечание |
Сырье |
|
Обрезная доска |
20х100х6000 |
м3 |
5840/6240 |
допуск |
сосна, ель |
|
25х100х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
25х150х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
40х100х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
40х150х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
40х200х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
50х100х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
50х150х6000 |
6000/6400 |
допуск |
|||
|
8500/7440 |
ГОСТ |
||||
|
50х200х6000 |
6000/6400 |
допуск |
Сколько штук обрезной доски в 1 кубе
Для определения нужного объема необходимо знать кубатуру и количество планок в кубе с учетом линейных размеров.
|
Ширина, мм |
Высота, мм |
Длина, мм |
м3/шт |
шт/м3 |
|
100 |
20 |
6000 |
0,012 |
83,3 |
|
150 |
20 |
6000 |
0,018 |
55,6 |
|
200 |
20 |
6000 |
0,024 |
41,7 |
|
100 |
25 |
6000 |
0,015 |
66,7 |
|
150 |
25 |
6000 |
0,023 |
43,5 |
|
200 |
25 |
6000 |
0,03 |
33,3 |
|
100 |
40 |
6000 |
0,024 |
41,7 |
|
150 |
40 |
6000 |
0,036 |
27,8 |
|
200 |
40 |
6000 |
0,048 |
20,9 |
|
100 |
50 |
6000 |
0,03 |
33,3 |
|
150 |
50 |
6000 |
0,045 |
22,2 |
|
200 |
50 |
6000 |
0,06 |
16,7 |
Технология производства и сортировка
Для изготовления используются хвойные породы дерева – сосна и ель. За счет высокой концентрации смол обрезная строганная доска получается прочной плотной и долговечной. Ее можно использовать даже на открытом пространстве без риска коробления или биологических повреждений.
За счет высокой концентрации смол обрезная строганная доска получается прочной плотной и долговечной. Ее можно использовать даже на открытом пространстве без риска коробления или биологических повреждений.
После сортировки бревна отправляются в камеры для просушивания. Высыхание длится неделю, в результате чего влажность падает до 18%. Температура и продолжительность сушки зависят от диаметра кругляка и его вида. «ЛесПрофиль» не продает в Междуреченске обрезную доску атмосферной сушки – этот материал не выдерживает проверку временем, в течение первых 3-х лет скручивается винтом.
После сушки пиловочник распускается на ламели, каждая из которых прогоняется через четырехсторонний станок. В результате по кромкам снимается обзол, а верхняя и нижняя пласти становятся ровными и гладкими.
Только после фрезеровки заготовок проводится сортировка по качеству. Что это означает? То, что обрезная доска 4 сорта (чернового) хорошего качества. Для определения сорта используются следующие квалифицирующие признаки (ГОСТ 8486–86):
|
Сорт |
Фото |
Характеристики |
|
I (высший, экстра) |
|
Идеальное состояние – равномерный цвет, минимальное количество сучков, до 5% обзола. |
|
II (В) |
|
Цвет может быть неравномерным. Допускаются здоровые сучки, обзол до 10%, невыпадающие карманы. |
|
III (С) |
|
Цвет неравномерный, встречаются здоровые и выпадающие сучки, незначительные потемнения, следы биологических повреждений, обзол до 25%, трещины, признаки старения древесины. |
|
IV (черновой) |
|
К качеству предъявляются минимальные требования – сучки, карманы, следы червоточин, жуков-короедов, заболони в виде пятен и полос, трещины, обзол долее 25%. |
Стандартная длина обрезной доски 6 метров.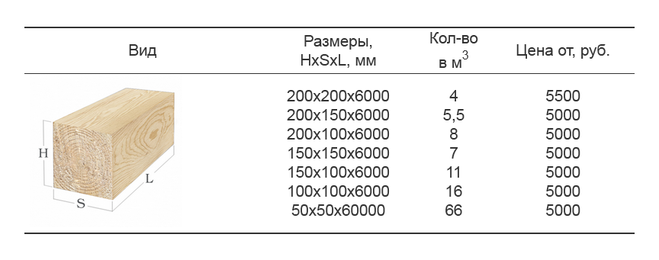 Возможна нарезка заготовок на длину от 1 метра с разным шагом. Высота 20-50 мм, ширина 100, 150 и 200 мм.
Возможна нарезка заготовок на длину от 1 метра с разным шагом. Высота 20-50 мм, ширина 100, 150 и 200 мм.
После сортировки весь пиломатериал проходит антисептическую и противопожарную защиту, после чего отправляется на склад для хранения. Из досок собираются штабеля, прокладываются брусьями для вентиляции. При подготовке заказа к отправке штабеля перемещаются на поддоны и упаковываются пленкой.
Стандартизация и сертификация
Каждый этап производства обрезной доски проводится в соответствии с регламентом конкретного государственного стандарта:
- заготовка сырья и сортировка по качеству – ГОСТ 8486-86 «Пиломатериалы хвойных пород»;
- камерная сушка и контроль влажности – ГОСТ 6782.1-75 «Пилопродукция из древесины хвойных пород».
- хранение на складе, упаковка и транспортировка – ГОСТ 3808.1-80 «Пиломатериалы хвойных пород. Атмосферная сушка и хранение».
К каждой партии выдается сертификат качества.
Где купить пиломатериал в Междуреченске
География заказов «ЛесПрофиль» охватывает всю территорию России. Стабильно низкие цены, грамотная логистика и собственный автопарк ежедневно расширяют зону заказов – даже в самые удаленные регионы поставляются наши изделия. Для удобства клиентов мы обрабатываем комплексные заявки и можем отправить в одной партии разноплановый товар – евровагонка, обрезная доска, профилированный брус и т.д.
Сомневаетесь в выборе или затрудняетесь с подсчетом, обращайтесь к нам. Специалисты дадут вам исчерпывающую консультацию, помогут с выбором, дадут рекомендации по монтажу и уходу.
Казино Cloudbet — играть на официальнос сайте Клаудбет
- 🏆 Преимущества проекта Cloudbet
- ♦ История Cloudbet
- 🎆 Промоакции от казино Cloudbet
- ✨ Инновационная платформа для ставок на криптовалюту
- 🎰 Азартные развлечения
- 💵 Как начать игру на деньги
- 🎮 Почему геймеры выбирают проект Cloudbet
- ✴ Лицензия
- 📝 Отзывы клиентов Cloudbet
Cloudbet – онлайн казино с лицензией, которая делает безопасной и честной игру в виртуальном заведении. Платформа ориентирована на держателей криптокошельков, которым предлагаются прогнозы на спорт и услуги крипто casino. Стать клиентом игорного заведения могут жители из разных стран.
Платформа ориентирована на держателей криптокошельков, которым предлагаются прогнозы на спорт и услуги крипто casino. Стать клиентом игорного заведения могут жители из разных стран.
Преимущества проекта Cloudbet
Cloudbet казино объединило в одно целое самые востребованные направления гэмблинга. Чтобы воспользоваться всем функционалом игорного заведения, посетителям сайта достаточно зарегистрировать аккаунт, пополнить баланс и начать играть на реальные деньги. Для проведения финансовых операций разрешается использовать разные цифровые монеты. Все транзакции осуществляются конфиденциально и за считанные секунды. К остальным преимуществам казино Cloudbet относятся следующие:
- регулярное проведение акций и турниров;
- моментальный вывод выигранных денег;
- индивидуальные поощрения в BTC;
- отличный выбор азартных игр;
- высокие лимиты на вывод;
- быстрая регистрация;
- лучшие коэффициенты на крупные матчи.

Поклонникам беттинга понравятся условия для ставок на исход спортивных мероприятий. Разрешается заключать пари перед началом и во время соревнований. Ставки принимаются на события по киберспорту и спортивные матчи. Каждый беттор сможет воспользоваться широким выбором рынков с максимально высокими коэффициентами.
Одним из плюсов казино Cloudbet считается его удобный пользовательский интерфейс. При входе на официальный сайт посетители увидят главную страницу, где разработчики опубликовали наиболее значимую информацию об онлайн-проекте. Здесь перечислены основные конкурентные преимущества виртуального заведения и указаны главные направления деятельности казино. На сайте разрешается играть только на криптовалюту.
История Cloudbet
Онлайн казино Cloudbet работает с 2013 года. Сразу после оформления лицензии оператор предложил своим клиентам отличную подборку развлечений, лайв-игры с участием реального крупье и прогнозы на спорт. Главный упор владелец проекта сделал на финансовые операции в биткоинах либо другой криптовалюте.
На сайте зарегистрированы пользователи со всего мира, поскольку на площадке практически отсутствуют территориальные ограничения – под запретом оказалось всего несколько стран. Управляет платформой компания Halcyon Super Holdings B.V., которая зарегистрирована на острове Кюрасао. Оператор оформил лицензию у местного регулятора (1668/JAZ).
Cloudbet работает на платформе Betsoft. Основным приоритетом для администрации казино выступает безопасность денежных средств клиентов. Компания активно использует технологию шифрования данных, гарантирующую, что все транзакции проходят безопасно и исключительно в частном порядке. Оператор активно использует современные методы безопасности для хранения полученной информации. Все средства пользователей направляются в автономный кошелек, недоступный потенциальным хакерам. За честность игрового процесса отвечает сертифицированный ГСЧ. Он регулярно проходит проверки независимых компаний.
Администрация Cloudbet казино регулярно раздает щедрые подарки. Обширная промо-программа рассчитана на новых и постоянных клиентов. Она предусматривает выдачу приветственных бонусов, бесплатных спинов и вознаграждений за пополнение счета. Весь список доступных поощрений отображается в разделе «Акции», который открывается после нажатия по соответствующей кнопке внизу страницы. Здесь же можно узнать о клубе лояльности и актуальных турнирах.
Обширная промо-программа рассчитана на новых и постоянных клиентов. Она предусматривает выдачу приветственных бонусов, бесплатных спинов и вознаграждений за пополнение счета. Весь список доступных поощрений отображается в разделе «Акции», который открывается после нажатия по соответствующей кнопке внизу страницы. Здесь же можно узнать о клубе лояльности и актуальных турнирах.
Приветственный бонус
В качестве приветственного бонуса можно получить до 5 BTC. Новичкам предлагается увеличить на 100% сумму первого перевода, сделанного в BNB, BCH, LTC, DASH, ETH, DOGE, BTC, USDT либо другой криптовалюте. Чтобы активировать поощрение от Cloudbet, новым пользователям необходимо:
- Перейти на основной домен или рабочее зеркало казино.
- Зарегистрировать учетную запись.
- Пополнить депозит с помощью криптовалюты.
- Получить вместе с деньгами приветственный бонус.
Минимальная сумма депозита зависит от используемой криптовалюты. Условия выдачи поощрений указаны в таблице:
Условия выдачи поощрений указаны в таблице:
| Цифровая монета | Минимальный депозит для получения бонуса |
| BTC | 0.001 |
| ETH | 0.01 |
| BCH | 0.03 |
| BNB | 0.05 |
| DASH / LTC | 0.1 |
Приветственный бонус остается активным в течение 60 дней. Следить за бонусными средствами можно на дополнительном счету, который предусмотрен в личном кабинете. После перевода бонусных денег на основной счет их можно будет вывести на криптокошелек.
Программа лояльности для гостей клуба
В казино Cloudbet действует программа лояльности, которая насчитывает 6 уровней. Новичкам после регистрации аккаунта присваивается статус «Bronze». По мере продвижения от одного уровня к другому гемблерам открывается доступ к более щедрым подаркам. Для перехода на новую ступень в программе лояльности требуется накапливать Lightning Point (LP). Начисление бонусных баллов не привязано к ставкам. Участники программы лояльности могут только следить за текущим прогрессом в персональном кабинете. С каждым новым уровнем увеличивается коэффициент выдаваемых LP. Чем выше будет уровень, тем быстрее можно накопить бонусные баллы.
Начисление бонусных баллов не привязано к ставкам. Участники программы лояльности могут только следить за текущим прогрессом в персональном кабинете. С каждым новым уровнем увеличивается коэффициент выдаваемых LP. Чем выше будет уровень, тем быстрее можно накопить бонусные баллы.
Шесть эксклюзивных уровней лояльности
Шесть уровней в программе лояльности указаны в таблице:
| Статус | LP-множитель | Поощрение |
| Bronze | х1 | — |
| Silver | х1,2 | 50% |
| Gold | х1,4 | 50% |
| Emerald | х1,6 | 50% |
| Sapphire | х1,8 | 100% |
| Ruby | х2 | 100% |
За текущим статусом можно следить в левом верхнем углу экрана. Нажав на него кнопкой мышки, гемблер увидит на странице окно с условиями программы лояльности. Здесь отображается прогресс игрока в процентах и главные преимущества уровня.
Здесь отображается прогресс игрока в процентах и главные преимущества уровня.
Преимущества вознаграждений за лояльность
Вознаграждения за лояльность представлены в виде фриспинов, реальных денег и других подарков. Воспользоваться каждым из них разрешается только после достижения определенного уровня, который предусмотрен системой поощрения клиентов.
Фриспины по вторникам
Каждый вторник зарегистрированные гости получают 20 бесплатных спинов за пополнение счета на 20 евро и более. Чтобы стать участником данной акции, гемблеру необходимо:
- Внести на баланс депозит в размере 20 евро и больше до вторника в течение недели.
- Дождаться зачисления неоплачиваемых спинов для слота Dead Riders Trail.
- Потратить призовые вращения барабанов в течение суток, начиная с момента их выдачи.
- Отыграть выигрыши с фриспинов с вейджером х40 в течение суток.
Данная акция проводится каждую неделю по вторникам. Увидеть призовые спины можно в разделе «Мой аккаунт». Они остаются активными в течение 24 часов после выдачи. Потратить бонусные вращения барабанов можно только на автомат, который указан на странице акции. Все выигрыши с фриспинов выдаются в виде бонусных денег. Их необходимо отыграть с вагером х40 перед подачей запроса на вывод средств.
Они остаются активными в течение 24 часов после выдачи. Потратить бонусные вращения барабанов можно только на автомат, который указан на странице акции. Все выигрыши с фриспинов выдаются в виде бонусных денег. Их необходимо отыграть с вагером х40 перед подачей запроса на вывод средств.
Ежедневный розыгрыш €300
Каждый день администрация казино Cloudbet разыгрывает €300 между бетторами, которые заключили пари на US Open. Стать участником данного розыгрыша может каждый авторизованный гость казино Cloudbet, который поставит минимум 10 евро на любую лайв-ставку любого матча US Open с 29 августа до 11 сентября. Ежедневные победители выбираются среди гемблеров, заключивших пари в рамках US Open. Засчитываются прогнозы на любые события Большого Шлема в режиме лайв.
Кто может участвовать?
Участвовать в данной акции могут все авторизованные гости игорного заведения. Главное условие для розыгрыша крупного призового фонда – наличие минимум одной ставки на US Open в этот день.
Можно ли участвовать в розыгрыше каждый день?
Игроки могут участвовать в розыгрыше €300 каждый день. Ограничений на количество прогнозов для авторизованных гемблеров Cloudbet казино не предусмотрено. Вне зависимости от исхода розыгрыша, его участники имеют все шансы выигрывать реальные деньги ежедневно.
Какая минимальная сумма ставки?
Для участия в розыгрыше 300 евро достаточно поставить на кон минимум 10 евро. Максимальный размер заключенного беттором пари ограничений не имеет. Не играют никакой роли и результаты прогноза.
Можно ли ставить бонусные деньги?
Нет, для участия в акции использовать бонусные деньги нельзя. Чтобы стать претендентом на реальный выигрыш, гемблеру потребуется внести на баланс минимальную сумму или воспользоваться ранее пополненным депозитом.
Когда объявляют победителя?
Никнейм победителя публикуется на странице акций онлайн-казино сразу после проведения розыгрыша. Уведомление о выигрыше также будет отправлено на электронную почту призера, которую он указал в личном кабинете. Победитель розыгрыша определяется на площадке случайным образом.
Победитель розыгрыша определяется на площадке случайным образом.
Ставки на спорт без ничьей
Администрация Cloudbet предлагает коэффициенты с нулевой маржой на разные соревнования, тем самым гарантируя своим клиентам лучшие условия для заключения пари на исходы в популярных видах спорта. Беттору достаточно следить за событиями, которые отмечены желтыми флажками. В рамках данной акции предусмотрены самые выгодные предматчевые коэффициенты на интересующие мероприятия.
Бонус на депозит каждый четверг
100% Reload-бонус доступен пользователям за депозит на минимальную сумму 10 евро. Максимальный размер поощрения ограничен суммой 5000 EUR. Вознаграждение выдается каждый четверг. Стать участником данной акции могут геймеры, которые имеют статус Ruby в действующей программе лояльности. Пользователи, которые достигли уровня Sapphire, получают 100% Reload-бонус, ограниченный суммой 2500 EUR. За пополнение счета на 10 евро гемблеры со статусом Emerald могут получить в качестве вознаграждения до 1 250 EUR.
Инновационная платформа для ставок на криптовалюту
Онлайн-казино Cloudbet ориентировано на гемблеров, предпочитающих играть на цифровую валюту. Клиентам игорного заведения предлагается воспользоваться не только биткоином. Также пользователям доступны и многие другие цифровые монеты. В их числе Bitcoin cash и Ethereum.
Использовать криптокошельки можно без опасений за безопасность денежных средств. Администрация Cloudbet гарантирует своим клиентам полную безопасность и оперативность финансовых транзакций. Деньги зачисляются на игровой счет практически моментально. Получить выигрыши также можно без задержек.
Среди главных особенностей казино Cloudbet – выгодные условия для спинов на реальные деньги. Новичкам предлагается активировать приветственный подарок. Он состоит из поощрения за первый депозит и предусматривает выдачу вознаграждения в размере до 5 BTC.
Азартные развлечения
В каталоге Cloudbet собраны популярные развлечения из мира гэмблинга. Отличный выбор киберспортивных и спортивных дисциплин дополняет коллекция лицензионных автоматов. Администрация казино предлагает только сертифицированные слоты, которые имеют разные тематики, высокие показатели отдачи, выгодные бонусы и широкий диапазон ставок. Средний показатель RTP в аппаратах онлайн-заведения составляет 95-98%.
Администрация казино предлагает только сертифицированные слоты, которые имеют разные тематики, высокие показатели отдачи, выгодные бонусы и широкий диапазон ставок. Средний показатель RTP в аппаратах онлайн-заведения составляет 95-98%.
Для удобства гостей сайта в отдельном разделе меню собраны карточные и настольные игры с участием реального крупье. Живой дилер принимает фишки за столом в режиме реального времени. Играть в лайв-казино интересно, выгодно и безопасно. Ставки принимаются только в криптовалюте.
Так как казино также выступает в качестве букмекерской платформы, здесь собраны многие дисциплины. Денежные средства списываются с главного счета. Они же используются и для запуска автоматов. Самые популярные виды спорта собраны в главном меню. Среди доступных для прогнозов дисциплин представлен бейсбол, теннис, футбол и ММА. В соответствующем разделе меню отображается весь список направлений. По ним проходят как крупные чемпионаты, так и небольшие соревнования. Любителям киберспортивных дисциплин предлагаются интересные события. В соответствующей категории с виртуальными играми можно найти такие популярные направления, как LoL, Starcraft, Valorant, Dota 2, FIFA, Call of Duty и многие другие.
В соответствующей категории с виртуальными играми можно найти такие популярные направления, как LoL, Starcraft, Valorant, Dota 2, FIFA, Call of Duty и многие другие.
Еще в одном разделе, который получил название «Доказуемо честные», можно увидеть дисциплины с необычными названиями. Некоторые из них вводят новичков площадки в заблуждение. В этой категории можно найти увлекательные азартные развлечения. Всего в каталоге собрано 8 тайтлов, среди которых представлен и хорошо знакомый гемблерам Aviator. Также в данной категории можно найти Plinko, Dice, Keno, Mines, Hilo и некоторые другие.
Баккара
В соответствующем разделе меню собрано пять версий баккары от ведущих производителей софта. Это тайтлы двух компаний – Betsoft и Evolution Gaming. Для удобства гемблеров рядом с каждым развлечением указан показатель теоретической отдачи. Понравившиеся версии баккары можно добавить в категорию «Избранное» нажатием на знак с изображением сердечка.
Блэкджек
Блэкджек представлен на портале 8 версиями. В соответствующей вкладке меню собраны разработки компаний Betsoft и Evolution Gaming. Рядом с каждой указывается показатель RTP. Для удобства посетителей предусмотрена возможность вывода развлечений на страницу определенных компаний.
В соответствующей вкладке меню собраны разработки компаний Betsoft и Evolution Gaming. Рядом с каждой указывается показатель RTP. Для удобства посетителей предусмотрена возможность вывода развлечений на страницу определенных компаний.
Игровые автоматы
В разделе с игровыми автоматами Cloudbet собраны сотни качественных слотов. Найти подходящий аппарат помогает удобная навигация по каталогу. Она реализована разработчиками в виде большого меню с десятками категорий, которое находится в левой части страницы. Одним кликом игрок выведет на экран автоматы, участвующие в розыгрыше прогрессивного джекпота. Есть возможность сформировать списки слотов по популярности, новизне, наличию опции покупки бонусов или большого количества линий выплат (Megaways games).
Настольные игры
В Cloudbet казино есть разные версии баккары, рулетки и блэкджека. Ставки принимаются на всевозможные настольные игры реальными деньгами и в виде демо-кредитов. Подходящее развлечение можно выбрать в левой части экрана. Также поиск нужных тайтлов допускается в поисковой строке по названию.
Также поиск нужных тайтлов допускается в поисковой строке по названию.
Рулетка
3 варианта онлайн-рулетки доступны в Cloudbet казино в соответствующем разделе меню. Рядом с каждым развлечением указан показатель отдачи и компания-производитель. В каталоге собраны такие популярные версии рулетки, как European Roulette, First Person European и First Person Lightning.
Live биткоин казино
Тайтлы с реальным крупье представлены на площадке компаниями Authentic Gaming, Evolution Gaming и Vivo. Для удобства все лайв-трансляции поделены на несколько разделов:
- Игровое шоу;
- Настольные игры;
- Блэкджек;
- Баккара;
- Рулетка.
Всего в каталоге собрано около 100 развлечений. Чтобы увидеть на экране весь список live-трансляций, достаточно попасть в лобби, где развлечения разделены по тематикам.
Как начать игру на деньги
Для получения доступа к игре на деньги в Cloudbet казино требуется зарегистрировать учетную запись. Создать игровой профиль игроки могут стандартным или альтернативным способом. Первый вариант предусматривает заполнение короткой анкеты. После ввода обязательных персональных данных останется определиться с подходящим слотом и запустить его барабаны. Для пополнения баланса авторизованным гостям сайта необходимо:
Создать игровой профиль игроки могут стандартным или альтернативным способом. Первый вариант предусматривает заполнение короткой анкеты. После ввода обязательных персональных данных останется определиться с подходящим слотом и запустить его барабаны. Для пополнения баланса авторизованным гостям сайта необходимо:
- В правом верхнем углу нажать кнопку «Купить BTC».
- Нажать «Покупайте BTC с помощью MoonPay».
- После перехода на страницу платежной системы указать сумму депозита.
- Кликнуть кнопку «Продолжить».
- Ввести электронную почту для авторизации в платежной системе.
- Подтвердить платеж и дождаться зачисления денежных средств.
Альтернативный способ создания аккаунта предусматривает использование упрощенной схемы. Она доступна посетителям, которые имеют профиль в социальных сетях. Авторизовавшись в системе через популярные мессенджеры, гемблер тем самым разрешит использовать личные данные, опубликованные на персональной странице. Этот процесс проходит автоматически после получения согласия от новичка.
Этот процесс проходит автоматически после получения согласия от новичка.
Почему геймеры выбирают проект Cloudbet
Профессионалы и новички выбирают безопасные и надежные ресурсы. Данные критерии нередко дополняет требование, касающееся доступности бонусных предложений. Все эти условия полностью соблюдены на сайте Cloudbet.
Оператор предоставляет азартные услуги на основании действующих лицензий. Документы на ведение законной игорной деятельности были получены от комиссий Curacao и Montenegro.
В онлайн-заведении принимаются прогнозы на спорт и запускаются автоматы с единого профиля. Переход между разделами занимает всего пару секунд. Крупные выигрыши выдаются за удачные спортивные прогнозы и беспроигрышные запуски игровых барабанов. Заработать криптовалюту позволяют сотни лицензионных слотов с высоким показателем отдачи.
Особое внимание администрация Cloudbet уделяет безопасности своих клиентов. Именно с этой целью на портале действует политика анонимности и конфиденциальности. Личные данные пользователей хранятся на сервере в зашифрованном виде. Указанная информация используется в рекламных целях.
Личные данные пользователей хранятся на сервере в зашифрованном виде. Указанная информация используется в рекламных целях.
Любой посетитель может на собственном опыте убедиться в достоинствах казино Cloudbet. Для этого достаточно зарегистрировать аккаунт и пополнить баланс. Играть на криптовалюту безопасно и удобно. Поскольку в любой момент гемблер сможет оформить запрос на получение выигранных денег.
Лицензия
Владелец лицензионного казино Cloudbet предлагает своим клиентам качественный софт, поскольку имеет для ведения законной игорной деятельности лицензии сразу двух регуляторов. Разрешение от Черногории для предоставления услуг в области гемблинга зарегистрировано под №02/01-118/4. Лицензия от игорной комиссии Кюрасао числится под номером 1668/JAZ. Данная информация позволяет всем желающим проверить на сайте регуляторов подлинность документов и убедиться в том, что их срок действия еще не истек.
Отзывы клиентов Cloudbet
Опубликованные в сети отзывы о Cloudbet казино подтверждают его честную и стабильную работу. Гости игорного зала отмечают не только легальную деятельность виртуальной площадки, которую гарантирует наличие 2 лицензий, но и большую коллекцию автоматов. Пользователей привлекает на сайте приветственный подарок и регулярные бонусы, наличие раздела со ставками на киберспорт и традиционные спортивные дисциплины. Особый интерес игорный зал представляет для держателей криптовалюты, которые тратят цифровые монеты на удачные ставки в режиме игры на реальные деньги.
Гости игорного зала отмечают не только легальную деятельность виртуальной площадки, которую гарантирует наличие 2 лицензий, но и большую коллекцию автоматов. Пользователей привлекает на сайте приветственный подарок и регулярные бонусы, наличие раздела со ставками на киберспорт и традиционные спортивные дисциплины. Особый интерес игорный зал представляет для держателей криптовалюты, которые тратят цифровые монеты на удачные ставки в режиме игры на реальные деньги.
Учебник по сборке кубика Рубика
Сборка кубика Рубика!
Легко, когда знаешь как.
Введение
Узнайте, как собрать кубик Рубика с помощью простых инструкций и интерактивных демонстраций.
Кубик Рубика может показаться почти невозможным, когда вы впервые начинаете с ним играть. Разместить первые несколько кусочков достаточно легко, но вскоре вы обнаружите, что ничего не можете сделать, не набивая другие области. Когда вы знаете шаги и вооружены правильными алгоритмами, это на самом деле довольно просто. На следующих страницах вы познакомитесь с простым и легким в применении набором алгоритмов (предварительно организованных шагов), которые помогут решить куб. (Кубик Рубика — это продукт, созданный компанией Rubik’s Brand Ltd. Это просто руководство по его сборке и никоим образом не связано с компанией.)
На следующих страницах вы познакомитесь с простым и легким в применении набором алгоритмов (предварительно организованных шагов), которые помогут решить куб. (Кубик Рубика — это продукт, созданный компанией Rubik’s Brand Ltd. Это просто руководство по его сборке и никоим образом не связано с компанией.)
Outline
Этот учебник по кубу разделен на 5 разделов. Остальная часть этой страницы знакомит вас с нотацией куба и знакомит с вашим кубом. Остальные страницы работают на решение куба.
Продолжайте читать ниже, чтобы начать работу, или перейдите к одному из следующих разделов.
- 1. Решите белый крест
- 2. Решите белые углы
- 3. Решить второй слой
- 4. Решите желтый крест
- 5. Решить последний слой
- Вызовы с узорами. Просто ради интереса посмотрите, сможете ли вы создать эти узоры из кубов (а затем бросьте вызов другим, чтобы решить их интуитивно).
- Шпаргалка — все алгоритмы на одной странице для удобства.

- Симулятор куба — полезен для обучения сборке куба.
На каждом шаге руководства перечислены алгоритмы и даны подробные пояснения. Если вы не хотите читать объяснения, вы можете их пропустить.
Знакомство с кубиком
Каждый берет кубик Рубика по-своему. Некоторые люди довольно быстро поймут, как манипулировать фигурами. Другим потребуется немного больше времени. С практикой манипулирования фигурами станет легче, и вы начнете понимать, как определенные ходы приводят к определенным результатам. То, что на первый взгляд кажется просто слепым следованием алгоритмам, начнет обретать смысл, и вы начнете модифицировать алгоритмы для создания ярлыков.
Прежде чем мы начнем собирать куб, может быть полезно получить представление о том, как ведет себя куб. Хорошим начальным упражнением является работа над сборкой только одной грани куба. Не волнуйтесь, если квадраты, примыкающие к этой грани, не выстраиваются правильно, просто работайте над решением одной грани. Вы должны быть в состоянии сделать это интуитивно (то есть без использования предопределенных алгоритмов). Это помогает понять, как части перемещаются и как можно расставлять их по местам, не затрагивая других. Вы должны потренироваться держать куб двумя руками, делая это и манипулируя кубом обеими руками. В качестве дополнительной задачи посмотрите, сможете ли вы собрать грань куба одной рукой.
Вы должны быть в состоянии сделать это интуитивно (то есть без использования предопределенных алгоритмов). Это помогает понять, как части перемещаются и как можно расставлять их по местам, не затрагивая других. Вы должны потренироваться держать куб двумя руками, делая это и манипулируя кубом обеими руками. В качестве дополнительной задачи посмотрите, сможете ли вы собрать грань куба одной рукой.
Кубики
Кубик Рубика состоит из трех различных типов деталей.
| Угловые элементы — 8 угловых элементов. Они имеют 3 панели и могут быть в любой из 3 ориентаций в каждом положении. | |
| Кромки — 12 кромок. У них есть 2 панели, и каждая может быть в любой из 2 ориентаций. | |
Центральные элементы — 6 центральных элементов. У каждого из них есть только одна панель, поэтому они могут быть в одной ориентации. Эти части также определяют шесть граней куба. например. лицо с синей центральной частью — синее лицо. например. лицо с синей центральной частью — синее лицо. |
Все это дает 26 частей, составляющих куб с 54 панелями на этих частях. Это приводит к ошеломляющим 43, 252, 003, 274, 489, 856, 000 возможным комбинациям . Несмотря на это большое количество, группа или исследователи с кучей свободного вычислительного времени фактически разработали оптимальное решение для каждой из этих комбинаций, установив, что максимальное необходимое количество ходов (см. Ниже) для решения любого куба составляет 20 ходов. Практически все эти комбинации требовали различных алгоритмов для оптимального решения, и мы не собираемся предлагать вам запоминать такое количество комбинаций и соответствующих алгоритмов.
Вместо этого мы познакомим вас с алгоритмами для начинающих. Они включают в себя более 20 ходов, но гарантированно решают любую комбинацию. В этом сила хорошо продуманных алгоритмов, они могут быть очень гибкими в том, что они могут решать. Вот почему этот учебник по кубику Рубика находится на веб-сайте с учебными пособиями по ИТ. Научиться собирать кубик Рубика — отличный способ изучить, как мы можем эффективно настраивать процессы, чтобы принимать широкий спектр возможных входных данных и надежно преобразовывать их в заданные выходные данные.
Научиться собирать кубик Рубика — отличный способ изучить, как мы можем эффективно настраивать процессы, чтобы принимать широкий спектр возможных входных данных и надежно преобразовывать их в заданные выходные данные.
Обозначение куба
Решение куба требует следования набору алгоритмов. Чтобы проиллюстрировать алгоритмы, мы будем использовать обозначение куба, как указано ниже. (Существует несколько вариантов обозначения куба, но как только вы узнаете один, приспособиться к другим довольно легко.)
Каждое из этих движений представляет собой поворот соответствующих фигур на 90 градусов. У каждого хода также есть соответствующий противоположный ход, который обозначается апострофом (‘).
U — Поверните верхнюю (вверх) сторону по часовой стрелке.
U’ — Поверните верхнюю (верхнюю) поверхность против часовой стрелки.
D — Поверните нижнюю (вниз) сторону по часовой стрелке.
D’ — Поверните нижнюю (вниз) сторону против часовой стрелки.
R — Поверните правую грань по часовой стрелке.
R’ — Поверните правую сторону против часовой стрелки.
L — Поверните левую грань по часовой стрелке.
L’ — Поверните левую сторону против часовой стрелки.
F — Поверните переднюю грань по часовой стрелке.
F’ — Поверните переднюю панель против часовой стрелки.
B — Поверните заднюю сторону по часовой стрелке.
B’ — Поверните заднюю поверхность против часовой стрелки.
M — Поверните вертикальный срез по часовой стрелке.
M’ — Поверните вертикальный срез против часовой стрелки.
E — Поверните горизонтальный срез по часовой стрелке.
E’ — Поверните горизонтальный срез против часовой стрелки.
S — Поверните верхний срез по часовой стрелке.
S’ — Поверните верхний срез против часовой стрелки.
Не беспокойтесь о попытках запомнить все это. Изображения, а также моделирование будут использоваться вместе с обозначениями при объяснении алгоритмов.
Часто просмотр ходов облегчает их понимание, поэтому вот куб, где вы можете увидеть каждый ход в действии.
Теперь вы готовы. Вы можете погрузиться в Шаг 1 — Решение белого креста или продолжить чтение ниже, если вам интересно.
Советы и рекомендации
Нередко вы чувствуете себя немного подавленным, когда впервые начинаете учиться собирать кубик Рубика. Со временем и практикой это быстро пройдет. Вот несколько советов и советов, которые помогут вам на пути к овладению кубом.
Со временем и практикой это быстро пройдет. Вот несколько советов и советов, которые помогут вам на пути к овладению кубом.
- Просто делайте понемногу каждый день — если вы начинаете расстраиваться, оставьте это на некоторое время и вернитесь на следующий день. Некоторое время может помочь прояснить ситуацию.
- Повторение — это хорошо — первые несколько раз, когда вы повторяете алгоритм шага, вам, вероятно, придется следовать руководству. Но скоро вы начнёте это вспоминать и сможете делать это самостоятельно. Повторение укрепит мышечную память, поэтому вам больше не нужно сознательно думать о выполнении этого шага. Это освободит ценные ресурсы вашего разума, которые вы сможете посвятить работе над следующим шагом.
- Смешайте это — Соберите куб несколько раз, используя учебник в качестве справочного материала, затем сделайте несколько шагов, которые вы можете запомнить сами.
- Во время обучения вы будете много раз ошибаться и забивать кубик.
 Если это произойдет, не беспокойтесь, вы можете попытаться отменить свои ходы и попробовать еще раз. Часто вы не помните, какие ходы вы на самом деле сделали, и просто еще больше запутаетесь, пытаясь отменить их. Не беспокойтесь, просто начните снова. Это хорошая практика.
Если это произойдет, не беспокойтесь, вы можете попытаться отменить свои ходы и попробовать еще раз. Часто вы не помните, какие ходы вы на самом деле сделали, и просто еще больше запутаетесь, пытаясь отменить их. Не беспокойтесь, просто начните снова. Это хорошая практика. - Эксперимент — Алгоритмы для каждого шага сосредоточены на размещении определенных фигур. Они также будут перемещать другие фигуры по кубу. При изучении нового алгоритма найдите время, чтобы посмотреть на другие части вашего куба и на то, как они перемещаются. Это поможет вам лучше понять, как работает алгоритм, а также может привести к сокращению пути.
Сокращение времени
Начнем с того, что вам понадобится совсем немного времени, чтобы собрать кубик Рубика. С практикой это можно сделать менее чем за минуту. Вот несколько советов, которые помогут в этом:
- Делайте движения пальцами, а не скручивая запястья. Это позволит вам делать движения намного быстрее и соединять движения вместе в быстрой последовательности.

- Получите кубик скорости (см. ниже). Они позволяют вам крутить детали намного проще, чем стандартный кубик Рубика, и это также поможет сократить ваше время.
- Изучите зеркальные отражения алгоритмов. Большинство алгоритмов можно сделать в зеркальном отображении и часто это позволяет более эффективно разместить фигуру.
- Научитесь выполнять алгоритмы на лицах, отличных от того, которое обращено к вам. Это сократит время, затрачиваемое на переворачивание куба, чтобы получить правильную грань перед вами, и немного сократит ваше время.
- Практика, практика, практика. Это, безусловно, лучший способ стать лучше, и многие из вышеперечисленных советов начнут происходить естественным образом с практикой.
Какой куб мне взять?
Стандартный кубик Рубика может легко стать довольно жестким, и его будет трудно поворачивать. Это может нарушить ваш поток и заставить работать с алгоритмами гораздо больше концентрации. На рынке есть много кубов других брендов, многие из которых продаются как Speed Cubes . Бренд Rubiks также продает один из них. У них часто есть детали с закругленными краями, которые обеспечивают более плавное вращение деталей. Вы также можете получить хороший скоростной куб очень дешево. Мой совет, чтобы получить один из них для гораздо лучшего опыта. Я не буду перечислять какие-либо конкретные сайты, на которых их можно купить. Выполните поиск в Google, и вы найдете множество розничных продавцов, продающих их.
Бренд Rubiks также продает один из них. У них часто есть детали с закругленными краями, которые обеспечивают более плавное вращение деталей. Вы также можете получить хороший скоростной куб очень дешево. Мой совет, чтобы получить один из них для гораздо лучшего опыта. Я не буду перечислять какие-либо конкретные сайты, на которых их можно купить. Выполните поиск в Google, и вы найдете множество розничных продавцов, продающих их.
Концепция раскрашенного куба, хитрости и ярлыки — Hitbullseye
В этой статье мы изучим концепцию разрезания куба или разрезания нарисованного куба. При решении этих вопросов наиболее важной частью является визуализация куба. Нарезка кубиком – важная концепция, так как вопросы по этой теме часто задают на ряде конкурсных экзаменов.
Предлагаемое действие
БЕСПЛАТНЫЕ живые мастер-классы от нашего звездного факультета с более чем 20-летним опытом. Зарегистрируйтесь сейчас
Давайте сначала изучим некоторые основные термины, например, грань , вершина и ребро куба.
В кубе 6 граней, 8 вершин и 12 ребер. Вершина означает углы, а край означает сторону.
Как правило, вопросы из этой темы относятся к типу, в котором куб со стороной, измеряемой единицей измерения «x», окрашивается на всех гранях и разрезается на более мелкие кубики со стороной, измеряемой единицей измерения «y». Затем вам нужно найти количество кубиков, имеющих n окрашенных граней.
Первое, что вам нужно выяснить, это количество меньших кубиков. Для этого вы смотрите на одно конкретное ребро большого куба и выясняете, сколько меньших кубов может в него поместиться. Это будет х/у. Таким образом, количество меньших кубиков будет (x/y) 3 .
Так как все меньшие кубы будут иметь хотя бы одну грань, обращенную внутрь, т.е. не на поверхность исходного куба, следовательно, ни у одного из меньших кубов не будут закрашены все грани. Далее, поскольку максимальное количество граней большего куба, пересекающихся в одной точке, равно 3 (по углам), следовательно, меньшие кубы могут иметь максимум 3 окрашенные грани.
Итак, количество меньших кубов с 3 окрашенными гранями = Количество углов большего куба = 8 (всегда), при условии, что ни одна из граней большего куба не осталась неокрашенной.
Применим эту теорию к заданным вопросам.
Примеры вопросов по резке куба
Пример 1: Куб со стороной 6 см окрашен в красный цвет со всех граней, а затем разрезан на более мелкие кубики по 1 см каждый. Найдите общее количество меньших кубиков, полученных таким образом.
Решение:
Как объяснялось выше, количество меньших кубиков = (6/1) 3 = 216 меньших кубиков.
(Здесь x=6 и y=1)
Пример 2: В приведенном выше примере у скольких кубов будут окрашены три грани?
Решение: Как объяснялось выше, только угловые кубы, то есть 8 кубов в углах исходного куба, будут иметь три окрашенные грани. Следовательно, ответ будет только 8.
Чтобы найти количество меньших кубов, у которых окрашены только 2 грани, нужно рассмотреть кубы, где сходятся 2 грани большего куба, т. е. ребра. Помните, что сюда входят и кубики, находящиеся в углах, поэтому вам нужно удалить эти 2 кубика из числа кубиков на каждом ребре.
е. ребра. Помните, что сюда входят и кубики, находящиеся в углах, поэтому вам нужно удалить эти 2 кубика из числа кубиков на каждом ребре.
Пример 3: В приведенном выше примере у скольких кубов будут окрашены только две грани?
Решение: Как обсуждалось выше, только кубы на краю большего куба могут иметь две окрашенные грани.
Большой куб имеет ребро 6 см, а меньший куб имеет ребро 1 см. Значит, на каждом ребре по 6 кубиков. Однако вам нужно учитывать только 4 средних куба, так как 2 куба в каждом углу будут иметь 3 окрашенные грани.
Значит, на каждом ребре по 4 таких кубика. Так как ребер 12, то будет 4*12 = 48 кубиков
.
Пример 4: В приведенном выше примере у скольких кубов будет только одна грань и ни одна грань?
Решение: Как обсуждалось выше, только у кубов на грани большего куба может быть только одна окрашенная грань. Так как больший куб имеет ребро 6 см, а меньший куб имеет ребро 1 см, следовательно, если вы посмотрите на одну из граней большего куба, вы увидите 6 * 6 = 36 кубов. Из них исключите кубики, лежащие на ребрах, так как у них две или более граней окрашены. Таким образом, на каждой грани исходного куба будет 4 * 4 = 16 кубов с окрашенной только одной гранью.
Из них исключите кубики, лежащие на ребрах, так как у них две или более граней окрашены. Таким образом, на каждой грани исходного куба будет 4 * 4 = 16 кубов с окрашенной только одной гранью.
Поскольку таких граней 6, количество таких меньших кубиков будет 16*6 = 96.
Наконец, количество кубиков, не имеющих окрашенных граней, можно найти, вычитая сумму окрашенных кубиков из общего числа кубиков. кубики меньшего размера. Следовательно, искомый ответ 216 – (8 + 48 + 96) = 64 куба.
Пример 5: Куб с ребром по 12 см каждый. Он окрашен в красный цвет на двух противоположных гранях, в синий цвет на другой паре противоположных граней, в черный цвет на еще одну грань и одна грань остается неокрашенной. Затем его нарезают более мелкими кубиками по 1 см каждый. Ответьте на следующие вопросы:
- Количество меньших кубов, у которых окрашены три грани.
- Количество меньших кубиков, у которых окрашены две грани.
- Количество меньших кубиков, окрашенных с одной стороны.

- Количество меньших кубов с нулевой гранью.
Решение:
- Общее количество кубов = (12*12*12)/(1*1*1)=1728
- Для куба со всеми окрашенными сторонами у нас есть 8 кубов с 3 окрашенными сторонами. Но здесь у нас 1 сторона не окрашена. Следовательно, у нас будет всего 4 кубика с 3 окрашенными сторонами. Остальные 4 кубика будут окрашены только с двух сторон.
- На 2 стороны окрашены, ищем края.
У куба 12 ребер.
8 ребер, каждое ребро с 10 кубиками будет иметь 2 окрашенные стороны. (4 края неокрашенной стороны не учитываются).
Мы также включим эти 4 кубика (которые мы не учитывали при подсчете 3 цветных сторон, так как у них 2 окрашенные стороны)
Кубы на 4 гранях неокрашенной стороны куба будут иметь 1 окрашенную сторону (из-за неокрашенная сторона).
Следовательно, всего кубиков с 2 окрашенными сторонами = 8*10 + 4= 84 кубика. - Для 1 окрашенной стороны ищем грани куба.

Куб имеет 6 граней.
5 граней, каждая из которых имеет (12-2)*(12-2) = 100 кубов, будет окрашена с одной стороны.
Нам нужно включить те кубики на ребрах, которые связаны с неокрашенной гранью.
10 кубиков на каждом из этих ребер будут окрашены с одной стороны.
Таким образом, общее количество кубиков с окрашенной 1 стороной = 5*100 + 4*10 = 540 кубиков. - Согласно формуле, кубы без окрашенной стороны = (12-2) 3 = 1000.
Но мы должны включить кубики и с неокрашенной стороны. Это будет 10*10=100
Итак, общее количество неокрашенных кубиков= 1000+100=1100.
Формулы быстрого доступа
- Для куба со стороной n*n*n, окрашенного со всех сторон, который равномерно разрезан на более мелкие кубики размерностью 1*1*1,
- Количество кубиков с окрашенной стороной 0= (n-2) 3
- Количество кубиков с окрашенной 1 стороной =6(n — 2) 2
- Количество кубиков с 2 окрашенными сторонами = 12(n-2)
- Количество кубиков с 3 окрашенными сторонами = 8 (всегда)
- Для прямоугольного параллелепипеда размерности a*b*c, окрашенного со всех сторон и разрезанного на более мелкие кубики размерностью 1*1*1,
- Количество кубиков с окрашенной стороной 0 = (a-2) (b-2) (c-2)
- Количество кубиков с окрашенной 1 стороной =2[(a-2) (b-2) + (b-2)(c-2) + (a-2)(c-2) ]
- Количество кубиков с 2 окрашенными сторонами = 4(a+b+c -6)
- Количество кубиков с 3 окрашенными сторонами = 8
БЕСПЛАТНЫЕ электронные книги
Получите доступ к тщательно отобранным академическими экспертами электронным книгам для сдачи конкурсных экзаменов. Загрузить сейчас
Загрузить сейчас
Ключ Обучение:
Подводя итог, количество трехгранных закрашенных кубов можно найти с помощью вершин, двухгранных закрашенных с помощью ребер и одногранных закрашенных с помощью граней. Используя это обучение, мы можем даже решать сложные вопросы по резке куба, например, куба, окрашенного в разные цвета.
Страница не найдена – Национальный музей математики
Страница не найдена – Национальный музей математикиНе найдено
К сожалению, эта страница не найдена.
Возвращение домой
В эссе Карима Джабера о головоломке 15 экспозиция строится от конкретного к общему и мягко знакомит читателя с этой классической головоломкой, а также с более широкими методами решения проблем. К концу становится ясно, что эта головоломка на самом деле представляет собой тематическое исследование теории групп о перестановках. Судьи сочли, что работа Карима особенно подходит для студентов, серьезно интересующихся математикой.
Нажмите здесь, чтобы прочитать эссе.
В этой впечатляющей коллекции записанных на видео лекций о математике нейронных сетей, глубоком обучении и искусственном интеллекте Адам Дхалла придерживается старой школы, стоя перед доской и используя цветные маркеры, но модернизирует классический стиль, добавляя полезные временные метки. в описании видео. Судьи также восхищались его сценическим присутствием, чистым голосом и качеством производства видеороликов.
Нажмите здесь, чтобы посетить сайт Адама
Судьи были поражены энергией и чувством юмора в работе Гриффина Хона «Случайные прогулки»! Это видео понравится детям всех возрастов, и оно отлично передает волнение, важность и универсальность случайных блужданий. Тема случайных блужданий всплывает во многих разделах математики и имеет приложения в самых разных областях, от финансов до физики, и все это было интересно представлено в видео Гриффина.
Нажмите здесь, чтобы посмотреть видео.
В «Оригаметрии» Рин Фукуока использует оригами для построения правильных многоугольников, а также для разделения угла пополам. Судьи сочли видео очень свежим, игривым и минималистичным (ни слова не сказано, а написано лишь несколько). Уровень преподавания особенно искусный (например, обратите внимание на соответствующие паузы в рассуждении о трисекции после риторического вопроса «а почему?»). В этот момент и в других местах Рин демонстрирует большую чувствительность к аудитории.
Судьи сочли видео очень свежим, игривым и минималистичным (ни слова не сказано, а написано лишь несколько). Уровень преподавания особенно искусный (например, обратите внимание на соответствующие паузы в рассуждении о трисекции после риторического вопроса «а почему?»). В этот момент и в других местах Рин демонстрирует большую чувствительность к аудитории.
Нажмите здесь, чтобы посмотреть видео
Анджела Ву получила поощрительный приз за напряженный трейлер фильма об особых параллелограммах: прямоугольниках, ромбах и квадратах. Это забавное и хорошо отредактированное видео, которое будет иметь широкую популярность.
Нажмите здесь, чтобы посмотреть видео
Используя тени самолета в качестве примера, иллюстрированное эссе Раунака Банерджи предлагает долгожданное введение в анализ главных компонентов, метод уменьшения размерности в науке о данных, а затем расшифровывает жаргон, который часто затрудняет понимание этого статистического метода.
Щелкните здесь, чтобы прочитать его эссе.
В этом изящно кратком стихотворении Таис Эстрада-Нуньес начинает со слов «Одно семя плюс одно семя — два семечка», и вскоре мы взлетаем (да и расположение самого стихотворения выглядит так, будто оно летит на странице). Общий эффект стильный, с оттенками тонкости и глубины.
Нажмите здесь, чтобы прочитать стихотворение.
Сайт Аруши Джа «Вокруг Кенигсберга» посвящен комбинаторике и оживлен красочными оригинальными рисунками Аруши. Зрителей привлечет изложение на веб-сайте таких интересных тем, как семь мостов Кенигсберга (основная проблема в развитии теории графов), а также история и рассуждения о магических квадратах.
Щелкните здесь, чтобы посетить веб-сайт.
Стихотворение Уайета Ренвика интригующе двусмысленно и открыто для интерпретаций: некоторые судьи прочитали его как любовное стихотворение, которое подмигивает читателю с помощью математических понятий и языка, в то время как другие увидели в нем поэтическую анимацию человеческих отношений, рассматриваемых как график функции. В любом случае, благодаря этому математика и поэзия кажутся более доступными для учащихся, которых в противном случае эти предметы не привлекли бы.
В любом случае, благодаря этому математика и поэзия кажутся более доступными для учащихся, которых в противном случае эти предметы не привлекли бы.
Нажмите здесь, чтобы прочитать стихотворение.
В своем проекте Мадлен использует музыкальный инструмент, известный как маримба, чтобы продемонстрировать нечто глубокое в музыке: музыкальная гармония тесно связана с отношениями небольших целых чисел, открытие, которое Пифагор и его последователи, как говорят, сделали 2500 лет назад. Судьи были впечатлены ясностью и элегантностью объяснений и демонстраций Мадлен.
Нажмите здесь, чтобы посмотреть видео Мэдлин.
У Джибрана есть сайт в Instagram, @creative_math, где он знакомит старшеклассников с темами, которые обычно предназначены для студентов-математиков. Судьи восхищались привлекательностью его постов и тем, как умело он объясняет передовые математические идеи, всегда дружелюбным голосом.
Нажмите здесь, чтобы прочитать сообщения Джибрана.
Алисса написала статью, в которой объясняет оптимальную стратегию игры в крестики-нолики, а также исследует варианты игры на сетке 4×4 и в кубической решетке 3x3x3 в трех измерениях.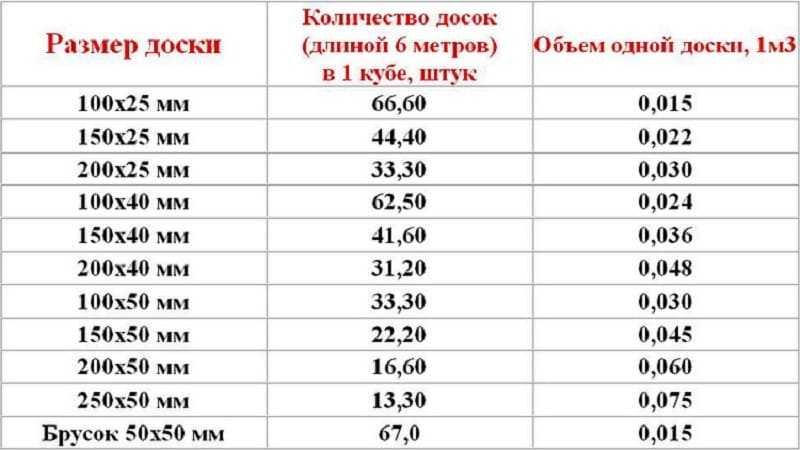 Судьи оценили ясность и оригинальность расследований Алисы.
Судьи оценили ясность и оригинальность расследований Алисы.
Нажмите здесь, чтобы прочитать статью Алиссы.
ПроектКоула представлял собой эссе о «несоответствии между тем, как математика обычно изображается, и тем, как она выполняется на самом деле». Учебники и статьи по математике обычно стараются выглядеть безупречно, но любой, кто занимается математикой, знает, насколько грязным и запутанным может быть то, что вы делаете на самом деле. Коул взял интервью у нескольких математиков об этом разрыве и выдвинул убедительный аргумент, что математическое общение будет более эффективным, если мы очеловечим его, показывая наши ошибки, а также наши идеи.
Щелкните здесь, чтобы прочитать эссе Коула
Для своего проекта Ян сконструировал песню из цифр иррационального числа, известного как золотое сечение (также известное как божественная пропорция из-за его красоты). Все судьи сочли проект интригующим как исследование и сочли саму песню удивительно красивой.
Нажмите здесь, чтобы послушать песню Яна.
Мадлен создала портрет математика Валери Томас. Судьи были впечатлены изобретательностью этого проекта: в нем используются только символы «3D» — искусно расположенные — для создания сильно вызывающего воспоминания портрета математика, известного своей работой над трехмерными спутниковыми изображениями.
Хелена написала «найденное стихотворение» — стихотворение, в котором каждое слово (кроме «вы» и «нас») взято из другого источника, в данном случае из статьи Эрика Вайсштейна MathWorld «Фундаментальные теоремы исчисления». Хелена переставила слова так, чтобы получилось что-то совершенно неожиданное, сдержанное маленькое стихотворение, от которого у судей перехватило дыхание.
Нажмите здесь, чтобы прочитать стихотворение Хелены.
Шрея и Эми объединились, чтобы воплотить в жизнь комбинаторную идентичность. Используя баскетбол в качестве математической площадки, они продемонстрировали два подхода к вычислению того, сколькими способами игрок может сделать или промахнуться 9 раз. н . Видео глупое и веселое: Эми пишет (и игриво болтает), пока Шрея стреляет, и, прежде чем вы это узнаете, они вычислили тождество для суммы биномиальных коэффициентов. Судьям понравилась простая, но умная видеосъемка, подшучивания между девушками и их аккуратные объяснения математики.
н . Видео глупое и веселое: Эми пишет (и игриво болтает), пока Шрея стреляет, и, прежде чем вы это узнаете, они вычислили тождество для суммы биномиальных коэффициентов. Судьям понравилась простая, но умная видеосъемка, подшучивания между девушками и их аккуратные объяснения математики.
Нажмите здесь, чтобы посмотреть видео
Заявка Джулии Шанан на соискание Строгацкой премии представляла собой стихотворение свободного стиха под названием «Человек-математик». Судьи были тронуты артистизмом и эмоциональной силой стихотворения, его глубиной и откровенной честностью, блестящим использованием языка и вниманием к неожиданным, но красноречивым деталям. «Математический человек» передает — одновременно красиво и навязчиво — изоляцию, которую Джулия чувствовала как одну из единственных девочек на Американском математическом конкурсе в 10-м классе, и, что более важно, интеллектуальную изоляцию, которую она все еще испытывает каждый день как человек, который все еще глубоко любит математику. не хватает друга, с которым можно было бы поделиться.
не хватает друга, с которым можно было бы поделиться.
Мама предлагает зайти в Panera, чтобы получить удовольствие от всех болезненных математических вычислений, которые я только что пережил.
Вот только это было не больно.
Я из тех, кто просидел медленную математику в средней школе, скучая и мечтая,
не видя, для чего все это было, желая — но никогда не напрягая дух, чтобы добиться большего.
Пока нет.
Теперь не хочу Panera.
Я не хочу, чтобы меня похлопывали по плечу и не понимали.
Я хочу вернуться в эту аудиторию, закончить экзамен и говорить об этом всю ночь.
Судьи сочли, что их собственных слов недостаточно, чтобы обобщить достижения Джулии в написании «Math Person». Скажем так, прочтите ее стихотворение и испытайте его на себе.
Нажмите здесь, чтобы прочитать стихи Джулии.
Апурва Панидапу — 16-летняя студентка-математик, художница и защитник интересов молодежи и гендерных меньшинств в STEAM. Она ведет блог под названием «Жемчужины STEM» и часто публикует эссе на Cantor’s Paradise, математическом сайте №1 на Medium.com. Она считает свой блог «местом, где можно узнать математические темы в доступной и беззаботной форме. Я предполагаю не более чем базовые математические знания и добавляю забавные факты для учащихся всех уровней опыта. Как для себя, так и для читателей, я вплетаю поп-культуру, пикапы и невероятные истории, чтобы познакомить людей с фантастическим миром математики и показать им, что любой может получать удовольствие от чего угодно».
Она ведет блог под названием «Жемчужины STEM» и часто публикует эссе на Cantor’s Paradise, математическом сайте №1 на Medium.com. Она считает свой блог «местом, где можно узнать математические темы в доступной и беззаботной форме. Я предполагаю не более чем базовые математические знания и добавляю забавные факты для учащихся всех уровней опыта. Как для себя, так и для читателей, я вплетаю поп-культуру, пикапы и невероятные истории, чтобы познакомить людей с фантастическим миром математики и показать им, что любой может получать удовольствие от чего угодно».
Судьи были очень впечатлены радостными, элегантно написанными сообщениями в блоге Апурвы по широкому кругу математических тем, от парадокса лжеца и разбиений до тесселяций и фракталов. Сочетая четкие объяснения с привлекательным макетом и хорошо подобранной графикой, Gems in STEM сама по себе является жемчужиной. Жюри понравилось разнообразие постов в блоге Апурвы. Они затрагивают историю, этимологию и головоломки, а также устанавливают связь со всем, от искусства и архитектуры до науки и природы. Воодушевляющее послание Апурвы состоит в том, что математика есть везде и доступна любому человеку с любым образованием.
Воодушевляющее послание Апурвы состоит в том, что математика есть везде и доступна любому человеку с любым образованием.
Нажмите здесь, чтобы прочитать сообщения Апурвы.
Анимационное видео
Ширли наполнено шутками и отсылками к поп-культуре, рассчитанными на более молодую аудиторию (хотя зрителям, состоящим из судей постарше, оно тоже очень понравилось). Ее цель, как она говорит в своем эссе, состоит в том, чтобы демистифицировать «математику с помощью юмора, забавных анимаций и реальных сценариев». В своем видео Ширли иллюстрирует технику комбинаторики, известную как «Палки и камни» (или «Звезды и бруски»), рассказывая историю о дилемме дедушки Боба: три его внучки. Благодаря отличной педагогике (в том числе попаданию в заманчивую математическую ловушку и последующему показу, как из нее выбраться) видео показывает зрителю, как посчитать все способы, которыми дедушка Боб может решить свою задачу. Видео веселое и динамичное, но уделяет нужное количество времени более сложным идеям и разбавляет их красочной графикой и выбором слов.
Нажмите здесь, чтобы посмотреть видео Ширли
ВидеоКэтрин было вдохновлено ее попытками понять, почему пустое множество является подмножеством каждого множества. Как она написала в своем эссе для этого конкурса: «Я никогда не принимала и не запоминала математическое понятие, если оно не имело для меня полного смысла, поэтому я решила выйти за рамки простых чисел и провести аналогию. Я понял, что наборы на моей странице могут быть связаны с моими занятиями в школе. Как элементами математического множества являются числа, так элементами класса являются ученики. Когда некоторые из них отсутствуют, существует только «подмножество» класса. И когда все отсутствуют, подмножество класса все еще существует, поскольку технически период класса все еще происходит. Эту аналогию я не хотел держать при себе, и поэтому она стала основой моего участия в конкурсе на Строгацкую премию!»
Судьи оценили ясные объяснения Кэтрин и сопроводительные иллюстрации. Теорию множеств часто считают одной из самых абстрактных частей математики, но в руках Кэтрин она становится осязаемой и яркой.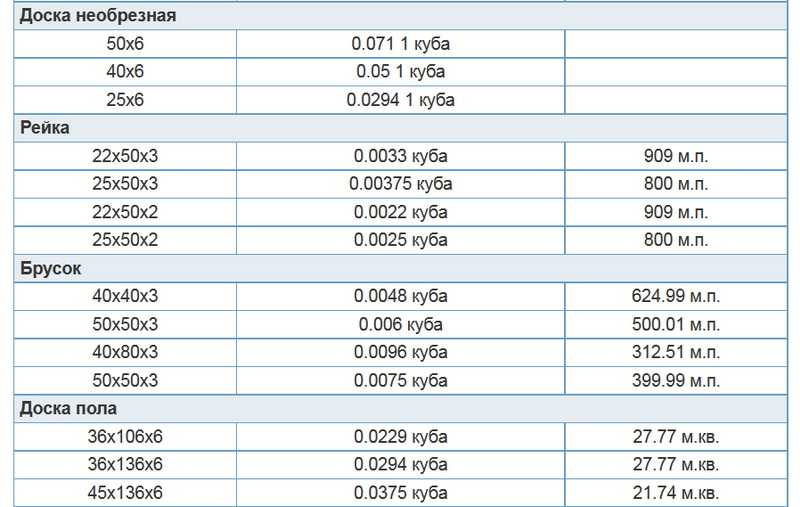 Ее аналогия с классной комнатой должна понравиться любому ученику. Кроме того, Кэтрин дает зрителю представление об универсальности теории множеств и о вкусе ее приложений в компьютерных науках.
Ее аналогия с классной комнатой должна понравиться любому ученику. Кроме того, Кэтрин дает зрителю представление об универсальности теории множеств и о вкусе ее приложений в компьютерных науках.
Нажмите здесь, чтобы посмотреть видео Кэтрин
В этом видео об известной теореме в теории графов и топологии Смаян красиво объясняет, почему любую плоскую карту можно раскрасить всего четырьмя цветами, так что соседние страны всегда будут разными цветами. Видео нежное и ясное, оживленное обильной графикой, аккуратно синхронизированной с повествованием Смаяна. Он дает зрителю полезную интуицию о том, как можно использовать неравенства (для вершин, ребер и граней плоских графов), чтобы сократить, казалось бы, бесконечную проблему до конечного числа случаев, которые затем могут быть проверены компьютером. Судьи сочли, что это была очень четкая презентация глубокого результата по продвинутой математике, объясненная таким образом, что каждый может понять и получить удовольствие.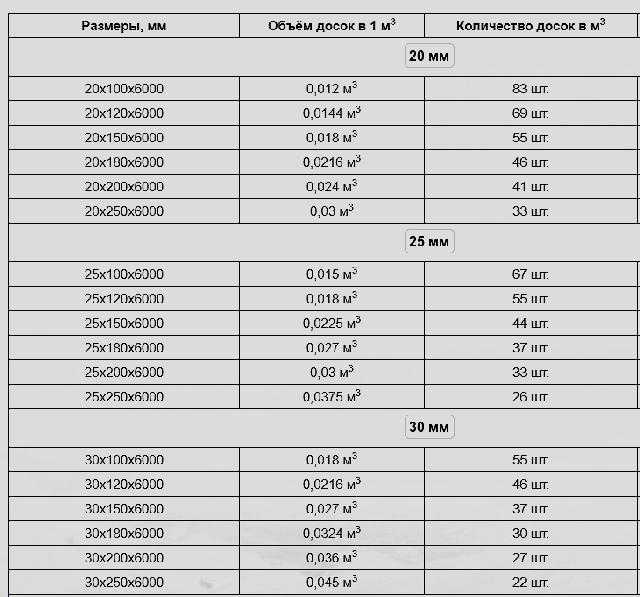
Нажмите здесь, чтобы посмотреть видео Смаяна
Джазовый саксофонист и математик Маркус Дж. Миллер поделится своими размышлениями о том, как математика и музыка могут сделать нас цельными.
Маркус Г. Миллер — музыкант и математик, живущий в Нью-Йорке.
Джон Уршель, нынешний кандидат математических наук в Массачусетском технологическом институте и бывший профессионал НФЛ, делится своей любимой логической головоломкой.
Джон Уршель играл в профессиональный футбол за Baltimore Ravens с 2014 по 2017 год, прежде чем уйти на пенсию, чтобы сосредоточиться на своей карьере в области математики. В настоящее время он является кандидатом наук в Массачусетском технологическом институте, где изучает теорию спектральных графов, числовую линейную алгебру и машинное обучение.
Приготовьтесь принять участие в сумасшедшей и забавной головоломке Kahoot со Стивом Шерманом. Это викторина, которая пощекочет ваши мозговые струны и бросит вызов вашим мыслительным способностям. Некоторые головоломки будут легкими, а другие заставят вас задуматься. Есть ли у вас что требуется, чтобы стать нашим чемпионом по головоломкам?
Некоторые головоломки будут легкими, а другие заставят вас задуматься. Есть ли у вас что требуется, чтобы стать нашим чемпионом по головоломкам?
Необходимые материалы:
- Смартфон, планшет или персональный компьютер с доступом в Интернет
Стив Шерман — директор по воображению и исполнительный мечтатель компании Living Maths.
Во время посещения MoMath покойный великий Джон Хортон Конвей произвел впечатление на людей, мгновенно указав им день недели, на который приходится или будет приходиться та или иная дата. И вы тоже можете это сделать! На какое число недели в следующем году выпадет твой день рождения? Или твой юбилей? Или любимый праздник? Когда следующая пятница 13-е? В какой день недели вы родились? Настройтесь на презентацию мастера головоломок MoMath Питера Винклера о чудесном «правиле Судного дня». Это легко и весело, и немного потренировавшись, вы сможете повторить подвиг Конвея. Это отличный трюк, и он продуман так, чтобы вы могли запомнить его и использовать, когда это необходимо.
Необходимые материалы:
- Бумага
- Карандаш
Питер Винклер в настоящее время является заслуженным председателем MoMath по общественному распространению математики и профессором математики и компьютерных наук в Дартмутском колледже.
Присоединяйтесь к Карлу Шафферу, пока мы играем с несколькими удивительными способами движения конечностями по кругу. Применяйте эти действия для создания последовательностей движений с идеальной математической опорой — обычным листом бумаги. Затем узнайте, как это связано с любопытной алгеброй кватернионов!
Необходимые материалы:
- Несколько листов бумаги для принтера размером 8,5″ на 11″
- Зона размером 5 на 5 футов для перемещения (предпочтительна зона без коврового покрытия)
Карл Шаффер — танцор, хореограф, математик и профессор математики в колледже Де Анза.
Какое отношение текучесть топологии и узлов может иметь к жесткости операций над дробями? Присоединяйтесь к Алексу Конторовичу, чтобы узнать об увлекательной связи, открытой покойным математиком Джоном Конвеем.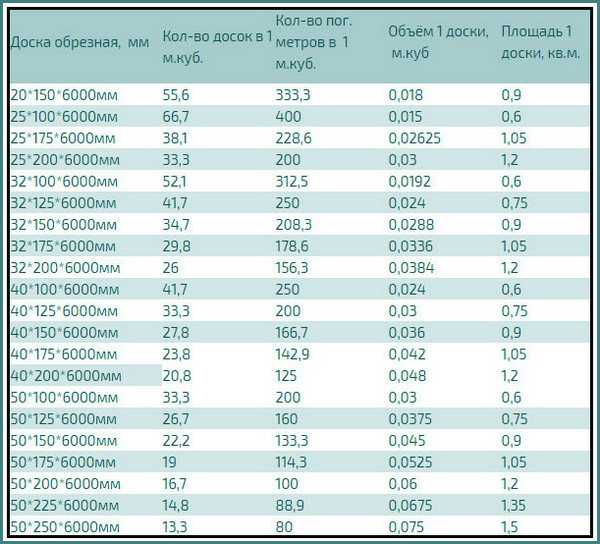
Необходимые материалы:
- 2 шнура разных цветов (можно также использовать провода или шнурки)
- Поверхность для укладки струн (например, пол или стол)
- Дополнительные материалы: бумага и карандаш
Алекс Конторович — декан академического содержания MoMath и профессор математики в Rutgers.
Эксперт по оригами Венди Зейхнер научит делать одну или две модели оригами, которые будут складываться из обычной бумаги для принтера. В каждой строчке есть математика!
Необходимые материалы:
- Несколько листов бумаги для принтера 8,5 x 11 дюймов
- Ручка или карандаш
- Ножницы
Венди Зейхнер — эксперт по оригами и президент OrigamiUSA.
Превратите два листа плотной бумаги и немного скотча в волчок и исследуйте его геометрию! Присоединяйтесь к Яне Моханти, доктору философии, математику и изобретателю Geometiles®, которая проведет вас через это увлекательное занятие по STEM. Вам будет предоставлен шаблон для печати и показано, как превратить его в свой спиннер. Как только вы освоите простую конструкцию, вы сможете украсить свой спиннер собственным дизайном.
Вам будет предоставлен шаблон для печати и показано, как превратить его в свой спиннер. Как только вы освоите простую конструкцию, вы сможете украсить свой спиннер собственным дизайном.
Необходимые материалы (метрические эквиваленты указаны в скобках) :
- 2 листа картонной бумаги размером 8,5 x 11 дюймов (размер A4), желательно двух цветов; манильские папки размером 8,5 x 11 дюймов также подойдут
- Ножницы
- Лента
- Дополнительно: этот проект также можно построить из мини-набора Geometiles® 2, который можно приобрести в Additions , интернет-магазине MoMath.
Яна Моханти — преподаватель математики, математик и создатель Geometiles®.
Если бы повторные подбрасывания монеты определяли, какой шаг вы предпримете, вы бы куда-нибудь попали? Шагните прямо (принесите свою монету) и узнайте!
Необходимые материалы:
- 1 монета
- Бумага
- Карандаш
Ральф Пантоцци — лауреат Премии Розенталя 2014 года и лауреат Президентской премии в области преподавания математики.
Давайте откроем для себя магию многогранной формулы Эйлера, создавая структуры из зубочисток и зефира.
Необходимые материалы:
- 1 коробка традиционных закругленных зубочисток с остриями на обоих концах
- 1 пакет мини-зефира
- Бумага
- Карандаш
Брюс Бэйли () — профессор математики в Аризонском университете и водитель автобуса, участвовавший в роуд-шоу Arizona Mathematics Road Show.
Присоединяйтесь к нам в онлайн-приключении по математике и бумаге! Годвин Моррис, директор образовательного центра Dazzling Discoveries STEM, продемонстрирует некоторые задачи по инженерному делу с бумагой. Вместе мы изучим пропорции, пропорции и масштабы, пока Годвин покажет вам, как создавать строения, мебель и персонажей из простых материалов.
Необходимые материалы:
- Бумага для принтера
- Лента
- Ножницы
Годвин Моррис — директор Образовательного центра Dazzling Discoveries STEM.
Доктор Артур Бенджамин поразит вас математической магией, а затем научит, как это делать. Принеси калькулятор!
Необходимые материалы:
- Калькулятор
Арт Бенджамин — отмеченный наградами популярный артист, математик и профессор математики в колледже Харви Мадда.
Возьмите с собой что-нибудь гибкое — галстук, шнурок, кусок веревки — и давайте повеселимся, изучая любопытную математику складывания.
Необходимые материалы:
- Гибкий предмет, например галстук, шнурок или веревка
Джеймс Тантон — всемирно известный педагог, популяризатор математики и математик.
Педагог и артист Джон Чейз покажет вам тесную связь между математикой и жонглированием. Математическое моделирование дало жонглерам множество новых моделей для жонглирования, и мы приглашаем вас посмотреть, на что способна математика. Принесите три предмета для жонглирования, чтобы присоединиться к веселью!
Необходимые материалы:
- 3 предмета для жонглирования
Джон Чейз — математический жонглер и преподаватель математики.
Манджул Бхаргава продемонстрирует интерактивный фокус, демонстрирующий, как можно создать удивительную сложность из чрезвычайной простоты. Зрителям предлагается участвовать из дома!
Необходимые материалы:
- 4 игральные карты
Манджул Бхаргава является первым заслуженным приглашенным профессором MoMath за общественное распространение математики, профессором математики в Принстонском университете и призером Филдса.
Приходите и насладитесь внеконкурсными исследованиями по математике.
Марк Сол — старший научный сотрудник Математического фестиваля Джулии Робинсон.
Синди Лоуренс, исполнительный директор MoMath, и Тим Ниссен, заместитель директора MoMath, приветствуют всех на пятом ежегодном нью-йоркском математическом фестивале, который включает часы математического веселья и развлечений. Присоединяйтесь к докладчикам со всего мира, чтобы разделить день оживленных и увлекательных мероприятий.
Джеймс Тэнтон, председатель Консультативного совета MoMath, открывает фестиваль, поделившись весьма интригующим «Международным математическим приветствием». Вы можете понять, как это работает?
Сайт фестиваля открывается в 13:30 по восточному поясному времени (Нью-Йорк). Войдите в любое время с 13:30 до 14:00, чтобы просмотреть любимую картинку MoMath прошлых лет. Мероприятия начинаются ровно в 14:00 по восточному поясному времени (Нью-Йорк).
Ознакомьтесь с нашей подборкой Geometiles® и найдите книги ведущих фестиваля Питера Винклера и Арта Бенджамина.
Специалист отдела розничной торговли MoMath всегда готов ответить на вопросы и дать квалифицированный совет по выбору всех ваших математических подарков.
Зайдите, чтобы посмотреть подборку кубиков Рубика, просмотреть восхитительные книги Кристофера Дэниелсона, Какой из них не принадлежит? и Сколько? и узнайте больше о фильме Человек, который познал бесконечность , в котором Манджул Бхаргава работал техническим консультантом, чтобы обеспечить точность математических расчетов, представленных в фильме.
Специалист по розничной торговле MoMath всегда готов ответить на вопросы и дать квалифицированный совет по выбору всех ваших математических подарков.
Ознакомьтесь с подборкой разноцветной бумаги для оригами MoMath, книгой Карла Шаффера Math Dance и другими замечательными предметами из Additions, интернет-магазина MoMath.
Специалист MoMath по розничной торговле всегда готов ответить на вопросы и дать квалифицированный совет по выбору всех ваших математических подарков.
Посмотрите, как Лорен Роуз собирает мозаику из кубика Рубика, и попытайтесь угадать, какой получится картинка. Математика встречается с искусством в этом творческом приложении популярного кубика Рубика.
Лорен Роуз — математик и профессор математики в Бард-колледже.
Дэниел Роуз-Левин продемонстрирует, как он собирает кубик Рубика ногами менее чем за 20 секунд.
Дэниел Роуз-Левин — бывший рекордсмен мира по сборке кубика Рубика с ногами.
Как невидимый мир пантомимы может исследовать математические идеи? Присоединяйтесь к Тиму Шартье, поскольку он использует пантомиму для исследования веса, величины силы и проективного движения с помощью искусства пантомимы. Вы также узнаете, как сделать бесконечную плитку шоколада. (Шоколадный батончик является настоящей опорой, но еда изображается пантомимой, поэтому удовольствие не содержит калорий.)
Тим Шартье — математический мим и профессор математики в колледже Дэвидсона. Он выступал по всему миру и прошел обучение в нескольких школах пантомимы, в том числе на мастер-классах у легендарного Марселя Марсо.
Симметрия вокруг нас. Мы видим симметрию в наших телах, автомобильных колесах, заборах, тканевых узорах, логотипе MoMath и многих других объектах! Мы узнаем о различных типах симметрии и весело проведем время, создавая симметричное искусство, используя обычные объекты.
Дэвид Рейманн — профессор математики и информатики колледжа Альбион, а также художник, использующий симметрию в своих работах.
Является ли лифт транспортным средством? Хот-дог — это бутерброд? Является ли сердце формой? Смайлик — это слово? Ответы на эти вопросы зависят от ваших определений транспортного средства, бутерброда, формы и слова. Точные определения являются важными инструментами математики, но немногие определения начинаются с такой точности, какой они потребуются позже. Поиграйте с границей между точностью и двусмысленностью в этой динамичной совместной сессии.
Кристофер Дэниэлсон () — отмеченный наградами писатель и преподаватель математики.
Присоединяйтесь к мистеру А., когда он поделится одним из своих многочисленных математических рэпов, расскажет, как он начал читать рэп о математике, и познакомит вас с некоторыми математическими идеями и ссылками в рэпе.
Майк Андрейковикс — учитель математики в средней школе из Лонг-Айленда, штат Нью-Йорк, который создает и исполняет рэп о математике на основе популярных хип-хоп треков.
Кристофер Дэниелсон — отмеченный наградами писатель и преподаватель математики.
Синди Лоуренс — исполнительный директор и генеральный директор Национального музея математики.
Тим Ниссен — заместитель директора Национального музея математики.
Стив Шерман — главный специалист по воображению и исполнительный мечтатель компании Living Maths.
Питер Винклер — почетный приглашенный профессор MoMath, занимающийся общественным распространением математики.
Карл Шаффер — танцор, хореограф, математик и профессор математики в колледже Де Анза.
Алекс Конторович — декан академического содержания MoMath и профессор математики в Rutgers.
Арт Бенджамин — отмеченный наградами популярный артист, математик и профессор математики в колледже Харви Мадда.
Брюс Бэйли — певец, скрипач и профессор математики Аризонского университета.
Дэниел Роуз-Левин — бывший рекордсмен мира по сборке кубика Рубика с ногами.
Дэвид Рейманн — профессор математики и информатики колледжа Альбион, а также художник, который использует симметрию в своих работах.
Годвин Моррис — директор Образовательного центра Dazzling Discoveries STEM.
Джеймс Тантон — всемирно известный педагог, популяризатор математики и математик-исследователь.
Джон Чейз — математический жонглер и преподаватель математики.
Лорен Роуз — танцовщица, хореограф, математик и профессор математики в колледже Де Анза.
Манджул Бхаргава — почетный приглашенный профессор MoMath за общественное распространение математики, профессор математики Принстонского университета и обладатель медали Филдса.
Марк Сол — исполнительный директор Математического фестиваля Джулии Робинсон.
Майк Андрейкович — учитель математики в старшей школе из Лонг-Айленда, штат Нью-Йорк, который создает и исполняет рэп о математике на основе популярных хип-хоп треков.
Эксперт по оригами Венди Зейхнер — исполнительный директор Origami USA.
Ральф Пантоцци — лауреат премии Розенталя 2014 года и преподаватель математики.
Яна Моханти — преподаватель математики, математик и создатель Geometiles®.
Кэролин Фигуэро — менеджер по розничной торговле Национального музея математики.
Тим Шартье — математический пантомимист, профессор математики в колледже Дэвидсона.
Детали ТК
Livingston, NJ
«Цель Math Musings, журнала, который я начал в старшей школе, — писал Рохан Джа, — заключалась в том, чтобы показать, что математика повсюду, но часто мы не осознаем этого. Это лежит в основе музыки, которую мы играем, или в том, как природа использует ее для своей собственной оптимальной выгоды, или это может быть в причудливом карточном фокусе, или математика может помочь нам уменьшить повсеместно наблюдаемое раздражение от пробок в часы пик». Журнал разными способами пытается очеловечить и оживить математику: рассказывая анекдоты об известных математиках; бросая вызов однокурсникам с веселыми головоломками; или подтолкнув их к более глубоким идеям, таким как головоломка с кувшинками, которая приводит к понятию обратной рекурсии в финансах. С помощью четких иллюстраций и пошаговых инструкций по фокусам и другим действиям Рохан пытается сделать математику увлекательной для всех… и у нее это прекрасно получается.
Coronado, CA
Проект, представленный Kyna Airriess, представляет собой «журнал», основанный на цитате из A Mathematician’s Lament , полемического эссе учителя средней школы Пола Локхарта. «Нет ничего более мечтательного и поэтичного, столь радикального, подрывного и психоделического, как математика», — писал Локхарт. Чтение эссе Локхарта, по словам Кины, «поспособствовало моему собственному превращению из ярого ненавистника математики в честолюбивого математика; Я никогда не слышал, чтобы кто-то описывал математику, предмет бесчувственных вычислений, такими словами, как «поэтический» и «радикальный». Прошло много времени, прежде чем я начал замечать эти черты для себя, но сегодня я идентифицирую себя как математика. ботаник, и я хочу изучать математику в колледже».
В журнале каждое из запоминающихся прилагательных Локхарта — мечтательный, поэтический, подрывной и психоделический — проиллюстрировано и связано с математическими идеями с использованием символов, истории, цвета и образов. Судьи были впечатлены страстной энергией, переданной словами и дизайном журнала. Общий эффект достигает того, что задумала Кина: воплотить «то, что те из нас, кто любит математику, хотят, чтобы мир понял. Дело вовсе не в холодных расчетах — это поле, полное творчества и красоты, и оно так же пропитано человечностью, как и любое другое».
Судьи были впечатлены страстной энергией, переданной словами и дизайном журнала. Общий эффект достигает того, что задумала Кина: воплотить «то, что те из нас, кто любит математику, хотят, чтобы мир понял. Дело вовсе не в холодных расчетах — это поле, полное творчества и красоты, и оно так же пропитано человечностью, как и любое другое».
Нью-Йорк, штат Нью-Йорк
«Лимерики и поэзия — нетипичный способ передать информацию о математике, — признает Сара Тау, — но я думаю, что это делает их более привлекательными, чем заучивание функций наизусть. Кто не любит лимерик?» Поэтому Сара создала серию коротких рифмованных стихотворений, чтобы перечислить некоторые основные свойства линейных, квадратичных, тригонометрических, полиномиальных, рациональных и других типов функций, встречающихся в алгебре и предварительном исчислении, и проиллюстрировала страницы примерами.
Судей поразила игривость этой работы. Лимерики — это беззаботная форма поэзии, в которой творчество исходит из работы в рамках ограничений и восхитительного их преодоления — и почти то же самое можно сказать о математике! В самом деле, как писала Сара: «Я люблю математику и всегда пытаюсь решать задачи, но это был новый тип задач. Тот, который не нуждался ни в алгебре, ни в моделировании. Каждое стихотворение становилось проблемой, которую нужно было решить, поскольку я пытался подобрать слова, чтобы свойства каждого функционального типа аккуратно рифмовались». Стихи освещают отличительные свойства различных видов функций и привлекают читателей уникальным, творческим и запоминающимся способом передачи математических идей.
Тот, который не нуждался ни в алгебре, ни в моделировании. Каждое стихотворение становилось проблемой, которую нужно было решить, поскольку я пытался подобрать слова, чтобы свойства каждого функционального типа аккуратно рифмовались». Стихи освещают отличительные свойства различных видов функций и привлекают читателей уникальным, творческим и запоминающимся способом передачи математических идей.
Honolulu, HI
Проект Джона Йошиды представляет собой карандашно-бумажную инфографику по теории графов. Он говорит: «Я задумал эту идею, когда читал о том, как Артур Кейли использовал деревья для представления структур углеводородов с n атомами углерода и 2n+2 атомами водорода. Вся структура имитирует один из этих углеводородов, этан (n=2), и внутри каждого атома заключено уникальное применение теории графов. Я разделил страницу на две части, чтобы атомы водорода, связанные с левым углеродом, содержали головоломки и забавные приложения теории графов, а те, которые связаны с правым водородом, больше касались непосредственных приложений, очень похожих на левое и правое полушария нашего мозга». Например, Теорема о четырех цветах (забавное приложение теории графов к раскрашиванию карт и давний исследовательский вопрос) появляется слева, а правая сторона включает приложения графов к информатике (нейронные сети и остовные деревья) и электротехнике ( принципиальные схемы).
Например, Теорема о четырех цветах (забавное приложение теории графов к раскрашиванию карт и давний исследовательский вопрос) появляется слева, а правая сторона включает приложения графов к информатике (нейронные сети и остовные деревья) и электротехнике ( принципиальные схемы).
Судьи высоко оценили оригинальную концепцию дизайна этого графического изображения, которое подчеркивает универсальность и междисциплинарный дух теории графов. Слова и изображения сочетают в себе историю, математику, химию и психологию, а вопросы в небольших текстовых полях приглашают читателя провести собственное исследование.
Toronto, ON
«Мой математический коммуникационный проект, Infinity Universe , — пишет Ивонн Хонг, — представляет собой иллюстративное, но математическое описание мира, в котором мы живем. Каждый показанный неодушевленный объект представляет простую, но вездесущую концепцию математики: при ближайшем рассмотрении монохроматическое дерево — это фрактальное дерево Пифагора, галактика на заднем плане построена с использованием последовательности Фибоначчи, а планета и комета — это разные вариации дерева Пифагора. Аполлоновская прокладка. Infinity Universe продвигает универсальность математической коммуникации посредством абстракции объектов и явлений, с которыми знакомы люди во всем мире».
Аполлоновская прокладка. Infinity Universe продвигает универсальность математической коммуникации посредством абстракции объектов и явлений, с которыми знакомы люди во всем мире».
Тщательно выполненная с большим вниманием к деталям картина, представленная Ивонн, привлекла внимание судей своими яркими цветами и гипнотическими узорами. Более того, тема бесконечности пронизывает картину, как и всю математику. Но здесь предположение о бесконечности скорее волшебное и потустороннее, чем научное и буквальное, и поэтому может понравиться аудитории, обычно не привлекающей математику.
New York, NY
Зои Маркман создала наглядное доказательство «формулы суммы квадратов», искусно используя три деревянные трехмерные пирамиды, которые соединяются друг с другом. Каждая пирамида состояла всего из 1 2 + 2 2 + … + n 2 одинаковых деревянных кубиков; таким образом, его объем визуально представлял собой сумму квадратов всех целых чисел от 1 до n. Чтобы найти формулу для этой суммы квадратов, Зоя манипулировала и переставила три пирамиды, чтобы сформировать прямоугольную призму, объем которой затем можно было легко вычислить, чтобы получить желаемую формулу суммы квадратов.
Чтобы найти формулу для этой суммы квадратов, Зоя манипулировала и переставила три пирамиды, чтобы сформировать прямоугольную призму, объем которой затем можно было легко вычислить, чтобы получить желаемую формулу суммы квадратов.
Судьи согласились с Зои в том, что такого рода визуальные, практические манипуляции «обеспечивают более глубокое понимание математики, чем то, которое дает письменный проект. Поскольку вы можете наблюдать, держать и манипулировать пирамидами (даже лично), аудитория способна понять, почему формула работает, а не просто принимать ее за чистую монету и произвольно принимать ее за истину. Во-вторых, презентацию могли понять даже люди, не обладающие значительными математическими знаниями. Он изложил то, что выглядит пугающей проблемой, в легко усваиваемой форме». Зои даже проверила презентацию на друзьях, которые сказали, что им не нравится математика. Это хорошая практика в любой форме общения. В целом, этот проект скромный, но очень хорошо сделанный и производит очень приятное «Ага!» момент для многих зрителей; действительно, это заставило одного из судей понять «формулу суммы квадратов» совершенно по-новому!
Santa Monica, CA
Чтобы выразить универсальность математики, Катарина Ченг перевела ее на другой универсальный язык: танец. «Точно так же, как танец существует как часть многих культур по всему миру для выражения абстрактных идей и эмоций через движение, математика бросает вызов культурным линиям, чтобы выражать абстрактные идеи через структуры и формы на странице», — написала она в описании своего проекта. Ее видео «Dancing the Dihedral Group» стремилось с помощью танца «представить визуальные симметрии, в первую очередь квадратные», а с помощью слов «то, как они перевели в алгебру, в первую очередь группу D8».
«Точно так же, как танец существует как часть многих культур по всему миру для выражения абстрактных идей и эмоций через движение, математика бросает вызов культурным линиям, чтобы выражать абстрактные идеи через структуры и формы на странице», — написала она в описании своего проекта. Ее видео «Dancing the Dihedral Group» стремилось с помощью танца «представить визуальные симметрии, в первую очередь квадратные», а с помощью слов «то, как они перевели в алгебру, в первую очередь группу D8».
Судьи хвалят Катарину за элегантность ее общения в видео. Особенно примечательной была эстетика минимализма — в том, как снимается видео, в выборе одежды, фона и цветов — все это идеально сочетается с минималистичной эстетикой теории групп. Интеграция математической графики с танцевальными движениями также выполнена изящно. Хотя другие в прошлом признавали сходство между математикой и танцем, немногие передавали эту аналогию с таким изяществом исполнения. Танцы и музыка тоже были искусно минимальными. Общий эффект заключается в усилении центральной идеи красоты в простоте.
Общий эффект заключается в усилении центральной идеи красоты в простоте.
Centreville, VA
Хамза Альсамраи любит Instagram, а также любит математику. Но когда он заметил, что в Instagram существует очень мало математических страниц, он попытался изменить это, запустив @daily_math, страницу, посвященную интригующим проблемам и идеям об алгебре, геометрии, исчислении, теории чисел и других разделах математики. «С помощью высококачественных образовательных постов, — говорит он, — я надеялся создать сообщество в Instagram, основанное на общей страсти к математике».
Судьи были впечатлены творчеством Хамзы, выраженным в умелом использовании визуальных эффектов, истории и головоломок, представленных в привлекательной форме. Его объяснения математических понятий ясны и проницательны, и он очень интерактивен со своими подписчиками, даже приглашая их публиковать сообщения. Судьи также высоко оценивают его рост как создателя и коммуникатора. Его страница в Instagram превратилась из сосредоточения внимания на сложных интегралах в первые дни на решение более доступных задач сейчас, и визуальное представление развивалось в тандеме.

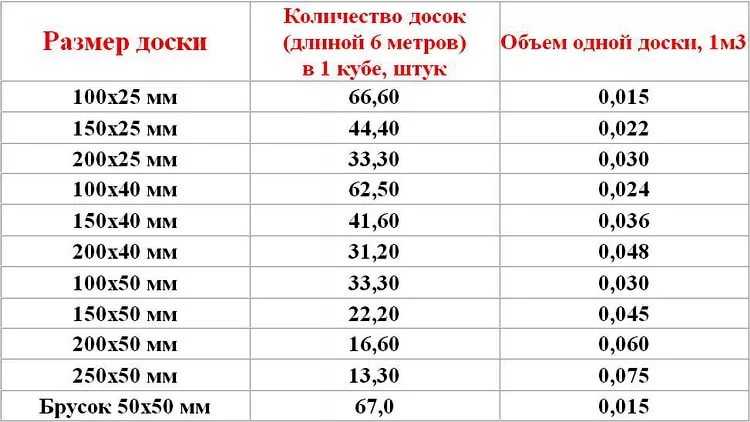




 Если это произойдет, не беспокойтесь, вы можете попытаться отменить свои ходы и попробовать еще раз. Часто вы не помните, какие ходы вы на самом деле сделали, и просто еще больше запутаетесь, пытаясь отменить их. Не беспокойтесь, просто начните снова. Это хорошая практика.
Если это произойдет, не беспокойтесь, вы можете попытаться отменить свои ходы и попробовать еще раз. Часто вы не помните, какие ходы вы на самом деле сделали, и просто еще больше запутаетесь, пытаясь отменить их. Не беспокойтесь, просто начните снова. Это хорошая практика.