Сколько в кубе будет 125? – Обзоры Вики
Поскольку кубический корень из 125 представляет собой целое число, 125 — это идеальный куб.
…
Кубический корень из 125 в радикальной форме: ∛125.
| 1. | Что такое кубический корень из 125? |
|---|---|
| 2. | Как вычислить кубический корень из 125? |
| 3. | Является ли кубический корень из 125 иррациональным? |
Итак, как вы работаете с кубиками? Чтобы найти куб коробки в кубических футах, сначала измерьте ее длину, ширину и высоту в дюймах. Далее умножьте все 3 цифры вместе, затем разделить результат на 1728, чтобы получить измерение куба вашего случая в кубических футах.
Дополнительно Какой куб равен 12? Список кубических чисел
| Число | Cubo,en | |
|---|---|---|
| 12 | 1728 | = 12 Х 12 Х 12 |
| 13 | 2197 | = 13 Х 13 Х 13 |
| 14 | 2744 | = 14 Х 14 Х 14 |
| 15 | 3375 | = 15 Х 15 Х 15 |
Что такое куб числа 81? Простая факторизация числа 81 равна 3 × 3 × 3 × 3, следовательно, кубический корень числа 81 в его низшей радикальной форме выражается как 3 ∛3 .
…
Кубический корень 81.
| 1. | Что такое кубический корень из 81? |
|---|---|
| 3. | Является ли кубический корень из 81 иррациональным? |
| 4. | Часто задаваемые вопросы о Cube Root of 81 |
Как вам кубический?
Чтобы рассчитать кубические дюймы, начните с измерения длины, ширины и глубины измеряемой коробки в дюймах. Потом, умножьте длину на ширину. Наконец, умножьте произведение длины и ширины на глубину коробки, чтобы найти объем в кубических дюймах.
Как найти площадь куба? 4 формулы для расчета кубических футов
Квадратные футы: Вы можете найти площадь или квадратные метры пространство путем умножения длины и ширины. Затем умножьте эту цифру на высоту, чтобы найти кубическое пространство или кубические метры внутри объекта.
Как вы работаете, если число является числом в кубе?
Числа куба
- Число куба — это число, умноженное на само себя 3 раза.
Это также можно назвать «числом в кубе». Символ куба — ³. - 2³ = 2 × 2 × 2 = 8.
- 3³ = 3 × 3 × 3 = 27.
- 4³ = 4 × 4 × 4 = 64.
- 5³ = 5 × 5 × 5 = 125.
- Числа в кубе до 100: 1, 8, 27, 64.
Это также можно назвать «числом в кубе». Символ куба — ³.Также Что такое куб от 1 до 20? От 1 до 20 числа 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 — четные кубические числа, а 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 — нечетные кубические числа.
Какие пять трехзначных кубических чисел?
Числа куба
- Первые пять кубических чисел: 1, 8, 27, 64 и 125.
- Каково число десятого кубика?
- Итак, 1000 — это десятое число куба.
Что такое куб числа 14? Кубы и кубические корни Список от 1 до 15
| Число | Куб (а 3 ) | Кубический корень ∛a |
|---|---|---|
| 12 | 1728 | 2.289 |
| 13 | 2197 | 2.351 |
| 14 | 2744 | 2. 410 |
| 15 | 3375 | 2.466 |
Что такое куб 27 года?
Поскольку кубический корень из 27 представляет собой целое число, 27 — это идеальный куб.
…
Кубический корень из 27 в радикальной форме: ∛27.
| 1. | Что такое кубический корень из 27? |
|---|---|
| 3. | Является ли кубический корень из 27 иррациональным? |
| 4. | Часто задаваемые вопросы о Cube Root of 27 |
Что такое куб 64 года?
Поскольку кубический корень из 64 представляет собой целое число, 64 — это идеальный куб.
…
Кубический корень из 64 в радикальной форме: ∛64.
| 1. | Что такое кубический корень из 64? |
|---|---|
| 3. | Является ли кубический корень из 64 иррациональным? |
| 4. | Часто задаваемые вопросы о Cube Root of 64 |
Что означает маленькая тройка в математике? В номер куба это число, умноженное само на себя 3 раза.
Это также можно назвать «числом в кубе». Символ куба — ³. 2³ = 2 × 2 × 2 = 8. 3³ = 3 × 3 × 3 = 27.
Сколько стоит кубический ярд? Кубический ярд — это объем куба с длиной, шириной и высотой в один ярд (3 фута или 36 дюймов). Один кубический ярд это равно 27 кубическим футам. Чтобы вы могли представить себе это, объем двух стиральных машин составляет чуть больше кубического ярда. Из-за их формы объем контейнера рассчитывается в кубических ярдах.
Насколько велика морозильная камера на 5 кубов?
【Размеры морозильного ларя】: отдельно стоящий морозильный ларь объемом 5.0 кубических футов, размеры: 23.2 × 29. 7 х 36.8 дюйма. Compact Frieza экономит пространство.
Насколько велика кубическая единица? В геометрии кубические единицы можно определить как единицы, используемые для измерения объема. Объем единичного куба, длина, ширина и высота которого равны 1 единице каждая. составляет 1 куб.
Сколько места в кубе?
Куб — это трехмерная фигура с квадратами на каждой из шести сторон.
3.
Какая единица объема? Объем — это мера трехмерного пространства, занятого материей или окруженного поверхностью, измеряемая в кубических единицах. СИ единица объема кубический метр (м3), которая является производной единицей. Литр (L) — это специальное название кубического дециметра (дм3).
Что такое кубы 1?
Кубики от 1 до 20
| Число | Куб (сущ. 3 ) |
|---|---|
| 1 | 1 |
| 2 | 8 |
| 3 | 27 |
| 4 | 64 |
Что такое куб _ 1? Так как кубический корень из 1 есть целое число , 1 — совершенный куб.
…
Кубический корень из 1 в радикальной форме: ∛1.
| 1. | Что такое кубический корень из 1? |
|---|---|
| 4. | Часто задаваемые вопросы о Cube Root of 1 |
Что такое куб от 1 до 10?
Числа в кубе от 1 до 100
| Число | Cubo,en |
|---|---|
| 8 | 512 |
| 9 | 729 |
| 10 | 1000 |
| 11 | 1331 |
• 4 июня 2020 г.
Объем и размеры резервуаров – как выбрать подходящую емкость
Наша компания является производителем резервуаров различных типов и назначения. Мы предлагаем емкости разной формы и объема, при этом на посвященных им страницах всегда указываем исчерпывающую информацию по характеристикам конкретной продукции, включая:
- объем в м3;
- форму – цилиндрическая, квадратная, прямоугольная;
- расположение – горизонтальное, вертикальное.
Тем не менее, мы достаточно часто получаем вопросы, связанные с габаритами наших изделий и их объемом. Поэтому рассмотрим данный вопрос более подробно.
Всем, кто прилежно изучал школьный курс физики, известно, что минимальной площадью поверхности при максимальном объеме обладает сосуд в форме шара. Но шарообразные емкости сложны в изготовлении и непрактичны, поэтому производители изготавливают емкости в форме цилиндра или куба (прямоугольника).
Цилиндрические емкости
Могут располагаться горизонтально или вертикально.
Пример: есть вертикальный цилиндрический резервуар диаметром 3 метра и высотой 5 метров. Рассчитываем объем: Радиус – 1,5 метра, в квадрате будет 2,25. Умножаем: 3,14159 ×2.25 ×5 (высота) = 35,34 м3. Итого, рабочий объем нашего резервуара будет равен 35 кубическим метрам, или 35 000 литрам (в 1 кубе – 1000 литров).
На практике конкретные размеры резервуара рассчитываются с учетом его функциональности. Например, горизонтальный резервуар диаметром 1 метр и длиной 10 метров будет просто неудобен в использовании. Его объем составит 7,8 куба. Если нам нужен резервуар такого объема, уместнее увеличить его диаметр и уменьшить длину – например, сделать диаметр 2 метра при длине 3 метра. Получим те же 7,8 куба при гораздо более функциональных размерах.
Прямоугольные емкости
Здесь все еще проще. Чтобы узнать полный объем, достаточно длину емкости умножить на ее ширину и высоту.
Например, кубический резервуар со стороной 1 метр будет вмещать 1 куб жидкости. Емкость размером 3000 мм × 2000 мм × 2500 мм будет иметь объем 15 кубометров.Почему большинство резервуаров имеют не квадратную или прямоугольную, а цилиндрическую форму? Потому что конструктивно такие емкости являются более прочными. Чтобы сварить куб, нужны 6 листов стали и 12 сварных швов. Цилиндрическая емкость имеет всего 3 поверхности: два круглых дна и цилиндрический корпус.
Корпус может быть сварен из одного листа металла, свернутого в цилиндр, для этого нужен всего 1 сварной шов. Плюс еще два круговых шва, чтобы приварить днища. Итого, в идеальном варианте всего 3 сварных шва – вместо 12 у куба.
Зачем тогда делают прямоугольные емкости? У них есть свои сферы использования. Например, их применяют в качестве пожарных емкостей – они обладают отличной эргономикой и хорошо вписываются в помещения, занимая минимум места.
В нашей компании вы можете заказать резервуар практически любого типа, формы и назначения.
Мы предлагаем как типовые варианты, так и изготавливаем продукцию на заказ. Зная основные принципы расчета размеров и объема резервуаров, вы можете оценить, какой вариант для вас окажется наиболее подходящим.
Преобразование 15 кубических дюймов в кубические футы
Насколько велики 15 кубических дюймов? Что такое 15 кубических дюймов в кубических футах? Преобразование 15 кубических дюймов в кубические футы.
От Баррели нефтиКубические сантиметрыКубические футыКубические дюймыКубические метрыКубические ярдыКубкиГаллоныИмперские галлоныИмперские пинтыЛитрыМиллилитрыУнцииПинтыКвартыСтоловые ложкиЧайные ложки
Бочки с масломКубические сантиметрыКубические футыКубические дюймыКубические метрыКубические ярдыКубкиГаллоныИмперские галлоныИмперские пинтыЛитрыМиллилитрыУнцииПинтыКвартыСтоловые ложкиЧайные ложки
поменять местами ↺
Сумма
15 кубических дюймов =
0,0086805556 Кубические футы
(округлено до 8 цифр)
Отображать результат как NumberFraction (точное значение)
Кубический дюйм — единица объема.
Это размер куба со стороной 1 дюйм. Это примерно 1,1 столовые ложки или около 16,4 кубических сантиметра.
Кубический фут — единица объема. Это размер куба со стороной 1 фут. Это около 7,5 галлонов или около 28,3 литров.
Преобразование кубических дюймов в кубические футы
(некоторые результаты округлены)
| у.е. дюйм | куб. футов |
|---|---|
| 15.00 | 0,0086806 |
| 15,01 | 0,0086863 |
| 15,02 | 0,0086921 |
| 15,03 | 0,0086979 |
| 15,04 | 0,0087037 |
| 15,05 | 0,0087095 |
| 15,06 | 0,0087153 |
| 15,07 | 0,0087211 |
| 15,08 | 0,0087269 |
| 15,09 | 0,0087326 |
| 15,10 | 0,0087384 |
15. 11 | 0,0087442 |
| 15,12 | 0,00875 |
| 15,13 | 0,0087558 |
| 15,14 | 0,0087616 |
| 15,15 | 0,0087674 |
| 15,16 | 0,0087731 |
| 15,17 | 0,0087789 |
| 15,18 | 0,0087847 |
| 15,19 | 0,0087905 |
| 15,20 | 0,0087963 |
| 15,21 | 0,0088021 |
| 15,22 | 0,0088079 |
| 15.23 | 0,0088137 |
| 15,24 | 0,0088194 |
| у.е. дюйм | куб. футов |
|---|---|
| 15,25 | 0,0088252 |
| 15,26 | 0,0088310 |
| 15,27 | 0,0088368 |
| 15,28 | 0,0088426 |
| 15,29 | 0,0088484 |
15. 30 | 0,0088542 |
| 15,31 | 0,0088600 |
| 15,32 | 0,0088657 |
| 15,33 | 0,0088715 |
| 15,34 | 0,0088773 |
| 15,35 | 0,0088831 |
| 15,36 | 0,0088889 |
| 15,37 | 0,0088947 |
| 15,38 | 0,0089005 |
| 15,39 | 0,0089063 |
| 15,40 | 0,0089120 |
| 15,41 | 0,0089178 |
| 15,42 | 0,0089236 |
| 15,43 | 0,0089294 |
| 15,44 | 0,0089352 |
| 15,45 | 0,0089410 |
| 15,46 | 0,0089468 |
| 15,47 | 0,0089525 |
| 15,48 | 0,0089583 |
| 15,49 | 0,0089641 |
у.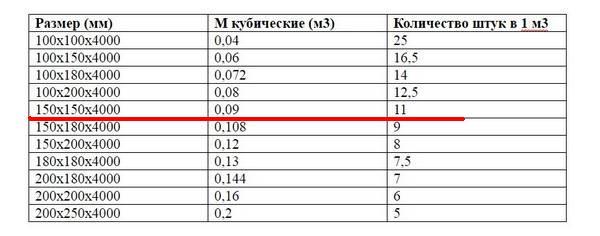 е. дюйм | куб. футов | |
|---|---|---|
| 15,50 | 0,0089699 | |
| 15,51 | 0,0089757 | |
| 15,52 | 0,0089815 | |
| 15,53 | 0,0089873 | |
| 15,54 | 0,0089931 | |
| 15,55 | 0,0089988 | |
| 15,56 | 0,00 | |
| 15,57 | 0,00 | |
| 15,58 | 0,00 | |
| 15,59 | 0,00 | |
| 15,60 | 0,00 | |
| 15,61 | 0,00 | |
| 15,62 | 0,00 | |
| 15,63 | 0,00 | |
| 15,64 | 0,00 | |
| 15,65 | 0,00 | |
| 15,66 | 0,00 | |
| 15,67 | 0,00 | |
| 15,68 | 0,00 | |
| 15,69 | 0,00 | |
| 15,70 | 0,00 | |
| 15,71 | 0,00 | |
| 15,72 | 0,0090972 | |
| 15,73 | 0,0091030 | |
| 15,74 | 0,0091088 |
у. е. дюйм | куб. футов |
|---|---|
| 15,75 | 0,0091146 |
| 15,76 | 0,0091204 |
| 15,77 | 0,0091262 |
| 15,78 | 0,0091319 |
| 15,79 | 0,0091377 |
| 15,80 | 0,0091435 |
| 15,81 | 0,0091493 |
| 15,82 | 0,0091551 |
| 15,83 | 0,0091609 |
| 15,84 | 0,0091667 |
| 15,85 | 0,0091725 |
| 15,86 | 0,0091782 |
| 15,87 | 0,0091840 |
| 15,88 | 0,0091898 |
| 15,89 | 0,0091956 |
| 15,90 | 0,0092014 |
| 15,91 | 0,0092072 |
| 15,92 | 0,0092130 |
| 15,93 | 0,0092188 |
| 15,94 | 0,0092245 |
| 15,95 | 0,0092303 |
| 15,96 | 0,0092361 |
| 15,97 | 0,0092419 |
| 15,98 | 0,0092477 |
| 15,99 | 0. |
Кубический корень из 15 — Как найти кубический корень из 15? [Решено]
Значение кубического корня из 15, округленное до 7 знаков после запятой, равно 2,4662121. Это действительное решение уравнения x 3 = 15. Кубический корень из 15 выражается как ∛15 в радикальной форме и как (15) ⅓ или (15) 0,33 в экспоненциальной форме. Разложение числа 15 на простые множители равно 3 × 5, следовательно, кубический корень из 15 в его низшей радикальной форме выражается как ∛15.
- Кубический корень из 15: 2,466212074
- Кубический корень из 15 в экспоненциальной форме: (15) ⅓
- Кубический корень из 15 в радикальной форме: ∛15
| 1. | Что такое кубический корень из 15? |
2. | Как вычислить кубический корень из 15? |
| 3. | Является ли кубический корень из 15 иррациональным? |
| 4. | Часто задаваемые вопросы о кубическом корне из 15 |
Что такое кубический корень из 15?
Кубический корень из 15 — это число, которое при трехкратном умножении само на себя дает произведение 15. Так как 15 можно выразить как 3 × 5. Следовательно, кубический корень из 15 = ∛(3 × 5) = 2,4662.
☛ Проверить: Калькулятор кубического корня
Как вычислить значение кубического корня из 15?
Кубический корень из 15 по методу Галлея
Его формула: ∛a ≈ x ((x 3 + 2a)/(2x 3 + a))
где,
a = число, кубический корень которого вычисляется
x = целочисленное предположение его кубического корня.
Здесь а = 15
Примем x как 2
[∵ 2 3 = 8 и 8 — ближайший совершенный куб, меньший 15]
⇒ х = 2
Следовательно,
∛15 = 2 (2 3 + 2 × 15)/(2 × 2 3 + 15)) = 2,45
⇒ ∛15 ≈ 2,45
Таким образом, кубический корень из 15 приблизительно равен 2,45.
Является ли кубический корень из 15 иррациональным?
Да, потому что ∛15 = ∛(3 × 5) и его нельзя выразить в виде p/q, где q ≠ 0. Следовательно, значение кубического корня из 15 является иррациональным числом.
☛ Также проверьте:
- Кубический корень из 45
- Кубический корень из 162
- Кубический корень из 529
- Кубический корень из 72
- Кубический корень из 16
- Кубический корень из 125
- Кубический корень из 53
Кубический корень из 15 решенных примеров
Пример 1. Найдите действительный корень уравнения x 3 − 15 = 0.
Решение:
x 3 − 15 = 0, т. е. x 3 = 15
Решение для x дает нам
x = ∛15, x = ∛15 × (-1 + √3i))/2 и x = ∛15 × (-1 — √3i))/2
где я называется мнимой единицей и равен √-1.
Игнорирование мнимых корней,
х = ∛15
Следовательно, действительный корень уравнения x 3 − 15 = 0 равен x = ∛15 = 2,4662.Пример 2: Объем сферического шара равен 15π в 3 . Каков радиус этого шара?
Решение:
Объем сферического шара = 15π в 3
= 4/3 × π × R 3
⇒ R 3 = 3/4 × 15
⇒ R = ∛(3/4 × 15) = ∛(3/4) × ∛15 = 0, × 2,46621 (∵ ∛(3/4) = 0, и ∛15 = 2,46621)
⇒ R = 2,2407 в 3Пример 3: Каково значение ∛15 ÷ ∛(-15)?
Решение:
Кубический корень из -15 равен минусу кубического корня из 15.
⇒ ∛-15 = -∛15Следовательно,
⇒ ∛15/∛(-15) = ∛15/(-∛15) = -1
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о кубическом корне из 15
Каково значение кубического корня из 15?
Мы можем выразить 15 как 3 × 5, т. е. ∛15 = ∛(3 × 5) = 2,46621. Следовательно, значение кубического корня из 15 равно 2,46621.
Чему равен куб кубического корня из 15?
Куб кубического корня из 15 — это само число 15, т.е. (∛15) 3 = (15 1/3 ) 3 = 15.
Почему значение кубического корня из 15 Иррациональный?
Значение кубического корня из 15 не может быть выражено в виде p/q, где q ≠ 0. Следовательно, число ∛15 иррационально.
Как упростить кубический корень из 15/216?
Мы знаем, что кубический корень из 15 равен 2,46621, а кубический корень из 216 равен 6. Следовательно, ∛(15/216) = (∛15)/(∛216) = 2,466/6 = 0,411.
Каково значение 15 плюс 11 кубический корень 15?
Значение ∛15 равно 2,466. Итак, 15 + 11 × ∛15 = 15 + 11 × 2,466 = 42,126000000000005.