Расчет крепежных резьбовых соединений
Расчет крепежных резьбовых соединений
Основным критерием работоспособности крепежных резьбовых соединений является прочность. Стандартные крепежные детали сконструированы равнопрочными по следующим параметрам: по напряжениям среза и смятия в резьбе, напряжениям растяжения в нарезанной части стержня и в месте перехода стержня в головку. Поэтому для стандартных крепежных деталей в качестве главного критерия работоспособности принята прочность стержня на растяжение, и по ней ведут расчет болтов, винтов и шпилек. Расчет резьбы на прочность выполняют в качестве проверочного лишь для нестандартных деталей.
Расчет резьбы. Как показали исследования, проведенные Н. Е. Жуковским, силы взаимодействия между витками винта и гайки распределены в значительной степени неравномерно, однако действительный характер распределения нагрузки по виткам зависит от многих факторов, трудно поддающихся учету (неточности изготовления, степени износа резьбы, материала и конструкции гайки и болта и т. д.). Поэтому при расчете резьбы условно считают, что все витки нагружены одинаково, а неточность в расчете компенсируют значением допускаемого напряжения.
д.). Поэтому при расчете резьбы условно считают, что все витки нагружены одинаково, а неточность в расчете компенсируют значением допускаемого напряжения.
Условие прочности резьбы на срез имеет вид
τср= Q/Acp < [τср]
где Q — осевая сила; Аср— площадь среза витков нарезки; для винта (см. рис. 3.1) Aср = πdlkHrдля гайки Аcp= πDkHr. Здесь Hr — высота гайки; к — коэффициент, учитывающий ширину основания витков резьбы: для метрической резьбы для винта к = 0,75, для гайки k = 0,88; для трапецеидальной и упорной резьб (см. рис. 3.3, 3.4) k= 0,65; для прямоугольной резьбы (см. рис. 3.5) к = 0,5. Если винт и гайка из одного материала, то на срез проверяют только винт, так как d1<D.
Условие прочности резьбы на смятие имеет вид
σСМ= Q/Acм <[ σСМ]
где Аcv— условная площадь смятия (проекция площади контакта резьбы винта и гайки на плоскость, перпендикулярную оси): Асм = πd2hz , где (см. рис. 3.1) πd2— длина одного витка по среднему диаметру; h — рабочая высота профиля резьбы; z = Hr /р — число витков резьбы в гайке высотой Hг; р — шаг резьбы (по стандарту рабочая высота профиля резьбы обозначена H1).
рис. 3.1) πd2— длина одного витка по среднему диаметру; h — рабочая высота профиля резьбы; z = Hr /р — число витков резьбы в гайке высотой Hг; р — шаг резьбы (по стандарту рабочая высота профиля резьбы обозначена H1).
Расчет незатянутых болтов. Характерный пример незатянутого резьбового соединения — крепление крюка грузоподъемного механизма (рис. 3.15). Под действием силы тяжести груза Q стержень крюка работает на растяжение, а опасным будет сечение, ослабленное нарезкой. Статическая прочность стержня с резьбой (которая испытывает объемное напряженное состояние) приблизительно на 10% выше, чем гладкого стержня без резьбы. Поэтому расчет стержня с резьбой условно ведут по расчетному диаметру dp=d-0,9р, где р — шаг резьбы с номинальным диаметром d (приближенно можно считать dp= d1).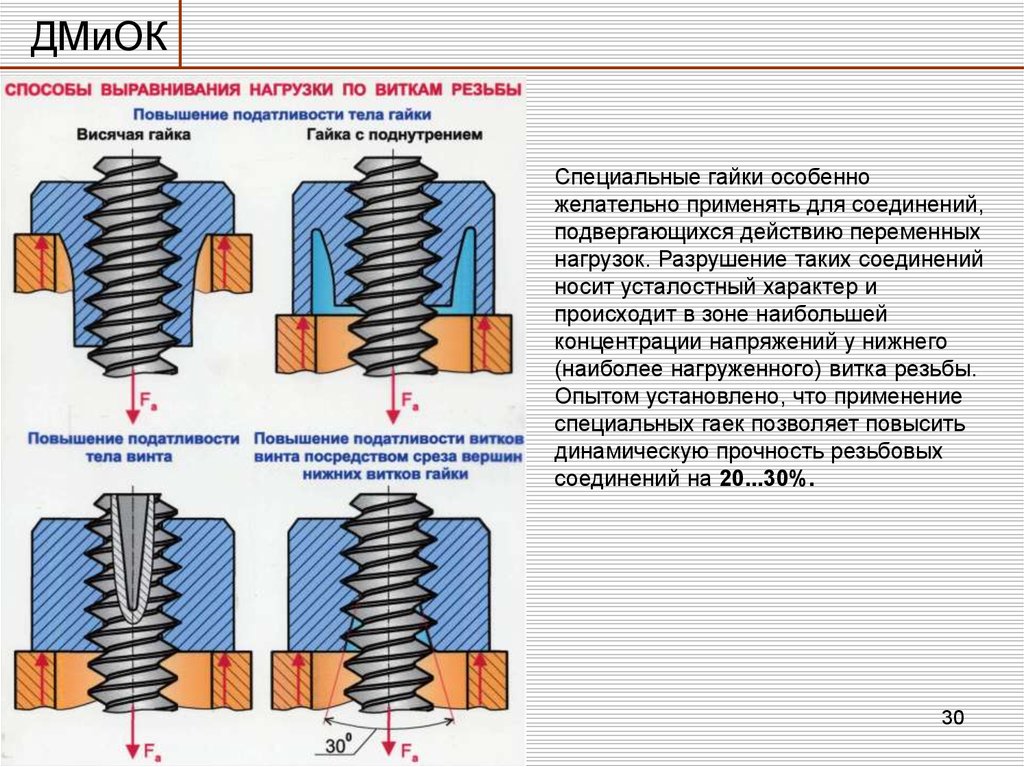 1/2
1/2
По найденному значению расчетного диаметра подбирается стандартная крепежная резьба.
Расчет затянутых болтов. Пример затянутого болтового соединения — крепление крышки люка с прокладкой, где для обеспечения герметичности необходимо создать силу затяжки Q (рис. 3.16). При этом стержень болта растягивается силой Q и скручивается моментом Мрв резьбе.
Напряжение растяжения σр = Q/(πdp2 /4) , максимальное напряжение кручения τк = Mp/Wp, где Wp= 0,2dp3 — момент сопротивления кручению сечения болта; Мр= 0,5 Q d2tg( ψ + φ’). Подставив в эти формулы средние значения угла подъема урезьбы, приведенного угла трения ф’ для метрической крепежной резьбы и применяя энергетическую теорию прочности, получим
σэкв=(σр2 + 3τк2)^1/2 = 1.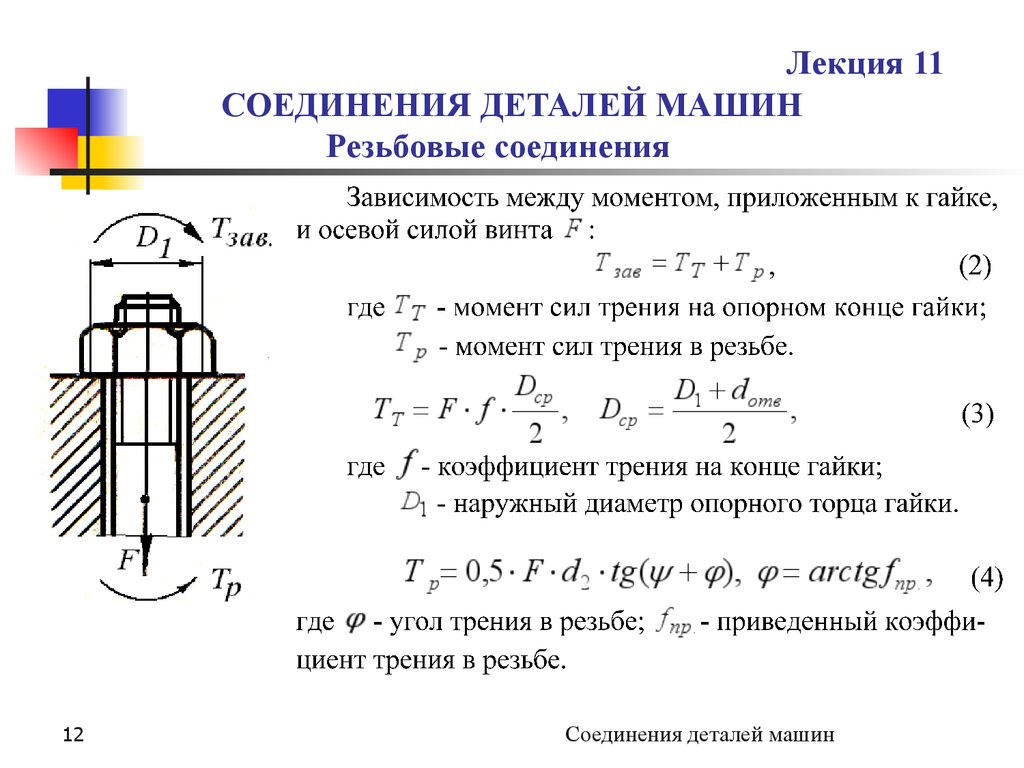 1/2
1/2
Здесь уместно отметить, что надежность затянутого болтового соединения в значительной степени зависит от качества монтажа, т. е. от контроля затяжки при заводской сборке, эксплуатации и ремонте. Затяжку контролируют либо путем измерения деформации болтов или специальных упругих шайб, либо с помощью динамометрических ключей.
Расчет затянутого болтового соединения, нагруженного внешней осевой силой.
Примером такого соединения может служить крепление z болтами крышки работающего под внутренним давлением резервуара (рис. 3.17). Для такого соединения необходимо обеспечить отсутствие зазора между крышкой и резервуаром при приложении нагрузки Rz, иначе говоря, обеспечить нераскрытие стыка. Введем следующие обозначения: Q — сила первоначальной затяжки болтового соединения; R — внешняя сила, приходящаяся на один болт; F — суммарная нагрузка на один болт (после приложения внешней силы R).
Очевидно, что при осуществлении первоначальной затяжки болтового соединения силой Q болт будет растянут, а соединяемые детали сжаты. После приложения внешней осевой силы R болт получит дополнительное удлинение, в результате чего затяжка соединения несколько уменьшится. Поэтому суммарная нагрузка на болт F < Q + R, а задача ее определения методами статики не решается.
После приложения внешней осевой силы R болт получит дополнительное удлинение, в результате чего затяжка соединения несколько уменьшится. Поэтому суммарная нагрузка на болт F < Q + R, а задача ее определения методами статики не решается.
Для удобства расчетов условились считать, что часть внешней нагрузки R воспринимается болтом, остальная часть — соединяемыми деталями, а сила затяжки остается первоначальной, тогда F = Q + xR, где х — коэффициент внешней нагрузки, показывающий, какая часть внешней нагрузки воспринимается болтом.
Так как до раскрытия стыка деформации болта и соединяемых деталей под действием силы R равны, то можно записать:
χ R λ6=(1-χ)R λд
λ6, λд — соответственно податливость (т. е. деформация под действием силы в 1 Н) болта и соединяемых деталей. Из последнего равенства получим
χ= λд (λд + λ6)
Отсюда видно, что с увеличением податливости соединяемых деталей при постоянной податливости болта коэффициент внешней нагрузки будет увеличиваться.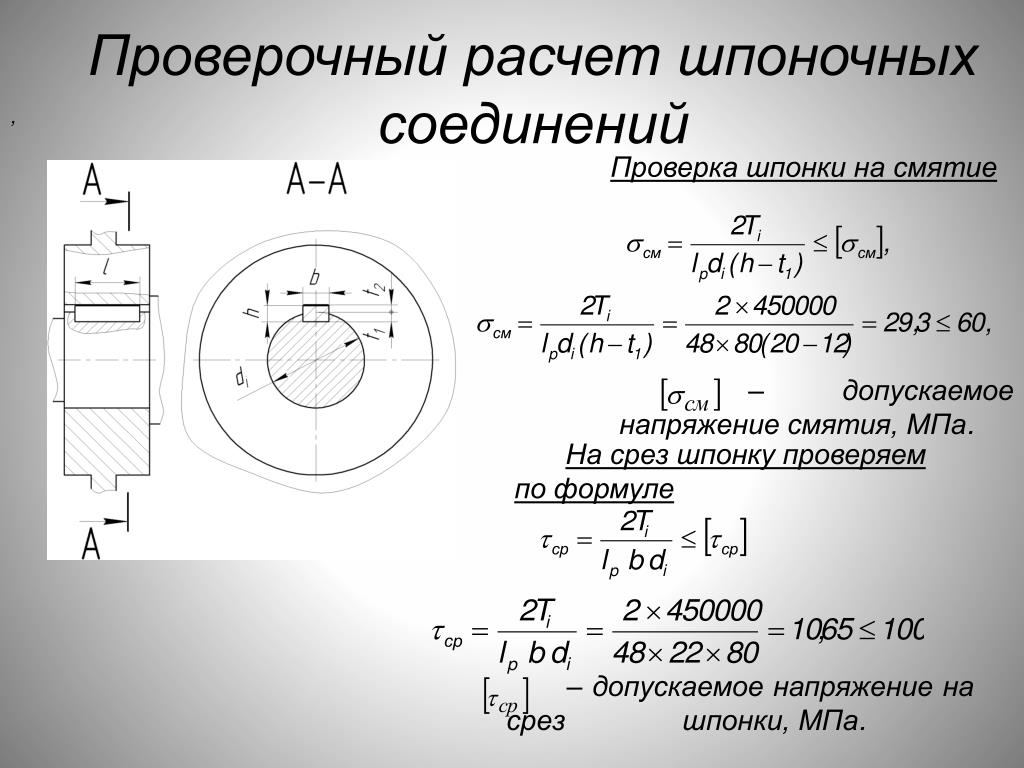 1/2
1/2
Расчеты деталей машин: Справ. пособие
Расчеты деталей машин: Справ. пособие
ОглавлениеПРЕДИСЛОВИЕРаздел I. СОЕДИНЕНИЯ ДЕТАЛЕЙ МАШИН Глава 1. ВАЛЬЦОВОЧНЫЕ СОЕДИНЕНИЯ 1.  1.3. Справочный материал 1.4. Примеры расчета Глава 2. СВАРНЫЕ, ПАЯНЫЕ И КЛЕЕВЫЕ СОЕДИНЕНИЯ 2.1. Общие сведения об основных видах сварных соединений и сварных швов 2.2. Расчет прочности сварных швов 2.3. Условное изображение сварных швов на чертежах 2.4. Паяные соединения 2.5. Клеевые соединения 2.6. Справочный материал 2.7. Примеры расчета Глава 3. РЕЗЬБОВЫЕ СОЕДИНЕНИЯ 3.2. Определение сил, действующих на один болт 3.3. Расчет болтового соединения плит и станин с фундаментом 3.4. Расчет стержня болта при постоянных нагрузках 3.5. Расчет стержня болта при переменных нагрузках 3.6. Расчет витков резьбы на прочность. Определение вращающего момента 3.7. Порядок расчета резьбовых соединений 3.9. Примеры расчета Глава 4. СОЕДИНЕНИЯ ВАЛ – СТУПИЦА (ШПОНОЧНЫЕ, ШЛИЦЕВЫЕ, С НАТЯГОМ) 4.2. Шлицевые соединения 4.3. Соединения с натягом 4.4. Справочный материал 4.5. Примеры расчета Раздел II.  МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ МЕХАНИЧЕСКИЕ ПЕРЕДАЧИГлава 5. КИНЕМАТИЧЕСКИЙ РАСЧЕТ ПРИВОДНЫХ УСТРОЙСТВ И ВЫБОР ЭЛЕКТРОДВИГАТЕЛЯ 5.2. Трехфазные асинхронные электродвигатели 5.3. Разбивка общего передаточного числа редуктора по ступеням 5.4. Справочный материал 5.5. Примеры расчета Глава 6. ФРИКЦИОННЫЕ ПЕРЕДАЧИ И ВАРИАТОРЫ 6.2. Кинематические расчеты фрикционных передач 6.3. Определение сил прижатия фрикционных тел и нагрузки на валы передачи 6.4. Расчет фрикционных тел на контактную прочность и КПД передач 6.5. Справочный материал 6.6. Примеры расчета Глава 7. РЕМЕННЫЕ ПЕРЕДАЧИ 7.2. Расчет клиноременных передач 7.3. Расчет передач поликлиновыми ремнями 7.4. Расчет зубчато-ременных передач 7.5. Справочный материал 7.6. Примеры расчета 8.2. Геометрический, кинематический и силовой расчеты цепных передач 8.3. Выбор основных параметров и расчет цепных передач 8.4. Справочный материал 8.5. Примеры расчета Глава 9.  ЗУБЧАТЫЕ ПЕРЕДАЧИ ЗУБЧАТЫЕ ПЕРЕДАЧИ9.2. Геометрия и кинематика эвольвентного цилиндрического зацепления 9.3. Зубчатые зацепления со смещением (корригированные) 9.4. Геометрия и кинематика конических передач 9.5. Материалы и допускаемые напряжения 9.6. Точность зубчатых передач 9.7. Коэффициент нагрузки 9.8. Расчет зубчатого зацепления на контактную прочность 9.9. Расчет зубьев колес на изгиб 9.10. Расчет открытых зубчатых передач 9.11. Проверка прочности зубьев колес при перегрузках 9.12. Определение размеров стальных зубчатых закрытых передач и проверка их прочности 9.13. Конструкции зубчатых колес 9.14. Справочный материал 9.15. Примеры расчета Глава 10. ПЛАНЕТАРНЫЕ ПЕРЕДАЧИ 10.2. Кинематический расчет 10.3. Условия собираемости соосных и многопоточных передач 10.4. Порядок подбора чисел зубьев при заданном передаточном отношении и числе сателлитов 10.5. Определение КПД планетарных передач 10.6. Определение сил, действующих в зацеплениях и в опорах осей и валов прямозубых передач 10.  7. Расчет зубьев планетарных передач на прочность 7. Расчет зубьев планетарных передач на прочность10.8. Конструкция и размеры деталей планетарных передач [14] 10.9. Смазочные системы планетарных редукторов 10.10. Порядок проектного расчета планетарного редуктора (схемы 1 и 2 табл. 10.1) 10.11. Порядок расчета планетарного мотор-редуктора (схема 1 табл. 10.1) 10.12. Справочный материал 10.13. Примеры расчета Глава 11. ВОЛНОВЫЕ ПЕРЕДАЧИ 11.3. Проектный расчет волновой зубчатой передачи 11.4. Конструкция и размеры основных деталей волновых передач 11.5. Порядок расчета волновой передачи с кулачковым генератором 11.6. Справочный материал 11.7. Пример расчета Глава 12. ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ 12.2 Геометрия и кинематика червячного зацепления 12.3. Червячные передачи со смещением (корригированные) 12.4. Материалы и допускаемые напряжения 12.5. Точность червячных передач 12.6. Коэффициент нагрузки 12.7. Расчет червячного зацепления на контактную прочность 12.  8. Расчет на изгиб 8. Расчет на изгиб12.9. Расчет открытых червячных передач 12.10. Проверка червячных редукторов на нагрев 12.11. Конструкция червяков и червячных колес 12.12. Справочный материал 12.13. Пример расчета Глава 13. ПЕРЕДАЧА ВИНТ – ГАЙКА 13.2. Кинематический и силовой расчеты 13.3. Передача винт—гайка с трением скольжения 13.4. Передача винт — гайка с трением качения 13.5. Справочный материал 13.6. Пример расчета Раздел III. ВАЛЫ, ИХ ОПОРЫ, МУФТЫ, ПРУЖИНЫ Глава 14. ВАЛЫ 14.2. Некоторые сведения по конструированию валов и выбору материалов 14.3. Расчет валов 14.4. Посадки основных деталей передач на валы по стандартам СЭВ 14.5. Справочный материал 14.6. Примеры расчета Глава 15. РАДИАЛЬНЫЕ ПОДШИПНИКИ СКОЛЬЖЕНИЯ 15.2. Упрощенный расчет подшипников скольжения 15.3. Расчет подшипников жидкостного трения 15.4. Сопротивление слоя масла вращению шипа 15.5. Тепловой расчет подшипника 15.6. Справочный материал 15. 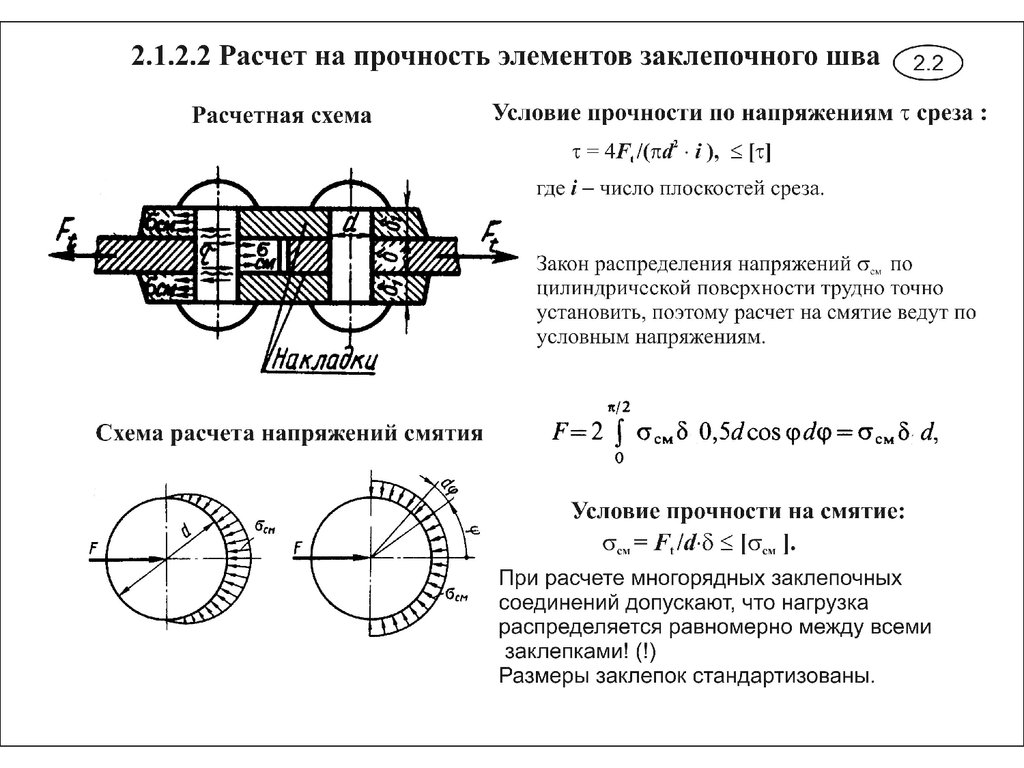 7. Примеры расчета 7. Примеры расчетаГлава 16. ПОДШИПНИКИ КАЧЕНИЯ 16.2. Условные обозначения и точность подшипников качения 16.4. Выбор подшипников качения по статической грузоподъемности 16.5. Справочный материал 16.6. Пример расчета Глава 17. МУФТЫ 17.2. Расчет муфт 17.3. Глухие муфты 17.4. Компенсирующие муфты 17.5. Управляемые (сцепные) муфты 17.6. Самоуправляемые муфты 17.7. Справочный материал 17.8. Примеры расчета Глава 18. ПРУЖИНЫ 18.2. Расчет винтовых пружин на прочность 18.3. Расчет винтовых пружин на жесткость 18.4. Подбор тарельчатых пружин 18.5. Справочный материал ЛИТЕРАТУРА |
Практический анализ прочности резьбы
Практический анализ прочности резьбы| Рекомендации по проектированию надежных винтовых соединений | ||||
| gif»> | ||||
| Шаг P, угол резьбы
60, средний диаметр d2=D2, большой диаметр наружной резьбы d, вспомогательный
диаметр внутренней резьбы d3, большой диаметр внутренней резьбы D, вспомогательный
диаметр внутренней резьбы D1, радиус впадины R, высота основной
треугольник Н. | ||||
| Критические зоны напряжения резьбовых соединений: | ||||
| Эффективная площадь поперечного сечения или площадь растяжения. | ||||
| Площадь среза наружной резьбы (винта, болта) | ||||
| Зона среза внутренней резьбы (гайка, резьбовое отверстие) | ||||
| ||||
| www.tribology-abc.com | ||||
Прочность резьбовых соединений
Прочность резьбовых соединений Неисправность крепежа на банке с продуктом
иметь потенциально катастрофические последствия. В попытке
гарантировать, что такие последствия не возникнут, строгие и обширные
тестирование продукта часто завершается. Однако во многих
приложений, обширные испытания не являются ни практичными, ни экономически выгодными. В таких случаях инженер обычно полагается на аналитические
анализ вместе с его опытом и суждениями, чтобы гарантировать
такого сбоя не происходит.
В таких случаях инженер обычно полагается на аналитические
анализ вместе с его опытом и суждениями, чтобы гарантировать
такого сбоя не происходит.
Выход из строя резьбового соединения в целом происходит в одном из трех режимов. Провал через хвостовик или резьбовая часть застежки, зачистка резьбы наружная резьба, или в-третьих, зачистка внутренней резьбы резьбовой член. Считая каждый по очереди:
Сбой через наружную резьбу или резьбу хвостовикБольшинство отказов крепежа происходит из-за перелома насквозь. мужская нить. При статических нагрузках прочность нити определяется площадью напряжения. Это основано на среднем малого и среднего диаметров резьбы. Инженерные справочники обычно имеют таблицы областей напряжений для различных размеров резьбы.

При затягивании болта хвостовик
выдерживает прямое напряжение из-за деформации растяжения вместе
с напряжением кручения из-за крутящего момента, действующего на резьбу.
Большинство таблиц моментов затяжки болтов не учитывают момент затяжки.
напряжение и предположить прямое напряжение в нитях некоторой пропорции
предел текучести болтов, обычно 75%. Для высокого трения
условиях величина напряжения кручения может быть такой
что в сочетании с прямым напряжением эквивалентное напряжение
может привести к чрезмерной урожайности, что приведет к неудаче. Более последовательный
подход заключается в определении величины прямого напряжения
что в сочетании с торсионным даст
эквивалентное напряжение некоторой доли выхода. Пропорция
обычно используется с этим подходом 90%.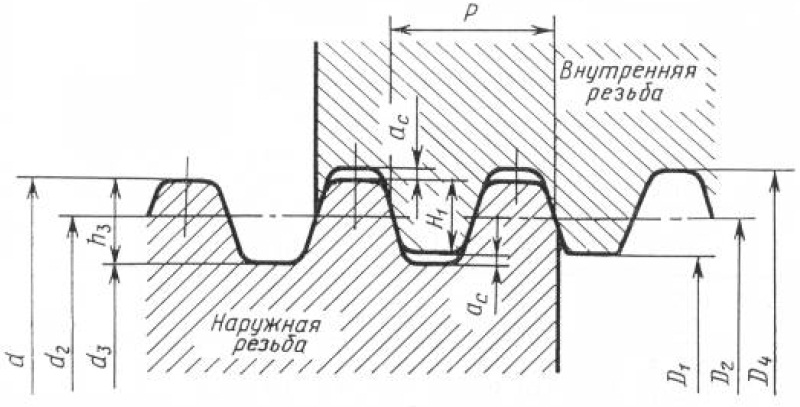 Компьютерная программа
TORQUE обеспечивает современное состояние
анализ момента затяжки резьбовых соединений.
Компьютерная программа
TORQUE обеспечивает современное состояние
анализ момента затяжки резьбовых соединений.
Высокопроизводительные болты часто разработан таким образом, что простой хвостовик меньше, чем напряжение диаметр резьбы. Это делается для того, чтобы растяжка, которая происходит под предварительным натягом, вызванным процессом затяжки максимально. С этим типом болта выход из строя при чрезмерной затяжке, произойдет в области плоского хвостовика, как показано на фотографии.
Снятие резьбы Обрыв резьбы может быть проблемой
во многих конструкциях, где требуются резьбовые отверстия в низкопрочных
материал. В общих чертах, зачистка внутренней резьбы
и наружной резьбы следует избегать, если надежная конструкция
должно быть достигнуто.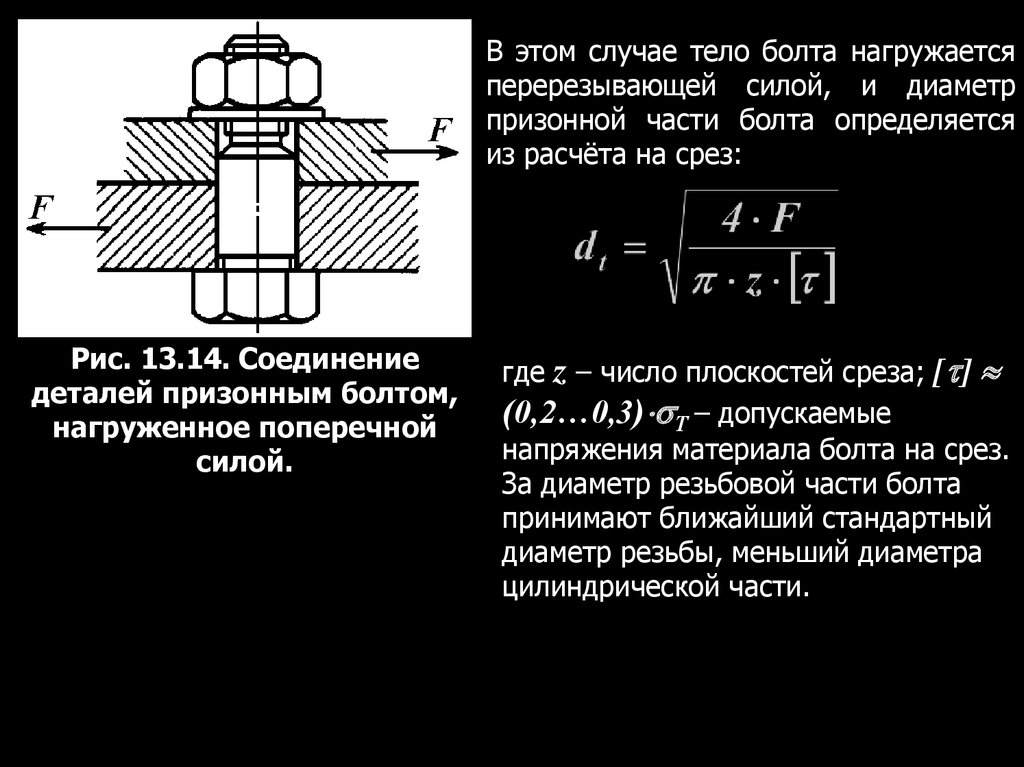 Если болт сломается при затяжке,
очевидно, что требуется замена. Обрыв резьбы имеет тенденцию
носить постепенный характер. Если режим обрезки нити может
случаются узлы, которые могут быть введены в эксплуатацию, которые частично
не удалось, это может иметь катастрофические последствия.
Если болт сломается при затяжке,
очевидно, что требуется замена. Обрыв резьбы имеет тенденцию
носить постепенный характер. Если режим обрезки нити может
случаются узлы, которые могут быть введены в эксплуатацию, которые частично
не удалось, это может иметь катастрофические последствия.
Фотография выше сделана со сканирования электронный микроскоп, показывающий резьбу болта, которая вот-вот сорвется. Интерфейс суставной поверхности находился с правой стороны. на изображении видно, что первая нить имеет наибольшую искажение. Механизм зачистки нити сложен и включает изгиб резьбы (что происходит при высоких нагрузках) и расширение гайки (что приводит к смещению плоскости сдвига).
Чтобы точно предсказать силу и
режим отказа резьбового узла требует рассмотрения
большого количества факторов. Снятие резьбы представляет собой комплекс
явление. Все следующие факторы оказывают важное влияние
на отрывную прочность резьбы:
Снятие резьбы представляет собой комплекс
явление. Все следующие факторы оказывают важное влияние
на отрывную прочность резьбы:
1. Разница в размерах резьбы (например, большой, шаг и второстепенный диаметры) оказывает значительное влияние как на внутренние, так и на внешние потоки отрывная прочность.
2. Изменения прочности на растяжение и сдвиг в материале как для внутренней, так и для внешней резьбы.
3. Эффект радиального смещения гайки или резьбового компонента (обычно называемого расширением гайки) в снижении прочности на сдвиг нитей. растяжение сила в застежке действует на резьбу и заклинивает создает радиальное смещение, которое снижает прочность резьбы.
4. Эффект изгиба нитей,
вызванное действием силы натяжения крепежного элемента, действующей
на V-образной резьбе, что приводит к заклиниванию, которое уменьшает
площадь среза нитей.
5. Влияние производственных вариаций в резьбовом узле, например, с небольшим конусом отверстия или раструбом, может иметь на прочность нити.
Прочность резьбы гайки или болта нельзя рассматривать изолированно, без учета взаимозависимости которые оба элемента имеют на прочность сборки. Одна из проблем прогнозирования прочности на отрыв резьбы заключается в том, что без учета таких эффектов, как изгиб нити, расширение ореха или раструб, возникает оптимистичный результат. Фактическая прочность на отрыв ниже расчетной. Программа FASTENER позволяет состояние арт-анализа, который должен быть выполнен для определения зачистки прочность резьбового соединения.
Эффекты громкого словца Осложняющий фактор, который может возникнуть
когда в просверленном отверстии нарезана резьба, это кричит. Это
небольшая конусность на отверстии, которая обычно встречается на большинстве
просверлены отверстия в некоторой степени. Этот конус проходит нормально
примерно на половину диаметра от начала отверстия.
причиной этого сужения является торсионная и поперечная гибкость
сверла вместе с нестабильностью вершины сверла
при входе в материал. Звонок можно свести к минимуму
с помощью плотно прилегающей, хорошо отцентрованной и жесткой дрели
втулки вместе с точной заточкой сверла.
Это
небольшая конусность на отверстии, которая обычно встречается на большинстве
просверлены отверстия в некоторой степени. Этот конус проходит нормально
примерно на половину диаметра от начала отверстия.
причиной этого сужения является торсионная и поперечная гибкость
сверла вместе с нестабильностью вершины сверла
при входе в материал. Звонок можно свести к минимуму
с помощью плотно прилегающей, хорошо отцентрованной и жесткой дрели
втулки вместе с точной заточкой сверла.
Отверстия с раструбом,
при постукивании ощущается переменная высота резьбы вдоль
длина отверстия. Это изменение может быть значительным на коротких
длина зацепления и мелкий шаг. Чистый эффект от
раструб заключается в уменьшении площади сдвига наружной резьбы. Чем тоньше нить, тем сильнее выражен эффект
болтовня.
Чем тоньше нить, тем сильнее выражен эффект
болтовня.
В резьбовых отверстиях высота резьбы
зависит от диаметра сверла. Уменьшить
риск неудачи, инженер-конструктор часто осторожничает
и определяет высокие проценты высоты резьбы в резьбовых
отверстия. С точки зрения производства эти более высокие проценты
высоты резьбы приводят к более высокому моменту нарезания резьбы, увеличению
поломки метчиков и, как таковые, не приветствуются. Для коротких длин
зацепления резьбы, размер меньшего диаметра — результирующий
от резьбонарезного сверла — оказывает существенное влияние на сборку
сила. Исследования показали, что для резьбовых соединений
обычных пропорций, размер резьбового сверла относительно неважен
до тех пор, пока процент высоты резьбы больше, чем
60%. Затраты на врезку, вероятно, будут ниже, если
используется высота резьбы.
Затраты на врезку, вероятно, будут ниже, если
используется высота резьбы.
Эффект низкой доли высота резьбы, чтобы уменьшить площадь сдвига внешней резьбы, это показано на рис. 1. Для очень низкой резьбы высоты, плоскость среза резьбы не обязательно должна быть параллельной к оси резьбы, это показано на рис. 2. Такие виды отказов трудно предсказать и их можно легко устранить поддерживая разумный процент высоты резьбы.
Гайка Расширение Сила растяжения, присутствующая в застежке
во время затяжки воздействует на V-образную резьбу, создавая заклинивание
действие, приводящее к радиальному смещению. Этот радиальный
смещение обычно известно как расширение гайки и происходит
в резьбовых бобышках, а также в обычных гайках.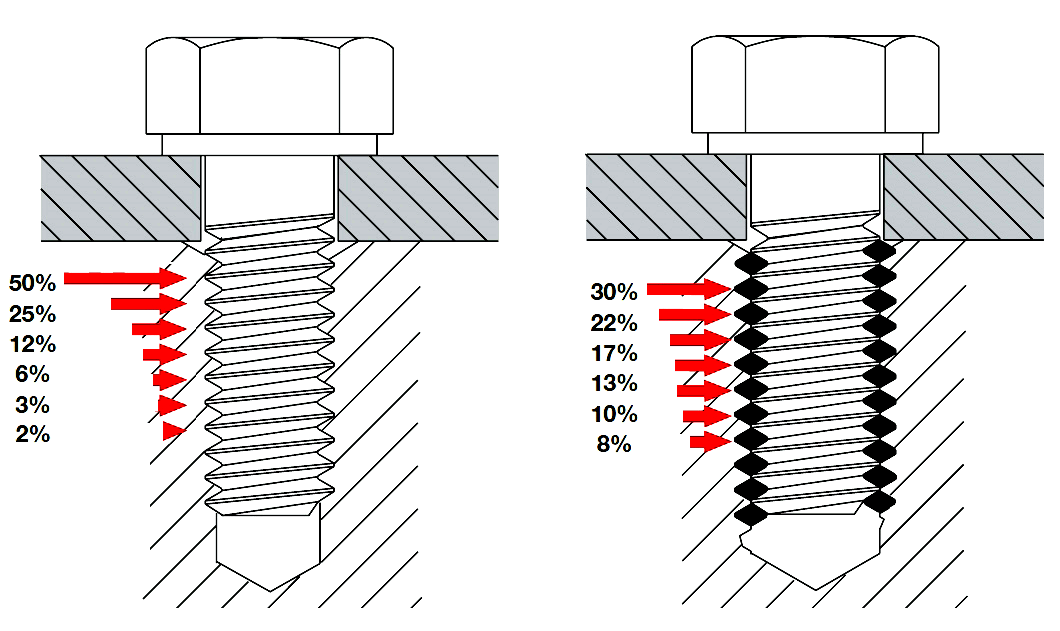 теоретический
и практические исследования этого явления свидетельствуют о том, что
верхняя поверхность гайки сжимается в радиальном направлении, в то время как
его опорная поверхность расширяется. Чистый эффект этого расширения
заключается в уменьшении площади сдвига как внутренней, так и внешней
нить.
теоретический
и практические исследования этого явления свидетельствуют о том, что
верхняя поверхность гайки сжимается в радиальном направлении, в то время как
его опорная поверхность расширяется. Чистый эффект этого расширения
заключается в уменьшении площади сдвига как внутренней, так и внешней
нить.
Прочность сборки на отрыв можно улучшить, увеличив ширину по плоскостям диаметр гайки или бобышки примерно в 1,9 раза больше номинальной резьбы диаметр. Это увеличивает жесткость локально вокруг внутренняя резьба и уменьшает радиальное расширение.
Изгиб резьбы Сила растяжения, присутствующая в застежке
во время процесса затяжки приводит к степени резьбы
изгиб между внутренней и внешней резьбой. Изгиб резьбы
уменьшает площадь сдвига как внутренней, так и внешней резьбы.

 е. выходит из строя винт, а не внутренняя или внешняя резьба
полоски. Длина резьбового зацепления должна быть, по крайней мере, достаточной, чтобы
нести полную нагрузку, необходимую для того, чтобы сломать винт. Если нет, зачистка нити
начинается с первой зацепленной нити и последовательно срезает последующие
потоки. Это может занять несколько часов, поэтому соединение может появиться
хорошо во время сборки, но выйдет из строя в эксплуатации. Размер
резьбовое крепление сначала устанавливают, рассчитав необходимое
зона растяжения с соответствующим запасом прочности. Если сустав зафиксирован
при использовании гайки и болта одного класса размер гайки не требуется
в то время как стандартная длина гайки такого размера, что винт выйдет из строя
до того, как нить будет сорвана. Если винт вкручивается в резьбовое отверстие
материала с низкой прочностью, то необходимо проверить длину зацепления резьбы.
необходимый.
е. выходит из строя винт, а не внутренняя или внешняя резьба
полоски. Длина резьбового зацепления должна быть, по крайней мере, достаточной, чтобы
нести полную нагрузку, необходимую для того, чтобы сломать винт. Если нет, зачистка нити
начинается с первой зацепленной нити и последовательно срезает последующие
потоки. Это может занять несколько часов, поэтому соединение может появиться
хорошо во время сборки, но выйдет из строя в эксплуатации. Размер
резьбовое крепление сначала устанавливают, рассчитав необходимое
зона растяжения с соответствующим запасом прочности. Если сустав зафиксирован
при использовании гайки и болта одного класса размер гайки не требуется
в то время как стандартная длина гайки такого размера, что винт выйдет из строя
до того, как нить будет сорвана. Если винт вкручивается в резьбовое отверстие
материала с низкой прочностью, то необходимо проверить длину зацепления резьбы.
необходимый.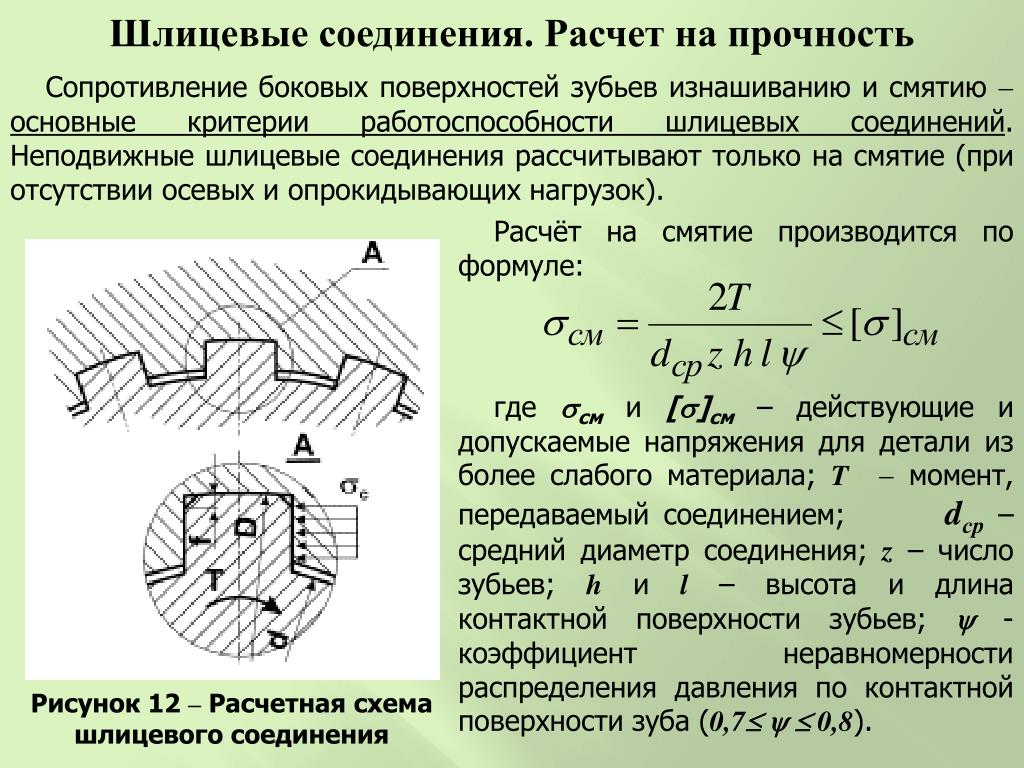
 чтобы убедиться, что прочность на растяжение является самой слабой.
прочность на отрыв определенной длины зацепления или материала может быть
получена из стандартной высоты гайки. Материал только с половинным сдвигом
прочность застежки требует двойной длины зацепления,
Le=2×0,75d.
чтобы убедиться, что прочность на растяжение является самой слабой.
прочность на отрыв определенной длины зацепления или материала может быть
получена из стандартной высоты гайки. Материал только с половинным сдвигом
прочность застежки требует двойной длины зацепления,
Le=2×0,75d. Отношение прочности на сдвиг к
предел прочности при растяжении чугуна ПГ принят равным τ/σ=0,9, где предел прочности при растяжении
прочность σ=500 МПа.
Отношение прочности на сдвиг к
предел прочности при растяжении чугуна ПГ принят равным τ/σ=0,9, где предел прочности при растяжении
прочность σ=500 МПа. 