14. Сдвиг. Основные понятия, напряжения и зависимости. Расчет на срез.
Чистый сдвиг — такой вид напряженного состояния, когда на 4 гранях выделенного элемента возникают только касательные напряжения. Соединения заклепом, штифтами, шпонками, сварные. Действие ножниц – 2 силы, действующие навстречу др. др. под дейчтвием 2 сил происходит перекашивание элемента abcd. Из Δbcc1: tgγ=δ/h≈γ (при малых углах деформации), где δ – переещение, h – расстояние действия сил. Перекашивание элемента abcd (деформация сдвига) предшествует деформации среза. Закон парности τ: τ на 2 взаимно перпендик. площадках равны по модулю и направлены к вершине или от нее этого параллелепипеда. Закон Гука для сдвига: τ=Gγ, где G – модуль упругости II рода, характ. физико-математич. св-ва материала, жесткость при кручении, γ – угол сдвига. G=E/2(1+μ), где Е – модуль упр. I рода (Юнга). Gстали=0,8∙105МПа. Расчет на срез
15. Смятие. Основные понятия, напряжения и зависимости. Расчет.
При небольшой толщине соединяемых брусьев и значит.нагрузке м/у пов-тью соединительной детали и стенками отверстия возник.большое взаимное давление, в рез-те кот.стенка отверстия может обмяться, форма отверстия измениться и соединение разрушиться. Давление, возникшее между пов-тями соединительной детали и отверстия, наз.напряжением смятия σсм. Допущ: силы давления распределены по пов-ти смятия равномерно и перпендикулярны ей. Условие прочности на смятие: σсм = F/Sсм≤[σсм], где F – нагрузка на соединительнй элемент, Sсм – площадь смятия, [σ см] – доп.напр.смятия, для низкоуглерод. стали [σсм]=60…120 МПа.
16. Основы теории напряжения и деформации состояний, все понятия и положения.
Напряженное состояние в точке тела – совокуп. напряжений во мн-ве площадок, проходящих через заданную точку. Исследование напряженного состояния необходимо для расчета на прочность в сложном случае напряжения. Моделью служит куб, параллелепипед. σij: i – перпендикулярная ось, j – вдоль. Из условия равновесия элементарного куба τyx=τxy. F=τ·S= τxy·(dz·dy)·dx; τyx=dx·dz·dy·τxy. => τyx=τxy. Напряженное состояние элементарного куба описывается 9 компонентами (3 нормальных, 6 касательных). Учитывая закон парности касат. напряжений (τyx=τxy), напряженное состояние описывается 6 компанентами. Понятие о главных напряжениях. Через заданную точку всегда можно провести только 3 взаимноперпендик. площадки, в которых τ=0. Это
1. действует только одно главное напряжение σ1 – одноосное напряженное состояние (растяжение). 2. действуют σ1, σ2 – плоское напряженное состояние (двуосное). 3. объемное напряженное состояние (трехосное).
studfiles.net
9. Основные типы резьбовых соединений.
1. болтовое: 1 – винт, 2 – гайка, 3 – шайба. Всегда действ. сдвиг. нагрузка F. Болт д.б. прочным, жестким, работосп. М.б. установлен с зазором (тело болта работает на растяжение) и без (на срез). Шайба – для лучшего распр-ния нагрузки на деталь 4; 2. винтовое – когда 1 деталь тонкостен., др.-мощная; 3. шпилечное.
10. Теория винтовой пары. Зависимость между моментом завинчивания и осевой силы винта.
Если винт нагружен осевой силойF, то для завинчивания гайки к ключу необходимо приложить момент Тзав, а к стержню винта реактивный момент Тр, кот. удерживает стержень от вращения. При этом можно записать Тзав=Тт+Тр, где Тт — момент сил трения на опорном торце гайки; Тр — момент сил в резьбе. Тт=Ff(Dср/2), где Dср=(D1+dотв)/2 – ср.радиус опорного торца гайки, D1 – наруж. диаметр опорного торца гайки, dотв — диаметр отверстия под винт; f – коэф. трения на торце гайки. Тр=0,5Fd2tg(ψ+φ), где ψ — угол подъема резьбы, φ=arctgfпр — угол трения в резьбе; fпр — приведенный коэф. трения в резьбе, учит. влияние угла профиля. Тзав=0,5Fd2[(Dср/)f+tg(ψ+φ)]. По этой ф-ле можно подсчитать отношение осевой силы винта F к силе Fk, приложенной на ручке ключа, F/Fk, кот. дает выигрыш в силе. Стержень винта не только растягивается силой F, но и закручивается моментом Тр. КПД винтовой пары η=tgψ/tg(ψ+φ) ↑ с ↑ψ и с ↓φ.
11. Расчет витков резьбы на срез и смятие.
Основ. виды разрушения резьб: крепежных – срез витков, ходовых – износ витков. В соотв. с этим ведут расчет для крепеж. резьб по напряжениям среза τ, для ходовых – по напряж. смятия σсм. Условия прочности по напряжениям среза: τ=F/(πdpHKKm)≤[τ], где dр – расчет. диаметр, Н≈0,8d – высота гайки, К – коэф. полноты резьбы, Km – коэф. неравномерности нагрузки по виткам резьбы. Условие износостойкости по напряжениям смятия: σсм=F/Sсм=F/(πd2hZ)≤[σсм], где Z=H/р – число рабочих витков
12. Расчет на прочность резьбы и стержня винта при нагружении резьбового соединения осевой растягивающей силе.
Примером служат болты для крепления ненагруженных герметич. крышек и люков корпусов машин. В этом случае стержень болта растягивается осевой силой Fзат, возникающей от затяжки болта, и закручивается моментом сил в резьбе Т р. Напряжение растяжения от силы Fзат: σ=Fзат/[(π/4)d21], напряж. кручения от момента Тр: τ=Тр/Wр=0,5Fзатd2tg(ψ+φ)/0,2d31. Fзат=Аσсм, А — площадь стыка деталей, приходящаяся на 1 болт. Прочность болта опр. по эквив. напр. σэкв=√[σ2+3τ2]≈1,3σ.,чности. Прочность болта: σэкв=1,3Fзат/[(π/4)d21]≤[σ].
13. Расчет на прочность стержня винта при нагружении резьбового соединения поперечной нагрузкой (болт поставлен без зазора).
Не
учитывают силы трения в стыке, т.к.
затяжка болта необязательна. Стержень
болта рассчитывают по напряжениям среза
и смятия. Условие прочности по напряжениям
среза: τ=F/[(π/4)d2i]≤[τ],
де 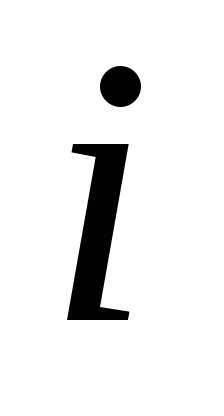
studfiles.net
Резьбовые расчеты резьбы на прочность
Основным критерием работоспособности крепежных резьбовых соединений является прочность. Стандартные крепежные детали сконструированы равнопрочными по следующим параметрам по напряжениям среза и смятия в резьбе, напряжениям растяжения в нарезанной части стержня и в месте перехода стержня в головку. Поэтому для стандартных крепежных деталей в качестве главного критерия работоспособности принята прочность стержня на растяжение, и по ней ведут расчет болтов, винтов и шпилек. Расчет резьбы на прочность выполняют в качестве проверочного лишь для нестандартных деталей. [c.43]Проверочные расчеты резьбы на прочность для стандартных крепежных деталей не проводятся. Проверочные расчеты витков резьбы на срез и смятие выполняют для деталей передачи винт — гайка и нестандартных резьбовых деталей, особенно имеющих мелкую резьбу. [c.355]
При одинаковых материалах сопрягаемых резьбовых деталей расчет резьбы на прочность производят по охватываемой детали по формулам [c.92]
Расчет резьбы на прочность. В случае применения низких гаек (высотой Ядлине свинчивания Н винтов и шпилек (с деталями стальными — Ж чугунными силуминовыми — Нрезьбовых соединений, может оказаться прочность резьбы. Наиболее характерный вид разрушения крепежной резьбы — срез ее витков (рис. 16.8). [c.303]
Если охватывающая резьбовая деталь изготовлена из материала менее прочного, чем материал охватываемой резьбовой детали, то расчет резьбы на срез следует выполнять для каждой из этих деталей. Условие прочности охватывающей детали на срез
При расчете на прочность резьбовых соединений определяют внутренний диаметр dj резьбы болта (винта, шпильки), все же остальные размеры болта, гайки, резьбы приводятся в стандартах. [c.410]
Расчет резьбовых соединений. Основным критерием резьбовых соединений является прочность. Все стандартные болты, винты и шпильки изготовляют равнопрочными на разрыв стержня по резьбе, на срез резьбы н на отрыв головки, поэтому расчет на прочность резьбового соединения обычно производится только по одному основному критерию работоспособности — прочности нарезанной части стержня, при этом определяют расчетный диаметр резьбы dp [c.377]
Все стандартные болты, винты и шпильки изготовляют равнопрочными на разрыв стержня по резьбе, на срез резьбы и отрыв головки, поэтому расчет на прочность резьбового соединения обычно производят только по одному основному критерию работоспособности — прочности нарезанной части стержня на растяжение. [c.62]
При использовании стандартных винтов и гаек из равнопрочных материалов прочность резьбы на участке свинчивания винта с гайкой выше прочности резьбового стержня, поэтому этот расчет для стандартных винтов и гаек не производят. [c.47]
Если в резьбовом соединении резьба нарезана непосредственно на соединяемых деталях, требуемую длину свинчивания L Определяют расчетом витков резьбы на срез. При близких по прочности материалах длину свинчивания определяют по внутренней резьбе (если прочность материала наружной резьбы меньше, чем внутренней, L определяется и для нее окончательно принимается большее значение) [c.38]
Все стандартные резьбы изготовляют равнопрочными на разрыв стержня, срез и смятие витков, поэтому при расчете на прочность определяют требуемый диаметр резьбового стержня.
Расчет резьбовых деталей. В приборостроении резьбовые детали, как правило, на прочность не рассчитывают. Внутренний диаметр резьбы болта по формуле [c.219]
Распределение рекомендуемых полей допусков внутренней и наружной резьбы с зазорами между классами точности приведено в табл. 8.5. Из таблицы видно, что одни и те же поля допусков относятся к разным классам точности при разных длинах свинчивания. Требования к точности разъемных неподвижных соедине НИИ вытекают нз условий свинчиваемости болта с гайкой и прочности. Разрушение резьбового соединения происходит чаще всего вследствие разрыва стержня или среза (а также смятия) витков резьбы. Стандартные значения элементов резьбовых деталей устанавливаются с учетом равнопрочности элементов. Поэтому расчет на прочность винтов обычно выполняют только по параметру di. Однако равнопрочность резьбы со стержнем обеспечивается только при определенной точности изготовления. В высоконапряженных и особо ответственных резьбовых соединениях часто материал ганки или резьбового гнезда бывает менее прочным, чем материал винта и тогда при недостаточной (для обеспечения равнопрочности) [c.255]
Основным критерием работоспособности резьбовых соединений является прочность. Все стандартные болты, винты и шпильки изготовляют равнопрочными на разрыв стержня по резьбе, на срез резьбы и на отрыв головки, поэтому расчет на прочность резьбового соединения обычно производится только по одному основному критерию работоспособности—прочности нарезанной части их стержня, при этом определяют внутренний диаметр резьбы 1- Длину болта, винта или шпильки принимают в завнсимости от толщины соединяемых деталей. Остальные размеры деталей резьбового соединения (гайки, шайбы и др.) принимают в зависимости от диаметра резьбы по ГОСТу. [c.53]
Расчет резьбовых соединений заключается в проверке на прочность и определении основных параметров резьбы (шага, длины резьбы, высоты профиля и т. д.). Слабым местом пластмасс является их низкая прочность при сдвиге (срезе). Проверку резьбы на срез можно выполнить по формуле [c.78]
Для цилиндров прессов, работающих от сети высокого давления, необходимо проводить поверочные расчеты ла прочность. При расчете на прочность цилиндра пресса проверяют запас прочности резьбового соединения, крышки с цилиндром и стенок цилиндра. Запас прочности выбранной резьбы определяется по формуле [c.221]
Коэффициенты запаса прочности находят по диаграмме предельных напряжений для резьбового соединения. При расчете используют диаграмму (рис. 8.1), аппроксимирующую с приемлемой для практики точностью реальную диаграмму для соединений с резьбой, накатанной на термообработанных заготовках. Если болты (шпильки) после накатывания резьбы подвергают термической обработке, а также если резьба деталей получена резанием, можно считать, что предельная амплитуда цикла не зависит от среднего напряжения, и диаграмма имеет вид, показанный штриховыми линиями на рис. 8.1. [c.261]
При расчете резьбовых соединений определяют диаметр стержня болта или винта из условия прочности на разрыв, а резьбу проверяют на срез и смятие. [c.347]
Расчеты резьбовых соединений. Резьбовые соединения могут выходить из строя вследствие разрушения (разрыва) стержня болта по резьбе или у головки, среза. резьбы, а также ее смятия или изгиба. Основным видом разрушения все же является разрушение стержня болта. Так как стандартизацию резьбы выполняют с использованием условия равнопрочности, то при применении стандартных крепежных деталей обычно можно ограничиваться расчетами по одному главному критерию работоспособности — прочности винта на растяжение. [c.71]
Влияние отклонений диаметров, шага и угла профиля метрической резьбы на прочность резьбовых соединений зависит от характера нагрузки, механических свойств материала и соотношения этих свойств болта и гайкн, а также от конструктивных и технологических факторов. В настоящее время еще не созданы методы расчета допускаемых отклонений параметрогз ре И)бы на прочность резьбовых соединений. Поэтому руководствуются экспериментальными данными [3, 84]. [c.161]
Расчеты соединений 1) заклепочные — при статической нагрузке заклепки (на срез и смятие), соединяемые элементы (на прочность в сечениях, ослабленных заклепками), и при переменной нагрузке — на предел выносливости 2) сварные — при статической нагрузке — на разрыв, сжатие или срез, и при переменной нагрузке — на предел выносливости 3) резьбовые — при статической нагрузке болт (на разрыв в опасном сечении, смятие, изгиб), резьба (на срез и смятие), и при переменной нагрузке — на предел выносливости 4) клиновые, щтифтовые, щпоночные, [c.144]
Расчет болтов, нагруженных осевой силой. Прочность является основным критерием работоспособности резьбовых соединений. Стандартные болты, винты, шпильки обладают равнопрочностьк> стержня на растяжение и резьбы на срез и смятие, поэтому расчет выполняют только для [c.352]
Расчет ненапряженного болтового соединения. Примером такого соединения является хвостовик грузоподъемного крюка е нарезан ной резьбой (рис. 81). В данном случае гайка свободно навинчена на хвостовик и зафиксирована от самоотворачивания шплинтом, проходящим через гайку и стержень хвостовика. Пренебрегая весом крюка, можно считать, что резьбовой хвостовик нагружается только растягивающей силой (Э, приложенной к крюку. Допуская, что напряжения в опасном сечении хвостовика (по внутреннему диаметру резьбы) распределяются равномерно, определяем внутренний диаметр резьбы Условие прочности на растяжение [c.110]
Расчет незатянутых болтов. Характерный пример незатянутого резьбового соединения — крепление крюка грузоподъемного механизма (рис. 3.15). Под действием силы тяжести груза Q стержень крюка работает на растяжение, а опасным будет сечение, ослабленное нарезкой. Статическая прочность стержня с резьбой (которая испытывает объемное напряженное состояние) приблизительно на 10% выше, чем гладкого стержня без резьбы. Поэтому расчет стержня с резьбой условно ведут по расчетному диаметру dp d—0,9p, где р — шаг резьбы с номинальным диаметром d (приближенно можно считать dpKdi). Условие прочности нарезанной части стержня на растяжение имеет вид [c.44]
mash-xxl.info
