Планетарный редуктор, устройство и расчет
По сравнению с традиционными редукторами можно выделить следующее преимущество этого устройства: они могут создавать огромные передаточные отношения скоростей при невысоком количестве шестеренок. Шестерни механизма имеют небольшой размер благодаря их количеству. Так, одно более массивное колесо распределяет равномерно нагрузку по нескольким сателлитам. Из этого следует, что устройство получается не очень большим и громоздким. Однако, расчет и практика показывают, что при высоких передаточных числах работоспособность и коэффициент полезного действия сильно снижаются.
Содержание
- Планетарный редуктор
- Преимущества планетарных устройств
- Планетарные редукторы в машиностроении
- Мотор-редукторы планетарного типа
- Расчет планетарного устройства
- Ремонт редуктора своими руками
Планетарный редуктор
Такой вид редукторов, как планетарный (планетарный мотор редуктор) относится к передачам крутящего момента посредством зубчатого (зубчатое устройство) зацепления шестерен. Как и любой другой редуктор, планетарный редуктор, предназначен для передачи крутящего момента от двигателей различных видов непосредственно к приводам, при этом происходит понижение скорости вращения валов и увеличение крутящего момента. Главное отличие, которое имеет устройство планетарного редуктора от обычных (червячного, цилиндрического, конического и т.д.) заключается в том, что он имеет перемещающиеся оси зубчатых колес. В состав редуктора набор шестеренок — сателлитов. В связи с тем, что эти сателлиты движутся вокруг одного центрального, и все это устройство напоминает солнечную систему, то соответственно и родилось название планетарный редуктор. Маленькие шестеренки, вращающиеся вокруг одной центральной, имеют ось в центре (водило).
Как и любой другой редуктор, планетарный редуктор, предназначен для передачи крутящего момента от двигателей различных видов непосредственно к приводам, при этом происходит понижение скорости вращения валов и увеличение крутящего момента. Главное отличие, которое имеет устройство планетарного редуктора от обычных (червячного, цилиндрического, конического и т.д.) заключается в том, что он имеет перемещающиеся оси зубчатых колес. В состав редуктора набор шестеренок — сателлитов. В связи с тем, что эти сателлиты движутся вокруг одного центрального, и все это устройство напоминает солнечную систему, то соответственно и родилось название планетарный редуктор. Маленькие шестеренки, вращающиеся вокруг одной центральной, имеют ось в центре (водило).
Преимущества планетарных устройств
По сравнению с традиционными редукторами можно выделить следующее преимущества, которые имеет это устройство: они могут создавать огромные передаточные отношения скоростей при невысоком количестве шестеренок. Шестерни механизма имеют небольшой размер благодаря их количеству. Так, одно более массивное колесо распределяет равномерно нагрузку по нескольким сателлитам. Из этого следует, что устройство получается не очень большим и громоздким. Однако, расчет и практика показывают, что при высоких передаточных числах работоспособность и коэффициент полезного действия сильно снижаются. И как вывод всего вышесказанного, основными преимуществами являются:
Шестерни механизма имеют небольшой размер благодаря их количеству. Так, одно более массивное колесо распределяет равномерно нагрузку по нескольким сателлитам. Из этого следует, что устройство получается не очень большим и громоздким. Однако, расчет и практика показывают, что при высоких передаточных числах работоспособность и коэффициент полезного действия сильно снижаются. И как вывод всего вышесказанного, основными преимуществами являются:
- Большие передаточные числа;
- Невысокая масса;
- Относительная компактность;
- Его можно чинить и собирать своими руками.
Такие преимущества требуют и соответствующего изготовления. Начиная с расчета, проектирования и заканчивая изготовлением — все должно быть прецизионно точно. Эти редукторы нашили очень широкий ряд применений в различных отраслях: прибостроительной, станкостроительной, машиностроительной и т.д. В данной статье остановимся более подробно на применении этого устройства в машиностроительной отрасли.
Планетарные редукторы в машиностроении
Широкое распространение редуктора, которые имеют устройство данного типа получили в ведущих мостах автомобилей и в автоматических коробках переключения передач. Колесный редуктор можно встретить в мостах таких автомобилей, как: МАЗ, Икарус, в некоторых троллейбусах, тракторах Т-150К, К-700. Этот колесный редуктор в мостах передает крутящий момент к ступицам колес от полуосей. Также они распространены в передаче бортового типа. Такое применение в бортовой передаче позволило существенно уменьшить как расчетный, так и практический диаметр основной передачи. Уменьшение диаметра отразилось повышенным просветом автомобиля и как следствие более высокой проходимостью. Использование планетарных коробок переключения передач набирает все большую популярность. Передаточное отношение устройства будет вытекать из расчета отношения числа зубьев на центральной шестерни к числу зубьев на коронной шестерне. Интересным моментом является расторможение коронной шестерни в коробке. В этом случае передаточное число равняется 1.
В этом случае передаточное число равняется 1.
Мотор-редукторы планетарного типа
Это устройство предназначено для использования в роли привода в горизонтальном либо вертикальном положении. Мотор-редукторы исполнены из нескольких модулей. Такая кинематическая схема, включающая сразу мотор и устройство планетарного редуктора, имеет целый ряд значительных преимуществ и позволяет выполнять следующие задачи:
- Вырабатывание высоких мощностей при невысоких габаритах;
- Большой коэффициент полезного действия;
- Масса в три раза меньше аналогов;
- Использование для специализированных установок;
- Расчет делать легче, чем у других редукторов;
- Невысокие затраты на обслуживание.
Расчет планетарного устройства
Обсудив в статье уже множество моментов по этому редуктору, стоит перейти и к основным моментам по его расчету перед проектированием. Расчет редуктора производится следующим образом:
- Определяем число передаточных ступеней;
- Расчет сателлитов и числа зубьев;
- Выбор материала шестерен;
- Определяем межосевое расстояние;
- Проверочный расчет;
- Расчет сил;
- Выбор подшипников;
- Определение толщины колес;
- Вычисление осей шестеренок.

Ремонт редуктора своими руками
Ремонт редуктора своими руками является весьма непростой задачей. Так, данный механизм очень непростой и состоит из множества частей. При ремонте своими руками часто можно даже при разборке не ведая, что внутри просто растерять целую кучу маленьких деталей, например, иголки моментально рассыпаются и теряются. Ремонт планетарного редуктора лучше всего оставить профессионалам.
Стоит отметить, что на сегодняшний день планетарный редуктор весьма распространен и используется в большинстве грузовых автомобилей в ведущих мостах, а также очень часто встречается в роли лебедок.
Как и все редукторы, он может быть как одноступенчатым, так и многоступенчатым. Если Вы собираетесь приобрести механизм данного типа, то лучше всего покупать его у проверенных производителей, так как ремонт своими руками очень затруднен, а если он будет часто выходить из строя, то денег на него будет уходить много. В данной статье мы попытались собрать общую информацию по устройствам планетарного типа использующихся для производства автомобилей. Также нужно сказать, что данный вид устройства очень интенсивно внедряется во многие сферы и отрасли благодаря своим очень весомым преимуществам.
Также нужно сказать, что данный вид устройства очень интенсивно внедряется во многие сферы и отрасли благодаря своим очень весомым преимуществам.
Как устроен планетарный мотор-редуктор: Статьи
Сферы применения планетарных редукторов
Планетарный редуктор работает на тех же самых прямозубых передачах, что и цилиндрический, поэтому у него максимально возможный КПД. Преимущество перед цилиндрическим — соотношение передаваемой мощности и веса. Именно по этой причине планетарные редукторы используются в авиации и в автомобилях.
Планетарные передачи в промышленности
Общепромышленные редукторы в основном имеют червяную и цилиндрическую кинематическую схему. Планетарный вариант все больше получает распространение. Установка этого типа редукторов оправдана в тех случаях, когда критичен вес агрегата. Это различные подвижные механизмы, электрокары, тележки, привод манипуляторов и так далее. В современном автоматизированном производстве таких сфер применения огромное множество.
В современном автоматизированном производстве таких сфер применения огромное множество.
Роботы-манипуляторы приводятся в движение либо волновыми редукторами (обеспечивают очень медленные и плавные движения, коэффициент замедления 1:1000) или же планетарными. Последние устанавливают там, где необходимо передаточное отношение от 10 до 100. Это привод различных исполнительных механизмов, размещаемых на головке универсального манипулятора.
Современный планетарный привод организуется по компоновке мотор-редуктора. Электродвигатели выбирают с торцевым фланцевым креплением, которое не требует горизонтальной плиты. Такая компоновка обеспечивает экономию материалов до 30-40% на корпуса и монтажные приспособления.
Использование планетарных передач в автомобилях
Планетарную кинематическую схему имеют современные автоматические коробки передач. Там ставится три одинаковые планетарные пары, обеспечивающие 7-9 ступеней. АКПП получается компактной и способной передавать значительный крутящий момент. Планетарные коробки ставят на военных автомобилях. Основное большинство все еще использует обычные КПП с параллельными валами, выполненными по схеме цилиндрического редуктора. Очень давно разработан и используется планетарный механизм поворота гусеничной техники: тракторов, бульдозеров и танков.
Планетарные коробки ставят на военных автомобилях. Основное большинство все еще использует обычные КПП с параллельными валами, выполненными по схеме цилиндрического редуктора. Очень давно разработан и используется планетарный механизм поворота гусеничной техники: тракторов, бульдозеров и танков.
Автоматическая планетарная КПП имеет четыре одинаковые шестерни-сателлита на каждой паре. В промышленных редукторах обычно реализована схема с тремя сателлитами. Увеличение их числа позволяет уменьшить размер шестерен, так как возрастает число зубьев, находящихся в зацеплении одновременно и большая нагрузка равномерно распределяется между ними. Больше 5 сателлитов на одной паре не ставится.
Велосипедистам хорошо знакомы планетарные втулки для велосипедов. Выбор такого решения объясняется главным преимуществом планетарной передачи — соотношением передаваемой мощности и веса.
Планетарные передачи ставятся в мотор-колесах — самом перспективном типе привода для электромобилей. Уже сейчас активно эксплуатируются электросамокаты с одной планетарной парой в колесе. Аналогичный привод подходит для электроскутеров, электроциклов, и электромобилей. При использовании перспективной гибридной схемы планетарная передача также остается актуальной, конструкция мотор-колеса не меняется.
Уже сейчас активно эксплуатируются электросамокаты с одной планетарной парой в колесе. Аналогичный привод подходит для электроскутеров, электроциклов, и электромобилей. При использовании перспективной гибридной схемы планетарная передача также остается актуальной, конструкция мотор-колеса не меняется.
Планетарные мотор-редукторы для металлообработки
Металлообработка является основным потребителем кинетической энергии в машиностроении. Электродвигатели имеют высокий КПД на скоростях вращения 50-25 об/сек, что является слишком высоким значением для резания металла. При такой скорости происходит искрообразование и перегрев резцов. Выход заключается в установке редуктора с небольшим передаточным числом, например, 8-20. Планетарная кинематическая схема тут подходит как нельзя лучше, так как именно это передаточное отношение обеспечивается одной парой шестерен с сателлитами.
Металлорежущие станки часто комплектуются цилиндрическими редукторами, но там есть существенный недостаток — несоответствие осей входного и выходного вала, плюс большие габариты картера. В планетарной схеме входной и выходной вал расположены строго по одной оси. Кроме того, сам корпус получается плоским и круглым, что позволяет его легко закрепить на торце электродвигателя. Получается оптимальная схема привода, когда система имеет минимальные габариты и простоту установки. Такой мотор-редуктор ставится на один фланец точно так же, как и обычный электродвигатель.
В планетарной схеме входной и выходной вал расположены строго по одной оси. Кроме того, сам корпус получается плоским и круглым, что позволяет его легко закрепить на торце электродвигателя. Получается оптимальная схема привода, когда система имеет минимальные габариты и простоту установки. Такой мотор-редуктор ставится на один фланец точно так же, как и обычный электродвигатель.
Планетарные редукторы для мобильной техники
Применение планетарных передач выгодно там, где критичен вес агрегата, а в эту категорию попадает вся дорожно-строительная и строительная техника: автобетоносместители «миксеры», асфальтоукладчики, гидродвигатели катков, кранов, экскаваторов. Редуктор исполняется в плоском стальном корпусе в форме блина с торцевым креплением к агрегату. Скорость вращения у ДВС и общепромышленных электродвигателей стараются делать одинаковой — 3000 об/мин, что соответствует сети 50 Гц 380 вольт и удобно для конструктивных расчетов по подбору редуктора.
Какие мотор-редукторы применяются в промышленности
Благодаря конструкции с применением планетарной передачи агрегаты превосходно справляются с перегрузками, возникающими во время эксплуатации. Именно поэтому механизмы на их основе повседневно применяются на многих промышленных заводах и фабриках. Популярным моделям российского производства можно отнести такие планетарные мотор-редукторы как: 3МП-40 или 3МП50. Эти агрегаты обладают превосходными характеристиками и невысокой стоимостью.
Именно поэтому механизмы на их основе повседневно применяются на многих промышленных заводах и фабриках. Популярным моделям российского производства можно отнести такие планетарные мотор-редукторы как: 3МП-40 или 3МП50. Эти агрегаты обладают превосходными характеристиками и невысокой стоимостью.
Для нужд хим. заводов были разработаны специальные мотор-редукторы МПО2М-15 с высокой степенью защиты. Для небольших буровых установок потребители выбирают малогабаритные редукторы 3МП-31,5 возможности питания от бытовой сети 220В.
Планетарная передача
Планетарная передача: тип передачи, используемый в механических и автоматических коробках передач. Помимо вращательного преобразования, «планетарка» способна добавлять и разлагать силы. Зная планетарный механизм: что это такое, как он работает, по каким критериям оценивается коробка передач, станет понятно устройство и характеристики АКПП. В случае поломки расчет трансмиссии поможет выбрать надежный и долговечный механизм.
Содержание
- Устройство и принцип работы
- Разновидности планетарных передач
- Характеристики основных разновидностей этого устройства
- Цилиндрические
- Конические
- Волновые
- Достоинства и недостатки планетарных передач
- Передаточное число планетарных передач
- Подбор чисел зубьев планетарных передач
- Расчет на прочность планетарных передач
- Советы по подбору планетарного редуктора
- Область применения планетарных передач
- Заключение
Устройство и принцип работы
Планетарная передача представляет собой конструкцию из шестерен, которые перемещаются относительно центра. По центральной оси расположены колеса разного диаметра:
- маленькие солнечные с наружными зубцами;
- крупная коронка или эпицикл с внутренними зубьями.
Сателлиты перемещаются между колесами. Его вращение напоминает движение планет Солнечной системы. Оси сателлитов механически связаны с водилой, которая вращается вокруг центральной оси.
Устройство простого планетарного блока:
- 1 эпицикл;
- 1 солнечное колесо;
- 1 перевозчик.
Планетарный механизм собирается каскадами из двух и более звеньев на валу для получения широкого диапазона передач. Основной кинематической характеристикой зубчатой передачи является передаточное число.
Принцип работы планетарной коробки заключается в блокировке одного из основных элементов и передаче вращения через ведущее колесо. Для остановки элемента используются тормозные ленты, стопорные муфты, конические шестерни. Передаточное число меняется в зависимости от схемы крепления. Принцип работы планетарного механизма удобнее описать на примере:
- Корона заблокирована.
- Вал передает крутящий момент на солнце.
- Вращение Солнца заставляет планеты вращаться вместе с ним.
- Водила становится ведомым, сообщая о пониженной передаче.

Управляя элементами простой «планетарки», они получают разные характеристики:
| Передача инфекции | Как работает планетарный редуктор в АКПП |
| а | Солнце вращает владельца, корона движется в противоположном направлении. |
| два | Корона вращает владельца, солнце садится. |
| 3 | Основной носитель передает вращение Солнцу. Корона заблокирована. |
| 4 | Владелец двигает корону. Солнце зафиксировано. |
| Прилавок | Перевозчик заблокирован. Солнечное колесо вращается, планеты поворачиваются и двигают корону в противоположном направлении. |
КПД одиночной передачи η достигает 0,97.
Набор планетарных шестерен с одной степенью свободы становится планетарной передачей. Две мощности образуют дифференциал. Дифференциал добавляет моменты на звездочку от звеньев главной передачи.
Дифференциал добавляет моменты на звездочку от звеньев главной передачи.
Ремонт акпп ниссан х трейл своими руками
Разновидности планетарных передач
По количеству ступеней планетарные механизмы делятся на:
- один ряд;
- многорядный.
Планетарная передача солнечной шестерни, одновентовых сателлитов, водила и эпицикла будут однорядными. Замена сателлитов на два ряда усложняет конструкцию, делая ее двухрядной.
Многоступенчатый планетарный редуктор представляет собой однорядный агрегат, установленный последовательно. Эта схема позволяет суммировать передаточные числа и получать большие значения. 4-ступенчатые АКПП состоят из двухрядных планетарных структур, 8-ступенчатые — из четырехрядных.
В автоматических коробках передач используются схемы, названные в честь изобретателей:
- Механизм Wilson представляет собой трехрядную конструкцию, в которой соединены заводная головка первого ряда, держатель второго ряда и заводная головка третьего ряда.
 Количество передач – 5 вперед и 1 назад.
Количество передач – 5 вперед и 1 назад. - Механизм Лепелетье состоит из 3 простых планетарных шестерен, расположенных соосно. Количество передач – 6 вперед и 1 назад.
- Схема Симпсона: 2 редуктора с общей солнечной шестерней. Багажник второго ряда оборудован тормозом. Венец и солнце переднего ряда жестко связаны с карданным валом через две блокировочные муфты. Механизм реализует следующие режимы: нейтральный; 1,2,3 передачи; прилавок.
По типу зубчатых конструкций планетарные редукторы делятся на:
- цилиндрический;
- конический;
- волна;
- червь.
Различные типы используются для передачи крутящего момента между валами, расположенными параллельно или под углом. А также в механизмах, требующих низкой или высокой кинематики.
Характеристики основных разновидностей этого устройства
В конструкции планетарного ряда автоматических коробок передач используются различные типы шестерен. Различают три основных наиболее распространенных: цилиндрический, конический и гофрированный.
Цилиндрические
Зубчатые механизмы передают крутящий момент между параллельными валами. В конструкцию цилиндрической передачи входят две и более пары колес. Форма зубьев шестерни может быть прямой, косой или шевронной. Цилиндрический контур прост в изготовлении и эксплуатации. Применяется в редукторах, бортовых передачах, трансмиссиях. Передаточное отношение ограничено размерами механизма: для одного комплекта колес оно достигает 12. КПД составляет 95%.
Конические
Колеса по конической схеме преобразуют и передают вращение между валами, расположенными под углом от 90 до 170 градусов. Зубья нагружены неравномерно, что снижает их предельный момент и прочность. Наличие сил на осях усложняет конструкцию опор. Для плавного соединения и повышенной прочности используется круглая форма зубьев.
Производство конических зубчатых колес требует высокой точности и, следовательно, является дорогостоящим. Угловые конструкции используются в редукторах, воротах, фрезерных станках. Передаточное отношение конических шестерен для средненагруженной техники не превышает 7. КПД: 98%.
Передаточное отношение конических шестерен для средненагруженной техники не превышает 7. КПД: 98%.
Волновые
В волновой передаче нет ни солнечных шестерен, ни планетарных шестерен. Внутри венца установлено гибкое зубчатое колесо овальной формы. Водило выполняет роль генератора волн и представляет собой овальный кулачок на специальном подшипнике.
Гибкое стальное или пластиковое колесо деформируется под действием конвейера. По большой геометрической оси зубья входят в зацепление с коронкой по всей рабочей высоте; шестерни на малой оси нет. Движение передается волной, создаваемой гибким зубчатым колесом.
В волновых механизмах КПД возрастает при передаточном числе больше 300. Волновая передача не работает в схемах с кинематической характеристикой меньше 20. Редуктор выдает КПД 85%, мультипликатор — 65%. Конструкция используется в промышленных роботах, манипуляторах, авиационной и космической технике.
Планетарная передача превосходит аналогичные по мощности однозубчатые механизмы компактными размерами и в 2-3 раза меньшей массой. За счет использования нескольких планетарных передач достигается зацепление зубьев на 80%. Увеличивается грузоподъемность механизма и уменьшается давление на каждый зуб.
Кинематическая характеристика планетарного механизма достигает 1000 при малом числе передач без применения многорядных конструкций. Помимо трансмиссии планетарная схема может выполнять функции дифференциала.
За счет соосности осей планетарного механизма монтировать станки проще, чем с другими редукторами.
Использование планетарного ряда в АКПП снижает уровень шума в автомобиле. Сбалансированная система обладает высокой устойчивостью к вибрациям за счет гашения колебаний. Следовательно, вибрация кузова снижается.
Недостатки планетарного механизма:
- сложное производство и высокоточная сборка;
- на сателлиты устанавливаются подшипники, которые выходят из строя быстрее шестерни;
- с увеличением передаточных чисел КПД падает, поэтому приходится усложнять конструкцию.

Продолжить чтение Как самостоятельно перейти с автоматического режима на ручной
Передаточное число планетарных передач
Передаточное число – это отношение частоты ведущего вала планетарной передачи к частоте ведомого. Визуально определить его значение не получится. Механизм приводится в движение по-разному, а значит, и передаточное отношение в каждом случае разное.
Для расчета передаточного числа планетарного редуктора учитывают количество зубьев и систему крепления. Допустим, у солнечной шестерни 24 зуба, у планетарной шестерни — 12, а у зубчатого венца — 48. Водило зафиксировано. Солнце ведет.
Сателлиты начнут вращаться со скоростью, передаваемой солнечной шестерней. Передаточное отношение: -24/12 или -2. Результат означает, что планеты вращаются в направлении, противоположном солнцу, с угловой скоростью 2 оборота. Сателлиты вращаются вокруг заводной головки, поворачивая ее на 12/48 или ¼ оборота. Колеса с внутренним штифтом вращаются в одном направлении, поэтому число положительное.
Сателлиты вращаются вокруг заводной головки, поворачивая ее на 12/48 или ¼ оборота. Колеса с внутренним штифтом вращаются в одном направлении, поэтому число положительное.
Общее передаточное число равно отношению числа зубьев на ведущем колесе к числу зубьев на ведущем колесе: -24/48 или -1/2 оборота, которые делает венец относительно солнца с водилом постоянный.
Если транспортное средство движется по путеводному солнцу, то передаточное число: (1+48/24) или 3. Это максимальное число, которое может предложить система. Наименьшее соотношение достигается установкой коронки и приложением крутящего момента к брекету: (1+/(1+48/24)) или 1/3.
Передаточные числа простой планетарной схемы: 1,25 — 8, многоступенчатой: 30 — 1000. С увеличением кинематической характеристики КПД снижается.
Подбор чисел зубьев планетарных передач
Число зубьев колес выбирается на первом этапе расчета планетарной схемы в соответствии с заданным передаточным числом. Особенностью конструкции планетарного ряда является выполнение требований по правильности монтажа, соосности и близости механизма:
Особенностью конструкции планетарного ряда является выполнение требований по правильности монтажа, соосности и близости механизма:
- зубья сателлитов должны совпадать с синусами солнца и эпицикла;
- планеты не должны касаться друг друга зубцами. На практике используется не более 6 спутников из-за сложности равномерного распределения нагрузки;
- оси водила, солнца и венца должны совпадать.
Основное соотношение выбора зуба шестерни через передаточное число выглядит следующим образом:
i = 1+Zкраун/Zsol,
где i — передаточное отношение;
Zn – количество зубьев.
Условие соосности соблюдается при равных межосевых расстояниях от солнечного колеса, венца и опоры. Для простой планетарной передачи проверяют расстояния между центрами центральных колес и сателлитов. Равенство должно удовлетворять формуле:
Zкорона= Zсол+2×Zспутник.
Чтобы между сателлитами оставался зазор, сумма радиусов соседних шестерен не должна превышать осевого расстояния между ними. Условие близости к солнечному колесу проверяется по формуле:
Условие близости к солнечному колесу проверяется по формуле:
sin (π/c)> (Zспутник+2)/(Zсол+Zспутник),
где c – количество спутников.
Планетарные колеса расположены равномерно, если отношение венца к солнечному зубу к числу сателлитов является целым числом:
Zсолн/с = Z;
Zкрон/с = Z,
где Z — целое число.
Расчет на прочность планетарных передач
Прочностной расчет планетарных передач проводят так же, как и прямозубых. Рассчитать каждую ссылку:
- внешний — между солнцем и планетарными колесами;
- внутренние — между планетами и макушкой.
Если колеса изготовлены из одного материала и силы сцепления равны, то рассчитывается наименее прочное соединение — внешнее.
Алгоритм расчета следующий:
- Выберите коробку передач.
- Определяются исходные данные: передаточное отношение i, крутящий момент Tвых и частота вращения выходного вала Uвых.

- Количество зубьев выбирают, проверяя условия монтажа и близость планетарных шестерен.
- Вычислите угловые скорости колес.
- Рассчитать КПД и моменты выходных валов.
- Рассчитайте прочность связи.
Расчет момента учитывает количество планетарных колес и неравномерность нагрузки на их зубья. Поправочный коэффициент η = 1,5… 2 вводится при отсутствии компенсационных мероприятий:
- повышенная точность изготовления;
- радиальная подвижность солнца, короны или носителя;
- применение эластичных элементов.
Расчет зубчатых колес ведется по двум критериям:
- контактное усилие, т.е сопротивление рабочих поверхностей зубьев под нагрузкой;
- напряжение изгиба, усталостное разрушение.
Расчет контактного усилия сводится к проверке условия, чтобы натяжение σn не превышало допустимого значения. Расчеты выполняются по формуле Герца для цилиндрических поверхностей с добавлением коэффициентов уточнения. 3)/(Ψ×d) ≤ [σн]
3)/(Ψ×d) ≤ [σн]
При расчете прогиба принимается условие, что вся нагрузка передается на одну пару зубьев и прилагается к их верхней части. Номинальное напряжение не должно превышать допустимого:
σf= (M/W) – (F/(b×s) ≤ [σf],
где М — изгибающий момент;
W — осевой момент сопротивления;
F — сила сжатия;
b, s — размеры зуба в сечении;
[σf] — допустимое напряжение изгиба. Это зависит от предела сопротивления, шероховатости, погрешности изготовления зубьев.
Советы по подбору планетарного редуктора
Перед выбором планетарного редуктора производится точный расчет нагрузки и режимов работы механизма. Определите тип трансмиссии, осевые нагрузки, диапазон температур и размеры редуктора. Для тяжелой спецтехники, где нужен высокий крутящий момент при малых скоростях, выбирают коробку передач с высоким передаточным числом.
Для замедления угловой скорости без снижения крутящего момента используется привод с электродвигателем и редуктором. При выборе мотор-редуктора необходимо учитывать:
При выборе мотор-редуктора необходимо учитывать:
- эксплуатационная нагрузка;
- момент вала на выходе;
- частота вращения входного и выходного валов;
- мощность электродвигателей;
- монтажный вариант.
Область применения планетарных передач
Планетарная схема используется в:
- редукторы;
- автоматические и механические коробки передач;
- в авиационных частях;
- дифференциалы машин, устройства;
- ведущие мосты тяжелой техники;
- кинематические схемы станков.
Планетарный редуктор применяется в агрегатах с переменным передаточным числом, тормозящим водило. В гусеничной технике для сложения потоков мощности элементы планетарной передачи не блокируются.
youtube.com/embed/BzigBpN9tD0?feature=oembed&wmode=opaque»/>Заключение
Планетарные передачи в автоматических коробках передач зарекомендовали себя десятилетиями эксплуатации начиная с Ford T: компактные размеры, малый вес, высокие скорости, надежность и прочность. Планетарная схема способна передавать вращение и управлять потоками энергии, поэтому нашла применение в авиации, машиностроении и промышленности.
Чтобы не запутаться с выбором конструкции, производится точный расчет геометрии и прочности зубчатого колеса в сравнении с допустимыми значениями. Ошибки в расчетах приводят к чрезмерным нагрузкам на шестерни, поломке и износу зубьев.
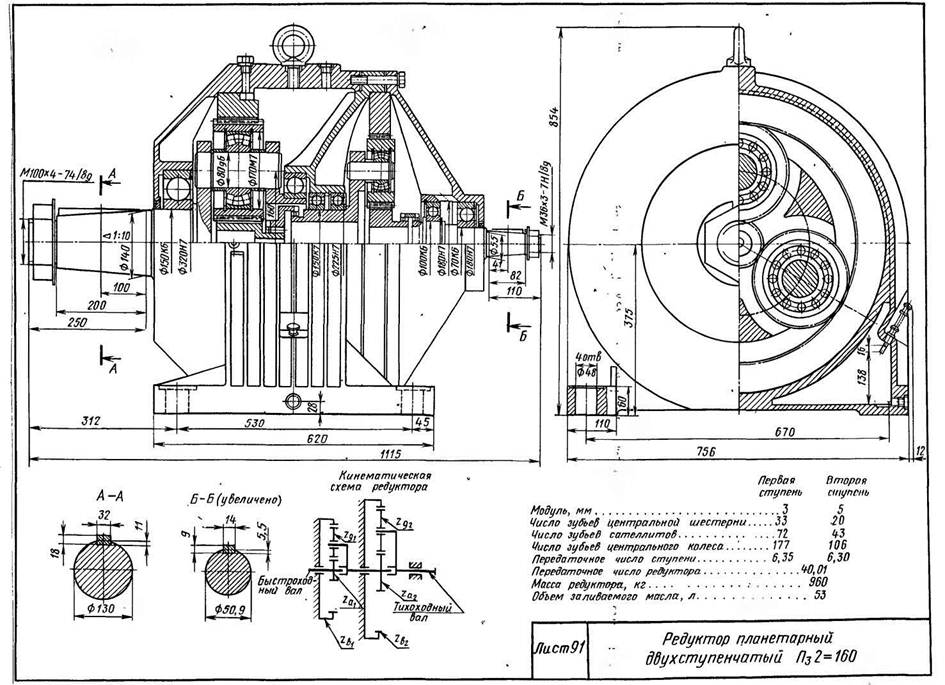
Планетарный Редуктор, Устройство и Принцип Работы, Кинематическая Схема одноступенчатого И двухступенчатого, Расчет и Ремонт Своими Руками
Двухступенчатый планетарный редуктор представляет собой конструкцию, составленную из шестеренок и других рабочих элементов, которые приводятся в движение посредством зубчатой передачи. При этом двигаются они по принципу, который заложен в механике вращения планет – вокруг одного центра. По этой причине центральная шестерня именуется «солнечной», промежуточные — «сателлитами», а внешняя с внутренним зубчатым сцеплением — «коронной». Кроме этого, самый простой планетарный редуктор состоит из водила. Оно предназначено для фиксации сателлитов относительно друг друга, чтобы они двигались вместе.
При этом двигаются они по принципу, который заложен в механике вращения планет – вокруг одного центра. По этой причине центральная шестерня именуется «солнечной», промежуточные — «сателлитами», а внешняя с внутренним зубчатым сцеплением — «коронной». Кроме этого, самый простой планетарный редуктор состоит из водила. Оно предназначено для фиксации сателлитов относительно друг друга, чтобы они двигались вместе.
Для правильной работы устройства необходимо, чтобы одна из составляющих его частей была жестко закреплена на корпусе. В планетарном редукторе, который оснащен водилом, статической частью является именно оно. Кроме этого, жестко закрепленным может быть коронная или солнечная шестеренки. В случае если ни одна из частей этого устройства не закреплена, имеется возможность расщепления одного движения на несколько, либо слияние двух в одно.
При этом в сцепке с ведущим и ведомым валом может быть как коронная, так и солнечная шестерни, или сателлиты.
Этот механизм может осуществлять повышение передаточного числа и снижение крутящего момента и на оборот.
За счет такой конструкции обеспечивается движение ведомого и ведущего валов в одном направлении.
Назначение и конструкция редуктора
Служит редуктор для обеспечения понижения передачи и при этом повышения силы крутящего момента. Для обеспечения работы этого механизма вращающийся вал присоединяется к его ведомому элементу.
Это устройство в классическом исполнении состоит из червячных или зубчатых пар, центрирующих подшипников, различных уплотнений, сальников и т.д. Примером планетарного редуктора является шариковый подшипник. Корпус устройства сложен из двух элементов:
- крышки;
- основания.
Смазка всех составных элементов этого устройства производится путем разбрызгивания масла, но в некоторых особенных устройствах это осуществляется при помощи масляного насоса в принудительном порядке.
Ремонт редуктора своими руками
Ремонт редуктора своими руками является весьма непростой задачей. Так, данный механизм очень непростой и состоит из множества частей. При ремонте своими руками часто можно даже при разборке не ведая, что внутри просто растерять целую кучу маленьких деталей, например, иголки моментально рассыпаются и теряются. Ремонт планетарного редуктора лучше всего оставить профессионалам.
Так, данный механизм очень непростой и состоит из множества частей. При ремонте своими руками часто можно даже при разборке не ведая, что внутри просто растерять целую кучу маленьких деталей, например, иголки моментально рассыпаются и теряются. Ремонт планетарного редуктора лучше всего оставить профессионалам.
Стоит отметить, что на сегодняшний день планетарный редуктор весьма распространен и используется в большинстве грузовых автомобилей в ведущих мостах, а также очень часто встречается в роли лебедок.
Как и все редукторы, он может быть как одноступенчатым, так и многоступенчатым. Если Вы собираетесь приобрести механизм данного типа, то лучше всего покупать его у проверенных производителей, так как ремонт своими руками очень затруднен, а если он будет часто выходить из строя, то денег на него будет уходить много. В данной статье мы попытались собрать общую информацию по устройствам планетарного типа использующихся для производства автомобилей. Также нужно сказать, что данный вид устройства очень интенсивно внедряется во многие сферы и отрасли благодаря своим очень весомым преимуществам.
Читать также: Как заточить лезвие бритвы джилет
Принцип работы
То, как будет функционировать этот агрегат зависит от кинематической схемы привода. Так подводку вращательного движения можно осуществлять к любому элементу этой системы, а снятие производить с какого-либо из оставшихся. Передаточное число зависит от того, согласно какой схемы организована подводка и съем вращательного движения.
Понимание того, как работает подобный редуктор, позволяет оценить сложность ремонта и восстановления.
Основными элементами планетарной передачи можно считать следующие:
- Солнечная шестерня: находится в центре;
- Водило: жёстко фиксирует друг относительно друга оси нескольких
- Планетарных шестерён (сателлитов) одинакового размера, находящихся в зацеплении с солнечной шестерней;
- Кольцевая шестерня (эпицикл): внешнее зубчатое колесо, имеющее внутреннее зацепление с планетарными шестернями.
Планетарная передача в режиме повышения скорости.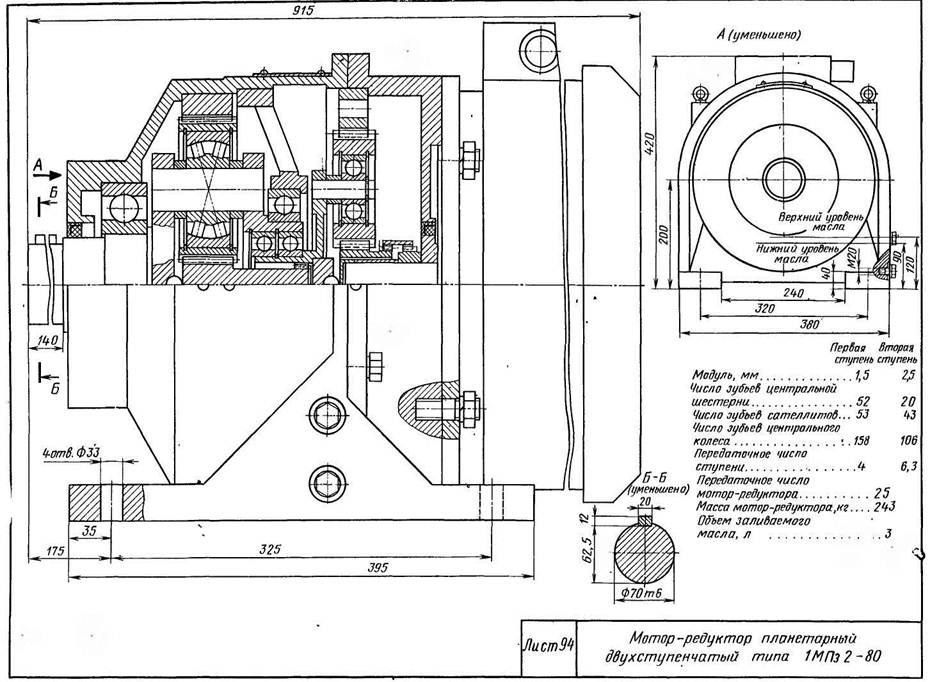 Водило (зелёное) вращается внешним источником. Усилие снимается с солнечной шестерни (жёлтая), в то время как кольцевая шестерня (красная) закреплена неподвижно. Красные метки показывают вращение входного вала на 45°.
Водило (зелёное) вращается внешним источником. Усилие снимается с солнечной шестерни (жёлтая), в то время как кольцевая шестерня (красная) закреплена неподвижно. Красные метки показывают вращение входного вала на 45°.
При использовании планетарной передачи в качестве редуктора один из трёх её основных элементов фиксируется неподвижно, другой элемент используется как ведущий, а третий – в качестве ведомого. Таким образом, передаточное отношение будет зависеть от количества зубьев каждого компонента, а также того, какой элемент закреплён.
Водило (зелёное) закреплено неподвижно, в то время как солнечная шестерня (жёлтая) вращается внешним источником. В данном случае передаточное отношение равно -24/16, или -3/2; каждая планетарная шестерня поворачивается на 3/2 оборота относительно солнечной шестерни, в противоположном направлении.
Часто планетарные передачи используются для суммирования двух потоков мощности (например, планетарные ряды двухпоточных трансмиссий некоторых танков и др. гусеничных машин), в этом случае неподвижно зафиксированных элементов нет. Например, два потока мощности могут подводиться к солнечной шестерне и эпициклу, а результирующий поток снимается с водила.
гусеничных машин), в этом случае неподвижно зафиксированных элементов нет. Например, два потока мощности могут подводиться к солнечной шестерне и эпициклу, а результирующий поток снимается с водила.
Разновидности планетарных редукторов
В зависимости от количества ступеней, которые они имеют планетарные редукторы подразделяют на:
- одноступенчатые;
- многоступенчатые.
Одноступенчатые более простые и при этом компактнее, меньше по размерам в сравнении с многоступенчатыми, обеспечивают более широкие возможности по передаче крутящего момента, достижения разных передаточных чисел. Обладающие несколькими ступенями являются достаточно громоздкими механизмами, при этом диапазон передаточных чисел, которые ими могут быть обеспечены, существенно меньше.
В зависимости от сложности конструкции они могут быть:
- простыми;
- дифференциальными.
Кроме этого, планетарные редукторы в зависимости от формы корпуса, используемых элементов и внутренней конструкции могут быть:
- коническими;
- волновыми;
- глобоидными;
- червячными;
- цилиндрическими.

Через них может передаваться движение между параллельными, пересекающимися и перекрещивающимися валами.
Общее описание [ править | править код ]
Конструкция [ править | править код ]
Механической основой планетарного редуктора может быть планетарная передача любой формы и состава. Принципиальная возможность работы планетарной передачи в режиме редуктора не зависит от формата распределения функций между тремя её основными звеньями (солнцем, водилом и эпициклом): любое звено может быть выбрано конструкторами как ведущее, и любое как ведомое. Но при этом, наличие у планетарной передачи двух степеней свобод требует снятия одной степени свободы для её работы в качестве редуктора; эта задача решается посредством блокировки третьего звена на корпус редуктора, а само звено получает название «опорное звено
».
Уникальные особенности [ править | править код ]
В контексте сравнения планетарной передачи с любыми другими типами зубчатых передач под использование их в качестве редуктора, таковыми особенностями являются: сходность входящего и исходящего потока мощности (например, валов) даже на однорядной планетарной передаче; возможность выбора из шести передаточных отношений даже на простой трёхзвенной планетарной передаче; две степени свободы любой планетарной передачи; возможность получения больших передаточных отношений в условиях ограниченного поперечного габарита.
Характеристики основных разновидностей этого устройства
Цилиндрические
Самые распространенные. Коэффициент полезного действия этих устройств достигает 95%. Они могут обеспечивать передачу достаточно больших мощностей. Передача движения осуществляется между параллельными и соосными валами. Они могут оснащаться прямозубными, косозубными и шевронными зубчатыми колесами. Коэффициент передачи может колебаться в пределах от 1,5 до 600.
Конические
Такое название они носят потому, что в них используются шестеренки, которые имеют коническую форму. Это обеспечивает плавность сцепки и способность выдерживать достаточно большие нагрузки. Могу иметь одну, две и три ступени. Валы в этой разновидности редукторов могут располагаться как горизонтально, так и вертикально.
Волновые
Они представляют собой конструкцию с гибким промежуточным числом. Состоят они из генератора волн, эксцентрика или кулачка, который обеспечивает растяжение гибкого колеса до достижения его контакта с неподвижным. При этом гибкое колесо имеет наружные зубья, а неподвижное — внутренние.
При этом гибкое колесо имеет наружные зубья, а неподвижное — внутренние.
К достоинствам такого типа редукторов относится:
- плавность хода;
- высокое передаточное число;
- возможность передачи движения через герметичные и сплошные стенки.
Они могут быть одно- и многоступенчатыми. Высокоскоростные оснащены подшипниками скольжения, а низкоскоростные — подшипниками качения.
Преимущества планетарных устройств
По сравнению с традиционными редукторами можно выделить следующее преимущества, которые имеет это устройство: они могут создавать огромные передаточные отношения скоростей при невысоком количестве шестеренок. Шестерни механизма имеют небольшой размер благодаря их количеству. Так, одно более массивное колесо распределяет равномерно нагрузку по нескольким сателлитам. Из этого следует, что устройство получается не очень большим и громоздким. Однако, расчет и практика показывают, что при высоких передаточных числах работоспособность и коэффициент полезного действия сильно снижаются. И как вывод всего вышесказанного, основными преимуществами являются:
И как вывод всего вышесказанного, основными преимуществами являются:
- Большие передаточные числа;
- Невысокая масса;
- Относительная компактность;
- Его можно чинить и собирать своими руками.
Такие преимущества требуют и соответствующего изготовления. Начиная с расчета, проектирования и заканчивая изготовлением – все должно быть прецизионно точно. Эти редукторы нашили очень широкий ряд применений в различных отраслях: прибостроительной, станкостроительной, машиностроительной и т.д. В данной статье остановимся более подробно на применении этого устройства в машиностроительной отрасли.
Усовершенствование механической бетономешалки или как сделать редуктор самому
При строительстве дома, нежилых сооружений, то есть сарая, гаража в качестве необходимого оборудования всегда выступает бетономешалка. Покупать её действительно накладно, тем более, что хозяин не собирается стоиться всю свою жизнь. Но изготовить её самостоятельно вполне возможно и не очень сложно, если использовать инструкции. Можно использовать готовую механическую конструкцию, а можно все изготовить самому. Конструкция может быть как для стационарного использования, так и передвижной. Тогда можно использовать старую тележку на колёсах.
Можно использовать готовую механическую конструкцию, а можно все изготовить самому. Конструкция может быть как для стационарного использования, так и передвижной. Тогда можно использовать старую тележку на колёсах.
Один из примеров изготовления самодельной бетономешалки
Изготовить планетарный редуктор своими руками, который будет вращать емкость бетономешалки, несложно. Скорость перемешивания бетона не должна быть высокой. Он является посредником между электродвигателем и нашим баком и будет регулировать скорость вращения через вал редуктора. При его изготовлении важную роль играет корпус редуктора, в котором будут находиться валы, оси с необходимой соосностью, а также шестерни должны быть выставлены с необходимым зазором. Если нет возможности подобрать необходимого размера корпус, нужно или переделать из готового или сварить новый. При сварке обязательно нужно учитывать деформацию металла.
Иные мастера советуют варить корпус полностью и использовать в качестве гнёзд для подшипников опоры обрезки труб, которые можно выставить в необходимом положении и закрепить или при помощи сварки или болтового соединения.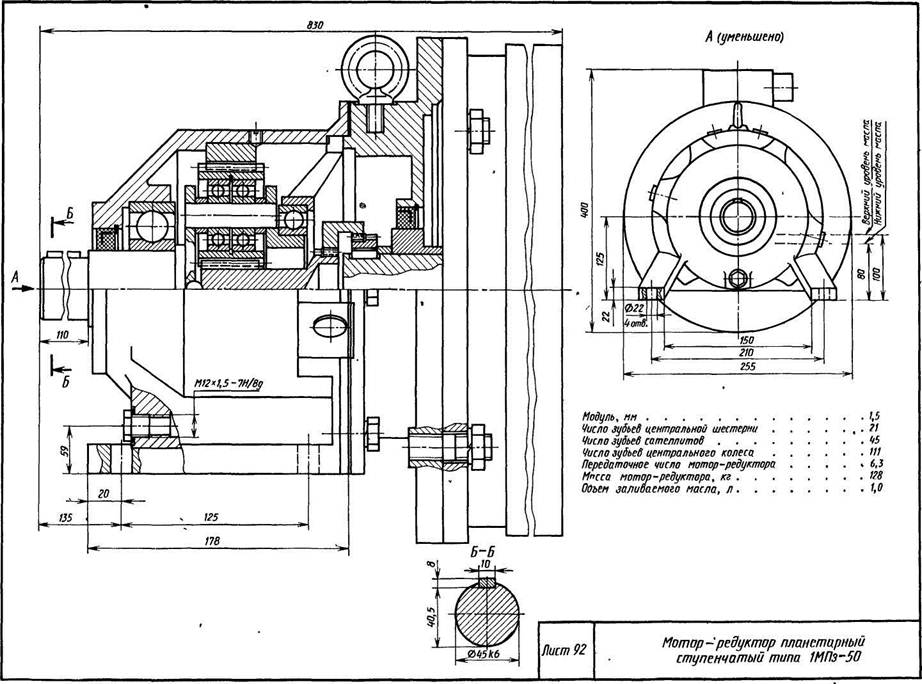 Что бы была возможность смазывать наш редуктор, крышку делают съемной.
Что бы была возможность смазывать наш редуктор, крышку делают съемной.
Изготавливают валы и оси, которые будут служить опорой шестерням, из стали с хорошими характеристиками по прочности. Шестерни на них должны быть закреплены жёстко. Ось используют в конструкции в случае, когда нужна в редукторе промежуточная шестерня, которую можно застопорить на оси или стопорной разрезной шайбой или гайкой с упорным буртиком.
Примерный набор валов и шестерен
Валы опираются на опорные подшипники и их правильный подбор влияет на работоспособность всего редуктора. Лучше всего выбрать закрытый подшипник, что бы не приходилось часто разбирать конструкцию и смазывать подшипники. Выбор подшипника зависит также и от вида зуба у шестерни. Прямозубые шестерни требуют обычных однорядных, лучше двухрядных шарикоподшипников, а косозубые работают лучше с радиально упорным подшипником, причем лучше выбрать роликовый.
Шестерни изготовить достаточно сложно, лучшим вариантом будет снять их со старого списанного оборудования.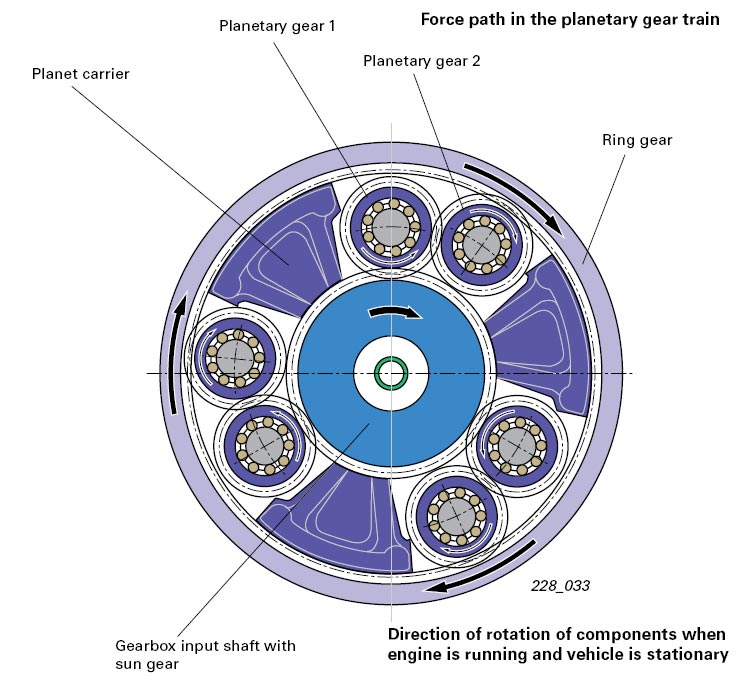 Главное, что бы они были парами и отвечали вашей задумке по количеству зубьев. Для этого нужно рассчитать передачу. Допустим, бетономешалка должна вращаться со скоростью 35 оборотов за одну минуту. Двигатель дает 1000 оборотов за одну минуту. Производим вычисление: 1000/35 = 28. Значит, диаметр одной шестерни и её зубьев должен также соотноситься в диаметром другой шестерни.
Главное, что бы они были парами и отвечали вашей задумке по количеству зубьев. Для этого нужно рассчитать передачу. Допустим, бетономешалка должна вращаться со скоростью 35 оборотов за одну минуту. Двигатель дает 1000 оборотов за одну минуту. Производим вычисление: 1000/35 = 28. Значит, диаметр одной шестерни и её зубьев должен также соотноситься в диаметром другой шестерни.
Смазываем их жидким маслом так, что бы нижние зубья были им покрыты и выставляем необходимый зазор, регулируя его так, для того, что бы уменьшить шум в работе, и выдерживалась необходимая нагрузка. Необходимо установить и сальниковые уплотнители, что бы не просачивалось масло. Также необходимо установить крышки подшипников, которые также можно подобрать уже готовыми.
Далее свариваем раму и устанавливаем на неё вашу емкость, предварительно убедившись в её герметичности, если вы используете подручный материал. Если будем изготавливать подвижной вариант бетономешалки, привариваем стойки к тележке и устанавливаем вашу емкость на тележку. Вы должны обеспечить возможность опрокидывания ёмкости для выгрузки бетона. Для этого крепление на раму делаем подвижным при помощи осей или болтов и сверху крепим штурвал. На основании закрепляем раму с прикреплённым двигателем и редуктором, собранным в одно целое и крепим наш узел на середину днища, на который предварительно при помощи сварки или болтов крепим так называемый венец. В принципе, вот и всё.
Вы должны обеспечить возможность опрокидывания ёмкости для выгрузки бетона. Для этого крепление на раму делаем подвижным при помощи осей или болтов и сверху крепим штурвал. На основании закрепляем раму с прикреплённым двигателем и редуктором, собранным в одно целое и крепим наш узел на середину днища, на который предварительно при помощи сварки или болтов крепим так называемый венец. В принципе, вот и всё.
| Внимание покупателей подшипников Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас: [email protected] Доставка подшипников по РФ и зарубежью. Каталог подшипников на сайте |
Внимание покупателей подшипников
Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас: +7 [email protected] Доставка подшипников по РФ и зарубежью. Каталог подшипников на сайте
themechanic. ru
ru
Видеокурс по этой теме
Планетарный Редуктор, Устройство и Принцип Работы, Кинематическая Схема одноступенчатого И двухступенчатого, Расчет и Ремонт Своими Руками
В классе редукторных механизмов планетарные редукторы занимают особое место. При довольно простой конструкции они могут создавать высокие передаточные числа и выдерживать значительные нагрузки. В чем особенность таких мотор-редукторов, как они работают и почему им отдают предпочтение крупные отрасли (приборо- и машиностроение, производство станков)? Разберемся.
Назначение и конструкция редуктора
Служит редуктор для обеспечения понижения передачи и при этом повышения силы крутящего момента. Для обеспечения работы этого механизма вращающийся вал присоединяется к его ведомому элементу.
Это устройство в классическом исполнении состоит из червячных или зубчатых пар, центрирующих подшипников, различных уплотнений, сальников и т. д. Примером планетарного редуктора является шариковый подшипник. Корпус устройства сложен из двух элементов:
д. Примером планетарного редуктора является шариковый подшипник. Корпус устройства сложен из двух элементов:
- крышки;
- основания.
Смазка всех составных элементов этого устройства производится путем разбрызгивания масла, но в некоторых особенных устройствах это осуществляется при помощи масляного насоса в принудительном порядке.
Обслуживание и ремонт
Компактные размеры и высокая эффективность планетарного редуктора – это результат его устройства, которое предполагает большое количество прямых контактов зубьев. А такие контакты при постоянной работе приводят к быстрому истиранию мелких деталей. Именно поэтому ресурс и качество долгосрочной работы становятся производной правильного обслуживания оборудования. Этот вид механизма требует большего внимания, чем многие аналоги. В центре сервисной программы:
- Контроль уровня и регулярное добавление масла. Смазка, заливаемая в корпус, работает на решение 2 главных проблем: интенсивной выработки тепла и истирания малых деталей (зубьев).
 Со временем она вырабатывается, засоряется металлической стружкой, теряет основные качества. Потому требует периодической полной замены или долива. Для планетарной передачи редуктора особенно важен грамотный выбор смазочного материала (по рекомендации производителя).
Со временем она вырабатывается, засоряется металлической стружкой, теряет основные качества. Потому требует периодической полной замены или долива. Для планетарной передачи редуктора особенно важен грамотный выбор смазочного материала (по рекомендации производителя). - Профессиональный плановый и внеплановый ремонт. Его должны производить специалисты, которые умеют работать с данным классом устройств. Часто в рамках регулярного или срочного ремонта проводится замена подвижных деталей – их выбор тоже необходимо производить с учетом рекомендаций компании, которая изготовила мотор-редуктор.
- Постоянный контроль состояния. Регулярная диагностика позволит выявить большинство поломок на раннем этапе и тем самым снизить риски технико-технологических процессов, в которых используется планетарный редуктор. Частые признаки неисправностей, которые можно определить, не имея специальных знаний: сильные нехарактерные шумы, усиливающаяся вибрация, работа рывками, перегрев корпуса.

Принцип работы
То, как будет функционировать этот агрегат зависит от кинематической схемы привода. Так подводку вращательного движения можно осуществлять к любому элементу этой системы, а снятие производить с какого-либо из оставшихся. Передаточное число зависит от того, согласно какой схемы организована подводка и съем вращательного движения.
Понимание того, как работает подобный редуктор, позволяет оценить сложность ремонта и восстановления.
Как правильно переключать передачи при движении на велосипеде с планетарной втулкой
Однако, если каждый тормоз наносится на каждое солнце одновременно, передача блокируется и не вращается. Каждый рычаг ограничивает вращение или останавливает свою соответствующую солнечную шестерню, взаимодействуя с ступенчатой областью солнечной шестерни, так что рычаг входит в зацепление с поверхностью ступени и ограничивает вращение солнца в одном направлении. Механизм может зацеплять солнечные шестерни радиально снаружи или радиально внутри в зависимости от требуемой конфигурации.
По мере изменения профиля рычаги перемещаются либо в качестве тормоза, либо в открытом состоянии, и обеспечивают свободное перемещение соответствующей солнечной шестерни. Сдвиговый кулачок 600 входит в зацепление с валиками 601 сдвига. Каждый валик сдвига 601 входит в зацепление с соответствующей подушкой или элементом 602. Шестерня Р2 закреплена на валу 201. Тормоз 1 содержит элемент 901 сдвига, который входит в зацепление с зубьями 212.
Велосипедами с планетарной втулкой это очень удобно управлять, и езда с этими приспособлениями очень упрощается, поскольку не возникает проблем с переключением скоростей. Поскольку эти приспособления сами переключают скорость, когда это необходимо. Однако следует ознакомиться с определенными принципами и правилами переключения скоростей:
- Лучше всего совершать переключение передачей, когда давление с цепи полностью снято, в противном случае можно просто не переключиться и сломать весь механизм и порвать цепь;
- Передачу нужно повышать прямо перед горой, а не во время преодоления ее;
- Не следует переключаться одновременно на несколько передач. Все нужно делать последовательно – сначала нужно переключать первую передачу и немного разогнаться, затем вторую по такому же принципу следует переходить на третью и так далее. Весь принцип работы такой же, как и у автомобильной коробки передач;
- Необходимо избегать все возможных перекосов цепи.
Процесс переключения:
- У всех современных велосипедах, в передней части расположены 2-3 звезды, а в задней 8-10 звезд;
- Нумерация звезд от 1 до 3 происходит в сторону увеличения звезд, а нумерация задних звезд от 1 до 6, в сторону уменьшения звезд.

Для того чтобы этот процесс стал ясен, можно рассмотреть на примере велосипеда с приводом 3х8:
- Большую переднюю звезду нужно использовать при движении на ровном асфальтовом покрытии. Совместно с этой звездой необходимо использовать задние звезды с номерами 8 до 4;
- Среднюю переднюю звезду применяют при движении на грунтовой дороге, с плохим асфальтовым покрытием. С ней используются задние звезды с 6 по 2;
- Маленькую переднюю звезду используют при езде на крутых подъемах и спусках, по ухабам и кочкам. С ней используют задние звезды с 5 по 1.
Разновидности планетарных редукторов
В зависимости от количества ступеней, которые они имеют планетарные редукторы подразделяют на:
- одноступенчатые;
- многоступенчатые.
Одноступенчатые более простые и при этом компактнее, меньше по размерам в сравнении с многоступенчатыми, обеспечивают более широкие возможности по передаче крутящего момента, достижения разных передаточных чисел.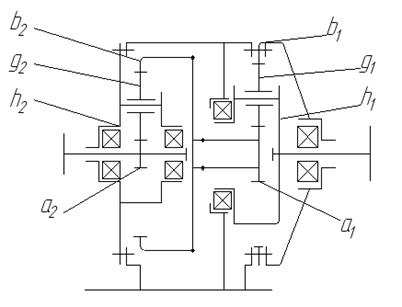 Обладающие несколькими ступенями являются достаточно громоздкими механизмами, при этом диапазон передаточных чисел, которые ими могут быть обеспечены, существенно меньше.
Обладающие несколькими ступенями являются достаточно громоздкими механизмами, при этом диапазон передаточных чисел, которые ими могут быть обеспечены, существенно меньше.
В зависимости от сложности конструкции они могут быть:
- простыми;
- дифференциальными.
Кроме этого, планетарные редукторы в зависимости от формы корпуса, используемых элементов и внутренней конструкции могут быть:
- коническими;
- волновыми;
- глобоидными;
- червячными;
- цилиндрическими.
Через них может передаваться движение между параллельными, пересекающимися и перекрещивающимися валами.
Достоинства и недостатки
Широкая область применения прежде всего связана с основными преимуществами механизма. Многие свойства такие же, как у цилиндрического варианта исполнения, так как в обоих случаях применяются шестерни. Преимущества следующие:
- Компактность. Многие модели характеризуются небольшими размерами, за счет чего упрощается установка.
 Небольшие габаритные размеры также позволяют создавать механизмы с небольшой массой. За счет этого существенно повышается эффективность рассматриваемого устройства.
Небольшие габаритные размеры также позволяют создавать механизмы с небольшой массой. За счет этого существенно повышается эффективность рассматриваемого устройства. - Сниженный уровень шума. Это свойство достигается за счет установки конических колес с косым зубом. За счет применения большого количества зубьев также обеспечивается точность хода основных элементов. Даже при большой нагрузке и скорости вращения основных элементов сильного гула не возникает, что и стало причиной широкого распространения планетарных редукторов.
- Малая нагрузка, оказываемая на опоры. Обычные редуктора характеризуются тем, что нагрузка оказывается на вал, который со временем может сорвать. Также нагрузка оказывает влияние на подшипники, повышая степень их износа. Со временем все приведенные выше причины приводят к необходимости выполнения обслуживания.
- Снижается нагрузка на зубья. Это достигается за счет ее равномерного распределения и большого количества задействованных зубьев. Часто встречается проблема, связанная с истиранием рабочей части зубьев.
 За счет этого они начинают не плотно прилегать друг к другу, последствия подобного явления заключается в повышенном износе и появлении шума.
За счет этого они начинают не плотно прилегать друг к другу, последствия подобного явления заключается в повышенном износе и появлении шума. - Обеспечивается равномерное разбрасывание масла на момент работы. Как и при функционировании любого другого редуктора, в рассматриваемом случае большое значение имеет степень смазки рабочей поверхности.
- Длительный эксплуатационный срок. Особенности расположения сателлитов приводит к взаимному компенсированию оказываемой силы.
- Повышенной передаточное отношение. Этот показатель считается основным. Передаточное соотношение может варьировать в достаточно большом диапазоне.
В целом можно сказать, что есть довольно большое количество причин, по которым применяется именно подобный механизм для передачи вращения. КПД планетарного редуктора относительно невысокое, что можно назвать существенным недостатком подобного варианта исполнения. Кроме этого, коэффициент полезного действия существенно падает при непосредственном использовании устройства, так как со временем оно изнашивается.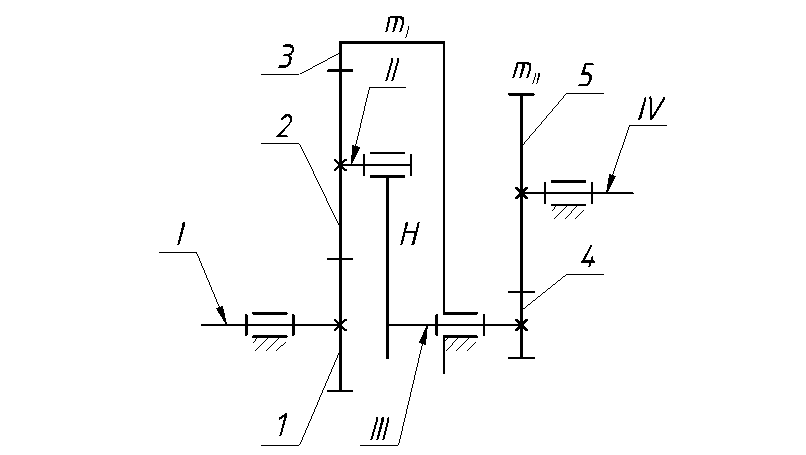
Кроме этого следует уделить внимание тому, что планетарный редуктор является сложной конструкцией, при изготовлении и установке которой возникают трудности.
Незначительное отклонение в размерах становится причиной уменьшения основных свойств, а также появления серьезных неисправностей.
Характеристики основных разновидностей этого устройства
Цилиндрические
Самые распространенные. Коэффициент полезного действия этих устройств достигает 95%. Они могут обеспечивать передачу достаточно больших мощностей. Передача движения осуществляется между параллельными и соосными валами. Они могут оснащаться прямозубными, косозубными и шевронными зубчатыми колесами. Коэффициент передачи может колебаться в пределах от 1,5 до 600.
Они могут обеспечивать передачу достаточно больших мощностей. Передача движения осуществляется между параллельными и соосными валами. Они могут оснащаться прямозубными, косозубными и шевронными зубчатыми колесами. Коэффициент передачи может колебаться в пределах от 1,5 до 600.
Конические
Такое название они носят потому, что в них используются шестеренки, которые имеют коническую форму. Это обеспечивает плавность сцепки и способность выдерживать достаточно большие нагрузки. Могу иметь одну, две и три ступени. Валы в этой разновидности редукторов могут располагаться как горизонтально, так и вертикально.
Волновые
Они представляют собой конструкцию с гибким промежуточным числом. Состоят они из генератора волн, эксцентрика или кулачка, который обеспечивает растяжение гибкого колеса до достижения его контакта с неподвижным. При этом гибкое колесо имеет наружные зубья, а неподвижное — внутренние.
К достоинствам такого типа редукторов относится:
- плавность хода;
- высокое передаточное число;
- возможность передачи движения через герметичные и сплошные стенки.

Они могут быть одно- и многоступенчатыми. Высокоскоростные оснащены подшипниками скольжения, а низкоскоростные — подшипниками качения.
Рабочий процесс
Если вращать коронную шестерню, соединенную с ведущим валом, при свободно вращающейся на подшипниках солнечной шестерне, то водило, соединенное с ведомым валом, не будет вращаться. В этом случае сателлиты будут передавать вращение солнечной шестерне в обратном направлении с передаточным числом, которое зависит от соотношения диаметров сцепленных шестерен.
В случае если солнечную шестерню затормозить, то при вращении коронной шестерни, сателлиты, обкатываясь по неподвижной солнечной шестерне, будут вести за собой водило, вращая ведомый вал с необходимым передаточным числом.
Если же жестко соединить между собой солнечную шестерню и водило, например, при помощи муфты сцепления, планетарный механизм будет замкнут — заблокирован и начнет вращаться, как одно целое. При этом число оборотов ведущего и ведомого валов будет одинаковым, передаточное число равно 1,0.
Возможны и другие случаи использования планетарной передачи, когда ведущая часть — солнечная шестерня, а ведомая — коронная.
Рассмотренная простейшая планетарная передача, у которой сателлиты одновременно входят в зацепление с солнечной и коронной шестернями, носит название передачи с внешним и внутренним зацеплением.
Ремонт редуктора своими руками
Ремонт редуктора своими руками является весьма непростой задачей. Так, данный механизм очень непростой и состоит из множества частей. При ремонте своими руками часто можно даже при разборке не ведая, что внутри просто растерять целую кучу маленьких деталей, например, иголки моментально рассыпаются и теряются. Ремонт планетарного редуктора лучше всего оставить профессионалам.
Как и все редукторы, он может быть как одноступенчатым, так и многоступенчатым. Если Вы собираетесь приобрести механизм данного типа, то лучше всего покупать его у проверенных производителей, так как ремонт своими руками очень затруднен, а если он будет часто выходить из строя, то денег на него будет уходить много. В данной статье мы попытались собрать общую информацию по устройствам планетарного типа использующихся для производства автомобилей. Также нужно сказать, что данный вид устройства очень интенсивно внедряется во многие сферы и отрасли благодаря своим очень весомым преимуществам.
В данной статье мы попытались собрать общую информацию по устройствам планетарного типа использующихся для производства автомобилей. Также нужно сказать, что данный вид устройства очень интенсивно внедряется во многие сферы и отрасли благодаря своим очень весомым преимуществам.
Ремонт планетарных втулок
Планетарные втулки – надежные детали. При правильной эксплуатации они способны прослужить в течение продолжительного времени. Покупая эту деталь у проверенного производителя, вероятность последующего возникновения проблем с ней минимальная.
Надо понимать, что планетарная втулка обладает очень сложной конструкцией. Без опыта и знаний провести обслуживание или ремонт подобного механизма невозможно. Поэтому при возникновении проблем обращайтесь к специалистам. Не пытайтесь самостоятельно провести ремонтные работы, с большой вероятностью после неквалифицированного обслуживания, деталь полностью выйдет из строя, ее придется заменять.
Не пытайтесь самостоятельно провести ремонтные работы, с большой вероятностью после неквалифицированного обслуживания, деталь полностью выйдет из строя, ее придется заменять.
Планетарный редуктор из деталей стартёра
Этот механизм можно назвать ключевым инженерно-техническим устройством. Его можно описать как механизм преобразования поступающего крутящего момента с последующей передачей на другие системы. Указанное определение характеризует общий принцип работы, а в более широком смысле редуктором можно назвать любой преобразователь направления движения, давления или вращающего момента.
Ключевыми характеристиками таких устройств считаются:
- КПД;
- количество вращательных валов;
- передаваемая мощность;
- назначение.
Существует множество видов редукторов: механические, газовые, редукторы давления воды, турбинные и другие. Они снижают давление жидкой или газообразной среды и способны изменять направление потока.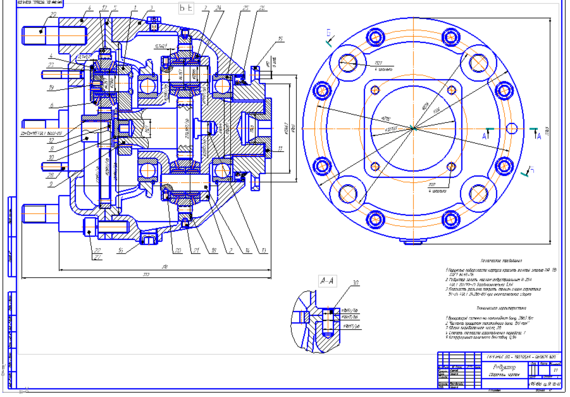 Их работа основывается на схожем принципе, однако внутреннее устройство и сам механизм преобразования отличаются. Корректная классификация редукторов возможна только при комплексном рассмотрении всех ключевых особенностей конкретного типа.
Их работа основывается на схожем принципе, однако внутреннее устройство и сам механизм преобразования отличаются. Корректная классификация редукторов возможна только при комплексном рассмотрении всех ключевых особенностей конкретного типа.
Классификация по основным признакам
Современные инженерно-технические стандарты предусматривают классификацию редукторов по следующим признакам:
- конструкция используемой передачи;
- пространственное расположение элементов;
- конструктивное исполнение.
По пространственному расположению ключевых элементов эти устройства подразделяются на редукторы вертикального исполнения и традиционные горизонтальные. Конструктивное исполнение предусматривает два дополнительных вида: чистый механический редуктор, и редуктор с двигательной установкой (мотор-редуктор). Однако общепринятой классификацией редукторов считается таковая по типу используемого передаточного узла (передачи).
Редукторы с цилиндрической и конической передачей
Коническо-цилиндрические редукторы
В качестве передаточного узла используется зубчатая передача цилиндрической или конической формы. Показатель КПД редукторов этого типа чрезвычайно высок: от 80 до 98% в зависимости от количества звеньев. Важной особенностью цилиндрических и конических редукторов считается отсутствие нагревающихся элементов. Из-за простоты своего внутреннего устройства они не нуждаются в дополнительном охлаждении или усилении конструкции, что объясняет их высокую надежность и простоту в эксплуатации.
Показатель КПД редукторов этого типа чрезвычайно высок: от 80 до 98% в зависимости от количества звеньев. Важной особенностью цилиндрических и конических редукторов считается отсутствие нагревающихся элементов. Из-за простоты своего внутреннего устройства они не нуждаются в дополнительном охлаждении или усилении конструкции, что объясняет их высокую надежность и простоту в эксплуатации.
Отзывы о комбинированных устройствах
Комбинированные редукторы, понижающие обороты, среди профессионалов высоко ценятся. Если верить отзывам, то модели хорошо подходят для асинхронных двигателей. Толкатели целесообразнее применять из стальных пластин. Для установки дисков используются упоры. Муфта у модификаций фиксируется за валом. Если верить отзывам экспертов, то фиксатор можно вырезать из обычной пластины. Также надо отметить, что крышку целесообразнее устанавливать с винтовым зажимом.
Планетарные редукторы
Планетарные редукторы
Здесь рабочим элементом выступает планетарная передача, которая преобразует поступающий на нее крутящий момент. Планетарные передачи отличаются от стандартных принципом своей работы: в основе преобразования лежит вращательное движение в пределах одной геометрической оси. Особенности строения планетарных узлов позволяют создавать крайне компактные редукторы, которые широко используются в различных отраслях приборостроения и промышленности.
Планетарные передачи отличаются от стандартных принципом своей работы: в основе преобразования лежит вращательное движение в пределах одной геометрической оси. Особенности строения планетарных узлов позволяют создавать крайне компактные редукторы, которые широко используются в различных отраслях приборостроения и промышленности.
По своим характеристикам планетарные редукторы занимают промежуточное звено между цилиндрическими и червячными. Они имеют меньший КПД, чем у цилиндрических, однако более компактны и значительно долговечнее редукторов червячного типа. Между собой планетарные редукторы отличаются количеством передач, их расположением относительно главной оси, конструктивным исполнением.
Достоинства и недостатки
Широкая область применения прежде всего связана с основными преимуществами механизма. Многие свойства такие же, как у цилиндрического варианта исполнения, так как в обоих случаях применяются шестерни. Преимущества следующие:
- Компактность.
 Многие модели характеризуются небольшими размерами, за счет чего упрощается установка. Небольшие габаритные размеры также позволяют создавать механизмы с небольшой массой. За счет этого существенно повышается эффективность рассматриваемого устройства.
Многие модели характеризуются небольшими размерами, за счет чего упрощается установка. Небольшие габаритные размеры также позволяют создавать механизмы с небольшой массой. За счет этого существенно повышается эффективность рассматриваемого устройства. - Сниженный уровень шума. Это свойство достигается за счет установки конических колес с косым зубом. За счет применения большого количества зубьев также обеспечивается точность хода основных элементов. Даже при большой нагрузке и скорости вращения основных элементов сильного гула не возникает, что и стало причиной широкого распространения планетарных редукторов.
- Малая нагрузка, оказываемая на опоры. Обычные редуктора характеризуются тем, что нагрузка оказывается на вал, который со временем может сорвать. Также нагрузка оказывает влияние на подшипники, повышая степень их износа. Со временем все приведенные выше причины приводят к необходимости выполнения обслуживания.
- Снижается нагрузка на зубья. Это достигается за счет ее равномерного распределения и большого количества задействованных зубьев.
 Часто встречается проблема, связанная с истиранием рабочей части зубьев. За счет этого они начинают не плотно прилегать друг к другу, последствия подобного явления заключается в повышенном износе и появлении шума.
Часто встречается проблема, связанная с истиранием рабочей части зубьев. За счет этого они начинают не плотно прилегать друг к другу, последствия подобного явления заключается в повышенном износе и появлении шума. - Обеспечивается равномерное разбрасывание масла на момент работы. Как и при функционировании любого другого редуктора, в рассматриваемом случае большое значение имеет степень смазки рабочей поверхности.
- Длительный эксплуатационный срок. Особенности расположения сателлитов приводит к взаимному компенсированию оказываемой силы.
- Повышенной передаточное отношение. Этот показатель считается основным. Передаточное соотношение может варьировать в достаточно большом диапазоне.
В целом можно сказать, что есть довольно большое количество причин, по которым применяется именно подобный механизм для передачи вращения. КПД планетарного редуктора относительно невысокое, что можно назвать существенным недостатком подобного варианта исполнения. Кроме этого, коэффициент полезного действия существенно падает при непосредственном использовании устройства, так как со временем оно изнашивается.
Кроме этого следует уделить внимание тому, что планетарный редуктор является сложной конструкцией, при изготовлении и установке которой возникают трудности.
Незначительное отклонение в размерах становится причиной уменьшения основных свойств, а также появления серьезных неисправностей.
Червячные редукторы
Червячные редукторы
В качестве основного конструктивного элемента здесь выступает червячная передача, которая способна преобразовывать не только прямой крутящий момент, но и угловую скорость. Своему названию червячный редуктор обязан несущему винту, который осуществляет преобразование. Он представляет собой массивный спиралевидный винт, внешне похожий на земляного червяка. КПД червяных редукторов значительно ниже, чем у традиционных цилиндрических.
Страдает и надежность: из-за сложной конструкции червячные редукторы требуют тщательного соблюдения технологических стандартов, а при повышенной нагрузке могут выходить из строя. Тем не менее, этот тип редукторов незаменим в тех случаях, когда требуется установить передаточное соединение с перпендикулярно соотносящимися осями.
Тем не менее, этот тип редукторов незаменим в тех случаях, когда требуется установить передаточное соединение с перпендикулярно соотносящимися осями.
Чертежи конической модели
Данный понижающий редуктор можно сделать с продольными толкателями. Диски чаще всего устанавливаются на короткой стойке. Для переключения сцепления устанавливается рычаг. Многие модификации собираются с переходным держателем. Вал при этом фиксируется за стойкой. Для регулировки натяжения используется муфта. В конце работы останется только закрепить крышку. Двигатель с понижающим редуктором способен работать при частоте 50 гц.
Волновые редукторы
Волновые редукторы
В конструктивном плане волновой редуктор состоит из неподвижного корпуса с внутренними зубьями и гибкого элемента, который соединяется с ведущим валом. Гибкий элемент имеет овальную форму и вращается внутри корпуса, создавая волнообразные возмущения.
Волновые редукторы обеспечивают очень большое передаточное отношение — гораздо выше, чем таковое у любых других видов редукторов. Кроме того, относительная простота и компактность позволяет использовать их для соединения герметично отделенных отсеков.
Кроме того, относительная простота и компактность позволяет использовать их для соединения герметично отделенных отсеков.
Как сделать самодельный редуктор для мотоблока
Для самостоятельной сборки преобразующего устройства на мотоблок необходимо запастись следующими инструментами:
- штангенциркуль и металлическая линейка;
- набор отверток разного размера, в том числе и косая;
- пассатижи и кусачки;
- пила по металлу;
- электродрель с набором сверл по металлу;
- тиски;
- молотки – большой и маленький;
- резиновые прокладки.
Если вы решили самостоятельно собрать редуктор для своего мотоблока, обязательно проведите приблизительный расчет. Это поможет определить, как минимум, передаточное число и тип преобразующего устройства, который вам нужен.
Также с помощью предварительных расчетов вы сможете оценить габариты будущего передаточного устройства.
Чтобы сделать правильный расчет, определитесь с параметрами вашего двигателя. Для расчетов необходимо уточнить несколько данных:
Для расчетов необходимо уточнить несколько данных:
- Число оборотов коленвала двигателя. Однако эта величина не является постоянной: стоит «прибавить газ», и она значительно увеличится
. Поэтому расчеты основываются на базе – количество холостых оборотов плюс 10%. - Расчетное число оборотов для оси подвески. Оно высчитывается с учетом диаметра колес для определения выбега за один полный оборот
. На основе этого можно посчитать, с какой скоростью должна вращаться ось, чтобы обеспечить максимально комфортную скорость движения мотоблока. Это в среднем от 3 до 5 км/час.
Рассмотрим простой пример: мощность двигателя на холостом ходу с учетом увеличения на 10% составляет 600 оборотов/мин, а для обеспечения скорости 3 км/час требуется скорость вращения 200 об/мин. Следовательно, расчетное передаточное отношение редуктора составляет 3:1
. Иными словами, для уменьшения скорости вращения оси в три раза, чтобы обеспечить скорость движения 3 км в час, в три раза увеличивается крутящий момент.
Общие особенности и дополнительные характеристики
Как было отмечено ранее, редукторы практически не встречаются в чистом виде. Так, вертикальные цилиндрические редукторы чаще всего имеют несколько конических передач, расположенных горизонтально. В червячных редукторах используются двухступенчатые винты с дополнительным выходным валом. Кроме того, все редукторы могут изготавливаться с двух конструктивных вариантах: чисто механические и мотор-редукторы. Последние получили самое широкое распространение и представляют собой единое устройство, совмещающее в себе электродвигатель, редукторный механизм и различные вспомогательные элементы.
Сборка двухступенчатых устройств
Двухступенчатый понижающий редуктор способен работать с асинхронными двигателями высокой мощности. Современные модели выпускаются с продольными толкателями. При необходимости двухступенчатую модификацию можно изготовить самостоятельно. С этой целью берется блок и помещаются рабочие диски.
Вал важно тщательно обточить и напаять широкую головку. Для фиксации шестерни используется небольшой шток. Фиксатор устанавливается чаще всего в переднюю часть редуктора. Упор можно выточить из обычной стальной пластины небольшой толщины. Вал модификации не должен соприкасаться с рабочими дисками.
Для фиксации шестерни используется небольшой шток. Фиксатор устанавливается чаще всего в переднюю часть редуктора. Упор можно выточить из обычной стальной пластины небольшой толщины. Вал модификации не должен соприкасаться с рабочими дисками.
Также надо отметить, что устройства складываются с муфтой и без нее. Если рассматривать первый вариант, то в блок устанавливается рычаг сцепления. При этом пружина подбирается небольшого диаметра. Нажимной упор лучше фиксировать на коробке устройства.
Использование редукторов различных типов
Редукторы выступают в качестве основного элемента большинства сложных устройств и агрегатов. Они нашли применение практически во всех областях промышленности. В тяжелой промышленности наибольшее распространение получили цилиндрические и червячные редукторы, которые используются для передачи крутящего момента на рабочий инструмент.
В автомобилях редуктор — самый распространенный элемент. Коробка передач, карданный вал, тормозные системы, бензиновые насосы и регуляторы — во всех этих узлах используются редукторы различного типа.
Газовые редукторы и редукторы давления воды используются как в газодобывающей и перерабатывающей промышленности, так и на бытовом уровне (см. Добыча природного газа: особенности и подводные камни). Они позволяют контролировать давление жидкости или газа, изменять его направление.
Мотор-редукторы являются ключевыми элементами бытовой техники: миксеры, комбайны, стиральные машины и дрели используют планетарные или волновые мотор-редукторы для создания оптимальных режимов работы.
Обслуживание и ремонт
Сложность рассматриваемого механизма определяет то, что возникает необходимость в своевременном обслуживании и проведении ремонта. Для начала уделим внимание тому, каким образом проводится расчет планетарного редуктора. Среди особенностей этого процесса отметим следующие моменты:
- Определяется требуемое число передаточных ступеней. Для этого применяются специальные формулы.
- Определяется число зубьев и расчет сателлитов. Зубчатые колеса могут иметь самое различное число зубьев.
 В рассматриваемом случае их число довольно много, что является определяющим фактором.
В рассматриваемом случае их число довольно много, что является определяющим фактором. - Уделяется внимание выбору наиболее подходящего материала, так как от его свойств зависят и основные эксплуатационные характеристики устройства.
- Определяется показатель межосевого расстояния.
- Делается проверочный расчет. Он позволяет исключить вероятность допущения ошибок на первоначальном этапе проектирования.
- Выбираются подшипники. Они предназначены для обеспечения плавного вращения основных элементов. При выборе подшипника уделяется внимание тому, на какую нагрузку они рассчитаны. Кроме этого, не рекомендуется использовать этот элемент без смазки, так как это приводит к существенному износу.
- Определяется оптимальная толщина колеса. Слишком большой показатель становится причиной увеличения веса конструкции, а также расходов.
- Проводится вычисление того, где именно должны быть расположены оси шестерен. Это проводится с учетом размеров зубчатых колес и некоторых других моментов.
 Как правило, в качестве основы применяется чертеж, который можно скачать из интернета. Самостоятельно разработать проект по изготовления планетарного редуктора достаточно сложно, так как нужно обладать навыками инженера для проведения соответствующих расчетов и проектирования.
Как правило, в качестве основы применяется чертеж, который можно скачать из интернета. Самостоятельно разработать проект по изготовления планетарного редуктора достаточно сложно, так как нужно обладать навыками инженера для проведения соответствующих расчетов и проектирования.
— схема, детали, принцип работы, преимущества, недостатки Это зубчатая передача, состоящая из одной или нескольких внешних шестерен (сателлитных шестерен), вращающихся вокруг центральной (солнечной шестерни). Планетарная шестерня установлена на подвижном рычаге (водиле), который сам может вращаться относительно солнечной шестерни. Системы эпициклических зубчатых передач могут также включать в себя использование внешнего зубчатого венца или кольцевого кольца, которое входит в зацепление с планетарными шестернями.
На рисунке показан пример планетарной передачи. Он используется для увеличения скорости вывода. Водило планетарной передачи приводится в действие входным крутящим моментом. Солнечная шестерня обеспечивает выходной крутящий момент, а зубчатый венец неподвижен.
Солнечная шестерня обеспечивает выходной крутящий момент, а зубчатый венец неподвижен.
Передаточное число в планетарной передаче может различаться конструкцией зубьев шестерни и способами входного вращения в шестерню.
Детали планетарного редуктора:
Три основных компонента планетарной передачи:
1. Солнце: центральная шестерня
2. Водило планетарной передачи: удерживает одну или несколько периферийных планетарных шестерен одинакового размера в зацеплении с солнечной шестерней
3. Кольцевая или зубчатая передача: внешнее кольцо с обращенными внутрь зубьями, которые входят в зацепление с планетарной шестерней или шестернями
Во многих планетарных передачах, среди трех основных компонентов, один компонент удерживается неподвижно; один компонент вводится, обеспечивает питание системы, а последний компонент выводится, получает питание от системы. Отношение входного вращения к выходному вращению зависит от количества зубьев в каждой шестерне и от того, какой компонент удерживается неподвижно.
Отношение входного вращения к выходному вращению зависит от количества зубьев в каждой шестерне и от того, какой компонент удерживается неподвижно.
Планетарная коробка передач Схема:
простая планетарная коробка передач СхемаКонструкция планетарной коробки передач:
В планетарной коробке передач планетарная зубчатая передача является очень общим термином. По сути, он включает в себя 3 шестерни: солнечную шестерню, планетарную шестерню и зубчатый венец, основная концепция заключается в том, что множество передаточных чисел можно получить из небольшого объема по сравнению с другими типами зубчатых передач, которые занимают больше места. В отличие от простых зубчатых передач, планетарная зубчатая передача требует определения более одного входа для получения конкретного выхода, что делает анализ немного сложным и неинтуитивным.
Работа эпициклического редуктора:
Принцип работы эпициклического редуктора основан на том факте, что фиксация любой из шестерен, то есть солнечной шестерни, планетарной шестерни и кольцевой шестерни, выполняется для получения требуемого крутящего момента или выходной скорости.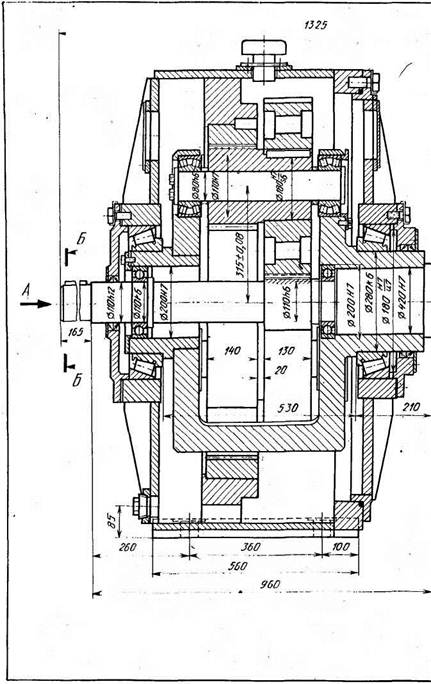 Поскольку фиксация любого из вышеперечисленных причин вызывает изменение передаточных чисел от высокого крутящего момента до высокой скорости. Итак, давайте посмотрим, как получаются эти передаточные числа.
Поскольку фиксация любого из вышеперечисленных причин вызывает изменение передаточных чисел от высокого крутящего момента до высокой скорости. Итак, давайте посмотрим, как получаются эти передаточные числа.
Первое передаточное число:
Это обеспечивает высокие передаточные числа крутящего момента для транспортного средства, которые помогают транспортному средству двигаться из его исходного состояния и получаются путем фиксации кольцевой шестерни, которая, в свою очередь, приводит планетарную передачу в движение. водило вращается за счет энергии, подаваемой на солнечную шестерню.
Второе передаточное число:
Обеспечивает высокие передаточные числа для транспортного средства, которые помогают транспортному средству развивать более высокую скорость во время движения. Эти передаточные числа получаются путем фиксации солнечной шестерни, которая, в свою очередь, делает водило планетарной передачи ведомым элементом. и кольцевой приводной элемент для достижения высоких передаточных чисел.
Передаточное число заднего хода:
Эта передача меняет направление выходного вала, что, в свою очередь, меняет направление движения автомобиля. солнечная шестерня водительского члена.
Примечание- Большее передаточное отношение скорости или крутящего момента может быть достигнуто за счет увеличения количества планетарной и солнечной шестерен в эпициклическом редукторе.
В одном случае водило планетарной передачи удерживается неподвижно, а солнечная шестерня используется в качестве входа. В этом случае планетарные шестерни просто вращаются вокруг своих осей со скоростью, определяемой количеством зубьев в каждой шестерне. Если солнечная шестерня имеет зубья S, а каждая планетарная шестерня имеет зубья P, то отношение равно -S/P. Это вращение планетарных шестерен может, в свою очередь, приводить в движение кольцевое пространство в соответствующем соотношении. Если кольцо имеет зубья P, то кольцо будет вращаться на число оборотов P/A за каждый оборот планетарных шестерен.
Итого:
1. Один оборот солнечной шестерни приводит к – S / P оборотам сателлитов
2. Один оборот планетарной шестерни приводит к P / A оборотам кольца
3. Один оборот солнечной шестерни приводит к -S / A оборотам кольца
В одной ситуации кольцо может также удерживаться фиксированным, с входом на водило планетарной передачи; выходное вращение затем производится солнечной шестерней. Эта конфигурация произведет увеличение передаточного числа, равное 1+A/S.
Все они описываются уравнением:
(2+n)ωa + 2ωs – 2(1+n) ωc = 0
Где n — коэффициент формы планетарной передачи, определяемый по формуле: n = Ns/ Np
Преимущества и недостатки планетарной передачиПреимущества планетарной коробки передач:
Планетарный редуктор предлагает ряд явных преимуществ, которые делают его интересной альтернативой традиционным типам передач, таким как редукторы с косозубыми и параллельными валами. в приложениях, требующих:
в приложениях, требующих:
- Высокие передаточные числа
- Компактный и легкий с передачей высокого крутящего момента
- Высокие радиальные нагрузки на выходной вал
- Работает тише
- Равномерное распределение нагрузки на все шестерни с большим контактом зубьев.
- Все шестерни постоянно находятся в зацеплении, поэтому смена одной шестерни на другую возможна без потерь.
• Сложность
• Сборка шестерен ограничена конкретными зубьями на передаточное число
• Расчеты эффективности затруднены
• Ведущее и ведомое оборудование должны быть на одной линии, чтобы избежать дополнительного зацепления
Применение планетарной зубчатой передачи:
- Хороший пример повседневное применение планетарной системы передач — автоматическая трансмиссия автомобиля.
- Планетарные зубчатые передачи используются в задней передаче токарных станков, дифференциалах автомобилей, подъемниках, шкивах, наручных часах и т.
 д.
д. - Планетарные зубчатые передачи используются для передачи высоких передаточных чисел с шестернями среднего размера в сравнительно меньшем пространстве.
Эл. к Сосудам под давлением Сосуды, резервуары и трубопроводы, которые транспортируют, хранят или получают жидкости, называются сосудами под давлением. Сосуд высокого давления определяется как сосуд с давлением…
Продолжить чтение
ссылка на Шарнирное соединение — детали, схема, расчет конструкции, применениеШарнирное соединение — детали, схема, расчет конструкции, применение
Шарнирное соединение Шарнирное соединение используется для соединения двух стержней, находящихся под действием растягивающих нагрузок. Однако, если соединение направляется, стержни могут выдерживать сжимающую нагрузку. Шарнирное соединение…
Продолжить чтение
Конструкция, детали, функции, соотношение и использование [PDF]
Из этой статьи вы узнаете что такое планетарная передача? Его конструкция, детали, функции, преимущества и использование объясняются Картинки . Если вам нужен файл PDF ? Скачать его можно в конце статьи.
Если вам нужен файл PDF ? Скачать его можно в конце статьи.
Что такое планетарная передача?
Планетарные передачи лежат в основе современного машиностроения и используются в основных промышленных машинах и электромобилях. Они также известны как эпициклические шестерни, состоят из двух шестерен, так что центр одной шестерни вращается вокруг центра другой.
Водило, соединяющее центры двух шестерен, вращает планетарную и солнечную шестерни так, что их делительные окружности катятся без проскальзывания. Точка делительной окружности планетарной передачи очерчивает эпициклоиду. В этом случае солнечная шестерня неподвижна, а планетарные шестерни вращаются вокруг солнечной шестерни.
В начале 1900-х годов первая трансмиссия с планетарными передачами была сделана на автомобиле Wilson-Pilcher, произведенном в Великобритании. В настоящее время большинство инженеров используют планетарные передачи в приложениях, требующих таких свойств, как высокая плотность крутящего момента, эффективность работы и долговечность.
Читайте также: Как работает распределитель зажигания в двигателе? [PDF]
Детали планетарной передачи
Ниже приведены основные части планетарной передачи:
- Солнечная шестерня (центральная шестерня)
- Несколько планетарных шестерен
- Кольцевая шестерня (внешняя шестерня)
- Водило планетарной передачи
№1 Солнечная шестерня (центральная шестерня)
В планетарной передаче солнечная шестерня приводит в движение окружающие ее планетарные шестерни, закрепленные на водиле во избежание проскальзывания во время работы. Когда солнечная шестерня приводится в движение, планетарные шестерни вращают зубчатый венец (также известный как внешняя шестерня).
#2 Многопланетарные шестерни
Обычно планетарная передача имеет две шестерни, одна планетарная шестерня входит в зацепление с солнечной шестерней, а другая входит в зацепление с планетарным зубчатым венцом. Они используются в качестве редукторов скорости. Они используются для замедления двигателей и увеличения крутящего момента.
Они используются для замедления двигателей и увеличения крутящего момента.
Основной и основной функцией планетарных передач является передача крутящего момента и изменение скорости вращения или крутящего момента между входным и выходным валами.
Зубчатый венец №3 (внешнее зубчатое колесо)
Нагрузка от солнечной шестерни распределяется на несколько планетарных шестерен, которые используются для привода внешнего кольца, вала или шпинделя. Зубчатый венец вращается в том же направлении, что и солнечная шестерня, обеспечивая тем самым обратное направление.
#4 Водило планетарной передачи
Водило планетарной передачи удерживает планетарную шестерню, которая вращается вокруг себя с вращением, противоположным водилу планетарной передачи. Обычно он соединяет центры двух шестерен и обеспечивает их вращение без проскальзывания.
Читайте также: Что такое шарнирный сустав и как он работает? [PDF]
Конструкция планетарной передачи
Планетарная передача — это очень общий термин, поскольку эта концепция очень адаптируема, в основном, она включает в себя. Три шестерни, солнечная шестерня, планетарная шестерня и зубчатый венец, а также множество передаточных чисел могут быть получены из небольшого объема по сравнению с другими типами зубчатых передач, которые занимают больше места.
Три шестерни, солнечная шестерня, планетарная шестерня и зубчатый венец, а также множество передаточных чисел могут быть получены из небольшого объема по сравнению с другими типами зубчатых передач, которые занимают больше места.
В отличие от простых зубчатых передач, планетарная передача требует определения более одного входа для получения конкретного выхода. Многие выходные данные можно получить, зафиксировав шестеренку, то есть сделав ее неподвижной, подав входную мощность на другую шестерню и получив выходную мощность от третьей шестерни.
Солнечная шестерня расположена в центре сборки. Он входит в зацепление с зубьями планетарных шестерен, планетарные шестерни представляют собой небольшие шестерни, встроенные в каркас, называемый водилом планетарной передачи.
Изготавливается из чугуна, алюминия или стали и имеет вал для каждой планетарной шестерни, планетарные шестерни окружают центральную ось солнечной шестерни и окружены кольцом, которое является самой большой частью простой набор.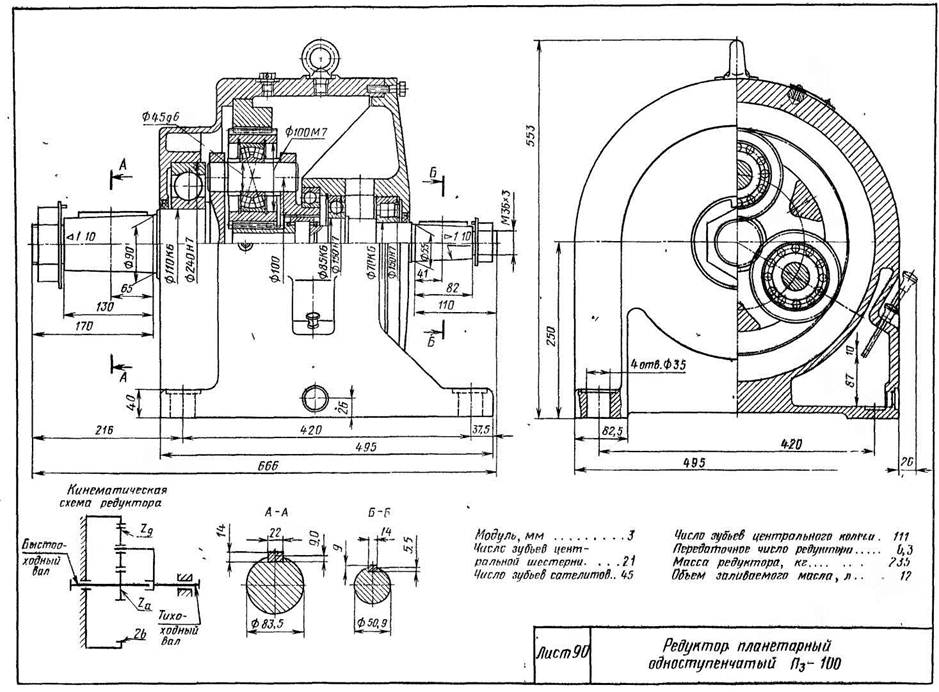
Солнце является центром Солнечной системы с планетами, вращающимися вокруг него, отсюда и название планетарной передачи.
Читайте также: Какие типы карданных валов используются в автомобилях?
Работа планетарной передачи
Каждый элемент планетарной передачи может вращаться или находиться в состоянии покоя, передача мощности возможна только через планетарную передачу. Поскольку один из членов находится в состоянии покоя, два члена сцеплены вместе.
Изображение: ВикипедияКогда ни один член не задержан или не заблокирован, существуют нейтральные условия. Любой из трех элементов может использоваться в качестве ведущего или входного элемента, в то время как другой элемент может быть удержан от вращения и, таким образом, становится неподвижным элементом, а третий элемент становится выходным элементом.
В зависимости от того, какой элемент является приводным, какой удерживается и какой приводится в движение, планетарная передача обеспечивает либо увеличение крутящего момента, либо увеличение скорости. Кроме того, направление вывода также может быть изменено с помощью различных комбинаций.
Кроме того, направление вывода также может быть изменено с помощью различных комбинаций.
В комбинациях и коронная шестерня, и солнечная шестерня являются входными элементами, они вращаются по часовой стрелке с одинаковой скоростью, внутренние зубья коронной шестерни, вращающейся по часовой стрелке, пытаются вращать планетарные шестерни по часовой стрелке, но солнечная шестерня, которая вращается по часовой стрелке, пытается вращать планетарные шестерни против часовой стрелки, эти противодействующие силы блокируют планетарные шестерни от вращения.
Таким образом, весь планетарный ряд вращается как единое целое, обеспечивая прямой привод.
Читайте также: Различные типы систем трансмиссии и их применение
Передаточное число планетарной передачи
Одноступенчатая планетарная передача состоит из кольцевого (кольца) с внутренними зубьями и окружающего его ленточного тормоза. В центре этой шестерни находится солнечная шестерня S, являющаяся частью входного вала. Солнечная шестерня и кольцевая шестерня соединены серией сателлитов P, установленных на водиле C и объединенных с выходным валом.
Солнечная шестерня и кольцевая шестерня соединены серией сателлитов P, установленных на водиле C и объединенных с выходным валом.
Для передачи крутящего момента солнечная шестерня, водило или кольцевая шестерня должны находиться в неподвижном состоянии.
Рассмотрена ситуация, когда неподвижна только кольцевая шестерня. При приводе вала входной солнечной шестерни с фиксированным ленточным тормозом кольцевой шестерни планетарные шестерни одновременно вращаются вокруг своих осей и вращаются вокруг оси входной солнечной шестерни по внутренней окружности кольцевой шестерни.
Таким образом, ведущий и вторичный валы поддерживают оси планетарной передачи, также вращаются, но с меньшей скоростью, чем входной вал.
Let,
- TA = количество зубьев на кольцевой, внутренней или кольцевой шестерне
- TS = количество зубьев на солнечной или центральной шестерне
- TP = количество зубьев на планетарной шестерне
- TC = количество эффективных зубьев на плече или водило планетарной передачи
Кроме того, TA = TS + 2TP и TC = TS + TA
Передаточное число первой передачи
Кольцевая шестерня удерживается в неподвижном состоянии, а водило планетарной передачи приводится в движение мощностью, подаваемой на солнечную шестерню.
Передаточное число второй передачи
Солнечная шестерня удерживается неподвижно. Водило планетарной передачи является ведомым элементом, а кольцевая шестерня — ведущим элементом.
Задняя передача
Здесь строгальный носитель удерживается неподвижно. Кольцевая шестерня приводится в движение солнечной шестерней, на которую подается мощность.
Преимущества планетарной передачи
- Обеспечивает более компактный узел, работающий вокруг общей центральной оси.
- Редукторы и корпуса редукторов имеют сравнительно меньшие габаритные размеры.
- Этот набор шестерен является более гибким по сравнению с обычным набором шестерен.
- Эти типы зубчатых передач занимают меньше места.
- Эта шестерня имеет высокое передаточное число и больший крутящий момент.
- Обычно имеет компактные размеры.
- Вместо нагрузки только на одну пару шестерен она распределяется по нескольким зубчатым колесам.
Недостатки планетарного редуктора
- Общая стоимость планетарного редуктора будет выше, чем у обычного редуктора.

- Конструкция и изготовление планетарных передач довольно сложны и сложны.
- Определение эффективности планетарной передачи было бы сложной задачей.
- Зубчатая передача требует точности передачи, поэтому это довольно сложно.
- Некоторые типы планетарных передач издают больше шума при работе.
- Чтобы игнорировать любую дополнительную передачу, ведущий и ведомый элементы должны сойтись.
Применение планетарной передачи
- Эти шестерни обычно используются для увеличения крутящего момента в роботах.
- Кроме того, он также используется в печатных машинах для уменьшения скорости роликов.
- Используется в упаковочных машинах для воспроизводимых продуктов в промышленности.
- Кроме того, он также используется в таких приводах, как колесный привод, гусеничный привод, конвейер, поворотный привод, привод подъемного устройства и привод лебедки.
- Они также используются в насосах, инжекторах ГНКТ и приводах режущих головок.

Подведение итогов
Планетарные передачи широко используются в различных отраслях промышленности. Поскольку шестерня является одним из важнейших компонентов планетарного механизма, эти шестерни будут влиять на всю систему трансмиссии.
Эти шестерни имеют много преимуществ, таких как повышенный крутящий момент, меньший сравнимый размер, меньший вес, более высокий КПД и многое другое.
Надеюсь, я рассказал все о « Планетарная передача ». Если у вас остались сомнения или вопросы по этой теме, вы можете связаться с нами или задать в комментариях, я вам отвечу. Если вам понравилось, поделитесь этим в кругу друзей и распространите знания.
Хотите получать бесплатные PDF-файлы прямо на свой почтовый ящик? Тогда подпишитесь на нашу рассылку.
Адрес электронной почты
Загрузить эту статью в формате PDF:
Щелкните здесь, чтобы загрузить
Кроме того, мы также написали множество статей, некоторые из которых упомянуты ниже:
- Как работает универсальный шарнир? Типы и применение
- Каков принцип работы маховика в двигателе?
- Типы шатунов: работа и применение
Внутреннее устройство коробки передач — Руководство по игре 0
Изменить эту страницуПереключить боковую панель оглавления
По сути, редуктор — это просто набор шестерен и корпус, который их соединяет. Редукторы имеют выходное передаточное число , конечное передаточное отношение между входным валом двигателя и конечным выходным валом.
Редукторы имеют выходное передаточное число , конечное передаточное отношение между входным валом двигателя и конечным выходным валом.
Клемма
- Редуктор
Также известен как передаточное число. В любой вращательной системе передачи мощности (обычно включающей двигатели и сервоприводы в FTC) передаточное отношение определяет как количество оборотов на входе системы, так и количество оборотов на выходе.
Например, мотор-редуктор NeveRest 20 состоит из немодифицированного мотора NeveRest и планетарного редуктора с передаточным числом 20:1 (или, если говорить, «20 к 1»). Это означает, что для того, чтобы выходной вал редуктора повернулся 1 раз, входной вал двигателя должен повернуться 20 раз. Передаточные числа являются одним из наиболее важных соображений при проектировании компонента силовой передачи.
Любой двигатель или сервопривод FTC имеет два свойства: скорость и крутящий момент (или вращательное усилие). Эти два свойства обратно пропорциональны, что означает, что увеличение скорости уменьшает крутящий момент, и наоборот.
Например, если кто-то хочет сделать механизм быстрее за счет крутящего момента, удвоив скорость этой коробки передач 20: 1, он уменьшит передаточное отношение в 2 раза. Поскольку 20 разделить на 2 равно 10, новое желаемое соотношение будет 10:1 (это называется ускорением). Однако, если кто-то хочет вместо этого удвоить крутящий момент, сделав систему более мощной и надежной за счет скорости, он должен увеличить передаточное число в 2 раза, оставив передаточное число 40:1 (это называется передаточным числом). вниз).
Наиболее распространенными способами повышения или понижения передачи являются редукторы, шестерни, звездочки и шкивы с ременным приводом, все из которых существуют в различных размерах.
В FTC редукторы могут быть более распространены, чем вы думаете — к каждому двигателю прикреплен редуктор. Эти редукторы относятся к одному из следующих двух типов: цилиндрические или планетарные. Ниже мы даем подробный анализ каждого из этих типов редукторов.
Цилиндрические редукторы
Term
- Цилиндрический редуктор
Цилиндрический редуктор имеет цилиндрические шестерни, которые расположены друг над другом. Редуктор достигается за счет шестерен разного размера в одной плоскости.
представляют собой набор передаточных чисел, часто наложенных друг на друга для достижения большого сложного передаточного числа (например, 40: 1). Каждое отдельное передаточное число имеет только две передачи — одна может быть 8:1, другая может быть 5:1, но конечное передаточное число будет 40:1. Эти редукторы используются в двигателях серии Andymark NeveRest Classic и goBILDA серии 5201, а также в двигателях REV HD Hex. Из-за особенностей конструкции этих коробок передач каждая передача имеет только несколько зубьев от каждой включенной шестерни, и эти зубья несут всю нагрузку коробки передач.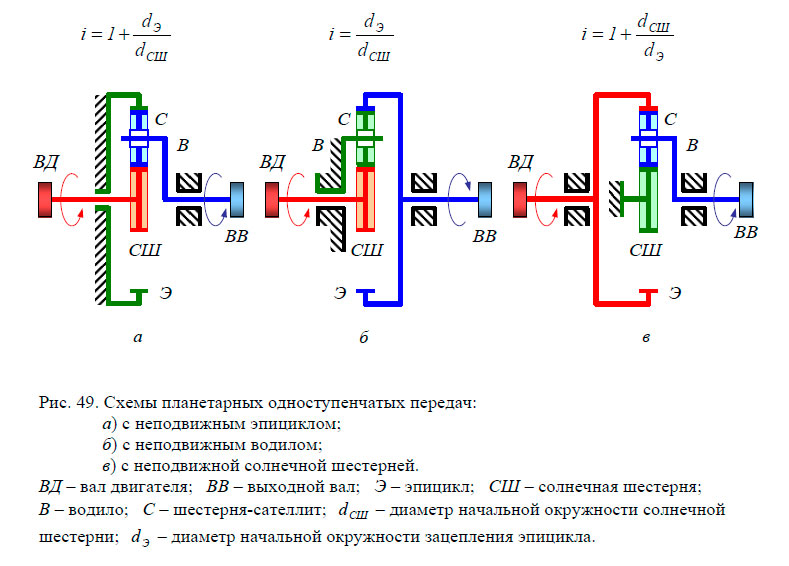
Наконечник
Не рекомендуется использовать цилиндрические редукторы в устройствах с высокими нагрузками, таких как трансмиссии или рычаги. Вместо этого используйте планетарные редукторы.
Пример цилиндрического редуктора. Обратите внимание, что все шестерни зацепляются только с одной другой шестерней.
Преимущества цилиндрических редукторов
Как правило, цилиндрические редукторы дешевле планетарных. Однако в FTC это изменение цены часто минимально. Планетарный редуктор 20:1 от REV всего на 4 доллара больше, чем цилиндрический редуктор 20:1
от разных производителей не взаимозаменяемы. Однако они сопоставимы и практически неотличимы по производительности. Здесь главное учитывать вашу желаемый редуктор, желаемые соединения двигателя и желаемый тип выходного вала .
Планетарные редукторы
В планетарных редукторах используется более сложная система зубчатых передач, обеспечивающая надежную передачу в компактном пространстве. В автомобильной технике планетарные редукторы могут достигать нескольких различных передаточных чисел без изменения размера шестерни, но все планетарные редукторы, которые вы увидите в FTC, достигают только одного передаточного числа.
В автомобильной технике планетарные редукторы могут достигать нескольких различных передаточных чисел без изменения размера шестерни, но все планетарные редукторы, которые вы увидите в FTC, достигают только одного передаточного числа.
Терминал
- Планетарный редуктор
Планетарная передача состоит из центральной шестерни (солнечной шестерни), вокруг которой вращаются шестерни меньшего размера (планетарные шестерни). Внешний радиус имеет зубчатый венец, который удерживает другие шестерни на месте.
используются в серии Andymark Orbital, некоторых планетарных и ультрапланетарных двигателях REV HD Hex, а также в широком ассортименте планетарных мотор-редукторов goBILDA. Кроме того, AndyMark продает несколько планетарных коробок передач на вторичном рынке под названием NeveRest Sport и 57 Sport, а VEXpro продает настраиваемую коробку передач VersaPlanetary. Как видно из рисунка ниже, на одну ступень зацепляется больше зубьев, чем в цилиндрическом редукторе.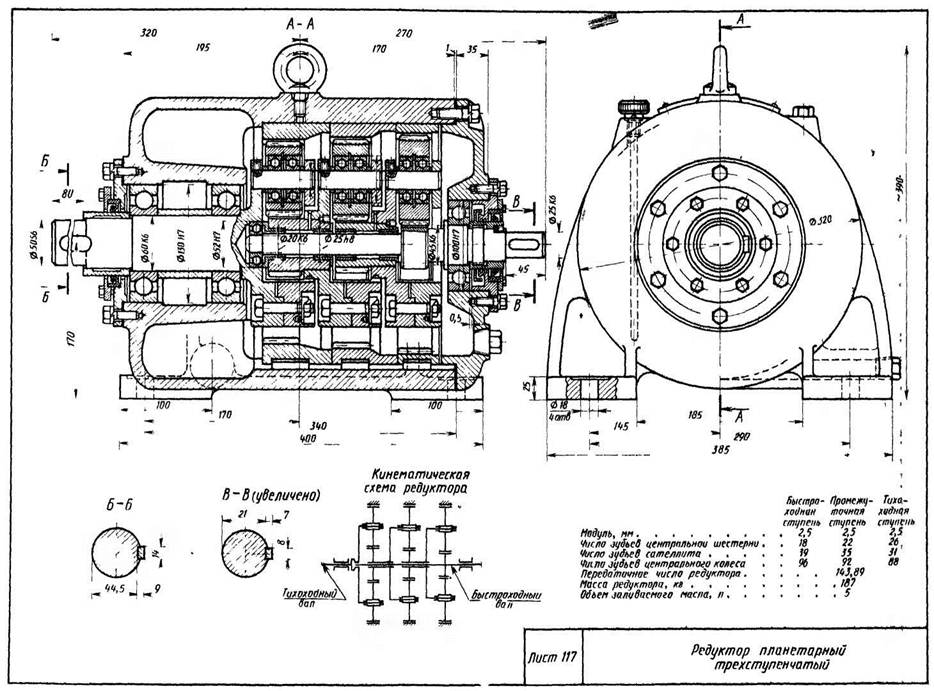
Пример ступени планетарного редуктора. Обратите внимание, как солнечная шестерня входит в зацепление с несколькими шестернями.
Преимущества планетарных редукторов
Люфт меньше, чем у аналогов с прямозубым редуктором. Люфт определяется как зазор или потеря движения, вызванные зазорами между деталями. Это легко объяснить, надев колесо или шестерню на вал двигателя и слегка вращая его. Деталь должна иметь возможность немного покачиваться без приложения к ней значительной силы. Это вызвано тем, что зубья шестерни внутри коробки передач не могут идеально сцепляться, и то же самое для цепи и звездочек или любой другой формы передачи мощности. Однако планетарные редукторы имеют меньший люфт, поскольку у них меньше ступеней передач.
Эффективность выше, чем у цилиндрических редукторов. Типичный двухступенчатый цилиндрический редуктор имеет КПД около 85%, тогда как большинство двухступенчатых планетарных редукторов имеют КПД 94%.
Грузоподъемность выше у планетарных редукторов.
Это связано с тем, что на каждой ступени задействовано несколько зубьев, что распределяет нагрузку.
Наконечник
Это означает, что планетарные редукторы не так легко ломаются при использовании в условиях высоких нагрузок, таких как трансмиссии.
Планетарная передача: Справочник | Журнал Gear Solutions Ваш ресурс для индустрии зубчатых передач
Для инженеров-конструкторов, которые только начинают свою карьеру, и даже для опытных профессионалов, которым не помешал бы курс повышения квалификации, в следующей статье предлагается базовый подход к обсуждению планетарных зубчатых передач.
В недавних статьях в Gear Solutions обсуждались планетарные передачи, но часто в контексте опытных инженеров. По мере того, как все больше и больше таких инженеров достигают пенсионного возраста, молодые инженеры должны продолжать работу с того места, на котором они остановились, и для многих планетарных зубчатых колес им не хватает опыта. Эпициклическая передача требует пошагового процесса, чтобы заставить ее работать, и некоторые из шагов не обязательно интуитивно понятны. Таким образом, эта статья призвана предоставить помощь и рекомендации для тех, кто впервые проектирует планетарные зубчатые передачи, и, возможно, если хотите, облегчить их страдания. Мы начнем с определения типов и механизмов, а затем обсудим, почему используются планетарные передачи. Далее мы рассмотрим уникальные особенности эпициклических передач, в том числе относительные скорости, распределение крутящего момента и особенности множественного зацепления. Наконец, мы обсудим, что можно и чего нельзя делать, и поделимся некоторыми советами по проектированию и подводными камнями, связанными с планетарными передачами.
Таким образом, эта статья призвана предоставить помощь и рекомендации для тех, кто впервые проектирует планетарные зубчатые передачи, и, возможно, если хотите, облегчить их страдания. Мы начнем с определения типов и механизмов, а затем обсудим, почему используются планетарные передачи. Далее мы рассмотрим уникальные особенности эпициклических передач, в том числе относительные скорости, распределение крутящего момента и особенности множественного зацепления. Наконец, мы обсудим, что можно и чего нельзя делать, и поделимся некоторыми советами по проектированию и подводными камнями, связанными с планетарными передачами.
Типы и компоновки
Начнем с изучения базовой терминологии. Планетарные передачи состоят из нескольких компонентов: солнца, водила, сателлитов и колец. Солнце представляет собой центральную шестерню, зацепленную с сателлитами, а водило содержит вал сателлита. Когда водило вращается, планеты вращаются на валах сателлитов, вращаясь вокруг солнца. Наконец, кольцо — это внутреннее зубчатое колесо, которое входит в зацепление с сателлитами.
Наконец, кольцо — это внутреннее зубчатое колесо, которое входит в зацепление с сателлитами.
Планетарные передачи можно разделить на три типа: простые планетарные эпициклические; сложный эпициклический; и связанные эпициклические множества. Есть несколько возможностей эпициклических расположений:
• Планетарные, с отношениями от 3:1 до 12:1 (см. рис. 1)
• Звездные, с отношениями от -2:1 до -11:1 (см. рис. 2)
• Солнечные, с отношениями от 1,2: 1 и 1,7:1 (см. рис. 3)
Почему планетарная передача?
Причины, по которым используются планетарные передачи, были освещены в этом журнале, поэтому мы расширим эту тему лишь в нескольких местах. Начнем с изучения важного аспекта любого проекта: стоимости. Планетарная передача обычно дешевле при правильном оснащении. Точно так же, как никто не рассматривает возможность изготовления партии шестерен из 100 штук на фрезерном станке с ЧПУ с фасонной фрезой или шаровой концевой фрезой, не следует рассматривать возможность изготовления партии из 100 штук планетарных водил на фрезерной машине с ЧПУ. Чтобы держатели не превышали разумных производственных затрат, они должны изготавливаться из отливок и обрабатываться на специализированных станках с несколькими резцами, одновременно удаляющими материал.
Чтобы держатели не превышали разумных производственных затрат, они должны изготавливаться из отливок и обрабатываться на специализированных станках с несколькими резцами, одновременно удаляющими материал.
Еще одним фактором является размер. Эпициклические зубчатые передачи используются, потому что они меньше, чем комплекты смещенных зубчатых колес, поскольку нагрузка распределяется между строгальными зубчатыми колесами. Это делает их легче и компактнее по сравнению с редукторами с промежуточным валом. Кроме того, при правильной настройке планетарные передачи более эффективны. Следующий пример иллюстрирует эти преимущества. Предположим, мы разрабатываем высокоскоростную коробку передач, удовлетворяющую следующим требованиям:
• Турбина выдает на первичный вал мощность 6000 л.с. при 16000 об/мин.
• Выход коробки передач должен управлять генератором со скоростью 900 об/мин.
• Расчетный срок службы должен составлять 10 000 часов.
Учитывая эти требования, давайте рассмотрим три возможных решения, одно из которых включает одноветвевой двухступенчатый косозубый набор. Второе решение использует исходный набор шестерен и разделяет двухступенчатую передачу на две ветви, а третье требует использования двухступенчатого планетарного или звездообразного планетарного редуктора. В данном случае мы выбрали звезду. Давайте рассмотрим каждый из них более подробно, взглянув на их соотношения и результирующие веса.
Второе решение использует исходный набор шестерен и разделяет двухступенчатую передачу на две ветви, а третье требует использования двухступенчатого планетарного или звездообразного планетарного редуктора. В данном случае мы выбрали звезду. Давайте рассмотрим каждый из них более подробно, взглянув на их соотношения и результирующие веса.
Первое решение — двухступенчатая косозубая шестерня с одной ветвью — имеет два одинаковых передаточных числа, полученных путем извлечения квадратного корня из конечного передаточного числа (7.70). (См. рис. 4.) В процессе рассмотрения этого решения мы заметили, что его размер и вес очень велики. Затем, чтобы уменьшить вес, мы изучаем возможность создания двух ответвлений аналогичного расположения, как показано во втором решении. Это снижает нагрузку на зуб и значительно уменьшает размер и вес (см. рис. 5). Наконец мы приходим к нашему третьему решению, которое представляет собой эпициклическую звезду с двумя ступенями. С тремя сателлитами эта зубчатая передача значительно снижает нагрузку на зубья при первом подходе и несколько меньше при втором подходе (см.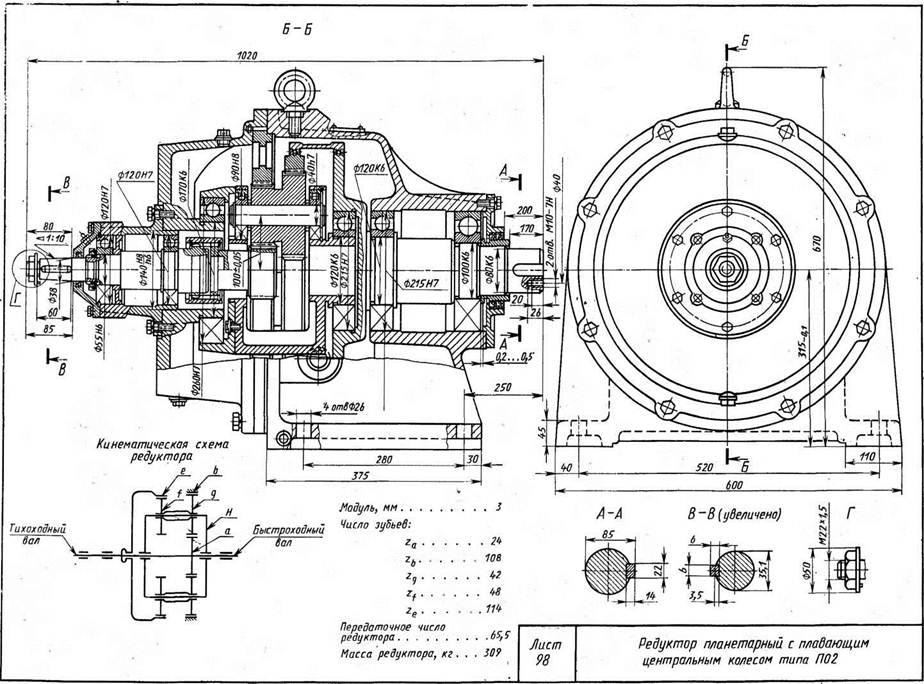 «методику» в конце и рисунок 6).
«методику» в конце и рисунок 6).
Уникальные конструктивные характеристики планетарных зубчатых колес во многом делают их такими полезными, однако именно эти характеристики могут усложнить их проектирование. В следующих разделах мы рассмотрим относительные скорости, распределение крутящего момента и особенности построения сетки. Наша цель — облегчить вам понимание и работу с уникальными конструктивными характеристиками планетарных передач.
Рис. 4: Передаточное число 1 = 4,216, Передаточное число 2 = 4,216, Вес = 5 293#Относительные скорости
Давайте начнем с рассмотрения того, как относительные скорости работают в сочетании с различными конфигурациями. В звездообразном расположении водило неподвижно, а относительные скорости солнца, планеты и кольца просто определяются скоростью одного элемента и количеством зубьев в каждой шестерне.
В планетарном механизме зубчатый венец неподвижен, и планеты вращаются вокруг Солнца, вращаясь на планетарном валу. В этом устройстве относительные скорости солнца и планет определяются количеством зубьев в каждой шестерне и скоростью водила.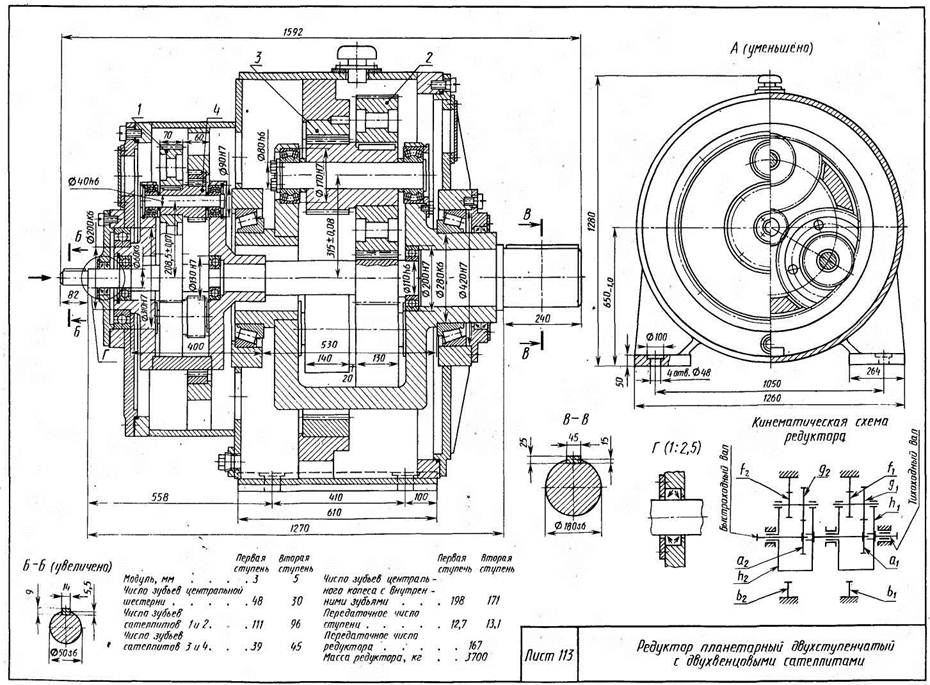
При работе с спаренными планетарными передачами все становится немного сложнее, поскольку относительные скорости могут быть непонятны. Поэтому крайне важно всегда рассчитывать скорость солнца, планеты и кольца относительно носителя. Помните, что даже в солнечном расположении, где солнце зафиксировано, его скорость связана с планетой — это не нулевой RPM в сетке.
Разделение крутящего момента
При рассмотрении разделения крутящего момента предполагается, что крутящий момент делится между сателлитами поровну, но это может быть неверным предположением. Опора стержня и количество планет определяют распределение крутящего момента, представленное «эффективным» количеством планет. Это число в планетарных наборах, построенных с двумя или тремя планетами, в большинстве случаев равно фактическому количеству планет. Однако при использовании более трех планет эффективное количество планет всегда меньше фактического количества планет.
Рис. 5: Передаточное число 1 = 3,925, Передаточное число 2 = 4,536, Вес = 3,228# Давайте посмотрим на распределение крутящего момента с точки зрения фиксированной и плавающей опоры элементов. При фиксированной опоре все элементы опираются на подшипники. Центры солнца, кольца и держателя не будут совпадать из-за производственных допусков. Из-за этого меньшее количество планет одновременно находится в зацеплении, что приводит к меньшему эффективному количеству планет, разделяющих нагрузку. При плавающей опоре одному или двум элементам предоставляется небольшая радиальная свобода или плавание, что позволяет солнцу, кольцу и держателю искать положение, при котором их центры совпадают. Этот поплавок может быть всего 0,001-0,002 дюйма. С плавающей опорой три планеты всегда будут в зацеплении, что приведет к большему эффективному количеству планет, разделяющих нагрузку.
При фиксированной опоре все элементы опираются на подшипники. Центры солнца, кольца и держателя не будут совпадать из-за производственных допусков. Из-за этого меньшее количество планет одновременно находится в зацеплении, что приводит к меньшему эффективному количеству планет, разделяющих нагрузку. При плавающей опоре одному или двум элементам предоставляется небольшая радиальная свобода или плавание, что позволяет солнцу, кольцу и держателю искать положение, при котором их центры совпадают. Этот поплавок может быть всего 0,001-0,002 дюйма. С плавающей опорой три планеты всегда будут в зацеплении, что приведет к большему эффективному количеству планет, разделяющих нагрузку.
Рассмотрение нескольких сеток
В этот раз давайте рассмотрим соображения о множественных сетках, которые следует учитывать при проектировании планетарных передач. Сначала мы должны перевести число оборотов в минуту в скорость сетки и определить количество циклов приложения нагрузки в единицу времени для каждого элемента.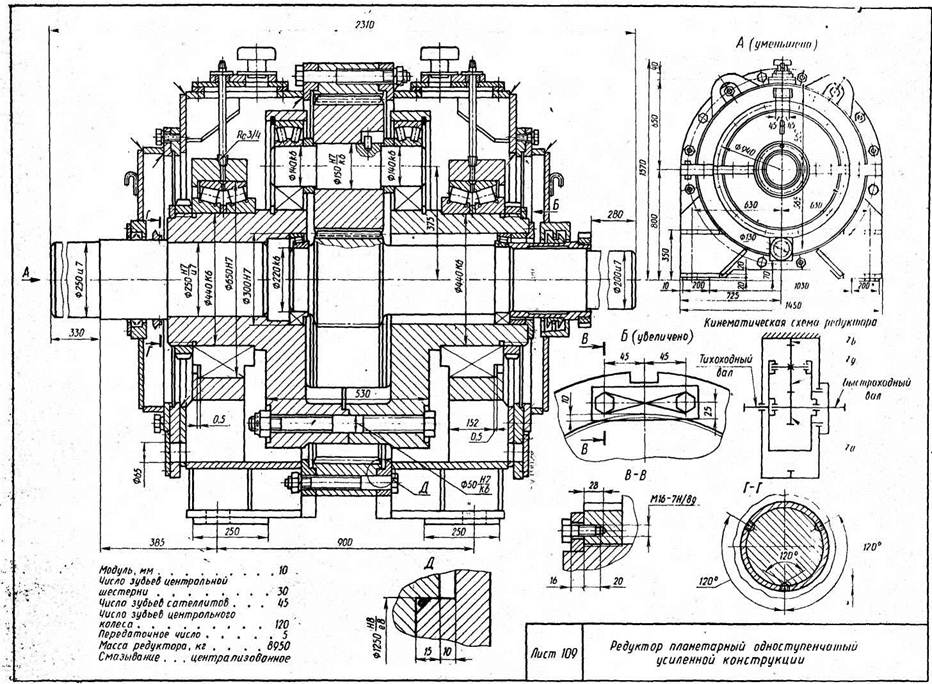 Первым шагом в этом определении является вычисление скоростей каждого из элементов относительно носителя. Например, если солнечная шестерня вращается со скоростью +1700 об/мин, а водило вращается со скоростью +400 об/мин, скорость солнечной шестерни относительно водила составляет +1300 об/мин, а скорости планетарной и кольцевой шестерен можно рассчитать по этому скорость и количество зубьев на каждой из шестерен. Здесь важно использование знаков для обозначения вращения по часовой стрелке и против часовой стрелки. Если солнце вращается со скоростью +1700 об/мин (по часовой стрелке), а водила вращается на -400 об/мин (против часовой стрелки), относительная скорость между двумя элементами составляет +1700-(-400) или +2100 об/мин.
Первым шагом в этом определении является вычисление скоростей каждого из элементов относительно носителя. Например, если солнечная шестерня вращается со скоростью +1700 об/мин, а водило вращается со скоростью +400 об/мин, скорость солнечной шестерни относительно водила составляет +1300 об/мин, а скорости планетарной и кольцевой шестерен можно рассчитать по этому скорость и количество зубьев на каждой из шестерен. Здесь важно использование знаков для обозначения вращения по часовой стрелке и против часовой стрелки. Если солнце вращается со скоростью +1700 об/мин (по часовой стрелке), а водила вращается на -400 об/мин (против часовой стрелки), относительная скорость между двумя элементами составляет +1700-(-400) или +2100 об/мин.
Второй шаг — определить количество циклов приложения нагрузки. Поскольку солнечная и кольцевая шестерни входят в зацепление с несколькими планетами, количество циклов нагрузки на один оборот относительно водила будет равно количеству планет. Однако планеты будут испытывать только одно двунаправленное приложение нагрузки за относительный оборот.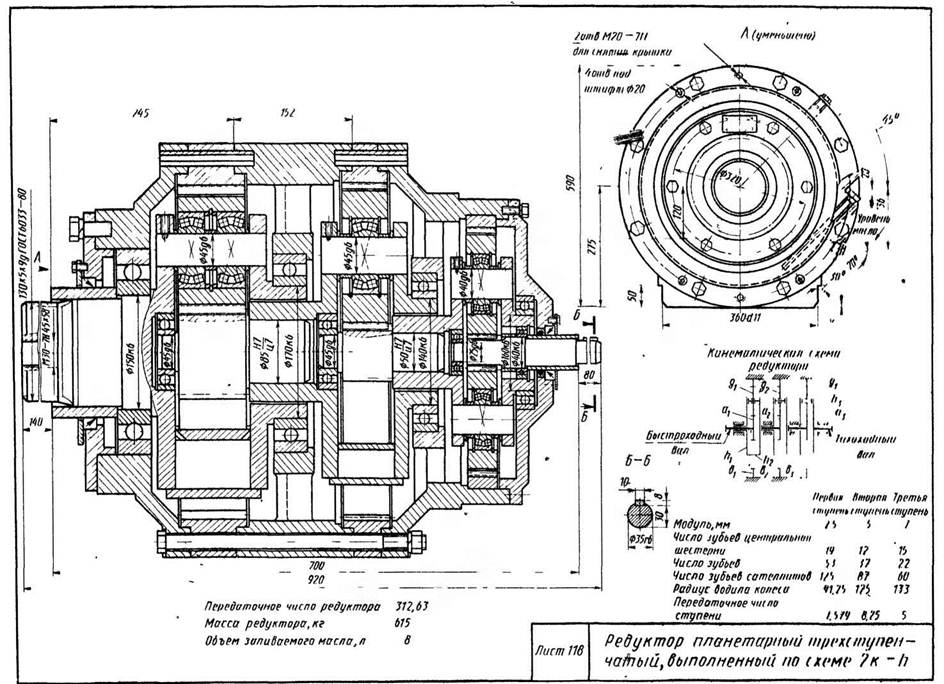 Он входит в зацепление с солнцем и кольцом, но нагрузка приходится на противоположные стороны зубьев, что приводит к одному полностью обращенному циклу напряжения. Таким образом, планета считается бездельником, и допустимое напряжение должно быть уменьшено на 30 процентов по сравнению со значением для приложения однонаправленной нагрузки.
Он входит в зацепление с солнцем и кольцом, но нагрузка приходится на противоположные стороны зубьев, что приводит к одному полностью обращенному циклу напряжения. Таким образом, планета считается бездельником, и допустимое напряжение должно быть уменьшено на 30 процентов по сравнению со значением для приложения однонаправленной нагрузки.
Как отмечалось выше, крутящий момент планетарных элементов распределяется между сателлитами. При анализе напряжения и срока службы элементов мы должны смотреть на результирующую нагрузку на каждую сетку. Мы считаем, что концепция крутящего момента на зацепление несколько сбивает с толку при анализе планетарных передач, и предпочитаем рассматривать тангенциальную нагрузку в каждом зацеплении. Например, рассматривая тангенциальную нагрузку на зацепление «солнечная планета», мы берем крутящий момент на солнечной шестерне и делим его на эффективное количество сателлитов и радиус рабочего шага. Эта тангенциальная нагрузка в сочетании с окружной скоростью используется для расчета мощности, передаваемой на каждую сетку, и с поправкой на количество циклов нагрузки на оборот, ожидаемого срока службы каждого компонента.
В дополнение к этим проблемам также могут возникнуть сложности при сборке, которые необходимо решить. Например, размещение одной планеты в положении между солнцем и кольцом фиксирует угловое положение солнца относительно кольца. Следующие планеты теперь могут быть собраны только в незаметных местах, где солнце и кольцо могут быть задействованы одновременно. «Наименьший угол зацепления» от первой планеты, который будет соответствовать одновременному зацеплению следующей планеты, равен 360 °, деленным на сумму количества зубцов на солнце и кольце. Таким образом, чтобы собрать дополнительные планеты, они должны быть расположены на расстоянии, кратном этому наименьшему углу сетки. Если кто-то хочет иметь равное расстояние между планетами в простом планетарном наборе, планеты могут быть расположены на одинаковом расстоянии друг от друга, когда сумма количества зубьев в солнце и кольце делится на число планет до целого числа. Те же правила применяются к составным эпициклам, но фиксированное соединение сателлитов добавляет еще один уровень сложности, а правильное расстояние между сателлитами может потребовать соответствующей маркировки зубьев.
Те же правила применяются к составным эпициклам, но фиксированное соединение сателлитов добавляет еще один уровень сложности, а правильное расстояние между сателлитами может потребовать соответствующей маркировки зубьев.
При наличии нескольких компонентов в сетке необходимо учитывать потери в каждой сетке, чтобы оценить эффективность устройства. Мощность, передаваемая в каждой сетке, а не входная мощность, должна использоваться для расчета потерь мощности. Для простых планетарных наборов общая мощность, передаваемая через сетку солнце-планета и сетка-кольцо-планета, может быть меньше входной мощности. Это одна из причин того, что простые планетарные планетарные эпициклы более эффективны, чем другие редукторы. Напротив, для многих связанных планетарных наборов общая мощность, передаваемая внутри каждой сетки, может быть больше, чем входная мощность.
Что с питанием в сетке? Для простых и составных планетарных наборов рассчитайте скорости линии шага и тангенциальные нагрузки, чтобы вычислить мощность в каждой сетке. Значения могут быть получены из относительной скорости крутящего момента планеты и диаметров рабочего шага с солнцем и кольцом. Связанные эпициклические наборы представляют более сложные проблемы. Элементы двух эпициклических наборов можно соединить 36 различными способами, используя один вход, один выход и одну реакцию. Некоторые устройства разделяют мощность, а некоторые рециркулируют энергию внутри. Для этих типов планетарных наборов касательные нагрузки в каждой сетке могут быть определены только с помощью диаграмм свободного тела. Кроме того, элементы двух эпициклических наборов могут быть соединены последовательно девятью различными способами, используя один вход, один выход и две реакции. Давайте посмотрим на некоторые примеры.
Значения могут быть получены из относительной скорости крутящего момента планеты и диаметров рабочего шага с солнцем и кольцом. Связанные эпициклические наборы представляют более сложные проблемы. Элементы двух эпициклических наборов можно соединить 36 различными способами, используя один вход, один выход и одну реакцию. Некоторые устройства разделяют мощность, а некоторые рециркулируют энергию внутри. Для этих типов планетарных наборов касательные нагрузки в каждой сетке могут быть определены только с помощью диаграмм свободного тела. Кроме того, элементы двух эпициклических наборов могут быть соединены последовательно девятью различными способами, используя один вход, один выход и две реакции. Давайте посмотрим на некоторые примеры.
В парном блоке с раздельной мощностью, показанном на , 85 процентов передаваемой мощности поступает на зубчатый венец №1 и 15 процентов на зубчатый венец №2. В результате этот спаренный набор шестерен может быть меньше, чем последовательно соединенные наборы, потому что мощность распределяется между двумя элементами. При последовательном соединении эпициклических наборов через каждый набор будет передаваться 0 процентов мощности (см. ).
При последовательном соединении эпициклических наборов через каждый набор будет передаваться 0 процентов мощности (см. ).
В следующем примере показана установка с «рециркуляцией мощности». Этот набор передач возникает, когда крутящий момент блокируется в системе, подобно тому, как это происходит в процедуре испытания «четыре квадрата» для ведущих мостов транспортных средств. Когда крутящий момент заблокирован в системе, мощность в каждой ячейке контура увеличивается по мере увеличения скорости. Следовательно, этот набор будет испытывать гораздо более высокие потери мощности в каждой сетке, что приведет к значительному снижению эффективности устройства (см. ).
На рис. 9 показана диаграмма свободного тела эпициклической конструкции, в которой происходит рециркуляция мощности. Беглый анализ этой диаграммы свободного тела объясняет 60-процентную эффективность системы рециркуляции, показанной на рис. Поскольку планеты жестко соединены друг с другом, сумма сил на двух шестернях должна равняться нулю. Сила в зацеплении солнечной шестерни возникает из-за крутящего момента, поступающего на солнечную шестерню. Сила во втором зацеплении зубчатого венца возникает из-за выходного крутящего момента на зубчатом венце. Соотношение составляет 41,1:1, выходной крутящий момент в 41,1 раза больше входного крутящего момента. С поправкой на разницу радиусов шага, скажем, 3:1, сила на второй планете будет примерно в 14 раз больше силы на первой планете в зацеплении солнечной шестерни. Следовательно, чтобы сумма сил равнялась нулю, тангенциальная нагрузка на первом зубчатом венце должна примерно в 13 раз превышать тангенциальную нагрузку на солнечную шестерню. Если предположить, что скорости линий тангажа одинаковы в солнечной сетке и кольцевой сетке, потери мощности на кольцевой сетке будут примерно в 13 раз выше, чем потери мощности на солнечной сетке (см. ).
Сила в зацеплении солнечной шестерни возникает из-за крутящего момента, поступающего на солнечную шестерню. Сила во втором зацеплении зубчатого венца возникает из-за выходного крутящего момента на зубчатом венце. Соотношение составляет 41,1:1, выходной крутящий момент в 41,1 раза больше входного крутящего момента. С поправкой на разницу радиусов шага, скажем, 3:1, сила на второй планете будет примерно в 14 раз больше силы на первой планете в зацеплении солнечной шестерни. Следовательно, чтобы сумма сил равнялась нулю, тангенциальная нагрузка на первом зубчатом венце должна примерно в 13 раз превышать тангенциальную нагрузку на солнечную шестерню. Если предположить, что скорости линий тангажа одинаковы в солнечной сетке и кольцевой сетке, потери мощности на кольцевой сетке будут примерно в 13 раз выше, чем потери мощности на солнечной сетке (см. ).
Дополнительные соображения
По мере увеличения скорости водила центробежные силы на планетарных шестернях становятся все более и более значительными; особенно если они имеют относительно большую массу. Эти силы должны быть уравновешены планетарным подшипником, и часто они выше, чем силы, передающие крутящий момент водилу. Их необходимо учитывать при расчетах планетарных подшипников.
Эти силы должны быть уравновешены планетарным подшипником, и часто они выше, чем силы, передающие крутящий момент водилу. Их необходимо учитывать при расчетах планетарных подшипников.
Смазка подшипников планетарной передачи может быть затруднена, особенно при более высоких скоростях каретки. Эти проблемы привели ко многим творческим решениям. Исследование патентов на эту тему окажется полезным. Удержание штифтов сателлитов в сильно нагруженных комплектах также может оказаться довольно сложной задачей. Изгибы ослабят прессовую посадку и растрескают сварные швы. Неплотная посадка может «завалить» отверстия в держателе, что приведет к большему, чем хотелось бы, смещению. Опять же, исследование патентов будет плодотворным.
Последняя проверка, которую необходимо сделать, особенно в планетарных передачах с высоким передаточным числом, — это зазор между наконечниками соседних сателлитов. Время найти этот ответ — на этапе проектирования, а не тогда, когда это усложняет сборку.
Что нужно и что нельзя делать
Теперь, когда мы рассмотрели типы и компоновки планетарных передач и их уникальные конструктивные характеристики, а также несколько примеров, давайте обсудим, что можно и чего нельзя делать при проектировании планетарных передач.
Сделать:
• Рассчитать расположение сателлитов
• Определить установочные метки сборки на чертеже
• Адресовать относительные скорости
• Правильно разделить крутящие моменты
• Анализировать сателлиты как холостые в простых планетарных установках
• Проверить сателлиты на наличие помех по внешнему диаметру
• Использовать свободное тело диаграммы
Не следует:
• Жестко закреплять все элементы, если это не требуется приложением
• Допустить разделение мощности
• Использовать сопряженные узлы с внутренней рециркуляцией мощности
• Забыть о центробежных нагрузках на планетарные подшипники
 8: Установка с рециркуляцией мощности, коэффициент = 41,1, эффективность = 61,6%. Расчеты выполнены с использованием программного обеспечения Integrated Gear.
8: Установка с рециркуляцией мощности, коэффициент = 41,1, эффективность = 61,6%. Расчеты выполнены с использованием программного обеспечения Integrated Gear.Советы по проектированию и подводные камни
В заключение приведем несколько советов по конструированию и подводных камней, которых следует избегать при проектировании планетарных передач. Помните, что проектирование на стандартных центрах приведет к более высокому удельному скольжению и более низкой эффективности. Если возникают проблемы с сетками, удаление одного зуба с планетарной шестерни улучшит как солнечную, так и кольцевую сетку. Убедитесь, что разрешено «плавание» или указано очень тесное расположение, а допуски на биение или распределение нагрузки будут меньше, чем ожидалось. Наконец, используйте тангенциальные нагрузки и скорости продольной линии для определения передачи мощности и потерь в сетке.
Рис. 9: Свободная диаграмма тела системы Как и любой навык, проектирование эпициклических передач становится легче с практикой. Уходящие на пенсию инженеры уносят с собой свои ноу-хау, а молодые инженеры продолжают работу с того места, на котором они остановились. Хотя этот краткий учебник не может охватить все нюансы планетарных передач, мы надеемся, что он послужит отправной точкой для инженеров, которым поручено спроектировать свой первый набор планетарных передач, и, возможно, даже послужит периодическим освежением знаний для более опытных проектировщиков.
Уходящие на пенсию инженеры уносят с собой свои ноу-хау, а молодые инженеры продолжают работу с того места, на котором они остановились. Хотя этот краткий учебник не может охватить все нюансы планетарных передач, мы надеемся, что он послужит отправной точкой для инженеров, которым поручено спроектировать свой первый набор планетарных передач, и, возможно, даже послужит периодическим освежением знаний для более опытных проектировщиков.
Методология
Для выполнения расчетов, показанных на Рисунке 7 и Рисунке 8, использовалось программное обеспечение UTS Integrated Gear Software (IGS). производственные затраты и сократить время выхода на рынок. См. ANSI/AGMA 6023-A-88 или ASME Paper 68-MECH-45 от P.W. Jensen для получения дополнительной информации о планетарных передачах.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Кинематический анализ систем планетарных передач с использованием блок-схем | Дж. Мех. Дес.
Пропустить пункт назначения навигации
Инновации в дизайне
Ми-Чинг Цай,
Ченг-Чи Хуан,
Бор-Джен Лин
Информация об авторе и статье
Дж. Мех. Дез . Июнь 2010 г., 132(6): 065001 (10 страниц)
Мех. Дез . Июнь 2010 г., 132(6): 065001 (10 страниц)
https://doi.org/10.1115/1.4001598
Опубликовано в Интернете: 25 мая 2010 г.
История статьи
Получен:
3 августа 2009 г.
Пересмотренный Просмотры
- Содержание артикула
- Рисунки и таблицы
- Видео
- Аудио
- Дополнительные данные
- Экспертная оценка
- MailTo
- Твиттер
Иконка Цитировать Цитировать
Разрешения
Цитирование
Цай М. , Хуан С. и Линь Б. (25 мая 2010 г.). «Кинематический анализ систем планетарных передач с использованием блок-схем». КАК Я. Дж. Мех. Дез . июнь 2010 г.; 132(6): 065001. https://doi.org/10.1115/1.4001598
, Хуан С. и Линь Б. (25 мая 2010 г.). «Кинематический анализ систем планетарных передач с использованием блок-схем». КАК Я. Дж. Мех. Дез . июнь 2010 г.; 132(6): 065001. https://doi.org/10.1115/1.4001598
Скачать файл цитаты:
- Рис (Зотеро)
- Менеджер ссылок
- EasyBib
- Подставки для книг
- Менделей
- Бумаги
- Конечная примечание
- РефВоркс
- Бибтекс
- Процит
- Медларс
Расширенный поиск
В этой статье используются методы управления для анализа кинематических взаимосвязей с помощью блок-схем для планетарных зубчатых передач. Выявленные уравнения касательной скорости в каждой точке контакта механических зубчатых передач используются для построения блок-схем. Затем используются концепции стратегий обратной связи и прямой связи, чтобы проиллюстрировать функции снижения и увеличения скорости в кинематике с анализом чувствительности. Конструктивное отличие необычных планетарных передач от обычных также объясняется на основе характеристического уравнения стратегий обратной связи для конструктивных ограничений по условиям устойчивости. Планетарная передача с кулачковым управлением дополнительно проиллюстрирована для ограничения и кинематического анализа с использованием метода блок-схемы и характеристического уравнения, и получены расчетные модели для чувствительности и выходного сигнала движения этой планетарной передачи. Благодаря взаимосвязи между управлением и кинематикой эта статья представляет собой руководство для инженеров в различных областях, позволяющее легко понять функцию механического проектирования.
Конструктивное отличие необычных планетарных передач от обычных также объясняется на основе характеристического уравнения стратегий обратной связи для конструктивных ограничений по условиям устойчивости. Планетарная передача с кулачковым управлением дополнительно проиллюстрирована для ограничения и кинематического анализа с использованием метода блок-схемы и характеристического уравнения, и получены расчетные модели для чувствительности и выходного сигнала движения этой планетарной передачи. Благодаря взаимосвязи между управлением и кинематикой эта статья представляет собой руководство для инженеров в различных областях, позволяющее легко понять функцию механического проектирования.
Раздел выпуска:
Инновационный дизайн
Ключевые слова:
графы потоков данных, инженерное проектирование, Обратная связь, прямая связь, шестерни, кинематика, график потока сигналов, блок-схема, планетарная передача, планетарная передача, кулачковый, кинематический, Обратная связь, прямая связь, характеристическое уравнение, планетарная передача с кулачковым управлением
Темы:
Планетарные передачи, Обратная связь, Кинематика, Шестерни, Упреждающее управление, Передаточные функции, Кинематический анализ
1.
Liu
,
YH
, 2004, «
Планетарный дифференциал
», патент США № 6, 777.
2.
Армингтон
,
S. F.
, 1960, «
Составной планетарный редуктор
», патент США № 2,941,423.
3.
Hsieh
,
WH
, 2007 г., «
Экспериментальное исследование планетарных зубчатых передач с кулачковым управлением
»,
3 ,
3 . Мах. Теория 0094-114X,
42
, стр.
513
–
525
.
4.
Мейсон
,
S. J.
J.
, 1953, «
Теория обратной связи: некоторые свойства графиков потока сигналов
»,
Proc. ИРЭ
0096-8390,
41
, стр.
1144
–
1156
.
5.
Wojnarowski
,
J.
и
Lidwin
,
A.
, 1975, «
.
»,
Мех. Мах. Теория
0094-114X,
10
(
1
), с.
6.
Войнаровски
,
Ж.
, 1976, «
Графовый метод определения нагрузок в сложных зубчатых передачах
»,
2.
 Мах. Теория
Мах. Теория 0094-114X,
11
, стр.
103
–
121
.
7.
Pennestrì
,
E.
и
Freudenstein
,
F.
, 1993, «
A Systemance Systeck Anyaly к мощности и STATIC-FORCIC. Цилиндрические зубчатые передачи
»,
ASME J. Mech. Дес.
0161-8458,
115
, стр.
639
–
644
.
8.
MA
,
R.
и
Gupta
,
K. C.
C.
, 1994, «
Графики сигнала для Spatial Gear Trains
966,. мех. Дес. 0161-8458,
116
, стр.
326
–
331
.
9.
Uematsu
,
S.
, 1997, “
Применение теории графов к кинематическому анализу планетарных зубчатых передач
»,
J. Jpn. соц. Точный англ.
0374-3543,
31
(
2
), стр.
141
–
66 036
10.
HSU
,
C. H.
и
LAM
,
K. T.
T.
, 1992, «
.
»,
ASME J. Мех. Дес.
0161-8458,
114
, стр.
196
–
200
.
11.
HSIEH
,
H. I.
и
TSAI
,
L. W.
, 1996, «
Kinematic Analysis of Epicyccric-type», 1996, «
Kinematic Analysis of Epicycric-type.
”,
ASME J. Mech. Дес.
0161-8458,
118
, стр.
294
–
299
.
12.
Nelson
,
C. A.
A.
и
CIPRA
,
R. J.
, 2005, «
Упрощенное кинематическое анализ BEVLICLICE Анализы
»,
ASME J. Mech. Дес.
0161-8458,
127
, стр.
278
–
286
.
13.
Wojnarowski
,
J.
,
Kopec
,
J.
, and
Zawislak
,
S.
, 2006, “
Gears и графики
»,
Journal of Theoretical and Applied Mechanics
1429-2955,
44
(
1
), стр.
139
–
162
; см. http://www.ptmts.org.pl/jtam.htmlhttp://www.ptmts.org.pl/jtam.html.
14.
Chesmond
,
C. J.
, 1984,
Технология системы управления
,
Edward Arnold
,
London
6.
15.
Куо
,
Б.К.
, 1991,
Системы автоматического управления
, 6-е изд.,
Prentice-Hall
,
Englewood Cliffs, NJ
.
16.
Phillips
,
C. L.
, и
Harbour
,
R. D.
D.
, 1991,
Presectcure Control Systems
, 2ND ED.,
, 2ND ED.
9000.-Hallce. , Энглвуд Клиффс, Нью-Джерси
.
17.
Склейтер
,
N.
и
Chironis
,
N. P.
, 1991,
Механизмы и механические устройства.
172
.
18.
Hopgood
,
A. A.
, 2001,
Интеллектуальные системы для инженеров и ученых
, 3
RC0003
Бока-Ратон, Флорида
, стр.
410
–
412
.
19.
Wilson
,
C. E.
,
Sadler
,
J. P.
, and
Michels
,
W. J.
, 1983,
Kinematics and Dynamics of Machinery
,
Harper & Row
,
Нью-Йорк
.
20.
Norton
,
R. L.
, 2002,
Справочник по проектированию и производству CAM
,
Industrial Press Inc.
,
New York
666, PP.
–
422
.
 J.
J. C.
C. T.
T. A.
A.
 D.
D.0003
Бока-Ратон, Флорида
, стр.
410
–
412
.
19.
Wilson
,
C. E.
,
Sadler
,
J. P.
, and
Michels
,
W. J.
, 1983,
Kinematics and Dynamics of Machinery
,
Harper & Row
,
Нью-Йорк
.
20.
Norton
,
R. L.
, 2002,
Справочник по проектированию и производству CAM
,
Industrial Press Inc.
,
New York
666, PP.
–
422
.



 Количество передач – 5 вперед и 1 назад.
Количество передач – 5 вперед и 1 назад. Этот механизм может осуществлять повышение передаточного числа и снижение крутящего момента и на оборот.
Этот механизм может осуществлять повышение передаточного числа и снижение крутящего момента и на оборот.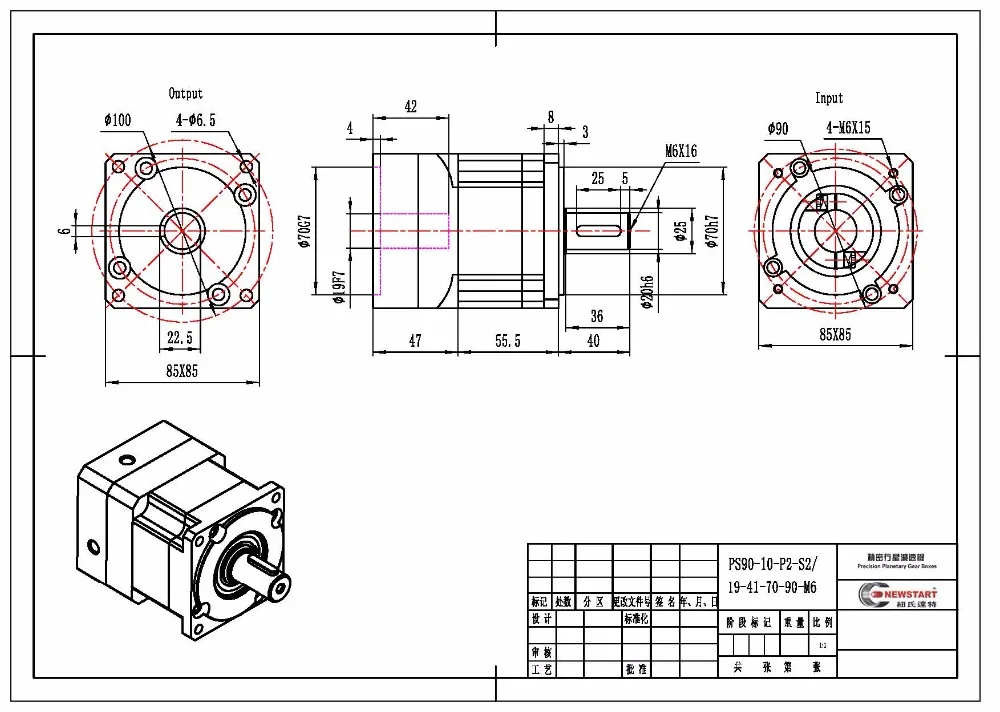
 Со временем она вырабатывается, засоряется металлической стружкой, теряет основные качества. Потому требует периодической полной замены или долива. Для планетарной передачи редуктора особенно важен грамотный выбор смазочного материала (по рекомендации производителя).
Со временем она вырабатывается, засоряется металлической стружкой, теряет основные качества. Потому требует периодической полной замены или долива. Для планетарной передачи редуктора особенно важен грамотный выбор смазочного материала (по рекомендации производителя).


 Небольшие габаритные размеры также позволяют создавать механизмы с небольшой массой. За счет этого существенно повышается эффективность рассматриваемого устройства.
Небольшие габаритные размеры также позволяют создавать механизмы с небольшой массой. За счет этого существенно повышается эффективность рассматриваемого устройства.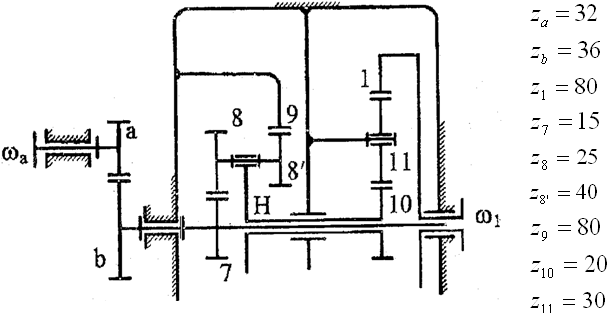 За счет этого они начинают не плотно прилегать друг к другу, последствия подобного явления заключается в повышенном износе и появлении шума.
За счет этого они начинают не плотно прилегать друг к другу, последствия подобного явления заключается в повышенном износе и появлении шума.
 Многие модели характеризуются небольшими размерами, за счет чего упрощается установка. Небольшие габаритные размеры также позволяют создавать механизмы с небольшой массой. За счет этого существенно повышается эффективность рассматриваемого устройства.
Многие модели характеризуются небольшими размерами, за счет чего упрощается установка. Небольшие габаритные размеры также позволяют создавать механизмы с небольшой массой. За счет этого существенно повышается эффективность рассматриваемого устройства. Часто встречается проблема, связанная с истиранием рабочей части зубьев. За счет этого они начинают не плотно прилегать друг к другу, последствия подобного явления заключается в повышенном износе и появлении шума.
Часто встречается проблема, связанная с истиранием рабочей части зубьев. За счет этого они начинают не плотно прилегать друг к другу, последствия подобного явления заключается в повышенном износе и появлении шума.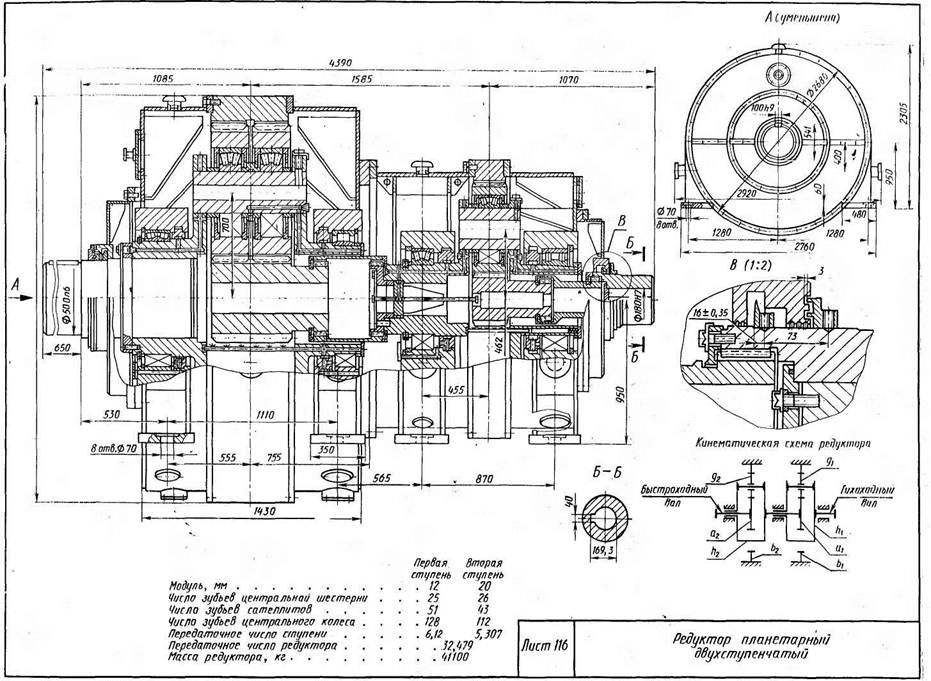 В рассматриваемом случае их число довольно много, что является определяющим фактором.
В рассматриваемом случае их число довольно много, что является определяющим фактором. Как правило, в качестве основы применяется чертеж, который можно скачать из интернета. Самостоятельно разработать проект по изготовления планетарного редуктора достаточно сложно, так как нужно обладать навыками инженера для проведения соответствующих расчетов и проектирования.
Как правило, в качестве основы применяется чертеж, который можно скачать из интернета. Самостоятельно разработать проект по изготовления планетарного редуктора достаточно сложно, так как нужно обладать навыками инженера для проведения соответствующих расчетов и проектирования.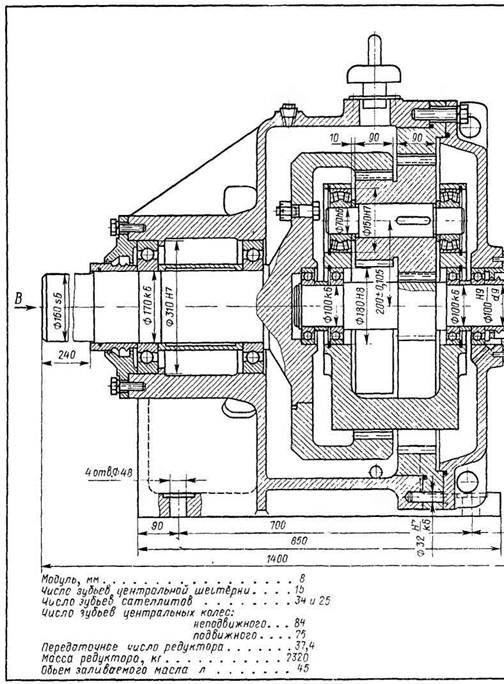 д.
д.