Объем воздушного шара: Подъёмная сила воздушного шара — задание. Физика, 7 класс.

Результат расчёта

• Объём: {$ result.v|number:4 $}
• Площать: {$ result.s|number:4 $}
• Площать: {$ result.s $}

Шар — это геометрическое тело вращения, образованное путем вращения круга или полукруга вокруг его диаметра. Также шар — это пространство, ограниченное сферической поверхностью. Существует множество реальных сферических объектов и связанных с ними задач, для решения которых требуется определить объем шара.

Шар и сфера

Круг — самая древняя геометрическая фигура, и античные ученые придавали ей сакральное значение. Круг — это символ нескончаемого времени и пространства, символ Вселенной и бытия. По мнению Пифагора, круг — прекраснейшая из фигур. В трехмерном пространстве окружность превращается в сферу, такую же идеальную, космическую и прекрасную, как и круг.

Сфера по-древнегречески означает «мяч». Сфера представляет собой поверхность, образованную бесконечным множеством точек, равноудаленных от центра фигуры. Пространство, ограниченное сферой, и есть шар. Шар — идеальная геометрическая фигура, форму которой принимают многие реальные объекты. К примеру, в реальной жизни форму шара имеют пушечные ядра, подшипники или мячи, в природе — капли воды, кроны деревьев или ягоды, в космосе — звезды, метеоры или планеты.

Объем шара

Определение объема сферической фигуры — сложная задача, ведь такое геометрическое тело нельзя разбить на кубы или треугольные призмы, формулы объемов которых уже известны. Современная наука позволяет вычислить объем шара при помощи определенного интеграла, однако каким образом была выведена формула объема в Древней Греции, когда об интегралах еще никто не слышал? Архимед вычислил объем шара при помощи конуса и цилиндра, так как формулы объемов этих фигур были уже определены древнегреческим философом и математиком Демокритом.

Архимед представил половину шара при помощи одинаковых конуса и цилиндра, при этом радиус каждой фигуры был равен ее высоте R = h. Античный ученый представил конус и цилиндр разбитыми на бесконечное количество маленьких цилиндров. Архимед понял, что если из объема цилиндра Vc вычесть объем конуса Vk, он получит объем одной полусферы Vsh:

0,5 Vsh = Vc − Vk

Объем конуса вычисляется по простой формуле:

Vk = 1/3 × So × h,

но зная, что So в данном случае — это площадь круга, а h = R, то формула трансформируется в:

Vk = 1/3 × pi × R × R² = 1/3 pi × R³

Объем цилиндра вычисляется по формуле:

Vc = pi × R² × h,

но считая, что высота цилиндра равна его радиусу, мы получаем:

Vc = pi × R³.

Используя эти формулы, Архимед получил:

0,5 Vsh = pi × R³ — 1/3 pi × R³ или Vsh = 4/3 pi × R³

Современное определение формулы объема шара выводится из интеграла от площади сферической поверхности, однако результат остается все тем же

Vsh = 4/3 pi × R³

Расчет объема шара может понадобиться как в реальной жизни, так и при решении абстрактных задач. Для вычисления объема шара при помощи онлайн-калькулятора вам понадобится узнать всего один параметр на выбор: диаметр или радиус сферы. Рассмотрим пару примеров.

Примеры из жизни

Пушечные ядра

Допустим, вы хотите узнать, сколько чугуна необходимо для отливки пушечного ядра шестифутового калибра. Вы знаете, что диаметр такого ядра составляет 9,6 сантиметров. Введите это число в ячейку калькулятора «Диаметр», и вы получите ответ в виде

V = 463,24

Таким образом, для выплавки пушечного ядра заданного калибра вам понадобится 463 кубических сантиметров или 0,463 литра чугуна.

Воздушные шары

Пусть вам любопытно, сколько воздуха необходимо для накачки воздушного шара идеальной сферической формы. Вы знаете, что радиус выбранного шарика составляет 10 см. Вбейте это значение в ячейку калькулятора «Радиус» и вы получите результат

V = 4188,7

Это означает, что для накачки одного такого шара вам понадобится 4188 кубических сантиметров или 4,18 литров воздуха.

Заключение

Необходимость определения объема шара может возникнуть в самых разных ситуациях: от абстрактных школьных задач до научных изысканий и производственных вопросов. Для решения вопросов любой сложности используйте наш онлайн-калькулятор, который мгновенно представит вам точный результат и необходимые математические выкладки.

Зависимость давления воздуха внутри шарика от его объема презентация, доклад

ЗАВИСИМОСТЬ ДАВЛЕНИЯ ВОЗДУХА ВНУТРИ ШАРИКА ОТ ЕГО ОБЪЕМА

,
Работа ученика 8-Ф класса Решельевского лицея г. Одессы
Бондаря Ильи

Слайд 2Текст слайда:

Как известно, вещества могут находиться в твердом, жидком и газообразном состоянии. При этом они характеризуются различными свойствами. Так свойства газов определяются такими параметрами, как давление, температура, занимаемый объем, масса и т.д. В отличие от твердых тел и жидкостей газы заполняют весь сосуд, в котором они находятся (например, стальной баллон для хранения газов, камеру автомобильной шины, шар из латекса и т. д.). При этом газ оказывает давление  на стенки, дно и крышку баллона или камеры, в которых он находится. Газы легко сжимаемы.
Причина давления газов связана с хаотичным быстрым движением молекул. Беспорядочно двигаясь, они сталкиваются друг с другом, а также со стенками сосуда, в котором находится газ. Газ состоит из огромного количества молекул, поэтому и число их ударов очень велико.
Таким образом, в газах давление создается множественными ударами беспорядочно движущихся молекул.

Газы занимают весь предоставленный им объем, так как их молекулы не связаны между собой. Понятно, что чем объем больше, тем количество молекул в единице объема будет меньше. Следовательно, меньше молекул будет ударять по поверхности, и, значит, давление газа будет меньше.
Следовательно, давление и объем газа находятся в обратно пропорциональной зависимости: чем больше объем, тем меньше давление, и чем меньше объем, тем больше давление.
При этом надо иметь в виду, что это справедливо в случае, когда масса газа и температура считаются неизменными.

---

Слайд 3Текст слайда:

Шарик заполненный воздухом или просто воздушный шарик является хорошим объектом для исследования зависимости давления газа от его занимаемого объема. Рассмотрим шарик с воздухом. Возьмем шарик и будем его надувать. Объем шарика растет до тех пор, пока сила давления воздуха внутри шарика не сравняется с силой упругости оболочки. При этом оболочка шарика принимает форму шара, то есть газ давит на его стенки по всем направлениям в среднем одинаково. Таким образом, в случае воздушного шарика давление газа на стенки вызывается ударами молекул газа и направлено во все стороны одинаково. 

Что происходит с давлением воздуха внутри шарика при изменении его объема? Это можно определить с помощью различных экспериментов. Рассмотрим один из таких экспериментов.

---

Слайд 4Текст слайда:

Тема: исследование зависимости давления воздуха внутри шарика от его объема.
Цель: определить зависимость давления воздуха внутри шарика от его объема.
Оборудование: шарик, линейка , жидкостный манометр.

Для исследования зависимость давления воздуха внутри шарика от его объема поместим в него некоторую массу воздуха (шарик находится в помещении при постоянной комнатной температуре). Для измерения давления используем жидкостный манометр, который состоит из двухколенной стеклянной трубки, в которую налита какая –нибудь жидкость. На правое колено U-образной трубки, в которую налита однородная жидкость, наденем шарик. Слегка сожмем шарик – высота жидкости в правом колене уменьшится, а в правом увеличится (рис.3). На уровне АВ давление в жидкости будет одинаковым. В точке В это будет давление воздуха рв в правом колене, а в точке А — атмосферное давление ра плюс давление ρgΔh столба жидкости Δh. Следовательно, рв=ра+ ρgΔh.  

Таким образом, с помощью U-образной трубки, заполненной однородной жидкостью, и линейки для измерения разности уровней жидкости в коленах трубки можно определить разницу Δp между давлением воздуха в сосуде и атмосферным давлением: Δp =рв — ра = ρgΔh, т.

е. разница компенсируется давлением столба жидкости.
Что происходит с давлением воздуха внутри шарика при изменении его объема? Это можно почувствовать, сжимая воздушный шарик в руке. Чтобы шарик становился меньше, необходимо давить сильнее. Таким образом, по мере уменьшения объема давление внутри шарика возрастает. Что и следует из показаний манометра.
Две величины, давление р и объем V обратно пропорциональны друг другу. Если между значениями давления и объема существует обратно пропорциональная зависимость: p=k/V, то их произведение остается неизменным, даже если эти величины будут изменяться: pV=k (где k – константа в обоих уравнениях).
Для воздуха и других газов эта зависимость называется законом Бойля–Мариотта. Данный закон справедлив для постоянной массы и неизменной температуры газа.

---

Слайд 5Текст слайда:

Измерение давления в воздушном шарике

---

Слайд 6Текст слайда:

Для изучения зависимости давления газа в воздушном шаре от его объема можно также провести следующий эксперимент.
Несильно надутый воздушный шарик положим в герметичную емкость, из которой можно откачать воздух.
Например, под колокол воздушного насоса помещают завязанный резиновый шарик. Он содержит небольшое количество воздуха и имеет неправильную форму (рис.а). Затем насосом откачивают воздух из-под колокола. Оболочка шарика, вокруг которой воздух становится все более разряженным, постепенно раздувается и принимает сферическую форму.
В эксперименте мы можем, как уменьшать, так и увеличивать внешнее давление, изменяя тем самым давления внутри шарика.
Как можно объяснить изменение давления в шарике от его объема в данном опыте? Температуру газа в данном опыте можно считать постоянной. Молекулы воздуха движутся и потому непрерывно ударяют о стенки шарика внутри и снаружи. При откачивании воздуха число молекул под колоколом вокруг оболочки шарика уменьшается. Но внутри шарика их число не изменяется, так как масса газа внутри шарика осталась неизменной. Поэтому число ударов молекул о внешнюю поверхность оболочки становится меньше числа ударов о внутреннюю поверхность.

Из-за этого шарик растет (раздувается) и принимает такие размеры, при которых сила упругости его резиновой оболочки становится равной силе давления газа, находящегося внутри его. При увеличении объема этой же массы газа шарика число молекул в каждом кубическом сантиметре, а значит, и число их ударов о стенки сосуда станет меньше. При этом давление газа внутри шарика становится меньше.
При этом оболочка шарика принимает сферическую форму (рис.б).
При увеличении внешнего давления объем шарика и соответственно ли объем газа в нем соответственно уменьшить, но так как его масса  осталась неизменной, то в каждом кубическом сантиметре газа молекул станет больше. Это означает, что плотность газа увеличится. Тогда число ударов молекул о стенки сосуда возрастет, и давление газа станет больше.

---

Слайд 7Текст слайда:

а) б)

Опыт, демонстрирующий зависимость давления газа от объема.

---

Слайд 8Текст слайда:

ВЫВОД:ПРИ НЕИЗМЕННОЙ МАССЕ И ТЕМПЕРАТУРЕ ВОЗДУХА ВНУТРИ ВОЗДУШНОГО ШАРИКА:

— уменьшение объема воздушного шарика, т. е. уменьшение объема занимаемого газом, приводит к увеличению давления внутри него;
V ↓ => удары чаще => p ↑

— и наоборот, при увеличении объема воздушного шарика давление в шарике уменьшается.

V ↓ => удары чаще => p ↑

---

Слайд 9Текст слайда:

Манометры – приборы для измерения давлений.
Манометры бывают:
а) жидкостные б) металлические

---

Слайд 10Текст слайда:

Жидкостный манометр состоит из двухколенной стеклянной трубки, в которую налита какая –нибудь жидкость.
Металлический манометр состоит из согнутой в дугу металлическая трубки, рычага, зубчатки, стрелки и крана.

---

Скачать презентацию

ФИЗИКА НА ВОЗДУШНЫХ ШАРИКАХ

• Авторы
• Руководители
• Файлы работы

Митрошин Д.В. 1

---

1МБОУ «Киясовская СОШ»

Бузанов Н. Г. 1

---

1МБОУ «Киясовская СОШ»

Текст работы размещён без изображений и формул.

Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Актуальность

Знакома ли вам ситуация, когда после дня рождения или какого-то другого праздника в доме появляется множество воздушных шаров? Сначала шарики детей радуют, они играют с ними, но вскоре на них перестают обращать внимание и шарики только путаются под ногами. Что с ними сделать, чтобы они не лежали без всякой цели, а принесли пользу? Конечно же, использовать в познавательной деятельности!

Вообще, воздушные шарики — прекрасный материал для демонстрации различных опытов и моделей. Было бы интересно написать книжку, в которой все физические понятия будут объяснятся через них. Ну а пока я хочу предложить вам провести больше десятка экспериментов из разных областей науки — от термодинамики до космологии, — в которых общим является реквизит: воздушные шары.

Цель: Исследовать воздушные шарики как бесценный подручный материал для наблюдения физических явлений и постановки различных физических экспериментов.

Задачи:

1. Изучить историю создания воздушных шариков.

2. Поставить ряд экспериментов с воздушными шариками.

3. Проанализировать наблюдаемые явления и сформулировать выводы.

4. Создать мультимедийную презентацию.

Объект исследования: воздушный шарик.

Методы исследования:

• Теоретические: изучение литературы по теме исследования.

• Сравнительно-сопоставительный.

• Эмпирические: наблюдение, измерение.

• Экспериментально-теоретические: эксперимент, лабораторный опыт.

Материалом данного исследования являются Интернет-источники, методические пособия по физике, учебники физики, задачники, данные архива и другая справочная литература.

Практическая значимость: результаты исследования могут быть использованы на уроках физики, на конференциях, при чтении элективных курсов и на внеклассных мероприятиях.

-3-

1. Теоретическая часть

История создания воздушных шариков

Глядя на современные воздушные шары, многие люди думают, что эта яркая, приятная игрушка стала доступной только недавно. Некоторые, более осведомленные, считают, что воздушные шары появились где-то в середине прошлого века, одновременно с началом технической революции. На самом деле это не так. История шаров, наполненных воздухом, началась гораздо раньше. Только выглядели предки наших шариков совсем не так, как сейчас. Первые, дошедшие до нас, упоминания об изготовлении летящих в воздухе шаров встречаются в карельских рукописях. В них описывается создание такого шара, сделанного из кожи кита и быка. А летописи XII века рассказывают нам о том, что в карельских поселках воздушный шар имела практически каждая семья. Причем именно с помощью таких шаров древние карелы частично решали проблему бездорожья — шары помогали людям преодолевать расстояния между населенными пунктами. Но такие путешествия были достаточно опасными: оболочка из шкур животных не могла выдерживать давление воздуха долгое время – то есть, говоря другими словами, эти воздушные шары были взрывоопасными. И вот, в итоге, от них остались только легенды. Но не прошло и 7 столетий с той полумифической эпохи, как в Лондоне профессором Майклом Фарадеем были изобретены резиновые воздушные шары. Ученый изучил эластические свойства каучука – и соорудил из этого материала две «лепешки». Для того чтобы «лепешки» не слипались, Фарадей обработал их внутренние стороны мукой. И после этого пальцами склеил их необработанные, оставшиеся липкими края. В итоге получилось нечто вроде мешочка, который можно было использовать для опытов с водородом. Лет через 80 после этого научный мешочек для водорода превратился в популярную забаву: каучуковые шары широко использовались в Европе во время городских праздников. За счет наполнявшего их газа они могли подниматься вверх – и это очень нравилось публике, еще не избалованной ни воздушными полетами, ни другими чудесами техники. Но эти воздушные шарики чем-то походили на своих легендарных предшественников: в них применялся водород (а он, как известно, газ взрывоопасный). Но, тем не менее, к водороду все привыкли – благо, что особых бед от шариков с этим газом не было вплоть до 1922 года. Тогда в США на одном из городских праздников некий шутник ради забавы взорвал художественное оформление праздника – то есть воздушные шарики. В результате этого взрыва пострадал чиновник, и поэтому органы правопорядка отреагировали достаточно оперативно. Забаву, оказавшуюся достаточно опасной,

-4-

наконец-то прекратили, запретив наполнять воздушные шарики водородом. От этого решения никто не пострадал – место водорода в шариках моментально занял гораздо более безопасный гелий. Этот новый газ поднимал шарики вверх ничуть не хуже, чем это делал водород. В 1931 году Нейлом Тайлотсоном был выпущен первый современный, латексный воздушный шарик (полимер латекс получают из водных дисперсий каучуков). И с тех пор воздушные шарики наконец-то смогли измениться! До этого они могли быть только круглыми – а с приходом латекса впервые появилась возможность создавать длинные, узкие шарики. Это новшество немедленно нашло применение: дизайнеры, оформляющие праздники, стали создавать из шаров композиции в виде собак, жирафов, самолетов, шляп… Компания Нейла Тайлотсона продавала через почту миллионы комплектов шаров, предназначенных для создания смешных фигурок. Качество воздушных шариков в то время было далеко не таким, как сейчас: при надувании шарики теряли часть своей яркости, они были непрочными и быстро лопалось. Поэтому воздушные шарики медленно утрачивали свою популярность – то, что они могут летать в воздухе, в двадцатом веке уже не казалось таким чудесным и интересным.Поэтому, еще задолго до конца 20 века, воздушные шарики стали раскупаться только для городских и детских праздников. Но изобретатели не забывали о воздушных шариках, работали над их улучшением. И ситуация изменилась. Сейчас промышленность выпускает такие шарики, которые не теряют цвет при своем надувании – и вдобавок стали гораздо более прочными, долговечными. Поэтому сейчас воздушные шарики вновь стали очень популярны – дизайнеры охотно используют их при оформлении разнообразных праздников, концертов, презентаций. Свадьбы, дни рождения, общегородские праздники, PR-компании, шоу… — обновленные, яркие шары везде на месте. Вот такая интересная, давняя история у простой, с детства знакомой нам забавы.

-5-

1. Практическая часть

Эксперимент №1

Качественное сравнение плотностей воды – горячей, холодной и соленой

Если исследовать не смешивающиеся и не вступающие в химическую реакцию жидкости, то достаточно просто слить их в один прозрачный сосуд, допустим, пробирку. О плотности можно судить по расположению слоев: чем ниже слой, тем выше плотность. Другое дело, если жидкости смешиваются, как, например, горячая, холодная и соленая вода.

Мы сравниваем поведение шариков, наполненных водой горячей, холодной и подсоленной в, соответственно, горячей, холодной и подсоленной воде. В результате опыта мы можем сделать вывод о плотностях этих жидкостей.

Оборудование: три шарика разных цветов, трехлитровая банка, холодная, горячая и соленая вода.

Ход эксперимента

1. Наливаем три порции разной воды в шарики – в синий горячую,

в зеленый холодную и в красный соленую воду.

2.Наливаем в банку горячую воду, помещаем туда по очереди шарики (Приложение №1).

3.Наливаем в емкость холодную воду, снова помещаем туда по очереди все шарики.

4.Наливаем в банку соленую воду, наблюдаем за поведением шариков.

Вывод:

1. Если плотность жидкостей различна, то жидкость с меньшей плотностью всплывает над жидкостью с большей плотностью, то есть

горячей воды < холодной воды < соленой воды

2. Чем больше плотность жидкости, тем больше ее выталкивающая сила:

F_А=Vg; так как V и g постоянны F_А зависит от величины .

Эксперимент №2

Худеющий и толстеющий шарик.То, что различные тела и газы расширяются от тепла и сжимаются от холода, можно легко продемонстрировать на примере воздушного шара.В морозную погоду возьмите с собой на прогулку воздушный шар и там туго надуйте его. Если потом внести этот шарик в теплый дом, то он, скорее всего, лопнет. Это произойдет из-за того, что от тепла воздух внутри шара резко расширится и резина не выдержит давления.

Оборудование: воздушный шарик, сантиметровая лента, холодильник, кастрюля с горячей водой

Ход эксперимента

Задание № 11. Надуваем в теплой комнате воздушный шарик.

-6-

2. С помощью сантиметровой ленты измерили его окружность (у нас получилось 80,6 см).

3. После этого положили шарик в холодильник на 20-30 минут.

4. Снова измерили его окружность. Мы обнаружили, что шарик «похудел» почти на сантиметр (в нашем опыте он стал 79,7 см). Это произошло из-за того, что воздух внутри шарика сжался и стал занимать меньший объем.

Задание № 2

1 С помощью сантиметровой ленты измерили окружность воздушного шарика (у нас получилось 80,6 см).

2.Кладем шарик в миску и обливаем его горячей водой из банки.

3.Измеряем новый объем шарика. Мы обнаружили, что шарик «потолстел» почти на сантиметр (в нашем опыте он стал 82 см). Это произошло из-за того, что воздух внутри шарика расширился и стал занимать больший объем.

Вывод: воздух, содержавшийся в шарике, при охлаждении сжимается, а при нагревании расширился, что доказывает наличие теплового расширения. Давления газов зависит от температуры. При уменьшении температуры, уменьшается давление воздуха в шарике, т.е. уменьшается объём шарика. При увеличении температуры, увеличивается давление воздуха в шарике, что доказывает зависимость объема и давления газов от температуры.

.

Эксперимент №3

«Шарик в банке»

Оборудование: шарик, трехлитровая банка, горячая вода.

Ход эксперимента.

1. Наливаем в шарик воду так, чтобы он не проходил в горлышко банки.

2. Наливаем в банку горячую воду, болтаем и выливаем ее. Оставляем банку на 5 минут.

3. Кладем шарик, наполненный водой, на банку. Ждем 20 минут. Шарик падает в банку

Вывод:так как шарик, наполненный водой и больший по диаметру, чем горлышко банки, провалился внутрь, значит, имеет место разница давлений: теплый воздух внутри банки имеет меньшую плотность, чем атмосферный воздух, давление внутри меньше; следовательно, большее атмосферное давление способствует проникновению шарика в банку.

-7-

Эксперимент №4

«Воздушный парадокс»

Этот опыт ставит многих в тупик.

Оборудование: два одинаковых воздушных шарика, трубочка длиной 10–30 см и диаметром 15–20 мм (на неё должен туго надеваться шарик). два воздушных шарика, по-разному надутых, трубка из пластика, подставка.

Ход эксперимента.

1. Несильно и НЕ ОДИНАКОВО надуваем шарики.

2. Натягиваем шарики на противоположные концы трубки. Чтобы шарики при этом не сдувались, перекручиваем их горловины.

3.Раскрываем горловины для свободного сообщения воздуха между шариками.

Наблюдение.Воздух перетекает из одного шарика в другой. Но… маленький шарик надувает большой!

Объяснение. Многие считают, что раз масса воздуха больше в шарике большего размера, то этот шарик будет сдуваться и надувать маленький шарик. Но такое рассуждение ошибочно. Причина наблюдаемого явления в давлении внутри шарика. (Вспомним сообщающиеся сосуды – вода перетекает не из того сосуда, где меньше воды, а из того, где давление больше. ) Кроме того, все знают, как трудно начинать надувать шарик, но когда «мёртвая» точка преодолена, дальше он надувается легко. Следовательно, и упругость резины играет немаловажную роль.

Вывод: давление газа внутри сферы тем больше, чем меньше ее радиус.

Эксперимент № 5

Шарик — йога

Мы настолько привыкли к тому, что надутый шарик, попав на остриё, с шумом лопается,

что шарик на гвоздях под тяжестью груза воспринимается нами как сверхъестественное явление. Тем не менее это факт.

Оборудование: доска с гвоздями, воздушный шарик, доска, гиря, два штатива.

Ход эксперимента.

1. На доску с гвоздями положить воздушный шарик и надавить его рукой сверху.

2. Надавливаем на шарик предварительно измеренным грузом.

3. Наблюдаем за поведением шарика.

-8-

Наблюдения: шарик остается цел. А все дело в площади опоры! Чем больше гвоздей, тем больше точек опоры для тела (т.е. больше площадь поверхности, на которую тело опирается). И вся сила распределяется по всем гвоздям так, что на отдельно взятый гвоздь приходится слишком мало силы для прокола шарика.

Вывод: давление распределяется равномерно по всей поверхности шарика, и до определенного момента давление это для шарика безобидно.

Эксперимент № 6

Индикатор электростатического поля

Информация. Электростатические поля удобно исследовать с помощью индикаторов, позволяющих оценить направление и величину кулоновской силы в каждой точке поля. Простейший точечный индикатор представляет собой лёгкое проводящее тело, подвешенное на нити. Раньше для изготовления лёгкого шарика рекомендовали использовать сердцевину ветки бузины. В настоящее время бузину целесообразно заменить пенопластом. Возможны и другие решения проблемы.

Задание. Разработать конструкцию и изготовить простейший индикатор электростатического поля. Экспериментально определить его чув­ствительность.

Ход эксперимента.

1. Из кусочка резины от детского воздушного шара выдуваем резиновый шарик 1 диаметром 1–2 см. Шарик привяжем к шёлковой нити 2, которая укреплена к резиновой пробке.

2. Поверхность шарика натираем до характерного металлического блеска графитовым порошком от грифеля мягкого простого карандаша.

3. Шарик зарядили от потёртой мехом эбонитовой палочки.

4. Ввели индикатор в поле сферического заряда и по величине действующей силы оцените чув­ствительность индикатора.

Вывод: маленький резиновый шарик, покрытый проводником является точечным индикатором электрического поля.

-9-

Эксперимент № 7

Шарик и кораблик

Оборудование: бумажный кораблик, металлическая пластмассовая крышка,

сосуд с водой.

Ход эксперимента.

1. Делаем бумажный кораблик и пускаем его на воду.

2. Электризуем шарик и подносим к кораблику.

Наблюдение. Кораблик последует за шариком.

3. Опускаем металлическую крышку на воду.

4.Электризуем шарик и подносим к крышке, не касаясь её.

Наблюдение. Металлическая крышка плывёт в сторону шарика.

5. Опускаем на воду пластмассовую крышку.

6. Электризуем шарик и подносим к крышке, не касаясь её.

Наблюдение. Тяжёлая крышка плывёт за шариком.

Вывод: В электрическом поле шарика бумага и пластмасса поляризуются и притягиваются к шарику. В металлической крышке также индуцируется заряд. Поскольку сила трения на воде незначительна, то кораблики легко приходят в движение

Эксперимент № 8

Попрыгунчики

Оборудование: воздушный шарик, мелко нарезанная металлическая фольга, лист картона.

Ход эксперимента.

1. Насыпаем на лист картона мелко нарезанную металлическую фольгу.

2. Электризуем шарик и подносим к фольге, но не касаемся её.

Наблюдение. Блёстки ведут себя как живые кузнечики-попрыгунчики. Подскакивают, касаются шарика и тут же отлетают в сторону.

Вывод:Металлические блёстки электризуются в поле шарика, но при этом остаются нейтральными. Блёстки притягиваются к шарику, подпрыгивают, при касании заряжаются и отскакивают как одноимённо заряженные.

-10-

Эксперимент № 9

Воздушный поцелуй по закону Бернулли

Оборудование: 2 воздушных шарика, 2 нитки длинной 1 м.

Ход эксперимента.

1.Надуваем шарики до одинакового размера и привязываем к каждому нитку.

2.Берём шарики за нитку правой и левой рукой так, чтобы они висели на одном уровне на некотором расстоянии друг от друга.

3.Не касаясь шариков руками, попробуйте соединить их.

Объяснение. Из закона Бернулли следует, что давление в струе воздуха ниже, чем атмосферное. Сила атмосферного давления с боков сблизит шарики.

Эксперимент № 10

Испытание на тепловую прочность

Оборудование: шарик и свеча

Ход эксперимента.

• Наливаем в шарик воды и вносим шарик с водой в пламя свечи.

Наблюдение. Резина только коптится.

Объяснение. Температура оболочки, пока в ней есть вода, не будет подниматься выше 100 °С, т.е. не достигнет температуры горения резины.

-11-

Эксперимент № 11

Как работают лёгкие?

Оборудование: пластиковая бутылка, воздушный шарик №1, воздушный шарик №2 ( вместо него я использовал целофановый пакет), скотч.

Ход эксперимента.

1.Отрезаем дно пластиковой бутылки

2.Помещаем воздушный шарик внутрь бутылки и натягиваем его на горлышко.

3.Отрезанную часть затягиваем тлёнкой от другого воздушного шарика (или целофановым пакетом) и закрепить скотчем.

4.Оттягиваем плёнку – шарик надувается, надавливаем на плёнку – шарик сдувается.

Объяснение. Объём воздуха внутри бутылки оказывается изолированным. При оттягивании плёнки этот объём увеличивается, давление уменьшается и становится меньше атмосферного. Шарик внутри бутылки надувается воздухом атмосферы. При надавливании на плёнку объём воздуха в бутылке уменьшается, давление становится больше атмосферного, шарик сдувается. Так же работают и наши лёгкие.

Эксперимент № 12

Воздушный шарик в качестве реактивного двигателя

Оборудование: воздушный шарик, трубочка, канцелярская резинка, скотч, машина.

Ход эксперимента.

1.Воздушный шарик надо закрепить на одном конце трубки при помощи канцелярской резинки.

2. Второй конец трубки надо закрепить на корпусе машинки при помощи скотча так, чтобы была возможность надувать шарик через трубку.

3. Модель готова, можно запускать! Для этого нужно через трубку надуть шарик, зажать пальцем отверстие трубки и поставить машинку на пол. Как только вы откроете отверстие, воздух из шарика станет вылетать и толкать машинку. -12-

Объяснение. Эта наглядная модель демонстрирует принцип работы реактивных двигателей. Принцип ее работы в том, что струя воздуха, вырывающаяся из шарика, после того, как его надули и отпустили, толкает машинку в противоположном направлении.

3.Заключение

На воздушных шариках можно изучать законы давления тел и газов, тепловое расширение (сжатие), теплопроводность, плотность жидкостей и газов, закон Архимеда; электризацию тел можно даже сконструировать приборы для измерения и исследования физических процессов.

Опыты, проведенные в данной исследовательской работе, доказывают, что шарик – отличное пособие для изучения физических явлений и законов. Использовать эту работу можно в школе на уроках при изучении разделов «Первоначальные сведения о строении вещества», «Реактивное движение», «Давление твердых тел, жидкостей и газов», «Тепловые и электрические явления». Собранный исторический материал применим на занятиях кружка по физике и внеклассных мероприятиях.

Созданная на основе практической части компьютерная презентация поможет школьникам быстрее понять сущность изучаемых физических явлений, вызовет большое желание проводить эксперименты с помощью простейшего оборудования.

Очевидно, что наша работа способствует формированию неподдельного интереса к изучению физики.

4.Литература

1. [Электронный ресурс]. Режим доступа: www.demaholding.ru

2. [Электронный ресурс]. Режим доступа: www.genon.ru

3. [Электронный ресурс]. Режим доступа: www.brav-o.ru

4. [Электронный ресурс]. Режим доступа: www.vashprazdnik.com

5. [Электронный ресурс]. Режим доступа: www.aerostat.biz

6. [Электронный ресурс]. Режим доступа: www.sims.ru

7. Туркина Г. Физика на воздушных шариках. // Физика. 2008. №16.

с.25-30.

 

Просмотров работы: 3410

Размеры воздушных шаров

Практические на всех сайтах размер воздушных шаров указан не в сантиметрах, а в дюймах. Поэтому понять, какого размера будет воздушный шарик заказчику сложно.

Дело в том, что в своей работе аэродизайнеры используют воздушные шары иностранного производства — Италия, Мексика, Колумбия. Эти страны используют единицу измерения дюйм, а не сантиметр. Аэродизайнеры упрощают себе жизнь и указывают у себя на сайте размеры, которые указывает на пачке изготовитель. Вообще один дюйм равен 2,5 сантиметрам.

Основные размеры воздушных шаров и их использование

1. Шарик 5 дюймов или 13 сантиметров — это шарики небольшого размера, напоминают апельсин. Их используют для изготовления фигур из шаров, например цифры, фигуры персонажей. Подходят только для наполнения воздухом, т.к. вес шарика выше подъемной силы гелия (малый объем гелия на вес шарика)

2. Шарик 9 дюймов или 23 сантиметра в диаметре. Такие шары могут надуваться воздухом (например цветы из шаров) или гелием. Это небольшие шары, подойдут они для украшения потолка зала, кафе или квартиры. Но эти шарики смотрятся «скромно» в пространстве из-за своего небольшого размера.

3. Воздушный шар 10 дюймов. Это самый распространенный размер шарика, часто просто говорят шар среднего размера или 25 сантиметров в диаметре. Такого размера воздушные шары на палочке раздают детям в Макдональдсе. Они хорошо подходят для украшения зала, кафе. Их можно надувать воздухом и гелием. Используют для сброса воздушных шаров или запуска гелиевых шаров. Бывают с рисунком или поздравительной надписью, например «С Днем Рождения»/

4. Шары большого размера 12 дюймов (основной размер шариков) или 30 сантиметров. Считается, что это шары большого размера, их можно надуть гелием. Напоминают по размеру небольшой арбузик. Если их надуть гелием и обработать ХайФлоат, то они летают от 2, 3 дней до месяца (зависит от условий эксплуатации). Так же используются, чтобы сделать арку из воздушных шаров.

5. Шары 14 дюймов или 35 сантиметров. Эти шарики используют так же как и 12 дюймовые, но по расходным материалам итоговая стоимость таких шариков с гелием и обработкой получается значительно выше, но большой разницы в объеме нет, поэтому выгоднее использовать 12ти дюймовые для обеих сторон (переплачивать нет смысла)

6. Шары большого размера (60см,90см) шар-гигант. Бывают шары еще большего размера, 1 метр и даже 2 метра в диаметре. используются чаще всего для декорирования помещений, фотосессии и шар-сюрприз (внутри шара находятся маленькие шарики или игрушки) или декорируются гирляндами- тассел. Отлично подходят для деккорирования большого пространства или помещения под торжественное мероприятие.

Размеры фольгированных шаров

1. Шары 4 дюйма или 10см. Эти маленькие шарики предназначены для наполнения воздухом. Используются при декорировании и составлении компазиций из воздушных шаров (сердечки, звездочки, цветочки).

2. Шары 9-10 дюймов или 23см. Маленькие фольгированные шарики наполняются исключительно воздухом, так как небольшой объем гелия в этих шариках не позволит им подняться в воздух из-за соотношения массы шарика и подъемной силы гелия. Так же Вы часто можете встретить в продаже эти шарики поштучно на входах в зоопарк или на детском мероприятии (различные формы в виде героев мультфильмов и животных) комплектуются удобной палочкой.

3. Шары 17 дюймов или 43см. Эти фольгированные шарики специальной формы используются для декорирования помещения. Исполненны в виде различных фигур (например- ромашка) которые можно легко и быстро прикрепить в помещении на стену, тем самым, преобразить его в красочное место для торжества.

4. Фольгированные шары 18 дюймов или 46 см. Это размер шаров, идеально подходящий для наполнения как воздухом, так и гелием. Благодаря такому качеству, шарики получили широкое применение у декораторов и компаний специализирующихся на доставке воздушных шаров. Самые популярные формы данных шариков: круги, звезды, сердца. Отличное дополнение к латексным шарикам, которые вместе составят красивый букет с яркими переливами красок.

5. Далее размеры фольгированных шариков варируются незначительно. Они могут отличаться по размеру лишь по причине их исполнения, так как размер обусловлен их формой. Исполнение шаров в виде героев мультфильмов, тортиков, зверей, машинок, самолетов и т.д.. Размеры: 20 дюймов- 51см, 22 дюйма- 56см, 34 дюйма- 86см и тд

6. Еще один распространенный размер фольгированных шаров- это фольгированные цифры. Размер этих шаров составляет 40 дюймов или 102 сантиметра.

7. Стоит так же упамянуть о фольгированных ходящих фигурах. Ходячие фигуры наполняются гелием и уравновешиваются специальными грузами (идут в комплекте). Благодаря грузам и гелию ходячая фигура парит над полом, создавая эффект движения от легкого дуновения ветра. Исполнены в виде героев мультфильмов или забавных жтвотных. Размеры ходячих фигур так же зависят от их формы. Бывают маленькие от 24 дюйма или 61см (собачки, кошечки и тд), а бывают и внушительного размера 44 дюйма 112 сантиметров (человек паук, бетмен, русалочка и тд).

НАШИ ШАРЫ С ГЕЛИЕМ

Динамика вертикального полёта летательного аппарата легче воздуха / Хабр

Введение

Определение скорости подъёма и спуска летательных аппаратов легче воздуха (ЛАЛВ) до настоящего времени является практически важной задачей, возникающей при проектировании таких аппаратов.

Большое количество публикаций посвящено ЛАЛВ, например, только на нашем ресурсе приведены две очень интересные статьи [1,2], касающиеся истории развития на примере конкретных конструкций дирижаблей и стратостатов. Однако очень мало расчётов динамики вертикального полёта таких устройств, позволяющих хотя бы ориентировочно определять скорости подъёма и спуска ЛАЛВ.

Последнее утверждение требует определённого пояснения, поскольку искушённый читатель хорошо помнит школьный курс физики, в котором решались задачи на высоту подъёма и другие параметры воздушных шаров, заполненных газами легче воздуха или самим подогреваемым во время полёта воздухом.

Все указанные задачи были основаны на равенстве двух сил: силы веса и выталкивающей силы. Газы считались идеальными и их параметры вычислялись по закону Менделеева Клапейрона. Однако, даже простой учёт третьей силы сопротивления воздуха уже приводит к системе дифференциальных уравнений, которая аналитически не решается. Необходимо так же учитывать изменение плотности атмосферного воздуха с высотой подъёма и температурой.

Кроме этого, если нужно рассмотреть не только подъём, но и зависание шара и его спуск на землю, то совсем уж не детская задача получается. Надеюсь, что рассмотрение решения подобной задачи средствами Python не только будет способствовать расширению знаний по физике, но и популяризации самого языка программирования Python. Что я и пытаюсь делать в своих публикациях на этом ресурсе.

Математическая модель полёта ЛАЛВ с оболочкой в форме шара, объём которого не изменяется с изменением высоты

Ограничимся рассмотрением движения его центра масс под действием следующих сил: силы тяжести (G), архимедовой силы (Fa) и силой аэродинамического сопротивления (Fc). Запишем соотношения для определения сил через параметры движения и воздушной среды[3]:

В приведенных формулах приняты обозначения: h – высота подъема шара, dh/dt – вертикальная скорость, m – масса, g – ускорение свободного падения, W – объем шара, c – коэффициент лобового сопротивления, S – характерная площадь сопротивления (площадь миделя).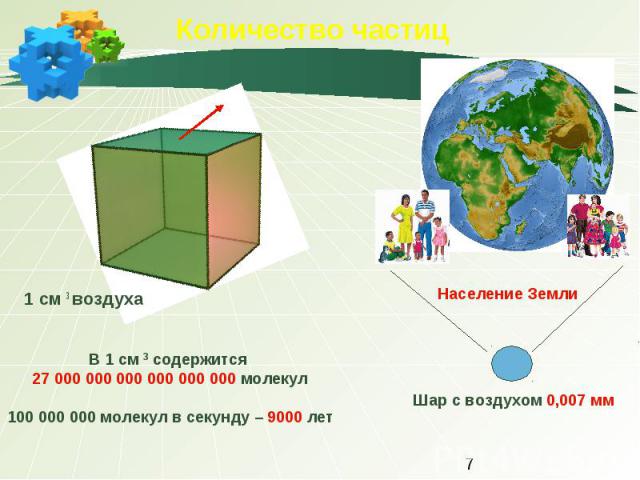
Зависимость плотности воздуха от высоты будем полагать экспоненциальной:

где – плотность воздуха на нулевой высоте, b–коэффициент. Сила тяжести направлена вниз, архимедова сила – вверх, а сила аэродинамического сопротивления всегда направлена «против движения», поэтому корректный учет этой силы в уравнениях движения требует введения множителя .

Однако, для наших целей этот факт не имеет принципиального значения, и мы ограничимся рассмотрением только этапа подъема шара, когда сила аэродинамического сопротивления направлена вниз и, следовательно, будет учтена в уравнениях движения со знаком минус. Теперь уравнение движения может быть записано в виде:

, (1)

Дополнительно предположим, что воздушный шар представляет собой однородное тело радиуса R с плотностью . Тогда величина площади, определяющая его аэродинамическое сопротивление, определится как , объем как , а масса, соответственно, как .

Теперь видно, что каждый член уравнения (1) содержит в качестве множителя величину S. Следовательно, каждый член уравнения движения может быть сокращен на величину множителя S, а само уравнение примет вид:

, (2)

Введём обозначения:

;
;

и перепишем (2) в виде следующей системы нелинейных уравнений:

, (3)

Влияние на скорость и высоту подъёма ЛАЛВ температуры атмосферного воздуха

Для этого сначала решим систему (3) с использованием следующего соотношения для зависимости плотности атмосферного воздуха от высоты без учёта температуры:

Повторим решение системы (3), но уже с использованием соотношения для зависимости плотности воздуха от высоты и температуры:

где: b=0.000125 — константа, связанная с плотностью воздуха в 1/м.;
a=0.0065 — константа, связанная с температурой воздуха в K/м.
– температура на уровне моря.

Листинг программы

 # -*- coding: utf8 -*-
from numpy import*
from scipy.integrate import odeint
import matplotlib. pyplot as plt
g=9.81# ускорение свободного падения на земле в м/с2.
rv=1.29# плотность атмосферного воздуха в кг/м3.
rg=0.17# плотность гелия в кг/м3.
R=8# радиус оболочки ЛАЛВ в м.
b=0.000125# константа, связанная с плотностью воздуха в 1/м
a=6.5*10**-3# константа, связанная с температурой воздуха в К/м
c=0.4#коэффициент лобового сопротивления
mo=240#масса в кг
V=(4/3)*pi*R**3
rs=rg+mo/V# суммарная плотность материала ЛАЛВ, массы гелия, и нагрузки
p1=rv/rs# введенный параметр
p2=3*c/(8*R)# введенный параметр
T0=300
def fun(y, t):
         y1, y2= y    
         return [y2,-g+g*p1*exp(-b*y1*T0/(T0-a*y1))-p1*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2]
t =arange(0,1100,0.01)
y0 = [0.0,0.0]
[y1,y2]=odeint(fun, y0,t, full_output=False).T
plt.title("Характеристики  подъёма ЛАЛВ  \n Объём: %s м3. Масса : %s кг. \n Подъёмная сила: %s kН. "%(round(V,0),mo,round(0.001*g*rv*V,0)))
plt.plot(t/60,y1,label='Максимальная высота подъёма: %s км. \n Максимальная скорость: % s м/с .\n С учётом температуры воздуха'%(round(max(y1)/1000,2),round(max(y2),2)))
def fun(y, t):
         y1, y2= y
         return [y2,-g+g*p1*exp(-b*y1)-p1*p2*exp(-b*y1)*y2**2]
[y1,y2]=odeint(fun, y0,t, full_output=False). T
plt.plot(t/60,y1,label='Максимальная высота подъёма: %s км. \n Максимальная скорость: % s м/с \n Без учёта температуры воздуха'%(round(max(y1)/1000,2),round(max(y2),2)))
plt.ylabel('Высота в м')
plt.xlabel(' Время в минутах')
plt.legend(loc='best')
plt.grid(True)
plt.show()

Получим:

Расчётное значение высоты подъёма ЛАЛВ с учётом температуры меньше, чем без учёта. Скорость подъёма аппарата при этом остаётся неизменной.

Определение характеристик всех фаз полёта ЛАЛВ от старта до приземления

Для построения программы полёта ЛАЛВ рассмотрим условия для следующих периодов времени:

Подъём — ;
Зависание — ;
Приземление — .

Листинг программы

# -*- coding: utf8 -*-
from numpy import*
from scipy.integrate import odeint
import matplotlib.pyplot as plt
g=9.81# ускорение свободного падения на земле в м/с2. 
rv=1.29# плотность атмосферного воздуха в кг/м3.
rg=0.17# плотность гелия в кг/м3.
R=8# радиус оболочки стратостата в м.
b=0.000125# константа, связанная с плотностью воздуха в 1/м
a=6.5*10**-3# константа, связанная с температурой воздуха в К/м
c=0.4# коэффициент лобового сопротивления
mo=240# масса в кг
V=(4/3)*pi*R**3
p2=3*c/(8*R)# введенный параметр
T0=300# температура на уровне моря
tz=4000# время зависания в секундах
rgu=1.2# плотность образовавшейся газовой смеси после  стравливания гелия в кг/м3 
tz=4000# время зависания
def fun(y, t):
         y1,y2= y
         if y2<=0:
                  if t<tz:
                            return [y2,-g+g*(rv/(rg+mo/V))*exp(-b*y1*T0/(T0-a*y1))+(rv/(rg+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2]
                  elif t>=tz:
                           return [y2,-g+g*(rv/(rgu+mo/V))*exp(-b*y1*T0/(T0-a*y1))+(rv/(rgu+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2]
         else:
                  return [y2,-g+g*(rv/(rg+mo/V))*exp(-b*y1*T0/(T0-a*y1))-(rv/(rg+mo/V))*p2*exp(-b*y1*T0/(T0-a*y1))*y2**2]
t =arange(0,tz+555,0. 1)
y0 = [0.0,0.0]
[y1,y2]=odeint(fun, y0,t, full_output=False).T
plt.title("Подъём, зависание, спуск ЛАЛВ \n с жёсткой оболочкой сферической формы  \n Объём: %s м3. Масса : %s кг. Подъёмная сила: %s kН. "%(round(V,0),mo,round(0.001*g*rv*V,0)))
plt.plot(t,y1,label='Максимальная высота подъёма: %s км. \n Максимальная скорость: % s м/с .\n Время зависания %s с.'%(round(max(y1)/1000,2), round(max(y2),2),tz-2*555))
plt.ylabel('Высота в м')
plt.xlabel(' Время в сек.')
plt.legend(loc='best')
plt.grid(True)
plt.show()

Получим:

Как следует из приведенного графика и листинга программы, для проведения вычислительного эксперимента достаточно ввести необходимые исходные данные.

Математическая модель полёта ЛАЛВ с оболочкой, объём которой изменяется с изменением высоты

К подобным ЛАЛВ относятся стратостаты. Стратостат нельзя полностью надуть гелием, придав ему максимальную подъёмную силу, которая превратит форму его оболочки в шар. Такой шар на большой высоте может лопнуть под действием возросшей разности внутреннего и наружного давлений.

По указанным причинам для расчётов максимально достижимой высоты подъёма вводят два значения его объёма: минимальный Vmin и максимальный Vmax соответственно. С учётом введенных переменных и зависимости плотности воздуха от высоты соотношения для выталкивающей силы Fa и силы тяжести Fт примут вид:

, (4)

, (5)

где: M — масса оболочки и оборудования стратостата; — плотность гелия.

Приравнивая соотношения (4) и (5), предполагая, что объем оболочки V является функцией от высоты подъёма ЛАЛВ, получим соотношение:

. (6)

Численные значения параметров входящих в соотношение (6) приводятся в листинге для построения графика, который приводится только с указанной целью.

Листинг графика с данными

# -*- coding: utf8 -*-
from numpy import*
from scipy.integrate import odeint
import matplotlib.pyplot as plt
g=9. 81# ускорение свободного падения на земле в м/с2.
rv=1.29# плотность атмосферного воздуха в кг/м3.
rg=0.17# плотность гелия в кг/м3.
Vmin=400# начальный объём шара в/м3.
b=0.000128# константа, связанная с плотностью воздуха в 1/м.
c=0.8#коэффициент лобового сопротивления
mo=40#масса в кг
rs=rg+mo/Vmin# суммарная плотность материала стратостата, массы гелия и нагрузки
p1=rv/rs# введенный параметр
h=[(10**-3)*log((rv*w)/(mo+rg*Vmin))*b**-1 for w in arange(1*10**3,1.8*10**5,1000)]
v=[(10**-3)*w for w in arange(1*10**3,1.8*10**5,1000)]
plt.title("Теоретическая зависимость высоты подъёма стратостата \n от его максимального объёма")
plt.plot(v,h)
plt.xlabel('Максимальный объём стратостата в тыс. м3')
plt.ylabel(' Максимальная высота подъёма в км.')
plt.grid(True)
plt.show()

Получим:

Изменяя параметры ЛАЛВ, приведенные в листинге программы, можно получить приведенный график и выбрать требуемый максимальный объём оболочки при проектировании. Уточнение результатов проводят с использованием огромного опыта по созданию подобных аппаратов.

Выводы:

1. Получены математические модели двух типов летательных аппаратов легче воздуха, которые позволяют проводить вычислительные экспериенты для оценочного определения параметров таких аппаратов в идеализированных условиях воздушной среды.
   
2. Предложенная многоступенчатая схема численного решения системы дифференциальных уравнений позволяет получить вертикальную траекторию летательных аппаратов легче воздуха на этапах подъёма зависания и спуска.
   

Ссылки

1. Пара слов про дирижабли
   
2. На пути в космос. Стратостаты
   
3. Рыжиков Ю.И. Современный Фортран. — СПб.: Корона принт, 2004. – 288 с.
   

Спрей для придания объема Balloon Dry Volume от R+Co подарил моим тонким, мягким волосам новую жизнь

Мы протестировали спрей для придания объема Balloon Dry Volume Spray от R+Co после получения бесплатного образца от бренда. Продолжайте читать наш полный обзор продукта.

В течение многих лет у меня были длинные волосы, и я использовала все, до чего могла дотянуться, чтобы они были гладкими и невероятно гладкими. Затем однажды я пошел на то, что я думал, было стандартным интервью для прессы с парикмахером. Следующее, что я знала, моя длина исчезла, и я вернулась в офис с бобом. Это освобождало, но и сбивало с толку, когда дело доходило до стиля. Я потратил годы на разглаживание и смягчение, и вдруг мне захотелось движения и твердости. Так началась моя любовь ко всему текстурирующему и объемному, в частности к спреям.

Прошло четыре года с момента отбивки, и за это время я перепробовала все средства для увеличения объема и текстуры на свете. Я чувствую, что это делает меня своего рода экспертом, когда дело доходит до отделения хороших продуктов от плохих, и поверьте мне, когда я говорю, что R+Co — одна из лучших. В частности, сегодня я смотрю на спрей для придания объема Balloon Dry Volume Spray, продукт, который, как утверждается, придает мгновенный объем и текстуру с великолепной отделкой и стойкостью. Как и все, что связано с R+Co, этот продукт сразил меня наповал, но если вам нужны подробности, читайте обзор.

R+Co Баллон Сухой Объемный Спрей

Подходит для: Нормальных и тонких волос.

Применение: В качестве объемного и текстурирующего спрея.  

Берди Чистый? Да

Цена: $32

О бренде: R+Co — это линия средств по уходу за волосами, созданная группой титулованных парикмахеров. Их предложение профессионального уровня, но все же удобное для пользователя. Бренд в основном известен своим крутым брендингом, простым подходом к уходу за волосами и невероятными ароматами.

О моих волосах: Мягкий, тонкий боб, который иногда может падать

Мои волосы — это ловушка-22. Поскольку я не крашу его и не использую часто термостайлеры, он мягкий и вполне здоровый (скромное хвастовство, я знаю). Но с моим бобом, касающимся плеч, мягкость может затруднить укладку. У меня тоже достаточно тонкие волосы. Он не тонкий, но имеет прекрасную текстуру (много тонких волос, как описывает его мой парикмахер). В любом случае, в целом я не могу жаловаться, но я сильно полагаюсь на текстурирующие и объемные спреи, чтобы придать им некоторую фиксацию и крутость, потому что нет ничего печальнее, чем плоская, вялая прическа.

Ингредиенты: минералы и другие трудолюбивые компоненты

Спрей для придания объема Balloon Dry Volume Spray от R+Co является выдающимся продуктом для волос, поскольку в нем особое внимание уделяется ингредиентам. Во-первых, это кремнезем, минерал, который, как известно, поглощает влагу (в том числе масло) и придает волосам шероховатость, которая является синонимом текстурирующих продуктов. Есть также цеолит, вулканический минерал, который добавляет сцепление, календула для увлажнения, полимеры для гибкой фиксации и слюда для тонкого блеска.

Вместе они работают вместе, чтобы создать спрей, который придает сухой объем без хрустящего ощущения. Он определенно матовый, но не пудровый и не тусклый. Это немалый подвиг в мире текстурирующих продуктов.

Как использовать: Экспериментирование — ключ к успеху

Я считаю, что спреи для текстурирования и придания объема — это продукт, с которым вам стоит поэкспериментировать, пока вы не найдете метод, который подходит для вашего типа и текстуры волос. Лично я предпочитаю грубую сушку, добавляю немного прически к корням и средней длине, правильно укладываю волосы и второй раз наношу корни, чтобы усилить эффект. Некоторые могут предпочесть только корни или среднюю длину, только если вы работаете над текстурированным пучком или пони. Прелесть этого в том, что нет универсального подхода, и вы действительно можете выбрать свое собственное приключение. Примечание: спрей для придания объема Balloon Dry Volume от R+Co также является хорошей альтернативой сухому шампуню для немытых волос, так как кремнезем удаляет излишки кожного сала.

Результаты: много объема и текстуры

Эмили Алгар/Дизайн Кристины Чанчи

Спрей для придания объема Balloon Dry Volume Spray от R+Co делает волосы такими объемными, что они могут быть полны секретов… Я шучу, но на самом деле это не так. Этот спрей дает действительно приятный, осязаемый, но очень полный объем. И великолепная, славная выдержка, которая является мечтой для низкорослых тонковолосых людей, таких как я. Он не такой матовый, как некоторые текстурирующие спреи, но мне это очень понравилось. Во всяком случае, это хорошая золотая середина.

Поэтому неудивительно, если я скажу, что это для тех, кто хочет густые, объемные волосы с большим количеством песка. Но каким-то волшебным образом он делает это, не оставляя волосы тусклыми или суперпудровыми (две мои любимые мозоли). Он относительно легкий, хорошо держится и расчесывается без какой-либо липкости.

Цена: дорого, но качество

Я полагаю, что единственный недостаток спрея для придания объема Balloon Dry Volume Spray от R+Co — это цена, но для профессиональной укладки волос это нормально. Лично я готов вкладывать деньги только в хороший текстурирующий или придающий объем спрей, поэтому я не против доплатить за что-то действительно хорошее. Но я думаю, что разные типы волос могут иметь разный опыт.

Похожие товары: У вас есть варианты

Oribe Dry Texturizing Spray: Самый известный и один из лучших, этот текстурирующий спрей Oribe (48 долларов США) действительно является иконой в области укладки волос. Я бы сказал, что у него меньше сцепления, чем у R+Co, но он по-прежнему обеспечивает невероятный объем, текстуру и движение.

Kristin Ess Dry Finish Working Texture Spray: Этот текстурирующий спрей от Кристин Эсс ($17) является доказательством того, что вам не нужно тратить кругленькую сумму, чтобы получить качественный текстурный спрей. Легкий и воздушный, он дает достойную зернистость и действительно хороший объем. Аромат не совсем на уровне R+Co, но все равно прекрасен.

Living Proof Full Dry Volume Blast: если вам нравится матовый эффект, вам понравится легкий спрей для объема Living Proof (30 долларов). Он пахнет чистотой и впитывает лишний жир.

Окончательный вердикт

Спрей для придания объема Balloon Dry Volume от R+Co — настоящее чудо для тонких и мягких волос. Он дает действительно крутой, текстурированный финиш, стойкий объем и не оставляет на волосах мелового или грязного ощущения. И, честно говоря, я бы купила его только из-за запаха. Скоро опустеет, точно.

Оптимальный объем пищеводного баллона для точной оценки плеврального давления в конце выдоха и в конце вдоха: лабораторный эксперимент in vitro | Медицина интенсивной терапии Экспериментальный

• Исследовательский
• Открытый доступ
• Опубликовано: 02 августа 2017 г.

• Ян-Лин Ян ^1,2 ,
• Сюань Хэ ¹ ,
• XIU-MEI SUN ¹ ,
• HAN Chen ^1,3 ,
• Zhong-Hua Shi ¹ ,
• Ming XU ¹ ,
• Ming XU ¹ ,
• 33333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333939.
• …
• Цзянь-Синь Чжоу ¹  

Экспериментальная медицина для интенсивной терапии том 5 , номер статьи: 35 (2017) Процитировать эту статью

• 2279 доступов

• 13 цитирований

• 11 Альтметрический

• Сведения о показателях

Abstract

История вопроса

Пищеводное давление, используемое в качестве заменителя плеврального давления, обычно измеряется с помощью наполненного воздухом баллона, и точность измерения зависит от правильного объема баллона. Было обнаружено, что больший объем заполнения требуется при более высоком окружающем давлении. В настоящем исследовании мы определили отношение давления баллона к объему в настольной модели, моделирующей плевральную полость во время контролируемой вентиляции. Цель состояла в том, чтобы подтвердить, существует ли оптимальный диапазон объема баллона, который мог бы обеспечить точные измерения как в конце выдоха, так и в конце вдоха.

Методы

Мы исследовали три пищеводных баллона разных размеров и материалов: катетеры Cooper, SmartCath-G и Microtek. Баллон вводили в стеклянную камеру, имитирующую плевральную полость, и начинали искусственную вентиляцию легких. Вентилятор был настроен на получение соответствующего давления в камере 5 и 20 см H ₂ O во время окклюзии в конце выдоха и в конце вдоха. Баллон постепенно надували и измеряли давление в баллоне и давление в камере. Трансмуральное давление в баллоне определяли как разницу между давлением в баллоне и в камере. Кривая давление-объем баллона была аппроксимирована с помощью сигмовидной регрессии, а минимальный и максимальный объем баллона, точно отражающие окружающее давление, были оценены с использованием нижней и верхней точки перегиба аппроксимированной сигмовидной кривой. Были исследованы объемы баллона в конце выдоха и конце вдоха, и диапазон объема баллона, обеспечивающий точное измерение в обеих фазах, был определен как оптимальный объем наполнения.

Результаты

Сигмовидная регрессия кривой давление-объем баллона была подтверждена подбором безразмерных переменных и анализом остаточного распределения. Все трансмуральные давления баллона находились в пределах ±1,0 см вод. ст. ₂ O при минимальном и максимальном объемах баллона. Минимальный и максимальный объемы баллона при окклюзии в конце вдоха были значительно больше, чем при окклюзии в конце выдоха, за исключением минимального объема в катетере Купера. Среднее значение (± стандартное отклонение) оптимального объема наполнения, подходящего как для измерения в конце выдоха, так и в конце вдоха, варьировалось от 0,7 ± 0,0 до 1,7 ± 0,2 мл по Куперу, 1,9от ± 0,2 до 3,6 ± 0,3 мл в SmartCath-G и от 2,2 ± 0,2 до 4,6 ± 0,1 мл в катетере Microtek.

Выводы

В каждом из протестированных баллонов был найден оптимальный диапазон объема наполнения, обеспечивающий точное измерение как при окклюзии в конце выдоха, так и при окклюзии в конце вдоха.

История вопроса

В течение многих лет давление в пищеводе использовалось в качестве заменителя плеврального давления при мониторинге дыхательной механики [1, 2]. Ранее измерение давления в пищеводе в основном применялось для оценки усилий дыхательных мышц и работы дыхания при спонтанной или вспомогательной вентиляции, особенно у пациентов с трудным отлучением от груди [3, 4]. Совсем недавно этот метод был расширен для проведения защитной вентиляции легких у пациентов с острым респираторным дистресс-синдромом [5,6,7,8].

Пищеводное давление обычно измеряют с помощью катетера с наполненным воздухом баллоном, и точность измерения зависит от правильного наполнения баллона [1, 2]. Исследования показали, что переполнение баллона может привести к завышению давления в пищеводе; напротив, недостаточное заполнение может привести к недооценке [9,10,11,12,13,14,15,16]. Теоретически оптимальный объем баллона — это диапазон с минимальным расхождением между давлениями, измеренными внутри и снаружи баллона, а именно минимальное трансмуральное давление баллона ( Р _ТМ ). Было обнаружено, что в лабораторных условиях для передачи давления при более высоком окружающем давлении требуется больший объем баллона [15]. Следовательно, при пассивной вентиляции оптимальный объем баллона, полученный в фазе конца выдоха (низкое давление), может одновременно не подходить для измерения в фазе конца вдоха (высокое давление), особенно у пациентов с высоким приводным давлением. Эта возможность требует дальнейшего изучения.

Предыдущие исследования показали нелинейную сигмовидную форму кривой давления-объема баллона в условиях in vitro и in vivo [9, 11,12,13,14,15,16,17]; однако ни в одном исследовании не предпринимались попытки такого типа регрессионного анализа. Мы предположили, что сигмовидная аппроксимация кривой давление-объем баллона может стать дополнительным методом определения оптимального объема баллона. В настоящем исследовании мы выбрали три коммерчески доступных пищеводных катетера с баллонами разных размеров и материалов. Данные о давлении и объеме баллона были подобраны с использованием уравнения сигмовидной регрессии, а оптимальный объем баллона был определен при атмосферном давлении и в динамической настольной модели, имитирующей плевральную полость во время вентиляции с контролируемым объемом. Оценивали общее соответствие сигмовидной регрессии и точность оценки объема баллона. Р _TM , а приемлемая точность измерения определена как P _TM в пределах ±1 см H ₂ O [15]. Мы стремились подтвердить, существует ли оптимальный диапазон объема баллона, который мог бы обеспечить точные измерения как в конце выдоха, так и в конце вдоха.

Методы

Пищеводные баллонные катетеры

Были протестированы три имеющихся в продаже пищеводных баллонных катетера с баллонами разных размеров и материалов: (1) катетер Купера (LOT 177405, Cooper Surgical, США) диаметром 5 Fr и длиной 85 см, в комплекте с полиэтиленовым баллоном и рекомендуемым производителем объемом надувания 1–2 мл; (2) катетер SmartCath-G (LOT 7003300, CareFusion Co. , США) диаметром 16 Fr и длиной 114 см, с полиэтиленовым баллоном и рекомендованным производителем объемом надувания 0,5–2,5 мл; и (3) катетер Microtek (LOT 20110815, Microtek Medical B.V., Нидерланды) диаметром 8 Fr и длиной 100 см, с латексным баллоном и без рекомендуемого производителем объема надувания.

Для каждого типа катетера случайным образом отобрали шесть образцов. Перед экспериментом каждый баллон проверяли на герметичность путем надувания под водой. Длину и диаметр баллона измеряли в одном случайно выбранном катетере каждого типа с помощью штангенциркуля с нониусом (CD67-S, PM/PS, Mitutoyo Measuring Instruments (Shanghai) Co., Ltd., Шанхай, Китай). Геометрический объем баллона рассчитывали на основе длины и диаметра баллона и с использованием корпуса капсулы в качестве приближения. Поскольку питательная трубка проходит через внутреннее пространство баллона катетера SmartCath-G, этот объем был вычтен при расчете геометрического объема баллона для этого типа катетера.

Измерения давления

Все измерения давления проводились с использованием датчиков давления (KT 100D-2, Kleis TEK, Италия, диапазон: ±100 смH ₂ O), подключенных к барокамере ICU-Lab (ICU Lab, KleisTEK Engineering, Бари, Италия) на 80-сантиметровых линиях из жестких труб. Датчики давления были откалиброваны с использованием водяного столба. Сигналы отображались непрерывно и сохранялись (программный пакет ICU-Lab 2.5, ICU Lab, KleisTEK Engineering, Бари, Италия) на портативном компьютере для дальнейшего анализа с частотой дискретизации 200 Гц.

Манипуляции с объемом баллона при атмосферном давлении

Соотношение давление-объем баллона определяли при атмосферном давлении с использованием ранее опубликованного метода с некоторыми модификациями [12, 13, 16]. Баллонный просвет катетера был соединен с трехходовым краном для манипуляции с объемом баллона, а два других канала были соединены с 1-мл газонепроницаемым шприцем (LOT JM00B25, оборудование для контроля жидкости Runze, C. O., Ltd. , Нанкин, Китай) и датчик давления. Воздушный шар сначала надували до геометрического объема, чтобы развернуть стенку воздушного шара. Затем баллон сдули, создав отрицательное давление примерно -10 см вод. ст. ₂ О, и запорный кран был закрыт. Эта процедура стандартизировала остаточный объем в баллоне, и мы произвольно определили объем баллона в этой ситуации как нулевой объем надувания [12, 13, 16]. После этого баллон постепенно надували с шагом 0,5 мл. После каждого надувания объема давление в баллоне измеряли после 3-минутного периода уравновешивания. Раздувание баллона прекращали до тех пор, пока давление в баллоне не превышало +10 см вод. ст. ₂ O. Поскольку эксперимент в статических условиях проводился при атмосферном давлении, Р _TM был равен давлению баллона.

Манипуляции с объемом баллона при имитации пассивной вентиляции

Была построена модель для имитации плевральной полости и легкого (рис. 1). Модель состояла из стеклянной камеры на 5000 мл (Shuniu Glass Instrument Co., Ltd., Сычуань, Китай) с тремя отверстиями, резинового легкого на 1000 мл (Puritan-Bennett Corporation, Калифорния, США) и тест-системы Мичигана. легкое (двойное тренировочное легкое для взрослых, модель 5600i, номер по каталогу 15090, Michigan Instruments, Гранд-Рапидс, Мичиган, США). Резиновое тестовое легкое было герметизировано в стеклянной камере через одно отверстие, имитирующее легкое, и было подключено к аппарату ИВЛ Servo-I (Maquet Critical Care, Solna, Швеция) с помощью эндотрахеальной трубки с внутренним диаметром 8,0 (LOT 1892776, Portex Tracheal Tube, Smiths). Medical International Ltd., Кин, США). Через второе отверстие стеклянная камера была соединена с тестовым легким Мичигана для имитации плевральной полости с изменяемой податливостью. Третье отверстие использовалось для введения баллона в стеклянную камеру и затем закрывалось. Давление измеряли с помощью различных датчиков давления в трех положениях (рис.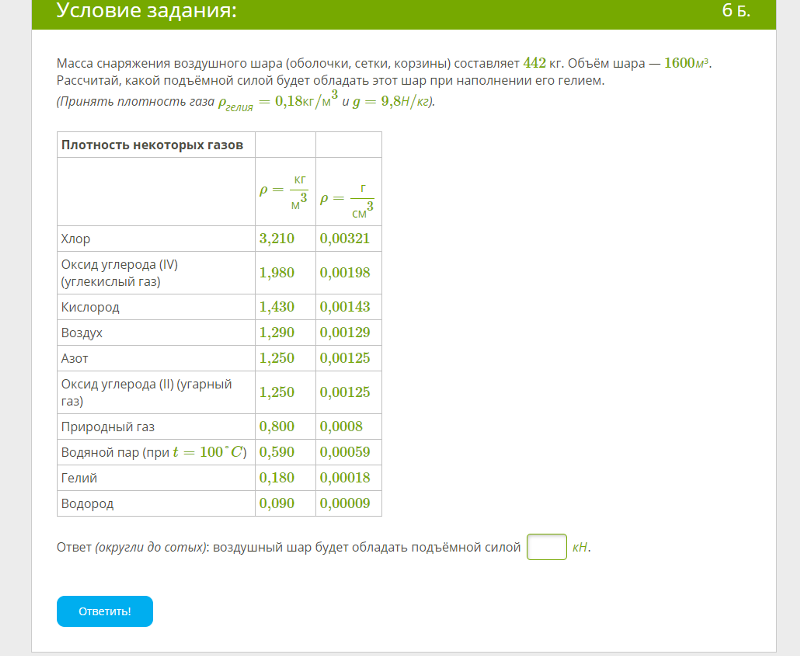 1): давление в дыхательных путях на проксимальном конце эндотрахеальной трубки, прямое измерение давления в камере для представления давления, окружающего баллон, и давление в баллоне.

Рис. 1

Схематическая модель с плевральной полостью и легким

Изображение в полный размер

Во время лабораторной процедуры механическая вентиляция была настроена как вентиляция с регулируемым объемом с постоянным потоком 60 л/мин; дыхательный объем 500 мл; время вдоха 0,5 с с временем паузы вдоха 0,5 с; частота дыхания 20 вдохов/мин; и положительное давление в конце выдоха (PEEP) 5 см H ₂ O. Триггер вдоха был установлен на -20 см H ₂ O, чтобы избежать автоматического срабатывания. Податливость тестового легкого в Мичигане была установлена ​​на уровне 20 мл/смH 9 .0159 2 O. Эти параметры аппарата ИВЛ и тестового легкого давали давление плато в дыхательных путях приблизительно 40 см вод. ст. ₂ O и давление в камере 20 см вод. , модель была протестирована двумя методами для подтверждения отсутствия систематической утечки: (1) дыхательный объем выдоха не менее дыхательного объема вдоха при ИВЛ и (2) снижение давления в дыхательных путях не менее 1 см вод.0159 2 O в течение 30 с окклюзии в конце выдоха при 30 см H ₂ O ПДКВ.

К просвету баллона катетера подсоединяли трехходовой кран. Искусственная вентиляция легких не прерывалась во время манипуляций с баллоном, чтобы имитировать реальный клинический сценарий. Баллон сначала сдули путем создания отрицательного давления, после чего баллон открыли в атмосферу на 3 минуты, чтобы стандартизировать остаточный объем, оставшийся в баллоне, и в просвете катетера. Затем баллон постепенно надували с шагом 0,5 мл до объема, который приводил к отклонению давления в баллоне от давления в камере, которое превышало 1 см H ₂ O. Раздувание баллона выполнено в конце выдоха. При каждом тестируемом объеме баллона после 3-минутного периода уравновешивания выполняли окклюзию в конце выдоха и конце вдоха (каждая по 10 с), а в последнюю секунду одновременно измеряли давление в баллоне и давление в камере.

Определение объема баллона с помощью сигмовидной регрессии

Объем баллона был построен в зависимости от давления в баллоне, и эти две переменные были подогнаны под следующее уравнение сигмовидной регрессии [18,19{-\left(\mathrm{Balloon}\ \mathrm{давление}-c\right)/d}} \) (1)

Кривая давление-объем баллона была подобрана с использованием итерационного алгоритма Левенберга-Марквардта, который был запускается до тех пор, пока изменение суммы квадратов остатков не станет меньше 10 ⁻⁸ . Пример графика рассеяния с подобранной линией показан на рис. 2а. Уравнение 1 имеет четыре подгоночных параметра: a в единицах объема (мл), представляющих нижнюю асимптоту подобранной сигмовидной кривой; b , также в единицах объема (мл), что представляет собой расстояние по вертикали от нижней до верхней асимптоты; c (cmH ₂ O), представляющее давление в средней точке сигмовидной кривой, где вогнутость меняет направление; и d (смH ₂ O), что пропорционально минимальному изменению давления в баллоне по мере увеличения объема баллона. Согласно характерным особенностям сигмовидной кривой, максимальные изменения кривизны вверх и вниз происходили в нижней и верхней точках перегиба при баллонных давлениях, равных c ± 1,317 d (рис. 2а) [21]. Внутри этих двух точек перегиба изменение давления в баллоне было минимальным во время постепенного надувания баллона. Мы выбрали более узкий диапазон для оценки оптимального объема баллона и определили объем баллона при давлении в баллоне c  −  d как минимальный объем наполнения ( V _MIN , равно [ a  +  b /2] − 0,231 b ) и c  +  d как максимальный объем ( V _MAX , равно [ a  +  b /2] + 0,231 b ). Баллон P _ТМ значения при В _МИН и В _MAX были рассчитаны как расчетное давление в баллоне минус среднее давление в камере. Приемлемая точность измерения определялась как Р _TM в пределах ±1 см H ₂ O [15]. Рабочий объем баллона ( V _РАБОТА ) рассчитывалась как разница между V _МИН и В _МАКС . В атмосферных условиях эластичность баллона оценивалась как разница давления в баллоне между и _МИН и В _МАКС разделить на В _РАБОТА .

Рис. 2

Пример аппроксимированной кривой объем-давление баллона с использованием уравнения сигмовидной регрессии. a Пример подбора давления и объема баллона в баллоне SmartCath-G при окклюзии в конце выдоха во время имитации искусственной вентиляции легких. Круги — это отдельные точки данных. сплошная линия представляет подобранную кривую. Уравнение (показанное в верхней части рисунка) имеет четыре подгоночных параметра: a в единицах объема (мл), представляющих нижнюю асимптоту подобранной сигмовидной кривой; b , также в единицах объема (мл), что представляет собой расстояние по вертикали от нижней до верхней асимптоты; c (cmH ₂ O), представляющее давление в средней точке сигмовидной кривой, где вогнутость меняет направление; и d (cmH ₂ O) пропорциональна минимальному изменению давления в баллоне по мере увеличения объема баллона. Мы определили объем баллона при давлении в баллоне c  −  d как минимальный объем наполнения ( V _MIN , равно [ a  +  b /2] − 0,231 b ) и c  +  d как максимальный объем ( V _MAX , равно [ a  +  b /2] + 0,231 b ). В этих двух точках изменение давления в баллоне было минимальным во время надувания баллона. Рабочий объем баллона ( V _РАБОТА ) определялась как разница между V _МИН и В _МАКС . б Анализ В _РАБОТА с во время окклюзии в конце выдоха (EEO) и в конце вдоха (EIO) в одном и том же баллоне в a . В _МИН и В _MAX оба удовлетворяющих двум фазам были определены как нижний и верхний предел оптимального диапазона объема баллона

Полноразмерное изображение

В каждом протестированном баллоне В Были исследованы значения _WORK во время окклюзии в конце выдоха и конце вдоха, а также V _МИН и В _MAX , обеспечивающие точное измерение на обеих фазах, были определены как нижний и верхний пределы оптимального диапазона объема баллона (рис. 2б). Визуальный осмотр промежуточного линейного участка кривой давление-объем баллона также выполняли с использованием метода, описанного Mojoli et al. [17]. Воздушный шар Р _ТМ значения при В _МИН и В _MAX , полученные методом визуального осмотра, также были рассчитаны.

Статистический анализ

При анализе кривой давление-объем баллона коэффициент наилучшего соответствия R ² и информационный критерий Акаике с поправкой на погрешность (AICc) сигмовидной регрессии были рассчитаны [22]. Чтобы оценить общее соответствие в уравнении регрессии для каждого типа баллона с использованием каждого соответствующего уравнения подбора, объем баллона и давление баллона были преобразованы в безразмерные переменные (объем баллона – 9{-\left(\mathrm{баллон}\ \mathrm{давление}-c\право)/d}} \) (2)

Среднее значение и стандартное отклонение (SD) остатка для (объем баллона −  a )/ b были рассчитаны и нанесены на график в зависимости от (баллонное давление —  c )/ d .

Категориальные переменные были выражены в виде количества и процентов. Непрерывные данные были проверены на нормальное распределение с использованием критерия Колмогорова-Смирнова и представлены как среднее значение ± стандартное отклонение или медиана (от 25-го до 75-го процентиля) в зависимости от ситуации. Данные об объеме баллона при атмосферном давлении сравнивались для различных типов баллонов с использованием однофакторного дисперсионного анализа и теста Стьюдента-Ньюмана-Кеулса для попарных сравнений. В динамических условиях во время симулированной пассивной вентиляции односторонний дисперсионный анализ также использовался для сравнения давления в камере и давления в баллоне при различном объеме баллона. Повторные измерения дисперсионного анализа использовались для сравнения данных об объеме баллона для разных типов баллонов и между окклюзией в конце выдоха и в конце вдоха. Парные t Тест использовался для сравнения разницы в абсолютных значениях P _ТМ на В _МИН или В _MAX между методами сигмовидного фитинга и визуальным контролем.

Все тесты значимости были на уровне значимости 5%. Анализы проводились с использованием SPSS V.20.0 (SPSS Inc., Чикаго, Иллинойс, США).

Результаты

Параметры установки сигмовидной кишки для всех протестированных баллонов и при всех стендовых условиях показаны в дополнительном файле 1: Таблица S1. Когда данные, полученные во всех тестируемых условиях для каждого типа баллона, были объединены и нормализованы в соответствии с параметрами в каждом соответствующем регрессионном уравнении (уравнение 1), безразмерная переменная (объем баллона – a )/ b был точно подогнан к (баллонное давление – c )/ d по стандартной сигмовидной кривой (дополнительный файл 1: рисунок S1). Среднее значение ± стандартное отклонение остаточного значения (объем баллона — a )/ b составило 0,000047 ± 0,0358, 0,00000 ± 0,0554 и 0,000028 ± 0,0648 для катетеров Cooper, SmartCath-G и Microtek соответственно. Остатки (объем баллона —  a )/ b были равномерно рассеяны по (давление баллона – c )/ d для катетера Cooper, но статистически положительная корреляция была обнаружена для катетеров SmartCath-G и Microtek (дополнительный файл 1: рисунок S2).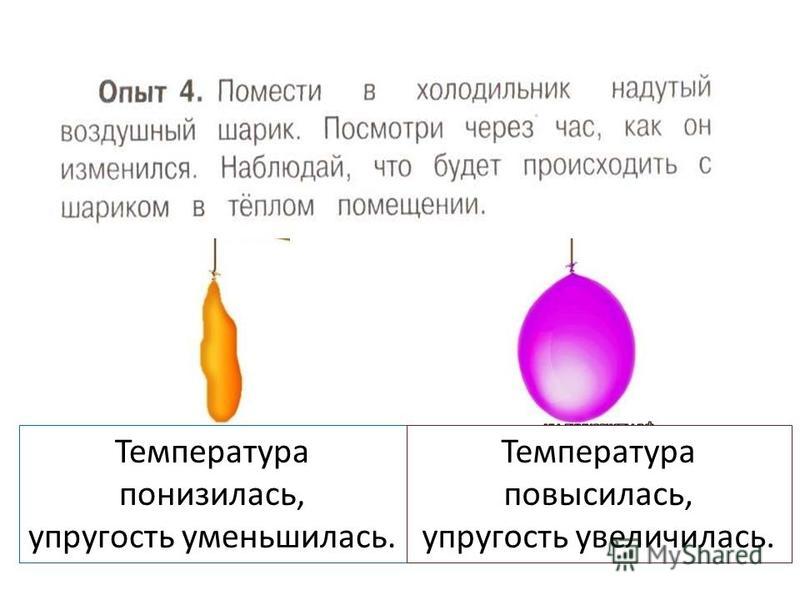

В таблице 1 приведены характеристики протестированных баллонов. Геометрический объем баллона составлял 2,8 мл для Cooper, 5,3 мл для SmartCath-G и 7,5 мл для катетера Microtek. При атмосферном давлении наблюдались существенные отличия V _МИН , В _МАКС , В _WORK и эластичность баллона разных типов ( p  < 0,001, рис. 3).

Полноразмерная таблица

a – d Данные об объеме баллона и его упругости в атмосфере. Данные представлены в виде среднего значения и стандартного отклонения. Значительная разница существовала в минимальном ( В _MIN , a ), максимальный объем наполнения баллона ( V _МАКС , б ), рабочий объем ( В _WORK , c ) и эластичность баллона между разными баллонами ( p  < 0,001, d ). Все значения p меньше 0,001 при попарном сравнении

Полноразмерное изображение

В динамической модели систематической утечки во время имитации пассивной вентиляции не было. С постепенным увеличением объема впрыскивания баллона давление в камере оставалось стабильным, но давление баллона значительно увеличивалось в каждом типе катетера в конце выдоха или в конце вдоха (все p  < 0,001) (дополнительный файл 2: рисунок S3). Данные об объеме баллона во время динамической вентиляции показаны на рис. 4. Имелись значительные различия между и . _МИН , В _МАКС и В _WORK для разных типов баллонов и между окклюзией в конце выдоха и в конце вдоха ( p  = 0,003 до <0,001). Во время окклюзии в конце выдоха или в конце вдоха V _МИН , В _МАКС и В _РАБОТА располагались в значимом порядке возрастания катетеров Cooper < SmartCath-G < Microtek, в соответствии с последовательностью геометрического объема. Три параметра объема баллона во время окклюзии в конце вдоха были значительно выше, чем во время окклюзии в конце выдоха, за исключением V _MAX в Cooper ( p = 0,062) и V _РАБОТА в Microtek ( p  = 0,363) (рис. 4). Во всех протестированных баллонах все Р Значения _TM при различных условиях испытаний (атмосферное давление и искусственная вентиляция) находились в пределах ±1,0 см H ₂ O (рис. 5). Все В _МИН и В _MAX , определенные сигмовидной регрессией, находились в пределах промежуточного линейного участка, полученного путем визуального изучения кривой давления-объема баллона (дополнительный файл 3: таблица S2). Для любого В _МИН или В _МАКС. , абсолютный P Значения _TM , измеренные с помощью сигмовидного фитинга, были ниже, чем значения, измеренные при проверке промежуточного линейного участка (дополнительный файл 3: рисунок S4).

Данные об объеме баллона во время имитации искусственной вентиляции легких. Данные представлены в виде среднего значения и стандартного отклонения. Существовали значительные различия в минимальном ( и ; В _МИН , p  < 0,001) и максимальное ( b ; В _MAX , p  < 0,001) объем накачивания баллона и рабочий объем ( c ; V _WORK , p  = 0,003) для разных типов баллонов и между окклюзией в конце выдоха и в конце вдоха. Показаны результаты попарного сравнения: * p  < 0,001, ** p  < 0,01 и *** p  < 0,05

Изображение в полный размер

Трансмуральное давление баллона при всех лабораторных условиях Баллонное трансмуральное давление ( P _ТМ ) при минимальном ( В _MIN ) и максимальный объем наполнения баллона ( V _MAX ) в атмосфере ( черный ) и в конце выдоха ( синий ) и в конце вдоха ( красный ) во время имитации пассивной вентиляции. Все P _TM находились в пределах ±1 см вод. ст. ₂ O. Также показаны среднее значение и стандартное отклонение

Полноразмерное изображение

Для каждого испытанного баллона существовал оптимальный диапазон объема баллона, который обеспечивал точные измерения как в конце выдоха, так и в конце выдоха. инспираторная окклюзия, которая составляла от 0,7 ± 0,0 до 1,7 ± 0,2 мл для Cooper, 1,9от ± 0,2 до 3,6 ± 0,3 мл для SmartCath-G и от 2,2 ± 0,2 до 4,6 ± 0,1 мл для катетера Microtek (рис. 6).

Нижний и верхний пределы оптимальных объемов баллона, которые обеспечивают точное измерение как во время окклюзии в конце выдоха, так и в конце вдоха. Нижний и верхний пределы были определены как минимальный и максимальный объем наполнения баллона, который обеспечивал точное измерение как во время окклюзии в конце выдоха, так и в конце вдоха

Полноразмерное изображение

Обсуждение

В настоящем исследовании мы использовали математический метод, сигмовидную регрессию, для анализа кривой давление-объем баллона и для определения оптимального объема баллона при различных лабораторных условиях. Наши основные выводы:

(1) Существует оптимальный диапазон объема баллона, который обеспечивает точное измерение как в конце выдоха, так и в конце вдоха для каждого из протестированных баллонов.

(2) Сигмовидная регрессия превосходно соответствует кривой давление-объем баллона и позволяет точно оценить оптимальный объем баллона. Этот метод обеспечивает дополнительный способ определения оптимального объема баллона.

Правильное титрование объема баллона имеет решающее значение для точного измерения давления в пищеводе [1, 2]. В лабораторных исследованиях оптимальный объем баллона определялся как диапазон объема, в котором P _TM находилась в пределах определенного порога [14, 15]. В настоящем исследовании мы оценили оптимальный объем и диапазон баллона, используя сигмовидную аппроксимацию кривой давления-объема баллона, которая использовалась для прогнозирования нижней и верхней точек перегиба при анализе кривой давления-объема дыхательной системы [19]. , 20]. После нормализации, основанной на параметрах уравнения регрессии, безразмерные переменные давления и объема баллона были близко распределены вдоль стандартной сигмовидной кривой, а средний остаток для безразмерных переменных объема был незначительным (дополнительный файл 1: рис. S1 и S2). Что еще более важно, все измерено P _ТМ значения при В _МИН и В _MAX находились в пределах ±1 см H ₂ O (рис. 5), что использовалось в качестве порога в предыдущем стендовом исследовании [15]. В совокупности эти результаты показывают, что сигмовидную регрессию давления и объема баллона можно использовать для точной оценки оптимального объема наполнения.

В настоящем исследовании, в дополнение к тестированию баллонов в атмосферных условиях, мы также проанализировали соотношение давление-объем баллона во время имитации пассивной вентиляции в модели дыхательной системы (рис. 1), о чем сообщалось в образовательных целях [23]. , 24]. Мы использовали эту модель в попытке имитировать реальные клинические сценарии. Используя наш метод сигмовидной подгонки, мы подтвердили два предыдущих основных открытия, касающихся взаимосвязи между объемом наполнения баллона, геометрическим объемом и окружающим давлением [14, 15]. Во-первых, объем наполнения баллона определяется геометрическим объемом баллона (рис. 3): чем больше геометрический объем, тем больший объем наполнения баллона необходим для отражения окружающего давления. Во-вторых, объем наполнения баллона, необходимый для точного измерения, увеличивается по мере увеличения давления вокруг баллона (рис. 4). Последний вывод имеет клиническое значение при мониторировании пищевода у пассивных пациентов на управляемой вентиляции. Поскольку плевральное давление увеличивается во время вдоха, объем баллона, пригодный для измерения в конце выдоха, может оказаться недостаточным для измерения в конце вдоха. К счастью, этого не произошло в нашей настольной модели с имитацией плеврального давления в диапазоне от 5 см H ₂ O во время окклюзии в конце выдоха до 20 см H ₂ O во время окклюзии в конце вдоха. Существовал оптимальный диапазон объемов, который позволял проводить точные измерения на обеих фазах (рис. 6).

Наклон промежуточного участка минимален в условиях in vitro и связан с эластичностью баллона [15, 16], но обычно наклонен in vivo из-за эластичности пищевода [17]. Мы оценили эластичность баллона на основе данных давления и объема подогнанного баллона, а также наших результатов (от 0,1 до 0,4 см H 9 ).0159 2 О/мл, рис. 3d) были сопоставимы с теми, о которых сообщают Cross et al. [16]. Необходимы дальнейшие исследования, чтобы определить, может ли этот метод повысить точность измерения эластичности пищевода и калибровки давления в пищеводе у постели больного.

В клинических условиях, поскольку трудно получить P _TM , надлежащий объем баллона обычно определяется визуальным осмотром промежуточного линейного участка кривой давление-объем баллона [17]. По сравнению с методом визуального контроля подгонка данных к сигмовидной кривой дала В _WORK с более узким диапазоном и P _TM ближе к нулю (дополнительный файл 3: таблица S2 и рисунок S4). Эти результаты позволяют предположить, что представленный нами метод может обеспечить более точную оценку оптимального объема баллона. Кроме того, подгонка сигмовидной является объективной и основана на математике. Однако, поскольку в настоящем исследовании метод сигмовидной подгонки изучался только на настольной модели, необходимы дальнейшие исследования, чтобы определить, может ли этот метод улучшить оценку оптимального объема баллона. Поскольку во избежание переполнения рекомендуется относительно небольшой адекватный объем баллона [2, 11], мы предлагаем использовать нижнюю границу оптимального диапазона объемов баллона (рис. 6), что позволяет избежать переполнения баллона на выдохе и одновременно избежать недополнения на вдохе. .

Настоящее исследование имеет ограничения. Во-первых, в нашей настольной модели мы моделировали только плевральную полость без пищевода. Было показано, что эластичность стенки пищевода существенно влияет на мониторинг эзофагеального давления [17]. Таким образом, наши результаты не могут быть непосредственно перенесены в клиническую практику. Кроме того, процедура выполнялась только при контролируемой вентиляции, и полученные данные нельзя применить к пациентам со спонтанным дыханием. Во-вторых, высокое давление вокруг баллона, смоделированное в настоящем исследовании, было несколько ниже, чем давление в пищеводе в конце вдоха у пациентов с острым респираторным дистресс-синдромом во время пассивной вентиляции [5,6,7]. Титрование объема баллона требует дальнейшего изучения в клинических исследованиях, особенно у пациентов с относительно высоким давлением в пищеводе и давлением в дыхательных путях.

Выводы

Кривая давление-объем баллона хорошо аппроксимируется сигмовидной регрессией и обеспечивает точную оценку объема баллона. В клинической практике следует проводить тщательное титрование объема наполнения, потому что достаточный объем баллона отличается для разных типов баллонов при различном окружающем давлении. В каждом протестированном баллоне существует оптимальный диапазон объема наполнения, который обеспечивает точное измерение как во время окклюзии в конце выдоха, так и в конце вдоха.

Сокращения

PEEP:

Положительное давление в конце выдоха

Р _ТМ :

Баллонное трансмуральное давление

SD:

Стандартное отклонение

В _МАКС :

Максимальный объем надувания баллона

В _МИН :

Минимальный объем надувания баллона

В _РАБОТА :

Рабочий объем баллона

Ссылки

1. «>

   Akoumianaki E, Maggiore SM, Valenza F, Bellani G, Jubran A et al (2014) Применение измерения давления в пищеводе у пациентов с дыхательной недостаточностью. Am J Respir Crit Care Med 189:520–531

   Статья пабмед Google ученый

2. Mauri T, Yoshida T, Bellani G, Goligher EC, Carteaux G et al (2016) Пищеводное и транспульмональное давление в клинических условиях: значение, полезность и перспективы. Intensive Care Med 42:1360–1373

   Статья пабмед Google ученый

3. Jubran A, Grant BJ, Laghi F, Parthasarathy S, Tobin MJ (2005)Прогноз прикорма: мониторинг давления в пищеводе дополняет тестирование готовности. Am J Respir Crit Care Med 171: 1252–1259

   Артикул пабмед Google ученый

4. Kallet RH, Hemphill JC 3rd, Dicker RA, Alonso JA, Campbell AR et al (2007)Спонтанное дыхание и работа дыхания у пациентов с острым респираторным дистресс-синдромом и острым повреждением легких. Respir Care 52:989–995

   PubMed Google ученый

5. Talmor D, Sarge T, O’Donnell CR, Ritz R, Malhotra A et al (2006) Пищеводное и транспульмональное давление при острой дыхательной недостаточности. Крит Уход Мед 34:1389–1394

   Артикул пабмед ПабМед Центральный Google ученый

6. Talmor D, Sarge T, Malhotra A, O’Donnell CR, Ritz R et al (2008) Механическая вентиляция под контролем давления в пищеводе при остром повреждении легких. N Engl J Med 359:2095–2104

   CAS Статья пабмед ПабМед Центральный Google ученый

7. Chiumello D, Carlesso E, Brioni M, Cressoni M (2016) Давление в дыхательных путях и стресс легких у пациентов с ОРДС. Критическая забота 20:276

   Артикул пабмед ПабМед Центральный Google ученый

8. «>

   Перссон П., Лундин С., Стенквист О. (2016)Транспульмональное и плевральное давление в модели дыхательной системы с эластичным возвратным легким и расширяющейся грудной стенкой. Intensive Care Med Exp 4:26

   Статья пабмед ПабМед Центральный Google ученый

9. Мид Дж., Макилрой МБ, Селверстоун, штат Нью-Джерси, Крит, Британская Колумбия (1955) Измерение внутрипищеводного давления. J Appl Physiol 7:491–495

   CAS пабмед Google ученый

10. Petit JM, Milic-Emili G (1958) Измерение внутрипищеводного давления. J Appl Physiol 13:481–485

    CAS пабмед Google ученый

11. Milic-Emili J, Mead J, Turner JM, Glauser EM (1964) Улучшенный метод оценки плеврального давления с помощью пищеводных баллонов. J Appl Physiol 19:207–211

    CAS пабмед Google ученый

12. «>

    Лемен Р., Бенсон М., Джонс Дж. Г. (1974) Измерение абсолютного давления с помощью изготовленных вручную пищеводных баллонов. J Appl Physiol 37:600–603

    CAS пабмед Google ученый

13. Beardsmore CS, Helms P, Stocks J, Hatch DJ, Silverman M (1980) Усовершенствованная техника пищеводного баллона для использования у младенцев. J Appl Physiol Respir Environ Exerc Physiol 49:735–742

    CAS пабмед Google ученый

14. Walterspacher S, Isaak L, Guttmann J, Kabitz HJ, Schumann S (2014) Оценка дыхательной функции зависит от механических характеристик баллонных катетеров. Respir Care 59:1345–1352

    Статья пабмед Google ученый

15. Mojoli F, Chiumello D, Pozzi M, Algieri I, Bianzina S и др. (2015) Измерение давления в пищеводе при различных условиях внутригрудного давления. Исследование in vitro баллонных катетеров второго поколения. Минерва Анестезиол 81: 855–864

    КАС пабмед Google ученый

16. Cross TJ, Lalande S, Hyatt RE, Johnson BD (2015) Характеристики отклика пищеводных баллонных катетеров, изготовленных вручную с использованием латексных и нелатексных материалов. Physiol Rep 3:e12426

    Артикул пабмед ПабМед Центральный Google ученый

17. Mojoli F, Iotti GA, Torriglia F, Pozzi M, Volta CA et al (2016)Калибровка давления в пищеводе in vivo у пациента на искусственной вентиляции легких делает измерения надежными. Критическая забота 20:98

    Артикул пабмед ПабМед Центральный Google ученый

18. Смит Г.К. (2002) Нелинейная регрессия. В: Эль-Шаарави А.Х., Пигорш В.В. (ред.) Энциклопедия экологии. John Wiley & Sons, Чичестер

    Google ученый

19. Venegas JG, Harris RS, Simon BA (1998) Комплексное уравнение для кривой давления в легких. J Appl Physiol 84: 389–395

    КАС пабмед Google ученый

20. Harris RS, Hess DR, Venegas JG (2000) Объективный анализ кривой давление-объем при остром респираторном дистресс-синдроме. Am J Respir Crit Care Med 161:432–439

    CAS Статья пабмед Google ученый

21. Narusawa U (2001) Общие характеристики уравнения сигмоидальной модели, представляющего квазистатические легочные кривые PV. J Appl Physiol 91:201–210

    CAS пабмед Google ученый

22. Spiess AN, Neumeyer N (2010)Оценка R2 как неадекватной меры для нелинейных моделей в фармакологических и биохимических исследованиях: подход Монте-Карло. BMC Pharmacol 10:6

    Артикул пабмед ПабМед Центральный Google ученый

23. Чинет А.Е. (1989) Статика грудной клетки и легких: реалистичный аналог для студенческой лаборатории. Am J Phys 257: S9–10

    КАС Google ученый

24. Андерсон Дж., Гоплен С., Мюррей Л., Морской берег К., Саундарраджан М. (2009) Демонстрационная модель дыхательной механики человека. Adv Physiol Educ 33:53–59

    Статья пабмед Google ученый

Скачать ссылки

Благодарности

Мы хотели бы поблагодарить профессора Йи-Лонг Ван (Центр клинических испытаний и исследований, Пекинская больница Тяньтань, Столичный медицинский университет) за его ценные предложения по статистическому анализу.

Финансирование

Это исследование было поддержано грантами Пекинского муниципального управления больниц (DFL20150502) и специальной программы Пекинской муниципальной комиссии по науке и технологиям (Z161100000116081). Спонсор не участвовал в разработке исследования, сборе данных, анализе данных, интерпретации данных или написании отчета.

Доступность данных и материалов

Подробные данные, подтверждающие выводы, доступны в наборе данных на сайте ResearchGate (https://www.researchgate.net/publication/31041519).6_Использование_сигмовидной_фитинги_для_определения_оптимального_баллонного_объема_пищеводного_баллонного_катетера_на_столике_in_vitro_experiment?ev=prf_pub).

Информация об авторе

Примечания автора

Авторы и аффилированные лица

1. Отделение интенсивной терапии, Пекинская больница Тяньтань, Столичный медицинский университет, № 6, Тяньтань Сили, округ Дунчэн, Пекин, 100050 Ян-

   5, Китай

   5 Линь Ян, Сюань Хэ, Сю-Мэй Сунь, Хан Чен, Чжун-Хуа Ши, Мин Сюй, Гуан-Цян Чен и Цзянь-Синь Чжоу

2. Отделение интенсивной терапии, Пекинская электроэнергетическая больница, Столичный медицинский университет, Пекин, 100073, Китай , Китай

   Han Chen

Авторы

1. Yan-Lin Yang

   Посмотреть публикации автора

   Вы также можете искать этого автора в PubMed Google Академия

2. Xuan He

   Посмотреть публикации автора

   Вы также можете искать этого автора в PubMed Google Scholar

3. Xiu-Mei Sun

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

4. Han Chen

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

5. Чжун-Хуа Ши

   Посмотреть публикации автора

   Вы также можете искать этого автора в PubMed Google Scholar

6. Ming Xu

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

7. Guang-Qiang Chen

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

8. Jian-Xin Zhou

   Посмотреть публикации автора

   Вы также можете искать этого автора в PubMed Google Scholar

Contributions

Дизайн исследования разработали YLY, XH, MX и JXZ. YLY, XH, MX и HC выполнили лабораторную процедуру и собрали экспериментальные данные. YLY, XH, ZHS и GQC проанализировали данные. XMS, XYL, KS и JXZ написали статью. JXZ рассмотрел документ и одобрил окончательный вариант рукописи. Все авторы прочитали и одобрили окончательный вариант рукописи.

Автор, ответственный за переписку

Связь с Цзянь-Синь Чжоу.

Декларация этики

Одобрение этики и согласие на участие

Неприменимо.

Согласие на публикацию

Не применимо.

Конкурирующие интересы

Авторы заявляют об отсутствии конкурирующих интересов.

Примечание издателя

Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и ​​институциональной принадлежности.

Дополнительные файлы

Дополнительный файл 1: Таблица S1.

Параметры настройки сигмовидной кишки при атмосферном давлении и окклюзии в конце выдоха и конце вдоха.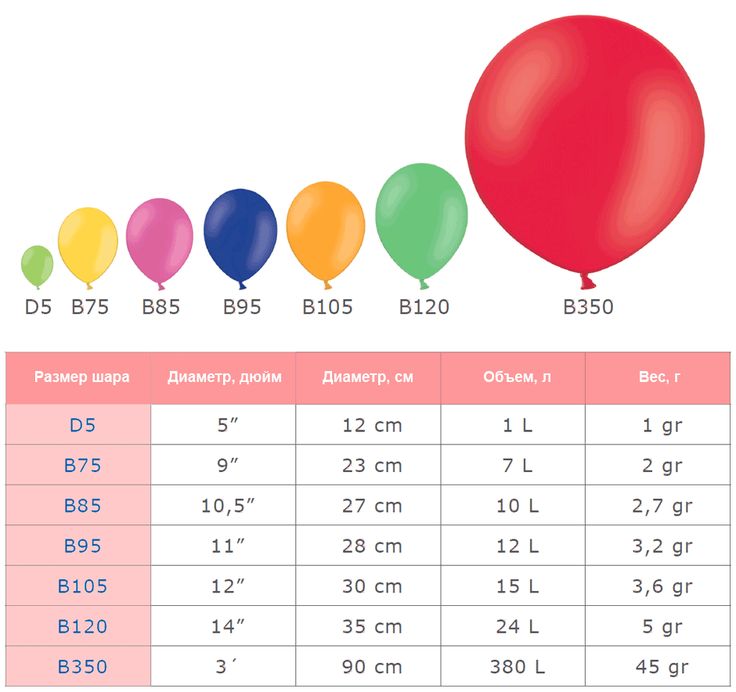 Рисунок S1. Подгонка безразмерных переменных в уравнении сигмовидной регрессии давление-объем баллона. Рисунок S2. График остаточного значения (объем баллона −  a )/ b , рассчитанный с помощью стандартной сигмовидной аппроксимации относительно (давления баллона −  c )/ d . (PDF 599 кб)

Дополнительный файл 2: Рисунок S3.

Давление в камере и давление в баллоне при манипулировании объемом баллона при атмосферном давлении и в условиях имитации пассивной вентиляции. (PDF 212 КБ)

Дополнительный файл 3: Таблица S2.

Минимальный и максимальный объем наполнения баллона, определяемый с помощью сигмовидного фитинга и визуального осмотра промежуточного линейного участка кривой давление-объем баллона во время окклюзии в конце выдоха и в конце вдоха. Рисунок S4. Абсолютное трансмуральное давление баллона при минимальном и максимальном объеме наполнения баллона. (PDF 329 КБ)

Права и разрешения

Открытый доступ Эта статья распространяется в соответствии с условиями международной лицензии Creative Commons Attribution 4. 0 (http://creativecommons.org/licenses/by/4.0/), которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии вы должным образом указываете автора (авторов) и источник, предоставляете ссылку на лицензию Creative Commons и указываете, были ли внесены изменения.

Перепечатки и разрешения

Об этой статье

Объем баллона доставки положительно коррелирует с диаметром и эффективной площадью отверстия имплантированного SAPIEN 3

. 2022 сен;80(3):190-196.

doi: 10.1016/j.jjcc.2022.03.011. Epub 2022 22 апр.

Такехиро Номура ¹ , Масаки Миясака ² , Масаки Накашима ³ , Макото Сайган ³ , Арата Иноуэ ³ , Юсуке Энта ³ , Юсуке Токи ³ , Кадзунори Исии ³ , Миэ Сакурай ³ , Йошико Мунехиса ³ , Июнь Ито ⁴ , Масаки Хата ⁵ , Масатака Тагури ⁶ , Норио Тада ⁷

Принадлежности

• ¹ Отделение кардиологии, больница Сендай Коусей, Сендай, Мияги, Япония; Кафедра сердечно-сосудистой хирургии, Медицинский факультет, Медицинский университет Доккио, Симоцуга-гун, Точиги, Япония. Электронный адрес: takehironomura0@gmail.com.
• ² Отделение кардиологии, больница Сендай Косей, Сендай, Мияги, Япония; Кафедра лабораторной медицины Медицинской школы Университета Дзикей, Токио, Япония.
• ³ Отделение кардиологии, больница Сендай Косей, Сендай, Мияги, Япония.
• ⁴ Отделение анестезиологии, больница Сендай Коусей, Сендай, Япония.
• ⁵ Отделение сердечно-сосудистой хирургии, больница Сендай Косей, Сендай, Мияги, Япония.
• ⁶ Кафедра биостатистики и эпидемиологии, Городской университет Йокогамы, Иокогама, Канагава, Япония.
• ⁷ Отделение кардиологии, больница Сендай Косей, Сендай, Мияги, Япония; Кафедра сердечно-сосудистой хирургии, Медицинский факультет, Медицинский университет Доккио, Симоцуга-гун, Точиги, Япония.
• PMID: 35469714
• DOI: 10.1016/j.jjcc.2022.03.011

Такехиро Номура и др. Дж Кардиол. 2022 Сентябрь

. 2022 сен;80(3):190-196.

doi: 10.1016/j.jjcc.2022.03.011. Epub 2022 22 апр.

Авторы

Такехиро Номура ¹ , Масаки Миясака ² , Масаки Накашима ³ , Макото Сайган ³ , Арата Иноуэ ³ , Юсуке Энта ³ , Юсуке Токи ³ , Казунори Исии ³ , Миэ Сакурай ³ , Йошико Мунехиса ³ , июнь Ито ⁴ , Масаки Хата ⁵ , Масатака Тагури ⁶ , Норио Тада ⁷

Принадлежности

• ¹ Отделение кардиологии, больница Сендай Коусей, Сендай, Мияги, Япония; Кафедра сердечно-сосудистой хирургии, Медицинский факультет, Медицинский университет Доккио, Симоцуга-гун, Точиги, Япония. Электронный адрес: takehironomura0@gmail.com.
• ² Отделение кардиологии, больница Сендай Косей, Сендай, Мияги, Япония; Кафедра лабораторной медицины Медицинской школы Университета Дзикей, Токио, Япония.
• ³ Отделение кардиологии, больница Сендай Косей, Сендай, Мияги, Япония.
• ⁴ Отделение анестезиологии, больница Сендай Коусей, Сендай, Япония.
• ⁵ Отделение сердечно-сосудистой хирургии, больница Сендай Косей, Сендай, Мияги, Япония.
• ⁶ Кафедра биостатистики и эпидемиологии, Городской университет Йокогамы, Иокогама, Канагава, Япония.
• ⁷ Отделение кардиологии, больница Сендай Косей, Сендай, Мияги, Япония; Кафедра сердечно-сосудистой хирургии, Медицинский факультет, Медицинский университет Доккио, Симоцуга-гун, Точиги, Япония.
• PMID: 35469714
• DOI: 10.1016/j.jjcc.2022.03.011

Абстрактный

Фон: При транскатетерной замене аортального клапана (TAVR) с использованием SAPIEN 3 (S3) (Edwards Lifesciences, Ирвин, Калифорния, США) некоторые клиницисты уменьшают или увеличивают объем баллона доставки (VOL) при развертывании S3 или проведении постдилатации. Однако влияние контроля VOL на диаметр транскатетерного сердечного клапана (THVD) и функцию клапана остается неясным. Мы оценили связь между VOL, THVD и эффективной площадью отверстия (EOA) S3.

Методы: Мы включили пациентов, перенесших TAVR с использованием 23- и 26-мм S3 в больнице Sendai Kousei в период с 2017 по 2019 год. VOL контролировали на основе предоперационной компьютерной томографии и интраоперационной чреспищеводной эхокардиографии (TEE). THVD определяли как диаметр транскатетерного сердечного клапана на среднем уровне, измеренный с помощью TEE.

Полученные результаты: Из 332 пациентов (23 мм, n = 188; 26 мм, n = 144) у одного (0,3%) и двух (0,6%) развился разрыв фиброзного кольца и умеренная/тяжелая параклапанная утечка соответственно. VOL при развертывании положительно коррелировал с THVD при развертывании (23 мм, r = 0,44, p < 0,001; 26 мм, r = 0,57, p < 0,001) и EOA (23 мм, r = 0,23, p = 0,0019).; 26 мм, r = 0,22, p = 0,0094). В множественном регрессионном анализе VOL и постдилатация были значимыми детерминантами THVD, хотя площадь кольца аорты, объем кальция и предварительная дилатация не были. Площади под кривой рабочей характеристики приемника, которые использовались для оценки точности индекса, полученного путем деления THVD на площадь поверхности тела (индексированного THVD) для прогнозирования несоответствия пациент-протез (PPM), составляли 0,744 и 0,811 в 23- и 26- мм когорт соответственно. Отсечка индексированного THVD ≤11,5 и 12,1 мм/м ² хорошо предсказанный PPM (23 мм, отношение шансов 5,20; 95% доверительный интервал, 1,33–20,3; 26 мм, отношение шансов 14,1, 95% доверительный интервал 2,40–81,0).

Вывод: VOL положительно коррелировал с THVD и EOA. Меньший индекс THVD был связан с более высокой частотой PPM. Контроль VOL при оценке THVD на месте может быть полезен для снижения частоты случаев PPM.

Ключевые слова: Расширяемый баллоном транскатетерный сердечный клапан; Объем баллона доставки; Эффективная площадь отверстия; Транскатетерная имплантация аортального клапана; Диаметр клапана.

Copyright © 2022 Elsevier Ltd. Все права защищены.

Заявление о конфликте интересов

org/1998/Math/MathML» xmlns:p1=»http://pubmed.gov/pub-one»> Декларация о конкурирующих интересах Норио Тада, Юсуке Энта и Масаки Накашима получили гонорары за лекции от Edwards Lifescience. Другие авторы не имеют конфликта интересов. Норио Тада — клинический инспектор Edwards Lifescience.

Похожие статьи

• Геометрические изменения в вентрикулоаортальном комплексе после транскатетерной замены аортального клапана и их связь с постпроцедурным несоответствием пациента и протеза: интрапроцедурное исследование 3D-TEE.

  Уцуномия Х., Михара Х., Итабаси Ю., Кобаяши С., Сигел Р.Дж., Чакраварти Т., Джилайхави Х., Маккар Р.Р., Сиота Т. Уцуномия Х. и др. Eur Heart J Cardiovasc Imaging. 2017 янв;18(1):1-10. дои: 10.1093/ehjci/jew039. Epub 2016 29 марта. Eur Heart J Cardiovasc Imaging. 2017. PMID: 27025512

• Частота и предикторы несоответствия протез-пациент после TAVI с использованием SAPIEN 3 в Азии: различия между новым и старым клапаном, расширяемым баллоном.

  Миясака М., Тада Н., Тагури М., Като С., Энта Ю., Хата М., Ватанабэ Ю., Наганума Т., Ямаваки М., Яманака Ф., Шираи С., Уэно Х., Мизутани К., Табата М., Такаги К., Ямамото М., Хаяшида К.; Следователи OCEAN-TAVI. Миясака М. и соавт. Открытое сердце. 2021 март;8(1):e001531. doi: 10.1136/openhrt-2020-001531. Открытое сердце. 2021. PMID: 33737333 Бесплатная статья ЧВК.

• Частота, предикторы и клиническое влияние несоответствия протез-пациент после транскатетерной замены аортального клапана у азиатских пациентов: регистр OCEAN-TAVI.

  Миясака М., Тада Н., Тагури М., Като С., Энта Ю., Отомо Т., Хата М., Ватанабэ Ю., Наганума Т., Араки М., Яманака Ф., Шираи С., Уэно Х., Мизутани К., Табата М., Хигашимори А., Такаги К., Ямамото М., Хаяшида К.; Исследователи ОКЕАН-ТАВИ. Миясака М. и соавт. JACC Cardiovasc Interv. 2018 23 апреля; 11 (8): 771-780. doi: 10.1016/j.jcin.2018.01.273. JACC Cardiovasc Interv. 2018. PMID: 29673509

• Индексированный размер кольца аорты на основе компьютерной томографии для прогнозирования несоответствия протеза пациенту.

  Хед С.Дж., Рирдон М.Дж., Диб Г.М., Ван Мигем Н.М., Попма Дж.Дж., Глисон Т.Г., Уильямс М.Р., Радхакришнан С., Фремес С., О Дж.К., Чанг И., Боулвар М.Дж., Каппетейн А.П. Head SJ и др. Circ Cardiovasc Interv. 2019 апр;12(4):e007396. doi: 10.1161/CIRCINTERVENTIONS.118.007396. Circ Cardiovasc Interv. 2019. PMID: 30929507

• Визуализация для прогнозирования и оценки несоответствия протеза пациенту после замены аортального клапана.

  Пибаро П., Магне Дж., Лейпсик Дж., Котэ Н., Бланке П., Турани В.Х., Хан Р. Пибаро П. и др. JACC Cardiovasc Imaging. 2019 Янв; 12 (1): 149-162. doi: 10.1016/j.jcmg.2018.10.020. JACC Cardiovasc Imaging. 2019. PMID: 30621987 Обзор.

Посмотреть все похожие статьи

термины MeSH

BALLOON Dry Volume Spray – R+Co

перейти к содержанию

${minicartMessage}

1. ${productTitles[item.productId].title}

   ${ключ}: ${значение}

   ${опция.имя}: ${ option.value }

   План продажи: ${item.selling_plan_allocation. selling_plan.name}

   Количество ${элемент.количество}

   БЕСПЛАТНО ${ товар.цена | в доллар США }

Расчетная сумма ${ корзинаВсего | вUSD }

Оформить заказПродолжить покупки

Оформляя заказ, я соглашаюсь с Условиями использования и подтверждаю, что ознакомился с Политикой конфиденциальности.

Доставка (рассчитывается при оформлении заказа)

В настоящее время ваша сумка пуста.

Включить файлы cookie для использования корзины

${cartItemCount}

Аромат

DARK WAVES

Кардамон
Ананас
Мандарин
Лаванда
Бамбук
Светлое дерево

Теплый романтический аромат

Shop Scent

Как использовать

Встряхнуть. Распылить на корни для объема. Чтобы придать законченный вид, переверните волосы и нанесите спрей от середины длины до кончиков.

отзывов

средний рейтинг 4,8 из 5

На основании 14 отзывов

• 5 звезд

  12 отзывов

• 4 звезды

  1 отзыв

• 3 звезды

  1 Обзор

• 2 звезды

  0 отзывов

• 1 звезда

  0 отзывов

100% рецензентов порекомендовали бы этот продукт другу

14 отзывов

Сортировать по Самые свежиеСтарые фото и видеоС наивысшим рейтингомСамый низкий рейтингСамые полезныеНаименее полезные0005

Грубое

Какова ваша главная цель прически?

Уход за цветом

Увлажнение + восстановление

Объем + текстура

Уход за локонами

Разглаживание

Уход за кожей головы

Natasha F. Отзыв от Natasha F.

Проверенный покупатель

Я рекомендую этот продукт

Тип волос

Волнистые

Плотность волос

Средняя длина

Какова ваша основная цель прически?

Увлажнение + восстановление

Оценка 5 из 5

Отзыв опубликован

Удивительно, ничего подобного!

Потрясающий продукт, всегда хотела спрей для объема на сухих волосах! Также хорошо подходит для финишной обработки естественных волн. Пришлось заказывать запасной продукт, на случай, если он закончится.. без этого продукта нельзя.

Загрузка…

это было полезно?

Большое спасибо, что нашли время оставить отзыв, Наташа! 🎈

Джоди Отзыв от Jody

Проверенный рецензент

Я рекомендую этот продукт

Тип волос

Вьющиеся

Плотность волос

Средняя

Какова ваша основная цель прически?

Уход за локонами

Оценка 5 из 5

Отзыв опубликован

Кудри имеют объем

Я получил это как образец и так рад, что я сделал. Я никогда не использовала средство типа спрея для своих локонов и, вероятно, не подумала бы его купить. Это придает моим кудрям объем без ощущения липкости. Переворачиваю голову, распыляю на корни, быстро перемешиваю и придаю объем! Мне нравится мини-размер, так как я могу носить его в сумочке. Спасибо, что предлагаете образцы продуктов, чтобы попробовать их первыми!

Загрузка…

это было полезно?

Большое спасибо, что нашли время оставить отзыв, Джоди!

DM

Даниэль М. Отзыв от Danielle M.

Проверенный покупатель

Я рекомендую этот продукт

Тип волос

Волнистые

Плотность волос

Средняя длина

Какова ваша основная цель прически?

Увлажнение + восстановление

Оценка 5 из 5

Отзыв опубликован

Дополнительный удар

У меня объем на сутки (слова стилиста, не мои). Но после несмываемого кондиционера, термозащиты и увлажняющего масла для волос мои волосы кажутся тяжелыми и ложатся немного плоско (у меня короткие волосы). Мне действительно не нравится ощущение или запах лака для волос, но я решила попробовать это средство. Голова/волосы перевернуты вверх дном, немного спрея на макушке, и я рада сообщить, что получила тот объем, который мне нравится, без традиционного или типичного лака для волос. В любое время в течение дня, когда я чувствую, что мне нужно, я быстро встряхиваю волосы, и объем возвращается.

Честно говоря, я не знаю, хорошо ли я это описываю, но мне действительно нравится этот продукт.

Загрузка…

это было полезно?

Кейт Отзыв от Kate

Проверенный покупатель

Я рекомендую этот продукт

Тип волос

Прямые

Плотность волос

Тонкие

Какова ваша основная цель прически?

Объем + Текстура

Оценка 5 из 5

Отзыв опубликован

Самый лучший!

Я люблю этот продукт! Он дает большое количество текстуры и объема, не будучи липким или жестким. Я буду использовать его для волос второго дня вместо сухого шампуня, и он не имеет такого белого эффекта и не так сильно сушит мои волосы.

Загрузка…

это было полезно?

Джейми Отзыв от Jamie

Я рекомендую этот продукт

Тип волос

Прямые

Плотность волос

Средняя

Какова ваша основная цель прически?

Объем + Текстура

Оценка 5 из 5

Отзыв опубликован

Обязательным

Пара брызг на мою челку и корону/слои, распушите их, и у вас будет идеальная сексуальная изголовье. Запах отличный, масло тоже впитывает. Я держу его в своей сумочке на те дни, когда твоя челка начинает делать свое дело, или когда ты хочешь снять шляпу и вернуть свой объем. Это меняет правила игры.

Загрузка…

это было полезно?

Использование анализа кривой давления-объема пищеводного баллона для определения эластичности стенки пищевода и калибровки необработанного пищеводного давления: лабораторный эксперимент и клиническое исследование | BMC Anesthesiology

• Исследовательская статья
• Открытый доступ
• Опубликовано: 14 февраля 2018 г.
• Сю-Мэй Сун ¹ ,
• Гуан-Цян Чен ¹ ,
• Hua-Wei Huang ¹ ,
• Xuan He ¹ ,
• Yan-Lin Yang ¹ ,
• Zhong-Hua Shi ¹ ,
• Ming Xu ¹ &
• …
• Цзянь-Синь Чжоу ORCID: orcid.org/0000-0003-1320-0979 ¹  

BMC Анестезиология том 18 , номер статьи: 21 (2018) Процитировать эту статью

• 2302 доступа

• 12 цитирований

• 5 Альтметрический

• Сведения о показателях

Abstract

История вопроса

Точное измерение пищеводного давления (Pes) зависит от правильного наполнения баллона. Эластичность стенки пищевода (Ees) также может влиять на измерение. Мы рассмотрели оценку эластичности окружающего баллона в стендовой модели и исследовали упрощенную процедуру калибровки Pes в баллоне относительно небольшого объема.

Методы

В настоящем исследовании использовался баллонный катетер Cooper (геометрический объем 2,8 мл). Баллон последовательно надували в разных газонепроницаемых стеклянных камерах с разным внутренним объемом. Эластичность камеры измеряли путем подбора давления в камере и объема баллона. Были получены кривые давление-объем баллона (P-V), а наклон промежуточного линейного участка был определен как расчетная эластичность камеры. Тесты объема баллона также были выполнены у 40 пациентов на контролируемой вентиляции. Наклон промежуточного линейного участка кривой P-V пищевода в конце выдоха рассчитывали как Ees. Объем баллона с наибольшим приливным размахом Pes определялся как наилучший объем. Давление, создаваемое стенкой пищевода при надувании баллона (Pew), оценивали как произведение Ees и наилучшего объема. Поскольку клинический промежуточный линейный участок включал объем наполнения от 0,6 до 1,4 мл у каждого пациента, мы упростили оценку Ees, используя только параметры для этих двух объемов наполнения.

Результаты

В лабораторном эксперименте погрешность (нижний и верхний пределы совпадения) составила 0,5 (от 0,2 до 0,8) см H ₂ О/мл между рассчитанной и измеренной эластичностью камеры. Промежуточный линейный участок на клинической и стендовой кривых P-V был похож друг на друга. Медиана (межквартильный размах) Ees составила 3,3 (2,5–4,1) см H ₂ О/мл. Клинический лучший объем составлял 1,0 (0,8–1,2) мл и колебался от 0,6 до 1,4 мл. Расчетное значение Pew при наилучшем объеме составило 2,8 (2,5–3,5) см вод. ст. ₂ O с максимальным значением 5,2 смH ₂ O. По сравнению с традиционным методом систематическая погрешность (нижний и верхний пределы совпадения) Ees, оцененных простым методом, составила − 0,1 (от − 0,7 до 0,6) смH ₂ O /мл.

Выводы

Наклон промежуточного линейного участка кривой P-V баллона коррелирует с упругостью, окружающей баллон. Оценка Ees и калибровка Pes были осуществимы для баллона небольшого объема.

Пробная регистрация

Идентификатор NCT02976844. Зарегистрирован задним числом 29 ноября 2016 г.

Отчеты экспертной оценки

История вопроса

Пищеводное давление (Pes), которое обычно измеряют с помощью катетера с наполненным воздухом баллоном, использовали для оценки плеврального давления [1, 2]. В последнее время к этой методике вновь привлекли внимание для проведения защитной вентиляции легких у пациентов с острым респираторным дистресс-синдромом [3, 4, 5, 6, 7]. Точное измерение Pes зависит от правильного наполнения баллона [8,9].,10,11,12,13]. В условиях in vitro при атмосферном давлении во время постепенного надувания баллона кривая давление-объем (P-V) баллона имеет почти плоский промежуточный участок, указывающий на диапазон объема с пренебрежимо малым давлением отдачи баллона [8,9,10,11]. Тем не менее, когда баллон помещается в пищевод, надувание баллона дает наклонный линейный промежуточный участок на кривой PV [8, 12, 13]. Считалось, что это явление связано с реакцией отдачи стенки пищевода на надувание баллона, а наклон промежуточного линейного участка считается равным эластичности стенки пищевода (Ees) [8, 12, 13]. Хотя для расчета относительного транспульмонального давления были предложены стратегии, основанные на высвобождении и эластичности [14], также может потребоваться устранение влияния окружающих баллон структур на абсолютное измерение Pes [3, 4, 7]. Основываясь на оценке Ees и давления, создаваемого стенкой пищевода во время надувания баллона (Pew), Моджоли и его коллеги ввели процедуру калибровки in vivo, чтобы сделать измерение Pes более надежным [13]. Однако, насколько нам известно, не проводилось никаких исследований, подтверждающих достоверность этого метода калибровки. Более того, исследовался только один тип баллона с относительно большим геометрическим объемом [13].

В настоящем исследовании мы создали лабораторную модель для имитации различных уровней эластичности окружающего баллона и провели тест объема баллона с использованием баллонного катетера малого объема. Эластичность вокруг баллона оценивалась по наклону промежуточного линейного участка кривой P-V баллона. В первую очередь мы стремились проверить соответствие между расчетной и измеренной эластичностью. Тест объема баллона также проводился у пассивных пациентов на контролируемой вентиляции. Баллонные кривые P-V, полученные in vitro и (в условиях in vivo), сравнивали. На основе ранее введенных методов [12, 13] мы разработали упрощенную процедуру для оценки Ees и калибровки Pes. Второстепенные цели включали оценку соответствия между стандартными и простые методы, а также сравнение откалиброванных значений Pes для разных объемов наполнения.

Методы

Подробные методы представлены в дополнительном файле 1.

В настоящем исследовании использовался коммерчески доступный пищеводный баллонный катетер (Cooper: LOT 177405, Cooper Surgical, США) [9,10,11]. Во время исследования формы волны давления измерялись и записывались с помощью специальной системы сбора данных [11].

Стендовый эксперимент

Пять стеклянных камер с внутренним объемом 1000, 500, 250, 175 и 125 мл использовали для получения пяти уровней эластичности камеры примерно от 1 до 8 см H ₂ О/мл (рис. 1а) [9, 15]. В каждой камере также устанавливали шесть уровней базового камерного давления (5, 10, 15, 20, 25 и 30 см H ₂ O) путем нагнетания в камеру различного количества воздуха. Таким образом, было смоделировано 30 условий вокруг баллона с пятью уровнями эластичности камеры и шестью уровнями базового давления в камере (рис. 1b).

Рис. 1

Модель стенда и протокол эксперимента. Панель ( a ) Каждая стеклянная камера имела два отверстия: одно для введения баллона в камеру, а другое для регулировки и измерения давления в камере. Панель ( b ) Тесты объема баллона проводились в пяти камерах с соответствующими внутренними объемами 1000, 500, 250, 175 и 125 мл. В каждой камере исходное давление доводили до 5, 10, 15, 20, 25 и 30 см вод. ст. ₂ O. Перед каждым испытанием объема баллона соединения в системе камер герметизировались силиконовым герметиком и проверялись систематические утечки

Изображение в полный размер

Пять катетеров Купера были отобраны и случайным образом введены в пять разных камер. Перед каждым тестом объема баллона остаточный объем баллона стандартизировали по методу, описанному в предыдущих исследованиях [16,17,18]. Вкратце, давление в камере было доведено до 5 см H ₂ O путем введения воздуха, и просвет баллона открывали в атмосферу на 3 мин. Мы условно определили объем баллона при этом условии как нулевой объем наполнения. Затем баллон периодически надували с шагом 0,2 мл до 2,4 мл. Тест объема баллона сначала проводили при атмосферном давлении, а затем в каждой камере с определенной эластичностью при разных уровнях базового давления в камере (рис. 1б).

Одновременно измерялись давление в баллоне и давление в камере. Трансмуральное давление в баллоне определяли как разницу между давлением в баллоне и давлением в камере (давление в баллоне — давление в камере) [9]., 10]. Объем баллона с трансмуральным давлением в пределах ±1,0 см вод. ст. ₂ O определяли как минимальный и максимальный объемы баллона (V _MIN и V _MAX ), которые представляли собой оптимальный объем наполнения с наименьшим влиянием давления отдачи баллона. 9, 10]. Рабочий объем баллона (V _WORK ) рассчитывали как разницу между V _MIN и V _MAX . Объем баллона с наиболее близким к нулю трансмуральным давлением определяли как наилучший объем наполнения (V _ЛУЧШИЙ ).

Давление в баллоне и давление в камере были нанесены на график в зависимости от объема баллона (рис. 2а). Давление в камере увеличивалось линейно в зависимости от объема баллона, а наклон, полученный методом наименьших квадратов, определялся как измеренная эластичность камеры. Кривая P-V баллона имела сигмовидную форму с промежуточным линейным участком, соответствующим диапазону от V _MIN до V _MAX . Мы использовали наклон этого линейного участка для оценки эластичности камеры. Базовое давление в камере оценивали как разницу между измеренным давлением в баллоне при V _BEST и произведение расчетной эластичности камеры и V _BEST .

Рис. 2

Примеры кривых давление-объем баллона. Панель ( a ) Давление в баллоне (кружки) и давление в камере (точки) были нанесены на график в зависимости от объема баллона в лабораторном эксперименте. Объем баллона с трансмуральным давлением (разницей между давлением в баллоне и давлением в камере) в пределах ±1,0 см вод. ст. ₂ O определяли как минимальный и максимальный объемы баллона (V _МИН и В _МАКС ). Объем баллона с наиболее близким к нулю трансмуральным давлением определяли как наилучший объем наполнения (V _BEST ). Также показана линия наименьших квадратов между давлением в камере и объемом баллона (черная линия) и между давлением баллона и объемом баллона в пределах от V _MIN до V _MAX (красная пунктирная линия). Панель ( b ) Давление в пищеводном баллоне в конце выдоха (кружки) и окклюзии в конце вдоха (квадраты) были нанесены на график в зависимости от объема баллона в клиническом исследовании. Нижний и верхний пределы промежуточного линейного участка на кривой давление-объем баллона выдоха визуально проверяли и определяли как клиническую V _МИН и В _МАКС . Клинический V _BEST определялся как объем баллона с наибольшей разницей между давлением внутрипищеводного баллона в конце выдоха и в конце вдоха. Также показана линия наименьшего квадрата между давлением баллона в конце выдоха и объемом баллона в клиническом диапазоне от V _MIN до V _MAX (красная пунктирная линия)

Полноразмерное изображение

Клиническое исследование

отделение интенсивной терапии, Пекинская больница Тяньтань, Столичный медицинский университет, Пекин, Китай. Протокол исследования был рассмотрен и одобрен местным Институциональным наблюдательным советом (KY-2016-11-22), и исследование было зарегистрировано на сайте ClinicalTrials. gov (NCT029).76844). Письменное информированное согласие было получено от пациента или соответствующих лиц, принимающих решения.

В исследование были включены послеоперационные пациенты с замедленным выходом из наркоза, поступившие в отделение искусственной вентиляции легких. У пациентов после плановых внутричерепных операций причинами отсроченной экстубации и ИВЛ в основном были резекция обширной опухоли ствола головного мозга, продолжительность операции более шести часов, массивное интраоперационное кровотечение или отек головного мозга [19].]. ИВЛ продолжали также у больных с тяжелыми черепно-мозговыми травмами после неотложных операций. Больным после ортопедических и сосудистых хирургических вмешательств экстубация проводилась отсроченно из-за большой длительности операции или массивного кровотечения. Пациентам с поражением ствола головного мозга и тяжелой черепно-мозговой травмой обычно требовалась длительная искусственная вентиляция легких. В нашем отделении мониторинг Pes обычно использовался у пациентов, находящихся на искусственной вентиляции легких, для управления настройками вентилятора и отлучением от него. Критериями исключения были следующие: 1) возраст до 18 лет; 2) противопоказания для введения пищеводного баллонного катетера, в том числе признаки тяжелой коагулопатии, диагностированный или предполагаемый варикоз вен пищевода, а также операции на пищеводе, желудке или легких в анамнезе; и 3) признаки активной утечки воздуха из легкого, включая бронхоплевральный свищ, пневмоторакс, пневмомедиастинум и существующую плевральную дренажную трубку. За время исследования у большинства больных не отошли от наркоза и нервно-мышечного паралича. В случае восстановления спонтанного дыхания проводили непрерывную внутривенную инфузию мидазолама 0,05–0,2 мг/кг/ч и фентанила 0,1 мг/ч, а векуроний 0,1 мг/кг внутривенно болюсно применяли по мере необходимости. Отсутствие спонтанного усилия на вдохе подтверждалось отсутствием колебаний отрицательного давления в дыхательных путях (Paw) во время 3-секундной окклюзии в конце выдоха. Пациентов вентилировали в режиме контролируемого объема с постоянным потоком, установленным как дыхательный объем 6–8 мл/кг прогнозируемой массы тела и клинического положительного давления в конце выдоха и фракции вдыхаемого кислорода. Гипоксемию документировали как отношение парциального давления артериального кислорода к фракции вдыхаемого кислорода менее 300. Острый респираторный дистресс-синдром (ОРДС) диагностировали по Берлинскому определению [20]. Отсутствие рентгенологического критерия определяли как острую гипоксическую дыхательную недостаточность (ОГДН).

Баллон Купера был помещен в нижние две трети пищевода, что было подтверждено наличием сердечных артефактов на трассировке Pes и рентгенологическом исследовании у постели больного.

Во время исследования пациенты находились в положении лежа на спине с приподнятым на 30° изголовьем кровати. Перед каждым испытанием объема баллона баллон надували до 3,0 мл, а затем сдували путем создания отрицательного давления с последующим открыванием в атмосферу на 3 мин. Баллон периодически надували с шагом 0,2 мл до 2,4 мл. При каждом тестируемом объеме после 3-минутного уравновешивания дыхательные пути перекрывались в конце выдоха и в конце вдоха, каждый на 3 с. При окклюзии в конце выдоха выполняли тест положительного давления и рассчитывали отношение изменения Pes к Paw (∆Pes/∆Paw) при сдавлении грудной стенки [21].

Давление в пищеводном баллоне наносили на график в зависимости от объема баллона (рис. 2b). Метод, представленный Mojoli et al. использовали для определения Ees и оптимального объема баллона [13]. Промежуточный линейный участок визуально проверяли на баллонных кривых P-V в конце выдоха, а нижний и верхний пределы определяли как клинические V _MIN и V _MAX . Диапазон между V _MIN и V _MAX был определен как V _WORK и рассматривался как оптимальный объем наполнения баллона для клинического измерения Pes. Клинический V _BEST определяли как объем баллона с наибольшей разницей между Pes в конце выдоха и в конце вдоха. Наклон промежуточного линейного участка на баллонной кривой P-V в конце выдоха определяли как Ees [13]. Давление отдачи стенки пищевода в ответ на наполнение баллона; т. е. Pew оценивали произведением Ees и объема баллона в пределах от V _MIN до V _MAX с использованием метода, ранее предложенного Milic-Emili et al. [12]. Необработанные значения Pes были откалиброваны путем экстраполяции к нулевому объему баллона, который также может быть выражен как: откалиброванное Pes = исходное Pes — Pew.

В каждом тесте объема баллона пациента промежуточный линейный участок на кривой P-V баллона в конце выдоха (т. е. диапазон клинических значений от V _MIN до V _MAX ) включает объем наполнения от 0,6 до 1,4 мл. Поэтому мы упростили оценку Ees, используя только параметры для этих двух объемов наполнения, как разницу давления баллона в конце выдоха между 0,6 мл и 1,4 мл, деленную на 0,8 мл (1,4–0,6 мл).

Статистический анализ

Категориальные переменные представлены в виде чисел и процентов. Непрерывные данные представлены в виде медианы и межквартильного размаха (IQR) и сравнивались с использованием теста Крускала-Уоллиса с апостериорным сравнением с поправкой Бонферрони.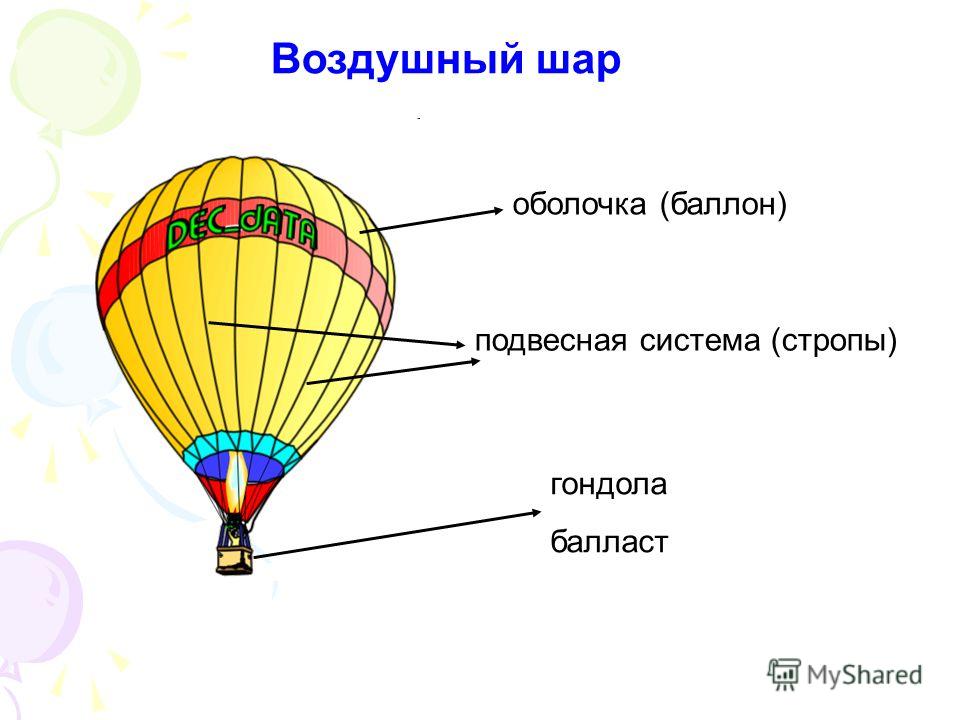

Проанализирована корреляция оптимального объема баллона с давлением баллона. Рассчитывали коэффициент корреляции Спирмена (ро).

Анализ Бланда-Альтмана использовался для проверки соответствия эластичности камеры и исходного давления в камере между оценочным и измеренным значением в лабораторном эксперименте, а также Ees между значениями, рассчитанными стандартным и простым методом в клиническом исследовании. Были рассчитаны систематическая ошибка и стандартное отклонение (SD) средней систематической ошибки. Верхний и нижний пределы согласия были определены как погрешность ±1,9.6 SD среднего отклонения. Размер выборки в стендовом эксперименте был основан на настройке условий ( n  = 30). Размер выборки в клиническом исследовании ( n  = 40) был выбран на основе предыдущих исследований [13, 21]. Соответствующий размер выборки дал 95% доверительный интервал соответствия предела как ±0,32 × SD и ±0,27 × SD [22].

Анализы проводились с использованием SPSS V. 20.0 (SPSS Inc., Чикаго, Иллинойс, США). Значение p < 0,05 считалось статистически значимым.

Результаты

Стендовый эксперимент

Подробные экспериментальные результаты представлены в дополнительном файле 2. Пример кривых P-V баллона при атмосферном давлении и различных уровнях эластичности камеры показан в дополнительном файле 3: рисунок S1. Наклон промежуточного линейного участка баллонной Р-V кривой при атмосферном давлении составил 0,4 (0,3–0,4) см вод. ст. ₂ О/мл. В соответствии с предыдущими исследованиями газонепроницаемые камеры с разным внутренним объемом давали разные уровни эластичности камеры (дополнительный файл 4: таблица S1).

Погрешность (нижний и верхний пределы совпадения) составила 0,5 (от 0,2 до 0,8) см H ₂ О/мл между наклоном линейного участка на кривой P-V баллона (оценочная эластичность камеры) и измеренной эластичностью камеры, и − 0,6 (от − 1,2 до 0,0) см H ₂ O между расчетным и измеренным базовым давлением в камере (рис. 3).

Рис. 3

Анализ пределов согласования по Бланду-Альтману для расчетной эластичности камеры (панель a ) и исходного давления в камере (панель б ). Горизонтальная ось представляет собой среднее значение расчетных и измеренных значений, а вертикальная ось представляет собой разницу расчетных и измеренных значений. Также показаны систематическая погрешность (сплошная линия), а также верхний и нижний пределы согласования (штриховые линии). линейно коррелирует с давлением в баллоне (rho = 0,715 и 0,674, p  = 0,010), но корреляции между V _BEST и баллонным давлением обнаружено не было (rho = 0,284, p  = 0,128).

Таблица 1 Оптимальный объем баллона (мл) в лабораторном эксперименте и клиническом исследовании

Полноразмерная таблица

Клиническое исследование

В исследование было включено 40 пациентов. Исходные характеристики представлены в таблице 2. Гипоксемия была представлена ​​у 13 (32,5%) пациентов, с диагнозом ОРДС и ОСН у 4 (10%) и 9 (22,5%) пациентов соответственно. Подробные результаты клинического исследования представлены в дополнительном файле 5.

Таблица 2 Исходные характеристики пациентов ( n  = 40)

Полноразмерная таблица

Промежуточный линейный участок был визуально идентифицирован на кривой P-V с баллоном пищевода в конце выдоха в каждом из клинических тестов. Оптимальные параметры объема баллона, полученные в ходе клинического исследования, также показаны в таблице 1 и дополнительном файле 6: таблица S2. V _MIN и V _MAX линейно коррелировали с давлением пищеводного баллона в конце выдоха или в конце вдоха (rho = 0,320–0,352, p  = 0,026 до 0,044). V _BEST составлял 1,0 (0,8–1,2) мл в диапазоне от 0,6 до 1,4 мл. Не было обнаружено значимой корреляции между V _BEST и давлением в пищеводном баллоне (rho = 0,096 и 0,176, p  = 0,557 и 0,279). Ees составляла 3,3 (2,5–4,1) см H 90 159 2 90 160 O/мл, в диапазоне от 1,2 до 5,8 см H 90 159 2 90 160 O/мл. Оценка Pew при V _BEST составила 2,8 (2,5–3,5) см вод. столба ₂ O в диапазоне от 1,4 до 5,2 см вод. в большинстве случаев кривая P-V in vivo поднималась раньше и более значительно, чем парная кривая in vitro. Примеры кривых PV пищеводного баллона in vivo во время окклюзии в конце выдоха в сочетании с кривыми in vitro в камерах с сопоставимой эластичностью и исходным давлением показаны в дополнительном файле 7: рисунок S2.

В тестах каждого пациента диапазон от V _MIN до V _MAX составлял от 0,6 до 1,4 мл, а V _BEST также находился в пределах от 0,6 до 1,4 мл (таблица 1). Отношения ∆Pes/∆Paw во время теста на окклюзию составляли 0,725 (0,251–0,848) при объемах баллона менее 0,6 мл, с 35,0% (42/120) в пределах от 0,8 до 1,2. Соотношения при объемах баллона выше 1,4 мл составляли 0,884 (0,734–1,041), а 59,4% (98/165) находились в пределах от 0,8 до 1,2. При объемах баллона от 0,6 до 1,4 мл соотношение ∆Pes/∆Paw составляло 92,5% (185/200) в пределах от 0,8 до 1,2, и не было обнаружено существенной разницы между различными объемами баллона в этом диапазоне ( p  = 0,067, таблица 3). Также не было существенной разницы в калиброванном Pes ( p  = 0,997) для объемов баллона в пределах от 0,6 до 1,4 мл (таблица 3).

Таблица 3 Откалиброванные результаты теста на пищеводное давление и окклюзию при объеме баллона от 0,6 до 1,4 мл в клиническом исследовании

Полноразмерная таблица

По сравнению со стандартным методом линейной регрессии, погрешность (нижний и верхний пределы совпадения) оцененных Ees простым методом было - 0,1 (от - 0,7 до 0,6) смH ₂ О/мл (Дополнительный файл 8: рисунок S3).

Обсуждение

Для катетера с баллоном малого объема, исследованного в настоящем исследовании, мы обнаружили, что: 1) наклон промежуточного линейного участка кривой P-V баллона согласуется с смоделированной эластичностью вокруг баллона в нашей настольной модели; и 2) Ees, оцененные простым методом, хорошо согласуются со стандартным методом линейной регрессии.

Хорошо известно, что надежное измерение Pes зависит от правильного наполнения баллона [9]., 10]. Однако даже в пределах оптимального диапазона объема баллона реакция стенки пищевода на наполнение баллона может повышать абсолютное значение Pes [12, 13]. Милич-Эмили и др. впервые предложил коррекцию необработанных значений Pes путем экстраполяции на нулевой объем баллона у здоровых добровольцев при спонтанном дыхании [12]. Моджоли и его коллеги дополнительно представили процедуру калибровки Pes путем оценки Ees и Pew у пассивных пациентов при контролируемой вентиляции [13]. В настоящем стендовом эксперименте использовались стеклянные камеры с разным внутренним объемом для имитации различной эластичности окружающего баллона (рис. 1). Упругость камер оценивали также по наклону промежуточного линейного участка на кривой P-V баллона при надувании баллона в камерах (рис. 2а). Анализ согласованности показал, что наклон промежуточного участка на кривой P-V баллона завышает эластичность камеры на среднее отклонение 0,5 см H ₂ О/мл (рис. 3а), что аппроксимировало наклон линейного участка баллонной Р-V кривой при атмосферном давлении (0,4 см H ₂ О/мл). Хотя при испытании воздушного шара в атмосфере не существовало эластичности окружающей среды, мы пришли к выводу, что небольшой наклон линейного участка на кривой P-V воздушного шара мог быть результатом тенденции воздушного шара возвращаться к своей первоначальной форме. Мы также обнаружили, что промежуточные участки на кривых PV баллона in vitro и in vivo почти перекрываются (дополнительный файл 7: рисунок S2), что дополнительно подтверждает рациональность методологии оценки Ees.

Предыдущие эксперименты in vitro показали, что V _WORK , т. е. диапазон объема баллона между V _MIN и V _MAX , был более узким у баллонов малого объема [9,10,11]. Среди протестированных типов пищеводных катетеров геометрический объем баллона Купера был наименьшим (2,8 мл). Таким образом, мы поставили под сомнение определение Ees in vivo и калибровку Pes, введенные Mojoli et al. может быть использован в этом типе воздушного шара. Хотя наш клинический V _WORK (медиана 1,2 мл, в диапазоне от 0,8 до 2,0 мл) была меньше, чем у баллона большого объема (соответственно среднее V _MIN и V _MAX 1,5 и 5,4 мл) [13], промежуточный линейный участок на кривую PV в конце выдоха можно было наблюдать в каждом клиническом тесте объема баллона с не менее чем пятью точками данных PV для линейной подгонки (рис. 2 и дополнительный файл 7: рис. S2). Этот промежуточный раздел подходит для расчета Ees. В соответствии с ранее опубликованными исследованиями in vitro и in vivo [10, 13], V _MIN напрямую коррелировало с давлением вокруг баллона в нашем настольном эксперименте и с Pes в нашем клиническом исследовании. Однако мы не обнаружили положительной связи между V _BEST и давлением в баллоне ни в условиях in vitro, ни в условиях in vivo. Кроме того, Mojoli et al. обнаружили, что V _BEST для баллона большого объема демонстрировал значительную вариабельность в различных условиях стола [10] и среди пациентов [13], в то время как в настоящем исследовании V _BEST был почти одинаковым среди пациентов (таблица 1). Эти результаты могут быть объяснены низкой изменчивостью баллона с малым геометрическим объемом.

Наши клинические результаты показали, что надувание баллона малого объема также вызывает реакции стенки пищевода. В нашей группе пациентов медиана Ees составила 3,3 (2,5–4,1) смH ₂ O/мл, что соответствует медиане Pew при V _BEST 2,8 (2,5–3,5) смH ₂ O при максимальном значении 5,2 см вод. ст. ₂ O. Этот уровень Pew может быть достаточно большим, чтобы значительно переоценить Pes и недооценить транспульмональное давление. Таким образом, мы рекомендуем проводить тест объема баллона и калибровку Pes даже при использовании баллона небольшого объема. Более того, можно было заметить, что in vivo V _BEST был заметно больше, чем значение in vitro (таблица 1), что может свидетельствовать о контактной реакции баллона на стенку пищевода. Однако это явление требует дальнейшего изучения.

Поскольку во всех клинических тестах диапазон от V _MIN до V _MAX составлял от 0,6 до 1,4 мл, мы упростили оценку Ees, используя только давление пищеводного баллона, измеренное при этих двух объемах баллона. Результаты, полученные простым методом, хорошо согласуются с результатами обычного метода линейной регрессии (дополнительный файл 8: рисунок S3). Для баллона малого объема, используемого в настоящем исследовании, все клинические V _BEST также располагались между 0,6 и 1,4 мл, и не было обнаружено существенной разницы ни в соотношении ∆Pes/∆Paw во время теста на окклюзию, ни в калиброванном Pes среди объемов баллона в этом диапазоне (таблица 3). Поэтому мы далее предлагаем простую процедуру проверки объема баллона и калибровки Pes для баллонного катетера Купера. Баллон можно надуть только до трех объемов: 0,6, 1,0 и 1,4 мл, и объем с наибольшим приливным колебанием давления в баллоне может быть выбран как V _ЛУЧШИЙ . Ees можно просто оценить только с использованием давления при объемах баллона 0,6 и 1,4 мл, а необработанные Pes на V _BEST можно откалибровать. Подходит ли эта процедура для других типов баллонов, особенно для баллонов большого объема, требует дальнейшего изучения.

Основным преимуществом нашего исследования является комбинированный отчет о лабораторных и клинических результатах. В нашем исследовании есть ограничения. Во-первых, несмотря на то, что в нашем стендовом эксперименте были успешно получены различные уровни эластичности вокруг баллона, мы определенно признали, что наша модель не имитировала реальный сценарий внутри пищевода, потому что контактная реакция пищевода на надувание баллона не учитывалась. Это ограничение можно проиллюстрировать на объединенных кривых PV баллона in vitro и in vivo (дополнительный файл 7: рисунок S2). При более высоких объемах баллона кривые in vivo поднимались раньше и более заметно, что может быть связано с контактной реакцией пищевода. Тем не менее, смоделированные нами уровни эластичности и давления вокруг баллона покрывают диапазоны Ees и Pes, зарегистрированные в клинических исследованиях [3, 4, 6, 7, 13, 21, 23]. При объединении результатов лабораторного эксперимента и клинического исследования мы обоснованно полагали, что этой упрощенной лабораторной модели достаточно, чтобы продемонстрировать взаимосвязь между наклоном кривой P-V промежуточного баллона и Ees.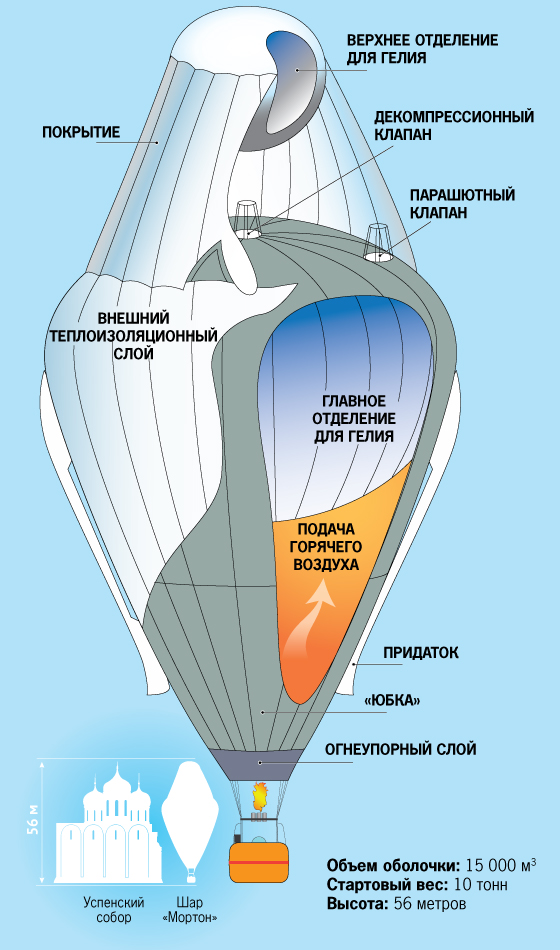 Во-вторых, мы исследовали только один конкретный тип баллона с относительно небольшим геометрическим объемом. В-третьих, исследовались только послеоперационные пациенты с нормальной оксигенацией и давлением в дыхательных путях. В-четвертых, тест объема баллона проводился только у пассивных пациентов на контролируемой вентиляции. Таким образом, наши результаты нельзя напрямую обобщить на другие баллонные катетеры и другие группы пациентов.

Выводы

Используя стендовую модель, состоящую из различных газонепроницаемых камер с различными внутренними объемами, мы оценили взаимосвязь между наклоном промежуточного линейного участка на кривой P-V баллона и упругостью, окружающей баллон. Методы оценки Ees и калибровки Pes также применимы для баллона относительно небольшого геометрического объема. Для баллонного катетера Купера можно использовать простую процедуру у постели больного для выбора оптимального объема баллона и калибровки Pes. Необходимы дальнейшие исследования, чтобы уточнить наши результаты для других типов баллонных катетеров и групп пациентов.

Сокращения

∆Pes/∆Paw:

Отношение изменений давления в пищеводе и давления в дыхательных путях при окклюзионном тесте с положительным давлением;

РАД:

Острая гипоксическая дыхательная недостаточность

АРДС:

Острый респираторный дистресс-синдром

Ees:

Эластичность стенки пищевода

IQR:

Межквартильный диапазон

МВ:

Механическая вентиляция

Лапа:

Давление в дыхательных путях

Пес:

Пищеводное давление

Скамья:

Давление, создаваемое стенкой пищевода во время надувания баллона

P-V кривая:

Кривая давление-объем

В _ЛУЧШИЙ :

Лучший объем наполнения баллона

В _МИН и В _МАКС :

Минимальный и максимальный объемы баллона, представляющие собой оптимальный объем наполнения с наименьшим влиянием давления отдачи баллона

В _РАБОТА :

Разница между V _MIN и V _MAX

Ссылки

1. «>

   Акумьянаки Э., Маджоре С.М., Валенца Ф., Беллани Г., Джубран А., Лоринг С.Х. и др. Применение измерения пищеводного давления у больных с дыхательной недостаточностью. Am J Respir Crit Care Med. 2014; 189: 520–31.

   Артикул пабмед Google ученый

2. Маури Т., Йошида Т., Беллани Г., Голигер Э.К., Карто Г., Риттаямаи Н. и др. Пищеводное и транспульмональное давление в клинических условиях: значение, полезность и перспективы. Интенсивная терапия Мед. 2016; 42:1360–73.

   Артикул пабмед Google ученый

3. Talmor D, Sarge T, O’Donnell CR, Ritz R, Malhotra A, Lisbon A, et al. Пищеводное и транспульмональное давление при острой дыхательной недостаточности. Крит Уход Мед. 2006; 34:1389–94.

   Артикул пабмед ПабМед Центральный Google ученый

4. «>

   Talmor D, Sarge T, Malhotra A, O’Donnell CR, Ritz R, Lisbon A, et al. Механическая вентиляция под контролем давления в пищеводе при остром повреждении легких. N Engl J Med. 2008;359: 2095–104.

   КАС Статья пабмед ПабМед Центральный Google ученый

5. Талмор Д.С., Фесслер Х.Э. Важны ли измерения давления в пищеводе для принятия клинических решений у пациентов, находящихся на искусственной вентиляции легких? Уход за дыханием. 2010;55:162–74.

   ПабМед Google ученый

6. Loring SH, O’Donnell CR, Behazin N, Malhotra A, Sarge T, Ritz R, et al. Давление в пищеводе при остром повреждении легких: представляют ли они артефакт или полезную информацию о транспульмональном давлении, механике грудной клетки и нагрузке на легкие. J Appl Physiol. 2010;108:515–22.

   Артикул пабмед Google ученый

7. «>

   Chen L, Chen GQ, Shore K, Shklar O, Martins C, Devenyi B, et al. Внедрение прикроватной оценки дыхательной механики у пациентов с острым респираторным дистресс-синдромом. Критический уход. 2017;21:84.

   Артикул пабмед ПабМед Центральный Google ученый

8. Мид Дж., Макилрой МБ, Селверстоун, штат Нью-Джерси, Крит, Британская Колумбия. Измерение внутрипищеводного давления. J Appl Physiol. 1955;7:491–5.

   КАС Статья пабмед Google ученый

9. Walterspacher S, Isaak L, Guttmann J, Kabitz HJ, Schumann S. Оценка дыхательной функции зависит от механических характеристик баллонных катетеров. Уход за дыханием. 2014;59:1345–52.

   Артикул пабмед Google ученый

10. Mojoli F, Chiumello D, Pozzi M, Algieri I, Bianzina S, Luoni S, et al. Измерение давления в пищеводе при различных условиях внутригрудного давления. Исследование in vitro баллонных катетеров второго поколения. Минерва Анестезиол. 2015; 81: 855–64.

    КАС пабмед Google ученый

11. Yang YL, He X, Sun XM, Chen H, Shi ZH, Xu M и др. Оптимальный объем пищеводного баллона для точной оценки плеврального давления в конце выдоха и в конце вдоха: лабораторный эксперимент in vitro. Интенсивная терапия Med Exp. 2017;5:35.

    Артикул пабмед ПабМед Центральный Google ученый

12. Милич-Эмили Дж., Мид Дж., Тернер Дж.М., Глаузер Э.М. Усовершенствованный метод оценки плеврального давления с помощью пищеводных баллонов. J Appl Physiol. 1964;19:207–11.

    КАС Статья пабмед Google ученый

13. Mojoli F, Iotti GA, Torriglia F, Pozzi M, Volta CA, Bianzina S, et al. Калибровка давления в пищеводе in vivo у пациентов, находящихся на искусственной вентиляции легких, делает измерения надежными. Критический уход. 2016;20:98.

    Артикул пабмед ПабМед Центральный Google ученый

14. Чиумелло Д., Крессони М., Коломбо А., Бабини Г., Бриони М., Кримелла Ф. и др. Оценка транспульмонального давления у больных ОРДС на ИВЛ. Интенсивная терапия Мед. 2014;40:1670–8.

    Артикул пабмед Google ученый

15. Хабертюр К., Мелиг А., Стовер Дж. Ф., Шуманн С., Мёллер К., Прибе Х. Дж. и др. Экспираторная автоматическая компенсация эндотрахеальной трубки уменьшает динамическую гиперинфляцию в модели физического легкого. Критический уход. 2009;13:R4.

    Артикул пабмед ПабМед Центральный Google ученый

16. Лемен Р., Бенсон М. , Джонс Дж.Г. Измерение абсолютного давления с помощью изготовленных вручную пищеводных баллонов. J Appl Physiol. 1974;37:600–3.

    КАС Статья пабмед Google ученый

17. Beardsmore CS, Helms P, Stocks J, Hatch DJ, Silverman M. Усовершенствованная техника пищеводного баллона для использования у младенцев. J Appl Physiol Respir Environ Exerc Physiol. 1980; 49: 735–42.

    КАС пабмед Google ученый

18. Cross TJ, Lalande S, Hyatt RE, Johnson BD. Характеристики отклика баллонных катетеров пищевода, изготовленных вручную из латексных и нелатексных материалов. Physiol Rep. 2015;3:e12426.

    Артикул пабмед ПабМед Центральный Google ученый

19. Wu YX, Chen H, Li Q, Hao JJ, Zhao LH, He X и др. Профилактическое использование ремифентанила для отсроченной экстубации после плановых внутричерепных операций: проспективное рандомизированное двойное слепое исследование. J Нейросург Анестезиол. 2017;29:281–90.

    Артикул пабмед Google ученый

20. Ranieri VM, Rubenfeld GD, Thompson BT, Ferguson ND, Caldwell E, Fan E, et al. Острый респираторный дистресс-синдром: берлинское определение. ДЖАМА. 2012;307:2526–33.

    ПабМед Google ученый

21. Чиумелло Д., Консонни Д., Коппола С., Фройо С., Кримелла Ф., Коломбо А. Тесты на окклюзию и давление в пищеводе в конце выдоха: измерения и сравнение при контролируемой и вспомогательной вентиляции. Энн Интенсивная терапия. 2016;6:13.

    Артикул пабмед ПабМед Центральный Google ученый

22. Бланд Дж. М., Альтман Д. Г. Статистические методы оценки соответствия между двумя методами клинических измерений. Ланцет. 1986;1(8476):307–10.

    КАС Статья пабмед Google ученый

23. «>

    Hedenstierna G, Järnberg PO, Torsell L, Gottlieb I. Эластичность пищевода у людей под наркозом. J Appl Physiol Respir Environ Exerc Physiol. 1983; 54: 1374–1378.

    КАС пабмед Google ученый

Ссылки на скачивание

Благодарности

Неприменимо.

Финансирование

Это исследование было поддержано грантами Специальной программы Пекинской муниципальной комиссии по науке и технологиям (Z161100000116081). Спонсор не участвовал в разработке исследования, сборе данных, анализе данных, интерпретации данных или написании отчета.

Доступность данных и материалов

Наборы данных, созданные и проанализированные в ходе текущего исследования, можно получить у соответствующего автора по обоснованному запросу.

Информация об авторе

Авторы и представители

1. Отделение реаниматологии, Пекинская больница Тяньтань, Столичный медицинский университет, Адрес: № 6, Тяньтань Сили, район Дунчэн, Пекин, 100050, Китай

   Сю-Мэй Сунь, Гуан-Цян Чен , Hua-Wei Huang, Xuan He, Yan-Lin Yang, Zhong-Hua Shi, Ming Xu & Jian-Xin Zhou

Авторы

1. Xiu-Mei Sun

   Просмотр публикаций авторов

   Вы также можете искать это автор в PubMed Google Академия

2. Guang-Qiang Chen

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

3. Hua-Wei Huang

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

4. Xuan He

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

5. Ян-Лин Ян

   Посмотреть публикации автора

   Вы также можете искать этого автора в PubMed Google Scholar

6. Zhong-Hua Shi

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

7. Ming Xu

   Просмотр публикаций автора

   Вы также можете искать этого автора в PubMed Google Scholar

8. Jian-Xin Zhou

   Посмотреть публикации автора

   Вы также можете искать этого автора в PubMed Google Scholar

Вклады

XMS, GQC и JXZ отвечали за концепцию и участвовали в разработке исследования. XMS, ZHS, YLY и JXZ участвовали в стендовом эксперименте. XMS, GQC, HWH, XH, YLY и MX участвовали в наборе пациентов и сборе данных. XMS, GQC и JXZ участвовали в анализе и интерпретации данных. XMS, GQC, YLY и JXZ участвовали в статистическом анализе. XMS и JXZ написали первый черновик рукописи. Все авторы прокомментировали исправления рукописи и одобрили окончательный вариант.

Автор, ответственный за переписку

Переписка с Цзянь-Синь Чжоу.

Декларация этики

Утверждение этики и согласие на участие

Протокол исследования был одобрен экспертным советом пекинской больницы Тяньтань Столичного медицинского университета (KY-2016-11-22). Письменное информированное согласие было получено от пациента или соответствующих лиц, принимающих решения.

Согласие на публикацию

Неприменимо

Конкурирующие интересы

Авторы заявляют об отсутствии конкурирующих интересов.

Примечание издателя

Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и ​​институциональной принадлежности.

Дополнительные файлы

Дополнительный файл 1:

Подробные методы лабораторного эксперимента и клинического исследования. (PDF 110 КБ)

Дополнительный файл 2:

Подробные результаты лабораторного эксперимента. (PDF 110 КБ)

Дополнительный файл 3:

Рисунок S1. Пример кривых P-V баллона при атмосферном давлении и различных уровнях эластичности камеры. (PDF, 468 КБ)

Дополнительный файл 4:

Таблица S1. Измеренная эластичность камеры (смH ₂ О/мл) в камерах с различным внутренним объемом. (PDF 62 КБ)

Дополнительный файл 5:

Подробные результаты клинического исследования (PDF 172 КБ)

Дополнительный файл 6:

Таблица S2. Индивидуальные данные объема баллона и эластичности стенки пищевода. (PDF, 71 КБ)

Дополнительный файл 7:

Рисунок S2. Примеры кривой давления-объема пищеводного баллона in vivo во время окклюзии в конце выдоха в сочетании с кривой in vitro в камере с сопоставимой эластичностью и исходным давлением. (PDF, 571 КБ)

Дополнительный файл 8:

Рисунок S3. Анализ пределов согласия Бланда-Альтмана для оценки эластичности пищевода с помощью простого и стандартного метода линейной регрессии. (PDF 287 КБ)

Права и разрешения

Открытый доступ Эта статья распространяется в соответствии с условиями международной лицензии Creative Commons Attribution 4.0 (http://creativecommons.org/licenses/by/4.0/), которая разрешает неограниченное использование, распространение, и воспроизведение на любом носителе, при условии, что вы укажете автора(ов) оригинала и источник, предоставите ссылку на лицензию Creative Commons и укажете, были ли внесены изменения. Отказ от права Creative Commons на общественное достояние (http://creativecommons.org/publicdomain/zero/1.0/) применяется к данным, представленным в этой статье, если не указано иное.

Перепечатка и разрешения

Об этой статье

Калькулятор характеристик воздушных шаров – высотная наука

Перед использованием нашего Калькулятора характеристик воздушных шаров важно, чтобы вы точно поняли, как он работает. Калькулятор производительности воздушного шара начинается со сбора трех элементов информации: размера вашего метеозонда, веса вашего полезного груза и того, какую положительную подъемную силу вы хотите использовать. С этими тремя значениями Калькулятор производительности воздушного шара точно определяет, сколько гелия вам нужно. Для этого калькулятор добавляет вес воздушного шара, вес полезной нагрузки и положительную подъемную силу. Затем он делит эту сумму на 27,82, чтобы получить необходимое количество гелия в кубических футах (1 кубический фут гелия может условно поднять 27,82 грамма). Затем Калькулятор производительности воздушного шара рассчитывает высоту, на которой воздушный шар лопнет. Он уже знает, каков начальный объем шара при запуске в кубических футах. и поэтому может предсказать, на какой высоте будет находиться воздушный шар, когда он достигнет своего максимального объема. Чем меньше первоначальный объем воздушного шара, тем выше он поднимется, прежде чем достигнет объема разрыва. Имейте в виду, что это только консервативная оценка.

Ссылка на калькулятор производительности баллона

tools.highaltitudescience.com/

Что вам нужно

1. Размер баллона, который вы собираетесь использовать, с нашим калькулятором Balloon 30 Размеры воздушных шаров 1200 г.
2. Вес вашей полезной нагрузки в граммах — Это вес всего, что подвешено под шаром, включая парашют. Вы можете использовать весы для запуска, входящие в комплект нашей инфляционной системы. чтобы получить точное измерение. Вес полезной нагрузки НЕ включает вес воздушного шара.
3. Ваш положительный подъем в граммах — Это число станет более понятным, когда вы научитесь пользоваться нашим Калькулятором производительности баллона. Пока просто начните с начального предположения в 100 граммов. Вы всегда можете изменить это число на основе результатов, полученных с помощью калькулятора.

Что такое положительный подъем?

Подъемная сила — это дополнительная подъемная сила, необходимая вашему метеозонду для подъема вверх в дополнение к подъемной силе, необходимой для удержания веса вашего полезного груза и веса самого шара. В качестве примера предположим, что вы хотите запустить полезную нагрузку весом 1200 граммов (включая вес парашюта, такелажа и т. д.). Предположим также, что вы используете наш 1200-граммовый метеозонд (который также весит 1200 грамм). Вы рассчитываете, сколько гелия вам нужно для запуска вашей полезной нагрузки, зная, что 1 куб. фут. гелия поднимет 28 грамм. Вы делите вес вашего воздушного шара и полезной нагрузки (2400 г) на 28 г/куб.фут. чтобы получить общее количество кубических футов гелия, необходимое для вашего запуска (2400 г ÷ 28 г/куб. фут = 86 куб. футов). Вы надуваете свой воздушный шар объемом 86 куб. футов. гелия и освободите свой груз. К вашему удивлению, он не лезет. Он просто плывет прямо перед вами, не поднимаясь и не опускаясь. Это потому, что в вашем воздушном шаре достаточно гелия, чтобы поднять собственный вес и вес полезной нагрузки. Это идеальное равновесие. Вам нужна сила, которая заставит воздушный шар и полезный груз подняться вверх. Самое простое решение — добавить в воздушный шар больше гелия. Этот дополнительный гелий обеспечит дополнительную подъемную силу, необходимую для подъема вашего воздушного шара. Подъемная сила, создаваемая этим дополнительным гелием, называется положительной подъемной силой. Чем больше гелия вы добавите в свой воздушный шар помимо гелия, используемого для подъема веса полезной нагрузки и самого воздушного шара, тем больше положительной подъемной силы вы получите. Чем выше положительная подъемная сила, тем быстрее будет подниматься ваш полезный груз.

О чем следует помнить

1. Наш калькулятор производительности шара консервативен при расчете прогнозируемой высоты взрыва. Мы хотим, чтобы наши клиенты были довольны достигнутой высотой и не разочаровывались, потому что они никогда не достигали теоретической высоты, рассчитанной нашим калькулятором.
2. Два воздушных шара одинакового размера, изготовленные одним и тем же производителем, обычно лопаются при одинаковом диаметре/объеме. Более дорогие воздушные шары имеют больший диаметр/объем взрыва, чем у более дешевых производителей.
3. Размеры воздушных шаров измеряются по их весу в граммах. 350-граммовый метеозонд весит ~350 грамм. 1200-граммовый метеозонд весит ~1200 грамм.
4. Чем больше размер воздушного шара (чем больше он весит), тем больше будет его диаметр/объем перед тем, как он лопнет.
5. Если вы запустите два груза с шаром одного размера, шар с наименьшим количеством гелия лопнет на большей высоте.

Шаг 1. Введите в калькулятор размер воздушного шара, вес полезной нагрузки и положительную подъемную силу 100 г. Выберите размер воздушного шара из выпадающего меню и введите вес полезной нагрузки (все, что подвешено под воздушным шаром, включая парашют, такелаж, камеры и т. д.). Поскольку мы не уверены, какая положительная подъемная сила нам нужна, мы пока просто введем 100 g. Для этого урока мы будем использовать наш 600-граммовый метеорологический шар и наш комплект Eagle Pro Kit, который весит ~ 600 г (включая батареи, камеру GoPro, парашют, радиожучок и т.  д.). Наш комплект для надувания погодного шара включает в себя весы для запуска, которые вы можете использовать для измерения веса вашей конкретной установки полезной нагрузки. Мы рекомендуем вам следовать этому руководству, вводя значения в свой собственный инструмент «Калькулятор производительности шара».

 

Шаг 2. Расчет. Щелкните Вычислить . На стороне калькулятора Output вы увидите, сколько гелия вам нужно, расчетную высоту взрыва, среднюю скорость подъема и время подъема (время, которое потребуется вашему воздушному шару, чтобы подняться с высоты 0 м до расчетной высоты взрыва). При положительной подъемной силе 100 г нашему воздушному шару массой 600 г с полезной нагрузкой 600 г потребуется 251 минута (4 часа 11 минут), чтобы достичь расчетной высоты взрыва 31 580 м (103 000 футов). Хотя мы рады видеть, как наш воздушный шар лопается на высоте более 100 000 футов, батарея нашей GoPro работает чуть менее трех часов. Предполагая, что полезному грузу требуется от 35 до 45 минут, чтобы спуститься под парашютом после того, как воздушные шары лопнут, нам нужно, чтобы наше всплытие заняло не более 120 минут, если мы хотим заснять весь полет на видео. Наша средняя скорость всплытия слишком медленная.

 

Шаг 3. Увеличьте положительную подъемную силу. Мы решаем посмотреть, что произойдет, если мы увеличим нашу положительную подъемную силу со 100 г до 1000 г, и пересчитаем (введите новое значение положительной подъемной силы 1000 г и нажмите Рассчитать ). Наше время восхождения составляет всего 84 минуты (1 час 24 минуты). Время подъема ниже нашей цели в 120 минут, но наша высота взрыва уменьшилась с 31 580 м до 28 090 м (92 000 футов). Есть еще большая проблема. Наша средняя скорость подъема составляет более 5 м/с. Любая скорость всплытия более 5 м/с значительно увеличивает риск того, что воздушный шар создаст нестационарное колебательное сопротивление в своем следе, когда он поднимается в атмосфере. Это заставит нашу полезную нагрузку сильно раскачиваться и может повредить полезную нагрузку и воздушный шар. Наша средняя скорость всплытия сейчас слишком высока.

 

Шаг 4. Увеличивайте/уменьшайте положительную подъемную силу до тех пор, пока не будете удовлетворены скоростью/временем подъема. Мы знаем, что нам нужна положительная подъемная сила от 100 до 1000 г. Наша цель — иметь время подъема 120 минут и скорость подъема менее 5 м/с. Мы экспериментируем с различными значениями положительной подъемной силы (просто введите разные значения положительной подъемной силы от 100 до 1000 g и нажмите Calculate ), пока не найдем, что 460 g дает нам время подъема ровно 120 минут. Наша высота взрыва 29,950 м. Это меньше, чем 100 000 футов, на которые мы рассчитывали, но калькулятор консервативен, поэтому наши шансы достичь 100 000 футов все еще высоки (у нас был клиент, достигший 115 000 футов с нашим комплектом Eagle Pro Kit и положительной подъемной силой 100 g, хотя калькулятор оценивает высота взрыва всего 103 000 футов для этой установки). Наша средняя скорость подъема значительно ниже 5 м/с, и нам нужно 60 куб. футов. гелий для нашего запуска.

 

Шаг 5. Продолжаем. Местный магазин товаров для вечеринок сдает в аренду 55 куб. футов. баллоны с гелием (обычный размер для Party City). Нам нужно 60 cu.ft. для нашего запуска, но что, если мы не хотим тратить деньги на аренду дополнительного резервуара на 55 куб. футов, когда нам нужно всего 5 дополнительных куб. футов? Мы уменьшаем нашу положительную подъемную силу до тех пор, пока наш калькулятор не скажет нам, что наша установка требует 55 кубических футов для запуска. При положительной подъемной силе 330 г нам нужно ровно 55 куб. футов. Это увеличило наше время восхождения со 120 до 140 минут. Это также увеличивает нашу высоту взрыва до 3049.0 м, что составляет ~100 000 футов. Нам не нравится добавлять 20 минут к времени всплытия. Какие еще варианты у нас есть?

 

Шаг 6. Что, если мы уменьшим размер нашего воздушного шара? Мы решили, что не хотим арендовать два 55 куб. фута. баллоны с гелием. Что произойдет, если мы уменьшим размер нашего воздушного шара с 600 г до 350 г? После расчета различных значений положительной подъемной силы мы обнаруживаем, что положительная подъемная сила 290 г дает нам 120-минутное время подъема, которое мы ищем, а общий требуемый объем гелия составляет всего 45 куб. футов. Однако наша расчетная высота взрыва упала до 26 060 м. Это меньше, чем 30 000 м ~ 100 000 футов, на которые мы рассчитывали. Вот лишь несколько вариантов, которые могут у вас быть. Если вы проявите творческий подход, вы, вероятно, сможете придумать еще больше вариантов.

1. Аренда двух 55 куб. футов. баллоны с гелием для нашего 600-граммового метеозонда и подняться на высоту 30 000 м за 120 минут, чтобы мы могли запечатлеть весь полет на нашу GoPro.
2. Аренда только одного 55 куб. футов. баллон с гелием на нашем 600-граммовом метеозонде и взлететь еще выше, но есть риск не заснять весь полет на нашу GoPro.
3. Возьмите напрокат только один баллон с гелием и используйте меньший 350-граммовый шар, чтобы не летать так высоко, но при этом снимать весь полет на нашу камеру GoPro.
4. Используйте наш 600-граммовый метеозонд и найдите способ уменьшить вес нашей полезной нагрузки, чтобы мы могли достичь высоты взрыва за 120 минут на 55 кубических футах. Поэкспериментируйте с Калькулятором производительности воздушного шара и посмотрите, сможете ли вы вычислить, сколько должен весить ваш полезный груз, чтобы достичь расчетной высоты взрыва за 120 минут с гелием объемом 55 куб. футов. Ответ находится внизу этой веб-страницы*.
5. Переместите стартовую площадку с уровня моря (расчет предполагает, что вы запускаете с высоты 0 м) на более высокую высоту. Здесь, в Колорадо, High Altitude Science обычно запускается на высоте 2200 м над уровнем моря. При средней скорости подъема 3,6 м/с время подъема сократится на 10 минут (2200 м разделить на 3,6 м/с, разделить на 60 с/мин = 10,2 минуты).

Какой вариант вы бы выбрали?

 

Далее

Чтобы узнать больше о запуске метеозондов, приобретите комплект Eagle Pro Weather Balloon Kit.