Объем газа в 50 литровом баллоне в м3: Сколько кубов газа в 50 литровом баллоне?

Содержание

Азот технический 99,6%, 40 л.

Новинки

Обмен газовых баллонов

Сварочное оборудование

Для строительства и дачи

Автономная газификация

Заправка погрузчиков

Заправка Доставка Газа

Главная » Заправка Аренда баллонов » Азот » Азот технический 99,6%, 40 л.

Азот технический 99,6%, 40 л.

Описание:

Купить . взять в Аренду и заправить газовые азотные баллоны в компании «diar-gas» возможно уже сегодя. Оперативная и срочная заправка и доставка азота в баллонах высокого давления по Москве и Московской области! Заказ по телефону 8 (495) 664-65-83 или на сайте нашего магазина в Москве.

Услуга: Аренда и Ответственное хранение азотных баллонов на нашем складе в Москве.

Закончился на стройке Азот, звоните 8-925-123-33-99.

Баллон азотный 40 л стальной. Предназначение: перевозка и хранение азота в баллонах ГОСТ 949-73.

Азот газообразный в баллонах 40 литров – нетоксичный и безопасный для человека технический газ. Азот полностью лишен цвета и запаха, он пожароустойчив, не взрывоопасен. Газ баллоны с азотом емкостью 40 литров не требуют особых, специальных условий для хранения, транспортировки и эксплуатации в отличие от взрыво- и пожароопасных технических газов: пропана, ацетилена и др. Благодаря своей высокой безопасности азот (в том числе в газовых баллонах 40 литров) перспективен во многих отраслях производства. Его широко используют в горнодобывающей промышленности, он пригоден для продувки систем кондиционирования и вентиляции при производстве пуско-наладочных работ, при резке и сварке некоторых металлов. Азоту находят применение в медицине, в электронике, в пожаротушении и т.д.

Заправка Азотом в баллоны в нашей компании осуществляется только после прохождения проверки баллона на специальном стенде на предмет его технической исправности и срока аттестации (освидетельствования) баллона (визуальный осмотр корпуса, резьбы вентиля, наличие разгерметизации резьбовых соединений), это обеспечивает безопасность при заправке и дальнейшей эксплуатации любого газового баллона 10 или 40 литров. Купить Азот газообразный или обменять баллон в Москве и Московской области можно оставив заявку на нашем сайте или связавшись с нами по телефону 8-495-664-65-83.

Азот технический ГОСТ 9293 — 74. (первый сорт)
Объёмная доля азота — не менее 99,6%
Объёмная доля кислорода — не более 0,4%
Содержание масла, механических примесей и влаги — выдерживает испытание
Зависимость давления азота в баллоне от температуры ГОСТ 26460-85
-50С-103 кгс/см2……… 0С- 137 кгс/см2
-40С-110 кгс/см2……… 10С-144 кгс/см2
-30С-117 кгс/см2……… 20С-150 кгс/см2
-20С-124 кгс/см2……… 30С-156 кгс/см2
-10С-131 кгс/см2……… 35С-159 кгс/см2
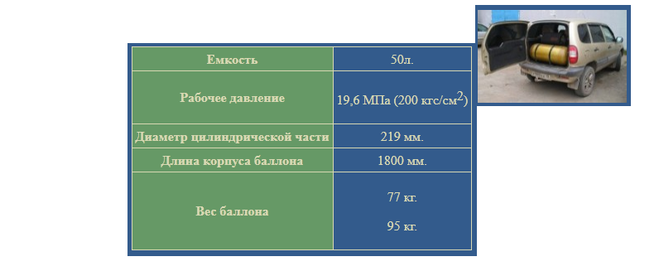
Характеристики баллона:
- Объем баллона — 40 л.
- Рабочее давление — 14,7 Мпа
- Испытательное давление — 19,6 МПа
- Диаметр — 219 мм.
- Высота — 1400 мм.
- Марка стали — 30ХГСА, 45, Д
- Масса баллона — 65 кг.
- Запорный вентиль ГОСТ 9909-81

Характеристики:

Объем баллона, л	40
Рабочее давление, МПа	14,7
Высота, мм	1400
Диаметр, мм	219
Материал	Сталь 45, Д
Масса баллона, кг	65 кг
Тип запорного устройства	вентиль
Объем газа м3	5,7
Вес газа	7,5 кг
ГОСТ	949-73

Объем, масса, плотность, удельный объем.

Приведение к нормальным и стандартным условиям и пересчет

Главная / Справочник / Приложения / Единицы физических величин, физико-химические понятия, соотношения, состав и характеристики газов / Объем, масса, плотность, удельный объем. Приведение к нормальным и стандартным условиям и пересчет

Приведение к нормальным и стандартным условиям

Единицей измерения объема газа является кубический метр (м³). Измеренный объем приводится к нормальным физическим условиям.

Нормальные физические условия: давление 101 325 Па, температура 273,16 К (0 °С).

Стандартные условия: давление 101 325 Па, температура 293,16 К (+20 °С).

В настоящее время эти обозначения выходят из употребления. Поэтому в дальнейшем следует указывать те условия, к которым относятся объемы и другие параметры газа. Если эти условия не указываются, то это значит, что параметры газа даны при 0 °С (273,16 °К) и 760 мм рт. ст. (1,033 кгс/см²). Иногда объем газа (особенно в иностранной литературе и нормах) при пользовании системой СИ приводится к 288,16 °К (+15 °С) и давлению 1 бар (105 Па).

Если известен объем газа при одних условиях, то пересчитать его в объемы при других условиях можно с помощью коэффициентов, приведенных следующей таблице.

Коэффициенты для пересчета объемов газа из одних условий в другие

Температура и даление газа	0 °С и 760 мм рт. ст.	15 °С и 760 мм рт. ст.	20 °С и 760 мм рт. ст.	15 °С (288,16 °К) и 1 бар
0 °С и 760 мм рт. ст. (норм. условия)	1	1,055	1,073	1,069
15 °С и 760 мм рт. ст. (в зар. литературе)	0,948	1	1,019	1,013
20 °С и 760 мм рт. ст. (ст. условия)	0,932	0,983	1	0,966
15 °С (288,16 °К) и 1 бар (СИ)	0,936	0,987	1,003	1

Для приведения объемов газа к 0 °С (273,16 °К) и 760 мм рт. ст. (1,033 кгс/см²), а также к 20 °С (293,16 °К) и 760 мм рт. ст. (1,033 кгс/см²) могут быть применены следующие формулы:

где V_{0 °С и 760 мм рт. ст.} — объем газа при 0 °С и 760 мм рт. ст., м³;
V_{20° С и 760 мм рт. ст.} — объем газа при 20 °С и 760 мм рт. ст., м³;
V_P — объем газа в рабочих условиях, м³;
р — абсолютное давление газа в рабочих условиях, мм рт. ст.;
Т — абсолютная температура газа в рабочих условиях, °К.

Пересчет объемов газа, приведенных к 0 °С и 760 мм рт. ст., а также к 20 °С и 760 мм рт. ст., в объемы при других (рабочих) условиях можно производить по формулам:

Любой газ способен расширяться. Следовательно, знание объема, который занимает газ, недостаточно для определения его массы, так как в любом объеме, целиком заполненном газом, его масса может быть различной.

Масса — это мера вещества какого-либо тела (жидкости, газа) в состоянии покоя; скалярная величина, характеризующая инерционные и гравитационные свойства тела. Единицы массы в СИ — килограмм (кг).

Плотность, или масса единицы объема, обозначаемая буквой p, — это отношение массы тела m, кг, к его объему, V, м³:

p = m/V

или с учетом химической формулы газа:

p = M/V_М = M/22,4,

где M — молекулярная масса,
V_М — молярный объем.

Единица плотности в СИ — килограмм на кубический метр (кг/м³).

Зная состав газовой смеси и плотность ее компонентов, определяем по правилу смешения среднюю плотность смеси:

p_см = (p₁V₁ + p₂V₂ + … + p_nV_n)/100,

где p₁, p₂, …, p_n — плотность компонентов газового топлива, кг/м³;
V₁, V₂, …, V_n — содержание компонента, об. %.

Величину, обратную плотности, называют удельным, или массовым, объемом (ν) и измеряют в кубических метрах на килограмм (м³/кг).

Как правило, на практике, чтобы показать, на сколько 1 м³ газа легче или тяжелее 1 м³ воздуха, используют понятие относительная плотность d, которая представляет собой отношение плотности газа к плотности воздуха:

d = p/1,293

d = M/(22,4×1,293).

Boyle’s Law Calculator

, созданный Wojciech SAS, PhD

, рассмотренная Bogna Szyk and Jack Bowater

Последнее обновление: 01 ноября, 2022

Соглашение:

.
Где применяется закон Бойля?
Прочие термодинамические процессы

Калькулятор закона Бойля отличный инструмент для оценки параметров газа в изотермическом процессе . Вы найдете ответ на вопрос «Что такое закон Бойля?» в тексте, поэтому читайте дальше, чтобы узнать о формуле закона Бойля , увидеть несколько полезных примеров упражнений по закону Бойля и узнать, как распознать, когда процесс удовлетворяет закону Бойля на графике.

Если вам нужно рассчитать результаты изобарического процесса, воспользуйтесь нашим калькулятором закона Чарльза.

Определение закона Бойля

Закон Бойля (также известный как закон Бойля-Мариотта) говорит нам о взаимосвязи между давлением газа и его объемом при постоянной температуре и массе газа . В нем говорится, что абсолютное давление обратно пропорционально объему .

Определение закона Бойля можно также сформулировать следующим образом: произведение давления и объема газа в замкнутой системе постоянно, пока не изменяется температура.

Закон Бойля описывает поведение идеального газа. Мы можем охарактеризовать этот газ уравнением идеального газа, о котором вы можете прочитать больше в нашем калькуляторе законов идеального газа. Закон Бойля говорит о изотермический процесс , что означает, что температура газа во время перехода остается постоянной, как и внутренняя энергия газа.

Формула закона Бойля

Уравнение закона Бойля можно записать следующим образом:

p₁ × V₁ = p₂ × V₂ ,

где p₁ и V соответственно начальное давление. Точно так же p₂ и V₂ являются конечными значениями этих параметров газа.

Мы можем записать формулу закона Бойля различными способами в зависимости от того, какой параметр мы хотим оценить. Допустим, мы изменили объем газа в изотермических условиях и хотим найти результирующее давление. Тогда уравнение закона Бойля утверждает, что:

p₂ = p₁ × V₁ / V₂ или p₂ / p₁ = V₁ / V₂ .

Как мы видим, соотношение конечного и начального давления является обратным отношением для объемов . Этот калькулятор закона Бойля работает в любом направлении, которое вам нравится. Просто введите любые три параметра, и четвертый будет рассчитан сразу!

Весь процесс можно представить на графике закона Бойля. Наиболее часто используется тип, когда давление является функцией объема. Для этого процесса кривая представляет собой гиперболу. Переход может происходить в обоих направлениях, поэтому и сжатие, и расширение газа удовлетворяют закону Бойля.

🔎 Если переход представляет собой изохорный процесс (постоянный объем), вам пригодится калькулятор закона Гей-Люссака Омни.

`Примеры закона Бойля`

Закон Бойля можно использовать несколькими способами, поэтому давайте рассмотрим несколько примеров:

Представьте, что у нас есть эластичный контейнер с газом. Начальное давление 100 кПа (или 10⁵ Па , если мы используем экспоненциальную запись), а объем сосуда равен 2 м³ . Решаем сжать ящик до 1 м³ , но общую температуру не меняем. Вопрос: «Как меняется давление газа?». Мы можем использовать формулу закона Бойля:
p₂ = p₁ × V₁ / V₂ = 100 кПа × 2 м³ / 1 м³ = 200 кПа .
После уменьшения объема вдвое внутреннее давление удваивается. Это является следствием того, что произведение давления на объем должно быть постоянным в течение этого процесса.
Следующий пример закона Бойля относится к газу под давлением

2,5 атм , занимая 6 литров пространства. Затем изотермически декомпрессируют до давления 0,2 атм . Узнаем его окончательный объем. Мы должны переписать уравнение закона Бойля: V₂ = p₁ × V₁ / p₂ = 2,5 атм × 6 л / 0,2 атм = 75 л . Вы всегда можете воспользоваться нашим калькулятором закона Бойля, чтобы проверить правильность своих оценок!

`Где применяется закон Бойля?`

Закон Бойля описывает все процессы, при которых температура остается постоянной. В термодинамике температура является мерой средней кинетической энергии, которой обладают атомы или молекулы. Другими словами, можно сказать, что средняя скорость частиц газа при этом переходе не меняется. Формула закона Бойля справедлива для широкого диапазона температур.

В расширенном режиме вы можете выбрать любую понравившуюся температуру, и мы рассчитаем количество молекул, содержащихся в газе. Вам нужно только убедиться, что вещество остается в газовой форме (например, не конденсируется и не кристаллизуется) при этой температуре.

  
 Есть несколько областей, где применим закон Бойля:
  Тепловая машина Карно  - Состоит из четырех термодинамических процессов, два из которых изотермические, удовлетворяющие закону Бойля. Эта модель может сказать нам, каков максимальный КПД тепловой машины.
  Дыхание  тоже можно описать законом Бойля. Всякий раз, когда вы делаете вдох, ваша диафрагма и межреберные мышцы увеличивают объем легких, что снижает давление газа. Когда воздух течет из области более высокого давления в область более низкого давления, воздух попадает в легкие и позволяет нам получать кислород из окружающей среды. При выдохе объем легких уменьшается, поэтому давление внутри выше, чем снаружи, поэтому воздух течет в обратном направлении.
 
  Шприц  - Всякий раз, когда вам нужно сделать инъекцию, врач или медсестра сначала набирают жидкость из маленького флакона. Для этого они используют шприц. При вытягивании поршня доступный объем увеличивается, что снижает давление и, согласно формуле закона Бойля, вызывает всасывание жидкости.
 Другие термодинамические процессы 
 Закон Бойля, наряду с законами Шарля и Гей-Люссака, относится к числу фундаментальных законов, описывающих подавляющее большинство термодинамических процессов.
 Помимо определения значений определенных параметров, таких как давление или объем, также можно узнать кое-что о теплопередаче и работе, совершаемой газом во время этих переходов, а также об изменении внутренней энергии. Мы собрали их все в нашем комбинированном газовом калькуляторе, где вы можете выбрать любой процесс и оценить результаты для реальных газов.
 Войцех Сас, доктор философии
 Начальные параметры
 Начальное давление (p₁)
 Начальный объем (v₁)
 Окончательные параметры
 Окончательное давление (P₂)
 Окончательный объем (V₂)
 Проверьте 39 аналогичных термодинамических калькуляторов 🌡
 Biot numberbltzmann Factorbt : определение, формула, примеры
 Сталкиваетесь ли вы с трудностями при нахождении объема цилиндра, если его форма искажена? Задумывались ли вы над тем, как найти объем таких цилиндров? Это то, что вы узнаете через мгновение.
 Объем цилиндра означает пространство внутри цилиндра, которое может вместить определенное количество материала. Проще говоря, способность цилиндра удерживать предмет — это его объем. Внутри пространства цилиндра вы можете удерживать любой из трех типов материи — твердое, жидкое или газообразное. Эту емкость можно наблюдать только в трехмерном цилиндре, т. е. вы не можете удержать ни жидкость, ни твердое тело, ни газ в двумерном цилиндре.
   Совершенный трехмерный цилиндр имеет два конгруэнтных и параллельных одинаковых основания. Это известно как правильный круговой цилиндр. В прямом круговом цилиндре основания круглые, а каждый отрезок является частью боковой криволинейной поверхности, перпендикулярной основаниям. Вы могли видеть правильные круглые цилиндры в своей повседневной жизни. Формы банок, формы рулонов бумаги, прямое стекло и многое другое.
 Однако, если форма стакана совершенно прямая, он будет называться правильным круглым цилиндром. Если форма нелинейна, то какой она будет?
 Если две конгруэнтные и идентичные параллельные стороны каким-то образом станут непараллельными или деформируются, вы получите любой из следующих цилиндров:
  Наклонный цилиндр – это цилиндр, стороны которого наклонены к основанию под углом, не равным равен прямому углу. Это будет форма искаженного стекла, о которой говорилось выше.
 Эллиптический цилиндр – это цилиндр, основания которого представляют собой эллипсы.
 Прямой круглый полый цилиндр. Имеет форму правильного круглого цилиндра. Однако в конце нет замкнутых кругов.
 Как найти объем цилиндра – традиционный метод   Найти объем цилиндра проще, чем вы думали. Если вам все еще интересно, как найти объем цилиндра, все, что вам нужно, это ведро с водой, весы и пустая плоская поверхность, на которую можно поставить ведро.
 Поставьте ванну на плоскую пустую поверхность и начните наполнять ее водой. Вы должны убедиться, что вода заполнена до краев. Как только ванна наполнится водой, поместите цилиндр, объем которого вам нужно найти, внутрь ванны. Вы увидите, как вода начнет выходить из ванны.
 Соберите выпавшую воду в стакан. Убедитесь, что вода не падает, пока вы делаете преобразование. Поставьте стакан на весы и запишите вес воды. Не забудьте вычесть вес стакана. Вы должны иметь только вес воды.
 Согласно закону Архимеда, вес воды, падающей из ванны, будет равен весу цилиндра. Следовательно, вес полученной воды будет равен весу цилиндра. Вам может быть интересно, как найти объем цилиндра?
 Согласно физике, если вы находитесь в помещении с комнатной температурой, вес будет равен объему. Это означает, что 1 кг будет эквивалентен 1 литру и так далее. Следовательно, вы получите объем цилиндра из объема воды.
 Но что, если вы живете в холодном или жарком регионе? Тогда вам придется использовать другой метод.
 Формула для нахождения объема цилиндра  Объем цилиндра можно найти с помощью формулы. Это универсально и может применяться независимо от вашего региона. Единицами объема являются кубические сантиметры, кубические дюймы или любые стандартные единицы с префиксом «кубический».
 Объем цилиндра можно найти двумя способами. Это:
 Использование площади и высоты
 Использование размеров
 Нахождение объема цилиндров с использованием площади и высоты представляет собой не что иное, как произведение площади и высоты любой формы. Это правило справедливо для всех трехмерных фигур, известных в математике. Например, в кубоиде, если вы знаете площадь одной его стороны, а затем умножаете ее на высоту или ширину, то есть на оставшуюся сторону, вы получите объем.
 В цилиндрах, V = площадь x высота
 Нахождение площади с известными размерами – Универсальная формула для нахождения объема цилиндра: π r ² h, где значение π (пи) равно 3,14 или 22/7, r – радиус вершины или дно цилиндра, а h - высота. Используя формулу, можно найти объемы прямых круговых цилиндров и косых цилиндров.
 Однако для эллиптических цилиндров формула другая. Поскольку эллиптические цилиндры имеют разные радиусы, формула для нахождения их объемов имеет вид: V = π abh, где π = 22/7 или 3,14, a и b — радиусы основания эллиптического цилиндра, а h — высота .
 Кроме того, формула также отличается для полых прямоугольных цилиндров. Объем полого прямоугольного цилиндра определяется формулой:  V = π (R ² – r ² ) h  , где R – внешний радиус круглого основания, r – внутренний радиус, а h – высота цилиндра.
 Если вы ищете формулу площади поверхности цилиндра, то вот она:  A = 2πr ² + 2πrh  , где r и h — радиус и высота цилиндра соответственно. Единицами площади поверхности будут квадратные единицы.
 Шаги для расчета объема цилиндра  Следуя приведенным ниже методам, вы можете найти объем цилиндра.
 Шаг 1: Определите тип цилиндра, данный вам в вопросе или в реальной жизни.
 Шаг 2: Когда у вас есть тип цилиндра, вам нужно выяснить формулу, по которой можно найти объем цилиндра.
 Шаг 3: Теперь у вас есть и формула. Проверьте, какие размеры вам нужны, чтобы найти объем. Убедитесь, что все размеры имеют одинаковые единицы измерения.
 Шаг 4: Разместите их на своих местах и рассчитайте объем.
 Шаг 5: Сохраните единицы измерения после расчетного значения как «кубические единицы». Используйте соответствующую единицу измерения, такую как метр, сантиметр или любую другую, вместо слова единица измерения.
  Примеры для нахождения объема цилиндра 
 Пример 1. Цилиндр имеет радиус 50 см и высоту 100 см. Как найти объем цилиндра?
 Решение: Мы знаем, что объем цилиндра находится по формуле – π r ² h, где r — радиус цилиндра, h — высота.
 Таким образом, подставив значения, получим
 Пример 2: Как найти объем цилиндра, у которого один из радиусов равен 40 см, а другой — 60 см? Цилиндр имеет высоту 200 см.
 Решение: Из приведенных данных видно, что цилиндр эллиптический, так как радиусы разные. Чтобы найти объем эллиптического цилиндра, используется формула V = π abh, где a и b — радиусы, а h — высота.
 Следовательно, объем цилиндра =  V = π abh 
 = π x 40 x 60 x 200 = 1507200 см ³ .
 Пример 3: Как найти объем полого цилиндра изнутри и имеет внешний и внутренний радиусы единиц 6 и 8 соответственно? Высота этого полого цилиндра составляет 15 единиц.
 Решение: Мы знаем, что формула объема полого цилиндра имеет вид  V = π (R ² – r ² ) h  .
 Следовательно, ставя значения, получаем,
 V = π (R ² – r ² ) ч
 = π (8 ² – 6 ² ) 15 = 1318,8 единиц ² .
 Пример 4: Однажды Алекс задался вопросом: «Как мне найти объем цилиндра, высота которого равна 6 дюймам, а радиус — 3 дюймам». Можете ли вы помочь ей найти объем этого цилиндра?
 Ответ: Да, можно! Вы знаете формулу для нахождения объема цилиндра: V = π r ² h.
 Таким образом, подставив значения, вы получите V = π r ² ч
 = π x 3 ² x 6 = 169,56 в ³ .
 Вы можете сказать Алексу, что объем цилиндра равен 169,56 в ³ .
 Часто задаваемые вопросы – Часто задаваемые вопросы  Какова площадь криволинейной поверхности цилиндра?
 Ответ) Площадь криволинейной поверхности цилиндра = 2πrh
 2. Каков объем цилиндра?
 Ответ) Объем цилиндра – это количество свободного места в нем. Его можно получить, умножив площадь основания на высоту. Объем цилиндра с радиусом основания «r» и высотой «h» равен V = πr2h.
 3. Каков объем полого цилиндра?
 Ответ) Измеряем два радиуса объема полого цилиндра, один для внутренней окружности, а другой для внешней окружности, образованной основанием полого цилиндра, и если «R» — внешний радиус, а «r» — внутренний радиус а «h» – высота, то объем полого цилиндра равен  V = πh (R2 – r2). 
 4. Какая единица измерения объема цилиндра?
 Ответ) Объем цилиндра измеряется в кубических единицах, таких как кубические сантиметры (см3), кубические метры (м3), кубические футы (фут3) и так далее.
 Практический вопрос  Вычислите объем заданного цилиндра высотой 30 см и радиусом основания 15 см. (Возьмите пи = 22/7)?
 Ответ) Дано:
 Высота = 30 см
 Радиус = 15 см
 мы это знаем;
 Объем, V = πr2h кубических единиц
 V=(22/7) × 15 × 15 × 30
 V= 212142,85 см3
 Следовательно, объем цилиндра = 212142,85 см3 A имеет цилиндр
3 9.