Цилиндические обечайки, производство цилиндрических обечаек в Екатеринбурге
8 (343) 288-77-05
г.Верхняя Пышма, ул.Петрова 59 б/2
Найти:
Цилиндрические обечайки
Обечайка представляет собой деталь цилиндрической формы с незаглушенными торцами. Поперечное сечение обечайки чаще всего представляет собой кольцо, либо в редких случаях сечение может иметь квадратную, треугольную, лекальную форму. Мы осуществляем производство обечаек, как методом холодной вальцовки, так и с предварительным подогревом материала («нагорячо»). По индивидуальному заказу мы готовы произвести обечайки посредством литья полуобечаек с их последующей сваркой.
- Диаметр внутренний D от 130 мм.
- Толщина S до 40 мм.
- Длина вала L 3000 мм.
- Сталь: углеродистая, низколегированная, коррозионностойкая, жаропрочная, и др.

Материал
Для изготовления обечаек применяется материал, поддающийся холодной деформации. В случаях, когда материал склонен к образованию дефектов при холодном формообразовании (в частности появление трещин, изломов), применяют метод горячей вальцовки.
Для производства обечаек, наряду с другими элементами сосудов, используются высококачественные материалы российского производства, соответствующие ГОСТ или ТУ, и импортные материалы, соответствующие AISI:
- углеродистые и низколегированные стали: Ст3, 09Г2С, 20, 13ХФА и др.
- котельные стали по ГОСТ 5520-79: 09Г2С, 20К, 17Г1С, 12ХМ и др.
- коррозионно-стойкие и жаропрочные стали: 08(12)Х18Н10Т, 10Х17Н13М2Т, 20Х23Н17 и др.
- зарубежные аналоги по AISI: 304, 316, 321 и др.
Заготовка для обечаек
Обечайки изготавливаются из цельной заготовки или сваренной из 2-х и более частей в соответствии с ГОСТ 34347-2017 ( Р 52630-2012) .
Любая обечайка будет иметь как минимум один продольный сварной шов. Наибольшее распространение при производстве обечаек получили следующие виды сварки:
- Механизированная дуговая сварка в защитном газе
- Автоматическая дуговая сварка под флюсом
Сварные соединения должны пройти обязательный контроль.
Применяются следующие методы контроля:
- Внешний осмотр и измерения
- Ультразвуковой
- Радиографический
По требованиям конструкторской документации осуществляются и другие виды контроля.
Формообразование
Для придания формы при изготовлении обечайки используют специальную листогибочную машину – вальцы. Такие машины представляют собой станину с расположенными на ней рабочими органами – валками. Валков может быть от 3-х и более. Наиболее точную форму обечайки позволяет получить четырехвалковая гибочная машина. В процессе изготовления конической обечайки заготовка подается в вальцы, и посредством постепенной прокатки с одновременной вертикальной подачей верхнего валка – изделию придается необходимая форма.
Ограничение технологических параметров обечаек обусловлено следующими факторами:
- Минимальный диаметр – ограничен диаметром верхнего валка листогибочной машины. Мы изготавливаем обечайки диаметром от 130мм.
- Максимальный диаметр – в варианте секционной сборки — не ограничен.
- Минимальная толщина стенки – не ограничена.
- Максимальная толщина стенки – ограничена пределом прочности верхнего валка, который установлен заводом-изготовителем вальцов.
 Мы изготавливаем обечайки толщиной стенки до 40 мм.
Мы изготавливаем обечайки толщиной стенки до 40 мм. - Минимальная высота – не ограничена.
- Максимальная высота – ограничена шириной валков гибочной машины. Мы изготавливаем обечайки высотой до 3000мм без кольцевого сварного шва.
Для того чтобы избежать прямого участка в области стыковки кромок обечайки используется набор оправок. В результате мы получаем равномерное кольцевое сечение обечайки.
Термическая обработка
Для придания необходимых механических свойств обечаек производят их термообработку.
Необходимость проведения термообработки при производстве устанавливается требованиями ГОСТ 34347-2017 ( Р 52630-2012) и конструкторской документации.
Механическая обработка
Для дальнейшего использования обечайки при изготовлении сосудов и аппаратов в ряде случаев необходимо произвести механическую обработку, например: обработку торца под приварку днища; под приварку штуцеров, отводов и др. элементов к обечайке и т.д.
элементов к обечайке и т.д.
Производители сосудов и аппаратов, имеющие станочный парк, выполняют механическую обработку самостоятельно. Таким предприятиям обечайки поставляются без механической обработки торцевой части.
Для производителей сосудов и аппаратов, не располагающих станочным парком или не имеющих специального оборудования, ООО «Реммашгрупп» выполняет механическую обработку любой сложности.
Оставить заявку
Цилиндрическая обечайка от производителя ООО ПКФ АрмаПром
- Главная
- Цилиндрическая обечайка
Товар сегодня
80% товара в наличии
Покупай у производителя
Цены ниже конкурентов до 15%
Доставка завтра
Оплати сегодня, а отгрузим уже завтра
Проверенно временем
8 лет мы производим продукцию
высокого качества.
Запросите цены, условия и сроки поставки
Я принимаю условия пользовательского соглашения
Получать новости о скидках и акциях
Прикрепите заявку и свои реквизиты — и мы сразу сможем выставить Вам счет.
Прикрепите заявку
Прикрепите реквизиты
Отправить заявку
| Товар | Диаметр, мм | Толщина стенки, мм | Заказ |
|---|---|---|---|
| Цилиндрические обечайки 325–1820 мм | 325–1820 | 8–30 | Оформить заявку |
Описание
Цилиндрическая обечайка — это открытый элемент трубопровода с незаглушенными торцевыми отверстиями, по форме напоминающий обод или отрезок трубы. Области эксплуатации: производство цельнометаллических ёмкостей, отраслевая промышленность, строительство нестандартных трубопроводных сетей.
Изделие выполняют из стального листа методом вальцовки. Сырьевым материалом является коррозионностойкая сталь, которая позволяет использовать арматуру в условиях воздействия агрессивных сред. Нормы производства деталей приведены в ГОСТ 34347-2017. Методы расчета стальных элементов на прочность изложены в ГОСТ 14249-89. Купить обечайку и оформить доставку можно по электронной почте или номеру телефона.
Сварка цилиндрических обечаек
Соединение элементов происходит кольцевым сварочным методом, с полным проплавлением свариваемых частей без прожогов. Основная задача — формирование прочной обратной стороны шва. При выборе сварочного способа учитывают толщину стальной заготовки.
Виды неразъемных соединений цилиндрической формы:
- контактная сварка: нагрев металла электрическим током под давлением;
- ручная дуговая сварка: проварка электрической дугой по внешнему контуру детали.
Глубина шва составляет 5-6 мм. При сваривании трубу делят на несколько участков. В зависимости от диаметра заготовку поворачивают на 90 или 180, последовательно нанося сварной шов.
В зависимости от диаметра заготовку поворачивают на 90 или 180, последовательно нанося сварной шов.
Устранение шлака и окалины после выполнения операции производят поэтапной зачисткой швов:
- очищение поверхности металла зубилом или молотком;
- полировка шлифовальной техникой;
- лужение пластичного соединения путем нанесения расплавленного олова.
Условия поставки
Цена, наличие товара, условия и гарантии
Мы работаем как с юридическими, так и с физическими лицами. Готовы поставить изделия на заказ.
У нас действует накопительная система скидок для постоянных клиентов.
Условия оплаты
Заказ вы можете оплатить 3 способами: наличными, безналичным расчетом, банковской картой.
Отсрочку платежа до 1 месяца предоставляем постоянным и хорошо зарекомендовавшим себя клиентам.
Доставка
Варианты: заказать у нас, воспользоваться услугами транспортной компании, организовать самовывоз.
При любом виде расчета отгружаем товар на следующий день после поступления оплаты.
Приемка и разгрузка товара
Вы должны обеспечить беспрепятственный подъезд нашего транспорта к разгрузочной площадке.
При разгрузке вы получаете пакет документов: накладная, счет-фактура и сертификат качества (по запросу).
Звоните
8-800-775-12-74
Мы ответим на ваш звонок с понедельника
9:00 — 18:00 — по Челябинску
07:00 — 16:00 — по Москве
Отправляйте заявку
Пишите нам в любое время.
Специалист свяжется с вами в рабочие часы в течение 20 минут после получения заявки.
Если вы
отправили заявку в нерабочее время, то наш специалист свяжется с вами на следующий день.
Запросите цены, условия и сроки поставки
Я принимаю условия пользовательского соглашения
Прикрепите заявку и свои реквизиты — и мы сразу сможем выставить Вам счет.
Получать новости о скидках и акциях
Прикрепите заявку
Прикрепите реквизиты
Отправить заявку
6.3: Объемы революции — цилиндрические оболочки
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2521
- Гилберт Странг и Эдвин «Джед» Герман
- OpenStax
Цели обучения
- Вычислить объем тела вращения, используя метод цилиндрических оболочек.

- Сравните различные методы расчета объема вращения.
В этом разделе мы рассмотрим метод цилиндрических оболочек, последний метод нахождения объема тела вращения. Мы можем использовать этот метод для тех же типов твердых тел, что и метод диска или метод шайбы; однако при использовании метода диска и шайбы мы интегрируем по оси координат, параллельной оси вращения. Методом цилиндрических оболочек интегрируем по координате ось перпендикулярна оси вращения. Возможность выбирать, какую переменную интегрирования мы хотим использовать, может быть значительным преимуществом для более сложных функций. Кроме того, специфическая геометрия твердого тела иногда делает метод использования цилиндрических оболочек более привлекательным, чем метод шайбы. В последней части этого раздела мы рассмотрим все методы определения объема, которые мы изучили, и изложим некоторые рекомендации, которые помогут вам определить, какой метод использовать в той или иной ситуации.
Метод цилиндрических оболочек
Опять же, мы работаем с телом вращения. Как и прежде, определим область \(R\), ограниченную сверху графиком функции \(y=f(x)\), снизу \(x\)-осью , а слева и справа от линий \(x=a\) и \(x=b\) соответственно, как показано на рисунке \(\PageIndex{1a}\). Затем мы вращаем эту область вокруг оси \(y\), как показано на рисунке \(\PageIndex{1b}\). Обратите внимание, что это отличается от того, что мы делали раньше. Ранее области, определяемые в терминах функций \(x\), вращались вокруг 9∗_i)\) и ширину \(Δx\). Репрезентативный прямоугольник показан на рисунке \(\PageIndex{2a}\). Когда этот прямоугольник вращается вокруг оси \(y\), вместо диска или шайбы мы получаем цилиндрическую оболочку, как показано на рисунке \(\PageIndex{2}\).
Рисунок \(\PageIndex{2}\): (a) Репрезентативный прямоугольник. (b) Когда этот прямоугольник вращается вокруг оси \(y\) , получается цилиндрическая оболочка. (c) Когда мы сложим все оболочки вместе, мы получим аппроксимацию исходного твердого тела. ∗_i\) и толщиной \(Δx\) (рисунок). Таким образом, объем оболочки примерно равен объему плоской пластины. Умножая высоту, ширину и глубину тарелки, получаем 9.b_a(2π\,x\,f(x))\,dx. \nonumber \]
∗_i\) и толщиной \(Δx\) (рисунок). Таким образом, объем оболочки примерно равен объему плоской пластины. Умножая высоту, ширину и глубину тарелки, получаем 9.b_a(2π\,x\,f(x))\,dx. \nonumber \]Это приводит к следующему правилу для метода цилиндрических оболочек .
Правило: метод цилиндрических оболочек
Пусть \(f(x)\) непрерывна и неотрицательна. Определим \(R\) как область, ограниченную сверху графиком \(f(x)\), снизу осью \(x\), слева линией \(x=a\) , а справа линией \(x=b\). Тогда объем тела вращения, образованного вращением \(R\) вокруг оси \(y\), равен 9b_a(2π\,x\,f(x))\,dx. \nonumber \]
Теперь рассмотрим пример.
Пример \(\PageIndex{1}\): Метод цилиндрических оболочек I
Определить \(R\) как область, ограниченную сверху графиком \(f(x)=1/x\) и снизу по оси \(x\) на интервале \([1,3]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг оси \(y\).
Решение
Сначала мы должны построить область \(R\) и связанное с ней тело вращения, как показано на рисунке \(\PageIndex{5}\).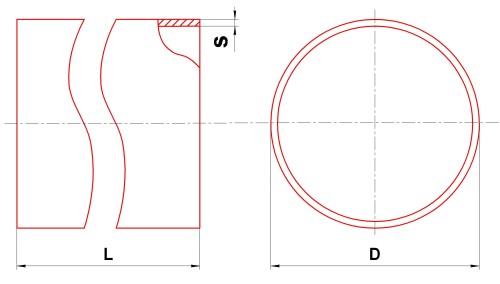 93\)
93\)
Как и в случае метода диска и метода шайбы, мы можем использовать метод цилиндрических оболочек с телами вращения, вращающимися вокруг оси \(x\), когда мы хотим проинтегрировать по \(y\). Аналогичное правило для этого типа твердого тела приведено здесь.
Правило: Метод цилиндрических оболочек для тел вращения вокруг оси \(x\)
Пусть \(g(y)\) непрерывна и неотрицательна. Определим \(Q\) как область, ограниченную справа графиком \(g(y)\), слева — осью \(y\), снизу линией \(y=c\) , а выше строкой \(y=d\). Тогда объем тела вращения, образованного вращением \(Q\) вокруг оси \(x\), равен 9d_c(2π\,y\,g(y))\,dy. \nonumber \]
Пример \(\PageIndex{3}\): Метод цилиндрических оболочек для твердого тела, вращающегося вокруг оси \(x\)
Определить \(Q\) как область, ограниченную справа по графику \(g(y)=2\sqrt{y}\) и слева по оси \(y\) для \(y∈[0,4]\). Найдите объем тела вращения, образованного вращением \(Q\) вокруг оси \(х\).
Решение
Во-первых, нам нужно изобразить область \(Q\) и связанное с ней тело вращения, как показано на рисунке \(\PageIndex{7}\). 93 \end{align*}\]
93 \end{align*}\]
Упражнение \(\PageIndex{3}\)
Определить \(Q\) как область, ограниченную справа графиком \(g(y)=3/y \) и слева по оси \(y\) для \(y∈[1,3]\). Найдите объем тела вращения, образованного вращением \(Q\) вокруг оси \(х\).
- Подсказка
Используйте процесс из примера \(\PageIndex{3}\).
- Ответить
\(12π\) единиц 9*_i)\left(\dfrac {x_i+x_{i-1}}{2}\right)(x_i-x_{i-1}).\end{align*}\]
Это было основано на оболочка с внешним радиусом \(x_i\) и внутренним радиусом \(x_{i−1}\). Однако если мы повернем область вокруг линии, отличной от оси \(y\), мы получим другой внешний и внутренний радиусы. Предположим, например, что мы вращаем область вокруг линии \(x=−k,\), где \(k\) — некоторая положительная константа. Тогда внешний радиус оболочки равен \(x_i+k\), а внутренний радиус оболочки равен \(x_{i−1}+k\). Подставляя эти члены в выражение для объема, мы видим, что при вращении плоской области вокруг линии \(x=−k,\) объем оболочки равен 9b_a(2π(x+k)f(x))dx.
 \nonumber \]
\nonumber \]Мы также можем вращать область вокруг других горизонтальных или вертикальных линий, таких как вертикальная линия в правой полуплоскости. В каждом случае формула объема должна быть скорректирована соответствующим образом. В частности, член \(х\) в интеграле должен быть заменен выражением, представляющим радиус оболочки. Чтобы увидеть, как это работает, рассмотрим следующий пример.
Пример \(\PageIndex{4}\): область вращения, вращающаяся вокруг линии
Определим \(R\) как область, ограниченную сверху графиком \(f(x)=x\) и снизу по оси \(x\) на интервале \([1,2]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг линии \(x=−1.\)
Решение
Сначала начертите область \(R\) и связанное с ней тело оборот, как показано на рисунке \(\PageIndex{8}\).
Рисунок \(\PageIndex{8}\): (a) Область \(R\) между графиком \(f(x)\) и осью \(x\) на интервале \([1 ,2]\). (b) Тело вращения, образованное вращением \(R\) вокруг линии \(x=−1. \) 92\) и ниже по оси \(x\) на интервале \([0,1]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг линии \(x=−2\).
\) 92\) и ниже по оси \(x\) на интервале \([0,1]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг линии \(x=−2\).- Подсказка
Используйте процесс из примера \(\PageIndex{4}\).
- Ответить
\(\dfrac {11π}{6}\) единиц 3
В качестве последнего примера в этом разделе рассмотрим объем тела вращения, область вращения которого ограничена графиками двух функций.
Пример \(\PageIndex{5}\): область вращения, ограниченная графиками двух функций
Определим \(R\) как область, ограниченную сверху графиком функции \(f(x)= \sqrt{x}\) и ниже по графику функции \(g(x)=1/x\) на интервале \([1,4]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг оси \(y\).
Решение
Сначала начертите область \(R\) и соответствующее тело вращения, как показано на рисунке \(\PageIndex{9}\).
Рисунок \(\PageIndex{9}\): (a) Область \(R\) между графиком \(f(x)\) и графиком \(g(x)\) на интервале \ ([1,4]\). (b) Тело вращения, образованное вращением \(R\) вокруг оси \(y\).
Обратите внимание, что осью вращения является ось \(y\), поэтому радиус оболочки задается просто \(x\). Нам не нужно вносить какие-либо коррективы в x-член нашего подынтегрального выражения. Однако высота оболочки определяется выражением \(f(x)−g(x)\), поэтому в этом случае нам нужно скорректировать член \(f(x)\) подынтегральной функции. Тогда объем твердого тела равен 92\) на интервале \([0,1]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг оси \(y\).
- Подсказка
Подсказка: используйте процесс из примера \(\PageIndex{5}\).
- Ответить
\(\dfrac {π}{6}\) единиц 3
Какой метод следует использовать?
Мы изучили несколько методов нахождения объема тела вращения, но как узнать, какой метод использовать? Часто все сводится к выбору того, какой интеграл проще всего вычислить.
Рисунок \(\PageIndex{10}\) Рисунок \(\PageIndex{10}\) описывает различные подходы для тел вращения вокруг оси \(x\). Вам предстоит разработать аналогичную таблицу для тел вращения вокруг оси \(y\).
Рисунок \(\PageIndex{10}\) описывает различные подходы для тел вращения вокруг оси \(x\). Вам предстоит разработать аналогичную таблицу для тел вращения вокруг оси \(y\).Давайте рассмотрим пару дополнительных задач и выберем наилучший подход к их решению.
Пример \(\PageIndex{6}\): выбор наилучшего метода
Для каждой из следующих задач выберите наилучший метод нахождения объема тела вращения, образованного вращением заданной области вокруг \(x \)-ось и настройте интеграл, чтобы найти объем (интеграл не оценивайте).
- Область, ограниченная графиками \(y=x, y=2−x,\) и осью \(x\). 92\) и оси \(х\).
Раствор
а.
Сначала нарисуйте область и тело вращения, как показано.
Рисунок \(\PageIndex{11}\): (a) Область \(R\), ограниченная двумя линиями и осью \(x\). (b) Тело вращения, образованное вращением \(R\) вокруг оси \(x\).Глядя на область, если мы хотим интегрировать по \(x\), нам придется разбить интеграл на две части, потому что у нас есть разные функции, ограничивающие область по \([0,1]\) и \([1,2]\).
 В этом случае, используя дисковый метод, мы получили бы 91_0 2π\,y[2−2y]\,dy. \nonumber \]
В этом случае, используя дисковый метод, мы получили бы 91_0 2π\,y[2−2y]\,dy. \nonumber \]Ни один из этих интегралов не является особенно обременительным, но поскольку метод оболочки требует только одного интеграла, а подынтегральная функция требует меньшего упрощения, в данном случае нам, вероятно, следует использовать метод оболочки.
б.
Сначала нарисуйте область и тело вращения, как показано.
Рисунок \(\PageIndex{12}\): (a) Область \(R\) между кривой и осью \(x\). (b) Тело вращения, образованное вращением \(R\) вокруг оси \(x\). 92\справа]\,dx\номер\]
Ключевые понятия
- Метод цилиндрических оболочек — еще один метод использования определенного интеграла для вычисления объема тела вращения. Этот метод иногда предпочтительнее либо метода дисков, либо метода шайб, потому что мы интегрируем по другой переменной. В некоторых случаях один интеграл существенно сложнее другого.
- Геометрия функций и сложность интегрирования являются основными факторами при принятии решения о том, какой метод интегрирования использовать.
 9b_a\left(2π\,x\,f(x)\right)\,dx\)
9b_a\left(2π\,x\,f(x)\right)\,dx\)Глоссарий
- метод цилиндрических оболочек
- метод расчета объема тела вращения путем деления тела на вложенные друг в друга цилиндрические оболочки; этот метод отличается от методов дисков или шайб тем, что мы интегрируем по противоположной переменной
Эта страница под названием 6.3: Volumes of Revolution — цилиндрические оболочки распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент. это было отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Теги
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- метод цилиндрических оболочек
- тело вращения
- источник@https://openstax.
 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1 - Объем по Shells
6.3 Volumes of Revolution: цилиндрические оболочки — исчисление, том 1
Цели обучения
- 6.3.1 Вычислите объем тела вращения методом цилиндрических оболочек.
- 6.3.2 Сравните различные методы расчета объема вращения.
В этом разделе мы рассмотрим метод цилиндрических оболочек, последний метод нахождения объема тела вращения. Мы можем использовать этот метод для тех же типов твердых тел, что и метод диска или метод шайбы; однако при использовании метода диска и шайбы мы интегрируем по оси координат, параллельной оси вращения. Методом цилиндрических оболочек интегрируем по оси координат перпендикулярно к оси вращения. Возможность выбирать, какую переменную интегрирования мы хотим использовать, может быть значительным преимуществом для более сложных функций.
 Кроме того, специфическая геометрия твердого тела иногда делает метод использования цилиндрических оболочек более привлекательным, чем метод шайбы. В последней части этого раздела мы рассмотрим все методы определения объема, которые мы изучили, и изложим некоторые рекомендации, которые помогут вам определить, какой метод использовать в той или иной ситуации.
Кроме того, специфическая геометрия твердого тела иногда делает метод использования цилиндрических оболочек более привлекательным, чем метод шайбы. В последней части этого раздела мы рассмотрим все методы определения объема, которые мы изучили, и изложим некоторые рекомендации, которые помогут вам определить, какой метод использовать в той или иной ситуации.Метод цилиндрических оболочек
Опять же, мы работаем с телом вращения. Как и ранее, определим область R,R, ограниченную сверху графиком функции y=f(x),y=f(x), снизу осью x, осью x, а слева и справа линиями x=ax=a и x=b,x=b соответственно, как показано на рис. 6.25(a). Затем мы вращаем эту область вокруг оси y , как показано на рис. 6.25(b). Обратите внимание, что это отличается от того, что мы делали раньше. Ранее области, определенные в терминах функций xx, вращались вокруг оси xx или линии, параллельной ей.
Рисунок 6,25 а) Область, ограниченная графиком функции от х.
 х. (b) Тело вращения, сформированное, когда область вращается вокруг оси y. ось y.
х. (b) Тело вращения, сформированное, когда область вращается вокруг оси y. ось y.Как мы уже делали много раз ранее, разобьем интервал [a,b][a,b] с помощью обычного разбиения P={x0,x1,…,xn}P={x0,x1,…,xn} и , для i=1,2,…,n,i=1,2,…,n выберем точку xi*∈[xi−1,xi].xi*∈[xi−1,xi]. Затем постройте прямоугольник на интервале [xi−1,xi][xi−1,xi] высоты f(xi*)f(xi*) и ширины ∆x.∆x. Типичный прямоугольник показан на рис. 6.26(а). Когда этот прямоугольник вращается вокруг у -оси вместо диска или шайбы получаем цилиндрическую оболочку, как показано на следующем рисунке.
Рисунок 6,26 (а) Репрезентативный прямоугольник. (b) Когда этот прямоугольник вращается вокруг оси y, получается цилиндрическая оболочка. (c) Когда мы сложим все оболочки вместе, мы получим аппроксимацию исходного твердого тела.
Чтобы рассчитать объем этой оболочки, рассмотрите рисунок 6.27.
Рисунок 6,27 Расчет объема скорлупы.
Оболочка представляет собой цилиндр, поэтому ее объем равен площади поперечного сечения, умноженной на высоту цилиндра.
 Поперечные сечения представляют собой кольца (области в форме колец — по сути, круги с отверстием в центре) с внешним радиусом xixi и внутренним радиусом xi−1.xi−1. Таким образом, площадь поперечного сечения равна πxi2−πxi−12,πxi2−πxi−12. Высота цилиндра равна f(xi*).f(xi*). Тогда объем оболочки
Поперечные сечения представляют собой кольца (области в форме колец — по сути, круги с отверстием в центре) с внешним радиусом xixi и внутренним радиусом xi−1.xi−1. Таким образом, площадь поперечного сечения равна πxi2−πxi−12,πxi2−πxi−12. Высота цилиндра равна f(xi*).f(xi*). Тогда объем оболочкиVshell=f(xi*)(πxi2−πxi−12)=πf(xi*)(xi2−xi−12)=πf(xi*)(xi+xi−1)(xi−xi−1)=2πf (xi*)(xi+xi−12)(xi−xi−1).Vshell=f(xi*)(πxi2−πxi−12)=πf(xi*)(xi2−xi−12)=πf(xi *)(xi+xi−1)(xi−xi−1)=2πf(xi*)(xi+xi−12)(xi−xi−1).
Обратите внимание, что xi−xi−1=Δx,xi−xi−1=Δx, поэтому мы имеем
Vshell=2πf(xi*)(xi+xi−12)Δx.Vshell=2πf(xi*)(xi+xi−12)Δx.
Кроме того, xi+xi−12xi+xi−12 одновременно является серединой интервала [xi−1,xi][xi−1,xi] и средним радиусом оболочки, и мы можем аппроксимировать это значением xi*. хх*. Тогда у нас есть
Vshell≈2πf(xi*)xi*Δx.Vshell≈2πf(xi*)xi*Δx.
Другой способ представить это — сделать вертикальный разрез в оболочке, а затем открыть ее, чтобы сформировать плоскую пластину (рис.
 6.28).
6.28).Рисунок 6,28 (а) Сделайте вертикальный разрез в репрезентативной раковине. (b) Откройте скорлупу, чтобы сформировать плоскую пластину.
В действительности внешний радиус оболочки больше внутреннего радиуса, поэтому задний край пластины будет немного длиннее переднего края пластины. Однако мы можем аппроксимировать уплощенную оболочку плоской пластиной высотой f(xi*),f(xi*), шириной 2πxi*, 2πxi* и толщиной ΔxΔx (рис. 6.28). Таким образом, объем оболочки примерно равен объему плоской пластины. Умножая высоту, ширину и глубину тарелки, получаем 9.0042
Vshell≈f(xi*)(2πxi*)Δx,Vshell≈f(xi*)(2πxi*)Δx,
, это та же формула, что и раньше.
Чтобы вычислить объем всего твердого тела, мы затем складываем объемы всех оболочек и получаем
V≈∑i=1n(2πxi*f(xi*)Δx).V≈∑i=1n(2πxi*f(xi*)Δx).
Здесь у нас есть еще одна сумма Римана, на этот раз для функции 2πxf(x).2πxf(x). Принимая предел как n→∞n→∞, мы получаем
V=limn→∞∑i=1n(2πxi*f(xi*)Δx)=∫ab(2πxf(x))dx.
 V=limn→∞∑i=1n(2πxi*f(xi*)Δx) =∫ab(2πxf(x))dx.
V=limn→∞∑i=1n(2πxi*f(xi*)Δx) =∫ab(2πxf(x))dx.Это приводит к следующему правилу для метода цилиндрических оболочек.
Правило: метод цилиндрических оболочек
Пусть f(x)f(x) непрерывна и неотрицательна. Определим RR как область, ограниченную сверху графиком f(x),f(x), снизу осью x, осью x, слева линией x=a,x=a и справа линией x=b.x=b. Тогда объем тела вращения, образованного вращением RR вокруг оси y , равен
V=∫ab(2πxf(x))dx.V=∫ab(2πxf(x))dx.
(6.6)
Теперь рассмотрим пример.
Пример 6.12
Метод цилиндрических оболочек 1
Определим RR как область, ограниченную сверху графиком f(x)=1/xf(x)=1/x и снизу по оси xx по оси x на интервале [1 ,3].[1,3]. Найдите объем тела вращения, образованного вращением RR вокруг оси у.
Решение
Сначала мы должны построить область RR и связанное с ней тело вращения, как показано на следующем рисунке.

Рисунок 6,29 (a) Область RR под графиком f(x)=1/xf(x)=1/x на интервале [1,3].[1,3]. (b) Тело вращения, образованное вращением RR вокруг оси y.
Тогда объем твердого тела определяется выражением
(x))dx=∫13(2πx(1x))dx=∫132πdx=2πx|13=4πединиц3.
Контрольно-пропускной пункт 6.12
Определить R как область, ограниченную сверху графиком f(x)=x2f(x)=x2 и снизу x — ось на интервале [1,2].[1,2]. Найдите объем тела вращения, образованного вращением RR вокруг оси у.
Пример 6.13
Метод цилиндрических оболочек 2
Определим R как область, ограниченную сверху графиком f(x)=2x−x2f(x)=2x−x2 и снизу по оси xx-ось на интервале [0,2].[0,2]. Найдите объем тела вращения, образованного вращением RR вокруг оси у.
Решение
Сначала нарисуйте область RR и связанное с ней тело вращения, как показано на следующем рисунке.

Рисунок 6.30 (a) Область RR под графиком f(x)=2x−x2f(x)=2x−x2 на интервале [0,2].[0,2]. (b) Объем вращения, полученный при вращении RR вокруг оси y.
Тогда объем твердого тела определяется как
V=∫ab(2πxf(x))dx=∫02(2πx(2x−x2))dx=2π∫02(2×2−x3)dx=2π[2×33 −x44]|02=8π3единиц3.V=∫ab(2πxf(x))dx=∫02(2πx(2x−x2))dx=2π∫02(2×2−x3)dx=2π[2×33−x44]|02 =8π3единиц3.
Контрольно-пропускной пункт 6.13
Определить RR как область, ограниченную сверху графиком f(x)=3x−x2f(x)=3x−x2 и снизу осью xx на интервале [0,2].[0,2 ]. Найдите объем тела вращения, образованного вращением RR вокруг оси у.
Как и в случае метода диска и метода шайбы, мы можем использовать метод цилиндрических оболочек с телами вращения, вращающимися вокруг оси x, оси x, когда мы хотим проинтегрировать по y.y. Аналогичное правило для этого типа твердого тела приведено здесь.
Правило: Метод цилиндрических оболочек для тел вращения вокруг оси
xПусть g(y)g(y) непрерывна и неотрицательна.
 Определим QQ как область, ограниченную справа графиком g(y),g(y), слева осью y, осью y, внизу линией y=c,y=c и вверху линией y=d.y=d. Тогда объем тела вращения, образованного вращением QQ вокруг оси xx, равен
Определим QQ как область, ограниченную справа графиком g(y),g(y), слева осью y, осью y, внизу линией y=c,y=c и вверху линией y=d.y=d. Тогда объем тела вращения, образованного вращением QQ вокруг оси xx, равенV=∫cd(2πyg(y))dy.V=∫cd(2πyg(y))dy.
Пример 6.14
Метод цилиндрических оболочек для твердого тела, вращающегося вокруг оси
xОпределить QQ как область, ограниченную справа графиком g(y)=2yg(y)=2y и слева y-осьy-ось для y∈[0,4].y∈[0,4]. Найдите объем тела вращения, образованного вращением QQ вокруг оси x.
Решение
Во-первых, нам нужно изобразить область QQ и связанное с ней тело вращения, как показано на следующем рисунке.
Рисунок 6.31 (а) Область QQ слева от функции g(y)g(y) на интервале [0,4].[0,4]. (b) Тело вращения, образованное вращением QQ вокруг оси x.x-ось.
Обозначьте заштрихованную область Q.
 Q. Тогда объем твердого тела определяется как
Q. Тогда объем твердого тела определяется какV=∫cd(2πyg(y))dy=∫04(2πy(2y))dy=4π∫04y3/2dy=4π[2y5/25]|04=256π5единиц3. V=∫cd(2πyg(y))dy=∫04(2πy(2y))dy=4π∫04y3/2dy=4π[2y5/25]|04=256π5единиц3.
Контрольно-пропускной пункт 6.14
Определим QQ как область, ограниченную справа графиком g(y)=3/yg(y)=3/y и слева осью y для y∈[1,3]. у∈[1,3]. Найдите объем тела вращения, образованного вращением QQ вокруг оси абсцисс.
В следующем примере мы рассмотрим тело вращения, для которого график функции вращается вокруг линии, отличной от одной из двух координатных осей. Чтобы установить это, нам нужно вернуться к развитию метода цилиндрических оболочек. Напомним, что мы нашли объем одной из оболочек равным
.Vshell=f(xi*)(πxi2−πxi−12)=πf(xi*)(xi2−xi−12)=πf(xi*)(xi+xi−1)(xi−xi−1)=2πf (xi*)(xi+xi−12)(xi−xi−1).Vshell=f(xi*)(πxi2−πxi−12)=πf(xi*)(xi2−xi−12)=πf(xi *)(xi+xi−1)(xi−xi−1)=2πf(xi*)(xi+xi−12)(xi−xi−1).
Основан на оболочке с внешним радиусом xixi и внутренним радиусом xi−1.
 xi−1. Однако если мы повернем область вокруг линии, отличной от оси Y, у нас будет другой внешний и внутренний радиус. Предположим, например, что мы вращаем область вокруг линии x=−k,x=−k, где kk — некоторая положительная константа. Тогда внешний радиус оболочки равен xi+kxi+k, а внутренний радиус оболочки равен xi−1+k.xi−1+k. Подставляя эти члены в выражение для объема, мы видим, что при вращении плоской области вокруг линии x=−k,x=−k объем оболочки равен
xi−1. Однако если мы повернем область вокруг линии, отличной от оси Y, у нас будет другой внешний и внутренний радиус. Предположим, например, что мы вращаем область вокруг линии x=−k,x=−k, где kk — некоторая положительная константа. Тогда внешний радиус оболочки равен xi+kxi+k, а внутренний радиус оболочки равен xi−1+k.xi−1+k. Подставляя эти члены в выражение для объема, мы видим, что при вращении плоской области вокруг линии x=−k,x=−k объем оболочки равенVshell=2πf(xi*)((xi+k)+(xi−1+k)2)((xi+k)−(xi−1+k))=2πf(xi*)((xi+xi −22)+k)Δx.Vshell=2πf(xi*)((xi+k)+(xi−1+k)2)((xi+k)−(xi−1+k))=2πf(xi *)((xi+xi−22)+k)∆x.
Как и прежде, мы замечаем, что xi+xi−12xi+xi−12 является серединой интервала [xi−1,xi][xi−1,xi] и может быть аппроксимировано с помощью xi*.xi*. Тогда примерный объем оболочки
Vshell≈2π(xi*+k)f(xi*)Δx.Vshell≈2π(xi*+k)f(xi*)Δx.
Дальнейшее развитие продолжается, как и прежде, и мы видим, что
V=∫ab(2π(x+k)f(x))dx.V=∫ab(2π(x+k)f(x))dx.
Мы также можем вращать область вокруг других горизонтальных или вертикальных линий, таких как вертикальная линия в правой полуплоскости.
 В каждом случае формула объема должна быть скорректирована соответствующим образом. В частности, x-termx-term в интеграле необходимо заменить выражением, представляющим радиус оболочки. Чтобы увидеть, как это работает, рассмотрим следующий пример.
В каждом случае формула объема должна быть скорректирована соответствующим образом. В частности, x-termx-term в интеграле необходимо заменить выражением, представляющим радиус оболочки. Чтобы увидеть, как это работает, рассмотрим следующий пример.Пример 6.15
Область революции вращается вокруг линии
Определить RR как область, ограниченную сверху графиком f(x)=xf(x)=x и снизу осью xx на интервале [1,2].[1,2]. Найдите объем тела вращения, образованного вращением RR вокруг линии x=−1.x=−1.
Решение
Сначала начертите область RR и связанное с ней тело вращения, как показано на следующем рисунке.
Рисунок 6.32 (a) Область RR между графиком f(x)f(x) и осью x на интервале [1,2].[1,2]. (b) Тело вращения, образованное вращением RR вокруг линии x=−1.x=−1.
Обратите внимание, что радиус оболочки равен x+1.x+1. Тогда объем твердого тела определяется как
V=∫12(2π(x+1)f(x))dx=∫12(2π(x+1)x)dx=2π∫12(x2+x) dx=2π[x33+x22]|12=23π3единиц3.
 V=∫12(2π(x+1)f(x))dx=∫12(2π(x+1)x)dx=2π∫12(x2+ x)dx=2π[x33+x22]|12=23π3единиц3.
V=∫12(2π(x+1)f(x))dx=∫12(2π(x+1)x)dx=2π∫12(x2+ x)dx=2π[x33+x22]|12=23π3единиц3.Контрольно-пропускной пункт 6.15
Определить RR как область, ограниченную сверху графиком f(x)=x2f(x)=x2 и снизу осью xx на интервале [0,1].[0,1]. Найдите объем тела вращения, образованного вращением RR вокруг линии x=−2.x=−2.
В качестве последнего примера в этом разделе рассмотрим объем тела вращения, область вращения которого ограничена графиками двух функций.
Пример 6.16
Область вращения, ограниченная графиками двух функций
Определим RR как область, ограниченную сверху графиком функции f(x)=xf(x)=x и снизу графиком функции g(x )=1/xg(x)=1/x на интервале [1,4].[1,4]. Найдите объем тела вращения, образованного вращением RR вокруг оси у.
Решение
Сначала начертите область RR и связанное с ней тело вращения, как показано на следующем рисунке.
Рисунок 6.
 33
(a) Область RR между графиком f(x)f(x) и графиком g(x)g(x) на интервале [1,4].[1,4]. (b) Тело вращения, образованное вращением RR вокруг оси y.
33
(a) Область RR между графиком f(x)f(x) и графиком g(x)g(x) на интервале [1,4].[1,4]. (b) Тело вращения, образованное вращением RR вокруг оси y.Обратите внимание, что осью вращения является ось Y, ось Y, поэтому радиус оболочки задается просто x.x. Нам не нужно вносить какие-либо коррективы в x — член нашего интеграла. Однако высота оболочки определяется как f(x)−g(x),f(x)−g(x), поэтому в этом случае нам нужно скорректировать член f(x)f(x) подынтегральная функция. Тогда объем твердого тела равен
V=∫14(2πx(f(x)−g(x))dx=∫14(2πx(x−1x))dx=2π∫14(x3/2 −1)dx=2π[2×5/25−x]|14=94π5единиц3.V=∫14(2πx(f(x)−g(x))dx=∫14(2πx(x−1x))dx= 2π∫14(x3/2−1)dx=2π[2×5/25−x]|14=94π5единиц3.
Контрольно-пропускной пункт 6.16
Определить RR как область, ограниченную сверху графиком f(x)=xf(x)=x и снизу графиком g(x)=x2g(x)=x2 на интервале [0,1]. [0,1]. Найдите объем тела вращения, образованного вращением RR вокруг оси у.
Какой метод следует использовать?
Мы изучили несколько методов нахождения объема тела вращения, но как узнать, какой из них использовать? Часто все сводится к выбору того, какой интеграл проще всего вычислить.
 На рис. 6.34 показаны различные подходы для тел вращения вокруг оси х. Вам решать разработать аналогичную таблицу для тел вращения вокруг оси y.ось y.
На рис. 6.34 показаны различные подходы для тел вращения вокруг оси х. Вам решать разработать аналогичную таблицу для тел вращения вокруг оси y.ось y.Рисунок 6.34
Давайте взглянем на пару дополнительных задач и выберем лучший подход к их решению.
Пример 6.17
Выбор наилучшего метода
Для каждой из следующих задач выберите наилучший метод для нахождения объема тела вращения, образованного вращением заданной области вокруг оси x, оси x, и подставьте интеграл к найти объем (интеграл не вычислять).
- Область, ограниченная графиками y=x,y=x,y=2−x,y=2−x и осью x.x-ось.
- Область, ограниченная графиками y=4x−x2y=4x−x2 и осью x.x-ось.
Решение
- Сначала нарисуйте область и тело вращения, как показано.
Рисунок 6,35 (а) Область RR, ограниченная двумя линиями и осью абсцисс. (b) Тело вращения, образованное вращением RR вокруг оси x.
 x-ось.
x-ось.
Глядя на область, если мы хотим интегрировать по x,x, нам придется разбить интеграл на две части, потому что у нас есть разные функции, ограничивающие область по [0,1][0,1] и [1,2].[1,2]. В этом случае, используя дисковый метод, мы получили быV=∫01(πx2)dx+∫12(π(2−x)2)dx.V=∫01(πx2)dx+∫12(π(2−x)2)dx.
Если бы мы использовали вместо этого метод оболочки, мы использовали бы функции yy для представления кривых, получаяV=∫01(2πy[(2−y)−y])dy=∫01(2πy[2−2y] )dy.V=∫01(2πy[(2−y)−y])dy=∫01(2πy[2−2y])dy.
Ни один из этих интегралов не является особенно обременительным, но поскольку метод оболочки требует только одного интеграла, а подынтегральная функция требует меньшего упрощения, в данном случае, вероятно, следует использовать метод оболочки. - Сначала нарисуйте область и тело вращения, как показано.
Рисунок 6,36 (а) Область RR между кривой и осью абсцисс. (b) Тело вращения, образованное вращением RR вокруг оси x.x-ось.

Глядя на область, было бы проблематично определить горизонтальный прямоугольник; область ограничена слева и справа одной и той же функцией. Поэтому можно отбросить метод снарядов. Твердое тело не имеет полости посередине, поэтому мы можем использовать метод дисков. ТогдаV=∫04π(4x−x2)2dx.V=∫04π(4x−x2)2dx.
Контрольно-пропускной пункт 6.17
Выберите наилучший метод для нахождения объема тела вращения, образованного вращением данной области вокруг оси x, оси x, и установите интеграл для нахождения объема (интеграл не вычислять): область ограничена графиками y=2−x2y=2−x2 и y=x2.y=x2.
Раздел 6.3 Упражнения
В следующих упражнениях найдите объем, возникающий при вращении области между двумя кривыми вокруг заданной оси. Используйте как метод оболочки, так и метод шайбы. Используйте технологию для построения графиков функций и нарисуйте типичный срез вручную.
114.

[T] Ограничен кривыми y=3x,x=0,y=3x,x=0 и y=3y=3, вращающимися вокруг оси y.ось y.
115.
[T] Ограничен кривыми y=3x,y=0,andx=3y=3x,y=0,andx=3, вращающимися вокруг оси y.ось y.
116.
[T] Ограничен кривыми y=3x,y=0,andy=3y=3x,y=0,andy=3, вращающимися вокруг оси x.ось x.
117.
[T] Ограничен кривыми y=3x,y=0,andx=3y=3x,y=0,andx=3, вращающимися вокруг оси x.ось x.
118.
[T] Ограничен кривыми y=2×3,y=0,andx=2y=2×3,y=0,andx=2, вращающимися вокруг оси y.ось y.
119.
[T] Ограничен кривыми y=2×3,y=0,andx=2y=2×3,y=0,andx=2, вращающимися вокруг оси x.ось x.
В следующих упражнениях используйте оболочки, чтобы найти объемы заданных твердых тел.
 Обратите внимание, что повернутые области лежат между кривой и осью xx и вращаются вокруг оси y.ось y.
Обратите внимание, что повернутые области лежат между кривой и осью xx и вращаются вокруг оси y.ось y.120.
y=1−x2,x=0,andx=1y=1−x2,x=0,andx=1
121.
y=5×3,x=0 иx=1y=5×3,x=0 иx=1
122.
y=1x,x=1,andx=100y=1x,x=1,andx=100
123.
y=1−x2,x=0,andx=1y=1−x2,x=0,andx=1
124.
y=11+x2,x=0 иx=3y=11+x2,x=0 иx=3
125.
y=sinx2,x=0,andx=πy=sinx2,x=0,andx=π
126.
y=11−x2,x=0,x=12y=11−x2,x=0,x=12
127.
y=x,x=0 иx=1y=x,x=0 иx=1
128.
y=(1+x2)3,x=0 иx=1y=(1+x2)3,x=0 иx=1
129.
y=5×3−2×4,x=0 иx=2y=5×3−2×4,x=0 иx=2
В следующих упражнениях используйте оболочки, чтобы найти объем, созданный вращением областей между заданной кривой и y=0y=0 вокруг оси x.
 x.
x.130.
y=1−x2,x=0,x=1y=1−x2,x=0,x=1 и x -ось
131.
y=x2,x=0,x=2y=x2,x=0,x=2 и x -ось
132.
y=x32,x=0,x=2,y=x32,x=0,x=2 и x -ось
133.
y=2×2,x=1,x=2,y=2×2,x=1,x=2 и x -ось
134.
х=11+у2,у=1,и=4х=11+у2,у=1,иу=4
135.
x=1+y2y,y=1,y=4,x=1+y2y,y=1,y=4 и y -ось
136.
x=уютно,x=0,andy=πx=уютно,x=0,andy=π
137.
х=у3-2у2,х=0,х=9х=у3-2у2,х=0,х=9
138.
x=y+1,x=1,x=3,x=y+1,x=1,x=3 и x -ось
139.

x=27y3andx=3y4x=27y3andx=3y4
В следующих упражнениях найдите объем, возникающий при вращении области между кривыми вокруг заданной оси.
140.
y=3−x,y=0,x=0,andx=2y=3−x,y=0,x=0,andx=2 повернуты вокруг оси y.ось y.
141.
y=x3,x=0,andy=8y=x3,x=0,andy=8 вращается вокруг оси y.ось y.
142.
y=x2,y=x,y=x2,y=x, вращается вокруг оси y.ось y.
143.
y=x,y=0,andx=1y=x,y=0,andx=1 повернуты вокруг линии x=2.x=2.
144.
y=14−x,x=1,x=2andy=0y=14−x,x=1,x=2andy=0 вращается вокруг линии x=4.x=4.
145.
y=xandy=x2y=xandy=x2 вращается вокруг оси y.ось y.
146.
y=xandy=x2y=xandy=x2 вращается вокруг линии x=2.x=2.
147.

x=y3,x=1y,x=1,andx=2x=y3,x=1y,x=1,andx=2 повернуты вокруг оси x.ось x.
148.
x=y2andy=xx=y2andy=x вращается вокруг линии y=2.y=2.
149.
[T] Слева от x=sin(πy),x=sin(πy), справа от y=x,y=x, вокруг оси y.ось y.
В следующих упражнениях используйте технологию построения графика области. Определите, какой метод, по вашему мнению, проще всего использовать для вычисления объема, генерируемого при вращении функции вокруг заданной оси. Затем используйте выбранный вами метод, чтобы найти объем.
150.
[T] y=x2y=x2 и y=4xy=4x повернуты вокруг оси y.ось y.
151.
[T] y=cos(πx),y=sin(πx),x=14,andx=54y=cos(πx),y=sin(πx),x=14,andx=54 вращается вокруг y-ось.y-ось. Это упражнение требует продвинутой техники. Вы можете использовать технологию для выполнения интеграции.

152.
[T] y=x2−2x,x=2,andx=4y=x2−2x,x=2,andx=4 вращается вокруг оси y.ось y.
153.
[T] y=x2−2x,x=2,andx=4y=x2−2x,x=2,andx=4 вращается вокруг оси x.x-ось.
154.
[T] y=3×3−2,y=x,andx=2y=3×3−2,y=x,andx=2 вращается вокруг оси x.x-ось.
155.
[T] y=3×3−2,y=x,andx=2y=3×3−2,y=x,andx=2 вращается вокруг оси y.ось y.
156.
[T] x=sin(πy2)x=sin(πy2) и x=2yx=2y вращается вокруг оси x.x-ось.
157.
[T] x=y2,x=y2−2y+1,andx=2x=y2,x=y2−2y+1,andx=2 повернуты вокруг оси y.ось y.
В следующих упражнениях используйте метод оболочек для аппроксимации объемов некоторых обычных объектов, изображенных на прилагаемых рисунках.

158.
Методом оболочек найдите объем сферы радиусом r.r.
159.
Методом оболочек найдите объем конуса радиусом rr и высотой h.h.
160.
Используйте метод оболочек, чтобы найти объем эллипсоида (x2/a2)+(y2/b2)=1(x2/a2)+(y2/b2)=1, повернутого вокруг оси x.ось x .
161.
Методом оболочек найдите объем цилиндра радиусом rr и высотой h.h.
162.
Используйте метод ракушек, чтобы найти объем бублика, который образуется при вращении окружности x2+y2=4×2+y2=4 вокруг линии x=4.x=4.
163.
Рассмотрим область, заключенную в графики y=f(x),y=1+f(x),x=0,y=0,y=f(x),y=1+f(x), х=0,у=0 и х=а>0.х=а>0. Каков объем твердого тела, образованного при вращении этой области вокруг оси y? оси y? Предположим, что функция определена на интервале [0,a].



 Мы изготавливаем обечайки толщиной стенки до 40 мм.
Мы изготавливаем обечайки толщиной стенки до 40 мм.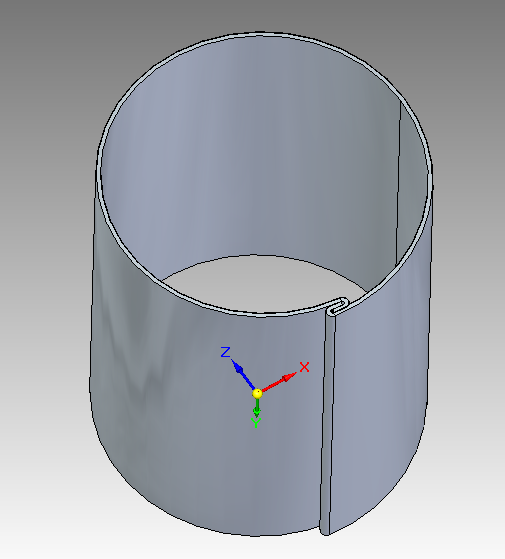
 \nonumber \]
\nonumber \] \) 92\) и ниже по оси \(x\) на интервале \([0,1]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг линии \(x=−2\).
\) 92\) и ниже по оси \(x\) на интервале \([0,1]\). Найдите объем тела вращения, образованного вращением \(R\) вокруг линии \(x=−2\).
 Рисунок \(\PageIndex{10}\) описывает различные подходы для тел вращения вокруг оси \(x\). Вам предстоит разработать аналогичную таблицу для тел вращения вокруг оси \(y\).
Рисунок \(\PageIndex{10}\) описывает различные подходы для тел вращения вокруг оси \(x\). Вам предстоит разработать аналогичную таблицу для тел вращения вокруг оси \(y\). В этом случае, используя дисковый метод, мы получили бы 91_0 2π\,y[2−2y]\,dy. \nonumber \]
В этом случае, используя дисковый метод, мы получили бы 91_0 2π\,y[2−2y]\,dy. \nonumber \] 9b_a\left(2π\,x\,f(x)\right)\,dx\)
9b_a\left(2π\,x\,f(x)\right)\,dx\) org/details/books/calculus-volume-1
org/details/books/calculus-volume-1 Кроме того, специфическая геометрия твердого тела иногда делает метод использования цилиндрических оболочек более привлекательным, чем метод шайбы. В последней части этого раздела мы рассмотрим все методы определения объема, которые мы изучили, и изложим некоторые рекомендации, которые помогут вам определить, какой метод использовать в той или иной ситуации.
Кроме того, специфическая геометрия твердого тела иногда делает метод использования цилиндрических оболочек более привлекательным, чем метод шайбы. В последней части этого раздела мы рассмотрим все методы определения объема, которые мы изучили, и изложим некоторые рекомендации, которые помогут вам определить, какой метод использовать в той или иной ситуации. х. (b) Тело вращения, сформированное, когда область вращается вокруг оси y. ось y.
х. (b) Тело вращения, сформированное, когда область вращается вокруг оси y. ось y. Поперечные сечения представляют собой кольца (области в форме колец — по сути, круги с отверстием в центре) с внешним радиусом xixi и внутренним радиусом xi−1.xi−1. Таким образом, площадь поперечного сечения равна πxi2−πxi−12,πxi2−πxi−12. Высота цилиндра равна f(xi*).f(xi*). Тогда объем оболочки
Поперечные сечения представляют собой кольца (области в форме колец — по сути, круги с отверстием в центре) с внешним радиусом xixi и внутренним радиусом xi−1.xi−1. Таким образом, площадь поперечного сечения равна πxi2−πxi−12,πxi2−πxi−12. Высота цилиндра равна f(xi*).f(xi*). Тогда объем оболочки 6.28).
6.28). V=limn→∞∑i=1n(2πxi*f(xi*)Δx) =∫ab(2πxf(x))dx.
V=limn→∞∑i=1n(2πxi*f(xi*)Δx) =∫ab(2πxf(x))dx.

 Определим QQ как область, ограниченную справа графиком g(y),g(y), слева осью y, осью y, внизу линией y=c,y=c и вверху линией y=d.y=d. Тогда объем тела вращения, образованного вращением QQ вокруг оси xx, равен
Определим QQ как область, ограниченную справа графиком g(y),g(y), слева осью y, осью y, внизу линией y=c,y=c и вверху линией y=d.y=d. Тогда объем тела вращения, образованного вращением QQ вокруг оси xx, равен Q. Тогда объем твердого тела определяется как
Q. Тогда объем твердого тела определяется как xi−1. Однако если мы повернем область вокруг линии, отличной от оси Y, у нас будет другой внешний и внутренний радиус. Предположим, например, что мы вращаем область вокруг линии x=−k,x=−k, где kk — некоторая положительная константа. Тогда внешний радиус оболочки равен xi+kxi+k, а внутренний радиус оболочки равен xi−1+k.xi−1+k. Подставляя эти члены в выражение для объема, мы видим, что при вращении плоской области вокруг линии x=−k,x=−k объем оболочки равен
xi−1. Однако если мы повернем область вокруг линии, отличной от оси Y, у нас будет другой внешний и внутренний радиус. Предположим, например, что мы вращаем область вокруг линии x=−k,x=−k, где kk — некоторая положительная константа. Тогда внешний радиус оболочки равен xi+kxi+k, а внутренний радиус оболочки равен xi−1+k.xi−1+k. Подставляя эти члены в выражение для объема, мы видим, что при вращении плоской области вокруг линии x=−k,x=−k объем оболочки равен В каждом случае формула объема должна быть скорректирована соответствующим образом. В частности, x-termx-term в интеграле необходимо заменить выражением, представляющим радиус оболочки. Чтобы увидеть, как это работает, рассмотрим следующий пример.
В каждом случае формула объема должна быть скорректирована соответствующим образом. В частности, x-termx-term в интеграле необходимо заменить выражением, представляющим радиус оболочки. Чтобы увидеть, как это работает, рассмотрим следующий пример. V=∫12(2π(x+1)f(x))dx=∫12(2π(x+1)x)dx=2π∫12(x2+ x)dx=2π[x33+x22]|12=23π3единиц3.
V=∫12(2π(x+1)f(x))dx=∫12(2π(x+1)x)dx=2π∫12(x2+ x)dx=2π[x33+x22]|12=23π3единиц3. 33
(a) Область RR между графиком f(x)f(x) и графиком g(x)g(x) на интервале [1,4].[1,4]. (b) Тело вращения, образованное вращением RR вокруг оси y.
33
(a) Область RR между графиком f(x)f(x) и графиком g(x)g(x) на интервале [1,4].[1,4]. (b) Тело вращения, образованное вращением RR вокруг оси y. На рис. 6.34 показаны различные подходы для тел вращения вокруг оси х. Вам решать разработать аналогичную таблицу для тел вращения вокруг оси y.ось y.
На рис. 6.34 показаны различные подходы для тел вращения вокруг оси х. Вам решать разработать аналогичную таблицу для тел вращения вокруг оси y.ось y. x-ось.
x-ось.

 Обратите внимание, что повернутые области лежат между кривой и осью xx и вращаются вокруг оси y.ось y.
Обратите внимание, что повернутые области лежат между кривой и осью xx и вращаются вокруг оси y.ось y. x.
x.

/1-700x700.jpg)

