|
Основные таблицы и графики, необходимые для механических расчетов Таблица 1 – Поправочный коэффициент η к нормативным допускаемым напряжениям
Таблица 2 – Нормативное допускаемое напряжение σ*
Таблица 3 – Определение расчетного давления р
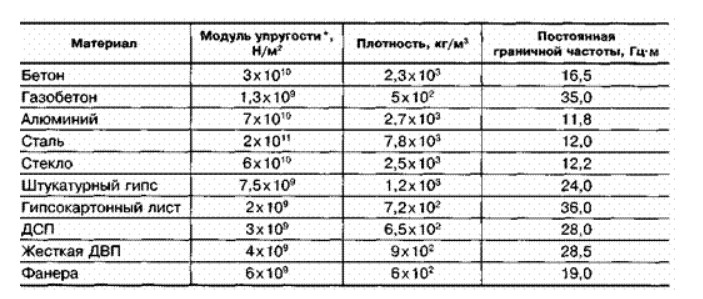
Таблица 4 – Модуль продольной упругости Е
Таблица 5 – Предел текучести материала
Таблица 6 – Шаг трубок при размещении их по вершинам равносторонних треугольников
Рисунок 1 – График для определения коэффициента Рисунок 2 – График для определения коэффициента k, зависящего от гибкости ребра Таблица 7 – Физические свойства черных металлов и сплавов Таблица 8 – Сортамент труб из теплостойкой стали 12ХМ Таблица 9 – Сортамент труб из углеродистой стали 10 и 20 Таблица 10 – Сортамент труб из высоколегированных сталей Таблица 11 – Линзы для компенсаторов из углеродистой стали* * Примечание Если МПа, то диаметр линзового компенсатора определяется по формуле где D – внутренний диаметр аппарата, мм — давление в межтрубном пространстве, МПа — допускаемое напряжение материала корпуса, МПа Таблица 12 – Коэффициенты при расчете линзового компенсатора
Таблица 13 – Величина удельного ветрового напора q
Рисунок 3 – График для определения коэффициента пульсации Рисунок 4 – График для определения коэффициента динамичности Рисунок 5 – График к расчету фундаментных болтов Таблица 14 – Коэффициенты ,
Таблица 15 – Масса колпачковой тарелки
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Круг сталевий гарячекатаний 80 мм сталь 09Г2С — купити за найкращою ціною в Запоріжжі від компанії «ТОВ фірма «Тера»»
Наявність документів
Знак Наявність документів означає, що компанія завантажила свідоцтво про державну реєстрацію для підтвердження свого юридичного статусу компанії або фізичної особи-підприємця.
У компанії підключені електронні платежі. Тепер ви можете купити будь-який товар не покидаючи сайту.
Опис
Характеристики
Інформація для замовлення
Круг гарячекатаний 80 мм сталь 09Г2С міра 6 м
Сталь конструкційна низьколегована для зварних конструкцій
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Матеріал | Документ | Замінник 1 | Замінник 2 | Замінник 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Сталь 09Г2С | ГОСТ 19281-89 |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Методика испытаний трубопроводных сталей на стойкость к канавочной коррозии | Виктор Иванович Болобов
Реферат
Предложена методика испытаний трубопроводных сталей, исходя из того, что для разрушения труб промысловых нефтепроводов по механизму канавочной коррозии необходимо одновременное выполнение таких условий, как возникновение царапин на нижней образующей трубы, перерастающих со временем в канал в виде канавки, обязательно обогащение эмульсии кислородом, наличие металла стенки трубы в напряженном состоянии, наличие хлор-иона в водонефтяной эмульсии. Испытания предлагается проводить в 3 % водном растворе NaCl при непрерывной аэрации воздухом на гнутых пластинах 150×15×3 мм из анализируемой стали, средняя часть которых находится под действием остаточных напряжений σост, близким к уровню максимальных эквивалентных напряжений σ экв в стенке нефтепровода, с наличием выреза на этом участке с внутренней стороны пластины как инициатора дополнительных механических напряжений. По значению модуля нормальной упругости анализируемой стали рассчитывают степень остаточной деформации упругопластического тела из этого материала, соответствующую величине необходимый угол отклонения, после чего на них наносится рез. После выдержки пластин в агрессивной среде для каждой из них анализируется увеличение глубины реза в результате коррозии стенок коррозионно-активной средой, из чего рассчитывается скорость стали К по механизму канавочной коррозии. с учетом продолжительности испытаний. Приведены значения скорости коррозии для двух марок трубной стали, определенные по предлагаемой методике.
Испытания предлагается проводить в 3 % водном растворе NaCl при непрерывной аэрации воздухом на гнутых пластинах 150×15×3 мм из анализируемой стали, средняя часть которых находится под действием остаточных напряжений σост, близким к уровню максимальных эквивалентных напряжений σ экв в стенке нефтепровода, с наличием выреза на этом участке с внутренней стороны пластины как инициатора дополнительных механических напряжений. По значению модуля нормальной упругости анализируемой стали рассчитывают степень остаточной деформации упругопластического тела из этого материала, соответствующую величине необходимый угол отклонения, после чего на них наносится рез. После выдержки пластин в агрессивной среде для каждой из них анализируется увеличение глубины реза в результате коррозии стенок коррозионно-активной средой, из чего рассчитывается скорость стали К по механизму канавочной коррозии. с учетом продолжительности испытаний. Приведены значения скорости коррозии для двух марок трубной стали, определенные по предлагаемой методике. Сравнение полученных значений К позволяет сделать вывод о более высокой стойкости к канавочной коррозии стали 09.Сталь Г2С.
Сравнение полученных значений К позволяет сделать вывод о более высокой стойкости к канавочной коррозии стали 09.Сталь Г2С.
Ключевые слова:
промысловые нефтепроводыметодика испытанийтрубопроводные сталистойкость к канавочной коррозиискорость коррозиимеханохимическое воздействие общий мировой энергетический баланс. Обеспечение бесперебойного транспорта нефти и нефтесодержащих продуктов по магистральным и промысловым трубопроводам является важной научно-технической задачей. Коррозия металлов является причиной аварий во многих отраслях промышленности, в том числе в нефтегазовой отрасли. Подсчитано, что в России ежегодно происходит более 80 000 аварий на трубопроводах [2] и резервуарах [34], и большинство из них связано с коррозионными повреждениями [8]. Опыт эксплуатации промысловых трубопроводов показывает, что основной причиной аварий является коррозия внутренней поверхности нижней образующей трубы, возникающая при перекачивании по трубопроводу водонефтяных эмульсий с тяжелой минерализованной водой, содержащей твердые абразивные частицы [5]. Этот вид коррозии называют канавочной коррозией из-за специфического вида места разрушения, напоминающего струйку, текущую по дну трубы (рис.1).
Этот вид коррозии называют канавочной коррозией из-за специфического вида места разрушения, напоминающего струйку, текущую по дну трубы (рис.1).
Рис.1. Типовой вид промыслового трубопровода, пораженного канавочной коррозией
Существует множество работ по коррозии канавок, например. [4, 9, 14], но механизм этого процесса и факторы, влияющие на его интенсивность, окончательно не установлены. В частности, это касается влияния напряженного состояния трубопровода на скорость коррозионного повреждения металла трубы и роль канавки в коррозионном процессе [3, 25]. Как показывает практика эксплуатации промысловых трубопроводов, существует ряд разработанных способов защиты (установка в участок трубопровода различных устройств, турбулизирующих поток эмульсии [12], нанесение ингибиторов [14], защитное покрытие внутренней поверхности трубы [16], применение установок предварительного водоотвода и др.) проблема канавочной коррозии в России и мире еще далека от полного решения. В наибольшей степени это актуально для длительно эксплуатируемых промысловых трубопроводов, где участки стальных труб, поврежденные канавочной коррозией, приходится периодически заменять новыми, требующими замены через некоторое время.
В данной работе предложена методика коррозионных лабораторных испытаний сталей [11] в условиях, моделирующих возможное межпромысловое повреждение стенки трубопровода при канавочной коррозии, которая позволяет подобрать стойкие к канавочной коррозии составы из существующих и инженерных трубопроводных сталей и в дальнейшем рекомендовать данные составы для использования в промысловых трубопроводах. Другим применением методики является изучение влияния напряженного состояния и наличия надреза на напряженной конструкции, имитирующего след канавочной коррозии, на скорость коррозии металлической конструкции в реакционной среде. Методика не предназначена для определения стойкости трубопроводных сталей в серосодержащих средах [24, 28, 32], а также в условиях, способствующих коррозии сталей под напряжением [25, 30, 33] и коррозионному растрескиванию под напряжением [22, 27]. , 29] в связи с существенными различиями в механизмах этих процессов.
Постановка задачи
При разработке методики предполагалось, что канавочная коррозия промысловых трубопроводов возникает при одновременном выполнении следующих основных условий:
- разделение водонефтяной эмульсии с промывкой водной фракцией образующая трубы;
- наличие растворенного кислорода в воде, контактирующей с металлом, в концентрации, достаточной для обеспечения электрохимической коррозионной реакции металла трубы с анодным контролем.
 (Это может происходить, например, при получении водонефтяных эмульсий с использованием пластовой воды, обогащенной кислородом, или при интенсивном перемешивании водонефтяной эмульсии в контакте с воздухом). Только при этом условии уровень напряжения трубы может влиять на скорость коррозии металла;
(Это может происходить, например, при получении водонефтяных эмульсий с использованием пластовой воды, обогащенной кислородом, или при интенсивном перемешивании водонефтяной эмульсии в контакте с воздухом). Только при этом условии уровень напряжения трубы может влиять на скорость коррозии металла; - наличие коррозионно-активных примесей в воде водонефтяных эмульсий, поступающих из пластовой воды, наиболее реакционноспособным из которых является хлор-ион [13] (влияние аниона S 2– аниона в данном методология) и высокоабразивные твердые частицы;
- воздействие растягивающих напряжений на стенку трубы, способствующее выходу ионов железа из стали в водный раствор на анодной фазе процесса и, как следствие, интенсификация процесса коррозии металла трубы;
- появление царапин на нижней образующей трубы в результате истирания твердыми частицами, содержащимися в эмульсии, перерастающих со временем в канавку, металл стенок и дна которой испытывает дополнительные растягивающие напряжения, максимальные в металле нижней части [4, 14, 26].

Методика
Для выполнения указанных условий предлагается испытывать стали на стойкость к канавочной коррозии в кислородсодержащей водно-хлоридной среде, на образцах, подвергнутых растягивающим напряжениям, близким к уровню эквивалентных напряжений в трубе, с канавкой вырезать на них по следующей методике.
Подготовка к испытаниям
Оценивается величина максимальных эквивалентных напряжений, возникающих в стенке трубы анализируемого промыслового трубопровода при перекачке водонефтяной эмульсии с учетом наличия на ней восходящих и нисходящих участков, вызывающих изгиб трубопровод [10, 23]:
σэкв =(σ1 + σ3)2 – (σ1+ σ3)σ2 + σ22,
где σ 1 – кольцевые напряжения от давления внутренней среды, МПа; σ 2 – продольные напряжения от изгибов трубопровода, МПа; о 3 – напряжения технологического происхождения, остающиеся в стенке после изготовления трубы, МПа [6, 19].
Для восходящего участка трубопровода 219×8 мм с радиусом изгиба 219 м, как одного из основных в номенклатуре промысловых трубопроводов, при рабочем давлении 4 МПа и температуре перекачиваемой эмульсии 60 °С значения σ 1 , σ 2 , σ 3 составляют 51, 95 и 35 МПа, параметр σ eqv имеет значение ~ 160 МПа, которое и использовалось в расчетах.
Рис.2. Графическая интерпретация решения задачи нахождения остаточного напряжения в упругопластическом теле σ el – напряжение, которое создалось бы в теле при условии идеальной упругости его материала; σ акт – фактическое напряжение, соответствующее заданному значению остаточной деформации на диаграмме растяжения материала
Листы размером 150×15×3 мм вырезают поперек направления прокатки (оси трубы) из прокатных трубопроводных сталей, используемых для изготовления сварных труб промысловых трубопроводов, или из тела трубы, в случае получения труб прокаткой. Пластины гнут в зажимах до остаточного прогиба, обеспечивающего остаточные напряжения σ res в средней, пластически деформированной дугообразной части пластин, близкой к σ eqv в трубе. Таким образом, как доказано в [35], на внутренней стороне пластин это растягивающие остаточные напряжения, а на внешней – напряжения сжатия. Условие равенства σ рез = σ экв достигается обеспечением металла в средней части пластины необходимой степени остаточной деформации ε рез , которая согласно теореме Генки [18] (рис. 2) для упругих -пластичность тела соответствует значению σ RES :
2) для упругих -пластичность тела соответствует значению σ RES :
ε RES = σ RES / E , (1)
, где E — Модуль нормальной эластичности для проанализированной стали.
Учитывая, что для всех трубопроводных сталей значение Е существенно не отличается (200 ГПа), требуемый уровень остаточных напряжений σ рез = σ экв = 160 МПа в упругопластическом теле из этих сталей, рассмотренном в примере, достигается при степени остаточной деформации металла ε рез ~ 0,0008 или 0,08 %.
Степень остаточной деформации ε res , воспринимаемой металлом в средней части дугообразных пластин, оценивается по радиусу окружности R, которую можно вписать в эту дугообразную часть (рис.3) . Значения ε рез и R относятся друг к другу
R=rεрез, (2)
где r – расстояние от нейтральной кромки пластины , мм.
В соответствии с выражением (2) при r = 1,5 мм требуемый уровень ε res = 0,0008 достигается загибанием средней части пластин до формы вписанной окружности с радиусом R ~ 1,8 м , что для пластин заданной геометрии (150×15 мм) соответствует прогибу пластины Н φ 8 мм.
После гибки пластин до достижения радиусом R требуемого значения принимают, что металл средней пластически деформируемой части испытывает те же остаточные напряжения, что и металл трубы промыслового трубопровода.
Дискообразным резцом толщиной 1 мм с режущей частью в виде полусферы радиусом 0,5 мм посередине пластин с внутренней стороны делают поперечный надрез глубиной ~ 0,2 мм и примерно канавкой -форма на нижней образующей трубопровода. Такой надрез на напряженной конструкции служит концентратором дополнительных растягивающих напряжений в окружающем металле [14, 17, 31] и, как можно заключить, должен интенсифицировать скорость коррозии. Например, при пропиле глубиной 0,2 мм на криволинейной пластине рассматриваемой конфигурации с σ res = 160 МПа В металле дна реза возникает остаточное напряжение, равное 200 МПа.
С помощью оптического микроскопа ЛабоМет-1 с шагом шкалы фокусных расстояний М = 0,003 мм определяют точную глубину реза в фиксированных точках. Для этого срез по всей его длине оптически делится на равные участки, т.е. 1 мм в длину. Положение граничных точек ( n = 13) фиксируют и для каждой из них определяют разность фокусных расстояний в делениях от дна реза до поверхности пластины вблизи реза вращением барабана точной подстройки Δ I = I bt – I sf с соответствующим пересчетом Δ I (используя M ) к исходной глубине резания в точке H 4. . Для предотвращения изменения фокусного расстояния до поверхности пластины вблизи реза в результате воздействия агрессивной среды эту поверхность перед коррозионными испытаниями покрывают защитным ацетатным лаком Ice Color.
Для этого срез по всей его длине оптически делится на равные участки, т.е. 1 мм в длину. Положение граничных точек ( n = 13) фиксируют и для каждой из них определяют разность фокусных расстояний в делениях от дна реза до поверхности пластины вблизи реза вращением барабана точной подстройки Δ I = I bt – I sf с соответствующим пересчетом Δ I (используя M ) к исходной глубине резания в точке H 4. . Для предотвращения изменения фокусного расстояния до поверхности пластины вблизи реза в результате воздействия агрессивной среды эту поверхность перед коррозионными испытаниями покрывают защитным ацетатным лаком Ice Color.
Проведение испытаний
Пластины помещают в термостат, заполненный 3 % водным раствором NaCl как типовую коррозионно-активную среду, используемую как в коррозионных исследованиях, как отечественных [5, 15, 20], так и зарубежных [21], для имитации состав водной составляющей водонефтяных эмульсий, перекачиваемых по промысловым нефтепроводам.
Пластины выдерживают в растворе при температуре 60 ± 5 °С (максимальная температура для перекачиваемых водонефтяных эмульсий) в течение времени, достаточного для возникновения заметной коррозии пластин (рекомендуемая продолжительность выдержки по ГОСТ Р 9.905-2007 « Единая система защиты от коррозии и старения. Методы испытаний на коррозию. Общие требования» 24; 48; 96 з).
Рис.5. Поперечный шлиф листа стали 09пс в месте реза после воздействия окружающей среды
В процессе выдержки для обеспечения анодного контроля электрохимической реакции, необходимого для демонстрации влияния напряженного состояния на скорость коррозии, рабочий раствор обогащают кислородом, что достигается непрерывным продуванием воздуха через решение.
Обработка результатов
По окончании термообработки нижняя поверхность среза пластины очищается от продуктов коррозии с помощью ластика, а поверхность пластин вокруг среза очищается от защитного лака. В тех же точках, что и до коррозионного испытания, повторно измеряют глубину реза пластин Н и * (см. таблицу) и определяют ее увеличение Δ Н и как результате агрессивного воздействия окружающей среды (рис.5). Боковые поверхности пластин полируются для получения шлифов, которые после травления используются для металлографического анализа стали.
таблицу) и определяют ее увеличение Δ Н и как результате агрессивного воздействия окружающей среды (рис.5). Боковые поверхности пластин полируются для получения шлифов, которые после травления используются для металлографического анализа стали.
Рассчитывается среднее арифметическое увеличения глубины резания по всем точкам:
$$ ΔНav = ΣΔНi /n,\qquad(3) $$
где n = 13; среднеквадратичное отклонение
S=1n∑i=1n(ΔHi – ΔHav)2, (4)
установлено фактическое увеличение глубины резания
$(0$09
и оценена скорость канавочной коррозии материалов пластин
K=ΔНactt⋅8760 = ΔНср ± St⋅8760, (6)
t – время температурного кондиционирования пластин; 8760 – часов в году.
Распределение изменения глубины реза по его длине и скорости коррозии, полученные на примерах трубопроводных сталей 09пс и 09Г2С, представлены в таблице.
Глубины резания в различных точках до и после воздействия агрессивной среды, изменение Δ
Н и и значений скоростей коррозии К трубопроводных сталей Сравнивая значения К, можно сделать вывод, что 09Сталь Г2С более устойчива к канавочной коррозии по сравнению со сталью 09пс.
Помимо определения сравнительной коррозионной стойкости сталей, предлагаемая методика позволяет исследовать влияние растягивающих и сжимающих напряжений в металле на скорость коррозии, а также наличие надреза на напряженной конструкции. Для этого наряду с поверхностью пластины вокруг среза защитным лаком наносят пластически деформированную криволинейную часть пластины с внешней ее стороны, где металл подвергается сжимающим напряжениям, а также на поверхность пластины. недеформированные части пластины, не подверженные каким-либо остаточным напряжениям. Защитное покрытие разрушают в указанных местах пластины в локальных точках, металл в которых будет подвергаться коррозионному воздействию при последующих испытаниях. После проведения коррозионных испытаний защитный лак с поверхности пластин вокруг этих точек удаляется. Затем определяют разность фокусных расстояний от нижней точки коррозионного повреждения до непораженной поверхности пластины, принимаемую за глубину повреждения в этой точке. Необходимые зависимости получают после проведения экспериментов на подготовленных таким образом пластинах, предварительно изогнутых на разные углы отклонения.
Необходимые зависимости получают после проведения экспериментов на подготовленных таким образом пластинах, предварительно изогнутых на разные углы отклонения.
Заключение
Разработана методика определения скорости коррозии трубопроводных сталей в условиях, имитирующих коррозионное повреждение стенки промыслового трубопровода: при нахождении металла стенки трубы в напряженном состоянии, наличии хлор-иона в водной составляющей водонефтяной эмульсии на нижней образующей трубы имеется канал в виде канавки, водная составляющая обогащена кислородом воздуха. В качестве примера применения предложенной методики приведены скорости коррозии двух трубопроводных сталей 09ps и 09G2S. Скорости коррозии (2,3 ± 0,8 и 1,8 ± 0,9 мм/год) оказались близкими к таковым для материалов промысловых трубопроводов, подвергшихся канавочной коррозии. Разработанная методика может быть использована при исследовании влияния растягивающих и сжимающих напряжений в металле, а также наличия разреза на напряженной конструкции, на скорость коррозии.
Список литературы
- Литвиненко В.С., Цветков П.С., Двойников М.В., Буслаев Г.В. Барьеры реализации водородных инициатив в контексте устойчивого развития мировой энергетики. Журнал Горного института. 2020. Том. 244, с. 428-438. DOI: 10.31897/ПМИ.2020.4.5
- Голдобина Л.А., Орлов П.С. Анализ причин коррозионного разрушения подземных трубопроводов и новые решения для повышения коррозионной стойкости стали. Журнал Горного института. 2016. Том. 219, с. 459-464. DOI: 10.18454/PMI.2016.3.459 (на русском языке).
- Зайнуллин Р.С. Кинетика механохимического разрушения и ресурс трубопроводных систем. Проблемы сбора, подготовки и транспорта нефти и нефтепродуктов. 2005. № 65, с. 44-63. DOI: 10.17122/ntj-oil-2005-65-44-63 (на русском языке).
- Бурков П.В., Бурков В.П., Фатьянов Д.С., Тимофеев В.Ю. Исследование напряженно-деформированного состояния нефтепромысловых трубопроводов, подверженных ручьевой коррозии. Вестник Кузбасского государственного технического университета.
 2018. № 3 (127), с. 5-12. DOI: 10.26730/1999-4125-2018-3-5-12 (на русском языке).
2018. № 3 (127), с. 5-12. DOI: 10.26730/1999-4125-2018-3-5-12 (на русском языке). - Виноградов С.Н., Волчихин В.И., Ширина Е.В., Мещеряков А.С. Исследование коррозионной стойкости конструкционных сталей в пластовой воде. Известия высших учебных заведений. Поволжский район. Технические науки. 2008. № 4, с. 139-144 (на русском языке).
- Коликов А.П., Лелетко А.С., Матвеев Д.Б. и другие. Исследование остаточных напряжений в сварных трубах. Известия высших учебных заведений. Черная металлургия. 2014. Том. 57. № 11, с. 48-53 DOI: 10.17073/0368-0797-2014-11-48-53 (на русском языке).
- Клисенко Л.Б., Лапшин А.П., Кудрин Д.В. Вероятные причины образования ребристой коррозии в нефтепромысловых трубопроводах, выявленные при техническом диагностировании. Современная наука: актуальные проблемы и решения. 2015. № 9(22), с. 58-61 (на русском языке).
- Любчик А.Н., Крапивский Е.И., Большунова О.М. Прогноз технического состояния трубопровода на основе анализа.
 Журнал Горного института. 2011. Том. 192, с. 153-156 (на русском языке).
Журнал Горного института. 2011. Том. 192, с. 153-156 (на русском языке). - Медведев А.П. Комплексная система безопасности трубопроводов Западно-Сибирского промысла: Автореф. дис. … д-ра техн. наук. Уфа: Институт проблем транспорта энергоресурсов, 2004, с. 44 (на русском языке).
- Фирстов А.А., Капачинских Ж.Ю., Середенок В.А. и другие. Обоснование возможности оценки уровня изгибающих напряжений в стенках трубы магистральных газонефтепроводов путем определения ее пространственного положения с поверхности земли. Наука и техника в газовой промышленности. 2020. № 2 (82).
- Болобов В.И., Попов Г.Г., Баталов А.П. и др. Патент № 2730102. Способ оценки стойкости трубопроводных сталей к «ручейковой» коррозии. опубл. 17.08.2020 (на русском языке).
- Подавалов А.К. Уменьшение канавочной коррозии нефтепроводов с помощью врезных муфт: Автореф. дис. … канд. техн. наук. СПб.: Санкт-Петербургский государственный горный институт им. Г.В.Плеханова, 2009, с. 20 (на русском языке).

- Подопригора А.А. Исследование коррозионных повреждений на поверхности нефтепровода после длительной эксплуатации. Вестник Югорского государственного университета. Том. 4 (23), с. 105-112 (на русском языке).
- Поподко Д.В. Оценка безопасности эксплуатации обечаек при ручьевой эрозии методом конечных элементов: Автореф. дис. … канд. техн. наук. Уфа: Уфимский государственный нефтяной технический университет, 2004, с. 24 (на русском языке).
- Скоромный В.И. Разработка методов и средств повышения безопасности эксплуатации нефтесборных трубопроводов: Автореф. дис. … канд. техн. наук. Уфа: Уфимский государственный нефтяной технический университет, 2004, с. 24 (на русском языке).
- Султанмагомедов С.М. Обеспечение безопасной эксплуатации и долговечности промысловых трубопроводов, подверженных ручьевой эрозии: Автореф. дис. … д-ра техн. наук. Уфа: Уфимский государственный нефтяной технический университет, 2003, с. 48 (на русском языке).
- Шаймухаметов М.
 Р. Напряжения в зоне разрушения канавок трубопроводов. Нефтегазовое дело. 2009. № 2, с. 115-120 (на русском языке).
Р. Напряжения в зоне разрушения канавок трубопроводов. Нефтегазовое дело. 2009. № 2, с. 115-120 (на русском языке). - Шинкин В.Н. Остаточные напряжения при пластическом кручении круглого стержня. Современные тенденции развития науки и технологий. 2016. № 3-3, с. 127-134 (на русском языке).
- Шинкин В.Н. Остаточные напряжения при расширении стальной трубы. Молодой ученый. 2015. № 20 (100). Часть 1, с. 88-93 (на русском языке).
- Щипачев А.М., Горбачев С.В. Влияние послесварочной обработки на скорость сплошной коррозии и микроструктуру сварных соединений сталей 20 и 30ХГСА. Журнал Горного института. 2018. Том. 231, с. 307-311. DOI: 10.25515/PMI.2018.3.307
- Рен Р.К., Чжан С., Пан С.Л., Гао К.В. Новое наблюдение взаимодействия между макроупругим напряжением и электрохимической коррозией низкоуглеродистой стали в 3,5% масс. растворе NaCl. Электрохимика Акта. 2012. Том. 85, с. 283-294. DOI: 10.1016/j.electacta.2012.08.079
- Абаев З.К., Галачиева С.
 В. Разработка математической модели влияния времени обжига на сопротивление коррозионному растрескиванию под напряжением. Международная конференция по промышленному инжинирингу, приложениям и производству (ICIEAM), 19-20 мая 2016 г., Челябинск, Россия. IEEE, 2016. Том. 2, с. 1-4. DOI: 10.1109/ICIEAM.2016.7911569
В. Разработка математической модели влияния времени обжига на сопротивление коррозионному растрескиванию под напряжением. Международная конференция по промышленному инжинирингу, приложениям и производству (ICIEAM), 19-20 мая 2016 г., Челябинск, Россия. IEEE, 2016. Том. 2, с. 1-4. DOI: 10.1109/ICIEAM.2016.7911569 - 23.Агиней Р.В., Фирстов А., Капачинских З.Ю. К вопросу об определении напряжения изгиба заглубленного трубопровода от поверхности земли. Международная конференция по инновациям, физическим исследованиям и цифровизации в горном деле (IPDME 2020),
23-24 апреля 2020 г., г. Санкт-Петербург, Российская Федерация. ИОП, 2020. Том. 1753. Вып. 1. N 012068. DOI: 10.1088/1742-6596/1753/1/012068 - Аль-Мансур М., Альфантази А.М., Эль-Буждаини М. Стойкость к растрескиванию под напряжением в сульфидах высокопрочной низколегированной стали API-X100. Материалы и дизайн. 2009. Том. 30, с. 4088-4094. DOI: 10.1016/j.matdes.2009.05.025
- Аскари М.А., Алиофхазраи М.
 , Афроухтех С. Комплексный обзор внутренней коррозии и трещинообразования нефтегазопроводов. Журнал науки и техники о природном газе. 2019. Том. 71. с. 1-25. DOI: 10.1016/j.jngse.2019.102971
, Афроухтех С. Комплексный обзор внутренней коррозии и трещинообразования нефтегазопроводов. Журнал науки и техники о природном газе. 2019. Том. 71. с. 1-25. DOI: 10.1016/j.jngse.2019.102971 - Синьхуа Ван, Синхуа Тан, Ливэй Ван и др. Коррозионное поведение трубопроводной стали Х80 при совместном воздействии напряжения и блуждающего тока. Международный журнал электрохимических наук. 2014. Том. 9. Вып. 8, с. 4574-4588. DOI: 10.3390/ma10070720
- Даровицки К., Орликовски Ю., Арутюнов А. Измерения спектроскопии динамического электрохимического импеданса растрескивания пассивного слоя под действием статических растягивающих напряжений. Твердотельная электрохимия. 2004. Том. 8, с. 352-359. DOI: 10.1007/s10008-003-0470-0
- Дергач Т.О., Сухомлин Г.Д. Методы повышения коррозионной стойкости труб из низколегированных сталей для нефтегазодобывающей промышленности. Материнская наука. 2021. Том. 56. Вып. 5, с. 684-690. DOI: 10.1007/s11003-021-00483-9
- Griggs J.
 , Gamboa E., Lavigne O. Обзор моделирования коррозионного растрескивания газопроводов высокого давления под напряжением при высоких значениях pH. Материалы и коррозия. 2015. Том. 67. Вып. 3, с. 251-263. DOI: 10.1002/maco.201508454
, Gamboa E., Lavigne O. Обзор моделирования коррозионного растрескивания газопроводов высокого давления под напряжением при высоких значениях pH. Материалы и коррозия. 2015. Том. 67. Вып. 3, с. 251-263. DOI: 10.1002/maco.201508454 - Хасан Ф., Икбал Дж., Ахмед Ф. Коррозионное разрушение газопровода высокого давления под напряжением. Анализ технических отказов. 2007. Том. 14. Вып. 5, с. 801-809. DOI: 10.1016/j.engfailanal.2006.11.002
- Чжан-Фэн Чен, Вэнь Ван, Хэ Ян и др. О влиянии протяженного коррозионного дефекта и осевого растяжения на разрывное давление подводных трубопроводов. Прикладные исследования океана. 2021. Том. 111. N 102637. DOI: 10.1016/j.apor.2021.102637
- Султанбеков Р., Исламов С., Мардашов Д. и др. Исследование влияния состава судового остаточного топлива на седиментацию из-за несовместимости. Журнал морской науки и техники. 2021. Том. 9. Исс. 10. N 1067. DOI: 10.3390/jmse9101067
- Салим Б., Ахмед Ф., Асиф Рафик М. и др. Стресс-коррозионное разрушение газопровода марки Х52.
 Анализ технических отказов. 2014. Том. 46, с. 157-165. DOI: 10.1016/j.engfailanal.2014.08.011
Анализ технических отказов. 2014. Том. 46, с. 157-165. DOI: 10.1016/j.engfailanal.2014.08.011 - Султанбеков Р.Р., Назарова М.Н. Влияние общего осадка нефтепродуктов на коррозионную активность металла резервуаров при хранении. Веб-конференция E3S. I Международная конференция «Коррозия в нефтегазовой отрасли», 22-24 мая 2019 г., Россия, Санкт-Петербург. E3S Web of Conferences, 2019. Том. 121. N 01015. DOI: 10.1051/e3sconf/201912101015
- Кривокрысенко Е.А., Попов Г.Г., Болобов В.И., Никулин В.Е. Применение метода магнитной анизотропии для оценки остаточных напряжений в металлоконструкциях. Ключевые инженерные материалы. 2020. Том. 854, с. 10-15. DOI: 10.4028/www.scientific.net/KEM.854.10
Похожие статьи
Оценка эффективности технологий извлечения тонкого золота на примере титаномагнетитовых пляжных россыпей западного побережья Камчатки
2021 Кунгурова Валентина Евгеньевна
Управление ресурсами подземных вод на трансграничных территориях (на примере Российской Федерации и Эстонской Республики)
2021 Головина Екатерина Ивановна, Гребнева Анастасия Викторовна
Возможности создания российского высокотехнологичного забойного оборудования
2021 Жданеев О. В., Зайцев А.В., Продан Т.Т.
В., Зайцев А.В., Продан Т.Т.
Online — Sixty Shades of Generalized Continua
В этой книге известные ученые обсуждают современные аспекты обобщенных континуумов, чтобы лучше понять современные материалы и передовые структуры. Они обладают сложной внутренней структурой, что требует разработки новых подходов к моделированию таких структур и вызываемых ими новых эффектов. В этой книге собраны фундаментальные работы в честь Виктора Еремеева и его 60-летия.
1 Влияние параметра плотности заполнения при 3D-печати на механические свойства PLA-полимера Реза Афшар, Саймон Джин и Билен Эмек Абали1.1 Введение 1.2 Аддитивное производство 1.3 Материалы и методы 1.3.1 Моделирование методом наплавления (FDM) 1.3. 2 Испытания на однонаправленное растяжение 1.3.3 Метод корреляции цифровых изображений 1.4 Результаты и обсуждение 1.5 Выводы Литература 2 Предварительные приближенные аналитические решения контактной задачи для неоднородного слоя С. М. Айзикович, Полина А. Лапина, С. С. Волков 2.1 Введение 2.2 Постановка задачи о сдвиге поверхности неоднородного слоя 2.3. Интегральные уравнения контактных задач 2.4. Численный анализ 2.5. Ссылки на замыкание 3. Прямой подход для пластин с учетом гигротермической нагрузки и остаточной кинетики 3.2 Система отсчета 3.3 Термические эффекты и гигроскопическое воздействие 3.4 Остаточная кинетика 3.5 Заключение Литература 4 Методика определения диаграмм истинного деформирования при динамическом растяжении с использованием ДИК Басалин Артем Викторович, Брагов Анатолий Михайлович, Брагов Александр Ю. Константинов, Филиппов А.Р. 4.1 Введение 4.2 Пневмодинамическая установка для испытаний материалов со скоростью деформации порядка 10-100 с 1 4.2.1 Схема установки 4.2.2 Методы получения и обработки информации в эксперименте 4.3 Результаты испытаний Лист (3 мм) Сталь 09G2S в широком диапазоне скоростей деформации 4.4 Заключение Ссылки 5 Упругость градиента деформации и двойные внутренние переменные Аркадий Березовский 5.
Айзикович, Полина А. Лапина, С. С. Волков 2.1 Введение 2.2 Постановка задачи о сдвиге поверхности неоднородного слоя 2.3. Интегральные уравнения контактных задач 2.4. Численный анализ 2.5. Ссылки на замыкание 3. Прямой подход для пластин с учетом гигротермической нагрузки и остаточной кинетики 3.2 Система отсчета 3.3 Термические эффекты и гигроскопическое воздействие 3.4 Остаточная кинетика 3.5 Заключение Литература 4 Методика определения диаграмм истинного деформирования при динамическом растяжении с использованием ДИК Басалин Артем Викторович, Брагов Анатолий Михайлович, Брагов Александр Ю. Константинов, Филиппов А.Р. 4.1 Введение 4.2 Пневмодинамическая установка для испытаний материалов со скоростью деформации порядка 10-100 с 1 4.2.1 Схема установки 4.2.2 Методы получения и обработки информации в эксперименте 4.3 Результаты испытаний Лист (3 мм) Сталь 09G2S в широком диапазоне скоростей деформации 4.4 Заключение Ссылки 5 Упругость градиента деформации и двойные внутренние переменные Аркадий Березовский 5. 1 Введение 5.2 Двойные внутренние переменные 5.2.1 Уравнения эволюции 5.2.2 Квадратичная свободная энергия 5.3 Заключительные замечания Ссылки 6 О коэрцитивной силе энергии деформации Функции в обобщенных моделях 6-параметрических оболочек Мирча Бирсан и Патрицио Нефф6.1 Введение 6.2 Общие 6-параметрические упругие оболочки. Управляющие уравнения 6.3 Модель порядка 3 6-параметрических оболочек, изготовленных из материала Коссера 6.3.1 Коэрцитивные результаты для модели порядка (3) 6.3.2 Существование минимизаторов 6.4 Модель высшего порядка 6-параметрических оболочек Коссера Ссылки 7 Решение задачи Уравнения нелинейной модели кристаллических сред со сложной решеткой и некоторые структуры плоской деформации Булыгин Анатолий Николаевич и Павлов Ю.В.7.1 Введение 7.2 Нелинейная модель деформации кристаллических сред 7.3 Общее решение динамических уравнений плоской деформации нелинейной модели 7.4 Решение уравнений микрополя 7.5. Заключение. Ссылки 8. Модальный анализ кольцевой пластины второго градиента, состоящей из ортогональной сети логарифмических спиральных волокон.
1 Введение 5.2 Двойные внутренние переменные 5.2.1 Уравнения эволюции 5.2.2 Квадратичная свободная энергия 5.3 Заключительные замечания Ссылки 6 О коэрцитивной силе энергии деформации Функции в обобщенных моделях 6-параметрических оболочек Мирча Бирсан и Патрицио Нефф6.1 Введение 6.2 Общие 6-параметрические упругие оболочки. Управляющие уравнения 6.3 Модель порядка 3 6-параметрических оболочек, изготовленных из материала Коссера 6.3.1 Коэрцитивные результаты для модели порядка (3) 6.3.2 Существование минимизаторов 6.4 Модель высшего порядка 6-параметрических оболочек Коссера Ссылки 7 Решение задачи Уравнения нелинейной модели кристаллических сред со сложной решеткой и некоторые структуры плоской деформации Булыгин Анатолий Николаевич и Павлов Ю.В.7.1 Введение 7.2 Нелинейная модель деформации кристаллических сред 7.3 Общее решение динамических уравнений плоской деформации нелинейной модели 7.4 Решение уравнений микрополя 7.5. Заключение. Ссылки 8. Модальный анализ кольцевой пластины второго градиента, состоящей из ортогональной сети логарифмических спиральных волокон. Введение 8.2 Модель оптоволоконной сети, организованной в виде логарифмических спиралей 8.3 Модальный анализ 8.4 Выводы и перспективы Ссылки 9Нелинейная простейшая приведенная среда Кельвина в окрестности сферического напряженного состояния: волны и неустойчивости Дрепин М.А., Грекова Елена Ф.9.1 Введение и обозначения9.2 Основные уравнения изотропной упругой приведенной среды Кельвина в окрестности предварительного Напряженное состояние 9.2.1 Законы динамики нелинейной приведенной среды Кельвина 9.2.2 Определяющие соотношения для нелинейной приведенной среды Кельвина 9.2.3 Простейшая нелинейная приведенная среда Кельвина. Энергия деформации 9.2.4 Среда в окрестности однородного нелинейного сферического деформационного состояния 9.3 Дисперсионные соотношения простейшей упругой приведенной среды Кельвина в окрестности предварительного сферического деформированного состояния для особых направлений распространения возмущений. Волны и устойчивость 9.3.1 Гармонические волны 9.3.2 Распространение гармонических волн вдоль оси точки тела (= +/- 0) 9.
Введение 8.2 Модель оптоволоконной сети, организованной в виде логарифмических спиралей 8.3 Модальный анализ 8.4 Выводы и перспективы Ссылки 9Нелинейная простейшая приведенная среда Кельвина в окрестности сферического напряженного состояния: волны и неустойчивости Дрепин М.А., Грекова Елена Ф.9.1 Введение и обозначения9.2 Основные уравнения изотропной упругой приведенной среды Кельвина в окрестности предварительного Напряженное состояние 9.2.1 Законы динамики нелинейной приведенной среды Кельвина 9.2.2 Определяющие соотношения для нелинейной приведенной среды Кельвина 9.2.3 Простейшая нелинейная приведенная среда Кельвина. Энергия деформации 9.2.4 Среда в окрестности однородного нелинейного сферического деформационного состояния 9.3 Дисперсионные соотношения простейшей упругой приведенной среды Кельвина в окрестности предварительного сферического деформированного состояния для особых направлений распространения возмущений. Волны и устойчивость 9.3.1 Гармонические волны 9.3.2 Распространение гармонических волн вдоль оси точки тела (= +/- 0) 9. 3.3 Распространение гармонических волн в направлении, ортогональном оси точки тела (0) 9.4 Заключение Литература 10 On Спектр времен релаксации связанных диффузионных и реологических процессов в средах с микроструктурой Дудин Д.С., Келлер И.Е. Коэффициенты диффузии в связанной системе 10.9Заключение Ссылки 11 Идентификация репрезентативного размера элемента объема и масштаба длины в обобщенной магнитоупругости Синан Эраслан, Инна М. Гитман, Минсю Сюй, Харм Аскес и Рене де Борст11.1 Введение 11.2 Формулировка 11.2.1 Гомогенизация и макроскопические характеристические параметры масштаба длины11. 2.2 Определение размеров RVE и идентификация характерных параметров масштаба длины 11.3 Численные результаты и обсуждение 11.4 Выводы Литература 12 Волны Рэлея в полупространстве Коссера (редуцированная модель) и полупространстве поврежденного материала Владимир Ерофеев, Артем Антонов, Анна Леонтьева, и Алексей Малханов. Разрушения плоскостей в каменных конструкциях Хосе Мануэль Торрес Эспино, Хайме Хеман Эспиноза Сандовал, Чуонг Энтони Тран , Роберто Феделе, Эмилио Турко, Франческо дель Изола, Лука Плачиди, Анил Мисра, Франсиско Джеймс Леон Трухильо и Эмилио Баркьези Законы 13.
3.3 Распространение гармонических волн в направлении, ортогональном оси точки тела (0) 9.4 Заключение Литература 10 On Спектр времен релаксации связанных диффузионных и реологических процессов в средах с микроструктурой Дудин Д.С., Келлер И.Е. Коэффициенты диффузии в связанной системе 10.9Заключение Ссылки 11 Идентификация репрезентативного размера элемента объема и масштаба длины в обобщенной магнитоупругости Синан Эраслан, Инна М. Гитман, Минсю Сюй, Харм Аскес и Рене де Борст11.1 Введение 11.2 Формулировка 11.2.1 Гомогенизация и макроскопические характеристические параметры масштаба длины11. 2.2 Определение размеров RVE и идентификация характерных параметров масштаба длины 11.3 Численные результаты и обсуждение 11.4 Выводы Литература 12 Волны Рэлея в полупространстве Коссера (редуцированная модель) и полупространстве поврежденного материала Владимир Ерофеев, Артем Антонов, Анна Леонтьева, и Алексей Малханов. Разрушения плоскостей в каменных конструкциях Хосе Мануэль Торрес Эспино, Хайме Хеман Эспиноза Сандовал, Чуонг Энтони Тран , Роберто Феделе, Эмилио Турко, Франческо дель Изола, Лука Плачиди, Анил Мисра, Франсиско Джеймс Леон Трухильо и Эмилио Баркьези Законы 13. 2.4 Принцип минимальной потенциальной энергии 13.2.5 Численная модель 13.2.6 Матрица жесткости 13.2.7 Алгоритм 13.3 Результаты 13.3.1 Сравнительный результат 13.3.2 Влияние толщины раствора на характеристики кладки 13.3.3 Изгиб и скольжение при сдвиге 13.3.4 Раскачивание 13.4 Выводы и будущие задачи Ссылки 14 Размерные эффекты в пластичности кристаллов Коссера Сэмюэл Форест и Флавьен Гильоне 14.1 Введение 14.2 Постановка задачи 14.2.1 Уравнения поля 14.2.2 Определяющие уравнения 14.2.3 Исследованная краевая задача 14.3 Упругопластичность Коссера на основе квадратичного потенциала 14.3.1 Простое скольжение в изотропной упругости 14.3.2 Пластичность кристалла на основе тензора полного напряжения 14.3.3 Закон Шмида, ограниченный t Симметричная часть тензора напряжений 14.3.4 Сравнение с моделью завитка 14.4 Энергетический потенциал первого ранга 14.4.1 Решение по упругости 14.4.2 Пластичность кристалла 14.4.3 Сравнение с моделью завитка 14.5 Комбинированный потенциал 14.6 Применение к поведению границ зерен 14.
2.4 Принцип минимальной потенциальной энергии 13.2.5 Численная модель 13.2.6 Матрица жесткости 13.2.7 Алгоритм 13.3 Результаты 13.3.1 Сравнительный результат 13.3.2 Влияние толщины раствора на характеристики кладки 13.3.3 Изгиб и скольжение при сдвиге 13.3.4 Раскачивание 13.4 Выводы и будущие задачи Ссылки 14 Размерные эффекты в пластичности кристаллов Коссера Сэмюэл Форест и Флавьен Гильоне 14.1 Введение 14.2 Постановка задачи 14.2.1 Уравнения поля 14.2.2 Определяющие уравнения 14.2.3 Исследованная краевая задача 14.3 Упругопластичность Коссера на основе квадратичного потенциала 14.3.1 Простое скольжение в изотропной упругости 14.3.2 Пластичность кристалла на основе тензора полного напряжения 14.3.3 Закон Шмида, ограниченный t Симметричная часть тензора напряжений 14.3.4 Сравнение с моделью завитка 14.4 Энергетический потенциал первого ранга 14.4.1 Решение по упругости 14.4.2 Пластичность кристалла 14.4.3 Сравнение с моделью завитка 14.5 Комбинированный потенциал 14.6 Применение к поведению границ зерен 14. 6.1 Модель фазового поля Коссера границ зерен 14.6.2 Аналитическое решение одной плоской границы зерен 14.6.3 Эталоны энергии границ зерен 15. О влиянии коэффициента Пуассона на фазовые превращения предельных поверхностей Александр Б. Фрейдин и Лия Л. Шарипова 15.1 Введение 15.2 Фазовые равновесия и зоны фазовых переходов для фаз с положительным и отрицательным коэффициентами Пуассона 15.3 Оптимальные ламинаты и предельные поверхности фазовых превращений 15.4 Результаты 15.5 Выводы Литература 16. Применение нелокального закона Фика в рамках микрополярного подхода Ксения Фролова, Николай Бессонов, Елена Вильчевская 16.1 Введение 16.2 Диффузия в средах, моделируемых микрополярным континуумом 16.3 Аксиально Симметричная задача 16.4 Результаты и обсуждение 16.5 Выводы Приложение. Некоторые замечания по численным аппроксимациям Ссылки 17 Геометрически нелинейная упругость Коссера с киральными эффектами, основанная на микромеханике гранул Иван Джорджио, Анил Мишра и Лука Плачиди 17.1 Введение 17.
6.1 Модель фазового поля Коссера границ зерен 14.6.2 Аналитическое решение одной плоской границы зерен 14.6.3 Эталоны энергии границ зерен 15. О влиянии коэффициента Пуассона на фазовые превращения предельных поверхностей Александр Б. Фрейдин и Лия Л. Шарипова 15.1 Введение 15.2 Фазовые равновесия и зоны фазовых переходов для фаз с положительным и отрицательным коэффициентами Пуассона 15.3 Оптимальные ламинаты и предельные поверхности фазовых превращений 15.4 Результаты 15.5 Выводы Литература 16. Применение нелокального закона Фика в рамках микрополярного подхода Ксения Фролова, Николай Бессонов, Елена Вильчевская 16.1 Введение 16.2 Диффузия в средах, моделируемых микрополярным континуумом 16.3 Аксиально Симметричная задача 16.4 Результаты и обсуждение 16.5 Выводы Приложение. Некоторые замечания по численным аппроксимациям Ссылки 17 Геометрически нелинейная упругость Коссера с киральными эффектами, основанная на микромеханике гранул Иван Джорджио, Анил Мишра и Лука Плачиди 17.1 Введение 17. 2 Дискретные и непрерывные модели для гранулированных систем 17.2.1 Идентификация с помощью анзаца Пиолы 17.2.2 Относительная межгранульная Смещение и связанные с ним меры деформации сплошной среды 17.2.3 О объективных (макро- и микро-макро) векторах смещения 17.2.4 О объективном тензоре 17.2.5 Объективные скалярные меры деформации 17.3 Функция упругой энергии 17.4 Идентификация неповрежденного изотропного случая 17.4. 1 Характеристика неповрежденного изотропного случая 17.4.2 Макроскопические изотропные матрицы жесткости 17.4.3 Идентификация макроскопических изотропных матриц жесткости 17.5 Заключение Литература 18 Исследование динамических свойств железобетона при высокоскоростном сжатии Гонов М.Е., Баландин В.В. , Анатолий М. Брагов и Александр Ю. Константинов 18.1 Введение 18.2 Метод испытаний 18.3 Характеристики испытуемых материалов 18.4 Результаты динамических испытаний на одноосное сжатие 18.5 Заключение Список литературы 19Мультистабильность конвективных течений в пористой оболочке Василий Говорухин, Межлум Сумбатян, Вячеслав Цыбулин19.
2 Дискретные и непрерывные модели для гранулированных систем 17.2.1 Идентификация с помощью анзаца Пиолы 17.2.2 Относительная межгранульная Смещение и связанные с ним меры деформации сплошной среды 17.2.3 О объективных (макро- и микро-макро) векторах смещения 17.2.4 О объективном тензоре 17.2.5 Объективные скалярные меры деформации 17.3 Функция упругой энергии 17.4 Идентификация неповрежденного изотропного случая 17.4. 1 Характеристика неповрежденного изотропного случая 17.4.2 Макроскопические изотропные матрицы жесткости 17.4.3 Идентификация макроскопических изотропных матриц жесткости 17.5 Заключение Литература 18 Исследование динамических свойств железобетона при высокоскоростном сжатии Гонов М.Е., Баландин В.В. , Анатолий М. Брагов и Александр Ю. Константинов 18.1 Введение 18.2 Метод испытаний 18.3 Характеристики испытуемых материалов 18.4 Результаты динамических испытаний на одноосное сжатие 18.5 Заключение Список литературы 19Мультистабильность конвективных течений в пористой оболочке Василий Говорухин, Межлум Сумбатян, Вячеслав Цыбулин19. 1 Введение 19.2 Математическая постановка задачи19.3 Численные методы и экстремальная мультистабильность 19.3.1 Спектральный глобальный метод Галеркина 19.3.2 Косимметрия, сохраняющая конечно-разностные аппроксимации19. 3.3. Продолжение метода скрытых параметров 19.4. Ссылки по мультистабильности 20. Перенос водорода в рамках подхода линейной неравновесной термодинамики. Неклассические модели изменения модуля Юнга геоматериалов при знакопеременных нагрузках Гузев М. А., Рябоконь Е. П., Турбаков М. С., Поплыгин В. В., Кожевников Е. В., Гладких Е. А. 31.1 Введение 21.2 Экспериментальная часть Исследования 21.3 Классическая модель изменений модуля Юнга us При переменной нагрузке 21.4 Неклассическая модель изменения модуля Юнга при переменной нагрузке 21.4.1 Формулировка неклассической модели 21.4.2 Построение решения 21.5 Заключение Литература22 Два подхода к моделированию вязкоупругих континуумов Коссера Елена А. Иванова22 .1 Введение 22.2 Кинематика и уравнения баланса 22.3 Дифференциальные уравнения, связывающие тензоры деформации с вектором скорости и вектором угловой скорости 22.
1 Введение 19.2 Математическая постановка задачи19.3 Численные методы и экстремальная мультистабильность 19.3.1 Спектральный глобальный метод Галеркина 19.3.2 Косимметрия, сохраняющая конечно-разностные аппроксимации19. 3.3. Продолжение метода скрытых параметров 19.4. Ссылки по мультистабильности 20. Перенос водорода в рамках подхода линейной неравновесной термодинамики. Неклассические модели изменения модуля Юнга геоматериалов при знакопеременных нагрузках Гузев М. А., Рябоконь Е. П., Турбаков М. С., Поплыгин В. В., Кожевников Е. В., Гладких Е. А. 31.1 Введение 21.2 Экспериментальная часть Исследования 21.3 Классическая модель изменений модуля Юнга us При переменной нагрузке 21.4 Неклассическая модель изменения модуля Юнга при переменной нагрузке 21.4.1 Формулировка неклассической модели 21.4.2 Построение решения 21.5 Заключение Литература22 Два подхода к моделированию вязкоупругих континуумов Коссера Елена А. Иванова22 .1 Введение 22.2 Кинематика и уравнения баланса 22.3 Дифференциальные уравнения, связывающие тензоры деформации с вектором скорости и вектором угловой скорости 22. 4 Приведенное уравнение баланса энергии и уравнение теплопроводности: метод Жилина 22.5 Интегральные уравнения, связывающие тензоры деформации с вектором скорости и вектор угловой скорости 22.6 Исходные члены в уравнениях баланса деформации 22.7 Приведенное уравнение баланса энергии и уравнение теплопроводности: новый метод 22.8 Сравнение двух подходов 22.9Ссылки для обсуждения 23 Модели пористых сред на основе обобщенных уравнений состояния с простыми примерами Анна Князева и Нелли Назаренко 23.1 Введение 23.2 Определения и общие соотношения 23.3 Термодинамические соотношения 23.4 Примеры частных задач 23.4.1 Сжимаемый невязкий газ 23.4.2 Сжимаемая жидкость с объемной вязкостью 23.4 .3 Неидеальный газ в неизотермических условиях 23.4.4 Бинарная невязкая несовершенная смесь 23.4.5 Диффузия и фильтрация в средах с двойной пористостью 23.4.6 Вязкая двухкомпонентная жидкость в средах с двойной пористостью 23.4.7 Невязкая двухкомпонентная жидкость в пористых средах с нано- и микропорами 23.
4 Приведенное уравнение баланса энергии и уравнение теплопроводности: метод Жилина 22.5 Интегральные уравнения, связывающие тензоры деформации с вектором скорости и вектор угловой скорости 22.6 Исходные члены в уравнениях баланса деформации 22.7 Приведенное уравнение баланса энергии и уравнение теплопроводности: новый метод 22.8 Сравнение двух подходов 22.9Ссылки для обсуждения 23 Модели пористых сред на основе обобщенных уравнений состояния с простыми примерами Анна Князева и Нелли Назаренко 23.1 Введение 23.2 Определения и общие соотношения 23.3 Термодинамические соотношения 23.4 Примеры частных задач 23.4.1 Сжимаемый невязкий газ 23.4.2 Сжимаемая жидкость с объемной вязкостью 23.4 .3 Неидеальный газ в неизотермических условиях 23.4.4 Бинарная невязкая несовершенная смесь 23.4.5 Диффузия и фильтрация в средах с двойной пористостью 23.4.6 Вязкая двухкомпонентная жидкость в средах с двойной пористостью 23.4.7 Невязкая двухкомпонентная жидкость в пористых средах с нано- и микропорами 23. 5. Гиперупругие мембраны 24.3 Численные результаты 24.4 Выводы Ссылки 25 Интегрировано как Имптотический подход к моделям строительной механики Колпаков А.Г., Ракин С.И. 25.1 Мотивация исследования 25.2 Современное состояние строительной механики 25.2.1 Деформация «основной» части рамы 25.2.2 Деформация соединительных узлов рамы 25.2 .3 «Бесконечная жесткость» соединительных узлов 25.2.4 Достижения и ограничения строительной механики 25.3 Комплексный подход к расчету тонкостенных конструкций 25.3.1 Перемещения в «основной» части балок 25.3.2 «Жесткие» перемещения Соединительный узел 25.3.3 Сопряжение перемещений в основной части балки с перемещениями «твердого тела» соединительного узла 25.3.4 Сборка однолучевых доменных функций в функцию в двумерном каркасе 25.3.5 Дополнение к Функции (25.5) с локальными возмущениями 25.4 Локальное напряженно-деформированное состояние в соединительных узлах 25.5 Репрезентативный фрагмент узла 25.6 Комплексная методика расчета каркаса 25.7 Актуальные задачи 25.
5. Гиперупругие мембраны 24.3 Численные результаты 24.4 Выводы Ссылки 25 Интегрировано как Имптотический подход к моделям строительной механики Колпаков А.Г., Ракин С.И. 25.1 Мотивация исследования 25.2 Современное состояние строительной механики 25.2.1 Деформация «основной» части рамы 25.2.2 Деформация соединительных узлов рамы 25.2 .3 «Бесконечная жесткость» соединительных узлов 25.2.4 Достижения и ограничения строительной механики 25.3 Комплексный подход к расчету тонкостенных конструкций 25.3.1 Перемещения в «основной» части балок 25.3.2 «Жесткие» перемещения Соединительный узел 25.3.3 Сопряжение перемещений в основной части балки с перемещениями «твердого тела» соединительного узла 25.3.4 Сборка однолучевых доменных функций в функцию в двумерном каркасе 25.3.5 Дополнение к Функции (25.5) с локальными возмущениями 25.4 Локальное напряженно-деформированное состояние в соединительных узлах 25.5 Репрезентативный фрагмент узла 25.6 Комплексная методика расчета каркаса 25.7 Актуальные задачи 25. 8 Заключение Использование Литература 26 Гомогенизированный критерий расслаивания для армированной волокном плиты Александр Г. Колпаков, Сергей И. Ракин и Игорь В. Андрианов 26.1 Введение 26.2 Пограничный слой 26.3 Результаты численных расчетов 26.3.1 Расширение вдоль оси 26.3.2 Сдвиг в 2-3-плоскости 26.4 Асимптотический гомогенизированный критерий прочности межфазной зоны 26.5 Построение критерия прочности на расслоение 26.6 Выводы Литература 27 Слегка нагруженный гидродинамический упорный подшипник, смазываемый неньютоновской жидкостью Кудиш Илья И., Волков С. С., Андрей С. Васильев 27.1 Введение 27.2 Постановка задачи смазки 27.3 Асимптотический анализ реологических уравнений и уравнений движения 27.4 Примеры некоторых конкретных решений задачи смазки и их обсуждение 27.5 Замыкающие ссылки 28 Идея использования адгезионных связей при формообразовании холоднодеформированных тонкостенных деталей Балки-колонныMarcin Kujawa, Antonio Cazzani, Lukasz Smakosz, ViolettaKonopinska-Zmyslowska, Karol Wi nkelmann, Faizullah Jan, and Czeslaw Szymczak 28.
8 Заключение Использование Литература 26 Гомогенизированный критерий расслаивания для армированной волокном плиты Александр Г. Колпаков, Сергей И. Ракин и Игорь В. Андрианов 26.1 Введение 26.2 Пограничный слой 26.3 Результаты численных расчетов 26.3.1 Расширение вдоль оси 26.3.2 Сдвиг в 2-3-плоскости 26.4 Асимптотический гомогенизированный критерий прочности межфазной зоны 26.5 Построение критерия прочности на расслоение 26.6 Выводы Литература 27 Слегка нагруженный гидродинамический упорный подшипник, смазываемый неньютоновской жидкостью Кудиш Илья И., Волков С. С., Андрей С. Васильев 27.1 Введение 27.2 Постановка задачи смазки 27.3 Асимптотический анализ реологических уравнений и уравнений движения 27.4 Примеры некоторых конкретных решений задачи смазки и их обсуждение 27.5 Замыкающие ссылки 28 Идея использования адгезионных связей при формообразовании холоднодеформированных тонкостенных деталей Балки-колонныMarcin Kujawa, Antonio Cazzani, Lukasz Smakosz, ViolettaKonopinska-Zmyslowska, Karol Wi nkelmann, Faizullah Jan, and Czeslaw Szymczak 28. 1 Введение 28.2 Современное состояние техники 28.2.1 Статический, динамический анализ и анализ устойчивости тонкостенных элементов 28.2.2 Влияние дефектов 28.2.3 Анализ отказов с учетом ползучести в металлических элементах, связанных клеем/ Структуры 28.3 Обоснование решения проблемы исследования 28.4 Выводы Список литературы 29Моделирование диссипативного механо-электромагнетизма в электронных компонентах Йиминг Лю, Вольфганг Х. Мюллер и Билен Эмек Абали 29.1 Введение 29.2 Основные уравнения 29.3 Конструктивные уравнения 29.4 Генерация слабых форм 29.5 Реализация и результаты 29.6 Заключение Ссылки 30 О возможной редукции градиентных теорий упругости Сергей А. Лурье, Петр А. Белов и Юрий О. Соляев 30.1 Введение 30.2 Вариационная формулировка градиентных теорий 30.3 Структура тензоров шестого ранга 30.4 Специальная структура градиентной части потенциальной энергии. Гипотеза об отсутствии расходящихся членов 30.5 Особенности вариационной формулировки градиентных моделей векторного типа 30.
1 Введение 28.2 Современное состояние техники 28.2.1 Статический, динамический анализ и анализ устойчивости тонкостенных элементов 28.2.2 Влияние дефектов 28.2.3 Анализ отказов с учетом ползучести в металлических элементах, связанных клеем/ Структуры 28.3 Обоснование решения проблемы исследования 28.4 Выводы Список литературы 29Моделирование диссипативного механо-электромагнетизма в электронных компонентах Йиминг Лю, Вольфганг Х. Мюллер и Билен Эмек Абали 29.1 Введение 29.2 Основные уравнения 29.3 Конструктивные уравнения 29.4 Генерация слабых форм 29.5 Реализация и результаты 29.6 Заключение Ссылки 30 О возможной редукции градиентных теорий упругости Сергей А. Лурье, Петр А. Белов и Юрий О. Соляев 30.1 Введение 30.2 Вариационная формулировка градиентных теорий 30.3 Структура тензоров шестого ранга 30.4 Специальная структура градиентной части потенциальной энергии. Гипотеза об отсутствии расходящихся членов 30.5 Особенности вариационной формулировки градиентных моделей векторного типа 30. 6 Система определяющих уравнений равновесия 30.7 О единственности редуцированных моделей векторного типа 30.8 Выводы Литература 31 Динамика прямоугольного твердого тела на подвижном основании В.С. Метрикин, Леонид А. Игумнов и Елена И. Комарова 31.1 Введение 31.2 Математическая модель 31.3 Построение точечного отображения поверхности Пуанкаре 31.3.1 Координаты неподвижной точки, соответствующие симметричному периодическому движению. Устойчивость 31.3.2 Уравнения для определения координат неподвижной точки, соответствующей асимметричным периодическим движениям. Устойчивость 31.4 Численные результаты для Y ( ) = sin( ) 31.5 Численные результаты 31.6 Заключение Ссылки 32 Асимптотически верная аналитическая модель для реакции на изгиб двухслойного материала Полоса с контрастными упругими константами Геннадий Михасев и Нгуен Ле32.1 Введение 32.2 Постановка задачи 32.3 Модель типа Бернулли-Эйлера для полосы, состоящей из слоев с близкими материальными константами 32.4 Модель типа Тимошенко-Рейсснера для полосы, состоящей из слоев с высококонтрастными упругими свойствами 32.
6 Система определяющих уравнений равновесия 30.7 О единственности редуцированных моделей векторного типа 30.8 Выводы Литература 31 Динамика прямоугольного твердого тела на подвижном основании В.С. Метрикин, Леонид А. Игумнов и Елена И. Комарова 31.1 Введение 31.2 Математическая модель 31.3 Построение точечного отображения поверхности Пуанкаре 31.3.1 Координаты неподвижной точки, соответствующие симметричному периодическому движению. Устойчивость 31.3.2 Уравнения для определения координат неподвижной точки, соответствующей асимметричным периодическим движениям. Устойчивость 31.4 Численные результаты для Y ( ) = sin( ) 31.5 Численные результаты 31.6 Заключение Ссылки 32 Асимптотически верная аналитическая модель для реакции на изгиб двухслойного материала Полоса с контрастными упругими константами Геннадий Михасев и Нгуен Ле32.1 Введение 32.2 Постановка задачи 32.3 Модель типа Бернулли-Эйлера для полосы, состоящей из слоев с близкими материальными константами 32.4 Модель типа Тимошенко-Рейсснера для полосы, состоящей из слоев с высококонтрастными упругими свойствами 32. 4.1 Опережающее приближение 32.4.2 Аппроксимация первого порядка 32.4.3 Одномерное управляющее уравнение 32.5 Свободные колебания 32.6 Выводы Литература 33 Об аналитическом моделировании намотки гибких листов с усилием натяжения Александр Морозов, Вильгельм Риккерт и Сергей Шубин 33.1 Введение 33.2 Общие предположения для задачи намотки 33.3 Намотка Первый слой 33.4 Намотка последующих слоев 33.5 Заключение Литература 34 Об использовании вращений в качестве основных переменных в нелинейной теории тонких упругих оболочек Войцех Петрашкевич 34.1 Введение 34.2 Геометрия и деформация базовой поверхности 34.3 Условия равновесия 34.4 Краевая задача с независимыми вращениями 34.5 Определяющие уравнения резиноподобных оболочек Литература 35 Описание континуума расширенных моделей метаматериала «масса в массе» Алексей В. Порубов 35.1 Введение 35.2 Классическая цепь «масса в массе» 35.3 Цепь с дополнительными присоединенными массами 35.4 Цепь с дополнительными внутренними присоединенными массами 35.
4.1 Опережающее приближение 32.4.2 Аппроксимация первого порядка 32.4.3 Одномерное управляющее уравнение 32.5 Свободные колебания 32.6 Выводы Литература 33 Об аналитическом моделировании намотки гибких листов с усилием натяжения Александр Морозов, Вильгельм Риккерт и Сергей Шубин 33.1 Введение 33.2 Общие предположения для задачи намотки 33.3 Намотка Первый слой 33.4 Намотка последующих слоев 33.5 Заключение Литература 34 Об использовании вращений в качестве основных переменных в нелинейной теории тонких упругих оболочек Войцех Петрашкевич 34.1 Введение 34.2 Геометрия и деформация базовой поверхности 34.3 Условия равновесия 34.4 Краевая задача с независимыми вращениями 34.5 Определяющие уравнения резиноподобных оболочек Литература 35 Описание континуума расширенных моделей метаматериала «масса в массе» Алексей В. Порубов 35.1 Введение 35.2 Классическая цепь «масса в массе» 35.3 Цепь с дополнительными присоединенными массами 35.4 Цепь с дополнительными внутренними присоединенными массами 35. 5 Прикрепленные массы через один элемент основной цепи 35.6. Заключение. и граничные условия 36.2.1 Равновесие Equat 36.2.2 Граничные и межфазные условия 36.2.3 Численные результаты 36.3 Параметрическое исследование толщины экранирующего устройства: предел возможностей для релаксированной микроморфной модели 36.4 Проектирование устройства с двойным экраном 36.5 Оптимизация нескольких экранов 36.6 Выводы Ссылки 37 О магнитно-индуцированном движении микрополярных феррожидкостей Вильгельм Риккерт, Маргарита Дементева, Грегор Ганцош, Елена Н. Вильчевская и Вольфганг Х. Мюллер 37.1 Введение 37.2 Задача о течении в сочетании с электромагнетизмом 37.3 Упрощения и нормализация 37.4 Плотность электромагнитной силы 37.5 Начальные значения, граничные условия и реализация 37.6 Результаты 37.6 .1 Скольжение 37.6.2 Отсутствие скольжения 37.6.3 Однородное магнитное поле 37.7 Резюме Список литературы 38 Оценка качества изготовления 3D-печатных матриксов из фотополимерной смолы с использованием микротомографии Евгений В.
5 Прикрепленные массы через один элемент основной цепи 35.6. Заключение. и граничные условия 36.2.1 Равновесие Equat 36.2.2 Граничные и межфазные условия 36.2.3 Численные результаты 36.3 Параметрическое исследование толщины экранирующего устройства: предел возможностей для релаксированной микроморфной модели 36.4 Проектирование устройства с двойным экраном 36.5 Оптимизация нескольких экранов 36.6 Выводы Ссылки 37 О магнитно-индуцированном движении микрополярных феррожидкостей Вильгельм Риккерт, Маргарита Дементева, Грегор Ганцош, Елена Н. Вильчевская и Вольфганг Х. Мюллер 37.1 Введение 37.2 Задача о течении в сочетании с электромагнетизмом 37.3 Упрощения и нормализация 37.4 Плотность электромагнитной силы 37.5 Начальные значения, граничные условия и реализация 37.6 Результаты 37.6 .1 Скольжение 37.6.2 Отсутствие скольжения 37.6.3 Однородное магнитное поле 37.7 Резюме Список литературы 38 Оценка качества изготовления 3D-печатных матриксов из фотополимерной смолы с использованием микротомографии Евгений В. Садырин, Андрей Л. Николаев, Сергей В. Чапек, Дмитрий В. Назаренко, Сергей М. Айзикович и Юнь-Че Ван 38.1 Введение 38.2 Материалы и метод ds 38.3 Результаты и обсуждение 38.4 Заключение Ссылки 39Сравнение методов гомогенизации в упругости градиента деформации для определения параметров материала Бекир Чагри Сарар, М. Эрден Йилдиздаг и Билен Эмек Абали 39.1 Введение 39.2 Определение параметров градиента деформации 39.3 Микроструктура 39.4 Результаты и обсуждение 39.5 Заключение Ссылки 40 Потеря устойчивости прямоугольной микрополярной пластины с Предварительно напряженные покрытия Денис Н. Шейдаков 40.1 Введение 40.2 Микрополярная пластина с предварительно напряженными покрытиями 40.3 Уравнения нейтрального равновесия 40.4 Микрополярная пластина с идентичными покрытиями 40.5 Заключение Ссылки 41 Модель Коссера для эластичных пластин, армированных волокном Дэвид Дж. Стейгманн, Мирча Бирсан и Милад Ширани 41.1 Введение 41.2 Трехмерная модель Коссера для упругих тел, армированных волокном 41.
Садырин, Андрей Л. Николаев, Сергей В. Чапек, Дмитрий В. Назаренко, Сергей М. Айзикович и Юнь-Че Ван 38.1 Введение 38.2 Материалы и метод ds 38.3 Результаты и обсуждение 38.4 Заключение Ссылки 39Сравнение методов гомогенизации в упругости градиента деформации для определения параметров материала Бекир Чагри Сарар, М. Эрден Йилдиздаг и Билен Эмек Абали 39.1 Введение 39.2 Определение параметров градиента деформации 39.3 Микроструктура 39.4 Результаты и обсуждение 39.5 Заключение Ссылки 40 Потеря устойчивости прямоугольной микрополярной пластины с Предварительно напряженные покрытия Денис Н. Шейдаков 40.1 Введение 40.2 Микрополярная пластина с предварительно напряженными покрытиями 40.3 Уравнения нейтрального равновесия 40.4 Микрополярная пластина с идентичными покрытиями 40.5 Заключение Ссылки 41 Модель Коссера для эластичных пластин, армированных волокном Дэвид Дж. Стейгманн, Мирча Бирсан и Милад Ширани 41.1 Введение 41.2 Трехмерная модель Коссера для упругих тел, армированных волокном 41. 2.1 Кинематические переменные и меры деформации в упругости Коссера 41.2.2 Материалы, армированные волокном 41.2.3 Равновесие и определяющие уравнения 41.3 Теория пластин для армированных волокном пластин 41 .4 Особая конститутивная Допущения 41.4.1 Коэрцитивность 41.4.2 Минимальное свойство Ссылки на приложение 42 О структуре решений в окрестности разрыва граничных условий для градиентных моделей Александр О. Ватулян, Сергей А. Нестеров, Виктор О. Юров, Оксана В. Явруян. Механическая усталость соединений и длительная прочность материала Волков И. А., Игумнов Л. А., Белов А. А., Волков А. И. 43.1 Введение 43.2 Определяющие соотношения математической модели механики повреждаемой среды 43.2.1 Определяющие Соотношения термовязкопластичности 43.2.2 Эволюционные уравнения для накопления повреждений 43.3 Численные результаты 43.4 ЗаключениеСсылки 44 Свойства запрещенной зоны класса хиральных и ахиральных метаматериалов Юн-Че Ван, Це-Чун Ляо, Кай-Вен Тан и Сергей М. Айзикович 54.1 Введение 44.
2.1 Кинематические переменные и меры деформации в упругости Коссера 41.2.2 Материалы, армированные волокном 41.2.3 Равновесие и определяющие уравнения 41.3 Теория пластин для армированных волокном пластин 41 .4 Особая конститутивная Допущения 41.4.1 Коэрцитивность 41.4.2 Минимальное свойство Ссылки на приложение 42 О структуре решений в окрестности разрыва граничных условий для градиентных моделей Александр О. Ватулян, Сергей А. Нестеров, Виктор О. Юров, Оксана В. Явруян. Механическая усталость соединений и длительная прочность материала Волков И. А., Игумнов Л. А., Белов А. А., Волков А. И. 43.1 Введение 43.2 Определяющие соотношения математической модели механики повреждаемой среды 43.2.1 Определяющие Соотношения термовязкопластичности 43.2.2 Эволюционные уравнения для накопления повреждений 43.3 Численные результаты 43.4 ЗаключениеСсылки 44 Свойства запрещенной зоны класса хиральных и ахиральных метаматериалов Юн-Че Ван, Це-Чун Ляо, Кай-Вен Тан и Сергей М. Айзикович 54.1 Введение 44.

 (Это может происходить, например, при получении водонефтяных эмульсий с использованием пластовой воды, обогащенной кислородом, или при интенсивном перемешивании водонефтяной эмульсии в контакте с воздухом). Только при этом условии уровень напряжения трубы может влиять на скорость коррозии металла;
(Это может происходить, например, при получении водонефтяных эмульсий с использованием пластовой воды, обогащенной кислородом, или при интенсивном перемешивании водонефтяной эмульсии в контакте с воздухом). Только при этом условии уровень напряжения трубы может влиять на скорость коррозии металла;
 2018. № 3 (127), с. 5-12. DOI: 10.26730/1999-4125-2018-3-5-12 (на русском языке).
2018. № 3 (127), с. 5-12. DOI: 10.26730/1999-4125-2018-3-5-12 (на русском языке). Журнал Горного института. 2011. Том. 192, с. 153-156 (на русском языке).
Журнал Горного института. 2011. Том. 192, с. 153-156 (на русском языке).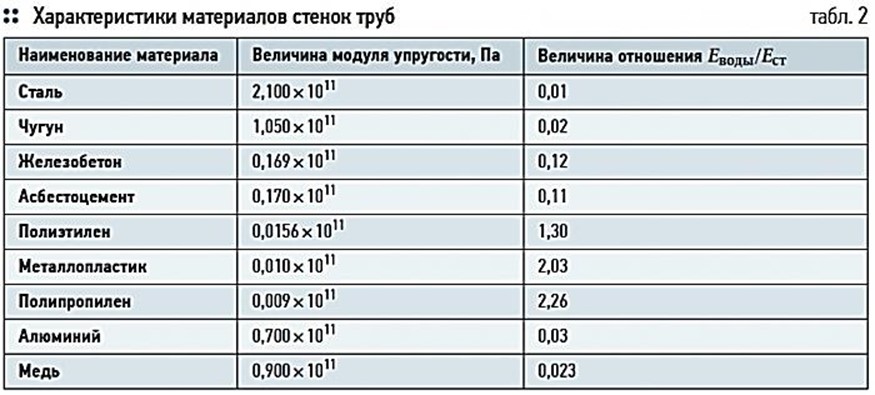
 Р. Напряжения в зоне разрушения канавок трубопроводов. Нефтегазовое дело. 2009. № 2, с. 115-120 (на русском языке).
Р. Напряжения в зоне разрушения канавок трубопроводов. Нефтегазовое дело. 2009. № 2, с. 115-120 (на русском языке). В. Разработка математической модели влияния времени обжига на сопротивление коррозионному растрескиванию под напряжением. Международная конференция по промышленному инжинирингу, приложениям и производству (ICIEAM), 19-20 мая 2016 г., Челябинск, Россия. IEEE, 2016. Том. 2, с. 1-4. DOI: 10.1109/ICIEAM.2016.7911569
В. Разработка математической модели влияния времени обжига на сопротивление коррозионному растрескиванию под напряжением. Международная конференция по промышленному инжинирингу, приложениям и производству (ICIEAM), 19-20 мая 2016 г., Челябинск, Россия. IEEE, 2016. Том. 2, с. 1-4. DOI: 10.1109/ICIEAM.2016.7911569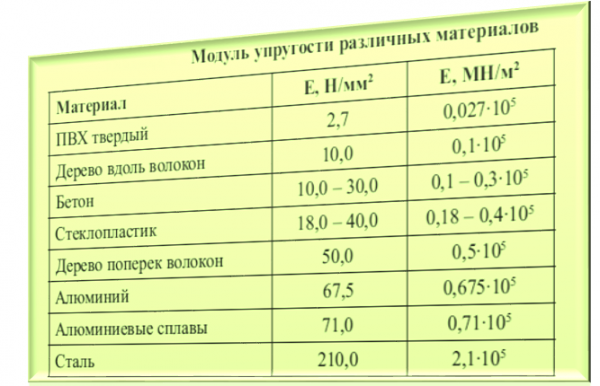 , Афроухтех С. Комплексный обзор внутренней коррозии и трещинообразования нефтегазопроводов. Журнал науки и техники о природном газе. 2019. Том. 71. с. 1-25. DOI: 10.1016/j.jngse.2019.102971
, Афроухтех С. Комплексный обзор внутренней коррозии и трещинообразования нефтегазопроводов. Журнал науки и техники о природном газе. 2019. Том. 71. с. 1-25. DOI: 10.1016/j.jngse.2019.102971 , Gamboa E., Lavigne O. Обзор моделирования коррозионного растрескивания газопроводов высокого давления под напряжением при высоких значениях pH. Материалы и коррозия. 2015. Том. 67. Вып. 3, с. 251-263. DOI: 10.1002/maco.201508454
, Gamboa E., Lavigne O. Обзор моделирования коррозионного растрескивания газопроводов высокого давления под напряжением при высоких значениях pH. Материалы и коррозия. 2015. Том. 67. Вып. 3, с. 251-263. DOI: 10.1002/maco.201508454 Анализ технических отказов. 2014. Том. 46, с. 157-165. DOI: 10.1016/j.engfailanal.2014.08.011
Анализ технических отказов. 2014. Том. 46, с. 157-165. DOI: 10.1016/j.engfailanal.2014.08.011