Луб | это… Что такое Луб?
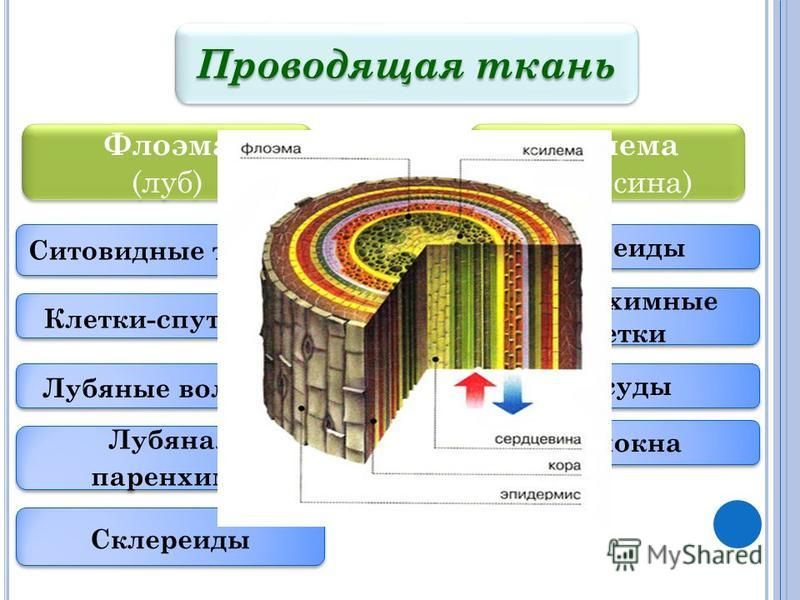
флоэма, сложная ткань высших растений, служащая для проведения органических веществ к различным органам. Л. выполняет также запасающую, нередко механическую и отчасти выделительную функции. В соответствии с многообразием функций для Л. характерно наличие различных элементов: ситовидных элементов, клеток запасающей и кристаллоносной лубяной паренхимы, лубяных волокон (См. Лубяные волокна) и склереид (См. Склереиды), радиальной паренхимы сердцевинных лучей. У некоторых растений в Л. имеются Млечники и смоляные ходы. Ситовидные элементы у покрытосеменных представлены ситовидными трубками. Они состоят из продольного ряда клеток (члеников), сообщающихся «ситечками» — тонкими участками в стенках со сквозными отверстиями. В протопластах ситовидных элементов рано отмирают ядра, цитоплазма становится вполне проницаемой для растворённых в воде органических веществ и минеральных солей; оболочка целлюлозная, часто с утолщением. Скорость передвижения пластических веществ по Л.
Запасающая ткань в Л. представлена клетками осевой лубяной и лучевой паренхимы. Лубяная паренхима образована удлинёнными клетками (веретеновидная паренхима) или короткими, соединёнными в вертикальный тяж (тяжевая паренхима). Клетки сердцевинных лучей образуются особыми инициальными клетками камбия (См. Камбий) и могут быть вытянуты в радиальном или в вертикальном направлении.
P. П. Барыкина.
П. Барыкина.
Анатомическое строение луба липы (поперечный срез): с. т. — ситовидные трубки; с. п. — ситовидные пластинки; сд — содержимое ситовидных трубок; с. к. — сопровождающие клетки; л. в. — лубяные волокна; п. с. л. — первичный сердцевинный луч; в. с. л. — вторичный сердцевинный луч; к. п. — кристаллоносные паренхимные клетки; кр — кристаллы оксалата кальция; др — друзы оксалата кальция; з. п. — клетки запасающей паренхимы.
Страница не найдена
Размер:
AAA
Цвет: C C C
Изображения Вкл. Выкл.
Обычная версия сайтаRUENBY
Гомельский государственный
медицинский университет
- Университет
- Университет
- История
- Руководство
- Устав и Символика
- Воспитательная деятельность
- Международное сотрудничество
- Система менеджмента качества
- Советы
- Факультеты
- Кафедры
- Подразделения
- Первичная профсоюзная организация работников
- Издания университета
- Гордость университета
- Выпускник-2021
- Первичная организация «Белорусский союз женщин»
- Одно окно
- ГомГМУ в международных рейтингах
- Структура университета
- Абитуриентам
- Приёмная комиссия
- Университетская олимпиада по биологии
- Целевая подготовка
- Заключение, расторжение «целевого» договора
- Льготы для молодых специалистов
- Архив проходных баллов
- Карта и маршрут проезда
- Порядок приёма на 2023 год
- Специальности
- Контрольные цифры приёма в 2022 году
- Стоимость обучения
- Информация о ходе приёма документов
- Приём документов и время работы приёмной комиссии
- Порядок приёма граждан РФ, Кыргызстана, Таджикистана, Казахстана
- Горячая линия по вопросам вступительной кампании
- Студентам
- Первокурснику
- Расписание занятий
- Расписание экзаменов
- Информация для студентов
- Студенческий клуб
- Спортивный клуб
- Общежитие
- Нормативные документы
- Практика
- Стоимость обучения
- БРСМ
- Профком студентов
- Учебный центр практической подготовки и симуляционного обучения
- Многофункциональная карточка студента
- Анкетирование студентов
- Выпускникам
- Интернатура и клиническая ординатура
- Докторантура
- Аспирантура
- Магистратура
- Распределение
- Врачам и специалистам
- Профессорский консультативный центр
- Факультет повышения квалификации и переподготовки
- Иностранным гражданам
- Факультет иностранных студентов
- Стоимость обучения
- Регистрация и визы
- Полезная информация
- Правила приёма
- Информация о возможностях и условиях приема в 2022 году
- Официальные представители ГомГМУ по набору студентов
- Страхование иностранных граждан
- Приём на Подготовительное отделение иностранных граждан
- Прием иностранных граждан для обучения на английском языке / Training of foreign students in English
- Повышение квалификации и переподготовка для иностранных граждан
- Научная деятельность
- Направления научной деятельности
- Научно-педагогические школы
- Инновационные технологии в ГомГМУ
- Научно-исследовательская часть
- Научно-исследовательская лаборатория
- Конкурсы, гранты, стипендии
- Научные мероприятия
- Работа комитета по этике
- В помощь исследователю
- Совет молодых ученых
- Студенчеcкое научное общество
- Диссертационный совет
- Патенты
- Инструкции на метод
- «Горизонт Европа»
- Госпрограмма (ЧАЭС)
- Главная
реальный анализ — Упорядоченное поле рациональных функций не обладает свойством LUB, может кто-нибудь привести пример?
спросил
Изменено 6 лет, 5 месяцев назад
Просмотрено 397 раз
$\begingroup$
S является набором некоторых рациональных функционалов и ограничен сверху, но S не имеет точной верхней границы.
Кто-нибудь может привести пример S?
- реальный анализ
- рациональные функции
$\endgroup$
2
$\begingroup$
Мы предполагаем, что вы имеете в виду рациональные функции с вещественными коэффициентами. Один из распространенных способов определения порядка — это сказать, что $r_1(x)\lt r_2(x)$, если для всех достаточно больших действительных $b$ мы имеем $r_1(b)\lt r_2(b)$.
Пусть $S=\{1,2,3,4,\dots\}$. Это множество ограничено сверху, например многочленом $x$, но не имеет точной верхней границы.
Схема доказательства: Предположим противное, что $r(x)=\frac{p(x)}{q(x)}$ является наименьшей верхней границей для $S$, где $p$ и $q$ являются многочленами без ограничения общности с положительными ведущими коэффициентами
Если $p$ имеет степень меньше степени $q$, то $p/q$ не является верхней гранью для $S$. 2}$, для которой $p_i()$, конечно, являются частичными разложениями Тейлора.)
2}$, для которой $p_i()$, конечно, являются частичными разложениями Тейлора.)
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Разница в определениях glb и lub в реальном анализе и абстрактной алгебре
спросил
Изменено 6 лет, 10 месяцев назад
Просмотрено 8к раз
$\begingroup$
Следующий текст взят из книги Abstract Algebra Т. В. Джадсона:
Пусть $X = {\{1,2,3,4,6,8,12,24}\}$ — множество делителей $24$ с частичным порядком, определяемым $a\preceq b$, если $a | б$. … Пусть $Y = {\{2, 3, 4, 6}\}$ содержится в множестве $X$. Тогда $Y$ имеет верхние границы $12$ и $24$, причем $12$ является наименьшей верхней границей. Единственная нижняя граница — $1$; следовательно, это должна быть наибольшая нижняя граница.
В реальном анализе наибольшая нижняя граница и нижняя верхняя граница ${\{2, 3, 4, 6}\}$ составляют $2$ и $6$ соответственно. Почему они не могут быть элементами самого множества в абстрактной алгебре?
- реальный анализ
- абстрактная алгебра
$\endgroup$
1
$\begingroup$
Г.л.б. и л.у.б. из анализа, который вы упоминаете, относятся к обычному частичному порядку (фактически, полному порядку) $\leq$. Действительно, у нас есть $2 \leq 3 \leq 4 \leq 6$, поэтому г.л.б. w.r.t. $\leq$ равен $2$, а л.у.б. составляет $6$.
В данной задаче указан другой частичный порядок , а именно $\preceq$ (или $\mid$). В этом случае у нас нет, например, ни $3 \preceq 4$, ни $4 \preceq 3$. Единственными элементами $x \in X$, такими что $2 \preceq x$, $3 \preceq x$, $4 \preceq x$ и $6 \preceq x$, являются $12$ и $24$, а также $12 \preceq 24$, поэтому $12$ — это луб.