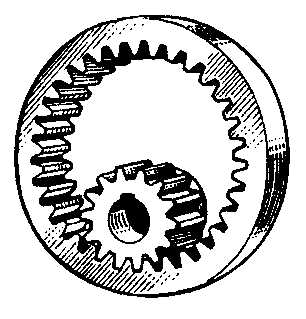
2 Общие сведения о зубчатых передачах
2.1 Описание зубчатых передач
Зубчатые передачи являются разновидностью механических передач, работающих на принципе зацепления. Их используют для передачи и преобразования вращательного движения между валами.
Зубчатые передачи отличаются высоким КПД (для одной ступени – 0,97-0,99 и выше), надежностью и длительным сроком службы, компактностью, стабильностью передаточного отношения из-за отсутствия проскальзывания. Зубчатые передачи применяют в широком диапазоне скоростей (до 200 м/сек), мощностей (до 300 МВт). Размеры зубчатых колес могут быть от долей миллиметра до нескольких метров.
К недостаткам можно отнести сравнительно высокую сложность изготовления, необходимость нарезания зубьев с высокой точностью, шум и вибрация при высоких скоростях, большую жесткость, не позволяющая компенсировать динамические нагрузки.
Передаточные числа в редукторных передачах могут достигать 8, в открытых передачах – до 20, в коробках передач – до 4.
По расположению зубьев различают передачи с наружным и внутренним зацеплением.
Конструктивно зубчатые передачи большей частью выполняются закрытыми в общем жестком корпусе, что обеспечивает высокую точность сборки. Лишь тихоходные передачи (v < 3 м/сек) с колесами значительных размеров, нередко встроенных в конструкцию машин (например, в механизмах поворота подъемных кранов, станков), изготавливаются в открытом исполнении.
Чаще всего зубчатые передачи применяют в качестве замедлительных (редукторов), т.е. для уменьшения частоты вращения и увеличения вращающего момента, но также с успехом используются для повышения скорости вращения (мультипликаторы).
Для предохранения рабочих поверхностей зубьев от заедания и абразивного износа, а также для уменьшения потерь на трение и связанного с этим нагревания, применяют смазку. Закрытые передачи обычно смазываются жидкими минеральными маслами, окунанием колес или принудительной подачей масла к зацепляющимся зубьям. Открытые передачи смазываются консистентными смазками, периодически наносимыми на зубья.
2.2 Виды зубчатых передач
Зубчатые передачи с параллельными валами называются цилиндрические (рис. 2.1), с пересекающимися валами – конические (рис. 2.2).
По расположению зубьев различают передачи с наружным (рис. 2.1а—в) и внутренним зацеплением (рис. 2.1г).
По профилю зубьев колес передачи подразделяют: на передачи с эвольвентным зацеплением, в котором профили зубьев очерчены эвольвентами; на передачи с циклоидальным профилем; на передачи с зацеплением Новикова. Далее в пособии будут описываться только передачи эвольвентного профиля с наружным зацеплением.
Шестерня – это зубчатое колесо передачи с меньшим числом зубьев (чаще всего – ведущее). Колесо – это зубчатое колесо передачи с большим числом зубьев. Термин «зубчатое колесо» можно применять как к шестерне, так и к колесу зубчатой передачи.
Цилиндрические зубчатые передачи бывают прямозубыми, косозубыми и шевронными.
Прямозубые колеса (рис. 2.1а) применяют преимущественно при невысоких и средних окружных скоростях, при большой твердости зубьев (когда динамические нагрузки от неточностей изготовления невелики по сравнению с полезными), в планетарных передачах, в открытых передачах, а также при необходимости осевого перемещения колес (в коробках передач).
|
|
| |
а | б | в | г |
Рис. 2.1. Виды цилиндрических зубчатых передач | |||
Косозубые колеса (рис. 2.1б) обладают более высокой нагрузочной способностью (за счет большей длины зуба при одинаковой ширине зубчатого венца), повышенной плавностью и пониженной шумностью, поэтому их применяют для ответственных передач при средних и высоких скоростях. Объем их применения – свыше 40 % объема применения всех цилиндрических колес в машинах.
Косозубые колеса с твердыми поверхностями зубьев требуют повышенной защиты от загрязнений во избежание неравномерности износа по длине контактных линий и опасности выкрашивания. В косозубом зацеплении возникает осевая сила, которую надо учитывать при проектировании опор и валов.
Шевронные колеса (рис. 2.1в) обладают всеми преимуществами косозубых колес, и при этом отсутствует вредная осевая сила, но их технология изготовления сложней.
Для прямозубых колес угол наклона зубьев = 0°, для косозубых — = 8…20°, для шевронных — = 25…40°.
В косозубых передачах редукторов для шестерен рекомендуют принимать направление зуба левое, для колес – правое.
Большинство серийных редукторов имеют косозубые колеса, причем и в быстроходных и в тихоходных ступенях.
Среди конических зубчатых передач наибольшее распространение в машиностроении имеют передачи с прямыми зубьями. Также часто применяются передачи с круговыми зубьями. Гораздо реже – с тангенциальными и другими криволинейными зубьями.
|
| ||
а | б | ||
Рис. 2.2. Виды конических зубчатых передач | |||
Прямозубые конические передачи (рис. 2.2а) применяют при невысоких окружных скоростях (до 2…3 м/сек, допустимо до 8 м/сек), как наиболее простые в монтаже.
Конические передачи с
studfiles.net
Конические зубчатые передачи, их применение и изготовление
Зубчатые передачи используются человечеством давно, такой способ сообщения энергии вращения является самым распространенным в механике.
Эти механизмы передают движение от одного вала другому, обычно с изменением частоты оборотов за единицу времени. Средством зацепления и непосредственными элементами сообщения движения служат либо колеса, либо рейки с нарезанными на их рабочих поверхностях углублениями и выступами особой формы.
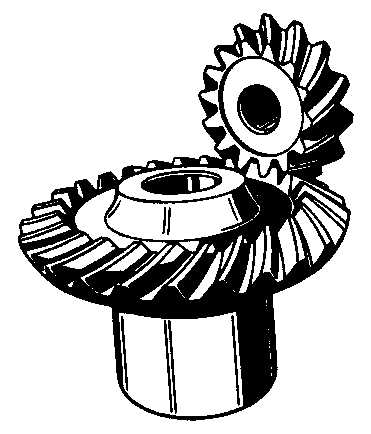
Из двух круглых элементов, взаимодействующих в передаче, один, большего диаметра, принято называть колесом, а второй – шестерней, хотя, в сущности, они оба представляют собой зубчатые колеса.
В зависимости от того, ставится ли в редукторе задача увеличения скорости вращения или, напротив, снижения, ведущим бывает либо колесо, либо шестерня.
Современные конструкционные материалы позволяют создавать зубчатые передачи, способные успешно трансформировать мощность до 36 миллионов Ватт.
Требования к механизмам различны, поэтому и разнообразие форм зубчатых зацеплений очень велико. Оси вращения могут быть параллельными, скрещивающимися или пересекающимися, в зависимости от этого существуют цилиндрические, винтовые, червячные или конические зубчатые передачи. Особенностью последних является способность сообщать вращение валу, расположенному под прямым углом по отношению к ведущей оси. Эта возможность часто нужна в самых различных механизмах, например, передача механической энергии от карданного вала автомобиля к ведущим колесам осуществляется именно по такой кинематической схеме.
Чаще всего коническая зубчатая передача имеет прямые зубья радиальной нарезки (тангенциальные). Если ведущая и ведомая ось не пересекаются, то такой редуктор называют гипоидным. Применение подобных механизмов в конструкции заднего моста вызвано стремлением разработчиков сделать ниже общий центр тяжести автомобиля для придания ему большей устойчивости.
Кроме прямозубых, используются и другие зубчатые передачи, например со спиралевидной нарезкой.
Кроме этого, конические передачи дают возможность сообщения вращения не только под прямым, но и практически под любым другим углом, тупым или острым.
Технология изготовления конических зубчатых колес примерно такая же, как и цилиндрических, но заготовка имеет довольно сложную форму. Она состоит как бы из двух усеченных конусов с общим большим основанием на одной оси. Образующие конусов находятся под прямым углом. Профиль зубьев хорошо виден с нерабочей стороны конического колеса, при этом ширина зуба уменьшается от периферии к центру. Материалом изготовления служит специальная сталь, стойкая к износу и очень твердая.
Профиль нарезки представляет собой линию эвольвенты, такая форма обеспечивает наиболее плавное вращение, равномерность износа и максимальное распределение механического напряжения в момент соприкосновения зубьев.
Зубчатые передачи с переменной по длине формой профиля сложны в изготовлении, и для их получения используются станки с программным управлением.
fb.ru
Виды зубчатых передач
Производство Виды зубчатых передачпросмотров — 123
Описание зубчатых передач
ОБЩИЕ СВЕДЕНИЯ О ЗУБЧАТЫХ ПЕРЕДАЧАХ
Зубчатые передачи являются разновидностью механических передач, работающих на принципе зацепления. Их используют для передачи и преобразования вращательного движения между валами.
Зубчатые передачи отличаются высоким КПД (для одной ступени – 0,97-0,99 и выше), надежностью и длительным сроком службы, компактностью, стабильностью передаточного отношения из-за отсутствия проскальзывания. Зубчатые передачи применяют в широком диапазоне скоростей (до 200 м/сек), мощностей (до 300 МВт). Размеры зубчатых колес бывают от долей миллиметра до нескольких метров.
К недостаткам можно отнести сравнительно высокую сложность изготовления, крайне важность нарезания зубьев с высокой точностью, шум и вибрация при высоких скоростях, большую жесткость, не позволяющая компенсировать динамические нагрузки.
Передаточные числа в редукторных передачах могут достигать 8, в открытых передачах – до 20, в коробках передач – до 4.
По расположению зубьев различают передачи с наружным и внутренним зацеплением.
Конструктивно зубчатые передачи большей частью выполняются закрытыми в общем жестком корпусе, что обеспечивает высокую точность сборки. Лишь тихоходные передачи (v < 3 м/сек) с колесами значительных размеров, нередко встроенных в конструкцию машин (к примеру, в механизмах поворота подъемных кранов, станков), изготавливаются в открытом исполнении.
Чаще всего зубчатые передачи применяют в качестве замедлительных (редукторов), ᴛ.ᴇ. для уменьшения частоты вращения и увеличения вращающего момента͵ но также с успехом используются для повышения скорости вращения (мультипликаторы).
Для предохранения рабочих поверхностей зубьев от заедания и абразивного износа, а также для уменьшения потерь на трение и связанного с этим нагревания, применяют смазку. Закрытые передачи обычно смазываются жидкими минеральными маслами, окунанием колес или принудительной подачей масла к зацепляющимся зубьям. Открытые передачи смазываются консистентными смазками, периодически наносимыми на зубья.
Зубчатые передачи с параллельными валами называются цилиндрические (рис. 2.1), с пересекающимися валами – конические (рис. 2.2).
По расположению зубьев различают передачи с наружным (рис. 2.1а—в) и внутренним зацеплением (рис. 2.1г).
По профилю зубьев колес передачи подразделяют: на передачи с эвольвентным зацеплением, в котором профили зубьев очерчены эвольвентами; на передачи с циклоидальным профилем; на передачи с зацеплением Новикова
. Далее в пособии будут описываться только передачи эвольвентного профиля с наружным зацеплением.Шестерня — ϶ᴛᴏ зубчатое колесо передачи с меньшим числом зубьев (чаще всего – ведущее). Колесо — ϶ᴛᴏ зубчатое колесо передачи с большим числом зубьев. Термин «зубчатое колесо» можно применять как к шестерне, так и к колесу зубчатой передачи.
Цилиндрические зубчатые передачи бывают прямозубыми, косозубыми и шевронными.
Прямозубые колеса (рис. 2.1а) применяют преимущественно при невысоких и средних окружных скоростях, при большой твердости зубьев (когда динамические нагрузки от неточностей изготовления невелики по сравнению с полезными), в планетарных передачах, в открытых передачах, а также при крайне важности осевого перемещения колес (в коробках передач).
| а | б | в | г |
| Рис. 2.1. Виды цилиндрических зубчатых передач |
Косозубые колеса (рис. 2.1б) обладают более высокой нагрузочной способностью (за счет большей длины зуба при одинаковой ширине зубчатого венца), повышенной плавностью и пониженной шумностью, в связи с этим их применяют для ответственных передач при средних и высоких скоростях. Объем их применения – свыше 40 % объема применения всех цилиндрических колес в машинах.
Косозубые колеса с твердыми поверхностями зубьев требуют повышенной защиты от загрязнений во избежание неравномерности износа по длине контактных линий и опасности выкрашивания. В косозубом зацеплении возникает осевая сила, которую нужно учитывать при проектировании опор и валов.
Шевронные колеса (рис. 2.1в) обладают всеми преимуществами косозубых колес, и при этом отсутствует вредная осевая сила, но их технология изготовления сложней.
Для прямозубых колес угол наклона зубьев b = 0°, для косозубых — b = 8…20°, для шевронных — b = 25…40°.
В косозубых передачах редукторов для шестерен рекомендуют принимать направление зуба левое, для колес – правое.
Большинство серийных редукторов имеют косозубые колеса, причем и в быстроходных и в тихоходных ступенях.
Среди конических зубчатых передач наибольшее распространение в машиностроении имеют передачи с прямыми зубьями. Также часто применяются передачи с круговыми зубьями. Гораздо реже – с тангенциальными и другими криволинейными зубьями.
| а | б | ||
| Рис. 2.2. Виды конических зубчатых передач |
Прямозубые конические передачи (рис. 2.2а) применяют при невысоких окружных скоростях (до 2…3 м/сек, допустимо до 8 м/сек), как наиболее простые в монтаже.
Конические передачи с круговыми зубьями (рис. 2.2б) имеют более плавное зацепление и в связи с этим большие быстроходность и несущую способность. Οʜᴎ более технологичны.
2.3Материалы зубчатых колес и термическая или химико-термическая обработка
Материалы зубчатых колес и термическая или химико-термическая обработка выбираются в зависимости от назначения передачи, условий эксплуатации и требований к габаритным размерам.
Для повышения несущей способности передач целесообразно повышение твердости поверхности зубьев, т.к. несущая способность передач по контактной прочности пропорциональна квадрату твердости поверхности зубьев. При этом повышение твердости материала отрицательно сказывается на изгибной прочности. Для повышения изгибной прочности желательно сохранять вязкую сердцевину зуба. По этой причине в основном применяется поверхностная термическая или химико-термическая обработка.
Способы упрочнения:
· Нормализация позволяет получить твердость 180…220 HB, в связи с этим нагрузочная способность относительно невелика, но при этом зубья колес хорошо прирабатываются и сохраняют точность, полученную при механической обработке. Нормализованные колеса обычно используют во вспомогательных механизмах, к примеру, в механизмах ручного управления.
Применяемые стали: 40, 45, 50 и др. Для повышения стойкости против заедания шестерни и колеса следует изготавливать из разных материалов.
· Улучшение позволяет получить твердость поверхности и сердцевины 200…240 HB (для небольших шестерен 280…320 HB), нагрузочная способность несколько выше, чем при нормализации, но зубья колес прирабатываются хуже. Обычно улучшенные колеса применяют в условиях мелкосерийного и единичного производства при отсутствии жестких требований к габаритам.
Применяемые стали: 40, 45, 50Г, 35ХГС, 40Х и др.
· Закалка токами высокой частоты (ТВЧ) дает среднюю нагрузочную способность при достаточно простой технологии упрочнения. Позволяет достигать поверхностной твердости 45…55 HRC при глубине упрочненного слоя до 3…4 мм. Закалке ТВЧ обычно предшествует улучшение, в связи с этим механические свойства сердцевины – как при улучшении. Изгибная прочность по сравнению с объемной закалкой выше в 1,5-2 раза. Из-за повышенной твердости зубьев передачи плохо прирабатываются. Размеры зубчатых колес практически неограниченны. Необходимо помнить, что при модулях менее 3…5 мм, зуб прокаливается насквозь, что приводит к значительному их короблению и снижению ударной вязкости.
Применяемые стали: 40Х, 40ХН, 35ХМ, 35ХГСА.
· Цементация (поверхностное насыщение углеродом) с последующей закалкой ТВЧ и обязательной шлифовкой позволяет получить поверхностную твердость 56…63 HRC при глубине упрочненного слоя 0,5…2 мм. Нагрузочная способность высокая, но технология упрочнения более сложная. Изгибная прочность по сравнению с объемной закалкой выше в 2-2,5 раза.
Широко применяют сталь 20Х, а для ответственных зубчатых колес, особенно работающих с перегрузками и ударными нагрузками, стали 12ХН3А, 20ХНМ, 18ХГТ, 25ХГМ, 15ХФ.
· Азотирование (поверхностное насыщение азотом) обеспечивает высокую твердость и износостойкость поверхностных слоев, при этом не требуется последующая закалка и шлифование. Азотирование позволяет получить поверхностную твердость 58…67 HRC при глубине упрочненного слоя 0,2…0,5 мм. Малая толщина упрочненного слоя не позволяет применять азотированные колеса при ударных нагрузках и при работе с интенсивным изнашиванием (при загрязненной смазке, попадании абразива). Длительность процесса азотирования достигает 40-60 часов. Обычно азотирование применяют для колес с внутренним зацеплением и других, шлифование которых затруднено.
Применяют молибденовую сталь 38Х2МЮА, но возможно азотирование сталей 40ХФА, 40ХНА, 40Х до меньшей твердости, но большей вязкости.
· Нитроцементация – насыщение поверхностных слоев углеродом и азотом в газовой среде с последующей закалкой обеспечивает высокую контактную прочность, износостойкость и сопротивление заеданиям, обладает достаточно высокой скоростью протекания процесса – около 0,1 мм/час и выше. В связи с малым короблением позволяет во многих случаях обойтись без шлифования. Содержание азота в поверхностном слое позволяет применять менее легированные стали, чем при цементации: 18ХГТ, 25ХГТ, 40Х и др.
2.4Конструкция зубчатых колес
Конструкция зубчатых колес зависит от их размеров, материала, технологии изготовления и эксплуатационных требований.
Шестерни малых размеров, у которых диаметр окружности впадин зубьев близок к диаметру вала, выполняются за одно целое с валом (вал-шестерня) (рис. 2.3).
| Рис. 2.3. Цилиндрические и коническая вал-шестерни. |
Колеса, допускающие посадку на вал, как правило, делаются насадными. Это дает возможность подбирать различные, наиболее подходящие материалы и термообработку для вала и колеса, упрощают технологию изготовления этих деталей, и позволяет после износа зубьев колеса производить его замену, сохраняя вал.
Шестерни небольшого диаметра (D £ 200 мм) обычно изготовляются из круглого проката (£ 150 мм), кованных или штампованных заготовок в виде сплошного диска или с выступающей ступицей и др. (рис. 2.4).
| Рис. 2.4. Цилиндрические и коническая шестерни. |
Колеса средних размеров (D £ 600 мм) изготовляются из поковок, штампованных или литых заготовок и большей частью имеют дисковую конструкцию (рис. 2.5).
| Рис. 2.5. Конструкция зубчатых колес. |
Зубчатые колеса больших размеров можно изготовлять цельнолитыми, с одним или двумя параллельными дисками, подкрепленными ребрами, или со спицами крестовидного, таврового, двутаврового, овального или другой формы сечения (рис. 2.6).
| Рис. 2.6. Цельнолитые цилиндрические зубчатые колеса. |
При использовании высококачественных сталей для изготовления зубчатого венца, в целях экономии, колеса могут выполняться бандажированными (посадка с гарантированным натягом) или сборными (на призонных болтах, с помощью сварки или клея) (рис. 2.7).
| Рис. 2.7. Бандажированное и сборные цилиндрические зубчатые колеса. |
Читайте также
Описание зубчатых передач ОБЩИЕ СВЕДЕНИЯ О ЗУБЧАТЫХ ПЕРЕДАЧАХ Зубчатые передачи являются разновидностью механических передач, работающих на принципе зацепления. Их используют для передачи и преобразования вращательного движения между валами. Зубчатые… [читать подробенее]
План Лекция № 7 Зубчатые передачи 1. Виды зубчатых передач и зубчатых колес. 2. Геометрические соотношения в эвольвентном зубчатом зацеплении. 3. Косозубые и шевронные колеса. 4. Силы, действующие в зацеплении. 5. Методы изготовление и материалы зубчатых колес. … [читать подробенее]
oplib.ru
Классификация зубчатых передач
Зубчатые передачи с параллельными валами называются цилиндрические (рис. 2.1), с пересекающимися валами – конические (рис. 2.2).
По расположению зубьев различают передачи с наружным (рис. 2.1а—в) и внутренним зацеплением (рис. 2.1г).
По профилю зубьев колес передачи подразделяют: на передачи с эвольвентным зацеплением, в котором профили зубьев очерчены эвольвентами; на передачи с циклоидальным профилем; на передачи с зацеплением Новикова. Далее в пособии будут описываться только передачи эвольвентного профиля с наружным зацеплением.
Цилиндрические зубчатые передачи бывают прямозубыми, косозубыми и шевронными.
Прямозубые колеса применяют преимущественно при невысоких и средних окружных скоростях, при большой твердости зубьев (когда динамические нагрузки от неточностей изготовления невелики по сравнению с полезными), в планетарных передачах, в открытых передачах, а также при необходимости осевого перемещения колес (в коробках передач).
| а | б | в | г |
| Рис. 2.1. Виды цилиндрических зубчатых передач |
Косозубые колеса обладают более высокой нагрузочной способностью (за счет большей длины зуба при одинаковой ширине зубчатого венца), повышенной плавностью и пониженной шумностью, поэтому их применяют для ответственных передач при средних и высоких скоростях. Объем их применения – свыше 40 % объема применения всех цилиндрических колес в машинах.
Косозубые колеса с твердыми поверхностями зубьев требуют повышенной защиты от загрязнений во избежание неравномерности износа по длине контактных линий и опасности выкрашивания. В косозубом зацеплении возникает осевая сила, которую надо учитывать при проектировании опор и валов.
Шевронные колеса обладают всеми преимуществами косозубых колес, и при этом отсутствует вредная осевая сила, но технология их изготовления сложней.
Для прямозубых колес угол наклона зубьев b = 0°, для косозубых — b = 8…20°, для шевронных — b = 25…40°.
В косозубых передачах редукторов для шестерен рекомендуют принимать направление зуба левое, для колес – правое.
Среди конических зубчатых передач наибольшее распространение в машиностроении имеют передачи с прямыми зубьями. Также часто применяются передачи с круговыми зубьями. Гораздо реже – с тангенциальными и другими криволинейными зубьями.
| а | б | ||
| Рис. 2.2. Виды конических зубчатых передач |
Прямозубые конические передачи (рис. 2.2а) применяют при невысоких окружных скоростях (до 2…3 м/сек, допустимо до 8 м/сек), как наиболее простые в монтаже.
Конические передачи с круговыми зубьями (рис. 2.2б) имеют более плавное зацепление и поэтому большие быстроходность и несущую способность. Они более технологичны.
2.3Конструкция зубчатых колес
Конструкция зубчатых колес зависит от их размеров, материала, технологии изготовления и эксплуатационных требований.
| Рис. 2.3. Цилиндрические и коническая вал-шестерни. |
Шестерни малых размеров, у которых диаметр окружности впадин зубьев близок к диаметру вала, выполняются за одно целое с валом (вал-шестерня) (рис. 2.3).
Колеса, допускающие посадку на вал, как правило, делаются насадными. Это дает возможность подбирать различные, наиболее подходящие материалы и термообработку для вала и колеса, упрощают технологию изготовления этих деталей, и позволяет после износа зубьев колеса производить его замену, сохраняя вал. Шестерни небольшого диаметра (D £ 200 мм) обычно изготовляются из круглого проката (£ 150 мм), кованных или штампованных заготовок в виде сплошного диска или с выступающей ступицей и др. (рис. 2.4).
| Рис. 2.4. Цилиндрические и коническая шестерни. |
Колеса средних размеров (D £ 600 мм) изготовляются из поковок, штампованных или литых заготовок и большей частью имеют дисковую конструкцию (рис. 2.5).
| Рис. 2.5. Конструкция зубчатых колес. |
| Рис. 2.6. Цельнолитые цилиндрические зубчатые колеса. |
Зубчатые колеса больших размеров можно изготовлять цельнолитыми, с одним или двумя параллельными дисками, подкрепленными ребрами, или со спицами (рис. 2.6).
Способы нарезания зубьев
Нарезание зубьев зубчатых колес можно производить методом копирования или методом огибания (обкатки).
По методу копирования впадина между зубьями образуется инструментом (дисковой фрезой (рис. 2.7а), пальцевой фрезой (рис. 2.7б), протяжкой, шлифовальным кругом), имеющим профиль впадины. Точность этого метода, особенно по шагу – пониженная. Метод копирования применяют для обработки крупномодульных шевронных колес, для нарезания и для шлифования колес в массовом производстве, а также в условиях ремонтных мастерских. Для нарезания колес с разным числом зубьев необходим комплект инструмента каждого модуля из 8…26 шт.
Методом копирования получают зубчатые колеса пониженной (9-ой) степени точности (см. ниже п. 2.5 «Нормы точности») без дополнительных отделочных операций. Колеса средней (8-ой) степени точности дополнительно отделываются или притираются в паре.
| а | б | в | г |
| Рис. 2.7. Способы нарезания зубьев |
Основное применение имеет метод огибания. По этому методу зубья нарезают инструментом в виде рейки-гребенки (рис. 2.7в), червячной фрезы (рис. 2.7г) или шестерни-долбяка. Нарезание происходит в процессе принудительного зацепления инструмента с заготовкой на зубофрезерном станке. Инструменту дополнительно сообщается движение, обеспечивающее резание.
Метод огибания обеспечивает повышенную производительность и точность по сравнению с методом копирования. Методом огибания изготавливают колеса 6 – 8 степени точности.
Нормы точности
Нормы точности (допуски и отклонения) для цилиндрических (ГОСТ 1643-81) и для конических (ГОСТ 1758-81) зубчатых передач предусматривают 12 степеней точности изготовления этих передач. Допуски на наиболее точные 1 и 2-ю степени (для конических передач – на 1 и 4-ю степени) пока не обусловлены, а на последнюю, наименее точную 12-ю степень не предусматривается, так как она относится к зубчатым колесам, не подвергающимся механической обработке.
Наибольшее практическое распространение имеют 6–9-е степени точности, соответствующие предельным окружным скоростям, приведенным в таблице 2.1. Если к зубчатым передачам предъявляются повышенные требования по плавности работы, бесшумности, более высокого к.п.д., степень точности может быть повышена.
Зубчатые передачи общего назначения обычно имеют 8-ю степень точности.
Зубчатые передачи для грубой работы, к которым не предъявляются требования нормальной точности (выполненные по конструктивным соображениям большими, чем следовало по расчету и т.п.) имеют 9-ю степень точности.
Ответственные скоростные судовые и авиационные передачи имеют 5–7-ю степень и лишь для некоторых специальных прецизионных и высокоскоростных передач назначаются более высокие степени точности или их комбинации.
Таблица 2.1
Степени точности зубчатых колес
infopedia.su
Коническая зубчатая передача.
Конической зубчатой передачей называется зубчатая передача с пересекающимися осями, у зубчатых колёс которой аксоидные, начальные и делительные поверхности конические. Угол между осями ОО1 и ОО2 шестерни и колеса называется межосевым углом (рис 20.1)
Если угол между осями равен 90°, то коническую зубчатую передачу называют ортогональной. В общем случае в не ортогональной передаче угол, дополненный до 180° к углу между векторами угловых скоростей и звеньев 1 и 2, называют межосевым углом (рис. 12.1, a)
Связь между и угловых скоростей 1 и 2 определяется соотношением:
(20.1)
Если через точку О пересечения осей О1О и О2О провести вектор то он совпадет с мгновенной осью ОР относительного движения ведущего и ведомого звеньев и определит конические поверхности аксоидов, называемых начальными конусами. При обозначении параметров, относящихся к начальному конусу, используют индекс . Углы и начальных конусов определяют при решении векторного соотношения (20.1) с использованием теоремы синусов (рис. 20.1, а):
Отношение модулей угловых скоростей | | и | | является передаточным отношением:
(20.3)
При заданных межосевом угле и передаточном отношении u12 углы начальных конусов определяют при совместном решении соотношений (20.2) и (20.3):
Искомые углы и начальных конусов находят по формулам:
(20.4)
(20.5)
 |
Для ортогональной передачи при =90° соотношения (20.4) и (20.5) имеют частный вид: (20.6)
Частным случаем неортогональной передачи является плоская коническая передача, в которой поверхность одного из начальных колес является плоскостью и угол при вершине=90° (рис 20.1, б)
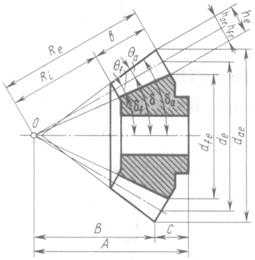Параметры, относящиеся к плоскому коническому колесу, обозначают с добавлением индекса с (например: число зубьев плоского колеса zс, угловая скорость c). Формирование колес, размеров зубьев и расположение их элементов проводят относительно базовой конической поверхности на каждом колесе, называемой делительным конусом. При проектировании конических передач углы 1и 2 делительных конусов принимают совпадающими с углами и начальных конусов, что упрощает расчетные соотношения. Зубья образуют на колесе зубчатый венец, который располагается между конусом вершин с углом a и конусом впадин с углом f (рис 20.2). При изготовлении заготовок и колес используют базовое расстояние А и размеры В до вершины конуса и С — до базовой плоскости.
Поверхность, отделяющая зуб от впадины, называется боковой поверхностью зуба. Пересечение боковой поверхности зуба с соосной поверхностью называют линией зуба. Линия зуба может совпадать с образующей делительного соосного конуса (прямые зубья) или иметь угол наклона линии зуба на делительной поверхности. Различают виды конических колес, отличающихся по форме линий зубьев на развертке делительного конуса (рис 20.3): a — с прямыми; b — тангенциальными; c — круговыми; d, e, f — криволинейными зубьями. Прямозубые передачи используют для работы при легких нагрузках и невысоких скоростях (обычно при частоте вращения <100 об/мин). Для работы в режиме максимальных нагрузок, при высоких скоростях и для обеспечения максимальной плавности работы и бесшумности используют передачи с криволинейными зубьями.
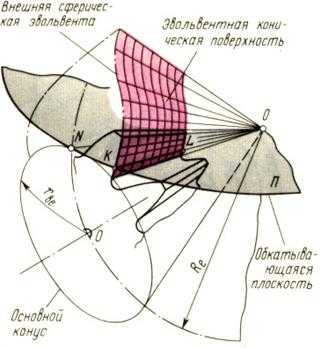Образование боковой поверхности зубьев можно проследить по рис. 20.4. Плоскость П касается основного конуса и перекатывается по нему без скольжения. Любая прямая KL на обкатывающейся плоскости П в пространстве опишет коничес-кую эвольвентную поверхность, а любая точка
Радиус Re внешнего торцевого сечения называют внешним конусным расстоянием. Расстояние между внешним и внутренним торцевыми сечениями конического колеса называют шириной зубчатого венца и обозначают b (см. рис. 20.2).
Взаимодействие сопряженных эвольвентных конических поверхностей при заданных начальных конусах представляет коническое эвольвентное зацепление (рис. 20.5).
Полюсная прямая РО, лежащая в плоскости N1ON2, касательной к основным конусам, может рассматриваться как образующая боковых поверхностей зубьев. Любые сопряженные сферические эвольвенты Э1 и Э2, имеют линию зацепления, расположенную на сфере (например, N1PN2) и являющуюся дугой большого круга сферы.
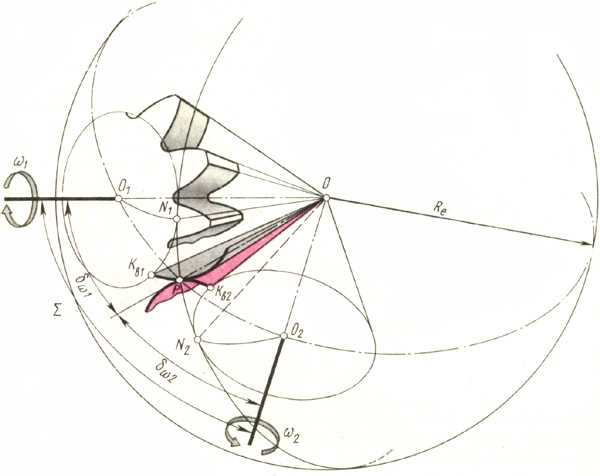
Взаимодействие сферических эвольвент описать в аналитической форме довольно сложно. Учитывая, что высотные размеры зубьев невелики по сравнению с радиусом сферы и профили зубьев расположены на узком сферическом поясе, используют инженерную методику расчета, которая заключается в использовании дополнительных конусов (рис. 20.6).
Дополнительным делительным конусом называют соосную коническую поверхность, образующая которого (например, РОv1 или Р0e2 на рис. 20.6) перпендикулярна образующей делительного конуса конического зубчатого колеса. Введение дополнительных конусов позволяет рассматривать взаимодействие профилей зубьев не на сфере, а на поверхности соприкасающихся со сферой дополнительных конусов. Если дополнительные конусы развернуть на плоскость, то профили зубьев становятся плоскими кривыми, достаточно близкими к обычным эвольвентам, соответствующим определенным размерам основных окружностей, радиусы 0ve1N1 и Ove2N2 которых находят для эквивалентной цилиндрической передачи. Параметры эквивалентной цилиндрической передачи имеют дополнительный индекс vt. Каждое из зубчатых колес такой передачи называют эквивалентным цилиндрическим зубчатым колесом с числами зубьев zvt1 и zvt2 в отличие от чисел зубьев z1 и z2 на конических колесах.
Связь между числами зубьев z1 и zvt1 или z2 и zvt2 легко установить при рассмотрении размеров концентрических окружностей конического и эквивалентного цилиндрического колес:
rvte1 = 0,5de1/cos 1 = 0,5mez1/cos 1 = 0,5mezvt1;
 |
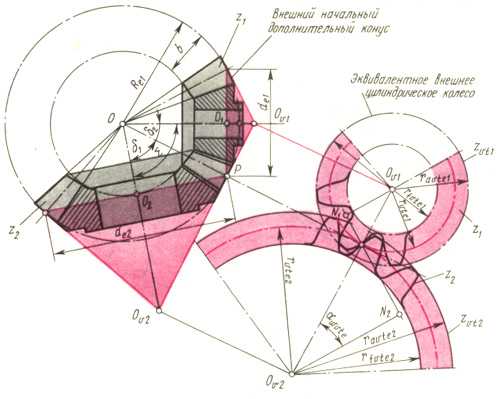rvte2 = 0,5de2/cos 2 = 0,5mez1/cos 2 = 0,5mezvt2
Внешний окружной модуль me, соответствующий расстоянию между одноименными профилями соседних зубьев по дуге концентрической окружности конического колеса на внешнем торце, равен модулю эквивалентной цилиндрической передачи. Поэтому числа зубьев zvt1и zvt2 можно выразить соотношениями:
zvt1 = z1/ cos 1 ; zvt2 = z2/ cos 2(20.7)
В общем случае числа zvt1и zvt2являются дробными и в процессе расчета не округляются, а вычисляются с точностью до 0,01.
Передаточное отношение эквивалентной цилиндрической передачи определяется следующим соотношением:
(20.8)
Угол зацепления wvte эквивалентной цилиндрической передачи, радиусы ravte1 и ravte2 окружностей вершин, радиусы rfvte1 и rfvte2 окружностей впадин (рис. 20.6) рассчитывают по формулам, аналогичным выведенным ранее для цилиндрических эвольвентных передач.
При расчете конических передач с криволинейной линией зуба (см. рис. 20.3) эквивалентная цилиндрическая передача является не прямозубой, а имеет винтовые зубья. Поэтому профили зубьев рассматривают в соответствующих нормальных сечениях. Прямозубое цилиндрическое зубчатое колесо, размеры и форма зубьев которого в главном сечении практически идентичны размерам и форме зубьев конического зубчатого колеса с тангенциальными и криволинейными зубьями в сечении, нормальном к средней линии зуба, называют биэквивалентным цилиндрическим колесом, число зубьев которого обозначают zvn (соответственно zvn1 и zvn2).
С достаточной для практических расчетов точностью коэффициент формы зубьев таких конических колес оценивают по аналогии с биэквивалентным цилиндрическим колесом, число зубьев которого:
zvn1 = z1/ cos 1 cos3n ; zvn2 = z2/ cos 2 cos3n(20.9)
где n — угол наклона средней линии зуба, соответствующий внешнему, среднему, внутреннему или другим расчетным нормальным сечениям зуба конического зубчатого колеса.
Геометрия боковых поверхностей и профилей зубьев теснейшим образом связана с технологией изготовления конических колес. Способ копирования фасонного профиля инструмента для образования профиля на коническом колесе не может быть использован, ибо размеры впадины конического колеса изменяются по мере приближения к вершине конуса. В связи с этим такие инструменты, как модульная дисковая фреза, пальцевая фреза, фасонный шлифовальный круг, могут использоваться только для черновой прорезки впадин или для образования впадин колес не выше 8-й степени точности.
Производящие колеса могут быть плоскими с woc = 90°(рис. 20.7, а, b) или плосковершинными с woc = 90° — fwo1 (рис. 20.7, c) при одном и том же угле wo1 при вершине аксоидного конуса станочного зацепления.
В первых двух случаях образуемые квазиэвольвентные конические колеса будут сопряженными, ибо производящие плоские колеса образуют совпадающую пару, у которой боковые производящие поверхности зубьев могут совпадать при наложении во всех своих точках (как отливка и форма или шаблон и контршаблон). Однако станок, реализующий схему станочного зацепления по рис. 20.7, а, должен иметь поворотные направляющие, допускающие установку резцовых направляющих под углом (90° — fwo1), где fwo1 – угол ножки зуба нарезаемого колеса в станочном зацеплении. Это усложняет конструкцию станка и используется ограниченно.
В случае движения резцов без учета угла fwo1 (рис. 20.7, б) высота ножки зуба по мере приближения к вершине конуса остается неизменной, что ослабляет зуб и приводит иногда к подрезу ножки.
Большинство моделей станков использует плосковершинное производящее колесо, у которого вершины зубьев расположены в плоскости, а угол аксоидного конуса в станочном зацеплении рассчитывается с учетом угла fwo1 ножки зуба нарезаемого колеса. Два плосковершинных колеса не образуют совпадающую производящую пару, и поэтому нарезаемые квазиэвольвентные колеса будут несопряженными. Эти погрешности обычно являются незначительными и ими обычно пренебрегают.
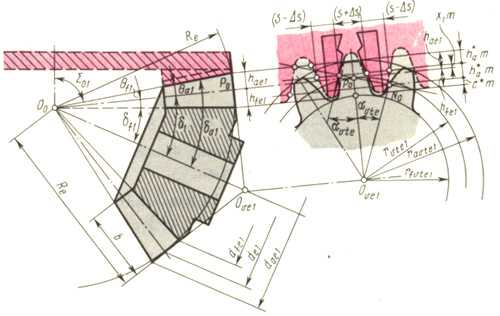
Расчетная схема, приведенная на рис. 20.8, позволяет на базе станочного зацепления конического колеса с производящим плосковершинным колесом перейти к эквивалентному станочному зацеплению с теоретическим исходным контуром. Исходный контур, совпадающий с реечным контуром, принятым в качестве базового для определения теоретических форм и размеров зубьев конических колес, регламентирован по ряду параметров: = 20°; h*a = 1,2 ; c* = 0,2 ; 0,3. Однако с учетом особенностей методов нарезания зубьев эти параметры можно изменять в пределах использования стандартного инструмента. Так, например, можно допускать неравенство толщины зуба и ширины впадины по делительной прямой за счет относительного расположения соседних резцов; не требуется строгого соответствия номинального модуля резцов модулю нарезаемого колеса. Внешний модуль может быть нестандартным и даже дробным. Можно изменять угол за счет наклона резцов,
Расчет параметров конической передачи проводят а такой последовательности (рис. 20.8):
число зубьев плоского колеса:
(20.10)
при =90°
(20.11)
внешнее конусное расстояние:
Re = 0,5mezc(20.12)
ширина зубчатого венца b 0,3Re или b 10me ; коэффициент ширины зубчатого венца kbe = b/Rwe = 0,2 0,3 ;
угол делительного конуса
1 = arctg ( sin /(z2/z1 + cos )) ; (20.13)
2 = — 1 ;(20.14)
при =90°
1 = arctg ( z1/z2 ); (20.15)
коэффициент смещения исходного контура x1 = 0 0,6в зависи-мости от числа зубьев z1 и передаточного отношения передачи ; x2 = — x1;
x1 x1min = 1,068 – 0,058z1/cos 1(20.16)
коэффициент изменения расчётной толщины зуба исходного контура
x 1 = 0,03 — 0,008(z2/z1 – 2,5) ; x 2 = — x 1 (20.17)
Расчёт параметров зубчатых колёс проводят по следующим расчётным формулам, вывод которых основан на расчётной схеме (рис 20.8)
внешняя высота головки зуба
hae1 = (h*a + x1)me ; hae2 = 2h*ame – hae1;(20.18)
внешняя высота ножки зуба
hfe1= hae2 + c*me ; hfe2 = hae1 + c*me ; (20.19)
внешняя высота зуба
he = hae + hfe;(20.20)
внешняя окружная толщина зуба
se1 = (0,5 + 2x1tg + x 1)me ; se2 = me – se1 ; (20.21)
угол ножки зуба
f1 = arctg hfe1/Re ; (20.22)
f2 = arctg hfe2/Re ; (20.23)
угол головки зуба
1 < f2 ; a2 < f1 (20.24)
угол конуса вершин
a1 = 1 + a1 ; a2 = 2 + a2 (20.25)
угол конуса впадин
f1 = 1 + f1 ; f2 = 2 + f2 (20.26)
внешний делительный диаметр
de1 = mez1 ; de2 = mez2 (20.27)
внешний диаметр вершин зубьев
dae1 = de1 + 2hae1 cos 1 ; dae2 = de2 + 2hae2 cos2 (20.28)
При выборе исходных данных учитывают заданные передаточные отношения u12 и его допустимое отклонение в связи с тем, что число зубьев – целые числа.
Рекомендуется назначать числа зубьев колёс в пределах от 12 до 100.
Для прямозубых конических передач передаточные отношения рекомендуется назначать: u12 < 5– для редуктора,u12 0,35– для мультипликатора.
Параметры исходного контура – по ГОСТ 13754-81
Контрольные вопросы к лекции N20.
1. Для каких целей используются конические зубчатые передачи?
2. Укажите достоинства и недостатки конических зубчатых передач
3. Каковы особенности расчёта геометрии конических колёс и передач?
4. Расскажите об особенностях технологии зуборезания конических колёс
5. Как определяются углы вершин начальных конусов в конической прямозубой передаче при известном передаточном отношении и межосевом угле?
Похожие статьи:
poznayka.org
1
44. Особенности расчета косозубых и шевронных колес на сопротивление контактной и изгибной усталости. Чем обуславливается повышение нагрузочной способности косозубых и шевронных передач по сравнению с прямозубыми.
Контактная усталость:
В косозубых и шевронных передачах зубья входят в зацепление постепенно. Расчет проводят с учетом геометрии в сечении, нормальном к направлению зуба. Результирующая сила в нормальной плоскости на делительной окружности . Суммарная длина контактных линий , . Радиус кривизны эвольвенты в полюсе зацепления в нормальном сечении .
Ψab – коэффициент относительной ширины колеса, KH – коэффициент нагрузки. Условие контактной прочности , максимальное расчетное напряжение , T1П – максимальный вращающий момент на шестерне, T1 – вращающий момент на шестерне, принятый при расчетах на выносливость при изгибе.
На изгибную усталость:
Для косозубых и шевронных передач характерно повышенное сопротивление усталости при изгибе.
— коэффициент, учитывающий торцевое перекрытие.
— коэффициент, учитывающий наклон зуба, получен экспериментально. — коэффициент осевого перекрытия.
Прочность зубьев при однократной нагрузке .
Максимальные расчетные напряжения , Tmax – максимальный вращающий момент на шестерне, T – вращающий момент на шестерне, принятый при расчетах на выносливость при изгибе.
45. Конические зубчатые передачи, достоинства и недостатки, Область применения. Типы зубчатых колес, основные геометрические параметры конического зубчатого колеса. Передаточное число конической зубчатой передачи.
Конические зубчатые передачи передают механическую энергию между валами с пересекающимися осями. Несмотря на сложность изготовления и монтажа, конические передачи получили широкое распространение в редукторах общего назначения, в металлообрабатывающих станках, вертолетах, автомобилях. (Это достоинства).
Недостатки: 1) необходимость регулировки передачи 2) меньшая нагрузочная способность 3) сложность изготовления и более высокие точности 4) большие осевые нагрузки.
Зацепление двух конических колес можно представить как качение без скольжения конусов с углами при вершинах 2δ1 и 2δ2. Эти конусы называют начальными. Линию касания этих конусов ОЕ называют полюсной линией или мгновенной осью в относительном вращении колес. Основное
применение получили передачи ортогональные с суммарным углом между осями δ1+ δ2 = 90°. Конические зубчатые передачи выполняют без смещения исходного контура (x1 = 0, х2=0) или равносмещенными (х2=-х1). Поэтому начальные конусы совпадают с делительными.
Конические колеса обычно выполняют прямозубыми или с круговыми зубьями Прямозубые передачи в основном применяют при окружных скоростях до 3 м/с, при более высоких скоростях применяют передачи с круговыми зубьями. Конические колеса с косыми зубьями применяют весьма редко из-за сложности изготовления и контроля.
Основные геометрические параметры.
К основным относятся следующие геометрические параметры конических зубчатых колес.
Углы, делительных конусов связаны с их диаметрами (и числами зубьев z).
Модуль конического колеса меняется по длине зуба. За основной принимают окружной модуль на внешнем торце mte, который удобно измерять. Внешние делительные диаметры колес равны
Внешнее конусное расстояние
Конусное расстояние до середины зуба
, где — коэффициент ширины зубчатого венца.
Средний делительный диаметр и модуль находят из подобных треугольников
Диаметр вершин зубьев
При расчете на прочность конические колеса заменяют на равнопрочные им цилиндрические колеса. Диаметр эквивалентного зубчатого колеса равен
.
Эквивалентное число зубьев из зависимости равно
.
Для передач с круговыми зубьями приводят еще косозубое колесо к прямозубому
Понижающие конические передачи можно выполнять с передаточным отношением u=1…10. Обычно u<6. Повышающие передачи имеют u не более 3. Большие передаточные отношения усложняют конструирование шестерни и ее опор. Число зубьев колеса .
nex7.narod.ru
Конические зубчатые передачи
Количество просмотров публикации Конические зубчатые передачи — 178
Общие сведения и характеристика. Конические зубчатые колеса применяют в передачах, у которых оси валов пересекаются под углом(рисунок 11.14). Чаще используются передачи с углом = 90°. Конические передачи сложнее цилиндрических в изготовлении и монтаже. Кроме допусков на размеры зубьев, здесь крайне важно выдерживать допуски на углы , 1 и 2, а при монтаже обеспечивать совпадение вершин делительных конусов. Пересечение осей валов усложняет размещение подшипниковых опор.
Размещено на реф.рф
Одно из конических колес, как правило, шестерня располагается консольно. При такой схеме увеличивается неравномерность распределения нагрузки по длине зуба (рисунок 11.5). В зацеплении конических колес действуют осевые силы. Из опыта эксплуатации установлено, что нагрузочная способность конической прямозубой передачи составляет около 0,85 цилиндрической.
Геометрические параметры. Аналогами делительных днаметров цилиндрических передач в конических являются делительные конусы с углами 1: и 2. Конусы, образующие которых перпендикулярны образующим делительных конусов (рисунок 11.15), называют дополнительными конусами. Сечение колеса дополнительным конусом называют торцовым сечением. Различают внешнее, внутреннее и среднее торцовые сечения.
Рисунок 11.14 – Коническая зубчатая передача
Размеры внешнего торцового сечения имеют индекс е, к примеру de, Reи т. д. Размеры в среднем сечении имеют индекс т: dm, Rmи др.
Размещено на реф.рф
Где Re – внешнее конусное расстояние, Rm – среднее конусное расстояние, b – длина зуба или ширина зубчатого венца.
Рисунок 11.15 – Схема приведения прямозубого конического колеса к эквивалентному прямозубому цилиндрическому
Размеры по внешнему торцовому сечению удобнее для измерения, в связи с этим их указывают на рабочих чертежах. Размеры в среднем торцовом сечении используют при расчетах на прочность. Зависимости размеров в среднем и внешнем торцовом сечениях:
. (11.36)
Передаточное число:
. (11.37)
Выразив d1 и d2через конусное расстояние R и углы делительных конусов и, получим
и при Σ==90° u = tg2=ctg1. (11.38)
Эти формулы используют для определения углов и
Силы в зацеплении прямозубой конической передачи. По нормали к поверхности зуба действует нормальная сила Fn, которую раскладывают на окружную силу Ft, радиальную силу Frи осевую силу Fa. Зависимость между этими силами можно увидеть на рисунке 11.14, где силы приложены к шестерне. Вначале силу Fnраскладывают на Ftи F’r(см. сечение зуба на рисунке 11.14). Далее F’rраскладывают на Fаи Fr(на рисунке 11.14 в зоне зацепления). В результате получим следующие зависимости для шестерни
, (11.39)
, ,
,
.
Для колеса силы направлены противоположно. Тогда радиальная сила для колеса равна осевой силе Faдля шестерни (Fr2 = Fa1),а осевая сила для колеса равна радиальной силе Frдля шестерни (Fa2= Fr1).
Приведение прямозубого конического колеса к эквивалентному прямозубому цилиндрическому. Параметры эквивалентных колес используют в расчетах на прочность. Форма зуба конического колеса в нормальном сечении (внешнее торцевое сечение) дополнительным конусом (рисунок 11.15) такая же, как у цилиндрического прямозубого колеса. Эквивалентное цилиндрическое колесо получается при развертке дополнительного конуса, которая ограничена углом . Тогда диаметры эквивалентных колес можно определить по формулам:
для шестерни
,
для колеса
. (11.40)
Выразив диаметры через z и m, получим , .
Тогда числа зубьев эквивалентных колес можно определить по формулам:
(11.41)
Расчет прямозубой конической передачи на контактную прочность. Для конических колес ρпр в формуле (1.4) определяют по радиусам эквивалентных колес. По формулам (11.40), для среднего торцового сечения зуба получим
.
Учитывая связь тригонометрических функций и формулу (11.38), находим
; .
После подстановки и преобразований получим
. (11.42)
Из формулы (11.42) видно, что приведенный радиус кривизны в различных сечениях зуба конического колеса изменяется пропорционально диаметрам этих сечений или расстоянию от вершины делительного конуса. Удельная нагрузка q также пропорциональна этим расстояниям. Следовательно, отношение постоянно для всех сечений зуба. Постоянными остаются и контактные напряжения по всей длине зуба, это позволяет выполнять расчет в любом сечении, в данном случае по среднему. Удельная нагрузка в данном сечении (рисунок 11.16)
. (11.43)
По сравнению с формулами для прямозубых цилиндрических передач видно, что формулы для q совпадают, а для различаются только числителями: вместо (и + 1).
Рисунок 11.16 м Удельная нагрузка сечения:
а) размеры поперечного сечения зуба конического колеса;
б) распределение нагрузки по длине зуба
Учитывая это различие, преобразовываем формулу (11.9) для проверочного расчета прямозубых конических передач в виде
, (11.44)
где – = 0,85 – опытный коэффициент, характеризующий понижение прочности конической прямозубой передачи по сравнению с цилиндрической.
Для проектного расчета формулу (11.44) преобразуют. Считают, что основными габаритными размерами для конических передач являются de2и Re, а нагрузка является моментом Т2на ведомом валу. После введения этих параметров и некоторых преобразований получают
, (11.45)
где – коэффициент ширины зубчатого венца относительно внешнего конусного расстояния. Рекомендуют Кbe < 0,З. Чаще принимают значение Кbe= 0,285. Тогда
. (11.46)
В формулах (11.45) и (11.46) принято: = 20°, KHv= 1,5. Коэффициент полезного действия. КПД зубчатой передачи
, (11.47)
где Р1, – мощность на входе, Р2 – мощность на выходе, Рr – мощность, потерянная в передаче.
При этом, Рr = Р3 + Рп +(–РГ), где Р3 – мощность, потерянная на трение, Рп – мощность, потерянная на трение в подшипниках, Рг – мощность, потерянная на разбрызгивание и перемешивание масла (гидравлические потери).
КПД зубчатой передачи можно записать в виде
, (11.48)
где 3 – КПД зацепления, п – КПД пары подшипников, г – КПД гидравлических потерь.
На практике определяют суммарные потери в передаче. В расчетах можно использовать следующие ориентировочные значения КПД одной ступени зубчатого редуктора на подшипниках качения при номинальной нагрузке:
Таблица 11.2 – Значения КПД одной ступени зубчатого редуктора на подшипниках качения
referatwork.ru