Как вычислить кубатуру бревна: способы вычислений, таблицы из нормативных документов

Как рассчитать объем бревна? |

Бревна очень часто используются для постройки домов из сруба, бань, беседок и других построек. Для того, чтобы закупить или заготовить правильное количество материала необходимо узнать его объем. Итак, как же рассчитать объем бревна?

Объем бревна измеряют в кубических метрах и называют кубатура бревна.

Необходимо знать объем бруса как при строительстве, так и при продаже- покупке дров.

Рассмотрим, как посчитать кубатуру круглого леса.

Существует несколько способов, которые широко используются для того, чтобы определить объем круглого леса.

Как определить объем бревна. Способ 1

этот метод заключается в измерении объема пространства в котором находятся бревна. Это может быть склад, сарай, поленница, кузов фуры и другие строения прямоугольной формы. Для того, чтобы определить объем бревна в помещении необходимо:

— измерить кубический объем пространства. Для этого измерьте высоту, и ширину помещения. Полученные значения нужно умножить друг на друга. Получение значение и есть объем.

— важно учитывать, что бревна, сложенные в помещении, не занимают все его пространство, между бревнами образуются прослойки воздуха, такие прослойки необходимо исключить из общего объема. Считается, что такие прослойки занимают примерно 20% пространства. Соответственно, восемьдесят процентов занимает древесина. Коэффициент пустот, который используют в формуле, составляет 0,8. Для того, чтобы рассчитать объем бруса необходимо умножить объем помещения на коэффициент пустот (0,8). Полученная цифра и будет кубатурой бревна.

Как определить объем бревна — способ 2

Второй метод расчета кубатуры бревна подходит для бруса одинаковой длинны и примерно одинакового диаметра.

Рассчитать объем бревна формула:

v = Pi*R*L,

Pi — 3,14

R — радиус бревна

L — длинна бревна

 

Так как бревна имеют похожий диаметр, но все же немного отличаются для более точного результата нам необходимо замерить какой объем занимают три бревна.

Вычисляем мы это по формуле, приведенной выше. После этого три полученных значения суммируем и делим на три, таким образом мы получим усредненное значение объема. Это значение умножаем на количество бревен, таким образом мы получим число обозначающее объем всего пиломатериала.

Как определить объем бруса способ 3

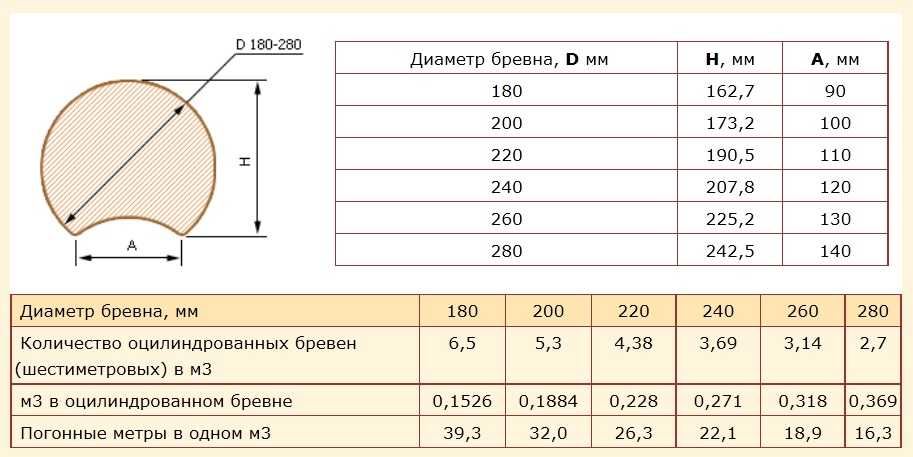
Третий способ часто используют в строительстве для того что бы определить какой объем бревна необходим для постройки того или иного здания. Представляет собой он готовые таблицы, в которых уже приведены посчитанные значения объема, наработанные строителями. Для того, чтобы найти необходимое значение вам потребуется замерить диаметр и длину имеющегося у вас бревна и подставить полученные значения в таблицу, на пересечении вы получите объем бревна.

 

Кубатура бревна таблица:

Диаметр, см / Длина, м	3	3,5	4	4,5	5	5,5	6	6,5	7	7,5	8
10	0,026	0,031	0,037	0,044	0,051	0,058	0,065	0,075	0,082	0,09	0,1
11	0,032	0,037	0,045	0,053	0,062	0,07	0,08	0,09	0,098	0,108	0,12
12	0,038	0,046	0,053	0,063	0,073	0,083	0,093	0,103	0,114	0,125	0,138
13	0,045	0,053	0,062	0,074	0,085	0,097	0,108	0,12	0,132	0,144	0,158
14	0,052	0,061	0,073	0,084	0,097	0,11	0,123	0,135	0,15	0,164	0,179
15	0,06	0,071	0,084	0,097	0,11	0,125	0,139	0,153	0,169	0,182	0,199
16	0,069	0,082	0,095	0,11	0,124	0,14	0,155	0,172	0,189	0,2	0,22
17	0,077	0,092	0,107	0,124	0,14	0,157	0,174	0,191	0,209	0,225	0,25
18	0,086	0,103	0,12	0,138	0,156	0,175	0,194	0,21	0,23	0,25	0,28
19	0,097	0,115	0,134	0,154	0,173	0,193	0,212	0,235	0,255	0,275	0,305
20	0,107	0,126	0,147	0,17	0,19	0,21	0,23	0,26	0,28	0,3	0,33
21	0,119	0,14	0,163	0,185	0,21	0,23	0,255	0,285	0,31	0,335	0,365
22	0,13	0,154	0,178	0,2	0,23	0,25	0,28	0,31	0,34	0,37	0,4
23	0,144	0,169	0,194	0,22	0,25	0,275	0,305	0,335	0,37	0,4	0,435
24	0,157	0,184	0,21	0,24	0,27	0,3	0,33	0,36	0,4	0,43	0,47
25	0,171	0,197	0,23	0,26	0,295	0,325	0,36	0,395	0,43	0,465	0,505
26	0,185	0,21	0,25	0,28	0,32	0,35	0,39	0,43	0,46	0,5	0,54
27	0,203	0,23	0,27	0,305	0,345	0,38	0,42	0,46	0,495	0,54	0,585
28	0,22	0,25	0,29	0,33	0,37	0,41	0,45	0,49	0,53	0,58	0,63
29	0,235	0,27	0,31	0,355	0,395	0,44	0,485	0,525	0,57	0,62	0,675
30	0,25	0,29	0,33	0,38	0,42	0,47	0,52	0,56	0,61	0,66	0,72
31	0,265	0,31	0,355	0,405	0,45	0,5	0,555	0,6	0,655	0,71	0,77
32	0,28	0,33	0,38	0,43	0,48	0,53	0,59	0,64	0,7	0,76	0,82
33	0,3	0,35	0,405	0,46	0,51	0,565	0,625	0,68	0,74	0,805	0,87
34	0,32	0,37	0,43	0,49	0,54	0,6	0,66	0,72	0,78	0,85	0,92
35	0,34	0,395	0,455	0,515	0,57	0,635	0,7	0,76	0,83	0,9	0,97
36	0,36	0,42	0,48	0,54	0,6	0,67	0,74	0,8	0,88	0,95	1,02
37	0,375	0,44	0,505	0,57	0,635	0,705	0,78	0,85	0,925	1	1,075
38	0,39	0,46	0,53	0,6	0,67	0,74	0,82	0,9	0,97	1,05	1,13
39	0,41	0,48	0,555	0,63	0,705	0,78	0,86	0,945	1,02	1,105	1,19
40	0,43	0,5	0,58	0,66	0,74	0,82	0,9	0,99	1,07	1,16	1,25
41	0,45	0,53	0,61	0,695	0,775	0,86	0,95	1,035	1,125	1,22	1,315
42	0,47	0,56	0,64	0,73	0,81	0,9	1	1,08	1,18	1,28	1,38
43	0,495	0,585	0,67	0,765	0,85	0,945	1,045	1,14	1,24	1,34	1,445
44	0,515	0,61	0,7	0,8	0,89	0,99	1,09	1,2	1,3	1,4	1,51
45	0,543	0,64	0,735	0,835	0,935	1,035	1,14	1,25	1,355	1,465	1,58
46	0,57	0,67	0,77	0,87	0,98	1,08	1,19	1,3	1,41	1,53	1,65
47	0,595	0,7	0,805	0,91	1,02	1,13	1,245	1,355	1,475	1,6	1,725
48	0,62	0,73	0,84	0,95	1,06	1,18	1,3	1,41	1,54	1,67	1,8
49	0,645	0,76	0,875	0,99	1,105	1,23	1,355	1,475	1,605	1,74	1,875
50	0,67	0,79	0,91	1,03	1,15	1,28	1,41	1,54	1,67	1,81	1,95
51	0,7	0,825	0,95	1,075	1,2	1,335	1,47	1,605	1,74	1,89	2,035
52	0,73	0,86	0,99	1,12	1,25	1,39	1,53	1,67	1,81	1,97	2,12
53	0,765	0,895	1,03	1,165	1,3	1,445	1,59	1,735	1,885	2,045	2,205
54	0,8	0,93	1,07	1,21	1,35	1,5	1,65	1,8	1,96	2,12	2,29
55	0,83	0,97	1,115	1,26	1,405	1,56	1,715	1,875	2,035	2,2	2,375
56	0,86	1,01	1,16	1,31	1,46	1,62	1,78	1,95	2,11	2,28	2,46
57	0,89	1,045	1,205	1,36	1,515	1,68	1,845	2,015	2,19	2,365	2,545
58	0,92	1,08	1,25	1,41	1,57	1,74	1,91	2,08	2,27	2,45	2,63
59	0,955	1,12	1,29	1,46	1,625	1,8	1,98	2,155	2,345	2,535	2,72
60	0,99	1,16	1,33	1,51	1,68	1,86	2,05	2,23	2,42	2,62	2,81
61	1,025	1,2	1,38	1,565	1,74	1,925	2,115	2,3	2,495	2,7	2,9
62	1,06	1,24	1,43	1,62	1,8	1,99	2,18	2,37	2,57	2,78	2,99
63	1,095	1,285	1,475	1,67	1,855	2,05	2,25	2,445	2,65	2,865	3,08
64	1,13	1,33	1,52	1,72	1,91	2,11	2,32	2,52	2,73	2,95	3,17
65	1,165	1,365	1,565	1,77	1,965	2,17	2,38	2,59	2,805	3,03	3,275
66	1,2	1,4	1,61	1,82	2,02	2,23	2,44	2,66	2,88	3,11	3,38
67	1,235	1,445	1,655	1,87	2,075	2,29	2,505	2,735	2,965	3,21	3,485
68	1,27	1,49	1,7	1,92	2,13	2,35	2,57	2,81	3,05	3,31	3,59
69	1,305	1,53	1,75	1,97	2,19	2,415	2,645	2,89	3,14	3,41	3,695
70	1,34	1,57	1,8	2,02	2,25	2,48	2,72	2,97	3,23	3,51	3,8
71	1,375	1,615	1,85	2,08	2,315	2,55	2,795	3,055	3,325	3,615	3,91
72	1,41	1,66	1,9	2,14	2,38	2,62	2,87	3,14	3,42	3,72	4,02
73	1,45	1,705	1,955	2,2	2,45	2,695	2,95	3,23	3,52	3,82	4,135
74	1,49	1,75	2,01	2,26	2,52	2,77	3,03	3,32	3,62	3,92	4,25
75	1,53	1,8	2,065	2,325	2,595	2,845	3,115	3,415	3,715	4,03	4,365
76	1,57	1,85	2,12	2,39	2,67	2,92	3,2	3,51	3,81	4,14	4,48
77	1,615	1,9	2,18	2,455	2,745	3	3,29	3,605	3,925	4,255	4,6
78	1,66	1,95	2,24	2,52	2,82	3,08	3,38	3,7	4,04	4,37	4,72
79	1,7	2	2,295	2,59	2,895	3,16	3,475	3,8	4,15	4,485	4,835
80	1,74	2,05	2,35	2,66	2,97	3,24	3,57	3,9	4,26	4,6	4,95
81	1,785	2,1	2,41	2,73	3,05	3,325	3,66	4,005	4,365	4,71	5,085
82	1,83	2,15	2,47	2,8	3,13	3,41	3,75	4,11	4,47	4,82	5,22
83	1,875	2,205	2,53	2,87	3,205	3,495	3,845	4,215	4,585	4,945	5,345
84	1,92	2,26	2,59	2,94	3,28	3,58	3,94	4,32	4,7	5,07	5,47
85	1,965	2,315	2,65	2,985	3,34	3,675	4,035	4,43	4,82	5,195	5,595
86	2,01	2,37	2,71	3,03	3,4	3,77	4,13	4,54	4,94	5,32	5,72
87	2,06	2,425	2,78	3,13	3,5	3,86	4,235	4,655	5,06	5,445	5,86
88	2,11	2,48	2,85	3,23	3,6	3,95	4,34	4,77	5,18	5,57	6
89	2,16	2,535	2,915	3,3	3,685	4,045	4,45	4,88	5,3	5,7	6,135
90	2,21	2,59	2,98	3,37	3,77	4,14	4,56	4,99	5,42	5,83	6,27
91	2,255	2,65	3,045	3,45	3,855	4,24	4,67	5,105	5,545	5,96	6,41
92	2,3	2,71	3,11	3,53	3,94	4,34	4,78	5,22	5,67	6,09	6,55
93	2,355	2,77	3,18	3,605	4,025	4,43	4,89	5,345	5,795	6,225	6,69
94	2,41	2,83	3,25	3,68	4,11	4,52	5	5,47	5,92	6,36	6,83
95	2,46	2,89	3,32	3,76	4,2	4,625	5,11	5,58	6,045	6,495	6,975
96	2,51	2,95	3,39	3,84	4,29	4,73	5,22	5,69	6,17	6,63	7,12
97	2,565	3,01	3,46	3,92	4,38	4,83	5,335	5,81	6,3	6,77	7,28
98	2,62	3,07	3,53	4	4,47	4,93	5,45	5,93	6,43	6,91	7,44
99	2,67	3,135	3,6	4,085	4,56	5,035	5,565	6,06	6,565	7,055	7,585
100	2,72	3,2	3,67	4,17	4,65	5,14	5,68	6,19	6,7	7,2	7,73

Ирина Железняк, Собкор интернет-издания «AtmWood. Дерево-промышленный вестник»

Как посчитать кубатуру бруса (объем)

Перед приобретением любого стройматериала необходимо как можно точнее определить нужное количество, иначе можно потерять какую-то сумму из-за оставшихся излишков либо потребности в дополнительном закупе, а также неучтенной возможности обмана со стороны недобросовестных продавцов. Брус, бревна, доски и подобные изделия из дерева, как известно, реализуют кубометрами, а значит надо во всех тонкостях знать расчеты определения объема этих материалов, а также перевода нужного их количества штук в кубы и обратно. А в случае приобретения бруса для строительства дома при подсчете требуемого количества этого стройматериала необходимо еще также учесть конструкцию и особенности будущей постройки.

Базовые расчеты – определение объема и перевод из штук в кубы и обратно

Рассчитать кубатуру бруса, доски и подобного пиломатериала очень просто. Для этого необходимо знать толщину, ширину (высоту) и длину изделия. И, как известно еще из школьного учебника по геометрии, надо перемножить эти размеры:

V = T ∙ H ∙ L, где

V – объем лесоматериала, м³;

T – толщина;

H – ширина;

L – длина.

Размеры перед вычислением следует привести какой-то одной единице измерения: мм, см или м. Лучше в метры, чтобы потом не делать перевод из мм³ или см³ в м³.

Таблица размеров бруса

Для примера рассчитаем кубатуру бруса 150×200. Эти размеры, как известно, указываются в мм. То есть толщина изделия 0,15 м, а ширина 0,2 м. Стандартная длина бруса и досок 6 м (иногда тоже указывают в мм – 6000). А может быть другой. Но для примера возьмем именно 6 м. Тогда объем этого пиломатериала:

0,15 ∙ 0,2 ∙ 6 = 0,18 м³.

Теперь можно перевести нужное количество (в штуках) этого изделия в кубы. Допустим, требуется 49 шт.:

0,18 ∙ 49 = 8,82 м³.

Зная объем одного изделия, можно также рассчитать куб бруса, то есть определить, сколько его единиц (штук) в 1 м³. Для этого надо поделить 1 куб на уже вычисленную или взятую из справочных таблиц кубатуру одного изделия (в рассматриваемом примере – 0,18 м³):

1 / 0,18 = 5,55555… шт.

Точно так же рассчитывается количество этого вида лесоматериалов для любого их объема.

Нюансы вычислений – как не ошибиться и не дать себя обмануть

Как следует из приведенных выше методики и примеров расчета, высчитывать нужный объем лесоматериала в штуках либо кубометрах очень легко. Однако при этом всегда надо помнить, что в 1 метре кубическом не целое количество этих изделий. Для приведенного в примере с размерами 150×200 длиной 6 м – 5,55555… шт. Недобросовестные, чаще всего розничные продавцы лесоматериалов ловко этим пользуются.

Например, надо 1 куб этого материала из примера. Продавец отпускает, разумеется, 5 изделий, но берет сумму как за целый куб. Переплата составит стоимость полбруса.

А допустим, для постройки дома нужны те же 49 брусьев из примера. И если продавец считает по следующей схеме, то придется уже существенно переплатить за полученный лесоматериал:

• 1 куб – 5 изделий 150×200 длиной 6 м;
•  49/5 = 9,8 кубов к оплате.

Это развод чистейшей воды на 5 единиц лесоматериала. Они лишние и не нужны, однако будут оплачены, но не получены. Выше в примерах расчета уже переведены данные 49 изделий в кубы – это 8,82 м³. То есть «особо предприимчивый» продавец обманет невнимательного покупателя на:

9,8 – 8,82 = 0,98 м³ лесоматериала,

что составляет 0,98/0,18 = 5,44444… шт. этого пиломатериала (0,18 – рассчитанный выше объем одного изделия).

Поэтому самым правильным будет заранее подсчитать именно количество единиц (штук) материала, а уже потом, используя эти данные и размеры бруса или доски, вычислить фактическую их кубатуру.

То есть в случае с приобретением одного кубометра в приведенном выше примере необходимо сначала определиться, сколько действительно нужно взять брусьев – 5 или 6. А затем считаем их кубатуру:

0,15 ∙ 0,2 ∙ 6 ∙ 5 (или 6 шт.) = 0,9 (или 1,08) м³.

А для 49 единиц этого лесоматериала:

0,15 ∙ 0,2 ∙ 6 ∙ 49 = 8,82 м³.

Тогда придется заплатить именно за эти 0,9 (1,08) или 8,82 куба, получив ровно 5 (6) либо 49 изделий. Причем и количество в штуках, и объем в м³ должны быть обязательно указаны в накладной на отпускаемый продавцом лесоматериал.

Готовый брус для строительства

 Другие особенности расчета кубатуры пиломатериалов

Еще одна важная особенность, которую следует знать для правильного расчета кубатуры бруса или досок при их приобретении. Фактическая длина пиломатериалов обычно всегда немного превышает стандартную или заявленную производителем этой продукции. Так, вместо 6 м средняя протяженность рассматриваемых лесоматериалов, как правило, составляет 6,05 м. Это обусловлено тем, что торцы пиломатериала после его распила не обрабатывают, из-за чего они могут оказаться неровными, идти под углами, причем разными или просто быть грязными. Разумеется, эти 5 см оплачивать не надо. Но некоторые ушлые продавцы, хотя и довольно редко, все-таки пытаются при расчете кубометров учесть даже это, что является чистым обманом.

Складирование бруса

И относительно расчетов для шпунтованных и профилированных лесоматериалов. Наличие у них шипов, пазов, а также других выступающих или выточенных мест не должно смущать. Расчет кубатуры таких материалов ничем не отличается от определения объема обычных ровных со всех сторон изделий. Для шпунтованных и профилированных пиломатериалов действует правило, что замеряется и берется в счет только основная часть (рабочая ширина) изделия, а все конструктивно-необходимые и/или декоративные элементы при вычислениях не учитываются. Это положение распространяется абсолютно на все виды лесоматериалов.

Закупка больших объемов материалов – расчет складочных и плотных кубометров

Когда необходимо закупить большое количество лесоматериалов, их кубатуру рассчитывают несколько иначе, чем было рассмотрено выше. Например, брус и доска нужны для возведения внушительного просторного дома, а также еще различных хозпостроек вблизи него. При этом необходимый пиломатериал, наверняка, будет разных размеров в поперечном сечении и длины. Перемерять и обсчитывать каждый вид требуемого материала при подобных объемах закупки – занятие, которое может отнять не один день.

Для таких случаев существует своя определенная методика расчета. Она основана на двух важных понятиях:

1. Плотный кубометр древесины. Так называют объем, занятый только древесиной и не имеющий в ней пустот, а также промежутков. Определяют его путем обмера отдельных лесоматериалов поштучно, а затем последующего расчета их общей кубатуры.
2. Складочный кубический метр. Так называют объем, занятый максимально плотно уложенными в штабель пиломатериалами и имеющий пустоты, а также промежутки между отдельными изделиями из дерева. Определяют его путем обмера штабеля, а затем последующего перемножения размеров последнего. Причем в таком пакете основное количество материала должно иметь примерно одинаковую длину, а остальные изделия могут быть короче, но не длиннее. Допускается наличие в штабелях коротких пиломатериалов, которые должны плотно укладываться друг за другом.

Чтобы быстро рассчитать большой объем требуемых закупаемых пиломатериалов, которые уже подготовлены и складированы в виде штабеля, последний сначала обмеряют, а потом рассчитывают его кубатуру. Это будет вычислена складочная кубатура. Затем ее величину надо умножить на специальный переводной коэффициент. В результате получится объем только древесины (плотный кубометр), то есть именно тех материалов, которые покупаются и будут оплачены.

Величина переводного коэффициента регулируется рядом стандартов на пиломатериалы: ГОСТ 6782.2-75, 6782.1-75, 6564-84, ОСТ 13-24-86 и другими. Для бруса и доски в зависимости от их влажности и породы дерева, из которого они изготовлены, составляет значение в пределах 0,74–0,82.

Считаем требуемую кубатуру бруса для постройки дома

Чтобы посчитать кубатуру бруса для дома, понадобится его проект, который уже должен быть готов до начала строительства.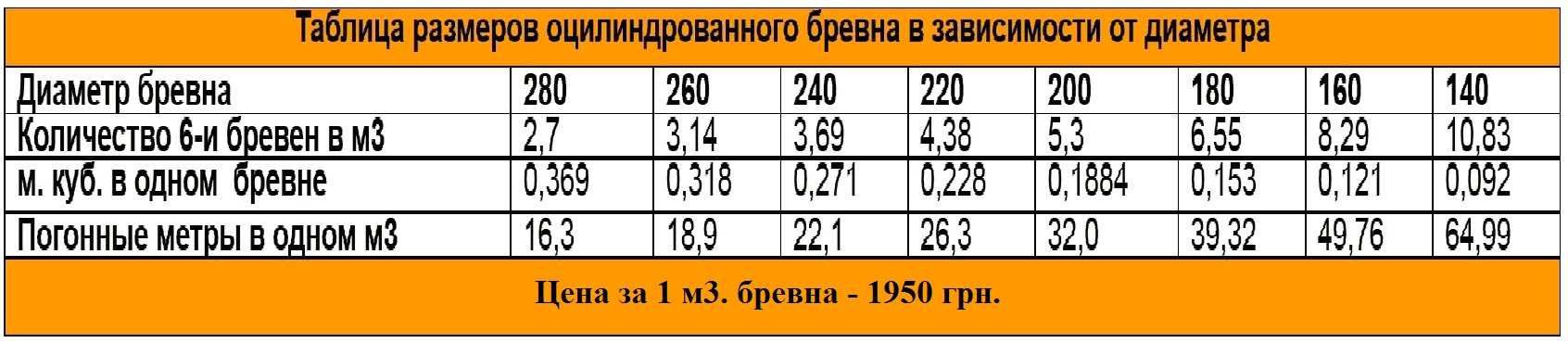 Из чертежей строения берем следующие данные:

• Высоту внешних стен, замеряемую от уровня фундамента. Обозначим как H.
• Высоту внутренних перегородочных стен, если они есть и должны быть из бруса.
• Длину наружных и внутренних стен.
• Количество и длину брусьев, используемых в стропильной системе, в качестве балок пола и потолка деревянного дома, а также в других его конструкциях – если это предусмотрено проектом.

Затем выбираем толщину материала для каждого из перечисленных выше элементов строения. Для наружных и внутренних несущих стен в зависимости от назначения возводимого дома и региона, где он строится. Для не несущих перегородок – по собственному усмотрению. Цокольный (самый нижний) венец внешних стен обычно немного толще, чем остальной лесоматериал для них. У остальных элементов строения толщина материала выбирается исходя из условий его эксплуатации, а также требуемой прочности конструкций, в которых он используется. В грамотно составленном проекте, кстати, уже должна быть указана толщина бруса, используемого для стен, цокольного венца, в деревянных перекрытиях и прочих конструкциях строения.

Теперь остается только чистая арифметика. Сначала вычисляем периметр дома – складываем длину всех его наружных стеновых конструкций. Для простого прямоугольного или квадратного строения надо просто сложить его ширину и длину, а полученное значение умножить на 2. Затем считаем кубатуру цокольного венца:

V_Ц = T_Ц ∙ Z_Ц ∙ I, где

V_Ц – общая кубатура цокольного пиломатериала, м³;

T_Ц – толщина цокольного изделия, м;

Z_Ц – его ширина (высота), м;

I – периметр наружных стен, м.

Рассчитываем оставшуюся высоту внешних стен, м:

h = H – Z_Ц, где

H – общая высота, м.

Вычисляем площадь внешних стеновых конструкций без цокольного венца, м²:

S_Н = h ∙ I.

Если толщина материала цокольного венца такая же, как у всей стены, то площадь последней, м²:

S_Н = H ∙ I.

Рассчитываем площадь внутренних стен, толщина пиломатериала у которых такая же, как у наружных, м²:

S_В1 = H_В ∙ L_В1, где

H_В – высота внутренних стен, м;

L_В1 – общая (суммарная) длина внутренних стен, толщина материала у которых такая же, как у наружных, м.

Рассчитываем площадь внутренних стен, толщина лесоматериала у которых другая, м²:

S_В2 = H_В ∙ L_В2, где

L_В2 — общая длина внутренних стен, толщина материала у которых другая, м.

Вычисляем кубатуру основного пиломатериала – для наружных стен и внутренних перегородок из такого же лесоматериала, м³:

V_S = (S_Н + S_В1) ∙ Z_S, где

Z_S – выбранная толщина изделия, м.

Определяем объем материала для внутренних перегородок из другого лесоматериала, м³:

V_В = S_В2 ∙ Z_В, где

Z_В — выбранная толщина материала для этих перегородок, м.

Полученные результаты (V_Ц, V_S и V_В) делим на длину закупаемого пиломатериала и его выбранную ширину (высоту). Получится количество материала в штуках. Округляем это значение до целой величины, а затем пересчитываем V_Ц, V_S и V_В , как это описано во второй главе.

Чтобы сэкономить на пиломатериале, следует подсчитать суммарные площади оконных, дверных и других проемов для соответствующих стен. Затем их величины надо отнять от S_Н, S_В1 и S_В2 соответственно. После этого делаем расчет V_S и V_В по тем же формулам. Затем увеличиваем полученные значения на 10–20 % – чтобы был запас на всякий случай.

Строительство дома из бруса

Кубатура бруса для остальных элементов дома, в которых он используется, подсчитывается еще проще. Вычисляется его общая длина, которую умножаем на выбранные для материала толщину и ширину.

{( j)} \in \Omega $, хотя это условие не обязательно. Для вычисления интеграла $I(f)$ по формуле (1) нужно только вычислить кубатурную сумму. Если $n = 1$ формула (1) и сумма в ее правой части известны как квадратурная формула и сумма (см. Квадратурная формула). {n} $ удовлетворяющее уравнению $ \phi ( x) = 0 $ называется алгебраической гиперповерхностью степени $m$. 9{( i)} ) = \delta _ {ij} $ ( $ \дельта _ {ij} $ символ Кронекера). Умножая приближенное равенство $ f ( x) \cong {\mathcal P} ( x) $ на $p(x)$ и интегрирование по $\Omega$ приводит к кубатурной формуле типа (1) с $N = \mu $ и

$$ \тег{2} C _ {j} знак равно я ( {\ mathcal L} _ {j}), \ \ j = 1 \точки \mu . $$

Существование интегралов (2) равносильно существованию моментов весовой функции, $ p _ {i} = I ( \phi _ {i} ) $, $ i = 1 \точки \mu $. Здесь и далее предполагается, что искомые моменты $ p ( x) $ существовать. Кубатурная формула (1), имеющая $ N = \mu $ узлов, не содержащихся ни в одной алгебраической гиперповерхности степени $ m $ и с коэффициентами, определяемыми формулой (2), называется интерполяционной кубатурной формулой. Формула (1) обладает $ m $-свойством, если она является точным равенством, когда $ f ( x) $ является полиномом степени не выше $m$; интерполяционная кубатурная формула обладает $m$-свойством. Кубатурная формула (1) с $ N \leq \mu $ узлов, обладающих свойством $m$, является интерполяционной формулой тогда и только тогда, когда матрица 9{( j)} ) = p _ {i} ,\ \ я = 1 \ точек \ мю . $$

Естественно требовать, чтобы количество неизвестных совпадало с количеством уравнений: $N ( n + 1) = \mu $. Это уравнение дает предварительную оценку количества узлов. Если $ N = \mu /( n + 1) $ не является целым числом, полагается $ N = [ \mu /( n + 1)] + 1 $, где $ [ \mu / ( n + 1)] $ обозначает целую часть $ \mu /( n + 1) $. Кубатурная формула с таким количеством узлов не всегда должна существовать. Если он существует, то количество его узлов равно $ 1/( n + 1) $ умноженное на количество узлов интерполяционной кубатурной формулы. Однако в этом случае сами узлы и коэффициенты определяются нелинейной системой уравнений (3). В методе неопределенных параметров кубатурную формулу строят, пытаясь придать ей вид, упрощающий систему (3). Это можно сделать, когда $ \Omega $ и $ р ( х) $ иметь симметрию. Положения узлов берутся совместимыми с симметрией $\Omega$ и $р(х)$, и в этом случае симметричным узлам присваиваются одинаковые коэффициенты. Упрощение системы (3) сопряжено с определенным риском: хотя исходная система (3) может быть разрешима, упрощенная система не обязательно.

Пример. Пусть $ \Omega = K _ {2} = \{ — 1 \leq x _ {1} , x _ {2} \leq 1 \} $, $ р ( х _ {1} , х _ {2} ) = 1 $. Одного просят построить кубатурную формулу со свойством $7$; $n = 2$, $ \mu = M ( 2, 7) = 36 $, и 12 узлов. Узлы расположены следующим образом. Первая группа узлов состоит из точек пересечения окружности радиуса $a$, с центром в начале координат, с осями координат. Вторая группа состоит из точек пересечения окружности радиуса $b$, также с центром в начале координат с прямыми линиями $ x _ {1} = \pm x _ {2} $. Аналогично строится и третья группа, радиус которой обозначается $c$. Коэффициенты, приписываемые узлам одной группы, одинаковы и обозначаются $A, B, C$ для узлов первой, второй и третьей группы соответственно. {2} $. Это дает нелинейную систему шести уравнений с шестью неизвестными $ a, b, c $, $А,В,С$. Решив эту систему, получим кубатурную формулу с положительными коэффициентами и с узлами, лежащими в $K_{2}$. 9{2} } $.

Теорема 1) Кубатурная формула, инвариантная относительно $ G $ обладает $m$-свойством тогда и только тогда, когда оно точно для всех многочленов степени не выше $m$ которые инвариантны относительно $G$ (см. [5]). Метод неопределенных коэффициентов можно определить как метод построения инвариантных кубатурных формул, обладающих $m$-свойством. В приведенном примере роль группы $G$ может играть группа симметрии квадрата. Теорема 1 имеет существенное значение при построении инвариантных кубатурных формул.

Для простых областей интегрирования, таких как куб, симплекс, шар или сфера, и для веса $ p (x) = 1 $, можно построить кубатурные формулы, многократно используя квадратурные формулы. Например, когда $ \Omega = K _ {n} = \{ {- 1 \leq x _ {i} \leq 1 } : {i = 1 \dots n } \} $ является кубом, можно использовать квадратурную формулу Гаусса с $ k $ узлы $ t _ {i} $ и коэффициенты $A_{i}$ чтобы получить кубатурную формулу

$$ \int\limits _ {K _ {n} } f ( x) dx \ cong \ \ сумма _ {я _ {1} \ точки я _ {п} = 1 } ^ {к} А _ {я _ {1} } \ точки А _ {я _ {п} } е ( т _ {я _ {1} } \ точки т _ {я _ {п} } ) $$ 9\альфа $ такое, что $ 0 \leq \alpha _ {i} \leq 2k — 1 $, $ i = 1 \ точек n $, и, в частности, для всех многочленов степени не выше $2k — 1$. Количество узлов таких кубатурных формул быстро увеличивается, что ограничивает их применимость.

В дальнейшем предполагается, что весовая функция имеет фиксированный знак, скажем

$$ \тег{4} р ( х) \geq 0 \ \ \mathop{\rm in} \Omega \ \ \textrm{ и } \ \ р _ {1} > 0. $$

Тот факт, что коэффициенты кубатурной формулы с такой весовой функцией положительны, является ценным свойством формулы.

Теорема 2) Если область интегрирования $ \Omega $ замкнут и $ p ( x) $ удовлетворяет (4), существует интерполяционная кубатурная формула (1), обладающая $ m $-свойством, $ N \leq \mu $, с положительными коэффициентами и с узлами в $\Omega$. Вопрос о реальном построении такой формулы пока открыт.

Теорема 3) Если кубатурная формула с весом, удовлетворяющим (4), имеет вещественные узлы и коэффициенты и обладает $m$-свойством, то не менее $\lambda = M(n,l)$ ее коэффициентов положительны, где $ l = [ m/2] $ — целая часть $ m/2 $. В условиях теоремы 3 число $ \lambda $ является нижней границей количества узлов: 9{(к)} $ и $C_{j}$ реальны.

Что касается кубатурных формул со свойством $ m $, то особенно интересны те, которые имеют минимальное количество узлов. При $ м = 1, 2 $ такие формулы легко найти для любых $n$, произвольный $\Omega$ и $ p ( x) \geq 0 $; минимальное количество узлов — это как раз нижняя граница $\lambda$: В первом случае он равен 1, а в $n+1$ В секунду. Когда $ m \geq 3 $, минимальное количество узлов зависит от домена и веса. Например, если $m = 3$, область центрально-симметрична, и если $p(x)=1$, количество узлов $2n$; для симплекса и $p(x)=1$, это $n+2$.

В силу (4),

$$ \тег{5} ( \ фи , \ фунтов на квадратный дюйм ) = \ I ( \phi \overline \psi \; ) $$

— скалярное произведение в пространстве многочленов. Пусть $ {\ mathcal P} _ {k} $ – векторное пространство полиномов степени $k$ которые ортогональны в смысле (5) всем полиномам степени не выше $k — 1$. Это пространство имеет размерность $ M (n — 1, k) $— количество мономов степени $k$. Многочлены от $ {\ mathcal P} _ {k} $ называются ортогональными многочленами для $ \Omega $ и $p(x)$. {n} ) $, где $m > n/2$, и в этом случае искомая кубатурная формула считается точной для всех многочленов степени не выше $m — 1$.

Литература

Крылов, Л.Т. Шульгина, «Справочник по численному интегрированию», Москва (1966) (на русском языке)

[1]	Н.М. Крылов, «Приближенное вычисление интегралов», Macmillan (1962) (Перевод с русского)
[2]
[3]	А.Х. 4]	С.Л. Соболев, Введение в теорию кубатурных формул, Москва (1974)
[5]	С.Л. Соболев, «Формулы механической кубатуры на поверхности сферы» Сиб. Мат. ж. , 3 : 5 (1962) с. 769–796
[6]	И.П. Мысовских, «Интерполяционные кубатурные формулы», М., 1981,

Комментарии

Многочлен влияния j-го узла» (т. {(j)}$).

«m-свойство» также известно в западной литературе как степень точности; кубатурная формула обладает $m$-свойством, если она имеет степень точности $m$.

Справочник [a1] является одновременно прекрасным введением и углубленным изучением кубатурных формул.

Литература

[a1]	Энгельс Г., «Численные квадратуры и кубатуры», акад. Press (1980)
[a2]	П. Дж. Дэвис, П. Рабинович, «Методы численного интегрирования», акад. Пресса (1984)

Как процитировать эту запись:
Кубатурная формула. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Cubature_formula&oldid=51796

Эта статья адаптирована из оригинальной статьи И.П. Мысовских (создатель), которая появилась в Математической энциклопедии — ISBN 1402006098. См. Оригинальную статью

Калькулятор объема древесины 2.

7.12.2 Скачать бесплатно

Описание издателя

Программа для:
— расчета кубатуры бревна по ГОСТ 2708-75, ИСО 4480-83, бревна цилиндрической формы;
— расчет кубатуры доски, количество досок в кубе;
— расчет средней массы объема древесины по основным породам древесины;
— две темы оформления: светлая и темная.

В любом режиме есть возможность подвести итоги, отменить последнюю операцию и скопировать любой расчет в буфер обмена.
Вы можете рассчитать вес вместе с расчетом бревен и досок, что поможет оценить грузоподъемность автомобиля.

О калькуляторе объема пиломатериалов

Калькулятор объема древесины — это бесплатное приложение для Android, опубликованное в списке приложений Office Suites & Tools, входящих в состав Business.

Компанией, разработавшей Калькулятор объема древесины, является Максим Бартош. Последняя версия, выпущенная разработчиком, — 2. 7.12.2. Это приложение было оценено 2 пользователями нашего сайта и имеет средний рейтинг 3,0.

Чтобы установить Timber Volume Calculator на Android-устройство, просто нажмите зеленую кнопку «Продолжить в приложении» выше, чтобы начать процесс установки. Приложение размещено на нашем сайте с 7 июля 2015 г. и было загружено 1073 раза. Мы уже проверили, безопасна ли ссылка для загрузки, однако для вашей собственной безопасности мы рекомендуем вам проверить загруженное приложение антивирусом. Ваш антивирус может определить Калькулятор объема древесины как вредоносное ПО, если ссылка для скачивания на maximsblog.blogspot.com.cubcalc не работает.

Как установить Timber Volume Calculator на Android-устройство:

• Нажмите кнопку «Продолжить в приложении» на нашем веб-сайте. Это перенаправит вас в Google Play.
• Как только Калькулятор объема древесины появится в списке Google Play вашего Android-устройства, вы можете начать его загрузку и установку. Нажмите на кнопку «Установить», расположенную под строкой поиска и справа от значка приложения.