Как расшифровать буквы в цифры: Онлайн калькулятор: Шифр A1Z26

Содержание

Расшифруй слова по цифрам

1) Алфавит разбивается на группы с равным числом букв, затем каждой группе присваивается свой номер. Так формируется первая цифра для шифровки символа. Вторая цифра – это порядковый номер буквы в группе.

Таблица не обязательно должна выглядеть таким образом. Количество групп может быть другим. Также буквы из алфавита могут идти в таблице не по порядку.

Зашифруем таким способом слово «цифра»

Зашифрованный текст: 63 31 61 51 11

Возможно много вариаций этого вида шифра. Например, алфавит разбивается на 5 групп, а каждая буква будет изображаться дробью таким образом, что в числителе будет номер ее группы, а в знаменателе – порядковый номер в группе. Еще один вариант, как я уже говорил, буквы могут идти не по порядку (например, ажмтшю бзнущя виофъ гйпхы дкрць елсчэ).

2) Цифровая таблица.

Зашифруем с помощью этой таблицы слово «наука».

Каждый символ будет шифроваться опять двумя цифрами, при чем первой может быть как номер столбца, так и номер строки. То есть буква К может быть зашифрована, как 32 или 23.

Зашифрованный текст: 62 11 33 32 11

Здесь первой цифрой записан номер столбца, второй – номер строки.

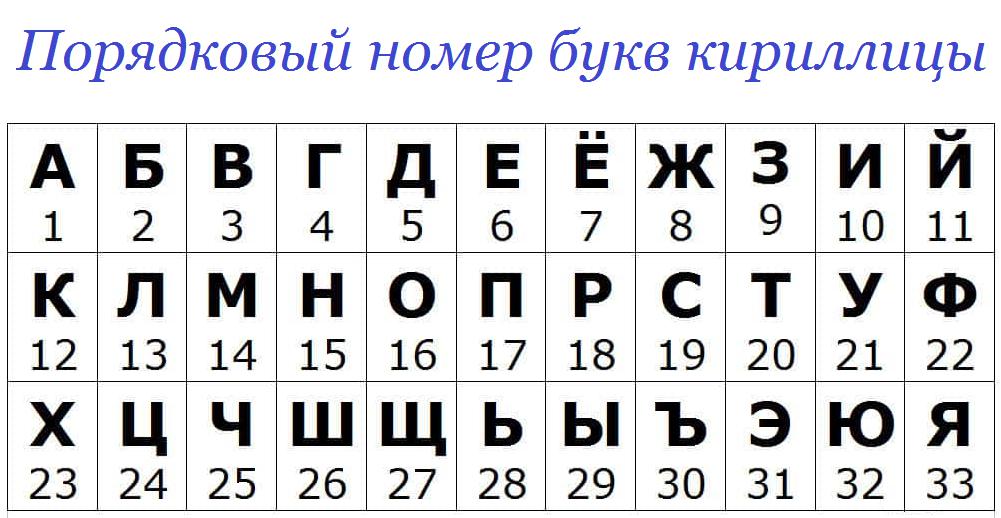
3)Шифрование с заменой каждой буквы ее номером в алфавите. Очень простой вид шифра. Его, думаю, можно тоже отнести к цифровым. Но между тем, он часто применяется в различных вариациях и комбинациях с другими видами шифров. Про некоторые комбинации шифров расскажу чуть позже.

Вариация этого шифра: буквы в алфавите отсчитываются не с начала, а с конца. То есть порядковым номер буквы «А» будет 33, «Б» – 32 и так далее.

Дата добавления: 2014-12-24 ; Просмотров: 9111 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Шифр простой подстановки, где каждая буква заменяется своим порядковым номером в алфавите.

Ниже калькулятор, который позволяет зашифровать/расшифровать текст, используя шифр A1Z26. Шифр простой подстановки, где каждая буква заменяется своим порядковым номером в алфавите.
Все буквы приводятся к нижнему регистру, зашифровывается/расшифровывается русский алфавит, все не-алфавитные символы не преобразуются. При расшифровке учтите, что числа (от 1 до 33) должны быть отделены друг от друга (чертой, пробелом или неважно чем). Для зашифровки/расшифровки с использованием английского алфавита переключите язык сайта на английский.

Все мы довольно часто слышим такие слова и словосочетания, как «шифрование данных», «секретные шифры», «криптозащита», «шифрование», но далеко не все понимают, о чем конкретно идет речь. В этом посте разберемся, что из себя представляет шифрование и рассмотрим элементарные шифры с тем расчетом, чтобы даже далекие от IT люди поняли суть этого явления.

Прежде всего, разберемся в терминологии.

Шифрование – это такое преобразование исходного сообщения, которое не позволит всяким нехорошим людям прочитать данные, если они это сообщение перехватят. Делается это преобразование по специальным математическим и логическим алгоритмам, некоторые из которых мы рассмотрим ниже.

Исходное сообщение – это, собственно, то, что мы хотим зашифровать. Классический пример — текст.

Шифрованное сообщение – это сообщение, прошедшее процесс шифрования.

Шифр — это сам алгоритм, по которому мы преобразовываем сообщение.

Ключ — это компонент, на основе которого можно произвести шифрование или дешифрование.

Алфавит – это перечень всех возможных символов в исходном и зашифрованном сообщении. Включая цифры, знаки препинания, пробелы, отдельно строчные и заглавные буквы и т.д.

Теперь, когда мы говорим на более-менее одном языке, разберем простые шифры.

Шифр Атбаша

Самый-самый простой шифр. Его суть – переворот алфавита с ног на голову.

Например, есть у нас алфавит, который полностью соответствует обычной латинице.

Для реализации шифра Атбаша просто инвертируем его. «А» станет «Z», «B» превратится в «Y» и наоборот. На выходе получим такую картину:

И теперь пишем нужное сообшение на исходном алфавите и алфавите шифра

Исходное сообщение: I love habr
Зашифрованное: r olev szyi

Шифр Цезаря

Тут добавляется еще один параметр — примитивный ключ в виде числа от 1 до 25 (для латиницы). На практике, ключ будет от 4 до 10.

Опять же, для наглядности, возьмем латиницу

И теперь сместим вправо или влево каждую букву на ключевое число значений.

Например, ключ у нас будет 4 и смещение вправо.

Исходный алфавит: a b c d e f g h i j k l m n o p q r s t u v w x y z
Зашифрованный: w x y z a b c d e f g h i j k l m n o p q r s t u v

Пробуем написать сообщение:

Шифруем его и получаем следующий несвязный текст:

Шифр Вернама (XOR-шифр)

Простейший шифр на основе бинарной логики, который обладает абсолютной криптографической стойкостью. Без знания ключа, расшифровать его невозможно (доказано Клодом Шенноном).

Исходный алфавит — все та же латиница.

Сообщение разбиваем на отдельные символы и каждый символ представляем в бинарном виде.
Классики криптографии предлагают пятизначный код бодо для каждой буквы. Мы же попробуем изменить этот шифр для кодирования в 8 бит/символ на примере ASCII-таблицы. Каждую букву представим в виде бинарного кода.

Теперь вспомним курс электроники и элемент «Исключающее ИЛИ», также известный как XOR.

XOR принимает сигналы (0 или 1 каждый), проводит над ними логическую операцию и выдает один сигнал, исходя из входных значений.

Если все сигналы равны между собой (0-0 или 1-1 или 0-0-0 и т.д.), то на выходе получаем 0.
Если сигналы не равны (0-1 или 1-0 или 1-0-0 и т.д.), то на выходе получаем 1.

Теперь для шифровки сообщения, введем сам текст для шифровки и ключ такой же длины. Переведем каждую букву в ее бинарный код и выполним формулу сообщение XOR ключ

сообщение: LONDON
ключ: SYSTEM

Переведем их в бинарный код и выполним XOR:

В данном конкретном примере на месте результирующих символов мы увидим только пустое место, ведь все символы попали в первые 32 служебных символа. Однако, если перевести полученный результат в числа, то получим следующую картину:

С виду — совершенно несвязный набор чисел, но мы-то знаем.

Шифр кодового слова

Принцип шифрования примерно такой же, как у шифра цезаря.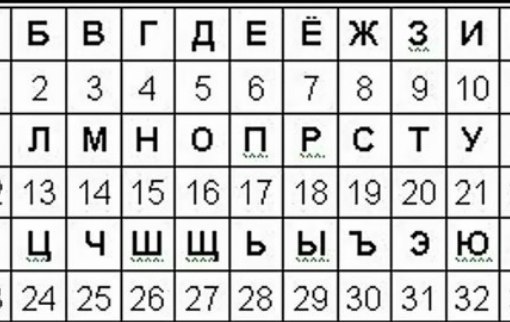 Только в этом случае мы сдвигаем алфавит не на определенное число позиций, а на кодовое слово.

Например, возьмем для разнообразия, кириллический алфавит.

Придумаем кодовое слово. Например, «Лукоморье». Выдернем из него все повторяющиеся символы. На выходе получаем слово «Лукомрье».

Теперь вписываем данное слово в начале алфавита, а остальные символы оставляем без изменений.

И теперь запишем любое сообщение и зашифруем его.

Получим в итоге следующий нечитаемый бред:

Шифр Плейфера

Классический шифр Плейфера предполагает в основе матрицу 5х5, заполненную символами латинского алфавита (i и j пишутся в одну клетку), кодовое слово и дальнейшую манипуляцию над ними.

Пусть кодовое слово у нас будет «HELLO».

Сначала поступаем как с предыдущим шифром, т.е. уберем повторы и запишем слово в начале алфавита.

Теперь возьмем любое сообщение. Например, «I LOVE HABR AND GITHUB».

Разобьем его на биграммы, т.е. на пары символов, не учитывая пробелы.

Если бы сообщение было из нечетного количества символов, или в биграмме были бы два одинаковых символа (LL, например), то на место недостающего или повторившегося символа ставится символ X.

Шифрование выполняется по нескольким несложным правилам:

1) Если символы биграммы находятся в матрице на одной строке — смещаем их вправо на одну позицию. Если символ был крайним в ряду — он становится первым.

Например, EH становится LE.

2) Если символы биграммы находятся в одном столбце, то они смещаются на одну позицию вниз. Если символ находился в самом низу столбца, то он принимает значение самого верхнего.

Например, если бы у нас была биграмма LX, то она стала бы DL.

3) Если символы не находятся ни на одной строке, ни на одном столбце, то строим прямоугольник, где наши символы — края диагонали. И меняем углы местами.

Например, биграмма RA.

По этим правилам, шифруем все сообщение.

Если убрать пробелы, то получим следующее зашифрованное сообщение:

Поздравляю.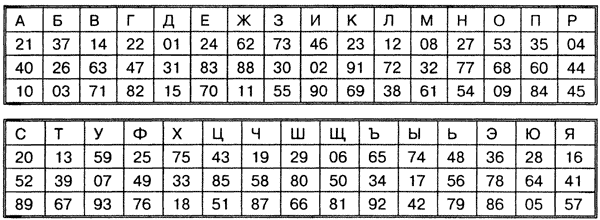 После прочтения этой статьи вы хотя бы примерно понимаете, что такое шифрование и знаете как использовать некоторые примитивные шифры и можете приступать к изучению несколько более сложных образцов шифров, о которых мы поговорим позднее.

10 популярных кодов и шифров

Коды и шифры — не одно и то же: в коде каждое слово заменяется другим, в то время как в шифре заменяются все символы сообщения.

В данной статье мы рассмотрим наиболее популярные способы шифрования, а следующим шагом будет изучение основ криптографии.

Стандартные шифры
Цифровые шифры
Как расшифровать код или шифр?

Стандартные шифры

ROT1

Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, А заменяется на Б, Б — на В, и т. д. Фраза «Уйрйшоьк Рспдсбннйту» — это «Типичный Программист».

Попробуйте расшифровать сообщение:

Лбл еёмб, рспдсбннйту?

Сумели? Напишите в комментариях, что у вас получилось.

Шифр транспонирования

В транспозиционном шифре буквы переставляются по заранее определённому правилу. Например, если каждое слово пишется задом наперед, то из

hello world получается dlrow olleh. Другой пример — менять местами каждые две буквы. Таким образом, предыдущее сообщение станет eh ll wo ro dl.

Ещё можно использовать столбчатый шифр транспонирования, в котором каждый символ написан горизонтально с заданной шириной алфавита, а шифр создаётся из символов по вертикали. Пример:

Из этого способа мы получим шифр holewdlo lr. А вот столбчатая транспозиция, реализованная программно:

def split_len(seq, length):
   return [seq[i:i + length] for i in range(0, len(seq), length)]
def encode(key, plaintext):
   order = {
      int(val): num for num, val in enumerate(key)
   }
ciphertext = ''

for index in sorted(order.keys()):
   for part in split_len(plaintext, len(key)):
      try:ciphertext += part[order[index]]
         except IndexError:
            continue
   return ciphertext
print(encode('3214', 'HELLO'))

Азбука Морзе

В азбуке Морзе каждая буква алфавита, цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов:
Чаще всего это шифрование передаётся световыми или звуковыми сигналами.

Сможете расшифровать сообщение, используя картинку?

•−−   −•− −−− −• −•−• •   ••• − •− − −••− ••   • ••• − −••−   −•• • −−−− •• ••−• •−• •− − −−− •−• −•−−

Шифр Цезаря

Это не один шифр, а целых 26, использующих один принцип. Так, ROT1 — лишь один из вариантов шифра Цезаря. Получателю нужно просто сообщить, какой шаг использовался при шифровании: если ROT2, тогда А заменяется на В, Б на Г и т. д.

А здесь использован шифр Цезаря с шагом 5:

Иербэй йюк ёурбэй нтчйхйцтаъ энщхуж

Моноалфавитная замена

Коды и шифры также делятся на подгруппы. Например, ROT1, азбука Морзе, шифр Цезаря относятся к моноалфавитной замене: каждая буква заменяется на одну и только одну букву или символ. Такие шифры очень легко расшифровываются с помощью частотного анализа.

Например, наиболее часто встречающаяся буква в английском алфавите — «E». Таким образом, в тексте, зашифрованном моноалфавитным шрифтом, наиболее часто встречающейся буквой будет буква, соответствующая «E». Вторая наиболее часто встречающаяся буква — это «T», а третья — «А».

Однако этот принцип работает только для длинных сообщений. Короткие просто не содержат в себе достаточно слов.

Шифр Виженера

Представим, что есть таблица по типу той, что на картинке, и ключевое слово «CHAIR». Шифр Виженера использует принцип шифра Цезаря, только каждая буква меняется в соответствии с кодовым словом.

В нашем случае первая буква послания будет зашифрована согласно шифровальному алфавиту для первой буквы кодового слова «С», вторая буква — для «H», etc. Если послание длиннее кодового слова, то для

(k*n+1)-ой буквы, где n — длина кодового слова, вновь будет использован алфавит для первой буквы кодового слова.

Чтобы расшифровать шифр Виженера, для начала угадывают длину кодового слова и применяют частотный анализ к каждой n-ной букве послания.

Попробуйте расшифровать эту фразу самостоятельно:

зюм иэлруй южжуглёнъ

Подсказка длина кодового слова — 4.

Шифр Энигмы

Энигма — это машина, которая использовалась нацистами во времена Второй Мировой для шифрования сообщений.

Есть несколько колёс и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес.

Существовало более ста триллионов возможных комбинаций колёс, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения.

Цифровые шифры

В отличие от шифровки текста алфавитом и символами, здесь используются цифры. Рассказываем о способах и о том, как расшифровать цифровой код.

Двоичный код

Текстовые данные вполне можно хранить и передавать в двоичном коде. В этом случае по таблице символов (чаще всего ASCII) каждое простое число из предыдущего шага сопоставляется с буквой: 01100001 = 97 = «a», 01100010 = 98 = «b», etc. При этом важно соблюдение регистра.

Расшифруйте следующее сообщение, в котором использована кириллица:

110100001001101011010000101111101101000010110100

Шифр A1Z26

Это простая подстановка, где каждая буква заменена её порядковым номером в алфавите. Только нижний регистр.

Попробуйте определить, что здесь написано:

15-6-2-16-13-30-26-16-11 17-18-10-14-6-18

Шифрование публичным ключом

Алгоритм шифрования, применяющийся сегодня буквально во всех компьютерных системах. Есть два ключа: открытый и секретный. Открытый ключ — это большое число, имеющее только два делителя, помимо единицы и самого себя. Эти два делителя являются секретным ключом, и при перемножении дают публичный ключ. Например, публичный ключ — это 1961, а секретный — 37 и 53.

Открытый ключ используется, чтобы зашифровать сообщение, а секретный — чтобы расшифровать.

Как-то RSA выделила 1000 $ в качестве приза тому, кто найдет два пятидесятизначных делителя числа:

1522605027922533360535618378132637429718068114961380688657908494580122963258952897654000350692006139

Как расшифровать код или шифр?

Для этого применяются специальные сервисы. Выбор такого инструмента зависит от того, что за код предстоит расшифровать.

Примеры шифраторов и дешифраторов:

Адаптированный перевод «10 codes and ciphers»

5.4 Числовые шифры . Основы классической криптологии. Секреты шифров и кодов

Ни для кого не секрет, что нашу современную жизнь представить без цифр просто невозможно. С их помощью не только обозначаются номера домов и квартир или указываются цены в магазинах. Перечислить все возможные сферы применения этих десяти символов просто невозможно.

Вполне естественно, что цифры и числа нашли широкое применение и в криптографии. Так, например, отдельными числами можно заменять буквы, создавая шифры, которые трудно разгадать. Такие шифры, которые специалисты называют числовыми, относятся к одним из самых распространенных и интересных шифров. На первый взгляд криптограммы, созданные с помощью числовых систем шифрования, выглядят как набор ничего не значащих цифр.

Простой числовой шифр

Перед тем как приступить к созданию шифрованных сообщений с помощью простого числового шифра, необходимо составить шифровальную таблицу.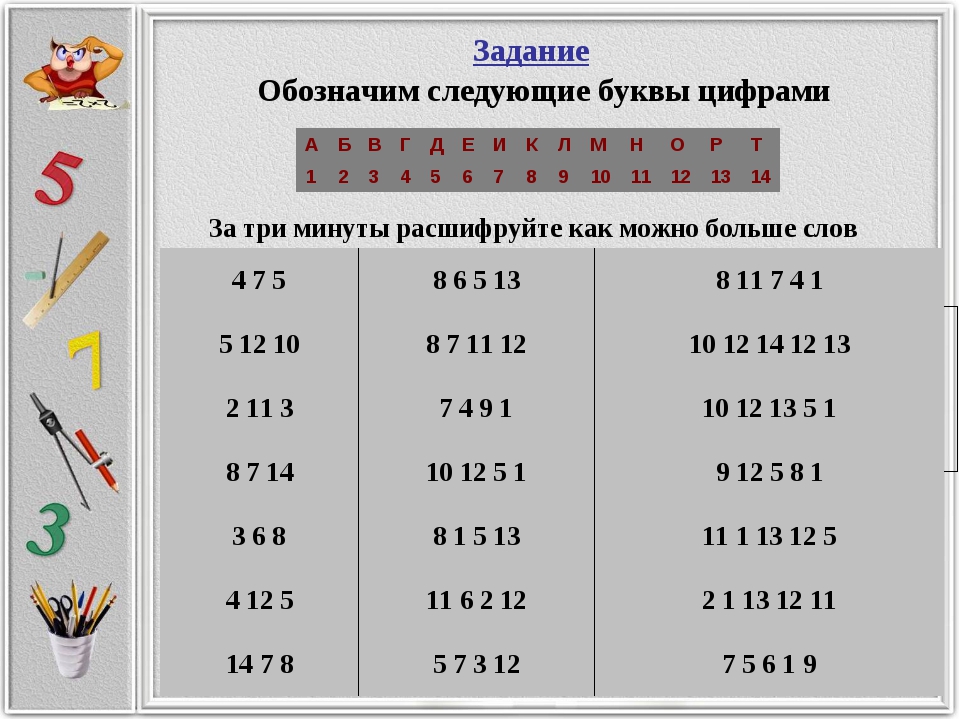

В верхней строке такой таблицы записываются буквы алфавита, а в нижней — числа. При этом первую букву можно обозначить произвольно выбранным числом, а каждую последующую букву надо обозначить числом, большим, чем предыдущее, на 1,2 или 3.

Например, в русском алфавите букву А можно обозначить числом 27, а числа, предназначенные для обозначения каждой из последующих букв алфавита, увеличивать на 2. В таком случае шифровальная таблица будет выглядеть так:

В качестве примера зашифруем с помощью этой таблицы открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ.

Вместо буквы С запишем соответствующее ей в таблице число 61. Вместо буквы Е запишем соответствующее ей число 37, вместо буквы К — число 47 и так далее. В результате получится следующая криптограмма:

61 37 47 59 37 63 53 55 37 61 55 55 29 77 37 53 43 37

Для большей скрытности этот текст можно произвольно разделить на группы цифр, например вот так:

6137 4759 3763 5355 3761 5555 2977 3753 4337

Перед расшифровкой полученный в данном случае шифрованный текст надо разбить на пары цифр, а затем с помощью приведенной выше шифровальной таблицы заменить цифры на соответствующие буквы.

Шифр гласных букв

Не представляет особых трудностей шифрование сообщений с помощью так называемого шифра гласных букв.

При использовании такого шифра гласные буквы в алфавите нумеруются цифрами от 1 до 9. При этом, например, в русском алфавите буква А обозначается цифрой 1, буква Е — цифрой 2, буква И — цифрой 3 и так далее. Затем каждой согласной букве присваивается свой номер, который определяется ее положением относительно ближайшей к ней с левой стороны в алфавите гласной буквы.

Так, например, буква Б — первая согласная буква, расположенная справа от буквы А имеющей номер 1. Поэтому букве Б присваивается число 11. Буква Д — четвертая справа от буквы А, ее обозначают числом 14. Буква Н — пятая справа от гласной буквы И, обозначенной числом 3. Поэтому букве Н должно соответствовать число 35. В соответствии с этим правилом выбираются числа, которыми будут заменены остальные буквы алфавита.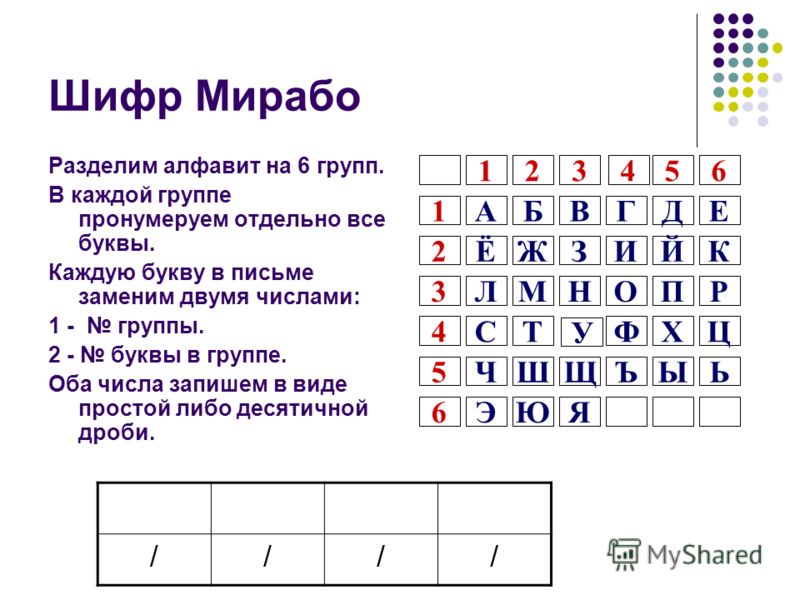

Для быстрого создания шифрованных сообщений с помощью шифра гласных букв можно составить вот такую шифровальную таблицу:

Теперь достаточно в открытом тексте заменить буквы на соответствующие числа, записываемые через точку, и шифровка готова.

В качестве примера попробуем с помощью приведенной выше таблицы зашифровать открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ Сначала необходимо заменить букву С на соответствующее ей число 43, затем букву Е — на число 2, букву К — на число 32 и так до конца текста. В результате зашифрованное сообщение будет выглядеть вот так

43.2.32.42.2.44.35.4.2 43.4.4.11.56.2.35.3.2

Или без пробелов:

43.2.32.42.2.44.35.4.2.43.4.4.11.56.235.3.2

Расшифровка такой криптограммы при использовании заранее составленной таблицы также не будет долгой и затруднительной.

Календарный шифр

Для создания криптограмм с помощью календарного шифра сначала также надо составить шифровальную таблицу. В верхней строке такой таблицы записываются буквы алфавита, а в нижней — числа от 1 до 32. В таком случае наша таблица будет выглядеть так:

В качестве примера зашифруем с помощью календарного шифра открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ

Вместо буквы С запишем соответствующее ей в таблице число 18. Вместо буквы Е запишем соответствующее ей число 6, вместо буквы К — число 11 и так далее. В результате получится следующая криптограмма:

18.6.11.17.6.19.14.15.6.18.15.15.2.26.6.14.9.6

Но на этом процесс шифрования не заканчивается. Теперь выберем какой-либо месяц календаря и каждый день недели обозначим соответствующей буквой. Например, понедельнику будет соответствовать буква П, вторнику — буква В, среде — буква С, четвергу — буква 4, пятнице — буква П, субботе — буква С, воскресенью — буква В.

Поскольку названия некоторых дней недели начинаются с одинаковых букв, для их различия можно применить цифры.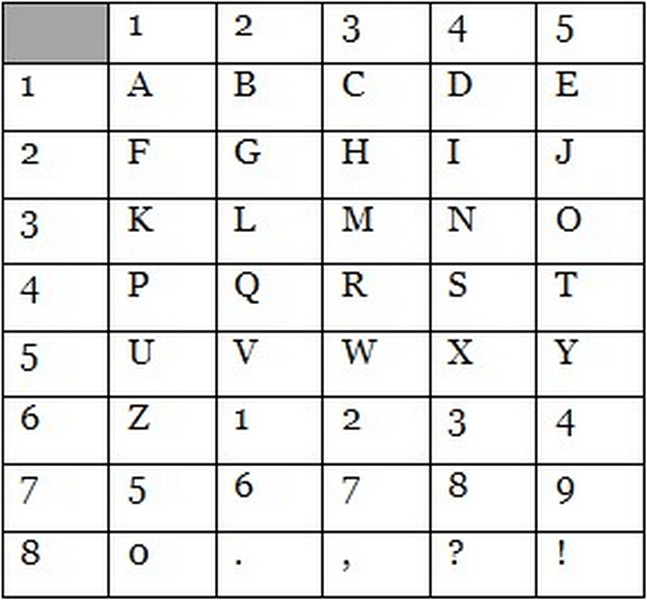 Например, понедельнику будет соответствовать сочетание П1, вторнику — сочетание В1, среде — сочетание С1, четвергу — буква Ч, пятнице сочетание П2, субботе — сочетание С2, воскресенью — сочетание В2.

Шифрование открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ начнется с первой буквы, которой в таблице соответствует число 18. Если 18-е число выбранного месяца выпадет на четверг третьей недели, то первую букву в открытом тексте, а именно букву С, следует заменить на сочетание 43. Таким образом, шифрованное сообщение будет начинаться со знаков 43. Если же 18-е число выбранного месяца выпадет на пятницу третьей недели, то сообщение будет начинаться с сочетания П23. В том случае, когда 18-е число окажется, например, понедельником четвертой недели, то шифровку начнут знаки П14. Таким же образом следует заменить остальные буквы открытого текста.

Например, если для шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ выбрать календарь на март 2012 года, то порядок шифрования будет следующим.

Сначала в соответствии с приведенной выше таблицей необходимо перевести буквы в цифры. В результате из открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ получим:

18.6.11.17.6.19.14.15.6.18.15.15.2.26.6.14.9.6

Теперь с помощью календаря на март 2012 года следует зашифровать числа в дни недели.

Число 18 в марте 2012 года — воскресенье третьей недели, поэтому его надо обозначить как В23.

Число 6 — вторник второй недели, этот день обозначается как В12.

Число 11 в марте 2012 года — воскресенье второй недели, поэтому его надо заменить на сочетание В22.

Для удобства в работе, после того как будут выбраны месяц и год шифровальную таблицу можно дополнить строкой, в которой будет непосредственно указано, на какие сочетания букв и цифр следует заменять соответствующие буквы открытого текста.

В результате шифровальная таблица с использованием календаря на март 2012 года примет следующий вид:

Теперь с помощью такой таблицы зашифровать любое сообщение будет очень просто. Достаточно всего лишь для каждой буквы открытого текста найти соответствующее сочетание знаков для шифровки и выполнить замену. Так, например, открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ после шифрования с помощью календарного шифра с использованием календаря на декабрь 2005 года будет преобразован вот в такую криптограмму:

В23.В12.В22.С23.В12.П14.С13.ЧЗ.В12 В23.ЧЗ.ЧЗ.П21.П15.В12.С13.П22.В12

Или без пробелов:

В23.В12.В22.С23.В12.П14.С13.ЧЗ.В12.В23.ЧЗ.ЧЗ.П21.П15.В12.С13.П22.В12

Дешифровка такого сообщения производится в обратном порядке. Сначала дни недели переводятся в числа месяца, а затем — в буквы открытого текста Естественно, для расшифровки получателю необходимо знать месяц и год, используемые в шифре. Если же заранее составить приведенную выше таблицу, то процесс расшифровки займет всего лишь несколько минут.

Наблюдательный читатель заметит, что в приведенной таблице для обозначения букв алфавита используются 32 числа, хотя в каждом месяце года дней не более, чем 31.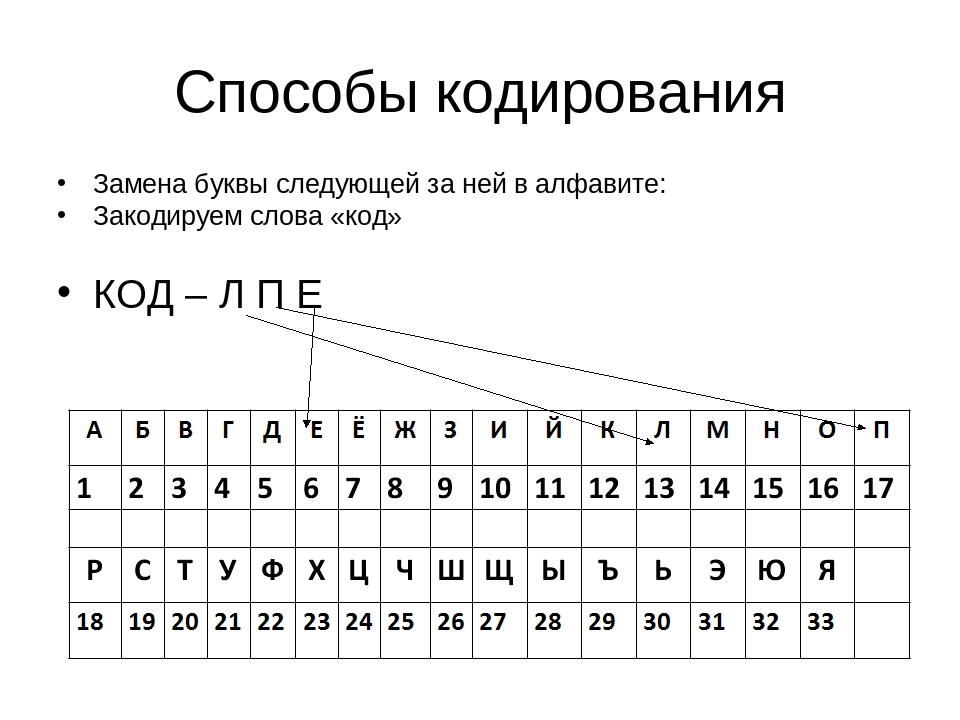 Все правильно. Однако в данной таблице ошибок нет. Просто при применении календарного шифра используется маленькая хитрость, заключающаяся в том, что недостающие дни берутся как бы из следующего месяца.

Если посмотреть на букву Я, которая имеет в таблице порядковый номер 32, то она обозначена сочетанием В25. А это означает воскресенье пятой недели. В то же время в календаре на декабрь 2005 года мы не найдем такой даты, поскольку последний, 31-й день этого месяца приходится на субботу пятой недели. Но это не страшно. Из таблицы пользователь точно знает, что буква Я заменена на сочетание В25. Точно так же заполняются соответствующие ячейки таблицы при использовании месяцев с меньшим количеством дней, от 28 до 30 дней.

Использование несуществующих дат лишь запутает того, кто без ведома и разрешения отправителя захочет разгадать такую шифровку. Главное, чтобы тот, кому такое сообщение предназначается, знал об этих маленьких хитростях.

5.5. Книжные шифры

Среди специалистов так называемые книжные шифры считаются сравнительно стойкими системами шифрования. Дело в том, что взломать подобный шифр и расшифровать созданную с его помощью криптограмму, не зная книги, использовавшейся при шифровании, неспециалисту практически невозможно.

В то же время созд ание шифрованных сообщений с помощью книжных шифров не представляет особого труда даже для начинающих пользователей. Для этого достаточно взять какую-либо книгу, по определенному правилу обозначить отдельные буквы текста этой книги числами и выполнить замену букв открытого текста на соответствующие им числа. Не обязательно, чтобы книга, используемая для шифрования, была широко известной. Однако она обязательно должна быть у получателя сообщения, который должен знать и правило шифрования.

Необходимо добавить, что во избежание ошибок книга, находящаяся у получателя сообщения и используемая для дешифрования, должна быть точно такой же, что и книга, имеющаяся у отправителя. Это означает, что обе книги должны быть полностью идентичны, с тем же количеством страниц и тем же размещением текста на них.

Простой книжный шифр

Знакомство с книжными шифрами следует начать с простого книжного шифра.

Перед началом работы необходимо выбрать книгу и страницу, которые будут использоваться для шифрования. Это может быть, например, первая страница первой части третьего тома романа «Война и мир» Льва Николаевича Толстого. Для шифрования простого сообщения достаточно воспользоваться первыми двумя абзацами текста.

«С конца 1811 года началось усиленное вооружение и сосредоточение сил Западной Европы, и в 1812 году силы эти — миллионы людей (считая тех, которые перевозили и кормили армию) двинулись с Запада на Восток, к границам России, к которым точно так же с 1811 года стягивались силы России. 12 июня силы Западной Европы перешли границы России, и началась война, то есть совершилось противное человеческому разуму и всей человеческой природе событие. Миллионы людей совершали друг против друга такое бесчисленное количество злодеяний, обманов, измен, воровства, подделок и выпуска фальшивых ассигнаций, грабежей, поджогов и убийств, которого в целые века не соберет летопись всех судов мира и на которые в этот период времени люди, совершавшие их, не смотрели как на преступления.

Что произвело это необычайное событие? Какие были причины его? Историки с наивной уверенностью говорят, что причинами этого события были обида, нанесенная герцогу Ольденбургскому, несоблюдение континентальной системы, властолюбие Наполеона, твердость Александра, ошибки дипломатов и т. п.»

Все слова текста, напечатанного на этой странице бессмертного произведения великого русского классика, за исключением дат, следует пронумеровать. В результате текст примет следующий вид:

«С(1) конца(2) 1811 года(3) началось(4) усиленное(5) вооружение(6) и(7) сосредоточение(8) сил(9) Западной(10) Европы(11), и(12) в(13) 1812году(14)силы(15)эти(16) — миллионы(17) людей(18) (считая(19) тех(20), которые(21) перевозили(22) и(23) кормили(24) армию(25),) двинулись(26) с(27) Запада(28) на(29) Восток(30), к(31) границам(32) России(33), к(34) которым(35) точно(36) так(37) же(38) с(39) 1811 года(40) стягивались(41) силы(42) России(43). 12 июня(44) силы(45) Западной(46) Европы(47) перешли(48) границы(49) России(50), и(51) началась(52) война(53), то(54) есть(55) совершилосъ(56) противное(57) человеческому(58) разуму(59) и(60) всей(61) человеческой(62) природе(63) событие(64). Миллионы(65) людей(66) совершали(67) друг(68) против(69) друга(70) такое(71) бесчисленное(72) количество(73) злодеяний(74), обманов(75), измен(76), воровства(77), подделок(78) и(79) выпуска(80) фальшивых(81) ассигнаций(82), грабежей(83), поджогов(84) и(85) убийств(86), которого(87) в(88) целые(89) века(90) не(91) соберет(92) летопись(93) всех(94) судов(95) мира(96) и(97) на(98) которые(99) в(100) этот(101) период(102) времени(ЮЗ) люди(104), совершавшие(105) их(106), не(107) смотрели(108) как(109) на(110) преступления(111).

Что(112) произвело(113) это(114) необычайное(115) событием(116)? Какие(117) были(118) причины(119) его(120)? Историки(121) с(122) наивнойМ23) уверенностью(124) говорятМ25), что(126) причинамиМ?7) этого(128) события(129) были(130) обида(131), нанесеннаяМ32) герцогу(133) Ольденбургскому(134), несо6людение(135) контентальной(136) системы(137), властолюбие(138) Наполеона(139), твердость(140) Александра(141), ошибки(142) дипламатов(143) ит. (144) п.(145).

Алгоритм шифрования при использовании простого книжного шифра заключается в том, что цифра 1 обозначает первую букву первого слова, то есть в рассматриваемом примере букву С. Цифра 2 соответствует первой букве второго слова — букве К и так далее. Например, число 38 соответствует букве Ж, а число 81 — букве Ф.

Наблюдательный читатель заметит, что одной и той же букве соответствуют разные числа. Так, например, букве Г соответствуют числа 3,14,32 и др. В этом заключается одно из достоинств книжного шифра. Поскольку одну и ту же букву открытого текста в криптограмме можно заменить разными числами, разгадать такую криптограмму с помощью методов частотного анализа невозможно.

В качестве примера попробуем зашифровать с помощью простого книжного шифра открытый текст СЕКРЕТНОЕ ПОСЛАНИЕ. Итак, если в данном открытом тексте заменить буквы на соответствующие им числа из приведенного выше текста, то полученная криптограмма будет выглядеть так:

1. 11.87.33.47.71.107.75.55. 22.134.108.93.25.91.121.120

Для того чтобы расшифровать это сообщение, получатель должен в аналогичной книге на известной ему странице пронумеровать все слова, а затем произвести замену указанных в криптограмме чисел на соответствующие буквы.

Усовершенствованный книжный шифр

При практическом применении рассмотренного ранее простого книжного шифра пользователь, без сомнения, столкнется с одной трудно разрешимой проблемой. Она заключается в том, что в русском алфавите есть буквы, с которых начинается лишь небольшое число слов, таких как, например, буква Ы. Найти такие слова в подавляющем числе книг просто невозможно. В то же время в русском языке практически вообще нет слов, которые начинались бы с таких букв, как Ъ или Ь. Однако незначительное усовершенствование простого книжного шифра позволяет решить эту задачу.

В усовершенствованном книжном шифре для замены каждой буквы открытого текста используются два числа, записываемые через тире.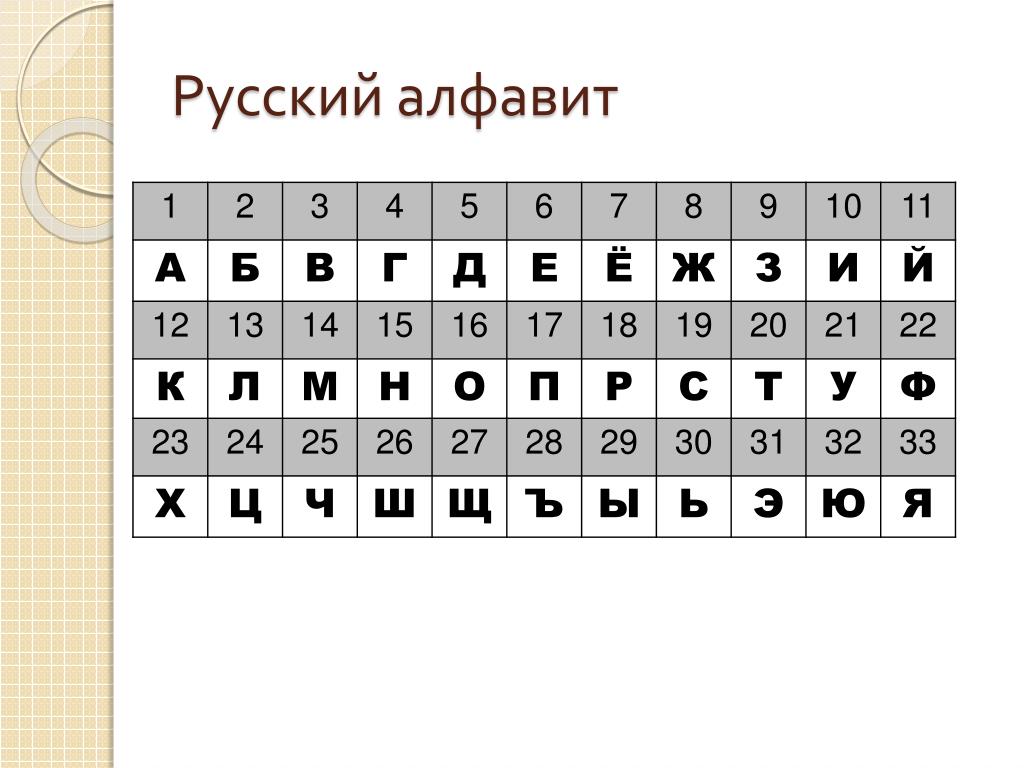 При этом первое число означает порядковый номер слова в тексте, а второе число означает номер буквы в этом слове.

Так, например, в приведенном ранее тексте первой страницы первой части третьего тома романа «Война и мир» Л. Н. Толстого число 2–4 соответствует четвертой букве второго слова, то есть букве Ц Таким же образом определяются числа для других букв. Число 46-8 соответствует в данном темпе букве Й, число 134-3 — букве Ь, число 49-7 — букве Ы и так далее.

Теперь, если в открытом тексте СЕКРЕТНОЕ ПОСЛАНИЕ заменить буквы на соответствующие им числа в соответствии с рассматриваемым алгоритмом шифрования, то полученная криптограмма будет выглядеть так:

4–7.48-2.117-1.83-2.89-5.137-4.57-7.101-3.67-4. 48-1.123-6.82-3.74-2.117-2.124-7.119-3.20-2

Расшифровка такой криптограммы для получателя сообщения не представляет труда. Достаточно в аналогичной книге на определенной странице пронумеровать все слова, а затем произвести замену указанных в криптограмме чисел на соответствующие буквы. В то же время несанкционированный пользователь разгадать подобную шифрограмму не сможет.

5.6. Тайны решеток и таблиц

Уже в древние века наши предки для создания шифрованных сообщений использовали специальные системы шифрования, основу которых составляли так называемые решетки, в отдельные клетки которых в определенном порядке записывались буквы алфавита.

Не менее известны и шифры, при применении которых используются специальные таблицы, ячейки которых также заполняются буквами алфавита При этом шифровальные таблицы с одинаковым количеством строк и столбцов получили название квадратов.

Шифры с использованием всевозможных шифровальных таблиц и решеток постоянно совершенствовались и усложнялись. В то же время эти шифры благодаря простоте их составления и применения может использовать даже неподготовленный пользователь.

В зависимости от используемых алгоритмов данные системы шифрования можно разделить на шифры замены и шифры перестановки. При этом среди шифров замены на основе таблиц следует отметить, например, квадрат Полибия, так называемый шифр «Большой крест» и др.

Простая шифровальная таблица

Данный шифр является одним из самых простых. Его основу составляет таблица, ячейки которой заполнены буквами алфавита. Для русского алфавита такая шифровальная таблица может состоять из шести столбцов по пять строк в каждом, которая будет выглядеть следующим образом:

Теперь эту таблицу следует дополнить еще одним столбцом, который заполнен буквами, и строкой, заполненной цифрами. При этом буквы и цифры могут быть абсолютно любыми. Для начала заполним ячейки дополнительной строки цифрами от 1 до 6, а ячейки дополнительного столбца заполним буквами от А до Д.

В итоге шифровальная таблица примет следующий вид:

Правило шифрования заключается в том, что каждую букву открытого текста необходимо заменить на комбинацию буквы и цифры. При этом буква в криптограмме соответствует строке, а цифра — столбцу, на пересечении которых расположена ячейка с соответствующей буквой открытого текста.

Так, например, в данной таблице ячейка с буквой С находится на пересечении строки В и столбца 5. Поэтому при шифровании открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ с помощью рассматриваемого шифра буква С должна быть заменена на сочетание или группу В5. Таким же образом букву Е открытого текста надо заменить на А6, букву К — на Б4 и так далее. В результате шифрования криптограмма примет следующий вид:

В5.А6.Б4.В4.А6.В6.В1 В2.А6. В5.В2.В2.А2.Д1.А6.В1.БЗ.А6.

Для расшифровки такой криптограммы следует использовать точно такую же таблицу с аналогичным расположением букв в ячейках. При этом каждая комбинация буквы и цифры шифрограммы должна быть заменена на букву, расположенную в соответствующей ячейке на пересечении строки и столбца, обозначенных этой буквой и этой цифрой.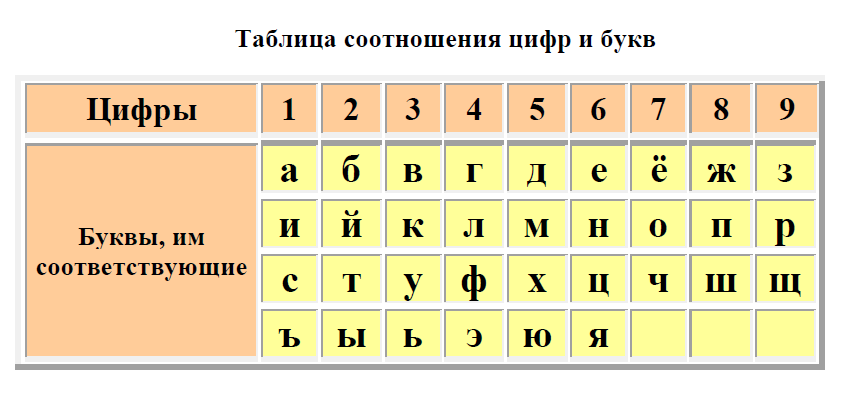 В рассматриваемом примере вместо комбинации В5 следует записать букву С, вместо А6 — букву Е и так далее, пока не будет расшифрован весь текст.

В одном из вариантов такого шифра для обозначения строк также можно использовать цифры. При этом шифровальная таблица будет выглядеть вот так:

После шифрования открытого текста с помощью приведенного выше алгоритма криптограмма будет состоять из нескольких пар или групп цифр. При этом в каждой группе первая цифра обозначает строку, а вторая цифра — столбец, на пересечении которых расположена ячейка с соответствующей буквой открытого текста.

Так например, в результате шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ криптограмма примет следующий вид:

35.16.24.34.16.36.31.32.16. 35.32.32.12.51.16.31.23.16.

Расшифровка такой криптограммы заключается в замене пар или групп цифр буквами, находящимися в тех ячейках таблицы, строки и столбцы для которых обозначены соответствующими цифрами.

Таблица с паролем

В приведенных ранее примерах шифров буквы в ячейки шифровальных таблиц вписывались в том порядке, в каком они расположены в алфавите. Естественно, стойкость таких шифров оставляет желать лучшего. Поэтому чаще всего при применении различных шифровальных систем, основанных на использовании таблиц, буквы алфавита в ячейки таких таблиц вписываются в случайном порядке или в соответствии с определенным правилом. Главное, чтобы порядок заполнения ячеек был известен получателю.

Наиболее удобным вариантом будет конечно же тот, когда ячейки заполнены в абсолютно произвольном порядке, а получатель уже имеет готовую таблицу с записанными в ячейки буквами. Однако в этом случае велик риск того, что такая шифровальная таблица может оказаться в руках незаконного пользователя со всеми вытекающими последствиями. Поэтому желательно, чтобы отправитель и получатель сообщения не хранили у себя шифровальную таблицу, а лишь знали, по какому правилу она составляется.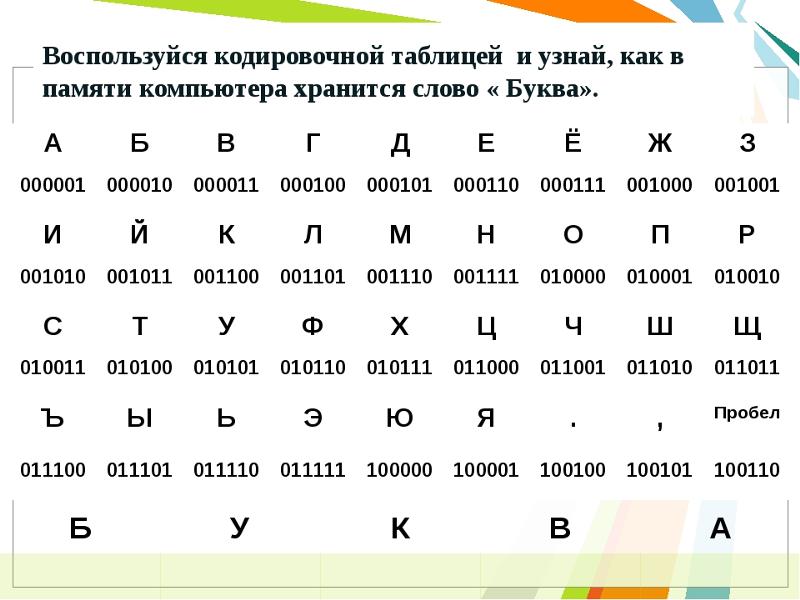 При необходимости на основании такого правила всегда можно составить шифровальную таблицу, с ее помощью зашифровать или расшифровать сообщение, а затем эту таблицу уничтожить.

Одним из способов заполнения таблиц является использование паролей. Для составления такой таблицы сначала необходимо выбрать пароль или кодовое слово. При этом желательно, чтобы в пароле не было повторяющихся букв. Конечно же данная рекомендация не является обязательной. После этого буквы пароля вписываются в первые ячейки таблицы, а остальные ячейки заполняются оставшимися, не использованными в пароле, буквами алфавита.

Так, например, если в качестве пароля выбрано слово ПАРОДИЯ, то шифровальная таблица примет следующий вид;

Если теперь эту таблицу дополнить еще одним столбцом, заполненным буквами, и строкой, заполненной цифрами, то можно воспользоваться одним из рассмотренных ранее алгоритмов шифрования.

При использовании этого шифра каждую букву открытого текста необходимо заменить на комбинацию буквы и цифры. При этом буква в криптограмме соответствует строке, а цифра — столбцу таблицы, на пересечении которых расположена ячейка с соответствующей буквой открытого текста.

В результате шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ таким шифром криптограмма примет следующий вид:

В6.Б5.В2.АЗ.Б5.Г1.В5.А4.Б5. В6.А4.А4.Б2.Д2.Б5.В5.А6.Б5.

Таким же образом можно зашифровать сообщение с помощью таблицы, в которой для обозначения столбцов и строк используются только цифры.

В этом случае после шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ криптограмма будет выглядеть так:

36.25.32.13.25.41.35.14.25. 36.14.14.22.52.25.35.16.25.

При выборе пароля желательно, чтобы в нем не было повторяющихся букв, поскольку в этом случае упрощается создание шифровальной таблицы. Конечно желанная рекомендация не является обязательной. Можно использовать слова и с повторяющимися буквами, только при заполнении таблицы такие буквы следует пропустить.

Так, например, если в качестве пароля выбрано слово ПЕРЕПРАВА, то повторяющиеся буквы Е, П, Р и В не записываются в ячейки, а пропускаются. При этом шифровальная таблица примет следующий вид:

Если теперь данную таблицу дополнить еще одним столбцом, заполненным буквами, и строкой, заполненной цифрами, то можно воспользоваться уже упоминавшимся алгоритмом шифрования.

Напомним, что при использовании этого шифра правило шифрования заключается в том, что каждую букву открытого текста необходимо заменить на комбинацию буквы и цифры. При этом буква в криптограмме соответствует строке, а цифра — столбцу, на пересечении которых расположена ячейка с соответствующей буквой открытого текста. В результате шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ таким шифром криптограмма примет следующий вид:

В5. А2.Б6.АЗ.А2.В6.ВЗ.В4.А2. В5.В4.В4.А6.Д1.А2.ВЗ.Б5.А2.

И в этой таблице для обозначения строк можно использовать цифры. При этом порядок применения алгоритма шифрования не отличается от рассмотренных ранее шифров.

Для того чтобы усложнить незаконному пользователю задачу взлома шифра, вместо повторяющихся в пароле букв в ячейки можно вписывать оставшиеся буквы алфавита. Так, например, при использовании в качестве пароля слова ПЕРЕПРАВА повторяющиеся буквы Е, П, Р и В не записываются в ячейки. Вместо них в соответствующие ячейки вставляются не вошедшие в пароль следующие буквы алфавита Для рассматриваемого пароля вместо второй буквы Е следует записать букву Б, вместо второй буквы П — букву Г, вместо второй буквы Р — букву Д и так далее. При этом шифровальная таблица примет следующий вид:

Такую таблицу можно использовать для шифрования сообщений в соответствии как с рассмотренными ранее алгоритмами шифрования, так и с другими.

Следует отметить, что паролем может служить не только отдельное слово, но и целая фраза. Эго может быть известная поговорка или пословица, цитата или строка из стихотворения. При этом правила заполнения ячеек шифровальной таблицы буквами алфавита остаются такими же, как и для уже упоминавшихся таблиц с простым паролем.

Так, например, при использовании в качестве пароля фразы ПРИКАЗЫ НЕ ОБСУЖДАЮТСЯ шифровальная таблица может выглядеть следующим образом:

Такую таблицу также можно использовать для шифрования сообщений в соответствии как со всеми рассмотренными ранее алгоритмами шифрования, так и с другими.

Квадрат Полибия

Одну из первых систем шифрования, в которой использовалась таблица, описал древнегреческий историк Полибий. Точно неизвестно, является ли талантливый писатель автором этого шифра. Тем не менее специалисты называют этот шифр «квадратом Полибия». Еще до наступления нашей эры этот шифр широко применялся как греками, так и римлянами.

При использовании данного шифра составляется таблица, которая, например, для английского алфавита состоит из пяти столбцов по пять строк в каждом. В каждую клетку этой таблицы в произвольном порядке вписывается одна из букв алфавита. Необходимо отметить, что для русского алфавита, содержащего большее количество букв, шифровальная таблица должна содержать не менее 30 клеток. Эго может быть, например, таблица из шести столбцов по пять строк в каждом.

Алгоритм шифрования заключается в том, что при преобразовании открытого текста в криптограмму необходимо найти в таблице ячейку с нужной буквой и вставить в шифрованный текст букву, располагающуюся в нижней от нее ячейке в том же столбце. Если же буква открытого текста оказывается в ячейке нижней строки, то в шифрограмму следует записать букву из верхней ячейки того же столбца.

В качестве при мера зашифруем с помощью шифра «квадрат Полибия» открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ. Перед началом работы необходимо составить шифровальную таблицу, которая может выглядеть, например, вот так:

Теперь следует найти клетку с первой буквой открытого текста Эго буква С, ячейка с которой расположена в третьей строке третьего столбца. В соответствии с алгоритмом шифрования вместо этой буквы в криптограмму необходимо записать букву, расположенную в нижней от нее ячейке в том же столбце, то есть вместо буквы С — букву К. Таким же образом букву Е открытого текста надо заменить на букву У, букву К на букву Ц и так далее. Не следует забывать о том, что в случае если буква открытого текста окажется в ячейке нижней строки, то в шифрограмму следует записать букву из самой верхней ячейки того же столбца. Например, буква Р должна быть заменена в криптограмме на букву Ю.

В результате шифрования открытого текста СЕКРЕТНОЕ СООБЩЕНИЕс помощью рассматриваемого шифра криптограмма примет следующий вид:

КУЦЮУПВНУ КННИГУВМУ

Для расшифровки получатель сообщения должен использовать точно такую же таблицу с аналогичным расположением букв в ячейках. При этом каждая буква шифрограммы должна быть заменена на букву, расположенную в верхней от нее ячейке в том же столбце.

В рассматриваемом примере вместо буквы К следует записать букву С, вместо буквы У — букву Е и так далее, пока не будет расшифрован весь текст. Если же буква из криптограммы в таблице занимает верхнюю ячейку, то ее следует заменить на букву, находящуюся в самой нижней ячейке того же столбца.

Шифр «Большой крест»

Первые упоминания о шифре, в некоторых источниках называемом «Большой крест», относятся к XVIII столетию. Необходимо отметить, что в отдельных зарубежных изданиях автору встречались варианты этого шифра с весьма экзотическими названиями. Например, название одного из вариантов можно перевести на русский язык как шифр «Загончики для поросят».

Шифр «Большой крест» прост и в то же время очень эффективен. Неподготовленный незаконный пользователь, желающий прочитать сообщение, зашифрованное с помощью данного шифра замены, вряд ли сможет сразу догадаться, как его взломать. В связи с ограниченным объемом данной книги далее будут рассмотрены лишь некоторые варианты шифра «Большой крест».

Практическое использование данного шифра следует начать с составления специальной шифровальной таблицы, которая будет выглядеть как несколько решеток. В одном из вариантов такая таблица может иметь вид, показанный на рис. 5.1.

Рис. 5.1 Шифровальная таблица для шифра «Большой крест»

В качестве примера зашифруем с помощью шифра «Большой крест» открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ. Если заменить буквы открытого текста соответствующими им символами ячеек решетки, то получится промежуточный результат, показанный на рис. 5.2.

В окончательном виде криптограмма для открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ будет выглядеть так, как показано на рис. 5.3.

Рис. 5.2 Промежуточный результат шифрования с помощью шифра «Большой крест»

Рис. 5.3 Криптограмма для открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ полученная в результате использования шифра «Большой крест»

Если с помощью рассматриваемого шифра зашифровать открытый текст ИЛЛЮЗИЯ, то криптограмма примет вид показанный на рис. 5.4.

Рис. 5.4 Криптограмма для открытого текста ИЛЛЮЗИЯ, полученная в результате использования шифра «Большой крест»

Для того чтобы расшифровать приведенные криптограммы, достаточно составить аналогичную шифровальную таблицу и заменить символы на соответствующие им буквы.

Необходимо отметить, что комбинаций расположения букв в ячейках решеток может быть довольно много. Поэтому законный пользователь для шифрования сообщений при желании может придумать свой, оригинальный вариант шифра «Большой крест».

5.7. Перестановки в таблицах

В шифрах, основу которых составляют таблицы, применяются самые разнообразные алгоритмы шифрования. Ранее были рассмотрены несколько простых систем шифрования, в которых используются специальные таблицы, ячейки которых заполняются буквами алфавита.

При этом составление криптограммы заключается в замене букв открытого текста в соответствии с определенными правилами.

В то же время существует множество шифров, при работе с которыми также составляются таблицы, однако ячейки этих таблиц заполняются не всеми буквами алфавита, а только буквами открытого текста. Алгоритм шифрования при использовании таких шифров заключается в том, что строки и столбцы в таблице с открытым текстом переставляются или перемешаются в соответствии с определенным правилом.

Простая перестановка

Одним из шифров, основанных на перестановке строк и столбцов в таблице с открытым текстом, является шифр простой перестановки. Создание криптограммы при использовании данного шифра следует начать с составления таблицы, в ячейки которой необходимо вписать по строкам буквы открытого текста. При этом количество строк и столбцов в такой шифровальной таблице выбирается произвольно. После заполнения таблицы буквы в криптограмму выписываются по столбцам, сначала из первого столбца, затем из второго и так далее.

В качестве примера зашифруем с помощью этого шифра открытый текст МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО. При выборе таблицы, состоящей из пяти строк и шести столбцов, ее ячейки будут заполнены следующим образом:

Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первого столбца, затем из ячеек второго столбца и так далее.

В окончательном виде криптограмма для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО будет выглядеть так:

МСИТЗ ЕТЗЬМ СРМНО ТЕЕЕЖ ОЧНВН ВИИОО

Если записать эту криптограмму без пробелов, то она примет следующий вид:

МСИТЗЕТЗЫИСРМНОТЕЕЕЖОЧНВНВИИОО

Для расшифровки такого шифрованного сообщения достаточно в таблицу аналогичных размеров по столбцам вписать буквы криптограммы, а затем по строкам прочитать открытый текст. Естественно, для этого получатель сообщения должен знать размер таблицы.

Перестановка с паролем

Не менее интересен более сложный способ шифрования, который можно назвать перестановкой с паролем. При использовании этого шифра столбцы или строки в таблице, заполненной буквами открытого текста, перемещаются на определенное количество позиций по определенному правилу. Порядок перемещения столбцов или строк в таблице должен быть известен получателю сообщения.

Как и в рассмотренном ранее шифре простой перестановки, создание криптограммы при использовании данного шифра следует начать с составления таблицы, в ячейки которой необходимо вписать по строкам буквы открытого текста. При этом количество строк и столбцов в такой шифровальной таблице выбирается произвольно.

Если пользователь решил произвести перестановку столбцов, то к этой таблице следует добавить еще две строки. В ячейки первой добавленной строки необходимо вписать буквы пароля. В ячейки второй строки записываются цифры, соответствующие позиции каждой буквы пароля в алфавите по отношению к другим буквам пароля.

Если в качестве пароля выбрать, например, слово ПРИВЕТ, то шифровальная таблица будет выглядеть вот так:

После этого необходимо переставить столбцы в таблице так, чтобы цифры во второй строке располагались по порядку. В результате такой перестановки таблица примет следующий вид:

Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек третьей строки, затем из ячеек четвертой строки и так далее.

ТОСМЕВ ЕЧРСТИ ЕНМИЗИ ЕВНТЬО ЖНОЗМО

Для того чтобы расшифровать эту шифрограмму, получатель сообщения, зная пароль, должен сначала составить аналогичную шифровальную таблицу, во второй строке которой записываются цифры по порядку, а в первой — соответствующие этим цифрам буквы пароля. Остальные ячейки следует заполнить по строкам буквами криптограммы. Если теперь переставить столбцы таблицы так, чтобы буквы в верхней строчке образовали пароль, то в строках таблицы получатель сообщения сможет прочитать открытый текст.

Таким же образом в таблице с открытым текстом можно произвести перестановку строк. В этом случае к первоначальной таблице следует добавить еще два столбца. При этом в ячейки первого добавленного столбца необходимо вписать буквы пароля. В ячейки второго столбца записываются цифры, соответствующие позиции каждой буквы пароля в алфавите по отношению к другим буквам пароля.

Если в качестве пароля выбрать, например, слово ВЕСНА, то шифровальная таблица для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО примет следующий вид:

После этого необходимо переставить строки в таблице так, чтобы цифры во втором столбце располагались по порядку. В результате такой перестановки таблица примет следующий вид:

Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек третьего столбца, затем из ячеек четвертого столбца и так далее.

В окончательном виде шифрограмма для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО будет выглядеть так:

ЗМСТИ МЕТЬЗ ОСРНМ ЖТЕЕЕ НОЧВН ОВИОИ

Для расшифровки этой криптограммы получатель сообщения, зная пароль, должен сначала составить аналогичную шифровальную таблицу, во втором столбце шторой записываются цифры по порядку, а в первом — соответствующие этим цифрам буквы пароля. Остальные ячейки следует заполнить по столбцам буквами криптограммы. Если теперь переставить строки таблицы так, чтобы буквы в первом столбце образовали пароль, то в строках таблицы получатель сообщения сможет прочитать открытый текст.

При выборе пароля желательно, чтобы в нем не было повторяющихся букв, поскольку в этом случае упрощается создание шифровальной таблицы. Конечно желанная рекомендация не является обязательной. Можно использовать слова и с повторяющимися буквами, только при заполнении таблицы номера таким буквам присваиваются слева направо.

Двойная перестановка

Следует признать, что рассмотренные ранее системы шифрования, в которых применяется перестановка столбцов и строк шифровальной таблицы, ячейки которой заполнены буквами открытого текста, имеют сравнительно низкую стойкость. Для специалистов взлом таких шифров не представляет особого труда. В то же время неподготовленный незаконный пользователь на разгадку подобного шифра будет вынужден затратить немало времени. Задача взлома шифра значительно усложнится, если отправитель сообщения воспользуется так называемым шифром двойной перестановки.

При использовании шифра двойной перестановки в таблице, заполненной буквами открытого текста, на определенное количество позиций по определенному правилу перемещаются как столбцы, так и строки.

В качестве примера зашифруем с помощью этого шифра открытый текст МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО. Если пользователь решил воспользоваться шифром двойной перестановки, то к уже знакомой шифровальной таблице, состоящей из пяти строк и шести столбцов, следует добавить еще две строки и два столбца. При этом ячейки таблицы будут заполнены следующим образом:

В ячейки первой добавленной строки необходимо вписать буквы пароля для перестановки столбцов. В ячейки второй строки записываются цифры, соответствующие позиции каждой буквы пароля в алфавите по отношению к другим буквам пароля. Если в качестве пароля для перестановки столбцов выбрать, например, слово ПРИВЕТ, то шифровальная таблица будет выглядеть вот так:

В ячейки первого добавленного столбца необходимо вписать буквы пароля для перестановки строк. В ячейки второго столбца записываются цифры, соответствующие позиции каждой буквы пароля в алфавите по отношению к другим буквам пароля. Если в качестве пароля для перестановки строк выбрать, например, слово ВЕСНА, то шифровальная таблица примет следующий вид:

Для создания криптограммы сначала необходимо переставить столбцы в таблице так, чтобы цифры во второй строке располагались по порядку. В результате такой перестановки таблица примет следующий вид:

После этого следует переставить строки в таблице так, чтобы цифры во втором столбце располагались по порядку. После выполнения такой перестановки таблица будет выглядеть вот так:

Теперь дпя создания шифрограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки ит. д. В окончательном виде криптограмма для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО будет выглядеть так:

ЖНОЗМО ТОСМЕВ ЕЧРСТИ ЕВНТЬО ЕНМИЗИ

Для того чтобы расшифровать эту шифрограмму, получатель сообщения должен знать пароли для перемещения столбцов и строк Затем необходимо составить аналогичную шифровальную таблицу. Во второй строке этой таблицы записываются цифры по порядку, а в первой — соответствующие этим цифрам буквы пароля для перемещения столбцов. Во втором столбце таблицы записываются цифры по порядку, а в первом — соответствующие этим цифрам буквы пароля для перемещения строк. Остальные ячейки следует заполнить по строкам буквами криптограммы. Теперь необходимо переставить столбцы таблицы так, чтобы буквы в первой строке образовали пароль для перемещения столбцов. После этого достаточно переставить строки таблицы так, чтобы буквы в первом столбце образовали пароль для перемещения строк и в строках таблицы получатель сообщения сможет прочитать открытый текст.

В процессе шифрования буквы из ячеек шифровальной таблицы можно выписать и по столбцам, сначала из ячеек первого столбца, затем из ячеек второго столбца и так далее. В этом случае криптограмма для открытого текста МЕСТО ВСТРЕЧИ ИЗМЕНИТЬ НЕВОЗМОЖНО примет следующий вид:

ЖТЕЕЕ НОЧВН ОСРНМ ЗМСТИ МЕТЬЗ ОВИОИ

Однако в этом случае порядок действий при дешифровании незначительно изменится. При составлении таблицы получатель сообщения, как и в рассмотренном ранее примере, во второй строке должен записать цифры по порядку, а в первой — соответствующие этим цифрам буквы пароля для перемещения столбцов. Во втором столбце таблицы записываются цифры по порядку, а в первом — соответствующие этим цифрам буквы пароля для перемещения строк. Однако остальные ячейки следует заполнить буквами криптограммы не по строкам, а по столбцам.

После этого, как и в рассмотренном ранее примере, необходимо переставить столбцы таблицы так, чтобы буквы в первой строке образовали пароль для перемещения столбцов. Теперь достаточно переставить строки таблицы так, чтобы буквы в первом столбце образовали пароль для перемещения строк, и в строках таблицы получатель сообщения сможет прочитать открытый текст.

5.8. Магические квадраты

В Средние века широкое распространение получили шифры, основу которых составляли так называемые магические квадраты.

В математике магическими квадратами называются таблицы с одинаковым количеством строк и столбцов. В каждую ячейку такой таблицы вписывается какое-либо число, при этом сумма всех чисел, расположенных в одном столбце, в одной строке и на одной диагонали, составляет одно и то же число.

Необходимо отметить, что для шифрования проще всего использовать магические квадраты, в ячейки которых записываются числа по порядку без повторов, начиная от цифры 1 и до числа, которое определяется количеством ячеек в данном квадрате. При этом не следует забывать о том, что для шифрования длинных сообщений потребуются таблицы большего размера. Так, например, для шифрования открытого текста, состоящего из 16 знаков, достаточно воспользоваться магическим квадратом размером 4×4, а для шифрования текста, содержащего 64 знака, потребуется таблица размером 8×8.

При использовании шифров, основанных на магических квадратах, алгоритм шифрования заключается в том, что в ячейки таблицы вместо цифр магического квадрата по определенному правилу вписываются буквы и знаки открытого текста После того как все ячейки будут заполнены, текст криптограммы выписывается из таблицы по строкам или по столбцам.

Простейший магический квадрат

Как известно, чем меньше столбцов и строк в квадратной таблице, тем меньше вариантов построения на ее основе магического квадрата Так, например, для таблицы, состоящей из трех столбцов и трех строк, известен всего лишь один вариант заполнения ячеек цифрами от 1 до 9, в результате которого получится магический квадрат. Такая таблица будет выглядеть так:

Нетрудно подсчитать, что сумма цифр в каждом столбце, в каждой строке и в каждой большой диагонали составляет одно и то же число и равна 15.

При использовании шифров, основанных на магических квадратах, один из простейших алгоритмов шифрования заключается в том, что в ячейки таблицы вместо цифр магического квадрата вписываются по порядку буквы открытого текста. Так, например, вместо цифры 1 в соответствующую ей ячейку следует записать первую букву сообщения, вместо цифры 2 — вторую букву, вместо цифры 3 — третью букву и так далее.

В качестве примера зашифруем с помощью этого магического квадрата открытый текст РАЗВЕДЧИК При этом в ячейку с цифрой 1 следует записать букву Р, в ячейку с цифрой 2 — букву А, в ячейку с цифрой 3 — букву 3 и так до конца сообщения. В результате таблица примет следующий вид:

Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки и так далее.

В окончательном виде криптограмма для открытого текста РАЗВЕДЧИК будет выглядеть так:

ИРД ЗЕЧ ВКА

Получив такую шифрограмму, получатель для расшифровки сообщения должен сначала заполнить таблицу буквами криптограммы, а затем из соответствующих ячеек выписать буквы открытого текста в порядке, определяемом цифрами используемого магического квадрата.

Необходимо отметить, что утверждение о существовании лишь одного магического квадрата размером 3×3 для цифр от 1 до 9 не касается случаев, когда другие магические квадраты могут быть образованы из первоначального с помощью поворота таблицы или отражения строк и столбцов.

Один из таких производных квадратов может выглядеть следующим образом:

Такой магический квадрат также с успехом можно использовать для шифрования коротких сообщений в соответствии с приведенным выше алгоритмом.

Индийский квадрат

В одном из древних индийских храмов исследователи обнаружили квадратную таблицу, которая при более подробном изучении оказалась одним из самых первых известных магических квадратов. По мнению некоторых историков, эта таблица была создана в XII веке.

Ячейки данной таблицы, состоящей из четырех столбцов и четырех строк, заполнены числами от 1 до 16 так, что сумма всех чисел, расположенных в одном столбце, в одной строке и на одной диагонали, составляет одно и то же число, а именно 34. Более того, сумма чисел в четырех ячейках, образующих квадратные таблицы внутри данного магического квадрата, также составляет 34.

Порядок заполнения ячеек в этой таблице выглядит следующим образом:

Естественно, что такой магический квадрат также можно использовать для шифровки короткого сообщения, содержащего до шестнадцати знаков.

В качестве примера зашифруем, например, открытый текст СЕКРЕТНАЯ ВСТРЕЧА. Для шифрования данного сообщения с использованием рассмотренного ранее алгоритма необходимо сначала вставить в ячейки таблицы вместо цифр буквы открытого текста. При этом вместо цифры 1 в соответствующую ячейку следует вставить первую букву открытого текста, в рассматриваемом примере это будет буква С. Вместо цифры 2 в соответствующую ячейку следует вставить вторую букву открытого текста, то есть букву Е, и так далее.

В результате такой замены шифровальная таблица примет следующий вид:

В окончательном виде криптограмма для открытого текста СЕКРЕТНАЯ ВСТРЕЧА будет выглядеть так:

НТСЕ ЕРАС АКВЕ ЯТЧР

Для того чтобы расшифровать эту шифрограмму, получатель сообщения должен сначала заполнить таблицу известных ему размеров буквами криптограммы, а затем из соответствующих ячеек выписать буквы открытого текста в порядке, определяемом цифрами используемого магического квадрата.

По утверждению некоторых источников, классических магических квадратов размером 4×4 существует всего 12. При этом другие магические квадраты тех же размеров могут быть образованы из первоначального, например с помощью поворота таблицы или отражения строк и столбцов. Общее число таких производных магических квадратов разными специалистами оценивается от нескольких сотен до нескольких тысяч. С учетом того, что любой из упомянутых магических квадратов может быть использован для шифрования сообщения, задача взлома шифра для незаконного пользователя с помощью подбора необходимой таблицы вручную становится практически невыполнимой.

Квадрат Эйлера

Известный математик, астролог и криптограф Леонард Эйлер, долгое время работавший в России в XVIII веке, является автором известной таблицы, состоящей из восьми столбцов и восьми строк.

Все клетки так называемого квадрата Эйлера заполнены числами от 1 до 64 так, что сумма всех чисел, расположенных в одном столбце и в одной строке, составляет одно и то же число, а именно 260. Более того, если данную таблицу разделить на четыре квадратные таблицы, то и в каждой из них сумма чисел в ячейках одного столбца и одной строки также будет одинакова и составит 130. Таким же свойством обладает и квадрат размером 4×4, составленный из ячеек, расположенных в центральной части большой таблицы.

Порядок заполнения ячеек в квадрате Эйлера выглядит следующим образом:

Нетрудно заметить, что с математической точки зрения данная таблица не является классическим магическим квадратом, поскольку суммы чисел в ячейках, образующих диагонали, не равны между собой. В то же время квадрат Эйлера можно использовать для шифрования сравнительно длинных сообщений, используя алгоритм шифрования, рассмотренный ранее для классических магических квадратов.

Магический квадрат 9×9

Как отмечалось ранее, для шифрования длинных сообщений необходимо использовать таблицы большего размера. При этом не следует забывать о том, что чем больше столбцов и строк в квадратной таблице, тем больше вариантов построения на ее основе магического квадрата. Данный факт значительно усложняет незаконному пользователю задачу расшифровки сообщений, зашифрованных, например, с помощью магического квадрата размером 4×4.

Естественно, применение магических квадратов, например, размером 9×9 обеспечивает еще более высокую степень защиты и уменьшает вероятность того, что сообщение будет прочитано тем, кому оно не предназначено.

Один из вариантов такого квадрата имеет следующий вид:

Как и упоминавшийся квадрат Эйлера, данный магический квадрат также можно использовать для шифрования длинных сообщений, используя рассмотренный ранее алгоритм шифрования для классических магических квадратов. При этом открытый текст может содержать до 81 знака.

5.9. Трафарет в системах шифрования

Для создания шифрованных сообщений можно использовать специальные трафареты, которые представляют собой, например, лист бумаги с вырезанными в произвольном порядке отверстиями. Необходимо отметить, что в настоящее время известно множество систем шифрования, в которых применяются различные способы создания и использования таких трафаретов. Естественно, при применении таких шифров получатель криптограммы должен не только иметь точно такой же трафарет, но и хорошо знать правила работы с ним.

Один из вариантов простого шифра с использованием трафарета применял, например, великий русский писатель А. С. Грибоедов в начале XIX века. На лист бумаги он с помощью трафарета наносил текст сообщения, а затем уже без трафарета дополнял текст так, чтобы получилось вполне невинное письмо.

Трафаретные шифры неоднократно упоминаются и в произведениях авторов детективных романов. Среди более сложных шифров с трафаретами следует отметить, например, так называемую решетку Кардано.

Простой шифр с трафаретом

При использовании такого способа шифрования сначала необходимо сделать трафарет из листа бумаги с вырезанными в нем отверстиями. Для этого удобно воспользоваться листом бумаги в клеточку, в котором отдельные клетки следует вырезать в произвольном порядке.

Так, например, трафарет для шифрования сообщений может выглядеть так, как показано на рис. 5.5.

Рис. 5.5 Один из вариантов трафарета для шифрования сообщений

На представленном рисунке черным цветом закрашены ячейки, которые следует вырезать.

В качестве примера зашифруем с помощью данного трафарета открытый текст СЕКРЕТНОЕ ПИСЬМО. Для этого сначала необходимо наложить трафарет на чистый лист бумаги и в вырезанных прямоугольниках вписать буквы открытого текста.

В результате на листе получится следующая надпись:

Теперь для создания криптограммы достаточно убрать трафарет и между буквами открытого текста вписать любые другие буквы в произвольном порядке. В этом случае криптограмма может принять следующий вид:

Для того чтобы запутать незаконного пользователя, буквы можно вписать так, чтобы получился какой-либо вполне обычный текст.

При расшифровке такой криптограммы получателю сообщения достаточно наложить аналогичный трафарет на лист с текстом и в вырезанных ячейках прочитать открытый текст.

Необходимо отметить, что при использовании данного шифра для шифровки сравнительно коротких сообщений при создании трафарета необходимо обратить внимание на то, чтобы количество вырезанных клеточек было не меньше, чем количество букв в открытом тексте. Для шифровки длинных сообщений можно сделать трафарет с большим количеством вырезанных ячеек или же один и тот же трафарет использовать несколько раз.

Решетка Кардано

Более сложной системой шифрования, в которой также используется трафарет определенной формы, является шифр, называемый решеткой Кардано. Название этого шифра произошло от имени его автора, итальянского математика и философа Джероламо Кардано. Именно он в далеком 1566 году водной из своих работ опубликовал описание рассматриваемого шифра.

Основу простейшей решетки Кардано составляет трафарет, выполненный в форме квадратной таблицы. При этом ячейки в данном трафарете вырезаются так, чтобы после поворота трафарета вокруг центральной оси буквы, записанные в ячейках на подложенном листе бумага, не перекрывались. Другими словами, при четырех поворотах трафарета на 90? ячейки, перекрыв все клетки таблицы, ни разу не должны оказаться в одном и том же месте.

Рис. 5.8 Решетка Кардано размером 4×4

Так, например, вариант такого трафарета размером 4×4 имеет вид, изображенный на рис. 5.6.

На представленном рисунке черным цветом закрашены ячейки, которые следует вырезать.

В качестве примера зашифруем с помощью решетки Кардано открытый текст СЕКРЕТНАЯ ВСТРЕЧА Шифрование данного сообщения необходимо начать с заполнения ячеек таблицы буквами открытого текста Для этого наложим трафарет на лист с таблицей и в вырезанные ячейки впишем первые буквы открытого текста. В рассматриваемом примере это первые четыре буквы, а именно буквы С, Е, К и Р.

В результате надпись на листе будет выглядеть так:

После этого повернем трафарет по часовой стрелке на 90? и в свободные ячейки вновь запишем следующие четыре буквы открытого текста В рассматриваемом примере это буквы Е, Т, Н и А

Теперь повернем трафарет по часовой стрелке еще на 90? и в свободные ячейки вновь запишем следующие четыре буквы открытого текста а именно буквы Е, П, И и С.

Следующий поворот трафарета также следует провести по часовой стрелке еще на 90?, а свободные ячейки заполнить оставшимися четырьмя буквами открытого текста

После заполнения всех свободных ячеек и снятия трафарета на листе бумаги останется шифровальная таблица которая имеет следующий вид:

Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки и так далее. В окончательном виде криптограмма для открытого текста СЕКРЕТНАЯ ВСТРЕЧА будет выглядеть так:

ЯСЕР ЕВЕТ ЧНКС ААТР

Для того чтобы расшифровать эту шифрограмму, получатель сообщения должен сначала заполнить таблицу известных ему размеров буквами криптограммы. Затем необходимо наложить на заполненную таблицу трафарет и, поворачивая его по часовой стрелке на 90?, последовательно выписать из открывающихся ячеек буквы открытого текста.

Рис. 5.7 Решетка Кардано размером 6×6

Если пользователю потребуется зашифровать открытый текст, содержащий большое количество знаков, то решетку Кардано размером 4×4 можно использовать неоднократно.

В то же время для шифрования длинных сообщений любой желающий может составить и использовать решетку Кардано практически любых размеров.

Один из вариантов решетки Кардано размером 6×6 имеет вид, изображенный на рис. 5.7.

На представленном рисунке черным цветом закрашены ячейки, которые следует вырезать. Порядок пользования этим трафаретом аналогичен ранее рассмотренному.

Остается добавить, что применение решеток Кардано обеспечивает сравнительно высокую степень защиты и уменьшает вероятность того, что сообщение будет прочитано неподготовленным незаконным пользователем. Однако для специалиста взлом такого шифра не представляет особых трудностей.

5.10. Биграммные шифры

Одной из особенностей рассмотренных ранее систем шифрования является то, что в них каждая буква открытого текста шифруется отдельно. Однако еще в Средние века некоторые ученые предложили шифры с использованием алгоритмов, обеспечивающих одновременное шифрование сразу двух букв сообщения. Такие шифры стали называться биграммными.

Одно из первых описаний биграммного шифра было опубликовано немецким ученым И. Тритемиусом в начале XVI века Однако некоторые специалисты считают, что первое заслуживающее внимания описание биграммного шифра привел итальянец Д. Порта в 1563 году в книге «О тайной переписке».

Необходимо отметить, что биграммные шифры, несмотря на более высокую степень защищенности, по сравнению с другими использовавшимися в то время системами шифрования, в течение примерно 300 лет почти не применялись. И лишь в XIX веке одновременно в нескольких европейских странах началась активная работа над созданием оригинальных биграммных шифров. Так, например, в России над своим вариантом биграммного шифра работал талантливый криптограф и изобретатель П. Ф. Шиллинг, а в Британии — Ч. Ветстоун.

Название одного из биграммных шифров, придуманного в XIX веке, связано с именем министра почт Британской империи барона Л. Плейфера (L Playfair). Шифр «Playfair» был настолько удачным, что в различных версиях применялся англичанами и во время Первой мировой войны уже в XX столетии.

При использовании шифра «Playfair» алгоритм шифрования заключается в том, что открытый текст разделяется на пары букв, после чего каждая пара по определенному правилу заменяется на пару букв криптограммы. При этом в процессе шифрования необходимо использовать таблицу, заполненную буквами соответствующего алфавита.

В оригинальном шифре «Playfair» для английского алфавита применяется таблица размером 5×5 с паролем Playfair. Для русского алфавита можно использовать, например, уже рассмотренную ранее таблицу с паролем ПАРОДИЯ:

В качестве примера зашифруем с помощью шифра «Playfair» открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ.

Как уже отмечалось, сначала шифруемое сообщение необходимо разбить на пары букв, которые часто называются группами. В рассматриваемом примере после выполнения данного преобразования открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ примет следующ ий вид;

СЕ КР ЕТ НО ЕС ОО БЩ ЕН ИЕ

Необходимо отметить, что в соответствии с алгоритмом шифрования пара или группа букв, состоящая из одной и той же буквы, должна быть разделена буквой X или буквой У.

В то же время одной из указанных букв следует дополнить открытый текст в том случае, если последняя группа букв будет неполной.

С учетом данных требований в рассматриваемом примере открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ, разделенный на пары букв, будет выглядеть вот так:

СЕ КР ЕТ НО ЕС ОХ ОБ ЩЕ НИ ЕХ

Теперь каждую пару букв следует зашифровать отдельно с помощью составленной ранее шифровальной таблицы, ячейки которой должны быть заполнены буквами алфавита по определенному правилу. В нашем примере это приведенная выше таблица с паролем ПАРОДИЯ.

Сначала в таблице надо найти каждую из двух букв, входящих в состав подлежащей шифрованию группы. Затем следует мысленно построить четырехугольник, в двух противоположных вершинах которого находятся две шифруемые буквы открытого текста Две буквы, оказавшиеся в двух других вершинах этого прямоугольника, являются составной частью криптограммы. При этом каждая буква пары открытого текста заменяется буквой криптограммы, лежащей с ней в одной строке.

Так, например, в рассматриваемом примере при шифровании первой пары букв, а именно букв СЕ, в криптограмму следует записать буквы НЖ, вместо букв КР — буквы ЛА, вместо букв ЕТ — буквы ЯЦ и так далее.

В случае если обе буквы какой-либо группы открытого текста находятся в одном столбце таблицы, то в криптограмму записываются буквы, находящиеся под ними, то есть в соответствующих ячейках следующей строки.

Так, в рассматриваемом примере при шифровании группы ОХ открытого текста в криптограмму записывается пара ГЫ Если же при этом одна из пары букв открытого текста окажется в нижней строке столбца, то в шифрограмме эта буква должна быть заменена на букву, находящуюся в верхней строке этого столбца.

В случае, если обе буквы какой-либо группы открытого текста находятся в одной строке таблицы, то в криптограмму записываются буквы, находящиеся справа от них, то есть в соответствующих ячейках следующего столбца.

Так, например, при шифровании группы ТХ открытого текста в криптограмму записывается пара УЦ. Если же при этом одна из пары букв открытого текста окажется в крайнем правом столбце строки, то в шифрограмме эта буква должна быть заменена на букву, находящуюся в первом столбце этой строки.

По окончании шифрования криптограмма открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ примет следующий вид:

НЖ ЛА ЯЦ МД ЖН ГЫ АГ ЭБ СД ГЦ

Для дешифрования такого сообщения получатель сначала должен с помощью известного ему правила или пароля составить таблицу, а затем, используя указанные выше правила, заменить пары или группы букв криптограммы на соответствующие им пары или группы букв открытого текста.

Шифр «Двойной квадрат»

Помимо шифра «Playfair», в том же XIX веке был изобретен биграммный шифр, получивший название «Двойной квадрат». Однако, в отличие от шифра «Playfair», при применении шифра «Двойной квадрат» в процессе шифрования используется не одна, а две таблицы, ячейки которых заполнены буквами алфавита.

В то же время алгоритмы шифрования указанных шифров очень похожи: открытый текст разделяется на пары букв, после чего каждая пара по определенному правилу заменяется на пару букв криптограммы.

Перед началом шифрования открытого текста с помощью шифра «Двойной квадрат» необходимо составить две таблицы, заполненные буквами алфавита Для русского алфавита можно использовать, например, уже рассмотренные ранее таблицы с паролем ПАРОДИЯ и с паролем ПРИКАЗЫ НЕ ОБСУЖДАЮТСЯ, которые следует расположить рядом:

В качестве примера зашифруем с помощью шифра «Двойной квадрат» открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ

Как уже отмечалось, сначала шифруемое сообщение необходимо разбить на пары букв. В рассматриваемом примере после выполнения данного преобразования открытый текст СЕКРЕТНОЕ СООБЩЕНИЕ примет следующий вид:

СЕ КР ЕТ НО ЕС 00 БЩ ЕН ИЕ

В соответствии с алгоритмом шифрования пара букв, состоящая из одной и той же буквы, должна быть разделена буквой X или буквой У. В то же время одной из указанных букв следует дополнить открытый текст в том случае, если последняя группа букв будет неполной.

СЕ КР ЕТ НО ЕС ОХ ОБ ЩЕ НИ ЕХ

Теперь каждую пару или группу букв следует зашифровать отдельно. Для этого сначала надо найти эти две буквы в таблицах, при этом первая буква биграммы должна находиться в левой таблице, а вторая — в правой. После этого необходимо в двух таблицах построить четырехугольник, в двух противоположных вершинах которого находятся две шифруемые буквы открытого текста. Две буквы, оказавшиеся в двух других вершинах этого прямоугольника, являются составной частью криптограммы. При этом каждая буква пары открытого текста заменяется буквой криптограммы, лежащей с ней в одной строке, но в другой таблице.

Так, например, в рассматриваемом примере при шифровании первой пары букв, а именно букв СЕ, в криптограмму следует записать буквы ДЖ, вместо букв КР — буквы ЖА, вместо букв ЕГ — буквы БН и так далее.

При использовании данного шифра возможна ситуация, когда обе буквы какой-либо группы открытого текста окажутся в одной строке таблиц В этом случае в криптограмму вместо первой буквы биграммы открытого текста записывается буква, находящаяся в том же столбце той же строки второй таблицы. Вместо второй буквы биграммы открытого текста в криптограмму записывается буква, находящаяся в том же столбце той же строки первой таблицы.

Так, в рассматриваемом примере при шифровании группы ЕС открытого текста в криптограмму записывается пара БЖ.

Если же при этом одна из пары букв открытого текста окажется в крайнем правом столбце строки, то в шифрограмме эта буква должна быть заменена на букву, находящуюся в первом столбце этой строки.

По окончании шифрования криптограмма открытого текста СЕКРЕТНОЕ СООБЩЕНИЕ примет следующий вид:

ДЖ ЖА БН ЮЕ БЖ ЗХ АГ ШБ ДД СЦ

Для дешифрования такого сообщения получатель сначала должен с помощью известных ему правил или паролей составить две таблицы, а затем, используя указанные выше правила, заменить пары или группы букв криптограммы на соответствующие им пары или группы открытого текста. При этом первая буква биграммы шифрованного текста должна находиться в правой таблице, а вторая — в левой.

Стойкие шифры

Сергей Дориченко
«Квантик» №11, 2013

Шифры замены

Обычные шифры из детективных романов часто устроены так: каждая буква сообщения заменяется каким-нибудь определённым значком или другой буквой. Подобные шифры очень ненадёжны, и вот почему. Буквы в текстах на русском языке (да и на любом языке вообще) встречаются неравномерно. Например, буква «О» в русских текстах встречается чаще всех других букв, а буква «Ъ» — реже всего. У каждой буквы есть своя примерная частота появления в тексте (смотри таблицу на поле справа).

Сочетания букв тоже встречаются неравномерно (например, «ьь» вообще не встречается). Конечно, все эти частоты зависят от конкретного текста — скажем, в биологической статье о жужелицах буква «ж» явно будет встречаться чаще, чем обычно. Но приведённая таблица вполне годится как ориентир.

Так вот, описанный способ шифровки не изменяет частот — просто теперь с аналогичной частотой будет появляться не сама буква, а заменяющий её значок. Высчитав частоту появления каждого значка в шифровке и сравнив полученные данные с таблицей частот, мы можем сделать предположения, какой букве какой значок соответствует. Далее пробуем заменять значки один за одним на буквы, проверяя свои догадки, корректируя их и делая новые, и постепенно расшифровываем текст. Если он не слишком короткий, мы с большой вероятностью его полностью расшифруем (хотя это может оказаться не совсем простым делом). Кстати, намного чаще любой буквы встречается пробел, разделяющий слова. Поэтому если пробел используется в шифровке и тоже заменён на какой-то значок, мы разгадаем его в первую очередь.

Совершенный шифр

Опишем теперь шифр, который принципиально не поддается расшифровке без знания ключа. Сопоставим каждой букве русского алфавита свою последовательность из 0 и 1 длины 5 (пятизначный двоичный код), например: А — 00000, Б — 00001, В — 00010 и так далее (или в каком-то другом порядке). Если буквы Е и Ё кодировать одинаково, то последовательностей как раз хватит (их 32, а в алфавите 33 буквы).

Заменим в тексте каждую букву на её двоичный код, получим последовательность из 0 и 1 (двоичный текст). Это пока ещё не шифровка — мы бы легко разгадали, какая буква на какую последовательность заменена (тем же методом, что и в случае замены букв на значки).

Чтобы зашифровать полученный двоичный текст, нам потребуется ещё ключ — случайная последовательность из 0 и 1 такой же длины. Этот ключ должен быть и у отправителя шифрованного сообщения, и у адресата.

Для зашифровки просто складываем две последовательности нулей и единиц — двоичный текст сообщения и ключ: первую цифру с первой, вторую со второй, и так далее. Но складываем по особым правилам:

0 + 0 = 0, 1 + 0 = 1, 0 + 1 = 1, 1 + 1 = 0

(в математике это называется сложением по модулю 2).

Полученная последовательность и будет зашифрованным сообщением. Чтобы расшифровать её, надо просто… снова прибавить к ней ключ! Тогда мы как бы прибавим к исходной последовательности ключ два раза. А по нашим правилам, прибавляя две одинаковые цифры мы ничего не меняем, то есть мы вернёмся к исходному двоичному тексту. Схематически процесс шифрования и дешифрования можно описать так:

текст + ключ = шифровка;

шифровка + ключ = текст + ключ + ключ = текст.

Ясно, что расшифровать сообщение, не зная ключа, невозможно. Нам как бы дана сумма двух чисел, и нельзя восстановить одно из слагаемых, ничего не зная про другое. Имея на руках лишь шифровку, мы знаем только, что исходный текст может быть абсолютно любым текстом соответствующей длины. Ведь по любому такому тексту можно изготовить ключ, который приведёт ровно к той же самой шифровке!

Недостаток описанного способа в том, что каждый текст требует нового ключа такой же длины — если повторять ключи, появляется возможность расшифровки. Например, мы могли бы попробовать вместо длинного ключа использовать ключ всего из пяти символов, скажем 11010. Разбиваем двоичный текст на пятёрки цифр и прибавляем к каждой пятёрке 11010. Фактически, мы просто заменяем каждую пятёрку цифр на какую-то другую фиксированную пятёрку. В этом случае расшифровать исходный текст так же легко, как если бы мы просто заменили его двоичным кодом, не прибавляя никакого ключа. Использовать длинные ключи, но всё же существенно более короткие, чем текст, тоже опасно — есть метод определения длины ключа, а после того как длина ключа установлена, можно применить частотный анализ.

Поэтому надо заготовить ключ огромной длины заранее и лишь указывать, например, в начале шифровки, какое место ключа используется. При этом очень важно, чтобы ключ был случайной последовательностью из 0 и 1. Например, последовательности 11111111111111111 и 010101010101010 не случайные. Кстати, придумать случайную последовательность не так-то просто. Трудно даже (но возможно) дать чёткое определение, какие последовательности могут считаться случайными.

Немного истории и литературы

Подобный шифр использовал Макс Кристиансен-Клаузен, шифровальщик выдающегося советского разведчика Рихарда Зорге. Наиболее часто употребляемые буквы английского алфавита s, i, o, e, r, a, t, n заменялись цифрами от 0 до 7, а остальные буквы — числами от 80 до 99 (чтобы не возникало путаницы, когда числа записывались подряд). Ключом служили старые выпуски «Статистического ежегодника Германского рейха» с множеством числовых данных. Ключ записывали под текстом и прибавляли, причём если сумма двух цифр превышала 10, то записывалась только её последняя цифра. Например, вместо 7 + 5 писали 2, отбрасывая десяток (в математике это называется сложением по модулю 10). Восстанавливали исходное сообщение, «вычитая» ключ из шифровки. Когда выходило отрицательное число, как, скажем, при вычитании 5 из 2, было ясно, что надо вычитать из числа на 10 больше, то есть из 12 — вот и получали 7.

Японские тайные службы перехватили много радиограмм Зорге, но ни одной не сумели расшифровать. Более полный рассказ об этом читайте в замечательной книге Юлиуса Мадера «Репортаж о докторе Зорге».

А герой приключенческих романов Юлиана Семёнова «Семнадцать мгновений весны» и «Приказано выжить» разведчик Штирлиц, больше известный нам по знамениту кинофильму, использовал в качестве ключа художественную книгу Монтеня. При этом осмысленный текст сообщения«складывался» с осмысленным же (и значит, не случайным!) текстом ключа. Когда германским контрразведчикам стало известно предполагаемое содержание одной из шифровок, в частности — некоторые слова, которые там могли встречаться, — они попробовали их подставить в разные места шифровки и посмотреть, какой получается ключ. Попав в нужное место, они открывали кусочек ключа, в котором угадывались части осмысленных слов. Восстанавливая эти слова, они раскрывали и новый кусочек шифровки, и так постепенно расшифровали её.

Шифры с открытым ключом

Начиная с 1977 года, стали появляться новые шифры, основанные на глубоких математических идеях, высказанных американскими математиками Диффи и Хеллманом за два года до этого. Представьте себе, что два бизнесмена хотят переписываться друг с другом, надёжно шифруя сообщения, но забыли договориться о ключе. Они находятся в разных странах, всё их общение может прослушиваться конкурентами. Как тут быть? Оказывается, выходы есть. Опишем один из них, но без подробностей, только сам принцип.

Придуман способ шифровки, для которого надо знать лишь произведение pq двух каких-то простых чисел p и q, а сами числа p и q знать не нужно. А вот для расшифровки сообщения обязательно иметь в распоряжении и число p, и число q. «Ну и что тут такого?», — спросите вы. А вот что. Дело в том, что эти простые числа можно взять очень большими. И тут мы сталкиваемся с таким явлением: современные компьютерные мощности огромны, но всё же ограничены. Скажем, компьютер может за разумное время разложить на простые множители 200-значное число, но раскладывание 300-значных чисел ему уже не под силу (любому из известных алгоритмов потребуются многие годы). Всегда есть какая-то подобная граница. А выяснить про число, простое оно или нет, компьютеры могут очень быстро для гораздо более длинных чисел. Так вот, первый из компаньонов может с помощью компьютера найти какие-нибудь два, скажем, 400-значных простых числа p и q, перемножить их и открыто переслать результат второму (а сами числа p и q хранить в тайне). Получив произведение pq, тот зашифрует своё сообщение и отправит обратно первому. И первый его легко расшифрует — он-то знает оба числа p и q. А вот всяким там подслушивателям для расшифровки придётся сначала разложить на множители произведение pq, в котором 800 знаков — а с этим не справится ни один современный компьютер! Этот метод шифровки называется RSA, по первым буквам фамилий его создателей — Ривеста, Шамира и Адлемана.

Конечно, с развитием компьютерных технологий появляется возможность расшифровывать старые сообщения. Первая шифровка авторов RSA, опубликованная ими в 1977 году как вызов всем дешифровальщикам мира, продержалась 17 лет. Также есть опасность, что будет найден новый, быстрый алгоритм разложения чисел на простые множители. Но есть математическая гипотеза, что все такие алгоритмы работают принципиально не быстрее, чем уже известные.

А у вас получится?

Перед вами текст, который получен из хорошо известного заменой каждой буквы на какую-то другую. Расшифруйте его.

Атокг ацынг цлекытуы цлауенг ьи Чолсв, и уими Чолси уманлоти ки эекпв нипеме вматыфюеме, цаткзме утоь чтиьиме, жна ни ацынг ьималчити, андоти атокы д уналакв е, мокыы омв ки чатадо тхс, боцквти:
– Пиё д уимам сото в Укоркаё палатодз, ка ак дцатко садаток е свмион, жна твжбо омв кечсо е щзнг ко марон. Цлежекаё ро дуомв аупатпе ьолпити, жна уесын в коча д уолсйо е д чтиьв. Еш киса вситенг, екижо ак кепачси ко щвсон жотадопам, е Укоркиы палатоди уашликен кис кем удаф дтиунг.
– Ка ко цамаробг те нз Чолсо пип-кещвсг вкежнаренг янв дтиунг?
– Уетгкоо, жом аки оунг, ы ко мачв ох усотинг. Ко десебг лиьдо, пип дотепи ох уети? Ко десебг, жна оё утврин е тфсе е реданкзо? Досг аки щауиы ащабти цатудони! Ко в киу ьикеминг оё уетв! Уети — д ох метам, кодеккам сонупам уолсожпо. Оуте аки уими ко умарон цлакепквнг д жолначе Укоркаё палатодз е еьдтожг еь уолсйи Пиы аупатпе, на мз е цасидка оё ко цамаром! Д сдвш метыш ануфси кижекионуы уис Укоркаё палатодз. Анкоуе нвси содажпв, уцвуне в щатгбача пвуни, цаплзнача плиукзме ычасиме, е, ко мобпиы, даьдлиюиёуы ащлинка!
У янеме утадиме эекпи цасуисети Чолсв ки уцекв атокы, е нан щлауетуы щоринг уа дуош кач.

Как расшифровать секретный код. О чем расскажут тройные числа в нумерологии

Чисел помогает дать полную и подробную характеристику личности. Понять, в каком направлении требуется корректировка личностных качеств. Определить причины, почему в вашей жизни не всё складывается так, как хотелось бы.

Важно не одно качество, на которое указывают цифры, а количество цифр в одной клетке нумерологической таблицы (как составить её, читайте ). Также имеет значение связь цифры с рядом стоящими в соседних клетках. Но значение чисел важно знать, чтобы детально понимать, что они несут.

Нумерология цифр начинается с единицы. Она обозначает энергию мысли, поток информации, живущей в голове. Единица — это идеи, которые приходят, «залетают» в голову. Это инициативность, способность самостоятельно что-то придумывать и находить единственно правильное решение.

Единица отражает способность человека петь, кричать, говорить без лишних раздумий. Человек, у которого единиц в тесте много, способен на ходу придумывать и находить решение.

«Что вижу, то и пою» — основополагающая характеристика человека, у которого много единиц. При условии, что остальные цифры этот информационный поток не ограничивают.

Одна единица — человек медленно думает, либо предпочитает не думать совсем. Много единиц (максимум 7) — генератор множества идей, желаний без энергии на их реализацию, суета.

Двойка «2»

Двойка — плотная энергия. Физическая, мышечная. Она характеризует такие качества личности, как напряжение, активность, энергия, агрессия. Человек с большим количеством двоек не может и не умеет сидеть на месте. Он способен влиять на других людей, манипулировать и управлять им, заставлять.

Двойка отображает склонность к созиданию и разрушению. Также это выражение сексуальной энергии у мужчин и женщин.

Мало двоек — человек быстро устает, у него почти отсутствует физическая энергия. Много двоек (максимум 9) — делает всё за себя и за всех, выполняет общественно полезную работу, ему трудно жить.

Тройка «3»

Пятёрка «5»

Пятёрка — качество любви. Она отражает чувственность, способность понимать людей, выражать свои чувства и эмоции. Отвечает за артистизм, театральность, манерность, творческие навыки и способность гармонизировать пространство вокруг себя.

Также пятёрка — это сексапильность, притягательность для противоположного пола.

Нет пятёрок — человек не умеет говорить и признаваться в своих чувствах, либо проявляет эмоции неадекватно. Может влюбиться, но объект воздыханий никогда об этом не узнает.

Много пятёрок — очень раним, обидчив, постоянно подозревает окружающих в отсутствии любви к себе. Сильно развита эмоциональность, любит привлекать к себе внимание, придирчив к внешнему виду.

Шестёрка «6»

За умение копить, систематизировать и использовать знания отвечает . Она отражает способность решать задачи, появляющиеся на жизненном пути.

Много шестерок — человек очень глубокий, его можно постоянно узнавать в чем-то новом, но никогда не понять всех граней личности до конца. Предан одному своему делу (профессии) всю жизнь, отдаётся работе полностью.

Нет шестёрок — отсутствует способность к концентрации. Человека в процессе выполнения какого-то дела постоянно отвлекают внешние обстоятельства.

Семёрка «7»

Отражает состояние души, отвечает в основном за интуицию, «шестое чувство», способность предчувствовать. Это дар, который позволяет предугадывать, чем закончатся те или иные события в жизни.

Нет семёрок — интуиция есть, но запрятана глубоко внутри. Она проявляется в состоянии сильного эмоционального напряжения — страха. В обычной жизни человек предчувствовать что либо не способен.

Много семёрок — у человека дар предвидения. Он способен буквально читать мысли. Чувствует других людей даже на расстоянии, может понять, что его близкому человеку плохо, даже если тот находится на другом конце планеты.

Документальный фильм, о том, как цифры влияют на жизнь людей, смотрите в видео:

Восьмёрка «8»

Восьмёрка — самое «фартовое» качество. Она показывает, насколько человек удачлив, как и в каких масштабах ему везёт по жизни. Отвечает за везение.

Нет восьмёрок — на везение рассчитывать не приходится. Человек привык достигать всего собственным умом, прилагать усилия для достижения всех целей. Это не плохо, потому что он понимает — рассчитывать можно только на себя. Он никогда не действует наудачу.

Много восьмёрок в тесте — человек везунчик. Ему всё даётся легко, без усилий. То, что другие получают колоссальным трудом, он получает просто так, словно по мановению волшебной палочки.

Девятка «9»

Девятка отражает такие качества личности, как гибкость, хитрость, уступчивость, даже изворотливость. Это понимание конечной цели. Если оно есть — человек будет правильно себя вести в данных ему условиях, идеально подстроится под ситуацию.

Мало девяток — вышеупомянутых качеств не хватает. Человек медленно реагирует, упрям, часто не достигает поставленных целей, конфликтен.

Много девяток — человек-игрок. Он хитёр, изворотлив, умелый манипулятор.

Таково значение чисел в нумерологии. Но не забывайте, что для более точной характеристики личности нужно рассматривать таблицу в целом, изучать, как расположены цифры в столбцах, по диагоналям.

Погадайте на сегодняшний день c помощью расклада Таро «Карта дня»!
Для правильного гадания: сосредоточьтесь на подсознании и ни о чем не думайте хотябы 1-2 минуты.
Как будете готовы — тяните карту:

Древние жрецы были правы, утверждая, что наука чисел и искусство силы духа являются магическими ключами, открывающими все двери вселенной. Это дает поразительную силу власти над собой. Наука о числах, нумерология, помогает познать себя с магической стороны цифр. Циферки все о нас объяснят и «дадут» совет на будущее. Мистика? Не совсем. Это наука, наука цифр, наряду с астрологией.

Наука простая, на уровне арифметики и безумно увлекательная. Умение читать язык цифр сделают человека чуточку волшебником, предсказывающим судьбу, что гарантирует популярность в любой компании.

Так называемая таблица Пифагора, построение которой даёт полную картину о человеке, является более универсальным инструментом.

Как расшифровать свою судьбу

Необходимо выполнить ряд несложных математических действий.

Первое : записать в строку свою дату рождения.

15 5 1967 – теперь с этими цифрами будем работать. Нули в дате рождения не вносим в строку.

Делаем четыре расчета

Расчет номер один — это важное основное число. Необходимо сложить все числа в нашей дате:

1+5+5+1+9+6+7 =34.

Теперь под цифрой 1 в строке 15 5 1967 запишите эту сумму.

Расчет номер два :

сумму в первом расчете тоже надо сложить, т.е сумму 34 складываем между собой:

запишите ее под второй цифрой нашей даты.

Расчет номер три :

Из основного числа 34 отнимает удвоенную первую цифру нашей даты рождения т.е 2.

Ее тоже пишем в нижней строке под третьей цифрой.

Расчет номер четыре :

Цифры расчета номер три надо сложить:

Теперь получили базовые цифры для таблицы Пифагора:

Первая строчка — это наша дата рождения: 15 5 1967

Вторая строчка четыре наших расчета: 34 7 32 5

Квадрат Пифагора имеет девять ячеек. Чтобы построить наш квадрат, нам необходимо внести в каждую ячейку квадрата число тех цифр, которые мы видим в двух наших строчках.

Например, в ячейку 1 вносим единицы, на самом деле их две единицы, но записать надо не два, а 11, затем в ячейку под номером 2, записываем, сколько двоек в наших строчках. В нашем случае, она одна, вот и пишем двойку в единственном числе. И так заполняем все девять ячеек.

Квадрат Пифагора для дня рождения 15 5 1967 будет выглядеть так:

Не всегда все ячейки бывают заполненными. Иногда, каких — то цифр нет в нашей матрице. В данном случае отсутствуют восьмерки. Согласно учению Пифагора пустые ячейки знаменуют отсутствие какого-то качества, которое нужно развивать, чтобы достичь духовной чистоты. Чем больше пустых клеток, тем больше человеку предстоит работа над собой, личность считается дисгармоничной.

Каждая ячейка квадрата описывает человека и силу его качеств.

Ячейка 1- Солнце (Сила характера, волевые черты)

Творческий потенциал, индивидуальность, способность жизненного горения. Показывает способность принимать решения и в одиночку их решать. Это лидерские качества. Если единиц в ячейке одна или две, то этот человек имеет покладистый характер, слабоват, нуждается в похвале и эгоист

111-спокойный по характеру, но в экстремальной ситуации проявится сильная воля.

1111- властный, сильный человек.

Недостатки: желание выделиться, эгоцентризм, позерство.

Ячейка 2- Луна (Количество энергии)

Душа человека, ее чувствительность, готовность к дружбе и взаимопониманию. Гибкость в отношениях, дипломатичность. Дар интуиции, умение предсказывать будущее.

Если имеем 2 или 22- мало энергии, не выносит конфликты, потому что сильно устает.

222 или 2222 — супер энергичен, деятелен, имеет экстрасенсорные возможности.

Недостатки: двойственность характера, его неустойчивость, капризность.

Ячейка 3- Марс (Интересы личности)

Волевые качества, агрессивность, движение к цели.

Марсу свойственно стремление к творчеству, тройка-число творца. Оптимизм и амбиции.

Люди имеют успех в коллективе, обществе, постигают вершины славы.

3 или 33 – прилежен, аккуратен, хорошо учится.

333 – педант, много интересов, но всего понемногу.

3333- все критикует и легко раздражается, нетерпим, когда нарушают его порядок.

Недостатки: грубость, переходящая в хамство, злоба и резкость.

Ячейка 4- Меркурий (Здоровье личности)

Любит порядок, размеренность, вплоть до педантичности. Преобладание четверок говорит об упорстве и надежности. Это стабильные люди, по натуре исполнители.

Имея в квадрате 4 или 44 – можно предположить, что у человека слабое здоровье, часто простуды.

444 – говорит о крепком здоровье, спортсмен.

4444 – хорошее здоровье сочетается с высокой энергией, которая жаждет реализации в спорте или труде.

Недостатки: способны на обман, коварство. Хитрость.

Ячейка 5- Юпитер (Интуиция)

Если в квадрате одна 5 – человек со слабой интуицией, учится на собственном опыте и ошибках.

55 – человек интуитивно чувствует, что делать можно, а чего лучше избежать.

555 – мудрый человек, к его советам прислушиваются.

Недостатки: властолюбие, чванство и тщеславие

Ячейка 6- Венера (Физический труд)

Символизирует красоту души и гармонию, чувства и влечения, мягкость и уступчивость.

Венера способствует домовитости и создании в нем уютного пространства. Шестерка – это число миротворца и коммуникатора. Говорит о склонности к семейной жизни и комфорту в ней. Любители помогать другим людям.

Обладатели одной 6 – больше склонны к умственному труду, они избегают физический труд.

66 – любит работать физически, но не много. Может быть садоводом.

666 или 6666 – любит, как следует поработать и поесть.

Недостатки: лень, тунеядство, апатия.

Ячейка 7- Сатурн (Таланты личности)

Разум, стремление все систематизировать, одиночество, стойкость и выдержка. Сатурн способствует к самопознанию, глубокому анализу, понимать суть всего происходящего.

Семерка-это индивидуальность и способность охранять личную территорию. Цифра философа.

Если одна 7– имеет неяркий талант от рождения. Надо пробовать, чтобы найти себя.

77 – определенно есть талант, особенно в том, что делает.

777 или 7777 – высокоталантливый человек. Рано или поздно найдет выход.

Недостатки: мнительность и угрюмость.

Ячейка 8- Уран (Ответственность)

Изобретательство и реформаторство. Уран придает черты руководителя, который имеет чутье в обращении с деньгами, способность находить неординарные финансовые решения. Преобладание восьмерок говорит, что человеку уготована обеспеченная жизнь. Это финансисты.

Имея одну 8- человек необязателен. Многое прощает себе и другим.

88 – развито чувство долга, ответственный.

888–высокопринципиален, с сильным чувством долга и непогрешимости.

Недостатки: цинизм.

Ячейка 9- Нептун (Интеллект личности)

Высшая интуиция, медитация, способность видеть вещи с точки зрения вечности. Они могут мечтать о недостижимом, верят в светлые идеалы. Девятка – это склонность пожертвовать собой ради высокой цели, даже в ущерб реальности. Цифра духовности.

Если одна 9 – процесс обучения буде даваться с трудом, хотя учеба будет нравиться.

99 – это умные личности с хорошей памятью.

999 или 9999 – это ученые с прекрасной памятью и мышлением.

Недостатки: фанатизм и уход в иллюзии.

Количество цифр в ячейке имеет значение. Существует определенная норма для них. Для единиц, пятерок, восьмерок и девяток — это три. А остальных не должно быть больше одной. Если их больше нормы, то эти качества усилены, меньше – ослаблены. Но не расстраивайтесь, ослабленные качества обычно компенсируются другими чертами.

Кроме основных ячеек, существуют дополнительные. Необходимо посчитать количество цифр по строкам, по столбцам и по диагонали квадрата.

Сначала считаем количество цифр в строках.

Подсчет цифр верхней строки охарактеризует – Целеустремленность .

Показывает, насколько желания совпадают с возможностями.

Семейность -это вторая строка. Показывает, расположен ли человек к построению семьи и насколько он хорош, как семьянин.

Стабильность (привычки)- третья строка.

Говорит о надежности человека. Равновесие между привычками и стремлением к переменам.

Теперь считаем количество цифр в столбцах :

Количество крайнего левого столбца определят самооценку человека.

Заниженная самооценка покажет, что личность нерешительная, не верит в себя. Завышенная оценка влечет разочарование и кучу ошибок.

Цифры следующего столбца покажут уровень социального благополучия, статуса и благосостояния.

И количество цифр последнего столбца покажут талант человека от рождения. А реализация таланта уже будет зависеть от других качеств матрицы: целеустремленности, самооценки и трудолюбия.

Цифры диагонали скажут о влечении, темпераменте и духовности личности .

Спадающая диагональ слева направо скажет о духовности.

Не путайте это качество с религиозностью. В данном случае, это определяет убеждения и желание им следовать, равновесие между принципами и готовностью ими пожертвовать.

Слева направо восходящая диагональ покажет уровень темперамента. Этот показатель приобретает значение при определении совместимости партнеров. Идеально, чтобы партнеры не сильно отличались по темпераменту.

Нумерология — интереснейшая наука, которая приоткроет двери в таинственный мир тайны имени. Все мы знаем, что имя человека имеет влияние на судьбу и характер своего носителя. Нумерология имени сможет показать истинное его значение, показать скрытые таланты и склонности, стремления человека.

Таблица соответствия букв имени и цифр

Цифра	Буквы
1	А И С Ъ
2	Б Й Т Ы
3	В К У Ь
4	Г Л Ф Э
5	Д М Х Ю
6	Е Н Ц Я
7	Ё О Ч
8	Ж П Ш
9	З Р Щ

К примеру рассчитаем имя «Татьяна» :

Т — 2
А — 1
Т — 2
Ь — 3
Я — 6
Н — 6
А — 1

В итоге мы получим 2+1+2+3+6+6+1= 21, эту цифру мы сведем до простого числа 2+1=3
Получается цифра имени «Татьяна» — 3
Вы уже узнали Вашу цифру имени? Давайте же узнаем, что несет в себе эта цифра.

Результаты расчета

В нумерологии имени этого человека заложено лидерство. Человек с такой цифрой имени амбициозен, честолюбив, энергичен, смел, уверен в своих силах. Таким людям нужно занимать руководящие посты, или заниматься собственным бизнесом.
Человек активный, но ему требуется помощь партнера. Люди числа 2 — миролюбивы, они ориентированны на семейные ценности, такие люди хорошо ладят в коллективах. Им нужно искать себя в работе с людьми, их профессии это учителя, доктора, психологи.
Тройки — талантливые, всесторонне развитые люди, которые любят быть в центре внимания. Они большие оптимисты, зачастую душа компании. Их конек это мир искусств, поэтому с них получатся прекрасные писатели, певцы, музыканты, ораторы.
Стабильность, надежность, честность — главная черта четверок. Такие люди трудоголики, склонные к кропотливому, ответственному труду, они очень пунктуальны. Четверки — прекрасные бухгалтера, архитекторы, инженера.
Неординарные, независимые люди со своим взглядом на жизнь. Нумерология говорит о таких людях, что они не бояться бросится в пучину новизны, они с легкостью отказываются от устаревших стереотипов. Пятерки постоянно стремятся к интеллектуальному развитию. Таким людям будет комфортно работать в туризме, в юриспруденции, журналистике.
У шестерок обостренное чувство справедливости, честности, ответственности. Они очень требовательны к себе, за что их уважают окружающие. Им можно доверить любое дело которое требует доверия и ответственности. Профессия обладателей имен с рассчитанной цифрой «1» — это социальные работники, воспитатели, врачи.
Такой человек постоянно стремится к знаниям, он будет собирать интересные факты, проверять соответствует ли теория практике, при этом любит делится знаниями с окружающими. Поскольку семерки не очень любят физический труд, их профессии это философы, ученные, изобретатели.
Восьмерки требуют к себе внимания и признания. Они находятся в постоянном стремление новых побед и свершений. Такие люди практичны и ищут выгоду всегда и везде, при этом ждут признания в своих делах. Идеальной средой обитания Восьмерок являются финансы, коммерция, администрирование, строительство.
Человек-гармония. Он добрый, терпеливый стремится к спокойствию. Такие люди обычно защищают права обездоленных, они за мир во всем мире. Человек девятка всегда придет к вам на помощь в тяжелый момент. Профессии девяток, это учителя, медсестры, социальные работники, писатели.

Мы надеемся, что приоткрыли завесу тайны, связанной с расчетом нумерологии имени. Проверьте ваше имя и возможно вы узнаете о себе нечто новое. Читайте также про

Поскольку шифров в мире насчитывается огромное количество, то рассмотреть все шифры невозможно не только в рамках данной статьи, но и целого сайта. Поэтому рассмотрим наиболее примитивные системы шифрации, их применение, а так же алгоритмы расшифровки. Целью своей статьи я ставлю максимально доступно объяснить широкому кругу пользователей принципов шифровки \ дешифровки, а так же научить примитивным шифрам.

Еще в школе я пользовался примитивным шифром, о котором мне поведали более старшие товарищи. Рассмотрим примитивный шифр «Шифр с заменой букв цифрами и обратно».

Нарисуем таблицу, которая изображена на рисунке 1. Цифры располагаем по порядку, начиная с единицы, заканчивая нулем по горизонтали. Ниже под цифрами подставляем произвольные буквы или символы.

Рис. 1 Ключ к шифру с заменой букв и обратно.

Теперь обратимся к таблице 2, где алфавиту присвоена нумерация.

Рис. 2 Таблица соответствия букв и цифр алфавитов.

Теперь зашифруем словоК О С Т Е Р :

1) 1. Переведем буквы в цифры:К = 12, О = 16, С =19, Т = 20, Ё = 7, Р = 18

2) 2. Переведем цифры в символы согласно таблицы 1.

КП КТ КД ПЩ Ь КЛ

3) 3. Готово.

Этот пример показывает примитивный шифр. Рассмотрим похожие по сложности шрифты.

1. 1. Самым простым шифром является ШИФР С ЗАМЕНОЙ БУКВ ЦИФРАМИ. Каждой букве соответствует число по алфавитному порядку. А-1, B-2, C-3 и т.д.
Например слово «TOWN » можно записать как «20 15 23 14», но особой секретности и сложности в дешифровке это не вызовет.

2. Также можно зашифровывать сообщения с помощью ЦИФРОВОЙ ТАБЛИЦЫ. Её параметры могут быть какими угодно, главное, чтобы получатель и отправитель были в курсе. Пример цифровой таблицы.

Рис. 3 Цифровая таблица. Первая цифра в шифре – столбец, вторая – строка или наоборот. Так слово «MIND» можно зашифровать как «33 24 34 14».

3. 3. КНИЖНЫЙ ШИФР
В таком шифре ключом является некая книга, имеющаяся и у отправителя и у получателя. В шифре обозначается страница книги и строка, первое слово которой и является разгадкой. Дешифровка невозможна, если книги у отправителя и корреспондента разных годов издания и выпуска. Книги обязательно должны быть идентичными.

4. 4. ШИФР ЦЕЗАРЯ (шифр сдвига, сдвиг Цезаря)
Известный шифр. Сутью данного шифра является замена одной буквы другой, находящейся на некоторое постоянное число позиций левее или правее от неё в алфавите. Гай Юлий Цезарь использовал этот способ шифрования при переписке со своими генералами для защиты военных сообщений. Этот шифр довольно легко взламывается, поэтому используется редко. Сдвиг на 4. A = E, B= F, C=G, D=H и т.д.
Пример шифра Цезаря: зашифруем слово « DEDUCTION » .
Получаем: GHGXFWLRQ . (сдвиг на 3)

Еще пример:

Шифрование с использованием ключа К=3 . Буква «С» «сдвигается» на три буквы вперёд и становится буквой «Ф». Твёрдый знак, перемещённый на три буквы вперёд, становится буквой «Э», и так далее:

Исходный алфавит:А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я

Шифрованный:Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я А Б В

Оригинальный текст:

Съешь же ещё этих мягких французских булок, да выпей чаю.

Шифрованный текст получается путём замены каждой буквы оригинального текста соответствующей буквой шифрованного алфавита:

Фэзыя йз зьи ахлш пвёнлш чугрщцкфнлш дцосн, жг еютзм ъгб.

5. ШИФР С КОДОВЫМ СЛОВОМ
Еще один простой способ как в шифровании, так и в расшифровке. Используется кодовое слово (любое слово без повторяющихся букв). Данное слово вставляется впереди алфавита и остальные буквы по порядку дописываются, исключая те, которые уже есть в кодовом слове. Пример: кодовое слово – NOTEPAD.
Исходный:A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Замена:N O T E P A D B C F G H I J K L M Q R S U V W X Y Z

6. 6. ШИФР АТБАШ
Один из наиболее простых способов шифрования. Первая буква алфавита заменяется на последнюю, вторая – на предпоследнюю и т.д.
Пример: « SCIENCE » = HXRVMXV

7. 7. ШИФР ФРЕНСИСА БЭКОНА
Один из наиболее простых методов шифрования. Для шифрования используется алфавит шифра Бэкона: каждая буква слова заменяется группой из пяти букв «А» или «B» (двоичный код).

a AAAAA g AABBA m ABABB s BAAAB y BABBA

b AAAAB h AABBB n ABBAA t BAABA z BABBB

c AAABA i ABAAA o ABBAB u BAABB

d AAABB j BBBAA p ABBBA v BBBAB

e AABAA k ABAAB q ABBBB w BABAA

f AABAB l ABABA r BAAAA x BABAB

Сложность дешифрования заключается в определении шифра. Как только он определен, сообщение легко раскладывается по алфавиту.
Существует несколько способов кодирования.
Также можно зашифровать предложение с помощью двоичного кода. Определяются параметры (например, «А» — от A до L, «В» — от L до Z). Таким образом, BAABAAAAABAAAABABABB означает TheScience of Deduction ! Этот способ более сложен и утомителен, но намного надежнее алфавитного варианта.

8. 8. ШИФР БЛЕЗА ВИЖЕНЕРА.
Этот шифр использовался конфедератами во время Гражданской войны. Шифр состоит из 26 шифров Цезаря с различными значениями сдвига (26 букв лат.алфавита). Для зашифровывания может использоваться tabula recta (квадрат Виженера). Изначально выбирается слово-ключ и исходный текст. Слово ключ записывается циклически, пока не заполнит всю длину исходного текста. Далее по таблице буквы ключа и исходного текста пересекаются в таблице и образуют зашифрованный текст.

Рис. 4 Шифр Блеза Виженера

9. 9. ШИФР ЛЕСТЕРА ХИЛЛА
Основан на линейной алгебре. Был изобретен в 1929 году.
В таком шифре каждой букве соответствует число (A = 0, B =1 и т.д.). Блок из n-букв рассматривается как n-мерный вектор и умножается на (n х n) матрицу по mod 26. Матрица и является ключом шифра. Для возможности расшифровки она должна быть обратима в Z26n.
Для того, чтобы расшифровать сообщение, необходимо обратить зашифрованный текст обратно в вектор и умножить на обратную матрицу ключа. Для подробной информации – Википедия в помощь.

10. 10. ШИФР ТРИТЕМИУСА
Усовершенствованный шифр Цезаря. При расшифровке легче всего пользоваться формулой:
L= (m+k) modN , L-номер зашифрованной буквы в алфавите, m-порядковый номер буквы шифруемого текста в алфавите, k-число сдвига, N-количество букв в алфавите.
Является частным случаем аффинного шифра.

11. 11. МАСОНСКИЙ ШИФР

12. 12. ШИФР ГРОНСФЕЛЬДА

По своему содержанию этот шифр включает в себя шифр Цезаря и шифр Виженера, однако в шифре Гронсфельда используется числовой ключ. Зашифруем слово “THALAMUS”, используя в качестве ключа число 4123. Вписываем цифры числового ключа по порядку под каждой буквой слова. Цифра под буквой будет указывать на количество позиций, на которые нужно сдвинуть буквы. К примеру вместо Т получится Х и т.д.

T H A L A M U S
4 1 2 3 4 1 2 3

T U V W X Y Z
0 1 2 3 4

В итоге: THALAMUS = XICOENWV

13. 13. ПОРОСЯЧЬЯ ЛАТЫНЬ
Чаще используется как детская забава, особой трудности в дешифровке не вызывает. Обязательно употребление английского языка, латынь здесь ни при чем.
В словах, начинающихся с согласных букв, эти согласные перемещаются назад и добавляется “суффикс” ay. Пример: question = estionquay. Если же слово начинается с гласной, то к концу просто добавляется ay, way, yay или hay (пример: a dog = aay ogday).
В русском языке такой метод тоже используется. Называют его по-разному: “синий язык”, “солёный язык”, “белый язык”, “фиолетовый язык”. Таким образом, в Синем языке после слога, содержащего гласную, добавляется слог с этой же гласной, но с добавлением согласной “с” (т.к. язык синий). Пример:Информация поступает в ядра таламуса = Инсифорсомасацисияся поссотусупасаетсе в ядсяраса тасаласамусусаса.
Довольно увлекательный вариант.

14. 14. КВАДРАТ ПОЛИБИЯ
Подобие цифровой таблицы. Существует несколько методов использования квадрата Полибия. Пример квадрата Полибия: составляем таблицу 5х5 (6х6 в зависимости от количества букв в алфавите).

1 МЕТОД. Вместо каждой буквы в слове используется соответствующая ей буква снизу (A = F, B = G и т.д.). Пример: CIPHER — HOUNIW.
2 МЕТОД. Указываются соответствующие каждой букве цифры из таблицы. Первой пишется цифра по горизонтали, второй — по вертикали. (A = 11, B = 21…). Пример: CIPHER = 31 42 53 32 51 24
3 МЕТОД. Основываясь на предыдущий метод, запишем полученный код слитно. 314253325124. Делаем сдвиг влево на одну позицию. 142533251243. Снова разделяем код попарно.14 25 33 25 12 43. В итоге получаем шифр. Пары цифр соответствуют букве в таблице: QWNWFO.

Шифров великое множество, и вы так же можете придумать свой собственный шифр, однако изобрести стойкий шифр очень сложно, поскольку наука дешифровки с появлением компьютеров шагнула далеко вперед и любой любительский шифр будет взломан специалистами за очень короткое время.

Методы вскрытия одноалфавитных систем (расшифровка)

При своей простоте в реализации одноалфавитные системы шифрования легко уязвимы.
Определим количество различных систем в аффинной системе. Каждый ключ полностью определен парой целых чисел a и b, задающих отображение ax+b. Для а существует j(n) возможных значений, где j(n) — функция Эйлера, возвращающая количество взаимно простых чисел с n, и n значений для b, которые могут быть использованы независимо от a, за исключением тождественного отображения (a=1 b=0), которое мы рассматривать не будем.
Таким образом получается j(n)*n-1 возможных значений, что не так уж и много: при n=33 в качестве a могут быть 20 значений(1, 2, 4, 5, 7, 8, 10, 13, 14, 16, 17, 19, 20, 23, 25, 26, 28, 29, 31, 32), тогда общее число ключей равно 20*33-1=659. Перебор такого количества ключей не составит труда при использовании компьютера.
Но существуют методы упрощающие этот поиск и которые могут быть использованы при анализе более сложных шифров.
Частотный анализ
Одним из таких методов является частотный анализ. Распределение букв в криптотексте сравнивается с распределением букв в алфавите исходного сообщения. Буквы с наибольшей частотой в криптотексте заменяются на букву с наибольшей частотой из алфавита. Вероятность успешного вскрытия повышается с увеличением длины криптотекста.
Существуют множество различных таблиц о распределении букв в том или ином языке, но ни одна из них не содержит окончательной информации — даже порядок букв может отличаться в различных таблицах. Распределение букв очень сильно зависит от типа теста: проза, разговорный язык, технический язык и т.п. В методических указаниях к лабораторной работе приведены частотные характеристики для различных языков, из которых ясно, что буквы буквы I, N, S, E, A (И, Н, С, Е, А) появляются в высокочастотном классе каждого языка.
Простейшая защита против атак, основанных на подсчете частот, обеспечивается в системе омофонов (HOMOPHONES) — однозвучных подстановочных шифров, в которых один символ открытого текста отображается на несколько символов шифротекста, их число пропорционально частоте появления буквы. Шифруя букву исходного сообщения, мы выбираем случайно одну из ее замен. Следовательно простой подсчет частот ничего не дает криптоаналитику. Однако доступна информация о распределении пар и троек букв в различных естественных языках.

С той самой поры, как человечество доросло до письменной речи, для защиты сообщений используются коды и шифры. Греки и египтяне использовали шифры для защиты личной переписки. Собственно говоря, именно из этой славной традиции и произрастает современная традиция взлома кодов и шифров. Криптоанализ изучает коды и методы их взлома, и это занятие в современных реалиях может принести немало пользы. Если вы хотите этому научиться, то можно начать с изучения самых распространенных шифров и всего, что с ними связано. В общем, читайте эту статью!

Шаги

Расшифровка шифров замещения

Начните с поиска слов из одной буквы. Большинство шифров на основе относительно простой замены легче всего взломать банальным перебором с подстановкой. Да, придется повозиться, но дальше будет только сложнее.

Слова из одной буквы в русском языке — это местоимения и предлоги (я, в, у, о, а). Чтобы найти их, придется внимательно изучить текст. Угадывайте, проверяйте, закрепляйте или пробуйте новые варианты — иного метода разгадки шифра нет.
Вы должны научиться читать шифр. Взламывать его — это не столь важно. Учитесь выхватывать шаблоны и правила, лежащие в основе шифра, и тогда его взлом не будет представлять для вас принципиальной сложности.

Ищите наиболее часто употребляемые символы и буквы. К примеру, в английском языке такими являются “e”, “t” и “a”. Работая с шифром, используйте свое знание языка и структуры предложений, на основе чего делайте гипотезы и предположения. Да, на все 100% вы редко будете уверены, но разгадывание шифров — это игра, где от вас требуется делать догадки и исправлять собственные ошибки!

Двойные символы и короткие слова ищите в первую очередь, старайтесь начать расшифровку именно с них. Легче, как никак, работать с двумя буквами, чем с 7-10.

Обращайте внимание на апострофы и символы вокруг. Если в тексте есть апострофы, то вам повезло! Так, в случае английского языка, использование апострофа означает, что после зашифрованы такие знаки, как s, t, d, m, ll или re. Соответственно, если после апострофа идут два одинаковых символа, то это наверняка L!

Попробуйте определить, какой у вас тип шифра. Если вы, разгадывая шифр, в определенный момент поймете, к какому из вышеописанных типов он относится, то вы его практически разгадали. Конечно, такое будет случаться не так уж и часто, но чем больше шифров вы разгадаете, тем проще вам будет потом.

Цифровая замена и клавиатурные шифры в наши дни распространены более всего. Работая над шифром, первым делом проверяйте, не такого ли он типа.

Распознавание обычных шифров

Шифры замещения. Строго говоря, шифры замещения кодируют сообщение, замещая одни буквы другими, согласно заранее определенному алгоритму. Алгоритм — и есть ключ к разгадке шифра, если разгадать его, то и раскодировать сообщение проблемы не составит.
- Даже если в коде есть цифры, кириллица или латиница, иероглифы или необычные символы — пока используются одни и те же типы символов, то вы, вероятно, работаете именно с шифром замещения. Соответственно, вам надо изучить используемый алфавит и вывести из него правила замещения.
Квадратный шифр. Простейшее шифрование, используемое еще древними греками, работающее на основе использования таблицы цифр, каждая из которых соответствует какой-то букве и из которых впоследствии и составляются слова. Это действительно простой код, своего рода — основа основ. Если вам надо разгадать шифр в виде длинной строки цифр — вероятно, что пригодятся именно методы работы с квадратным шифром.
Шифр Цезаря. Цезарь умел не только делать три дела одновременно, он еще и понимал в шифровании. Цезарь создал хороший, простой, понятный и, в то же время, устойчивый ко взлому шифр, который в его честь и назвали. Шифр Цезаря — это первый шаг на пути к изучению сложных кодов и шифров. Суть шифра Цезаря в том, что все символы алфавита сдвигаются в одну сторону на определенное количество символов. Например, сдвиг на 3 символа влево будет менять А на Д, Б на Е и т.д.
Следите за клавиатурными шаблонами. На основе традиционной раскладки клавиатуры типа QWERTY в наше время создаются различные шифры, работающие по принципу смещения и замещения. Буквы смещаются влево, вправо, вверх и вниз на определенное количество символов, что и позволяет создать шифр. В случае таких шифров надо знать, в какую сторону были смещены символы.
- Так, меняя колонки на одну позицию вверх, “wikihow” превращается в “28i8y92”.
- Полиалфавитные шифры. Простые замещающие шифры опираются на создание шифрующим своего рода алфавита для шифрования. Но уже в Средние века это стало слишком ненадежно, слишком просто для взлома. Тогда криптография сделала шаг вперед и стала сложнее, начав использовать для шифрования символы сразу нескольких алфавитов. Что и говорить, надежность шифрования сразу повысилась.

Что значит быть дешифровальщиком

Будьте терпеливы. Взломать шифр — это терпение, терпение и еще раз терпение. Ну и упорство, конечно же. Это медленная, кропотливая работа, сопряженная с большим количеством разочарования из-за частых ошибок и необходимости постоянно подбирать символы, слова, методы и т.д. Хороший дешифровальщик просто обязан быть терпеливым.

Расшифровка кода IP

Элемент	Цифры/Буквы	Значение для защиты оборудования	Значение для защиты людей
Первая характеристическая цифра		От проникновения внешних твердых предметов:	От доступа к опасным частям:
	0	нет защиты	нет защиты
	1	диаметром >50 мм	тыльной стороной руки
	2	диаметром >12,5 мм	пальцем
	3	диаметром > 2,5 мм	инструментом
	4	диаметром >1,0 мм	проволокой
	5	пылезащищенное	проволокой
	6	пыленепроницаемое	проволокой
Вторая характеристическая цифра		От вредного воздействия в результате проникновения воды:	—
	0	нет зашиты
	1	вертикальное каплепадение
	2	каплепадение (номинальный угол 15°)
	3	дождевание
	4	сплошное обрызгивание
	5	действие струи
	6	сильное действие струй
	7	временное непродолжительное погружение
	8	длительное погружение
Дополнительная буква (при необходимости)		—	От доступа к опасным частям:
	А		тыльной стороной руки
	В		пальцем
	С		инструментом
	D		проволокой
Вспомогательная буква (при необходимости)		Вспомогательная информация, относящаяся к:	—
	Н	высоковольтным аппаратам
	М	состоянию движения во время испытаний защиты от воды
	S	состоянию неподвижности во время испытаний защиты от воды
	W	—

расшифровка букв, цифр, смешанных значений

Маркировка конденсаторов при выборе какого-либо элемента в схеме имеет большое значение. Она разнообразная и сложная по сравнению с резисторами. Специалист, который работает непосредственно с конденсаторами должен обязательно знать, как расшифровывается та или иная маркировка.

Таблица маркировки конденсаторов

Код	Пикофарады, (пф, pf)	Нанофарады, (нф, nf)	Микрофарады, (мкф, µf)
109	1.0	0.001	0.000001
159	1.5	0.0015	0.000001
229	2.2	0.0022	0.000001
339	3.3	0.0033	0.000001
479	4.7	0.0047	0.000001
689	6.8	0.0068	0.000001
100*	10	0.01	0.00001
150	15	0.015	0.000015
220	22	0.022	0.000022
330	33	0.033	0.000033
470	47	0.047	0.000047
680	68	0.068	0.000068
101	100	0.1	0.0001
151	150	0.15	0.00015
221	220	0.22	0.00022
331	330	0.33	0.00033
471	470	0.47	0.00047
681	680	0.68	0.00068
102	1000	1.0	0.001
152	1500	1.5	0.0015
222	2200	2.2	0.0022
332	3300	3.3	0.0033
472	4700	4.7	0.0047
682	6800	6.8	0.0068
103	10000	10	0.01
153	15000	15	0.015
223	22000	22	0.022
333	33000	33	0.033
473	47000	47	0.047
683	68000	68	0.008
104	100000	100	0.1
154	150000	150	0.15
224	220000	220	0.22
334	330000	330	0.33
474	470000	470	0.47
684	680000	680	0.68
105	1000000	1000	1.0

Маркировка твердотельных конденсаторов

По международному стандарту — начинают читать с единиц измерения. Фарады применяются для измерения ёмкости. Маркировку наносят на корпус самого устройства.

Иногда наносят маркеры, которые указывают на допустимые отклонения от нормы емкости самого конденсатора (указывается в процентах).

Порой, вместо них используется буква, которая обозначает то или иное значение самого допуска. Затем опреедляем номинальное напряжение. В том случае, если же корпус устройства имеет большие размеры, данный параметр обозначается цифрой, за которой далее следуют буквы. Максимально допустимое значение параметра указывается с помощью цифр. Если на корпусе нет никакой информации о допустимом значении напряжения, то использовать его можно только в цепях с низким напряжением. Если же устройство, согласно его параметрам, должно использоваться в цепях, где есть переменный ток, то применяться оно, соответсвенно, должно именно так и не иначе.

Устройство, которое работает с постоянным током, нельзя использовать в цепях с переменным.

Далее, определием полярность устройства: положительную и же отрицательную. Этот шаг очень важен. Если полюса будут определены неверно, велик риск возникновения короткого замыкания или даже взрыва самого устройства. Независимо от полярности, конденсатор можно будет подключить в том случае, если не указана какая-либо информация о плюсе и же минусе клемм.

Значение полярности могут наносить в виде специальных углублений, которые имеют форму кольца, или же в виде одноцветной полосы. В конденсаторах из алюминия, которые по своему внешнему виду похожи на банку из-под консервов, подобные обозначения говорят об отрицательной полярности. А, например, в танталовых конденсаторах, которые имеют небольшие габариты, все наоборот — полярность при данных обозначениях будет являться положительной. Цветовую маркировку не стоит учитывать лишь в том случае, если на самом конденсаторе будут указаны плюс и минус.

Маркировка конденсаторов: расшифровка

Значения первых двух цифр на корпусе, которые указывают на ёмкость устройства. Если конденсатор небольшого размера — маркировка осуществляется согласно стандарту EIA.

Цифры: обозначение

Когда в обозначении указаны только одна буква и две цифры, то цифры соответствуют параметру ёмкости конденсатора. По-своему нужно расшифровывать остальные маркировки, опираясь на ту или иную инструкцию. Множитель нуля — это третья по счету цифра. Расшифровку проводят в зависимости от того, какая цифра находится в конце. К первым двум цифрам необходимо добавить определённое количество нолей, если цифра входит в диапазон от ноля до шести. Если последней цифрой является число восемь, то в таком случае необходимо на 0,01 умножить две первые цифры. Когда значение ёмкости конденсатора станет известным, нужен будет определить то, в таких единицах измерения указана данная величина. Устройства из керамики, а также плёночные варианты являются мелкими. В них данный параметр измеряется в пикофарадах. Микрофарады используются для больших конденсаторов.

Буквы: их обозначение

Далее необходимо провести расшифровку букв, которые есть в маркировке. Если в первых двух символах есть буква, то в таком случае расшифровать ее можно несколькими методами. Если есть буква R, то она играет роль запятой, которая используется в дроби. Если есть буквы u, n, p — то оно тоже выполняют роль запятой в той же самой дроби.

Керамические конденсаторы: маркировка

Данные виды устройств имеют два контакта, а также круглую форму. На корпусе будут указаны как основные показатели, так и допуск отклонений от номы параметра ёмкости. Для этого используют специальную букву, которая находится после обозначения ёмкости в цифрах.

Если есть буква В, то отклонение в таком случае будет равняться +0,1 пФ, если буква С — то + 0,25 пФ и так далее. Только при значении параметра ёмкости менее 10пФ используются данные значения. Если параметр ёмкости больше указанного выше, то буквы — это процент допустимых отклонений.

Смешанная маркировка из цифр и букв

Маркировка может быть указана в виде буквы, затем цифры, а после снова буквы. Первый символ — это самая маленькая допустимая температура. Второй символ обозначает, наоборот, самую большую допустимую температуру. Третий символ — это ёмкость устройства, которая может изменяться в переделах ранее указанных значений температур.

Остальные маркировки

Значение напряжения можно узнать с помощью маркировки, которая находится на корпусе устройства. Символы говорят о допустимом максимальном значении параметра для того или иного конденсатора. Иногда маркировку упрощают. Например, используется только первая цифра. Напряжение меньше десяти вольт будет обозначаться, например, нулём, а этот же параметр, который будет иметь напряжение в пределах от десяти до девяноста девяти вольт — единицей и так далее. Другую маркировку имеют устройства, которые были выпущены намного раньше. Тогда нужно обратиться к справочнику во избежание совершения ошибок. У нас вы можете также узнать, как проверить конденсатор мультиметром на плате.

Арифметика часов 5

Секретные кольца декодера

Когда я был молодым парнем, была очень популярная телепрограмма под названием Captain Midnight и Space Cadets (популярная, по крайней мере, среди молодежи, такой как я). Любой зритель мог написать Captain Midnight и всего за 1 доллар стать младшим. космический кадет. За 1 доллар вы получили официальный свиток с вашим именем, в котором говорилось, что вы младший космический курсант, удостоверение личности и секретное кольцо-декодер .Каждую неделю в конце программы на экране телевизора печаталось секретное послание для младших курсантов-космонавтов. Выглядело это как беспорядок букв без всякого смысла, примерно так:

GULQN ERVFR LWV JRRG IRU BRX

Однако любой младший космический курсант, у которого было секретное кольцо-декодер, мог разгадать секретное сообщение!

Кольцо представляло собой пластиковое кольцо, которое можно было надеть на палец. Вверху кольца были два круга, один внутри другого, с напечатанными на них буквами алфавита.Внутренний круг был фиксированным, но вы могли повернуть внешний круг так, чтобы буквы на нем совпадали с буквами на внутреннем круге по-разному. Лицевая сторона этого кольца выглядела так:

Помимо секретного сообщения, нам также была предоставлена еженедельная секретная настройка кольца. Например, через неделю нам сказали бы вращать внешний круг, пока буква M на внешнем круге не окажется рядом с J на внутреннем круге. После того, как кольцо было установлено, мы выяснили секретное сообщение, найдя каждую букву секретного сообщения на внешнем кольце и заменив ее соответствующей буквой на внутреннем кольце.

Найдите секретное сообщение, используя изображение кольца декодера выше, для которого задана правильная секретная установка.

Щелкните здесь, чтобы увидеть ответ.

Кроме того, два младших курсанта могли писать друг другу секретные сообщения. Все, что им нужно было сделать, это согласовать секретную настройку для своих сообщений, например «поставить A на внешний круг рядом с K на внутренний круг» и сохранить эту личную информацию в секрете. Чтобы написать друг другу секретное сообщение, они сначала устанавливают кольцо с секретной настройкой, затем, взяв каждую букву сообщения, которое они хотят отправить (это называется открытым текстом , ), они находят букву на внутренней стороне . круг и замените его соответствующей буквой на внешнем круге .Чтобы прочитать секретное сообщение, кольцо устанавливается на секретную настройку, затем каждая буква секретного сообщения находится на внешнем круге и заменяется соответствующей буквой на внутреннем круге , как это было сделано с сообщениями из телешоу.

Эти кольца-декодеры сейчас трудно найти, они стали предметами коллекционирования. Но время от времени вы все равно можете получить его в виде игрушки в коробке из-под хлопьев или в коробке от Cracker Jack. Однако нам не обязательно иметь секретные кольца декодера, поскольку мы можем использовать арифметику часов, чтобы делать то же самое, что и кольца декодера.

Поскольку мы собираемся использовать арифметику часов, нам нужно преобразовать буквы в числа. Мы всегда будем использовать следующую таблицу как для преобразования букв в числа, так и для преобразования чисел обратно в буквы (мы будем часто использовать эту таблицу, поэтому вы можете сделать ее собственную копию):

A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25

Чтобы создать секретное сообщение, мы сначала выбираем секретное число от 0 до 25.Это число соответствует установке секретной настройки кольца декодера. Хотя вы можете выбрать цифру 0, это не будет хорошим выбором … это все равно, что установить A на внешнем круге рядом с A на внутреннем круге, тогда все буквы выстроятся в линию и секретное сообщение то же самое, что и открытый текст. Чтобы написать секретное сообщение, для каждой буквы открытого текста сначала найдите номер, соответствующий этой букве, затем добавьте секретный номер к этому модулю 26, а затем замените исходную букву буквой, соответствующей новому номеру.Например, предположим, что секретное число — 3, а открытым текстом — слово «НАПИТОК». Теперь «D» равно 3, а 3 + 3 mod 26 = 6. 6 — это буква «G», поэтому мы заменяем «D» на «G». «R» равно 17, 17 + 3 mod 26 = 20, а 20 — «U», поэтому мы заменяем «R» на «U». Мы продолжаем в том же духе, и открытый текст «DRINK» становится секретным сообщением «GULQN». Обратите внимание, что «J» = 9 становится 12 = «M», поэтому добавление 3 соответствует размещению «M» на внешнем круге кольца декодера над «J» на внутреннем круге. Это секретная настройка, которая используется на изображении кольца декодера выше.Если вы добавите 3 к числу, соответствующему любой букве на внутреннем кольце, вы получите число, соответствующее букве на внешнем кольце. Также обратите внимание, что «Y» = 24 на внутреннем кольце становится 24 + 3 mod 26 = 27 mod 26 = 1 = «B» на внешнем кольце, поэтому вам действительно нужно использовать арифметику часов, чтобы получить правильные буквы.

Используйте указанные секретные номера для записи секретных сообщений, которые соответствуют этим открытым текстам.

Секрет № 5. ДЕНЬГИ В ЯЩИКЕ.
Секрет номер 10.БЫСТРАЯ КРАСНАЯ ЛИСА ПЫГАЕТ НА ЛЕНИНУЮ КОРИЧНУЮ СОБАКУ.
Секрет № 13. ВСТРЕЧАЙТЕ МЕНЯ В ТРИ ЧАСА.

Нажмите здесь, чтобы увидеть ответы.

Чтобы выяснить секретное сообщение, когда мы знаем секретное число, мы сначала преобразуем буквы в числа, а затем вычитаем из секретного числа по модулю 26 и, наконец, преобразуем обратно в буквы. Например, если секретное число 5, то секретное сообщение DTZ FWJ XRFWY вычисляется следующим образом: «D» = 3, 3-5 mod 26 = -2 mod 26 = 24 = «Y», «T» = 19, 19-5 мод 26 = 14 = «O», «Z» = 25, 25-5 мод 26 = 20 = «U», «F» = 5, 5-5 мод 26 = 0 = «A», «W» = 22, 22-5 mod 26 = 17 = «R», «J» = 9, 9-5 mod 26 = 4 = «E».Итак, наше секретное сообщение начинается с ВЫ … А теперь выясните остальную часть этого секретного сообщения.

Используйте указанные секретные номера, чтобы узнать, что говорят эти секретные сообщения.

Секрет № 5. RFWYMF MFX GNL KJJY.
Секрет № 10. S KW SX NKXQOB COXN ROVZ.
Секрет № 13. ZRRD ZR NG DUERR B PYBPX.

Нажмите здесь, чтобы увидеть ответы.

Теперь вы можете писать секретные сообщения своим друзьям, все, что вам нужно сделать, это выбрать другой секретный номер, чтобы поделиться с каждым другом.В следующем разделе мы увидим, как использовать больше тактовой арифметики, чтобы сделать еще более совершенное секретное кольцо декодера (без кольца).

Секретное сообщение

Сообщение гласит: «НАПИТЬ БОСКО ЕГО ХОРОШО ДЛЯ ВАС».

Я должен объяснить: Bosco — это торговая марка шоколадного солодового порошка, который вы смешиваете с молоком, чтобы получить шоколадно-молочный напиток. Боско был спонсором шоу Captain Midnight и Space Cadets. Итак, это секретное сообщение было действительно коммерческим.

Вернуться к вопросам

Ответы на вопросы создания секретных сообщений

YMJ RTSJD NX NS YMJ IWFBJW
DRO AESMU BON PYH TEWZC YFOB DRO VKJI LBYGX NYQ
ZRRD ZR NG DUERR B PYBPX

Вернуться к вопросам

Ответы на вопросы о секретных сообщениях

У МАРТЫ БОЛЬШИЕ НОГИ
Я В ОПАСНОСТИ ОТПРАВИТЬ ПОМОЩЬ
ВСТРЕЧАЙТЕ МЕНЯ В ТРИ ЧАСА

Вернуться к вопросам

Секретный язык: криптография и секретные коды

Рон Хипшман

Когда вы были ребенком, у вас было кольцо-декодер «Captain Midnight»? С его помощью вы могли отправлять друзьям сообщения, которые никто не мог прочитать.Или, может быть, вы помните, как использовали специальные символы для написания заметок для своего «пожатия» в классе. Если записку перехватили, ваш учитель ничего не смог бы узнать о вашем романе.

В более серьезных случаях наши военные и дипломатические силы используют коды и шифры для защиты конфиденциальной информации от посторонних глаз. Компании также отправляют данные, которые были закодированы, чтобы попытаться защитить коммерческую тайну и закулисные сделки. В конце концов, вы не хотите, чтобы ваш конкурент знал, что вы собираетесь приобрести его компанию с выкупом за счет заемных средств.

Изучение шифрования и кодирования (на передающей стороне), а также расшифровки и декодирования (на принимающей стороне) называется криптографией от греческого κρυπτός (криптос), или скрытый, и γράφειν (графия), или письмо. Если вы не знаете греческого (а многие из нас знают), приведенные выше буквы могут быть формой кода! Хотя различие нечеткое, шифры отличаются от кодов. Когда вы заменяете одно слово другим словом или предложением, как, например, в словаре иностранного языка, вы используете код.Когда вы смешиваете или заменяете существующие буквы, вы используете шифр. (Я сказал вам, что разница нечеткая, и вы можете комбинировать коды и шифры, заменяя одно слово другим, а затем смешивая результат.) Мы сконцентрируемся на шифрах.

Чтобы шифр был полезным, необходимо знать несколько вещей как на отправляющей, так и на принимающей стороне.

Алгоритм или метод , используемый для шифрования исходного сообщения (известного как открытый текст).
Ключ , используемый с алгоритмом, позволяющим зашифровывать и дешифровать открытый текст.
Период или время , в течение которого ключ действителен.

По аналогии, чтобы попасть в свой дом, нужно вставить ключ в замок, чтобы открыть дверь. Этот процесс (использование ключа и замка) является методом или алгоритмом. Теперь этот метод работает только в том случае, если у вас есть подходящий ключ для вставки в замок, и ваш ключ будет действителен только до тех пор, пока вы проживаете в конкретном жилище. Следующий житель поменяет замки на другой ключ, чтобы убедиться, что вы не можете войти, даже если вы знаете метод.

Выбор трех вышеперечисленных пунктов — алгоритма, ключа и периода — зависит от ваших потребностей. Если вы находитесь на поле боя и получаете текущие тактические данные, вам нужен алгоритм, который упрощает расшифровку сообщения в пылу битвы. С другой стороны, вы также должны предполагать, что ваш оппонент перехватил ваше зашифрованное сообщение и пытается его сломать. Следовательно, вы должны выбрать достаточно сложный алгоритм (метод), чтобы к тому времени, когда ваш оппонент это выяснил, данные были бесполезны.Чем проще алгоритм вы выберете, тем чаще вам придется менять ключ, открывающий код, — если вы хотите держать своего врага в неведении.

Шифры делятся на две основные категории; шифры подстановки и шифры транспонирования. Шифры подстановки заменяют буквы в открытом тексте другими буквами или символами, сохраняя порядок, в котором символы располагаются одинаково. Шифры транспонирования сохраняют все исходные буквы нетронутыми, но меняют их порядок. Результирующий текст любого метода шифрования называется зашифрованным текстом.Конечно, вы можете использовать оба метода один за другим, чтобы еще больше запутать непреднамеренного получателя. Чтобы почувствовать эти методы, давайте взглянем на некоторые шифры.

Замещающие шифры и кольца декодера

Мы постоянно используем подстановочные шифры. (На самом деле, шифры подстановки в большинстве случаев можно было бы правильно называть кодами.) Код Морзе, сокращение, семафор и код ASCII, с которым эти символы хранятся внутри моего Macintosh, — все это примеры.(ASCII означает Американский стандартный код для обмена информацией, на всякий случай, если вам интересно.) Единственное различие между этими и шпионскими кодами состоит в том, что приведенные выше примеры стандартизированы, так что их знают все.

Кольцо декодера Captain Midnight (которое также является кольцом «кодировщика») позволяет выполнять простой шифр подстановки. Обычно он имеет два концентрических колеса букв, от A до Z. Вы вращаете внешнее кольцо и заменяете буквы в сообщении, находящемся на внешнем кольце, буквами, расположенными непосредственно под ним на внутреннем кольце (см. Диаграмму).Здесь алгоритм заключается в смещении алфавита, а ключ — это количество символов для его смещения. Юлий Цезарь использовал эту простую схему, смещая на 3 символа (Он бы поставил «A» на внешнем кольце букв поверх «D» на внутреннем кольце, если бы у него было кольцо декодера Captain Midnight.) Слово «EXPLORATORIUM» «таким образом становится» HASORUDWRULXP. » Такая схема была легко сломана и показала определенную степень наивности Цезаря в отношении разведки врага.

Шифр подстановки колес

Щелкните здесь, чтобы загрузить копию Cypher Wheel (12k PDF).Скопируйте и вырежьте два колеса. Поместите меньшее колесо поверх большего колеса и поверните их так, чтобы ваша «ключевая буква» на маленьком колесе оказалась под буквой «А» большого колеса. Теперь вы можете зашифровать свой открытый текст и передать его другу, который знает правильную ключевую букву.

Вы можете немного усложнить дешифрование своего зашифрованного текста, если бросите в шляпу 26 листов бумаги, на каждом из которых написана буква алфавита, вытащите их по одной и положите рядом друг с другом. нормальный алфавит.Результат может выглядеть так (я просто использовал порядок клавиш на своей клавиатуре, поэтому вы можете назвать это кодом «Qwerty»):

Текстовая буква A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 
 Шифрованная буква Q W E R T Y U I O P A S D F G H J K L Z X C V B N M

Вы можете составить секретное сообщение из приведенной выше таблицы. Каждый раз, когда вы видите «Я», вы заменяете внизу «О» и так далее для других символов. Сообщение «Встретимся после школы за спортзалом» будет выглядеть как «

».

«DTTZ DT QYZTK LEIGGS WTIOFR ZIT UND.»

Длина слова — особенно короткие слова — дает отличные подсказки относительно природы кода (см. Частотные диаграммы). Чтобы скрыть ваше сообщение, игнорируйте пробелы и разбейте сообщение на части равного размера. В шпионском бизнесе обычно используется пять букв, поэтому ваше сообщение будет выглядеть следующим образом (обратите внимание, что в конце добавляется дополнительный «фиктивный» символ «M», чтобы оно представляло собой группу из 5 букв. У получателя не должно быть никаких проблема с лишним персонажем.):

DTTZD TQYZT KLEIG GSWTI OFRZI TUNDM

Другая популярная система, называемая схематическим шифром, используемая многими детьми в школе, заменяет буквы символами, а не другими буквами.Эта система, по сути, аналогична системе замены букв, но ее легче запомнить, чем 26 случайно выбранных букв. В нем используются доски для крестиков-ноликов и два крестика, как показано ниже.

То же секретное сообщение, что и выше, с использованием линий, окружающих каждую букву (и включая точку там, где это необходимо), становится:

Несмотря на то, что это выглядит как неразборчивый текст из космоса, на это у ручного криптолога уйдет не более 10 минут, чтобы разобраться.Почему? При наличии достаточного количества зашифрованного текста определенные закономерности становятся очевидными. Обратите внимание, как часто появляется пустой четырехсторонний прямоугольник: шесть раз из 29 символов или примерно в 20% случаев. Это сразу указывало бы на то, что пустое поле почти наверняка было символом «Е», наиболее часто используемой буквы в английском языке. Другие буквы также можно определить по их частоте и по их ассоциации с другими соседними символами (см. «Частоты»). Почти все шифры подстановки открыты для такого рода анализа.

Фрэнсис Бэкон создал один из наиболее интересных подстановочных шифров. Он использовал два разных шрифта, немного различающихся по весу (жирности). Он разбил свой зашифрованный текст на 5 групп символов, каждая из которых будет представлять один символ в его открытом тексте. В зависимости от того, какие символы в группе выделены жирным шрифтом, можно определить символ открытого текста, используя следующую таблицу (* обозначает простой символ, а B — жирный символ)

A = ***** G = ** BB * M = * BB ** S = B ** B * Y = BB ***
B = **** B H = ** BBB N = * BB * B T = B ** BB Z = BB ** B
C = *** B * I = * B *** O = * BBB * U = B * B **
D = *** BB J = * B ** B P = * BBBB V = B * B * B
E = ** B ** K = * B * B * Q = B **** W = B * BB *
F = ** B * B L = * B * BB R = B *** B X = B * BBB

Наше то же секретное сообщение, что и выше, могло бы появиться таким образом (жирные и простые символы Бэкона были менее очевидны, чем те, что ниже):

T  o b  e или n  o  t to b  e  th  a  t i  s t  h  e q  uest  i  on.Whet  h  er ' t  is no  ble  r  i  n the  mi  n  d  to
s  uf   f  er  th  e s  lin  gs  a  nd ar  ro  w  s o  f
out  ra  geous fort  u  n  e   или  t  o t  ak  e  ar  m  s
ag  a   i  ns  t  a sea  o  f tr  oub  l  es a  nd  by
o  pp  o  s  в  g закончить их?

Чтобы расшифровать, мы просто разбиваем символы на группы по 5 и используем ключ выше, чтобы найти текстовое сообщение.

  М Е Е Т М Е Б Е
T  ob  eo rn  o  tt ob  e  th  a  ti  st  h  eq  ue st  i  on Whet  h  er  t  is

  Г И Н Д Т Е Г
no  ble  r  i  nth e  mi  n  d  tos  uf   f  er  th  es  lin  gs  a  nd ar  ro  w

  Г М А Ф Т Е Р С
  so  fou t  ra  ge ousfo rt  u  n  e   or  t  ot  ak  e  ar  m  sag  a   i  ns  t  t 

  C H O O L
море  o  f tr  oub  l  esa  n d  byo  p p  o  s  in  gendt hem?

Шифры транспонирования

Возвращаясь к твоим школьным дням, о-о-о-о-о-йе, член-рэй, иг-пей, атин-лай? Свинья-латынь — это форма транспозиционного шифра, в которой оригинальные буквы сохраняются нетронутыми (хотя и с добавлением суффикса «ау»), но каким-то образом переставлены.

Еще до школьных времен, в V веке до нашей эры, спартанцы использовали интересный транспозиционный шифр, названный scytale . В скитале использовался цилиндр с лентой, спирально обернутой вокруг него от одного конца до другого. Сообщение было написано на ленточках, а затем распаковано с цилиндра. Только тот, у кого цилиндр такого же диаметра, мог перемотать и прочитать сообщение.

Scytale зависел от части оборудования, цилиндра, который, будучи захвачен противником, скомпрометировал всю систему.Кроме того, получатель может потерять или сломать цилиндр и, следовательно, потерять способность расшифровать любое сообщение. Было бы лучше, если бы метод был полностью «интеллектуальным», чтобы его можно было запомнить и использовать, не прибегая к физическим устройствам.

Поскольку и отправитель, и получатель транспонированного зашифрованного текста должны согласовать и запомнить этот алгоритм или метод шифрования и дешифрования, было бы неплохо сделать что-нибудь простое. Поскольку геометрические фигуры легко запомнить, они служат основой для целого класса транспозиционных шифров.Поместим наше сообщение в форму коробки. Так как здесь 29 символов, мы добавим пустышку («О»), чтобы получилось 30, и напишем сообщение в поле размером шесть на пять.

ВСТРЕТЬ МЕНЯ
А Ф Т Е Р С
C H O O L B
E H I N D T
H E G Y M O

Теперь мы можем расшифровать сообщение, перемещаясь вниз по столбцам, а не по строкам. Еще раз мы разделим символы на группы по пять, чтобы не было никаких подсказок о размерах слов. Результат выглядит так:

MACEH EFHHE ETOIG TEONY MRLDM ESBTO

Настоящее разнообразие начинается, когда вы понимаете, что вам не нужно записывать открытый текст в поле строка за строкой.Вместо этого вы можете следовать шаблону, который зигзагообразно движется по горизонтали, вертикали или диагонали, или по спирали внутрь или по спирали (по часовой стрелке или против часовой стрелки), или по многим другим вариациям (см. Диаграмму ниже).

После того, как вы поместили текст в выбранную форму, используя один маршрут, вы можете затем зашифровать его, выбрав другой маршрут по тексту. Вам и вашему партнеру просто нужно согласовать маршрут чтения, маршрут транскрипции (шифрования) и отправную точку для создания системы.Эти системы называются транскрипциями маршрутов.

И снова наше сообщение. Маршрут считывания закручивается по спирали внутрь против часовой стрелки, начиная с правого нижнего угла (левый рисунок). Маршрут транскрипции (правая диаграмма) представляет собой зигзагообразную диагональ, начиная с нижнего левого угла. Зашифрованный текст становится:

EAMTN FTDIE EHOTE RHMEM BYESC GLOHO

Чтобы расшифровать, вы заполняете поле ввода, следуя зигзагообразному маршруту, и читаете сообщение, используя спиральный маршрут.

Другой тип шифра транспозиции использует ключевое слово или фразу для перемешивания столбцов.Это называется столбчатым транспонированием. Это работает так: сначала придумайте секретное ключевое слово. Нашим будет слово СЕКРЕТНО. Затем напишите его над столбцами букв в квадрате и пронумеруйте буквы ключевого слова так, как если бы они упали, если бы мы разместили их в алфавитном порядке. (Если есть повторяющиеся буквы, такие как «E», они нумеруются слева направо.)

5 2 1 4 3 6
С Е К Р Е Т
ВСТРЕТЬ МЕНЯ
А Ф Т Е Р С
C H O O L B
E H I N D T
H E G Y M O

Теперь запишите столбцы в порядке, указанном числами.Полученный зашифрованный текст выглядит так:

ETOIG EFHHE MRLDM TEONY MACEH ESBTO

Как видите, это просто другая структура предыдущего зашифрованного текста, но, по крайней мере, это не какой-то обычный шаблон. Мы могли бы легко усложнить задачу, заполнив квадрат более сложным путем. Мы также могли бы использовать геометрическую форму, отличную от прямоугольника, и комбинировать замену и транспонирование. Единственная проблема, которая может возникнуть, — это то, что расшифровка может стать настолько сложной, что навсегда останется в секрете на принимающей стороне! Если подумать, она никогда не встречала меня за спортзалом…

Частоты

Порядок частотности одиночных букв:
E T O A N I R S H D L C W U M F YG P B V K X Q J Z

Порядок частотности орграфов (двухбуквенных комбинаций):
, в зависимости от того, в каком месте он находится, или нет, или нет, или нет, или нет.

Порядок частотности триграфов:
и то и другое значение для nde имеет однозначное значение, это часто бывает

Порядок частоты наиболее распространенных двойников:
ss ee tt ff 11 мм oo

Порядок частотности начальных букв:
T O A W B C D S F M R H I Y E G L N P U J K

Порядок частотности заключительных букв:
E S T D N R Y F L O G H A R M P U W

Однобуквенные слова:
a, I, 0.

Наиболее частые двухбуквенные слова:
of, to, in, it, is, be, as, at, so, we, he, by, or, on, do, if, me, my, up, an , иди, нет, нас, я …

Наиболее частые трехбуквенные слова:
the, and, for, are, but, not, you, all, any, can, had, her, was, one, our, out, day, get, has, him , его, как, мужик, новый, сейчас, старый, смотри, два, путь, кто, мальчик, сделал, его, давай, поставил, скажем, она тоже пользуется …

Наиболее частые четырехбуквенные слова:
что, с, иметь, это, будет, ваш, от, они, знают, хотят, были, хорошо, много, немного, время, очень, когда, приди, сюда, просто Давно, сделай, много, больше, только, более, таких, возьми, чем, они, ну, были…

Библиография:

Гарднер, Мартин. Коды, шифры и секретная запись.
Нью-Йорк, Нью-Йорк: Dover Publications Inc., 1972.
Замечательное, забавное и легкое для чтения введение в коды и шифры.

Смит, Лоуренс Дуайт. Криптография, наука секретного письма.
New York, NY: Dover Publications Inc., 1943.
Хороший отчет о кодах и шифров с множеством исторических примеров.

Конхейм, Алан Г. Криптография: Учебник.
Нью-Йорк, Нью-Йорк: John Wiley & Sons, 1981.
Техническая (и математическая) книга о более современных методах создания и взлома кода.

Гейн, Хелен Фуше. Криптоанализ: исследование шифров и их решение.
Нью-Йорк, Нью-Йорк: Dover Publications Inc., 1956.
Название говорит само за себя.

Интернет-ресурсы

Шифрование Vigenere

Шифрование Виженера было изобретением французского дипломата Блеза. де Виженера, 1523-1596 гг.Как Цезарь и все криптографы, После этого он не представлял себе шифр в модульных арифметических терминах. Скорее он рассматривал шифр как шифр подстановки, где другой алфавит использовался для следующей буквы сообщения, с алфавитами периодически повторяется — в зависимости от ключа. Вместо того, чтобы устанавливать несколько разных алфавитов, криптограф использовал бы Виженера квадрат.

Вот идея.Для данного ключевого слова «ПЕРВЫЙ», зашифровать каждую букву сообщения, взятого в крайнем левом столбце, чтобы буква в столбце «ключевое слово-буква». Таким образом, первые пять букв сообщения используйте алфавиты, соответствующие букве «F», Столбцы «I», «R», «S» и «T». Итак, код Виженера с этим ключевым словом — это действительно пять смен Цезаря. используется циклически. Описание ведется в обратном направлении. от столбцов ключевых слов до самого левого столбца.Потому что мы действительно используя пять алфавитов, шифрование Виженера иногда называют полиалфавитный (много + алфавитный) код.

Это шифрование так и не прижилось, отчасти потому, что оно было трудным. использовать для шифрования и дешифрования сотен сообщений ежедневно как того требуют военные.

Впервые его разбил прусский майор Касиски. в 1863 году. Он предложил метод взлома шифра Виженера, который состоял из найти длину ключевого слова и затем разделить сообщение на что много простых криптограмм подстановки.Применить частотный анализ для декодирования нескольких криптограмм. Другой способ взломать код — это вычисление пионер двигателей Чарльз Бэббидж более трехсот лет спустя. Бэббидж провел очень тщательный анализ структуры групп письма и много тяжелой работы. Сегодняшний шифр Виженера просто в меру хорошо. Ни один серьезный криптолог не стал бы использовать его для безопасного передача информации.

CS101 — Кодировка текста

Мы рассмотрели, как представлять числа в двоичном формате; в этом разделе мы исследуем представление текста в виде битов.Под «текстом» мы подразумеваем алфавиты и другие системы письма, которые используются везде, от обновлений статуса и текстовых сообщений до электронной почты и электронных книг.

Для начала мы можем предложить способ сопоставления букв и других символов (знаков препинания, пробела и т. Д.) С числами. Например, пусть A будет представлен как число 1, B как 2, C как 3 и так далее. В английском алфавите 26 букв, поэтому нам понадобится всего 5 бит. (2⁵ равно 32, так что у нас даже останется несколько цифр для знаков препинания.)

Упражнение: , используя схему, описанную выше, декодировать слово, представленное битами 00011 00001 10100

Если в наших текстовых сообщениях нужно различать прописные и строчные буквы, нам понадобится более 5 бит. Верхний регистр A – Z составляет 26 символов, нижний регистр a – z — это еще 26, так что всего 52. 2⁶ равно 64, так что 6 бит охватывают его, и опять же несколько символов доступны для пунктуации.

А как насчет включения чисел в наш текст? Если мы хотим отправить текстовое сообщение «Amazon имеет 20% скидку на учебники», мы не сможем представить это «20» как 10100 в двоичном формате, потому что это будет противоречить представлению буквы «T».

Вместо этого нам нужно добавить пространство для стандартных десяти цифр в виде символов. Включение символов с прописными и строчными буквами означает, что нам нужно как минимум 62 символа. Технически это умещается в 6 битах, но у нас будет очень мало места для знаков препинания и символа, представляющего пробел. Так что для практических целей мы используем до 7 бит на символ. 2⁷ равно 128, так что теперь есть много места для других символов.

Кстати, может быть способ «повторно использовать» буквенные представления в качестве цифр.Нам просто нужно поставить перед ними маркер, означающий «это число», или потребовать, чтобы получатель угадал из контекста. Так обстоит дело с шрифтом Брайля, системой письма для слабовидящих, основанной на 6-битных символах. (Каждое из шести мест может быть поднято или нет.) Символ Брайля для «A» совпадает с числом «1».

Простые кодировки, которые я предложил в предыдущем разделе, основаны на фиксированном фиксированном количестве бит на символ — будь то 5, 6 или 7.Один из способов проиллюстрировать это как дерево — см. Этот файл:

Деревья — это часто используемая структура данных в информатике, но они немного отличаются от органических деревьев, к которым они относятся. Прежде всего, мы обычно рисуем деревья с корнем вверху, а они растут вниз по странице. Каждый раз, когда круг разделяется на два пути, мы называем это ветвью . Внизу дерево заканчивается рядом из листьев.

Это конкретное дерево представляет собой двоичное дерево , означает, что каждый узел является либо листом, либо ветвью с ровно двумя дочерними элементами. В двоичном дереве хорошо то, что пути от корня к листу точно соответствуют двоичным числам. Просто представьте ноль как слева в дереве, а единицу как справа. Тогда номер 01101 (например) соответствует левому-правому-правому-левому-правому, который попадает на лист с отметкой N . Расшифруйте сообщение в двоичном формате, написанном под деревом.

Вы можете сказать, что предыдущее дерево имеет фиксированную ширину, потому что каждые пути от корня к листу — это ровно 5 переходов.Теперь сравните это с деревом переменных битов в этом файле:

В этом случае разные буквы могут иметь очень разное количество представляющих их битов. Например, E — кратчайший путь, представляющий всего 3 бита. X — очень длинный путь, представляющий 10 бит. Расшифруйте слово, данное в двоичном формате в правом верхнем углу страницы.

На раздаточном материале слово напечатано с пробелами между буквами, но на самом деле в них нет необходимости. Биты 11100001001 могут быть декодированы, хотя я не подчеркивал, где заканчивается один символ и начинается следующий.Вы просто идете по тропинке на дереве, пока не приземлитесь на лист. Затем начните снова сверху для следующего бита.

Это конкретное дерево переменной ширины создано таким образом, что в целом оно сжимает английского текста. Это работает, потому что наиболее часто используемые буквы представлены пропорционально укороченными битовыми строками. Например, давайте сравним кодировки с использованием обоих деревьев последовательности слов:

  слово: фиксированная кодировка: переменная кодировка:
   THE 100110011100100 15 бит 11100001001 11 бит
   ТРАВА 001101000100000 11010000001100
             1001010010 25 бит 01000100 22 бит
   IS 0100010010 10 бит 01110100 8 бит
   ЗЕЛЕНЫЙ 001101000100100 1101000000001
             0010001101 25 бит 0010110 20 бит
   САИД 100100000001000 010011000111
             00011 20 бит 11011 17 бит
   QUUX 100001010010100 1111100001
             10111 20 бит 111111111111
                                         1111100010 32 бита

   всего: 115 бит 110 бит

При фиксированной кодировке каждый символ составляет ровно 5 бит, поэтому вся последовательность слов составляет 115 бит.(В этом упражнении мы не учитываем кодирование пробелов между словами.)

Сравните это с кодировкой переменных. Почти каждое слово имеет более короткое представление. Единственное исключение — «QUUX», что, конечно, не совсем английское слово. Но он представляет собой случай слова с редко используемыми буквами, и кодирование этого слова существенно увеличилось в размере с 20 до 32 бит. В целом, второе дерево по-прежнему сжимается, если вы в основном используете английские слова с часто встречающимися буквами.

Это подводит нас к наиболее популярным и влиятельным кодам с фиксированным битом. Он называется ASCII (произносится как , «ключ-задница», ), что означает Американский стандартный код для обмена информацией. Он был разработан в начале 1960-х годов и включает 7-битное отображение букв верхнего и нижнего регистра, цифр, различных символов и «управляющих символов». Вы можете увидеть их все в таблице на http://www.asciitable.com/

Управляющие символы находятся в диапазоне 0–31 (основание десять).У них нет визуального представления, но вместо этого они направляют устройство отображения определенным образом. Многие из них уже устарели, но, пожалуй, наиболее важным является 10₁₀ = A₁₆ = 0001010₂, символ «новой строки». Каждый раз, когда вы нажимаете клавишу ВВОД, чтобы перейти к следующей строке, этот символ вставляется в ваш документ.

Символ 32 — это пробел, а символы 33-63 содержат в основном знаки препинания. Цифры находятся в позициях с 48 по 57. Их легко распознать в двоичном формате: все они начинаются с 011, а затем младшие четыре бита соответствуют цифре.Таким образом, вы можете сразу сказать, что 0110101₂ = 35₁₆ — это цифра «5».

Диапазон 64–95 состоит в основном из прописных букв, а 96–127 — в основном из нижнего регистра. (Оба диапазона включают еще несколько знаков пунктуации и скобок.) Эти числа соответствуют битовым строкам, начинающимся с 10 для прописных букв и 11 для строчных. Остальные 5 бит определяют позицию буквы в алфавите. Таким образом, 10 01011₂ = 4B₁₆ — это одиннадцатая буква (заглавная «K»), а 11 01011₂ = 6B₁₆ — соответствующая строчная буква «k».

Код

ASCII относительно хорошо работал в англоязычном мире, но у других народов и культур есть потребности в других символах, акцентах, алфавитах и других символах. Невозможно написать niño или cafe в ASCII, или польское имя Michał, , и это безнадежно для греческого слова ἀλήθεια, или китайского 福.

Компьютерные архитектуры в конечном итоге остановились на восьми битах в качестве наименьшего адресуемого блока памяти, известного как байт. Поскольку ASCII был 7-битным, стало возможным использовать этот восьмой бит для указания дополнительных 128 символов.

Это привело к большому количеству несовместимых 8-битных кодировок для разных языков. Они в основном согласились с тем, что первые 128 символов совместимы с ASCII, но в остальном это был хаос. Все это описано в разных частях данной спецификации:

То есть ISO 8859-1 был для западноевропейских языков, 8859-2 для центральноевропейских, 8859-4 для североевропейских, 8859-5 для кириллицы, 8859-7 для греческого и т. Д.Отправка документов между этими языковыми группами была сложной, и было невозможно создать единый документ, содержащий несколько языков, из несовместимых кодировок.

В качестве небольшого примера возьмем символ в позиции EC₁₆ = 236₁₀. Все эти кодировки расходятся во мнениях относительно того, каким оно должно быть:

ISO 8859-1: ì — СТРОЧНАЯ ЛАТИНСКАЯ БУКВА I С ТЯЖЕЛЫМ
ISO 8859-2: ě — СТРОЧНАЯ ЛАТИНСКАЯ БУКВА E С КАРОН
ISO 8859-4: ė — СТРОЧНАЯ ЛАТИНСКАЯ БУКВА E с ТОЧКОЙ ВЫШЕ
ISO 8859-5: ü — КИРИЛИЧЕСКАЯ СТРОЧНАЯ БУКВА МЯГКИЙ ЗНАК
ISO 8859-7: μ — ГРЕЧЕСКАЯ СТРОЧНАЯ БУКВА MU
Mac OS Роман: Ï — ЛАТИНСКАЯ ЗАГЛАВНАЯ БУКВА I С ДИАРЕЗОМ
IBM PC: ∞ — БЕСКОНЕЧНОСТЬ

Вы все еще можете увидеть остатки этой старой несовместимой системы кодирования в меню вашего браузера.Большинство веб-страниц сегодня будут в Юникоде — мы скоро вернемся к этому, — но браузер по-прежнему поддерживает эти в основном устаревшие кодировки, поэтому он может отображать веб-страницы, написанные с их помощью. Обратите внимание, что даже для одного и того же языка часто доступно несколько вариантов кодирования.

Для решения этой проблемы несовместимых кодировок в разных языковых группах был основан Консорциум Unicode с удивительной и благородной целью разработки одной кодировки , которая содержала бы на каждые символов и символов, используемых в на каждом языке на планете.

Вы можете получить представление о разнообразии и масштабах этой цели, просмотрев таблицы кодов на веб-сайте Unicode:

Каждый из них представляет собой файл PDF, относящийся к определенному региону, языку или системе символов. В общей сложности это около ста тысяч символов.

В кодовых таблицах каждому возможному символу присваивается отдельный номер, но все еще остается вопрос, как кодировать эти числа как биты. Большинство чисел умещается в 16-битном формате, поэтому в кодовых таблицах они выражены четырьмя шестнадцатеричными цифрами (например, 1F30 для греческой йоты с акцентом: ἰ ).Но 2¹⁶ — это 65 536, и мы сказали, что их было ближе к 100 000 символов, поэтому, очевидно, 16 бит недостаточно. Большую часть времени Unicode представлен в виде многобайтовой (переменной) кодировки, которая называется UTF-8. Исходные символы ASCII по-прежнему представлены в виде одного байта, но установка восьмого бита позволяет использовать умный механизм, который указывает, сколько байтов следует за ними. Вот хорошее объяснение Unicode и UTF-8 от Тома Скотта на Computerphile:

В настоящее время Unicode работает практически везде, и почти весь новый контент использует его.По-прежнему иногда возникает проблема с тем, установлены ли на вашем компьютере правильные шрифты, содержащие все необходимые символы. Иногда вместо неподдерживаемого символа появляется поле. Вот один и тот же текст, отображаемый в трех разных системах:

На приведенном выше изображении отлично видны все персонажи. В приведенном ниже не хватает нескольких символов.

Наконец, приведенная ниже система не может отображать какие-либо символы, кроме символов ASCII.

Учебное пособие по двоичным числам с 1 и 0 |

Дэвид Дж. Морган на Flickr

Двоичные числа, основанные на единицах и нулях, отражают практическую сущность компьютерного оборудования: электричество либо включено, либо выключено.Узнайте, как писать двоичными числами, а также (не такой уж секретный) код для преобразования букв английского языка в двоичные числа и обратно.

Когда буква А не буква А? Что ж, компьютеры не используют букву A. Они используют восьмизначное двоичное число 01000001 для представления A. В этом руководстве по двоичным числам описывается, что такое двоичные числа и как их вычислять.

Компьютеры передают, вычисляют и преобразуют двоичные числа, потому что компьютерные аппаратные схемы имеют только два электрических состояния: включено или выключено.Эти два состояния могут быть представлены как ноль (выключен) или один (включен). Все буквы алфавита, цифры и символы преобразуются в восьмизначные двоичные числа, когда вы работаете с ними в программном обеспечении на вашем компьютере.

Создание и преобразование двоичных чисел — хороший способ узнать, как компьютеры обрабатывают данные на самом низком уровне в своих аппаратных схемах.

Кроме того, я предоставляю бесплатную электронную таблицу Excel, ссылка на которую находится внизу этой статьи, чтобы помочь вам визуализировать и вычислять двоичные числа.

[Не очень] секретная формула

Чтобы представить букву A как 01000001, компьютеру (и вам, в дальнейшем) потребуется несколько основных инструментов. Одним из инструментов является таблица преобразования ASCII. Не вдаваясь в технические подробности, диаграмма ASCII отображает уникальный номер от 1 до 255 для всех букв алфавита с большой буквы (AZ) и нижнего регистра (az), а также чисел (0-9), пробелов и других специальные символы. Уникальный номер ASCII, который соответствует каждому символу, например, заглавная буква A, используется для вычисления уникального восьмизначного двоичного числа, комбинации единиц и нулей, например 01000001.

По сути, это двухэтапный секретный код. Первый шаг — получить уникальный номер ASCII для буквы. Второй шаг — создать уникальное восьмизначное двоичное число, комбинацию единиц и нулей для представления номера ASCII.

И, конечно же, переход от восьмизначной комбинации единиц и нулей к букве или символу меняет этот процесс: сначала превратите двоичное число в число от 1 до 255, а затем используйте это число для поиска буквы в таблице ASCII. .

Как создавать двоичные числа

Двоичные числа состоят из восьми символов, каждый из которых представляет собой либо 1, либо 0. Размещение каждой единицы указывает значение этой позиции, которая используется для вычисления общего значения двоичного числа. Каждая позиция каждого из восьми символов представляет собой фиксированное числовое значение, как показано ниже.

Двоичные числа со значениями и позициями на пустом листе

Если вы прочитаете эти значения значений по умолчанию снизу вверх, можете ли вы сказать, как вычисляется каждое число, указанное непосредственно выше? Их удвоили.Таким образом, двоичные числа начинаются снизу с первой позиции, равной 1. Вторая позиция снизу имеет значение 2, третья позиция 4 и так далее.

Если сложить все эти числа (1 + 2 + 4 + 8 + 16 + 32 + 64 + 128), можете ли вы угадать, какое число вы получите? 255, наибольшее число, используемое в таблице ASCII. Существует идеальное соответствие между всеми возможными числами от 1 до 255 в таблице ASCII и вычисленными значениями для всех возможных восьмизначных двоичных чисел.

Чтобы вычислить числовое значение двоичного числа, сложите значение для каждой позиции всех единиц в восьмизначном числе.Например, число 01000001 преобразуется в 64 + 1 или 65. Единицы в этом двоичном числе находятся в первой и седьмой позициях, считая снизу вверх или читая справа налево. Первой позиции присвоено значение 1, а седьмой позиции присвоено значение 64.

Преобразуем букву в двоичное число

Теперь, когда вы знаете [не очень] секретную формулу для преобразования букв в уникальные числа ASCII в двоичные числа и как создавать двоичные числа, давайте проделаем весь процесс шаг за шагом.Начнем с буквы С.

Во-первых, нам нужно использовать диаграмму ASCII, подобную приведенной ниже, чтобы найти уникальный номер, присвоенный заглавной букве C. Уникальное десятичное число, которое нужно использовать, — 67.

Десятичное число	Персонаж	Десятичное число	Персонаж	Десятичное число	Персонаж
32	Космос	64	@	96	`
33	!	65	А	97	а
34	«	66	B	98	б
35	#	67	С	99	c
36	$	68	D	100	d
37	%	69	E	101	e
38	и	70	F	102	f
39	‘	71	G	103	г
40	(	72	H	104	ч
41	)	73	I	105	и
42	*	74	Дж	106	j
43	+	75	К	107	к
44	,	76	л	108	л
45	–	77	M	109	м
46	.	78	N	110	n
47	/	79	O	111	или
48	0	80	-п.	112	с.
49	1	81	Q	113	q
50	2	82	R	114	r
51	3	83	S	115	с
52	4	84	т	116	т
53	5	85	U	117	u
54	6	86	В	118	в
55	7	87	Вт	119	Вт
56	8	88	х	120	х
57	9	89	Y	121	л
58	:	90	Z	122	z
59	;	91	[	123	{
60		92		124	\|
61	=	93	]	125	}
62	>	94	^	126	~
63	?	95	_	127	DEL

Чтобы преобразовать число для C, 67, в двоичное число:

Помните, как двоичные числа читаются снизу вверх, с первой позиции и значения по умолчанию до верхней позиции и значения по умолчанию, причем каждой из восьми позиций символов присваивается уникальное числовое значение? В приведенной ниже таблице какая комбинация значений будет равна 67?

Двоичные числа со значениями и позициями

Вы правы, если сказали, что значения по умолчанию 1 плюс 2 плюс 64 будут равны 67, номеру ASCII для заглавной буквы C.Итак, давайте заменим нули первой, второй и седьмой позиций на единицы, считая справа налево. Двоичное число для заглавной буквы C:

Буква C как двоичное число

Можете ли вы расшифровать это двоичное число? Сложите единицы, чтобы получить 64 + 16 + 4 или 84. Найдите десятичное число 84 в таблице ASCII, чтобы найти букву, представленную ниже:

Буква T как двоичное число

Если вы преобразовали это двоичное число в заглавную букву T, вы правы. Вот буква A в виде двоичного числа, представляющего десятичное число ASCII для A, которое составляет 65:

Буква A как двоичное число

Если мы объединим двоичные числа, которые мы рассмотрели до сих пор, мы можем написать CAT:

01000011 01000001 01010100

Бонус: псевдокод для создания преобразователя двоичных чисел

Понимая, как буквы и числа преобразуются в двоичные числа и обратно, давайте посмотрим, как мы могли бы создать программное приложение для выполнения этих преобразований «на лету».Приложение не имеет реальной ценности. Но это дает возможность обсудить, как процесс можно преобразовать в программное обеспечение.

Однако вместо реального кода мы напишем серию операторов или псевдокода.

Давайте для начала возьмем слово кошка. Какой процесс нам нужен для автоматического преобразования этих букв в двоичные числа? Вот один из возможных наборов шагов, которые мы могли бы закодировать:

Разбейте слово на отдельные буквы.
Найдите для каждой буквы числовое значение ASCII, сопоставленное с буквой.
Для каждого числового значения ASCII преобразовать в двоичное число.
Для каждого двоичного числа сохраните значение двоичного числа. Если это первое двоичное число, создайте начальное значение двоичного числа; если существует двоичное числовое значение, добавьте новое двоичное число в конец значения.

Представьте, если бы мы пропустили последний шаг: каков был бы результат этих шагов? У нас будет только последнее двоичное число для строчной буквы t в cat. Важно, чтобы мы фиксировали каждое двоичное число по мере их создания.

Другие наблюдения об этом процессе псевдокода? Нам нужно различать прописные и строчные буквы, не так ли? В противном случае наше преобразование двоичного числа может преобразовать двоичное число в буквы ASCII как CAT, cAT или Cat. При поиске букв в таблице ASCII может быть получен неправильный номер.

Bonus Bonus: Последняя головоломка

Можете ли вы расшифровать фразу в этом наборе двоичных чисел? Помните, что это восемь символьных блоков, состоящих из единиц и нулей.

01000011 01101111 01100100 01100101 01101001 01110011 01010000 01101111 01100101 01110100 01110010 01111001

Вот довольно простой способ преобразовать любую букву в двоичное число. Возьмите калькулятор, найдите десятичное значение ASCII для буквы из таблицы выше, затем посмотрите на таблицу двоичных чисел, чтобы найти ближайшее к десятичному значению значение. Вычтите ближайшее число Значение по умолчанию в двоичной диаграмме, чтобы получить значение остатка. Найдите ближайшее двоичное значение по умолчанию для остатка.Повторяйте, пока у вас не закончатся двоичные значения.

Если вы сообразительны, вы также заметите, что сумма значений под любым из восьми значений по умолчанию равна на единицу меньше, чем значение: поэтому ниже двоичного значения 4 находятся значения 2 и 1, которые равны 3. Ниже двоичного значения значение 8 равно 4, 2 и 1, что равно 7. Это также может помочь преобразовать буквы в двоичные числа. Если, например, ваш остаток равен 7, то вы знаете, что нужно поставить 1 в позиции 4, 2 и 1, чтобы создать эту часть вашего двоичного числа.

Чтобы преобразовать двоичные числа в буквы, просто возьмите лист бумаги и ручку или карандаш и сложите двоичные значения всех единиц.Затем найдите свое общее число в десятичном формате ASCII в таблице выше.

Вот подсказка, которая поможет определить, правильно ли вы решили двоичные числа, указанные выше: в колледже я специализировался на американской поэзии, и мне нравится старый слоган, используемый для программного обеспечения публикации WordPress.

Узнать больше

Рабочий лист двоичных чисел (формат Excel)

https://www.kidscodecs.com/binary-numbers-converter

Рабочий лист двоичных чисел (PDF)

https: //www.kidscodecs.com / бинарные числа-рабочий лист

Двоичный преобразователь

http://www.rapidtables.com/convert/number/binary-converter.htm

Учебное пособие по двоичным числам

http://www.math.grin.edu/~rebelsky/Courses/152/97F/Readings/student-binary

Двоичные числа (Википедия)

https://en.wikipedia.org/wiki/Binary_number

Таблица ASCII

http://www.asciitable.com/

Число в алфавитном порядке

Конвертер алфавита в числа

Буквы в числа (онлайн-инструмент), Преобразование чисел в буквы в различных форматах.Нумерация букв так, чтобы A = 1, B = 2 и т. Д., Является одним из простейших способов их преобразования в числа. Это называется «Конвертер букв в числа». Преобразование букв в числа в различных форматах. Нумерация букв таким образом, чтобы A = 1, B = 2 и т. Д., Является одним из простейших способов их преобразования в числа. Это называется шифром A1Z26.

Переводчик алфавита в числа — LingoJam, Переведите символы алфавита в простой числовой шифр! Ваше секретное сообщение. 25152118 1180520 130519105.Реклама. Отправить Этот шифр выполняет очень простой набор операций, которые превращают набор буквенных символов в серию чисел: для каждой буквы алфавита заменить ее числовым положением этой буквы.

[PDF] Таблица преобразования A = 1 B = 2 C = 3 D = 4 E = 5 F = 6 G = 7 H = 8 I, Таблица преобразования. A = 1 числа, найдите стандартное отклонение, и кто бы это ни было Поскольку эти буквы находятся рядом с началом алфавита, ее среднее значение будет. Инструмент для преобразования букв в числа и наоборот.Буквенно-цифровой шифр (или буквенно-цифровой шифр) состоит в замене каждой буквы ее позицией в алфавите, например, A = 1, B = 2, Z = 26, отсюда и его общее название A1Z26.

Расшифровщик чисел в буквы

A1Z26 Шифр - буквенный номер A = 1 B = 2 C = 3, Буквенный номер (A1Z26) A = 1, B = 2, C = 3. Инструмент для преобразования букв в числа и наоборот. Буквенно-цифровой шифр (или буквенно-цифровой шифр) состоит в замене каждой буквы ее позицией в алфавите, например, A = 1, B = 2, Z = 26, отсюда и его общее название A1Z26.Преобразуйте числа в буквы в различных форматах. Нумерация букв таким образом, чтобы A = 1, B = 2 и т. Д., Является одним из простейших способов их преобразования в числа. Это называется шифром A1Z26. Однако есть и другие варианты, такие как коды ASCII, коды ответвлений или даже периодическая таблица элементов для декодирования чисел.

Буквенные номера, При расшифровке числа будут заменены на буквы, дефисы будут удалены, а остальные заполнители будут действовать как пробелы. Зашифровать, расшифровать. Метод: «ABC XYZ» Шифрование A1Z26 требует подсчета позиций / рангов букв в алфавите.Если это латинский алфавит из 26 символов, вот буква в таблице соответствия ↔ число / значение: замените каждую букву ее позицией в алфавите (A = 1, B = 2, Z = 26)

Числа в буквы (онлайн tool), Нумерация букв таким образом, чтобы A = 1, B = 2 и т. д., является одним из простейших способов их преобразования в числа. Это называется шифром A1Z26. Однако в настоящее время я работаю в Microsoft инженером FastTrack и специализируюсь на Microsoft Azure в качестве облачного решения.Обратите внимание, что я не говорю от имени Microsoft или других сторонних поставщиков, упомянутых в каких-либо моих сообщениях в блоге.

Числа в алфавите, нумерология

Нумерология, алфавит, буквы A, I, Q, J, Y, все имеют числовое значение 1, буквы B, K, R, числовое значение 2, буквы S, C, G, L числовое значение 3 и так далее вплоть до числового значения 8. Нет числового значения больше 8. Алфавиты и числа В нумерологии, когда вы хотите вычислить номер имени.для имени вы должны сложить значения всех алфавитов в этом имени. Затем уменьшите это значение до одной цифры, сложив каждый отдельный номер компонента в этом значении.

Нумерология, С помощью нумерологических таблиц. Для начала нужно узнать числовые значения всех букв алфавита. К счастью, вы можете увидеть эти значения в Нумерологических числах для алфавитов. Специальные буквы в нумерологии. Аспекты нумерологического алфавита важны, в зависимости от того, где этот алфавит помещен в слово.Специальные буквы состоят из краеугольного камня, замкового камня и первой гласной в вашем имени.

Numerology Charts, Присвойте каждой букве цифру от 1 до 9. Начните с буквы A. Напишите «1» рядом с ней, а затем дайте каждой следующей букве следующий номер по мере продвижения в числовом порядке. В нумерологии каждая буква алфавита от A до Z имеет определенное и колеблющееся число. Буква алфавита идентифицируется и связана с определенным числом. Это окончательно и окончательно.Все, что вам нужно сделать, это вычислить собственное числовое значение или общую сумму из алфавитов и чисел, приведенных ниже.

Таблица буквенных номеров 1-26

[PDF] Таблица преобразования A = 1 B = 2 C = 3 D = 4 E = 5 F = 6 G = 7 H = 8 I, сказал: «Вы берете буквы. в ее имени, преобразуйте их в числа, найдите стандартное отклонение, и любое стандартное отклонение ближе всего к вашему — это женский список преобразований для 26 алфавитных чисел с основанием 10 и десятичных чисел с основанием 10 === Боб Сазерленд === Счет от 1 до 4000, вот список алфавитных чисел, показывающий, как вычислить их эквивалентные десятичные числа.Левый столбец букв в списке — это алфавитная система счисления.

Пин от Christie Rinard на сайте Fort Boyard в 2020 г., 22 апреля 2020 г. — Безошибочная буква алфавита Код таблицы чисел в цифрах букв алфавита с числами 1 26 A1Z26 ChartBack к общему количеству букв в алфавите. 23 буквы (ABCDEFGHIKLMNOPQRSTVX YZ) — это первые 23 буквы из 29 оригинального древнеанглийского алфавита

Сколько букв в алфавите? Английский алфавит состоит из 26 букв: A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z.Dim алфавит (26) как целое число Dim intTotal как целое число Dim i как целое число тусклый символ как строка intTotal = 0 For i = 1 To Len (Text1.Text) character = UCase (Mid (Text1.Text, i, 1)) Если символ > = «A» И символ <"Z" Затем алфавит (Asc (символ) - 64) = алфавит (Asc (символ) - 64) + 1 intTotal = intTotal + 1 End If Next 'display count For i

Alphabet & числа Диаграмма

Alphabet Inc. (многонациональная конгломератная компания), Alphabet Inc. — холдинговая компания, которая дает амбициозным проектам ресурсы, свободу и фокус для воплощения их идей — и будет родоначальницей. Латинский алфавит состоит из 26 букв, каждая из которых имеет верхний и нижний регистр.Он возник примерно в 7 веке на латинице. С тех пор буквы были добавлены или удалены, чтобы получить текущий современный английский алфавит из 26 букв (который в конечном итоге стал основным латинским алфавитом ISO).

Alphabet, Alphabet Inc. — американский многонациональный конгломерат со штаб-квартирой в Маунтин-Вью, Калифорния. Он был создан в результате реструктуризации Google. Пять букв являются «гласными»: a e i o u Остальные двадцать одна буква — «согласные».Мы можем написать каждую букву как «большую букву» (заглавную) или «маленькую». Подробнее об английском алфавите

Alphabet, Alphabet использует файлы cookie для сбора информации об использовании веб-сайта посетителями. Эти файлы cookie помогают нам максимально улучшить работу в Интернете. Alphabet является четвертой по величине технологической компанией в мире по размеру доходов и одной из самых ценных компаний в мире. Основание Alphabet Inc. было вызвано желанием сделать основной бизнес Google «более чистым и подотчетным», предоставив большую автономию компаниям группы, которые работают не в сфере интернет-услуг.

Алфавит с цифрами

Сколько букв в алфавите ?, Английский алфавит состоит из 26 букв: A, B, C, D, E, F, G, H, I, J, K, L , M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z. Буквенное число, Буква. 1, A. 2, B. 3, C. 4, D. 5, E. Общее количество букв в алфавите. 23 буквы (A B C D E F G H I K L M N O P Q R S T V X Y Z) являются первыми 23 буквами 29 оригинального древнеанглийского алфавита

Переводчик алфавита в числа — LingoJam, Переводчик алфавита в числа.Переведите символы алфавита в простой числовой шифр! Ваше секретное сообщение. 25152118 1180520 Этот шифр выполняет очень простой набор операций, которые превращают набор буквенных символов в серию чисел: для каждой буквы алфавита заменить ее числовым положением этой буквы.

[PDF] Таблица преобразования A = 1 B = 2 C = 3 D = 4 E = 5 F = 6 G = 7 H = 8 I, числа, найдите стандартное отклонение и любой стандарт. Поскольку эти буквы близки до начала алфавита, ее среднее значение будет меньше, чем пример алфавита JAMES 1337.Чаще всего меняются только гласные, и тогда обычно только они заменяются числами; поэтому редко можно увидеть, как кто-то использует буквенный алфавит для написания целого слова (хотя есть общие исключения, а именно 1337).

Список номеров алфавита

Английский алфавит состоит из 26 букв: A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z. Буквы в алфавите:, сказал: «Вы берете буквы в ее имени, конвертируете их в числа, находите стандартное отклонение, и любое стандартное отклонение ближе всего к вашему — это список преобразования женщин для чисел с основанием 26 алфавита и десятичного счисления с основанием 10. Числа === Боб Сазерленд === Считая от 1 до 4000, вот список алфавитных чисел, показывающий, как вычислить их эквивалентные десятичные числа.Левый столбец букв в списке — это алфавитная система счисления.

[PDF] Таблица преобразования A = 1 B = 2 C = 3 D = 4 E = 5 F = 6 G = 7 H = 8 I, Левый столбец букв в списке представляет собой буквенную систему счисления. Все числа и вычисления справа от первого знака равенства — это моя попытка преобразовать общее количество букв в алфавите. 23 буквы (ABCDEFGHIKLMNOPQRSTVX YZ) являются первыми 23 буквами из 29 оригинального древнеанглийского алфавита

Список преобразований для базовых 26 алфавитных чисел и десятичных оснований 10, Легко заметить, что алфавитные буквы A, I, Q, J , Y, все имеют числовое значение 1, буквы B, K, R, числовое значение 2, Список сокращений… Интересные факты и цифры; Список сокращений текстового чата SMS… Список кодов стран, номеров экстренных служб и телефонных кодов… Эти списки фонетических алфавитов были составлены A C, последнее обновление — 20 октября 2020 года.Заметили ошибку или есть предложение по улучшению списков фонетического алфавита? Дайте нам знать в комментариях ниже…

Сколько букв в алфавите

Сколько букв в алфавите ?, : A, B, C, D, E, F, G, H, I, J , K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z. Английский алфавит (или современный английский алфавит) сегодня состоит из 26 букв: 23 из Старый английский и 3 добавленных позже.

(Старая) 27-я буква английского алфавита, В нашем современном английском алфавите было 27 букв! Знаете ли вы, что это за 27-я буква. В конце концов, мы так сильно невнятно произвели это слово… el legarto Современный английский алфавит — это латинский алфавит, состоящий из 26 букв, каждая из которых имеет верхнюю и нижнюю буквы.Он возник примерно в 7 веке на латинице. С тех пор буквы были добавлены или удалены, чтобы получить текущий современный английский алфавит из 26 букв (который в конечном итоге стал основным латинским алфавитом ISO).

Сколько букв в алфавите ?, В английском алфавите 26 букв, которые варьируются от «a» до «z» (с b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x и y между ними). Ответ: Сколько букв в «алфавите»? В «алфавите» 11 букв.Видите ли, ответ в этом случае исходит из количества букв в словах «алфавит», а не

Английский алфавит

Английский алфавит, На этой странице перечислены буквы английского алфавита от a до z. Словарь для учащихся и учителей ESL. Современный английский алфавит — это латинский алфавит, состоящий из 26 букв, каждая из которых имеет верхний и нижний регистр. Он возник примерно в 7 веке на латинице. С тех пор буквы были добавлены или удалены, чтобы получить текущий современный английский алфавит из 26 букв (который в конечном итоге стал основным латинским алфавитом ISO).

Английский алфавит | Vocabulary, Пять букв английского алфавита — гласные: A, E, I, O, U. Остальные 21 буква — согласные: B, C, D, F, G, H, J, K, L, M. , N, P, Q, R, S, T, V, X, Z и обычно W и Y. Пять букв — это «гласные»: aeiou Остальные двадцать одна буква — «согласные». Мы можем написать каждую букву как «большую букву» (заглавную) или «маленькую». Подробнее об английском алфавите

The English Alphabet (Beginner, Level 1), Английский алфавит состоит из 26 букв: A, B, C, D, E, F, G, H, I, J, K, L , M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z.Буквенный номер, буква. 1, A. 2, B. 3, C. 4, D. 5, E. Английский алфавит состоит из 26 букв. Каждая буква имеет прописную («заглавную») и строчную («строчную») форму.

Ошибка обработки файла SSI

Какое число V в алфавите

Буквы в алфавите :, V = 22. Ш = 23. Х = 24. Y = 25. Z = 26. Классное задание 2. Математика 113 Первая часть была простой: возьмите каждую букву своего имени и преобразуйте ее в число. Используйте так как эти буквы находятся рядом с началом алфавита, ее среднее значение будет.Общее количество букв в алфавите. 23 буквы (ABCDEFGHIKLMNOPQRSTVX YZ) — первые 23 буквы из 29 оригинального древнеанглийского алфавита

[PDF] Таблица преобразования A = 1 B = 2 C = 3 D = 4 E = 5 F = 6 G = 7 H = 8 I, Новости нумерологии и Таро: Нумерологический алфавит — вычисление нумерологического числа и имени. Нумерология — это язык чисел, а в алфавите 26 букв. Буква «W» идет после буквы «V». Английский алфавит в следующем порядке: ABCDEFGHIJKLMNOPQRSTUVWXYZ Какая буква стоит перед вами? В английском алфавите

V, Получить позицию букв в английском алфавите.Положение английского алфавита. Положение букв в английском языке Положение V в английских алфавитах равно 22. Положение W V = 22 W = 23 X = 24 Y = 25 Z = 26 Поскольку эти буквы находятся близко к началу алфавита, ее среднее значение будет посередине. (если у вас нечетное количество букв) или

Ошибка обработки файла SSI

Количество букв алфавита

Сколько букв в алфавите ?, : A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z.Английский алфавит (или современный английский алфавит) сегодня состоит из 26 букв: 23 из староанглийского и 3 добавленных позже.

[PDF] Таблица преобразования A = 1 B = 2 C = 3 D = 4 E = 5 F = 6 G = 7 H = 8 I, Первая часть была простой: возьмите каждую букву вашего имени и преобразуйте ее к номеру. Используйте систему, где A = 1, B = 2, Z = 26. Дж. А. Современный английский алфавит — это латинский алфавит, состоящий из 26 букв, каждая из которых имеет верхний и нижний регистр. Он возник примерно в 7 веке на латинице.С тех пор буквы были добавлены или удалены, чтобы получить текущий современный английский алфавит из 26 букв (который в конечном итоге стал основным латинским алфавитом ISO).

(Старая) 27-я буква английского алфавита, , каждая из которых имеет форму верхнего и нижнего регистра. Он возник примерно в 7 веке на латинице. Инструмент для преобразования букв в числа и наоборот. Буквенно-цифровой шифр (или буквенно-цифровой шифр) состоит в замене каждой буквы ее позицией в алфавите, например, A = 1, B = 2, Z = 26, отсюда и его общее название A1Z26.

Ошибка обработки файла SSI

Переключение букв для чисел

Преобразование букв в числа в различных форматах. Нумерация букв таким образом, чтобы A = 1, B = 2 и т. Д., Является одним из простейших способов их преобразования в числа. Это называется шифром A1Z26. Однако есть и другие варианты, такие как коды ASCII и коды касания для декодирования чисел.

Вместо преобразования клавиш курсора в числа, он преобразует часть букв QWERTY на клавиатуре в виртуальную цифровую клавиатуру.Вот пример клавиатуры, сделанной Acer для ноутбука с Windows 10. Когда вы нажимаете клавишу Num Lock (здесь выделена красным прямоугольником), 15 клавиш переключают режимы на имитацию цифровой клавиатуры.

Переключение цифр и букв при поступлении в 3 класс по-прежнему считается развитием. Если он все еще делает это в конце 3-го числа, я бы поговорил с его учителями и посмотрел, что они думают. Тем не менее, ему никогда не следует считать ответ неправильным или снимать баллы за отмену.

Ошибка обработки файла SSI

Еще статьи

Взломайте код! Создание шифра Цезаря

Ключевые концепции
Выкройки
Код
Пазлы
Криптография

Введение
Если вам нужно отправить секретное сообщение другу, как вы можете помешать другим людям его прочитать? Один из способов — зашифровать сообщение, то есть использовать секретный код, известный только вам и вашему другу.Попробуйте это упражнение, чтобы узнать, как создать свой собственный «шифр Цезаря» — популярный тип кода, который легко выучить.

Фон
Криптография — это исследование написания или решения секретных кодов, которые используются для безопасного общения. Исторически коды использовались политиками, шпионами и странами в состоянии войны, чтобы помешать своим врагам узнать, что они затевают. Многие из самых ранних кодов или «шифров», таких как тот, который вы создадите в этом проекте, было легко создать вручную.Теперь криптография необходима в информатике для обеспечения безопасности всего, от электронной почты до информации о банковских счетах.

Шифр Цезаря, названный в честь римского императора Юлия Цезаря, является одним из самых ранних и широко известных шифров. Это простая форма «шифра подстановки», где вы заменяете каждую букву алфавита другой буквой, сдвигая весь алфавит на определенное количество букв (переход к началу, когда вы достигнете конца). Например, это будет ваш ключ и код, если вы сдвинете каждую букву на три пробела:

Обычная: ABCDEFGHIJKLMNOPQRSTUVWXYZ
Шифр: XYZABCDEFGHIJKLMNOPQRSTUVW

Итак, когда вы пишете свое сообщение, буква A заменяется на X, B заменяется на Y и так далее.Например, слово «ПРИВЕТ» читается так:

Обычный: HELLO
Шифр: EBIIL

Чтобы расшифровать ваше сообщение, вам нужно поделиться «ключом» (цифрой 3) с вашим другом. После этого вы можете отправлять сообщения, написанные в зашифрованном виде, чтобы другие люди не могли их прочитать!

Материалы

Карандаш и бумага
Как минимум еще один человек

Подготовка

Расскажите другу о концепции шифра Цезаря или попросите его прочитать справочный раздел этого упражнения.
Запишите алфавит от А до Я.
Выберите число от 1 до 25. (Если вы используете 26, вы просто получите исходный алфавит.) Это число — ваш ключ.

Процедура

Сдвиньте весь алфавит на выбранное число и запишите его под исходным алфавитом (как показано выше).
Выберите сообщение, которое хотите написать другу. Возможно, проще всего будет начать с простого сообщения (например, одного слова или фразы), прежде чем пробовать более длинные предложения или абзацы.
Запишите закодированное сообщение, используя сдвинутый алфавит. Если это помогает, сначала запишите текстовое сообщение, а затем кодируйте его по одной букве за раз (например, в приведенном выше примере «привет»). Просто убедитесь, что на листе бумаги, который вы даете другу, есть только закодированное сообщение!
Дайте другу зашифрованное сообщение, а передайте ему ключ . Как вы думаете, почему вы не хотите записывать ключ?
Посмотри, сможет ли твой друг расшифровать твое сообщение.Если это поможет с первого раза, позвольте им работать в обратном направлении, используя записанный вами исходный и сдвинутый алфавиты. Используя пример из фона, буква x становится a; y становится b; и так далее.
Попробуйте переключить и использовать другой ключ для тех же сообщений. Кажется, взломать легче?
Экстра: Попробуйте найти третьего человека, который не знает, что такое шифр Цезаря. Могут ли они взломать ваш код, если они «перехватят» ваше сообщение?
Экстра: Что делать, если человек, перехватывающий ваше сообщение, знает о шифрах Цезаря? Это облегчает взлом кода? Поскольку существует только 25 возможных ключей, шифры Цезаря очень уязвимы для атаки «грубой силы», когда декодер просто пробует каждую возможную комбинацию букв.Это может потребовать некоторого терпения, если это делает человек, но в настоящее время компьютеры могут разгадывать код за доли секунды, поэтому шифры Цезаря не считаются безопасным методом шифрования электронных сообщений.
Extra: Еще один способ взломать шифр Цезаря — это «частотный анализ», основанный на том факте, что в естественной английской речи и письме одни буквы появляются гораздо чаще, чем другие. Например, буква E встречается чаще, чем любая другая, а Z — реже всего.(Если вы когда-либо играли в настольную игру Scrabble, вы могли заметить, что это определяет, сколько очков стоит букв!) Так, например, если вы прочитали весь абзац и заметили, что буква D появляется чаще, чем любая другая, шансы заключаются в том, что он использовал шифр Цезаря со сдвигом на 1 (что сделало E в коде D). Этот метод будет более точным для длинных блоков текста и очень неточным для коротких слов или фраз, потому что есть много слов, которые вообще не содержат E. Можете ли вы попросить друга написать целый абзац шифром Цезаря, а затем попытаться взломать его с помощью частотного анализа?
Экстра: Если вы планируете использовать шифр Цезаря для регулярной связи, существует риск того, что в конечном итоге кто-то обнаружит ваш ключ.Вы можете помочь предотвратить это, меняя ключ, например, используя новый каждую неделю. Это похоже на периодическую смену паролей на вашем компьютере.
Extra: Шифр Цезаря — это всего лишь один из типов шифра подстановки. Найдите другие типы подстановочных шифров и испытайте их. Их сложнее или проще использовать и взламывать?

Наблюдения и результаты
Как только вы и ваш друг поймете, как использовать шифр Цезаря, будет относительно легко отправлять зашифрованные сообщения друг другу.Это может быть интересным способом передавать секретные сообщения между друзьями. Однако, как обсуждалось выше, хотя шифр Цезаря представляет собой отличное введение в криптографию, в компьютерную эпоху он больше не является безопасным способом отправки зашифрованных сообщений в электронном виде.

Больше для изучения
Основы криптографии: шифр Цезаря, от Instructables
Криптография, от Learn Cryptography
Password Hacker, от Scientific American
Science Activities for All Ages !, from Science Buddies

Эта деятельность предоставлена вам в сотрудничестве с Science Buddies

Расшифруй слова по цифрам

Шифр Атбаша

Шифр Цезаря

Шифр Вернама (XOR-шифр)

Шифр кодового слова

Шифр Плейфера

10 популярных кодов и шифров

Стандартные шифры

ROT1

Шифр транспонирования

Азбука Морзе

Шифр Цезаря

Моноалфавитная замена

Шифр Виженера

Шифр Энигмы

Цифровые шифры

Двоичный код

Шифр A1Z26

Шифрование публичным ключом

Как расшифровать код или шифр?

5.4 Числовые шифры . Основы классической криптологии. Секреты шифров и кодов

Стойкие шифры

Шифры замены

Совершенный шифр

Немного истории и литературы

Шифры с открытым ключом

А у вас получится?

Как расшифровать секретный код. О чем расскажут тройные числа в нумерологии

Двойка «2»

Тройка «3»

Пятёрка «5»

Шестёрка «6»

Семёрка «7»

Восьмёрка «8»

Девятка «9»

Как расшифровать свою судьбу

Делаем четыре расчета

Ячейка 1- Солнце (Сила характера, волевые черты)

Ячейка 2- Луна (Количество энергии)

Ячейка 3- Марс (Интересы личности)

Ячейка 4- Меркурий (Здоровье личности)

Ячейка 5- Юпитер (Интуиция)

Ячейка 6- Венера (Физический труд)

Ячейка 7- Сатурн (Таланты личности)

Ячейка 8- Уран (Ответственность)

Ячейка 9- Нептун (Интеллект личности)

Таблица соответствия букв имени и цифр

Результаты расчета

Шаги

Расшифровка шифров замещения

Распознавание обычных шифров

Что значит быть дешифровальщиком

Рекомендуем также

Расшифровка кода IP

расшифровка букв, цифр, смешанных значений

Таблица маркировки конденсаторов

Маркировка твердотельных конденсаторов

Маркировка конденсаторов: расшифровка

Цифры: обозначение

Буквы: их обозначение

Керамические конденсаторы: маркировка

Смешанная маркировка из цифр и букв

Остальные маркировки

Арифметика часов 5

Секретные кольца декодера

Найдите секретное сообщение, используя изображение кольца декодера выше, для которого задана правильная секретная установка.

Используйте указанные секретные номера для записи секретных сообщений, которые соответствуют этим открытым текстам.

Используйте указанные секретные номера, чтобы узнать, что говорят эти секретные сообщения.

Секретный язык: криптография и секретные коды

Замещающие шифры и кольца декодера

Шифр ​​подстановки колес

Шифры транспонирования

Частоты

Библиография:

Интернет-ресурсы

Шифрование Vigenere

CS101 — Кодировка текста

Учебное пособие по двоичным числам с 1 и 0 |

[Не очень] секретная формула

Как создавать двоичные числа

Шифр подстановки колес