Формула относительного показателя преломления общий случай. Понятие показателя преломления
Закон преломления света был установлен опытным путем в XVII веке. При переходе света из одной прозрачной среды в другую направление света может меняться. Изменение направления света на границе разных сред называется преломлением света. Вседствие преломления происходит кажущееся изменение формы предмета. (пример: ложка в стакане с водой). Закон преломления света: На границе 2ух сред преломленный луч лежит в плоскости падения и образует с нормальню к границе раздела,восстановленной в точке падения, угол приломления, такой, что: =n 1-падения, 2 отражения,n-показатель преломления (ф. Снелиуса) — относительный показатель Показатель преломления луча, падающего на среду из безвоздушного пространства, называется его абсолютным показателем преломления. Угол падения, при котором преломленный луч начинает скользить по границе раздела двух сред без перехода в оптически более плотную среду – предельный угол полного внутреннего отражения.
ПРЕЛОМЛЕНИЯ ПОКАЗАТЕЛЬ (преломления коэффициент)
— оптич. характеристика среды, связанная с преломлением света на границе
раздела двух прозрачных оптически однородных и изотропных сред при переходе
его из одной среды в другую и обусловленная различием фазовых скоростей распространения
света
и в средах.
Величина П. п., равная отношению этих скоростейназ.
относительным
П. п. этих сред. Если свет падает на вторую пли
первую среду из (где скорость распространения света с) , то величинынназ.
абсолютными П. п. данных сред. При этом
а закон преломления может быть записан в виде
где и-
углы падения и преломления.
Величина абсолютного П. п. зависит от природы и строения вещества, его агрегатного состояния, темп-ры, давления и др. При больших интенсивностях П. п. зависит от интенсивности света (см.
Поккельса эффект — в кристаллах).Для данной среды П. п. зависит от длины волны
света l, причём в области полос поглощения эта зависимость носит аномальный
характер (см. Дисперсия света ).В рентг. области П. п. практически для
всех сред близок к 1, в видимой области для жидкостей и твёрдых тел — порядка
1,5; в ИК-области для ряда прозрачных сред
4,0 (для Ge).
Характеризуются двумя П. п.: обыкновенным (аналогично изотропным средам) и — необыкновенным, величина к-рого зависит от угла падения луча и, следовательно, направления распространения света в среде (см. Кристаллооптика ).Для сред, обладающих поглощением (в частности, для металлов), П. п. является комплексной величиной и может быть представлен в виде где га — обычный П. п., — показатель поглощения (см.
Поглощение света, Металлооптика) .П. п. является макроскопич. характеристикой среды
и связан с её диэлектрической проницаемостью н
магн. проницаемостью
Классич.
электронная теория (см. Дисперсия
света )позволяет связать величину П. п. с микроскопич. характеристиками
среды — электронной поляризуемостью атома (или молекулы)
зависящей от природы атомов и частоты света, и среды:
где N — число атомов в единице объёма.
Действующее на атом (молекулу) электрич. полесветовой
волны вызывает смещение оптич. электрона из положения равновесия; атом приобретает
индуциров. дипольный момент
изменяющийся во времени с частотой падающего света, и является источником вторичных
когерентных волн, к-рые. интерферируя с падающей на среду волной, образуют результирующую
световую волну, распространяющуюся в среде с фазовой скоростьюи
потому
Интенсивность обычных (не лазерных) источников
света относительно невелика, напряжённость электрич. полясветовой
волны, действующего на атом, много меньше внутриатомных электрич. полей, и электрон
в атоме можно рассматривать как гармонич. осциллятор.
В этом приближении величина
и П. п.
Являются величинами постоянными (на данной частоте), не зависящими от интенсивности
света. В интенсивных световых потоках, создаваемых мощными лазерами, величина
электрич. поля световой волны может быть соизмерима с внутриатомными элект-рич.
полями и модель гармония, осциллятора оказывается неприемлемой. Учёт ангармоничности
сил в системе электрон — атом приводит к зависимости поляризуемости атомаа
следовательно и П. п., от интенсивности света. Связь межу иоказывается
нелинейной; П. п. может быть представлен в виде
Где — П. п.
при малых интенсивностях света;
(обычно принятое обозначение) — нелинейная добавка к П. п., или коэф. нелинейности.
П. п. зависит
от природы среды, напр. для силикатных стёкол
На П. п. влияет высокая интенсивность ещё и в результате эффекта электрострикции , изменяющего плотность среды, высокочастотного для анизотропных молекул (в жидкости), а также в результате повышения темп-ры, вызванного поглощением
Законы физики играют очень важную роль при проведении расчетов для планирования определенной стратегии производства какого-либо товара или при составлении проекта строительства сооружений различного назначения.
Многие величины являются расчетными, так что перед стартом работ по планированию производятся измерения и вычисления. Например, показатель преломления стекла равен отношению синуса угла падения к синусу угла преломления.
Так что вначале идет процесс измерения углов, затем вычисляют их синус, а уже только потом можно получить искомое значение. Несмотря на наличие табличных данных, стоит каждый раз проводить дополнительные расчеты, так как в справочниках зачастую используются идеальные условия, которых добиться в реальной жизни практически невозможно. Поэтому на деле показатель обязательно будет отличаться от табличного, а в некоторых ситуациях это имеет принципиальное значение.
Абсолютный показатель
Абсолютный показатель преломления зависит от марки стекла, так как на практике имеется огромное количество вариантов, отличающихся по составу и степени прозрачности. В среднем он составляет 1,5 и колеблется вокруг этого значения на 0,2 в ту или иную сторону. В редких случаях могут быть отклонения от этой цифры.
Опять-таки, если важен точный показатель, то без дополнительных измерений не обойтись. Но и они не дают стопроцентно достоверного результата, так как на итоговое значение будет влиять положение солнца на небосводе и облачность в день измерений. К счастью, в 99,99% случае достаточно просто знать, что показатель преломления такого материала, как стекло больше единицы и меньше двойки, а все остальные десятые и сотые доли не играют роли.
На форумах, которые занимаются помощью в решении задач по физике, часто мелькает вопрос, каков показатель преломления стекла и алмаза? Многие думают, что раз эти два вещества похожи внешне, то и свойства у них должны быть примерно одинаковыми. Но это заблуждение.
Максимальное преломление у стекла будет находиться на уровне около 1,7, в то время как у алмаза этот показатель достигает отметки 2,42. Данный драгоценный камень является одним из немногих материалов на Земле, чей уровень преломления превышает отметку 2. Это связано с его кристаллическим строением и большим уровнем разброса световых лучей.
Огранка играет в изменениях табличного значения минимальную роль.
Относительный показатель
Относительный показатель для некоторых сред можно охарактеризовать так:
- — показатель преломления стекла относительно воды составляет примерно 1,18;
- — показатель преломления этго же материала относительно воздуха равен значению 1,5;
- — показатель преломления относительно спирта — 1,1.
Измерения показателя и вычисления относительного значения проводятся по известному алгоритму. Чтобы найти относительный параметр, нужно разделить одно табличное значение на другое. Или же произвести опытные расчеты для двух сред, а потом уже делить полученные данные. Такие операции часто проводятся на лабораторных занятиях по физике.
Определение показателя преломления
Определить показатель преломления стекла на практике довольно сложно, потому что требуются высокоточные приборы для измерения начальных данных. Любая погрешность будет возрастать, так как при вычислении используются сложные формулы, требующие отсутствия ошибок.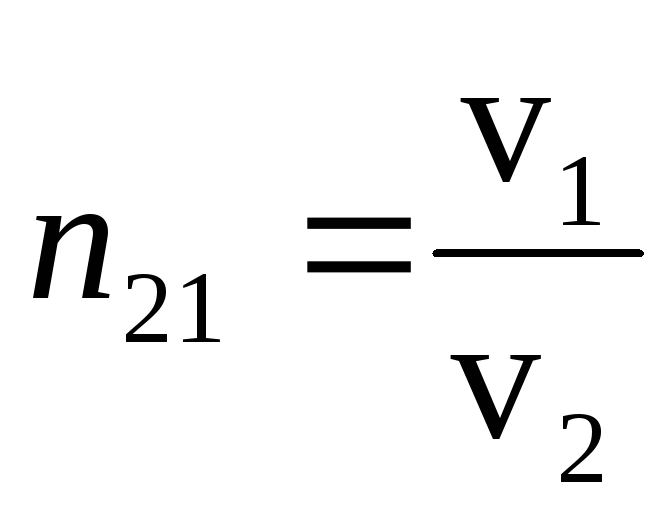
Вообще данный коэффициент показывает, во сколько раз замедляется скорость распространения световых лучей при прохождении через определенное препятствие. Поэтому он характерен только для прозрачных материалов. За эталонное значение, то бишь за единицу, взят показатель преломления газов. Это было сделано для того, чтобы можно было отталкиваться от какого-нибудь значения при расчетах.
Если солнечный луч падает на поверхность стекла с показателем преломления, который равен табличному значению, то изменить его можно несколькими способами:
- 1. Поклеить сверху пленку, у которой коэффициент преломления будет выше, чем у стекла. Этот принцип используется в тонировке окон автомобиля, чтобы улучшить комфорт пассажиров и позволить водителю более четко наблюдать за дорожной обстановкой. Также пленка будет сдерживать и ультрафиолетовое излучение.
- 2. Покрасить стекло краской. Так поступают производители дешевых солнцезащитных очков, но стоит учесть, что это может быть вредно для зрения.
В хороших моделях стекла сразу производятся цветными по специальной технологии. - 3. Погрузить стекло в какую-либо жидкость. Это полезно исключительно для опытов.
В хороших моделях стекла сразу производятся цветными по специальной технологии.Если луч света переходит из стекла, то показатель преломления на следующем материале рассчитывается при помощи использования относительного коэффициента, который можно получить, сопоставив между собой табличные значения. Эти вычисления очень важны при проектировке оптических систем, которые несут практическую или экспериментальную нагрузку. Ошибки здесь недопустимы, потому что они приведут к неправильной работе всего прибора, и тогда любые полученные с его помощью данные будут бесполезны.
Чтобы определить скорость света в стекле с показателем преломления, нужно абсолютное значение скорости в вакууме разделить на величину преломления. Вакуум используется в качестве эталонной среды, потому что там не действует преломление из-за отсутствия каких-либо веществ, которые могли бы мешать беспрепятственному движению световых лучей по заданной траектории.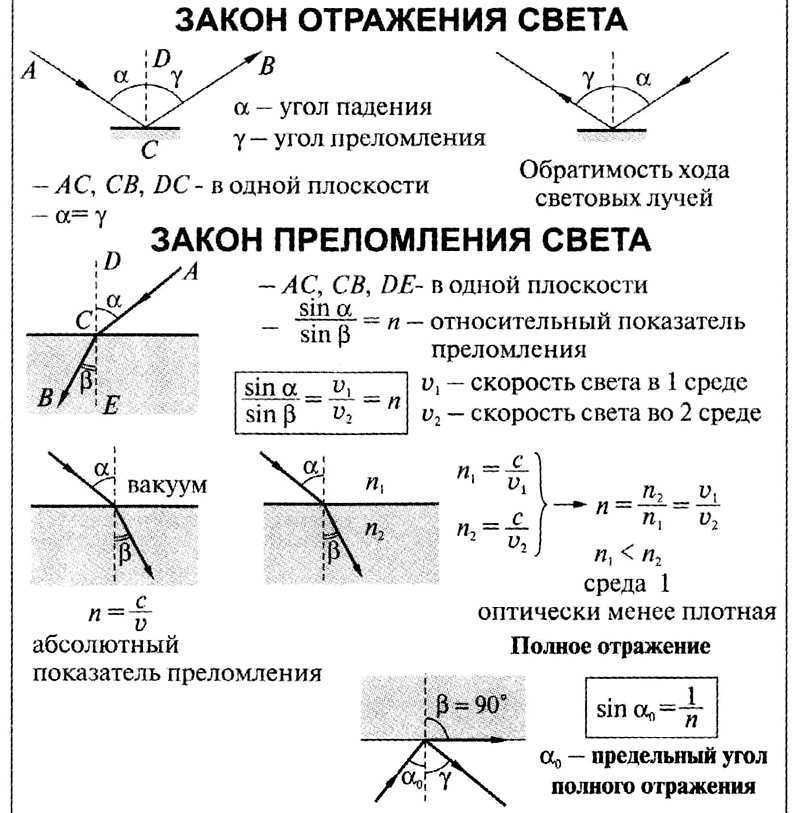
В любых расчетных показателях скорость будет меньше, чем в эталонной среде, так как коэффициент преломления всегда больше единицы.
Преломление света — явление, при котором луч света, переходя из одной среды в другую, изменяет направление на границе этих сред.
Преломление света происходит по следующему закону:
Падающий и преломленный лучи и перпендикуляр, проведенный к границе раздела двух сред в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред:
,
где α — угол падения,
β — угол преломления,
n — постоянная величина, не зависящая от угла падения.
При изменении угла падения изменяется и угол преломления. Чем больше угол падения, тем больше угол преломления.
Если свет идет из среды оптически менее плотной в более плотную среду, то угол преломления всегда меньше угла падения: β
Луч света, направленный перпендикулярно к границе раздела двух сред, проходит из одной среды в другую без преломления.
абсолютный показатель преломления вещества — величина, равная отношению фазовых скоростей света (электромагнитных волн) в вакууме и в данной среде n=c/v
Величина n, входящая в закон преломления, называется относительным показателем преломления для пары сред.
Величина n есть относительный показатель преломления среды В по отношению к среде А, а n» = 1/n есть относительный показатель преломления среды А по отношению к среде В.
Эта величина при прочих равных условиях больше единицы при переходе луча из среды более плотной в среду менее плотную, и меньше единицы при переходе луча из среды менее плотной в среду более плотную (например, из газа или из вакуума в жидкость или твердое тело). Есть исключения из этого правила, и потому принято называть среду оптически более или менее плотной, чем другая.
Луч, падающий из безвоздушного пространства на поверхность какой-нибудь среды В, преломляется сильнее, чем при падении на нее из другой среды А; показатель преломления луча, падающего на среду из безвоздушного пространства, называется его абсолютным показателем преломления.
(Абсолютный — относительно вакуума.
Относительный — относительно любого другого вещества (того же воздуха, например).
Относительный показатель двух веществ есть отношение их абсолютных показателей.)
Полное внутреннее отражение — внутреннее отражение, при условии, что угол падения превосходит некоторый критический угол. При этом падающая волна отражается полностью, и значение коэффициента отражения превосходит его самые большие значения для полированных поверхностей. Коэффициент отражения при полном внутреннем отражении не зависит от длины волны.
В оптике это явление наблюдается для широкого спектра электромагнитного излучения, включая рентгеновский диапазон.
В геометрической оптике явление объясняется в рамках закона Снелла. Учитывая, что угол преломления не может превышать 90°, получаем, что при угле падения, синус которого больше отношения меньшего показателя преломления к большему показателю, электромагнитная волна должна полностью отражаться в первую среду.
В соответствии с волновой теорией явления, электромагнитная волна всё же проникает во вторую среду — там распространяется так называемая «неоднородная волна», которая экспоненциально затухает и энергию с собой не уносит. Характерная глубина проникновения неоднородной волны во вторую среду порядка длины волны.
Законы преломления света.
Из всего сказанного заключаем:
1 . На границе раздела двух сред различной оптической плотности луч света при переходе из одной среды в другую меняет своё направление.
2. При переходе луча света в среду с большей оптической плотностью угол преломления меньше угла падения; при переходе луча света из оптически более плотной среды в среду менее плотную угол преломления больше угла падения.
Преломление света сопровождается отражением, причём с увеличением угла падения яркость отражённого пучка возрастает, а преломлённого ослабевает. Это можно увидеть проводя опыт, изображённом на рисунке. Следовательно, отражённый пучок уносит с собой тем больше световой энергии, чем больше угол падения.
Пусть MN -граница раздела двух про зрачных сред, например, воздуха и воды, АО -падающий луч, ОВ — преломленный луч, -угол падения, -угол преломления, -скорость распространения света в первой среде, — скорость распространения света во второй среде.
Преломление или рефракция — это явление, при котором происходит изменение направленности луча света, или иных волн, когда они переходят границу, разделяющую две среды, как прозрачные (пропускающие эти волны), так и внутри среды, в которой непрерывно изменяются свойства.
С явлением преломления мы сталкиваемся довольно часто и воспринимаем обыденным явлением: можем увидеть, что палочка, находящаяся в прозрачном стакане с окрашенной жидкостью, «переломлена» в месте раздела воздуха и воды (рис. 1). При преломлении и отражении света во время дождя мы радуемся, увидев радугу (рис. 2).
Показатель преломления — важная характеристика вещества, связанная с его физико-химическими свойствами. Он находится в зависимости от значений температур, а также от длины световых волн, при которых проводится определение.
По данным контроля качества в растворе на показатель преломления влияет концентрация растворенного в нем вещества, а также природа растворителя. В частности, на показатель преломления кровяной сыворотки влияет количество белка, содержащегося в ней.Это происходит из-за того, что при разной скорости распространения световых лучей в средах, имеющих различную плотность, их направление изменяется в месте раздела двух сред. Если мы разделим световую скорость в вакууме на световую скорость в исследуемом веществе, получится показатель преломления абсолютный (индекс рефракции). Практически определяется показатель преломления относительный (n
), представляющий собой отношение световой скорости в воздухе к световой скорости в исследуемом веществе.
Количественно показатель преломления определяют, используя специальный прибор — рефрактометр.
Рефрактометрия — один из наиболее легких методов физического анализа и может применяться в лабораториях контроля качества при производстве химической, пищевой, биологически активных добавок к пище , косметической и других видов продукции с минимальными затратами времени и количества исследуемых проб.
Конструкция рефрактометра основана на том, что лучи света полностью отражаются, когда переходят через границу двух сред (одна из них – это призма из стекла, другая – исследуемый раствор) (рис. 3).
| Рис. 3. Схема рефрактометра |
От источника (1) световой луч падает на зеркальную поверхность (2), затем, отражаясь, переходит в верхнюю призму осветительную (3), потом в нижнюю призму измерительную (4), которая изготовлена из стекла, обладающего большим показателем преломления. Между призмами (3) и (4) с помощью капилляра наносят 1–2 капельки пробы. Чтобы не нанести призме механических повреждений, необходимо не касаться капилляром ее поверхности.
В окуляр (9) видят поле с перекрещенными линиями, чтобы установить границу раздела. Перемещая окуляр, точку пересечения полей нужно совместить с границей раздела (рис. 4).Плоскость призмы (4) играет роль границы раздела, на поверхности которой преломляется световой луч.
Так как лучи рассеиваются, граница света и тени получается расплывчатой, радужной. Это явление устраняется компенсатором дисперсии (5). Затем луч пропускается объективом (6) и призмой (7). На пластине (8) имеются штрихи визирные (две прямые линии, пересеченные крестообразно), а также шкала с показателями преломления, которая наблюдается в окуляр (9). По ней и отсчитывается показатель преломления.
Линия раздела границ полей будет соответствовать углу внутреннего полного отражения, зависящего от показателя преломления пробы.
Рефрактометрия применяется с целью установления чистоты и подлинности вещества. Этот метод применяется также, чтобы при контроле качества определить концентрацию веществ в растворах, которую вычисляют по градуировочному графику (график, показывающий зависимость показателя преломления пробы от ее концентрации).
В компании «КоролёвФарм» показатель преломления определяется согласно утвержденной нормативной документации при входном контроле сырья , в экстрактах собственного производства , а также при выпуске готовой продукции.
Определение производится квалифицированными сотрудниками аккредитованной физико-химической лаборатории с помощью рефрактометра ИРФ – 454 Б2М.
Если по результатам входного контроля сырья показатель преломления не соответствует необходимым требованиям, отделом контроля качества оформляется Акт о несоответствии, на основании которого данная партия сырья возвращается поставщику.
Методика определения
1. Перед началом измерений проверяется чистота поверхностей призм, соприкасающихся между собой.
2. Проверка точки нуля. На поверхность призмы измерительной наносим 2÷3 капли воды дистиллированной, осторожно закрываем призмой осветительной. Открываем осветительное окошко и, применяя зеркало, устанавливаем световой источник в наиболее интенсивном направлении. Вращая винты окуляра, получаем в его поле зрения четкое, резкое разграничение темного и светлого полей. Вращаем винт и наводим линию тени и света так, чтобы она совпала с точкой, в которой пересекаются линии в верхнем окошке окуляра.
На вертикальной линии в нижнем окошке окуляра видим нужный результат – показатель преломления воды дистиллированной при 20 ° С (1,333). Если показания другие, устанавливаем винтом показатель преломления на значение 1,333, и с помощью ключа (снять винт регулировочный) приводим границу тени и света к месту точки пересечения линий.
3. Определяем коэффициент преломления. Приподнимаем камеру призмы осветительной и бумагой фильтровальной или салфеткой марлевой снимаем воду. Далее наносим 1-2 капли испытуемого раствора на поверхность призмы измерительной и закрываем камеру. Вращаем винты до момента, пока границы тени и света не совпадут с точкой пересечения линий. На вертикальной линии в нижнем окошке окуляра видим нужный результат – показатель преломления исследуемой пробы. Производим подсчет коэффициента преломления по шкале в нижнем окошке окуляра.
4. Используя градуировочный график, устанавливаем взаимосвязь между концентрацией раствора и показателем преломления.
Чтобы построить график необходимо приготовить стандартные растворы нескольких концентраций, используя препараты химически чистых веществ, измерить их показатели преломления и отложить полученные значения на оси ординат, на оси абсцисс отложить соответствующие концентрации растворов. Необходимо выбирать интервалы концентраций, при которых между концентрацией и показателем преломления наблюдается зависимость линейная. Измеряем показатель преломления исследуемой пробы и с помощью графика определяем его концентрацию.
Оптика и волны
|
Дисперсия света — это зависимость показателя преломления n вещества от длины волны света (в вакууме)
|
12)или, что то же самое, зависимость фазовой скорости световых волн от частоты:
|
|
(6.13) |
|
Дисперсией вещества называется производная от n по
|
14)Дисперсия — зависимость показателя преломления вещества от частоты волны – особенно ярко и красиво проявляет себя совместно с эффектом двойного лучепреломления (см. Видео 6.6 в предыдущем параграфе), наблюдаемом при прохождении света через анизотропные вещества. Дело в том, что показатели преломления обыкновенной и необыкновенной волн различно зависят от частоты волны. В результате цвет (частота) света прошедшего через анизотропное вещество помещенное между двумя поляризаторами зависит как от толщины слоя этого вещества, так и от угла между плоскостями пропускания поляризаторов.
Видео 6.8 Дисперсия и анизотропия: пластинки слюды между поляризаторами.
Видео 6.9 Дисперсия и анизотропия: полимерная пленка между поляризаторами.
Видео 6.10 Дисперсия и анизотропия: болванка CD-диска.
Видео 6.11 Дисперсия и анизотропия: нагруженная «балка».
Видео 6.12 Дисперсия и анизотропия: мятая целлофановая обертка.
Видео 6.13 Дисперсия и анизотропия: слюдяная бабочка и…
Для всех прозрачных бесцветных веществ в видимой части спектра с уменьшением длины волны показатель преломления увеличивается, то есть дисперсия вещества отрицательна: . (рис. 6.7, области 1-2, 3-4)
|
Нормальная дисперсия вещества — это отрицательная дисперсия |
Если вещество поглощает свет в каком-то диапазоне длин волн (частот), то в области поглощения дисперсия
оказывается положительной и называется аномальной (рис.
6.7, область 2–3).
Рис. 6.7. Зависимость квадрата показателя преломления (сплошная кривая) и коэффициента поглощения света веществом
(штриховая кривая) от длины волны l вблизи одной из полос поглощения ()
Изучением нормальной дисперсии занимался ещё Ньютон. Разложение белого света в спектр при прохождении сквозь призму является следствием дисперсии света. При прохождении пучка белого света через стеклянную призму на экране возникает разноцветный спектр (рис. 6.8).
Рис. 6.8. Прохождение белого света через призму: вследствие различия значений показателя преломления стекла для разных
длин волн пучок разлагается на монохроматические составляющие — на экране возникает спектр
Наибольшую длину волны и наименьший показатель преломления имеет красный свет, поэтому красные лучи отклоняются призмой меньше других.
Рядом с ними будут лучи оранжевого, потом желтого, зеленого, голубого, синего и, наконец, фиолетового света. Произошло разложение падающего на призму сложного белого света на монохроматические составляющие (спектр).
Ярким примером дисперсии является радуга. Радуга наблюдается, если солнце находится за спиной наблюдателя. Красные и фиолетовые лучи преломляются сферическими капельками воды и отражаются от их внутренней поверхности. Красные лучи преломляются меньше и попадают в глаз наблюдателя от капелек, находящихся на большей высоте. Поэтому верхняя полоса радуги всегда оказывается красной (рис. 26.8).
Рис. 6.9. Возникновение радуги
Используя законы отражения и преломления света, можно рассчитать ход световых лучей при полном отражении и дисперсии в дождевых каплях. Оказывается, что лучи рассеиваются с наибольшей интенсивностью в направлении, образующем угол около 42° с направлением солнечных лучей (рис. 6.10).
Рис.
6.10. Расположение радуги
Геометрическое место таких точек представляет собой окружность с центром в точке 0. Часть ее скрыта от наблюдателя Р под горизонтом, дуга над горизонтом и есть видимая радуга. Возможно также двойное отражение лучей в дождевых каплях, приводящее к радуге второго порядка, яркость которой, естественно, меньше яркости основной радуги. Для нее теория дает угол 51°, то есть радуга второго порядка лежит вне основной. В ней порядок цветов заменен на обратный: внешняя дуга окрашена в фиолетовый цвет, а нижняя — в красный. Радуги третьего и высших порядков наблюдаются редко.
Элементарная теория дисперсии. Зависимость показателя преломления вещества от длины электромагнитной волны (частоты) объясняется на основе теории вынужденных колебаний. Строго говоря, движение электронов в атоме (молекуле) подчиняется законам квантовой механики. Однако для качественного понимания оптических явлений можно ограничиться представлением об электронах, связанных в атоме (молекуле) упругой силой.
При отклонении от равновесного положения такие электроны начинают колебаться, постепенно теряя энергию на излучение электромагнитных волн или передавая свою энергию узлам решетки и нагревая вещество. В результате этого колебания будут затухающими.
При прохождении через вещество электромагнитная волна воздействует на каждый электрон с силой Лоренца:
|
|
(6.15) |
где v — скорость колеблющегося электрона. В электромагнитной волне отношение напряженностей магнитного и электрического полей равно
|
|
(6. |
16)Поэтому нетрудно оценить отношение электрической и магнитной сил, действующих на электрон:
|
|
(6.17) |
Электроны в веществе движутся со скоростями, много меньшими скорости света в вакууме:
Таким образом, можно считать, что при прохождении через вещество электромагнитной волны на каждый электрон действует только электрическая сила:
|
|
(6.18) |
где — амплитуда напряженности электрического поля в световой волне, — фаза волны, определяемая положением рассматриваемого электрона.
Для упрощения вычислений пренебрежем затуханием и запишем уравнение движения электрона в виде
|
|
(6.19) |
где, — собственная частота колебаний электрона в атоме. Решение такого дифференциального неоднородного уравнения мы уже рассматривали ранее и получили
|
|
(6.20) |
Следовательно, смещение электрона из положения равновесия пропорционально напряженности электрического поля.
Смещениями ядер из положения равновесия можно пренебречь, так как массы ядер весьма велики по сравнению с массой электрона.
Атом со смещенным электроном приобретает дипольный момент
(для простоты положим пока, что в атоме имеется только один «оптический» электрон, смещение которого вносит определяющий вклад в поляризацию). Если в единице объема содержится N атомов, то поляризованность среды (дипольный момент единицы объема) можно записать в виде
|
|
(6.21) |
В реальных средах возможны разные типы колебаний зарядов (групп электронов или ионов), вносящих вклад в поляризацию. Эти типы колебаний могут иметь разные величины заряда еiи массы тi, а также различные собственные частоты (мы будем обозначать их индексом k), при этом число атомов в единице объема с данным типом колебаний Nkпропорционально концентрации атомов N:
Безразмерный коэффициент пропорциональности fkхарактеризует эффективный вклад каждого типа колебаний в общую величину поляризации среды:
|
|
(6. |
22)С другой стороны, как известно,
|
|
(6.23) |
где — диэлектрическая восприимчивость вещества, которая связана с диэлектрической проницаемостью e соотношением
В результате получаем выражение для квадрата показателя преломления вещества:
|
|
(6.24) |
Вблизи каждой из собственных частот функция , определяемая формулой (6.
24), терпит разрыв. Такое поведение показателя преломления обусловлено тем, что мы пренебрегли затуханием. Аналогично, как мы видели ранее, пренебрежение затуханием приводит к бесконечному росту амплитуды вынужденных колебаний при резонансе. Учет затухания избавляет нас от бесконечностей, и функция имеет вид, изображенный на рис. 6.11.
Рис. 6.11. Зависимость диэлектрической проницаемости среды от частоты электромагнитной волны
Учитывая связь частоты с длиной электромагнитной волны в вакууме
или
можно получить зависимость показателя преломления вещества п от длины волны в области нормальной дисперсии (участки 1–2 и 3–4 на рис. 6.7):
|
|
(6. |
25)где
— длины волн, соответствующие собственным частотам колебаний , — постоянные коэффициенты.
В области аномальной дисперсии () частота внешнего электромагнитного поля близка к одной из собственных частот колебаний молекулярных диполей, то есть возникает резонанс. Именно в этих областях (например, участок 2–3 на рис. 6.7) наблюдается существенное поглощение электромагнитных волн; коэффициент поглощения света веществом показан штриховой линией на рис. 6.7.
Понятие о групповой скорости. С явлением дисперсии тесно связано понятие о групповой скорости. При распространении в среде с дисперсией реальных электромагнитных импульсов, например известных нам цугов волн, испускаемых отдельными атомными излучателями, происходит их «расплывание» — расширение протяженности в пространстве и длительности во времени. Это связано с тем, что такие импульсы представляют собой не монохроматическую синусоидальную волну, а так называемый волновой пакет, или группу волн — совокупность гармонических составляющих с разными частотами и с разными амплитудами, каждая из которых распространяется в среде со своей фазовой скоростью (6.
13).
Если бы волновой пакет распространялся в вакууме, то его форма и пространственно-временная протяженность оставались бы неизменными, а скоростью распространения такого цуга волн была бы фазовая скорость света в вакууме
Из-за наличия дисперсии зависимость частоты электромагнитной волны от волнового числа k становится нелинейной, и скорость распространения цуга волн в среде, то есть скорость переноса энергии, определяется производной
где — волновое число для «центральной» волны в цуге (обладающей наибольшей амплитудой).
Мы не будем выводить эту формулу в общем виде, но на частном примере поясним ее физический смысл. В качестве модели волнового пакета примем сигнал, состоящий из двух плоских волн, распространяющихся в одном направлении с одинаковыми амплитудами и начальными фазами , но различающихся частотами, сдвинутыми относительно «центральной» частоты на небольшую величину . Соответствующие волновые числа сдвинуты относительно «центрального» волнового числа на небольшую величину .
Эти волны описываются выражениями:
|
|
(6.26) |
Для результирующей волны
после применения тригонометрической формулы для суммы двух косинусов получим выражение:
|
|
(6.27) |
Мы убеждаемся, что результирующую волну можно представить как плоскую волну с «центральными» частотой и волновым числом , амплитуда которой A(t) есть медленно меняющаяся (в силу малости сдвигов и ) функция времени и координаты.
Похожий результат ранее был получен при изучении биений. Видно, что сама эта переменная амплитуда есть плоская волна, распространяющаяся со скоростью
В пределе бесконечно малых сдвигов частоты приходим к обсуждаемой формуле
|
|
(6.28) |
Эта скорость называется групповой скоростью. Поскольку, как мы уже знаем, энергия колебаний определяется их амплитудой, «перемещение» последней и означает, что групповая скорость является скоростью переноса энергии волновым пакетом.
Фазовая же скорость волны есть отношение частоты к волновому числу:
|
|
(6. |
29)Дифференцируя это соотношение по k, находим связь фазовой и групповой скоростей:
|
|
(6.30) |
Учитывая связь волнового числа с длиной волны
формулу (6.30) можно переписать в виде
|
|
(6.31) |
Очевидно, что в отсутствие дисперсии
и групповая скорость не отличается от фазовой.
Групповая скорость как скорость распространения энергии в среде не может быть больше скорости света в вакууме, то есть всегда , в то время как фазовая скорость света в среде не является предельной и может оказаться меньше скорости движения частиц в среде, например электронов. В этом случае, как мы уже знаем, возникает излучение Черенкова — Вавилова.
Расплывание волновых пакетов при их распространении в среде с дисперсией можно понять, если представить себе компактную группу из достаточно большого числа марафонцев, одновременно берущих старт, которая при приближении к финишу из-за разной скорости участников превратится в расплывшуюся в пространстве совокупность спортсменов, время прихода на финиш которых будет характеризовать временное расплывание этого аналога цуга волн. Таким образом, при перемещении в среде волнового пакета в целом с групповой скоростью происходит перемещение отдельных его волновых составляющих внутри пакета — ведь разные «участники» процесса движутся с разной «фазовой» скоростью.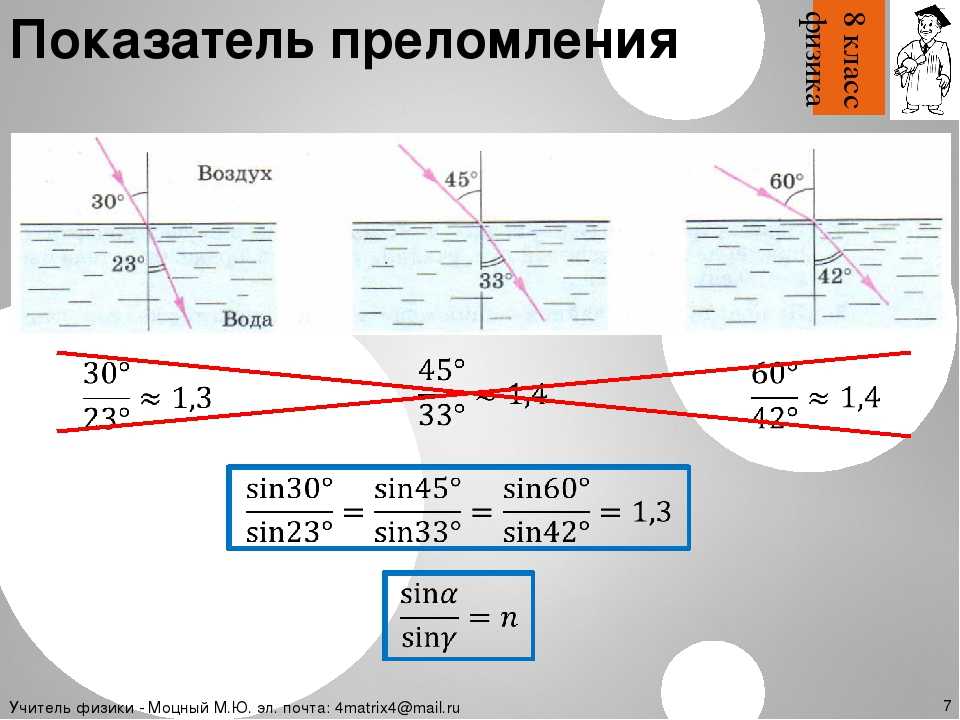
Показатель преломления – формула и пример
Ключевые понятия- Причина отклонения света.
- Абсолютный показатель преломления
- Углы падения, преломления и выхода.
Известно, что луч света искривляется при переходе из одной среды в другую. Однако причина этого изгиба и мера этого изгиба будут обсуждаться в этом разделе.
Объяснение:Причина преломления света:
- Когда свет, путешествуя по воздуху, попадает в стеклянную пластину, она изгибается. Это потому, что когда свет переходит из одной среды в другую, он преломляется.
- Когда свет попадает в стеклянную среду из воздуха, ему становится трудно проходить через нее, так как стекло плотнее воздуха. Следовательно, скорость света уменьшает в стекле.
- Скорость света в воздухе или вакууме 3 × 10 8 м/с , что сокращается примерно до
- Таким образом, свет проходит более короткий путь через стеклянную пластину, слегка изгибаясь по направлению к нормали.
- Таким образом, свет проходит через стеклянную пластину в то же время , что и в отсутствие стеклянной пластины.
- Точно так же, когда свет покидает стеклянную среду и попадает в воздух, ему становится легче проходить через нее, поскольку воздух реже, чем стекло. Следовательно, скорость света снова увеличивает до исходного значения,
- Следовательно, свет отклоняет от нормали , так как он снова достиг той же скорости.
- Таким образом, луч света смещается вбок на при преломлении через стеклянную пластинку.
Показатель преломления:
- Показатель преломления – это мера величины изгиба или изменения скорости света, когда он попадает в среду из воздуха.
- Обычно обозначается буквой n .
- Абсолютный показатель преломления среды представляет собой отношение скорости света в вакууме или воздухе и в среде.
То есть n = c/v
- Где c (= 3 × 10 8 м/с ) — скорость света в вакууме или воздухе, а v — его скорость в среде.
- Показатель преломления воздуха равен
n воздуха = c/c = 1, что является минимальным значением из всех.
- Так как здесь первая и вторая среда, обе являются воздухом, скорость остается c = (= 3 × 10 8 м/с).
- Показатель преломления любой другой среды больше 1 , так как скорость v в этой среде всегда меньше c . В результате n >= 1 .
- Показатель преломления среды безразмерный .
- Абсолютный показатель преломления стекла IS,
- , который IS, N Стекло = C/V = 3 x 108 м/с/2 x 108 м/с = 1,5
Так как здесь первая и вторая среда, обе являются воздухом, скорость остается c = (= 3 × 10 8 м/с).
- Абсолютный показатель преломления воды можно рассчитать аналогично выходу 1,33 .
n water = 1.33
- Therefore, n glass > n water
- This means that 9Стекло 0003 преломляет световой луч сильнее, чем вода .
Углы падения, преломления и выхода:
Угол падения не равен углу преломления, так как преломленный луч либо отклоняется к нормали, либо отклоняется от нее, меняя свой наклон с линией нормали. Следовательно,
∠ i ≠ ∠r
Нормальное падение:
Однако в нормальном падении падающий луч идет по нормали или параллельно нормали , как показано. Здесь световой луч проходит через вторую среду совсем не преломляясь.
Следовательно, в данном случае ∠ i = ∠r = 0 градусов.
Во всех остальных случаях вышеприведенное соотношение , а не выполняется.
Падающий луч всегда параллелен выходящему лучу в случае преломления через стеклянную пластину.
Следовательно, ∠ i = ∠e.
Резюме:1. Скорость света в вакууме или воздухе составляет 3 x 108 м/с.
2. Свет отклоняется к нормали при входе в более плотную среду, чтобы преодолеть более короткий путь за то же время, так как его скорость в этой среде уменьшается.
3. Скорость света увеличивается до 3 x 108 м/с, когда он выходит из более плотной среды обратно в воздух. Таким образом, он отклоняется от нормального.
4. Пучок света претерпевает латеральное смещение при прохождении через стеклянную пластинку после преломления.
5. Показатель преломления является мерой степени изгиба или изменения скорости света, когда он входит в среду из воздуха.
6. Абсолютный показатель преломления среды – это отношение скорости света в вакууме или воздухе и в среде. То есть n=$, где c — скорость света в воздухе, а скорость посещения — в среде.
7. Показатель преломления воздуха или вакуума равен 1, что является минимальным значением из всех.
8. Угол падения не равен углу преломления, за исключением нормального падения.
9. Угол падения всегда равен углу выхода.
5 things to know about refractive index
Introduction
1 Introduction
2 Refractive Index Review
3 Wavelength Dependence
4 Maxwell’s Equations
5 Negative Refractive Index
The refractive index is one of the basic concepts in оптические науки. Так же, как объем и плотность, показатель преломления является фундаментальным свойством всех материалов. Однако не только материалы, которые используются в оптике, имеют показатель преломления. Например, показатель преломления воды составляет 1,33, а показатель преломления воздуха составляет около 1,0.
В сегодняшней статье мы немного подробнее поговорим о показателе преломления. Эта статья немного тяжеловата по математике, но если вы хотите прочитать короткую версию, мы подготовили небольшое резюме прямо здесь:
Пять основных вещей, которые нужно знать о показателе преломления
Показатель преломления положительный. безразмерное число больше 1,0
Это может помочь вам рассчитать скорость света, когда он движется внутри материала
Показатель преломления материала изменяется в зависимости от температуры
Материал будет иметь разные значения показателя преломления для разных цветов.
Ученым удалось создать материалы с отрицательным показателем преломления.
Обзор показателя преломления
Основное определение показателя преломления состоит в том, что это безразмерное число, которое связывает скорость света в среде со скоростью света в вакууме. В общем случае это можно выразить следующим уравнением:
, где n — показатель преломления, v — скорость света в материале, а c — скорость света в вакууме. Некоторые важные свойства могут быть получены из этой простой формулы.
1.- Поскольку мы не можем превысить скорость света в вакууме, n всегда будет больше 1
2.- Показатель преломления всегда будет положительным
Зависимость от длины волны
Однако это уравнение не является полным. Мы знаем, например, что каждая длина волны имеет свой показатель преломления, но мы не видим этой зависимости от длины волны в приведенном выше уравнении. Поэтому необходимо расширить нашу простую формулу, чтобы учесть эти изменения. Это цель уравнения Коши
, где n — показатель преломления, l — длина волны света в вакууме, а A, B и C — коэффициенты, полученные прямым измерением. Уравнение Коши обычно сводится к первым двум слагаемым, поэтому вам нужно вычислить только коэффициенты А и В. Хотя уравнение Коши точнее исходного, оно справедливо только в видимом диапазоне и только для материалов с низкой дисперсией. Улучшение по сравнению с этим уравнением можно найти в уравнении Селлмейера:
Одно важное отличие в этом уравнении состоит в том, что знаменатель в сумме представляет собой линии поглощения на определенных длинах волн. При работе на длинах волн, далеких от этих линий поглощения (это l >> C), уравнение Селлмейера упрощается до:
Это подводит нас к другому важному свойству показателя преломления, а именно к его взаимосвязи с электрической и магнитной проницаемостями.
Уравнения Максвелла
Используя уравнения Максвелла, мы можем вывести и выразить скорость электромагнитной волны в среде, что приводит к выражению:
где ?r – электрическая диэлектрическая проницаемость, ?r – магнитная проницаемость (обычно с значение 1 для немагнитных материалов на оптических длинах волн). В поглощающих материалах возможна комплексная диэлектрическая проницаемость, приводящая к комплексному показателю преломления
где κ — коэффициент экстинкции
Отрицательный показатель преломления
В природе мы нашли материалы только с положительными показателями преломления, но можно создать материалы и с отрицательными. Эти материалы называются метаматериалами и являются детищем Виктора Весалаго из Московского физико-технического института в 1967 году. Он предсказал, что если материал имеет отрицательную электрическую и отрицательную магнитную проницаемость, он будет иметь отрицательный показатель преломления. Прошло более 30 лет, прежде чем его предсказания были подтверждены в 2000 году доктором Дэвидом Р. Смитом из UCSD. Его исследовательская группа создала новый класс материалов , демонстрирующих необычные физические свойства , которые никогда не наблюдались в природе. Эти материалы подчиняются законам физики, но ведут себя не так, как обычные материалы (например, инвертируют закон Снеллиуса).
Материал с отрицательным показателем преломления
Когда дело доходит до конструкции осветительных или воображающих линз, у нас есть обширный каталог стекла, из которого мы можем выбирать. Выбор правильного материала может быть сложной задачей, и нет стандартной процедуры.
Выбор подходящего материала из стекла или пластмассы будет зависеть от нескольких факторов, таких как рабочая длина волны, диапазон температур, при которых будет работать система, наличие абразивных материалов, механическое напряжение, стоимость материалов, частота расплавления стекла и многое другое.