Электропроводность металлов и сплавов – . —

Электропроводность металлических сплавов

В металлических сплавах концентрация носителей также не зависит от температуры. Поэтому температурная зависимость электропроводности сплавов целиком определяется зависимостью подвижности носителей от температуры. Рассмотрим этот вопрос подробнее.

Предположим, что в идеальной решетке металла, имеющей строго периодический потенциал, часть узлов беспорядочно замещена атомами другого элемента. Так как потенциал поля примесных атомов отличен от потенциала основных атомов, то периодичность потенциала будет нарушена. Такое нарушение приводит к рассеянию носителей и дополнительному электрическому сопротивлению.

Для удельного сопротивления бинарных сплавов получается следующее выражение:

, (3.15)

где и– относительные доли металлов, образующих сплав,

– коэффициент пропорциональности. Функцияимеет максимум при, то есть при равном содержании в сплаве обеих компонент.

Кроме того, абсолютное значение удельного сопротивления сплава значительно выше, чем чистого металла. Это объясняется тем, что примеси вызывают значительно более сильное нарушение периодичности потенциала решетки, чем тепловые колебания. Если, однако, сплавляемые металлы при определенном соотношении компонент образуют соединение с упорядоченной внутренней структурой, то периодичность потенциала решетки восстанавливается и сопротивление, обусловленное рассеянием на примесях, практически полностью восстанавливается. Это подтверждает квантовую теорию электропроводности, согласно которой причиной электрического сопротивления твердых тел является не столкновение свободных электронов с атомами решетки, а рассеяние их на дефектах решетки, вызывающих нарушение периодичности ее потенциала. Идеально правильная решетка, имеющая строго периодический потенциал, не способна рассеивать свободные носители заряда и поэтому должна обладать нулевым сопротивлением.

При небольшом содержании примеси в (3.15) можно положить , тогда. Это удельное сопротивление не зависит от температуры и сохраняется при абсолютном нуле.

Рассмотрим теперь температурный коэффициент сопротивления , выражающий относительное изменение сопротивления проводника при нагревании его на 1 К. Так как для чистых металлов согласно (3.13), то

.

Для сплавов , поэтому

,

так как от температуры не зависит. Это выражение можно преобразовать следующим образом:

, (3.16)

где – температурный коэффициент сопротивления чистых металлов.

Из (3.16) видно, что должен быть меньшечистого металла, причем тем меньше, чем большепо сравнению с. Обычнона порядок и более выше, поэтомуможет быть на порядок и более нижечистого металла, что в основном подтверждается опытом. Однако во многих случаях температурная зависимость сопротивления сплавов является значительно более сложной, чем это вытекает из простой аддитивной закономерности (3.15), и температурный коэффициент сопротивления сплавов может быть много меньше, чем это следует из (3.16).

Высокое удельное сопротивление и низкий температурный коэффициент сопротивления сплавов нашли широкое применение в технике.

studfiles.net

4.2.2. Электропроводность сплавов

Как известно, причинами рассеяния электронных волн в металле являются не только тепловые колебания узлов решетки, но и статические дефекты структуры, которые также нарушают периодичность потенциального поля кристалла. Наиболее существенный вклад в уменьшение электропроводности металлов вносят рассеяния на примесях, которые всегда присутствуют в реальном проводнике либо в виде загрязнения, либо в виде легирующего (преднамеренно вводимого) элемента. Следует заметить, что любая примесная добавка приводит к повышению удельного электросопротивления, даже если она обладает повышенной проводимостью по сравнению с основным металлом.

4.2.3. Влияние механических воздействий на электропроводность

металлов и сплавов

Большое влияние на электропроводность металлов и сплавов оказывают механические воздействия. При всестороннем сжатии у большинства металлов удельное сопротивление уменьшается. Это объясняется сближением атомов и уменьшением амплитуды тепловых колебаний решетки.

При упругом растяжении и кручении межатомные расстояния увеличиваются. Это сопровождается усилением рассеяния электронов и возрастанием удельного электросопротивления. Влияние упругого растяжения или сжатия при условии пропускания тока вдоль действующей силы учитывается формулой [2]

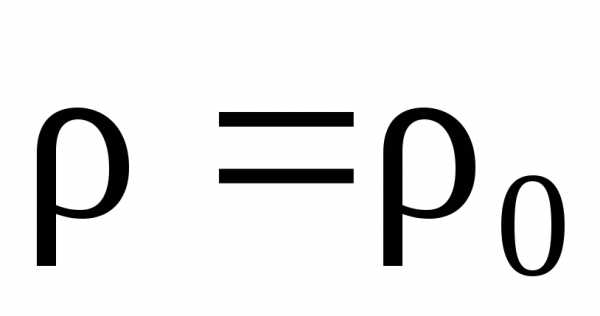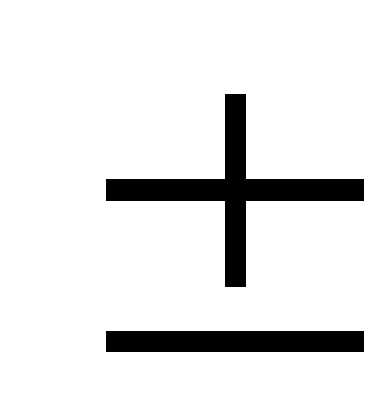(1φσ),

где ρ — удельное электросопротивление образца при механическом воздействии; ρ₀ — удельное электросопротивление образца при отсутствии механического воздействия; φ — коэффициент удельного электросопротивления по давлению; σ — механическое напряжение в сечении образца.

4.2.4. Влияние термообработки на электропроводность металлов и сплавов

Термическая закалка приводит к повышению удельного электросопротивления, что связано с искажениями кристаллической решетки, появлением внутренних напряжений. При рекристаллизации путем термической обработки (отжига) удельное электросопротивление может быть снижено до первоначального значения, поскольку происходит “залечивание” дефектов и снятие внутренних напряжений.

4.2.5. Мостовой метод измерения малых сопротивлений

Основная погрешность мостов постоянного тока определяется его чувствительностью, погрешностью значений сопротивлений плеч, сопротивлений монтажных проводов и контактов. Дополнительная погрешность возникает при изменении температуры и за счет сопротивлений внешних проводов и контактов, при помощи которых присоединяется резистор с неизвестным сопротивлением. Для уменьшения погрешности величину сопротивления соединительных проводов и контактов измеряют этим же мостом отдельно и вычитают из полученного результата. Для уменьшения погрешности измерения сопротивлений соединительных проводов и контактов при измерении сопротивлений, меньших одного Ома, разработаны так называемые двойные мосты. На рис. 4.1 показана схема двойного моста.

В этой схеме один контакт гальванометра Г присоединен к добавочной цепи, в которую введены два значительных по сравнению с Х и N сопротивления R₂ и R₄

.

Сопротивления R₁ и R₃ также велики по сравнению с R_Х и R_N. В такой схеме влияние сопротивления соединительных проводов и зажимов практически исключается.

Действительно, благодаря наличию значительных сопротивлений R₁, R₂, R₃, R₄, сила тока в них мала по сравнению с силой тока в R_Х и R_N. Следовательно, падение напряжения на соединительных проводах на всех участках мало. Если мост сбалансирован, то через гальванометр ток не идет. Тогда через сопротивления R₁ и R₃ идет одинаковый ток I₁, через сопротивления R₂ и R₄ ток I₂, а через сопротивления

R_Х и R_N ток I₀. По закону Кирхгофа

R_N I₀+R₂I₂ = R₃I₁; R_Х I₀+R₄I₂= R₁I₁.

Откуда получим

.

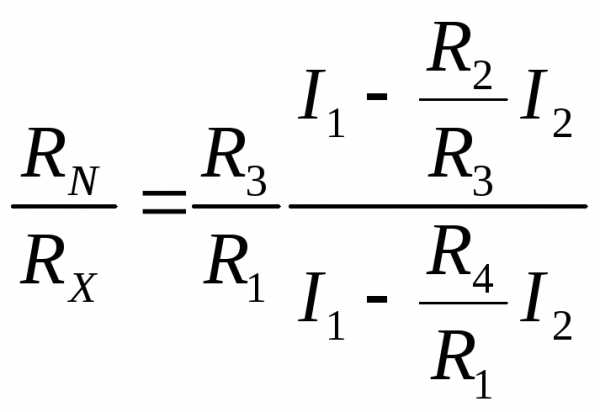Подбираем резисторы так, чтобы выполнялось условие R₂/R₃= R₄/R₁.

Тогда получим R_N/R_Х= R₃/R₁; R_Х = R_N R₁/R₃.

Откуда для удельного электросопротивления имеем

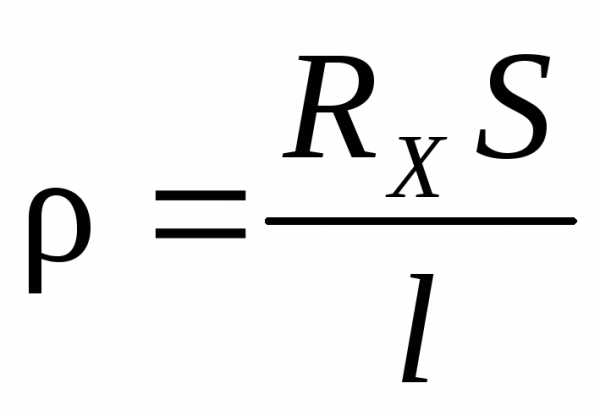. (4.8)

studfiles.net

Электропроводность металлов и сплавов Содержание

Электропроводность металлов и сплавов

Содержание : • Электропроводность проводников • Электропроводность полупроводников • Электропроводность диэлектриков • Электропроводность металлов • Электропроводность сплавов

Теоретические сведения 1) Проводник — тело, в котором имеются свободные носители заряда, то есть заряженные частицы, которые могут свободно перемещаться внутри этого тела. 2) Полупроводник — материал, который по своей удельной проводимости занимает промежуточное место между проводниками и диэлектриками и отличается от проводников сильной зависимостью удельной проводимости от концентрации примесей, температуры и воздействия различных видов излучения. 3) Диэлектрик — вещество, плохо проводящее электрический ток. 4) Электропроводность — способность тела проводить электрический ток, а также физическая величина, характеризующая эту способность и обратная электрическому сопротивлению. 5) Сплав — макроскопически однородный металлический материал, состоящий из смеси двух или большего числа химических элементов с преобладанием металлических компонентов.

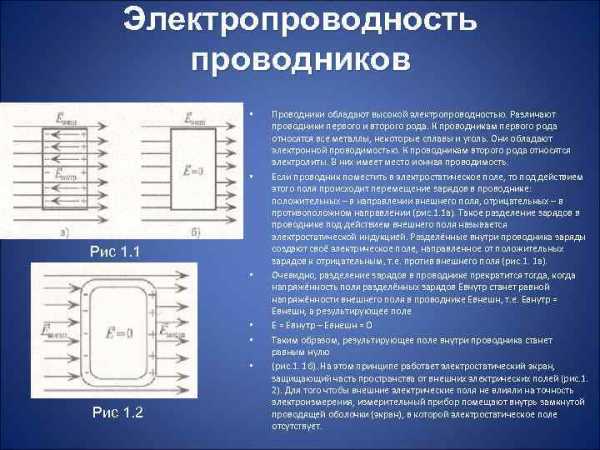Электропроводность проводников • • Рис 1. 1 • • Рис 1. 2 Проводники обладают высокой электропроводностью. Различают проводники первого и второго рода. К проводникам первого рода относятся все металлы, некоторые сплавы и уголь. Они обладают электронной проводимостью. К проводникам второго рода относятся электролиты. В них имеет место ионная проводимость. Если проводник поместить в электростатическое поле, то под действием этого поля происходит перемещение зарядов в проводнике: положительных – в направлении внешнего поля, отрицательных – в противоположном направлении (рис. 1. 1 а). Такое разделение зарядов в проводнике под действием внешнего поля называется электростатической индукцией. Разделённые внутри проводника заряды создают своё электрическое поле, направленное от положительных зарядов к отрицательным, т. е. против внешнего поля (рис. 1. 1 а). Очевидно, разделение зарядов в проводнике прекратится тогда, когда напряжённость поля разделённых зарядов Eвнутр станет равной напряжённости внешнего поля в проводнике Eвнешн, т. е. Eвнутр = Eвнешн, а результирующее поле Е = Eвнутр – Eвнешн = 0 Таким образом, результирующее поле внутри проводника станет равным нулю (рис. 1. 1 б). На этом принципе работает электростатический экран, защищающий часть пространства от внешних электрических полей (рис. 1. 2). Для того чтобы внешние электрические поля не влияли на точность электроизмерения, измерительный прибор помещают внутрь замкнутой проводящей оболочки (экран), в которой электростатическое поле отсутствует.

Электропроводность полупроводников • • В примесном полупроводнике n ¹ p, поэтому электропроводность выражается следующей формулой: • Рис. 2. 1 Полупроводник, не содержащий примесей, в нормальных условиях обладает так называемой собственной проводимостью или проводимостью типа i. Собственная проводимость обусловлена генерацией пар «электрон-дырка». Если концентрация электронов в зоне проводимости – ni , а дырок в валентной зоне – pi и ni = pi, то собственная проводимость полупроводника: В широком диапазоне температур и для различного содержания примесей имеют место температурные зависимости концентрации носителей заряда в полупроводнике n-типа, изображенные на рис. 2. 1. В области низких температур участок нижней ломаной между точками а и б характеризует только концентрацию носителей, обусловленную примесями. Наклон прямой на этом участке определяется энергией активации примесей. С увеличением температуры число носителей, поставляемых примесями, возрастает, пока не истощатся электронные ресурсы примесных атомов (точка б). На участке б – в примеси уже истощены, перехода электронов через запрещенную зону еще не обнаруживается. Участок кривой с постоянной концентрацией носителей заряда называют областью истощения примесей. В дальнейшем температура настолько велика, что начинается быстрый рост концентрации носителей вследствие перехода электронов через запрещенную зону ( участок в – и). Наклон этого участка характеризует ширину запрещенной зоны полупроводника. Угол наклона участка а – б зависит от концентрации примесей. Вторая компонента, обуславливающая электропроводность полупроводников – подвижность носителей заряда. При повышении температуры энергия электронов, а следовательно, и подвижность увеличивается. Но, начиная с некоторой температуры Т усиливаются колебания узлов кристаллической решетки полупроводника, которые мешают перемещению свободных носителей зарядов. Следовательно, их подвижность падает (рис. 2. 2. ). • • Рис. 2. 2

Электропроводность диэлектриков • • Рис. 3. 1 • • Электропроводность диэлектриков практически равна нулю в силу весьма сильной связи между электронами и ядром атомов диэлектрика. Если диэлектрик поместить в электростатическое поле, то в нём произойдёт поляризация атомов, т. е. смещение разноимённых зарядов в самом атоме, но не разделение их (рис. 3. 1 а). Поляризованный атом может рассматриваться как электрический диполь (рис. 3. 1 б), в котором «центры тяжести» положительных и отрицательных зарядов смещаются. Диполь – это система двух разноимённых зарядов, расположенных на малом расстоянии друг от друга в замкнутом пространстве атома или молекулы. Электрический диполь – это атом диэлектрика, в котором орбита электрона вытягивается в направлении, противоположном направлению внешнего поля Eвнешн (рис. 3. 11 б). Поляризованные атомы создают своё электрическое поле, напряжённость которого направлена против внешнего поля. В результате поляризации результирующее поле внутри диэлектрика ослабляется. Интенсивность поляризации диэлектрика зависит от его диэлектрической проницаемости. Чем она больше, тем интенсивнее поляризация в диэлектрике и тем слабее электрическое поле в нём. Е = Eвнешн – Eвнутр Если диэлектрик поместить в сильное электрическое поле, напряжённость которого можно увеличивать, то при каком-то значении напряжённости произойдёт пробой диэлектрика, при этом электроны отрываются от атома, т. е. происходит ионизация диэлектрика, и он становится проводником. Напряжённость внешнего поля, при которой происходит пробой диэлектрика, называется пробивной напряжённостью диэлектрика. А напряжение, при котором происходит пробой диэлектрика, называют напряжением пробоя, или электрической прочностью диэлектрика.

Электропроводность металлов • Электрический ток в металлах согласно классической электронной теории проводимости это упорядоченное движение электронов под действием сторонних сил. Согласно этой теории металл состоит из положительных ионов находящихся в узлах кристаллической решётки. А в свободном пространстве между ними движутся электроны подобно одноатомному идеальному газу. • Однако если в газе атомы соударяются между собой то в проводнике электроны ударяются об узлы решетки, отдавая таким образами им свою энергию. Как же была получена эта теория. Для начала нужно было выяснить, что является носителями зарядов в проводнике. С этой целью ученый Рикке в 1899 году провел такой эксперимент. Он взял три одинаковых цилиндра с тонко обработанными торцами. Два из них были медные, а третий алюминиевый. Сжал их между собой так, чтобы алюминиевый цилиндр оказался посередине и включил всю это конструкцию в главный питающий провод на трамвайной подстанции. • Рис. 4. 1 строение металла • Спустя год он разобрал конструкцию и тщательно обследовал места соединения цилиндров. И обнаружил, что диффузии металлов друга не произошло. То есть атомы меди не проникли в алюминий и наоборот. Из этого эксперимента можно сделать вывод что под действием электрического тока по проводнику не перемещаются ионы. А движутся лишь свободные электроны.

Электропроводность металлов • • • Рис. 4. 2 катушка с проводом вращаемая вокруг продольной оси • • То, что по проводнику движутся электроны, было установлено благодаря еще одному опыту. Для него необходимо взять катушку из проволоки и раскрутить ее. К катушке должен быть подключен амперметр. В момент резкой остановки катушки прибор покажет кратковременный ток. Этот ток обусловлен тем, что электроны продолжают двигаться по инерции, в то время как катушка уже остановилась. То есть наблюдается движение электронов по проводу хоть и кратковременное. В проводнике без электрического поля свободные электроны находятся в непрерывном хаотическом движении как молекулы газа. Но при создании внешнего электрического поля электроны сохраняя свое хаотическое движение, начнут двигаться под действием сил поля. Вот это направленное движение и называется током. Сами электроны под действием поля движутся достаточно медленно. Приблизительно пару миллиметров в секунду. Так как же лампочка, которую мы включаем, загорается так быстро ведь провод, которым она подключена достаточно длинный. И электрон от выключателя как минимум пару минут должен двигаться к спирали лампы. На самом деле все немного по другому. Ведь провода спираль и выключатель состоят из проводника и в них присутствуют электроны по всей длине. И при замыкании выключателя чтобы ток начал оказывать действие необязательно, чтобы электрон от выключателя попал в спираль. Ведь электроны в ней уже есть. При замыкании по проводникам начинает двигаться электрическое поле практически со скоростью света вот оно та и передает энергию. Представьте себе тонкую трубку набитую шариками внешним диаметром чуть меньше диаметра трубы. Когда мы всунем еще шарик с одной стороны, то с другого конца выпадет другой шарик. То есть по трубке двигалось усилие, передаваясь от шарика к шарику, а не ток шарик, который мы впихнули.

Электропроводность сплавов Идеальная решётка металла имеет строго периодический потенциал (рис. 2. 2, а). Если часть атомов меди беспорядочно замещена атомами другого элемента, то поле вблизи примесных атомов не такое, как вблизи собственных. Потенциал решётки становится непериодическим (рис. 2. 2, б). Он нарушается беспорядочно распределёнными примесями, что приводит к рассеянию носителей и дополнительному электрическому сопротивлению. В сплавах примеси вызывают более сильное нарушение периодичности потенциала решётки, чем тепловые колебания. Поэтому сопротивление сплава ρ(спл) значительно больше сопротивления ρ чистых металлов и определяется в основном рассеянием носителей на примесях. Как показал Нордгейм, подвижность для бинарных сплавов, обусловленная рассеянием их на нарушениях периодичности потенциала решётки, определяется следующим приближённым соотношением: где p и 1− p – относительные доли металлов, образующих сплав. Подставим в выражение σ = qnµ соотношение для подвижности сплава, учитывая, что ρ=1/σ, получим выражение удельного сопротивления для бинарного (двойного) сплава: где β – коэффициент пропорциональности. Функция p(1− p) имеет максимум при p = 1/2, т. е. при равном содержании в сплаве обоих компонентов. Если сплавляемые металлы при определённом соотношении компонентов образуют соединение с упорядоченной внутренней структурой, то периодичность решётки восстанавливается (рис. 2. 2, в) и сопротивление, обусловленное рассеянием на примесях, практически полностью исчезает. Этот факт является подтверждением квантовой теории электропроводности, согласно которой причиной электрического сопротивления твёрдых материалов является не столкновение свободных электронов с атомами решётки, а рассеяние их на дефектах решётки, вызывающих нарушение периодичности потенциала

Вывод: • Мы изучили электропроводность проводников, полупроводников, диэлектриков, также в частности металлов и сплавов, узнали какие факторы влияют на их электропроводность.

Контрольные вопросы: 1) Дать определение проводника 2) Какие вы знаете виды проводников? 3) Дайте определение собственной проводимости полупроводника. 4) Что такое диполь? 5) Дайте определение электрического диполя. 6) Что такое электропроводность? 7) Дайте определение электрического тока в металлах согласно классической электронной теории проводимости. • 8) Дайте определение сплава. • 9) Напишите уравнение подвижности для бинарных сплавов. • 10) Дайте определение диэлектрика. • •

present5.com

Электропроводность металлов и сплавов

Описание презентации Электропроводность металлов и сплавов по слайдам

Электропроводность металлов и сплавов

• Электропроводность проводников • Электропроводность полупроводников • Электропроводность диэлектриков • Электропроводность металлов • Электропроводность сплавов Содержание :

1) Проводник — тело, в котором имеются свободные носители заряда, то есть заряженные частицы, которые могут свободно перемещаться внутри этого тела. 2) Полупроводник — материал, который по своей удельной проводимости занимает промежуточное место между проводниками и диэлектриками и отличается от проводников сильной зависимостью удельной проводимости от концентрации примесей, температуры и воздействия различных видов излучения. 3) Диэлектрик — вещество, плохо проводящее электрический ток. 4) Электропроводность — способность тела проводить электрический ток, а также физическая величина, характеризующая эту способность и обратная электрическому сопротивлению. 5) Сплав — макроскопически однородный металлический материал, состоящий из смеси двух или большего числа химических элементов с преобладанием металлических компонентов. Теоретические сведения

Электропроводность проводников • Проводники обладают высокой электропроводностью. Различают проводники первого и второго рода. К проводникам первого рода относятся все металлы, некоторые сплавы и уголь. Они обладают электронной проводимостью. К проводникам второго рода относятся электролиты. В них имеет место ионная проводимость. • Если проводник поместить в электростатическое поле, то под действием этого поля происходит перемещение зарядов в проводнике: положительных – в направлении внешнего поля, отрицательных – в противоположном направлении (рис. 1. 1 а). Такое разделение зарядов в проводнике под действием внешнего поля называется электростатической индукцией. Разделённые внутри проводника заряды создают своё электрическое поле, направленное от положительных зарядов к отрицательным, т. е. против внешнего поля (рис. 1. 1 а). • Очевидно, разделение зарядов в проводнике прекратится тогда, когда напряжённость поля разделённых зарядов Eвнутр станет равной напряжённости внешнего поля в проводнике Eвнешн, т. е. Eвнутр = Eвнешн, а результирующее поле • Е = Eвнутр – Eвнешн = 0 • Таким образом, результирующее поле внутри проводника станет равным нулю • (рис. 1. 1 б). На этом принципе работает электростатический экран, защищающий часть пространства от внешних электрических полей (рис. 1. 2). Для того чтобы внешние электрические поля не влияли на точность электроизмерения, измерительный прибор помещают внутрь замкнутой проводящей оболочки (экран), в которой электростатическое поле отсутствует. Рис 1. 1 Рис 1.

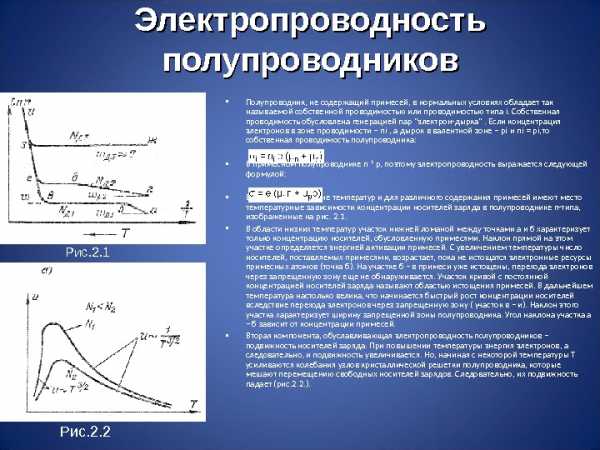Электропроводность полупроводников • Полупроводник, не содержащий примесей, в нормальных условиях обладает так называемой собственной проводимостью или проводимостью типа i. Собственная проводимость обусловлена генерацией пар «электрон-дырка». Если концентрация электронов в зоне проводимости – ni , а дырок в валентной зоне – pi и ni = pi, то собственная проводимость полупроводника: • В примесном полупроводнике n ¹ p, поэтому электропроводность выражается следующей формулой: • В широком диапазоне температур и для различного содержания примесей имеют место температурные зависимости концентрации носителей заряда в полупроводнике n-типа, изображенные на рис. 2. 1. • В области низких температур участок нижней ломаной между точками а и б характеризует только концентрацию носителей, обусловленную примесями. Наклон прямой на этом участке определяется энергией активации примесей. С увеличением температуры число носителей, поставляемых примесями, возрастает, пока не истощатся электронные ресурсы примесных атомов (точка б). На участке б – в примеси уже истощены, перехода электронов через запрещенную зону еще не обнаруживается. Участок кривой с постоянной концентрацией носителей заряда называют областью истощения примесей. В дальнейшем температура настолько велика, что начинается быстрый рост концентрации носителей вследствие перехода электронов через запрещенную зону ( участок в – и). Наклон этого участка характеризует ширину запрещенной зоны полупроводника. Угол наклона участка а – б зависит от концентрации примесей. • Вторая компонента, обуславливающая электропроводность полупроводников – подвижность носителей заряда. При повышении температуры энергия электронов, а следовательно, и подвижность увеличивается. Но, начиная с некоторой температуры Т усиливаются колебания узлов кристаллической решетки полупроводника, которые мешают перемещению свободных носителей зарядов. Следовательно, их подвижность падает (рис. 2. 2. ). Рис. 2. 1 Рис. 2.

Электропроводность диэлектриков • Электропроводность диэлектриков практически равна нулю в силу весьма сильной связи между электронами и ядром атомов диэлектрика. • Если диэлектрик поместить в электростатическое поле, то в нём произойдёт поляризация атомов, т. е. смещение разноимённых зарядов в самом атоме, но не разделение их (рис. 3. 1 а). Поляризованный атом может рассматриваться как электрический диполь (рис. 3. 1 б), в котором «центры тяжести» положительных и отрицательных зарядов смещаются. • Диполь – это система двух разноимённых зарядов, расположенных на малом расстоянии друг от друга в замкнутом пространстве атома или молекулы. • Электрический диполь – это атом диэлектрика, в котором орбита электрона вытягивается в направлении, противоположном направлению внешнего поля Eвнешн (рис. 3. 11 б). Поляризованные атомы создают своё электрическое поле, напряжённость которого направлена против внешнего поля. В результате поляризации результирующее поле внутри диэлектрика ослабляется. Интенсивность поляризации диэлектрика зависит от его диэлектрической проницаемости. Чем она больше, тем интенсивнее поляризация в диэлектрике и тем слабее электрическое поле в нём. • Е = Eвнешн – Eвнутр • Если диэлектрик поместить в сильное электрическое поле, напряжённость которого можно увеличивать, то при каком-то значении напряжённости произойдёт пробой диэлектрика, при этом электроны отрываются от атома, т. е. происходит ионизация диэлектрика, и он становится проводником. Напряжённость внешнего поля, при которой происходит пробой диэлектрика, называется пробивной напряжённостью диэлектрика. А напряжение, при котором происходит пробой диэлектрика, называют напряжением пробоя, или электрической прочностью диэлектрика. Рис. 3.

Электропроводность металлов • Электрический ток в металлах согласно классической электронной теории проводимости это упорядоченное движение электронов под действием сторонних сил. Согласно этой теории металл состоит из положительных ионов находящихся в узлах кристаллической решётки. А в свободном пространстве между ними движутся электроны подобно одноатомному идеальному газу. • Однако если в газе атомы соударяются между собой то в проводнике электроны ударяются об узлы решетки, отдавая таким образами им свою энергию. • Как же была получена эта теория. Для начала нужно было выяснить, что является носителями зарядов в проводнике. С этой целью ученый Рикке в 1899 году провел такой эксперимент. Он взял три одинаковых цилиндра с тонко обработанными торцами. Два из них были медные, а третий алюминиевый. Сжал их между собой так, чтобы алюминиевый цилиндр оказался посередине и включил всю это конструкцию в главный питающий провод на трамвайной подстанции. • Спустя год он разобрал конструкцию и тщательно обследовал места соединения цилиндров. И обнаружил, что диффузии металлов друга не произошло. То есть атомы меди не проникли в алюминий и наоборот. Из этого эксперимента можно сделать вывод что под действием электрического тока по проводнику не перемещаются ионы. А движутся лишь свободные электроны. Рис. 4. 1 — строение металла

• То, что по проводнику движутся электроны, было установлено благодаря еще одному опыту. Для него необходимо взять катушку из проволоки и раскрутить ее. К катушке должен быть подключен амперметр. В момент резкой остановки катушки прибор покажет кратковременный ток. Этот ток обусловлен тем, что электроны продолжают двигаться по инерции, в то время как катушка уже остановилась. То есть наблюдается движение электронов по проводу хоть и кратковременное. • В проводнике без электрического поля свободные электроны находятся в непрерывном хаотическом движении как молекулы газа. Но при создании внешнего электрического поля электроны сохраняя свое хаотическое движение, начнут двигаться под действием сил поля. Вот это направленное движение и называется током. • Сами электроны под действием поля движутся достаточно медленно. Приблизительно пару миллиметров в секунду. Так как же лампочка, которую мы включаем, загорается так быстро ведь провод, которым она подключена достаточно длинный. И электрон от выключателя как минимум пару минут должен двигаться к спирали лампы. • На самом деле все немного по другому. Ведь провода спираль и выключатель состоят из проводника и в них присутствуют электроны по всей длине. И при замыкании выключателя чтобы ток начал оказывать действие необязательно, чтобы электрон от выключателя попал в спираль. Ведь электроны в ней уже есть. При замыкании по проводникам начинает двигаться электрическое поле практически со скоростью света вот оно та и передает энергию. • Представьте себе тонкую трубку набитую шариками внешним диаметром чуть меньше диаметра трубы. Когда мы всунем еще шарик с одной стороны, то с другого конца выпадет другой шарик. То есть по трубке двигалось усилие, передаваясь от шарика к шарику, а не ток шарик, который мы впихнули. Рис. 4. 2 — катушка с проводом вращаемая вокруг продольной оси Электропроводность металлов

Идеальная решётка металла имеет строго периодический потенциал (рис. 2. 2, а). Если часть атомов меди беспорядочно замещена атомами другого элемента, то поле вблизи примесных атомов не такое, как вблизи собственных. Потенциал решётки становится непериодическим (рис. 2. 2, б). Он нарушается беспорядочно распределёнными примесями, что приводит к рассеянию носителей и дополнительному электрическому сопротивлению. В сплавах примеси вызывают более сильное нарушение периодичности потенциала решётки, чем тепловые колебания. Поэтому сопротивление сплава ρ ( спл ) значительно больше сопротивления ρ чистых металлов и определяется в основном рассеянием носителей на примесях. Как показал Нордгейм, подвижность для бинарных сплавов, обусловленная рассеянием их на нарушениях периодичности потенциала решётки, определяется следующим приближённым соотношением: где p и 1− p – относительные доли металлов, образующих сплав. Подставим в выражение σ = qnµ соотношение для подвижности сплава, учитывая, что ρ =1/ σ , получим выражение удельного сопротивления для бинарного (двойного) сплава: где β – коэффициент пропорциональности. Функция p(1− p ) имеет максимум при p = 1/2 , т. е. при равном содержании в сплаве обоих компонентов. Если сплавляемые металлы при определённом соотношении компонентов образуют соединение с упорядоченной внутренней структурой, то периодичность решётки восстанавливается (рис. 2. 2, в) и сопротивление, обусловленное рассеянием на примесях, практически полностью исчезает. Этот факт является подтверждением квантовой теории электропроводности, согласно которой причиной электрического сопротивления твёрдых материалов является не столкновение свободных электронов с атомами решётки, а рассеяние их на дефектах решётки, вызывающих нарушение периодичности потенциала. Электропроводность сплавов

Вывод : : • Мы изучили электропроводность проводников, полупроводников, диэлектриков, также в частности металлов и сплавов, узнали какие факторы влияют на их электропроводность.

Контрольные вопросы : : • 1) Дать определение проводника • 2) Какие вы знаете виды проводников? • 3) Дайте определение собственной проводимости полупроводника. • 4) Что такое диполь? • 5) Дайте определение электрического диполя. • 6) Что такое электропроводность? • 7) Дайте определение электрического тока в металлах согласно классической электронной теории проводимости. • 8) Дайте определение сплава. • 9) Напишите уравнение подвижности для бинарных сплавов. • 10) Дайте определение диэлектрика.

present5.com

ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ И СПЛАВОВ — КиберПедия

Электропроводность чистых металлов. Так как в металлах концентрация электронного газа n практически не зависит от температуры, то зависимость удельной электропроводности ơ от температуры полностью определяется температурной зависимостью подвижности электронов вырожденного электронного газа. В достаточно чистом металле концентрация примесей невелика и подвижность вплоть до весьма низких температур определяется рассеянием электронов на колебаниях решетки.

В области высоких температур u и ơ электронов обратно пропорциональны Т.

При температурах, близких к абсолютному нулю основное значение приобретает рассеяние на примесных атомах, подвижность электронов в этом случае не зависит от Т, поэтому удельное сопротивление, ρ приобретает постоянное значение, которое называют остаточным сопротивлением ρ _Ост

На рис. 7.6, а схематически показана кривая зависимости удельного сопротивления чистых металлов от температуры.

Рис. 7.6. Зависимость удельного сопротивления чистых металлов от температуры

ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛИЧЕСКИХ СПЛАВОВ.

При температуре, отличной от абсолютного нуля, к остаточному сопротивлению р_ост = Рв присоединяется сопротивление р_т , обусловленное рассеянием на тепловых колебаниях решетки, и общее сопротивление проводника

(7.29)

Это соотношение выражает известное правило Матиссена об аддитивности сопротивления. Для сплавов вплоть до высоких температур удельное сопротивление меняется с температурой значительно слабее, чем у чистых металлов, и температурный коэффициент сопротивления сплавов, как правило, значительно ниже температурного коэффициента сопротивления чистых металлов.

СОБСТВЕННАЯ И ПРИМЕСНАЯ ПРОВОДИМОСТИ ПОЛУПРОВОДНИКОВ

Полупроводники высокой степени очистки в области не слишком низких температур обладают электрической проводимостью, обусловленной наличием в них собственных носителей заряда — электронов и дырок. Эту проводимость называют собственной проводимостью полупроводников.

В собственном полупроводнике имеется два типа носителей — электроны и дырки, удельная проводимость его описывается соотношением

(7.30)

где n_i, p_i — концентрации электронов и дырок в собственном полупроводнике; μ_n, μ_р — их подвижности. Подставляя в (7.30) n_i и p_i из (6.12) и μ_n и μ_р из (7.16), получаем

(7.31)

где через ơ₀ обозначены сомножители, стоящие перед экспонентой. Зависимость ơ_t от Т удобно представить в полулогарифмических координатах:

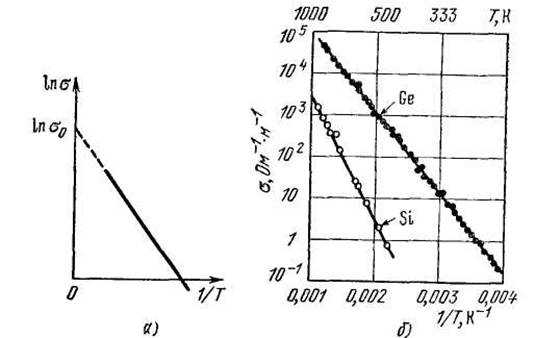
Рис. 7.8. Температурная зависимость электропроводности собственных полупроводников: а — теоретическая зависимость; 6 —кривые для германия и кремния

Если по оси абсцисс отложить 1/Т, а по оси ординат ln ơ_i ,то получится прямая, отсекающая на оси ординат отрезок, равный ln ơ₀ {рис. 7.8, а). Угловой коэффициент этой прямой равен —E_gl2k, Строя такой график, можно определить постоянную ơ₀ и ширину запрещенной зоны E_g.

Таким образом, у металлов концентрация носителей заряда практически не зависит от температуры, и температурная зависимость проводимости определяется температурной зависимостью подвижности; в полупроводниках концентрация резко зависит от температуры и температурная зависимость проводимости практически полностью определяется температурной зависимостью концентрации.

Примесная проводимость полупроводников. Температурная зависимость электропроводности примесных полупроводников определяется в основном температурой зависимостью концентрации носителей. На рис. 7.9,а схематически показаны кривые зависимости ơ (Т) для примесного полупроводника, содержащего различные количества активной примеси.

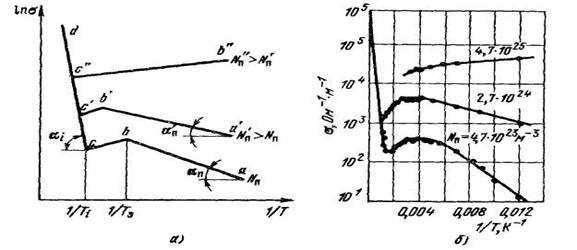
Рис. 7.9. Зависимость электропроводности примесных полупроводников от температуры: а — теоретические кривые; б —кривые для кремния, содержащего различные концентрации фосфора

На этих кривых можно выделить три характерные области: первая соответствует низким температурам – до температуры истощения примеси T_s. Концентрация носителей заряда в этой области описывается формулой

(6.15)

cyberpedia.su

ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ И СПЛАВОВ

 

2.2.1. Почему удельное сопротивление металлов увеличивается с повышением температуры?

2.2.2. Что называют температурным коэффициентом удельного сопротивления? Является ли он константой для данного металла?

2.2.3. Как влияют примеси на удельное сопротивление металлов? Сформулируйте правило Матиссена.

2.2.4. Как меняется средняя длина свободного пробега электронов в идеально чистом металле и в металле с примесями при увеличении температуры (от абсолютного нуля)?

2.2.5. Почему металлические сплавы типа твердых растворов обладают более высоким удельным сопротивлением, чем чистые компоненты, образующие сплав?

2.2.6. Объясните, как изменяется удельное сопротивление двухкомпонентного металлического сплава, представляющего неупорядоченный твердый раствор, в зависимости от его состава.

2.2.7. Изобразите (качественно) график зависимости удельного сопротивления от состава бинарного сплава, компоненты которого обладают ограниченной взаимной растворимостью в твердой фазе.

2.2.8. Почему при термической закалке удельное сопротивление металлов возрастает, а при термическом отжиге — уменьшается? Почему металлоидные примеси сильнее влияют на удельное сопротивление металлов, чем примеси металлических элементов?

2.2.9. Как и почему изменяется удельное сопротивление металлов при плавлении?

2.2.10. Почему ферромагнитные металлы обладают нелинейной зависимостью удельного сопротивления от температуры?

2.2.11. Почему в формулы для плотности тока и удельной проводимости металлов входит концентрация всех свободных электронов, хотя реально в электропроводности участвует лишь небольшая часть электронов, имеющих энергию, близкую энергии Ферми?

2.2.12. Объясните зависимость удельного сопротивления тонких металлических пленок от их толщины.

2.2.13. Объясните поведение проводников в электромагнитном поле на высоких частотах. Нарисуйте (качественно) график распределения плотности тока по сечению цилиндрического проводника при воздействии на него напряжения высокой частоты. Укажите на графике глубину проникновения электромагнитного поля в проводник.

2.2.14. Какие металлы, и в каких условиях могут переходить в состояние сверхпроводимости? Что является причиной образования куперовских пар?

2.2.15. Как влияет магнитное поле на критическую температуру перехода в состояние сверхпроводимости? Чем различаются сверхпроводники первого и второго рода?

2.2.16. В каких материалах обнаружено явление высокотемпературной сверхпроводимости? Какие перспективы открываются в случае широкого применения этих материалов в технике?

2.2.17. Как и почему изменяется удельное сопротивление металлов при механических воздействиях (сжатие, растяжение, изгиб, пластическая деформация)?

2.2.18. Определить максимальную частоту тепловых колебаний атомов в кристаллах алюминия, для которого температура Дебая . Какую длину волны будет иметь фотон с эквивалентной энергией?

2.2.19. Вычислить длину свободного пробега электронов в меди при , если ее удельное сопротивление при этой температуре равно .

 

Решение

Согласно представлениям квантовой теории, удельное сопротивление металлов связано с длиной свободного пробега электронов соотношением

 

.

 

Концентрация свободных электронов в меди

 

 

Отсюда следует, что длина свободного пробега

 

м.

 

2.2.20. Удельное сопротивление серебра при комнатной температуре равно , а температурный коэффициент удельного сопротивления составляет . Определить, как и во сколько раз изменится длина свободного пробега электронов при нагревании проводника от до .

2.2.21. В медном проводнике под действием электрического поля проходит электрический ток плотностью . Определить скорость дрейфа и отношение ее к средней суммарной скорости движения электронов при температуре .

2.2.22. При включении в электрическую цепь проводника диаметром и длиной разность потенциалов на концах проводника составила при токе . Определить удельное сопротивление материала проводника.

2.2.23. Определить время, в течение которого электрон пройдет расстояние по медному проводу, если удельное сопротивление меди , а разность потенциалов на концах проводника . За какое время электрон пролетит это же расстояние, двигаясь без соударений, при той же разности потенциалов? Каково время передачи сигнала?

 

Решение

 

Из закона Ома следует, что удельная проводимость . Концентрация свободных электронов в меди (см. решение задачи 2.2.19). Тогда средняя скорость дрейфа электронов

 

м/с.

 

Время дрейфа электрона по проводнику с.

При отсутствии столкновений с узлами решетки электрон движется равноускоренно и время пролета

 

Передача энергии вдоль проводов линии осуществляется электромагнитным полем, распространяющимся вдоль проводов со скоростью света с. Полагая, что средой, окружающей провод, является воздух, время передачи сигнала

 

.

 

2.2.24. Вычислить удельное сопротивление металлического проводника, имеющего плотность и молярную массу , если известно, что средняя скорость дрейфа электронов в электрическом поле напряженностью составляет . Можно полагать, что на каждый атом кристаллической решетки приходится один электрон.

2.2.25. В металлическом проводнике с площадью поперечного сечения и сопротивлением концентрация свободных электронов равна . Определить среднюю скорость дрейфа электронов при напряжении .

2.2.26. К медной проволоке длиной и диаметром приложено напряжение . Сколько электронов пройдет через поперечное сечение проводника за , если удельное сопротивление меди равно ?

2.2.27. Одинаковым ли будет относительное изменение удельного сопротивления меди для двух температурных интервалов: и (но отношению к начальному значению в каждом из этих интервалов)?

2.2.28. Удельное сопротивление чистой меди при и равно соответственно и . Пользуясь линейной аппроксимацией зависимости , определить температурный коэффициент удельного сопротивления при .

2.2.29. Доказать, что между температурными коэффициентами сопротивления проводника удельного сопротивления материала и линейного расширения существует следующая взаимосвязь: .

2.2.30. Определить температурный коэффициент линейного расширения и удлинение нихромовой проволоки, если известно, что при повышении температуры от до электрическое сопротивление проволоки изменяется от до . Длина проволоки в холодном состоянии . Температурный коэффициент удельного сопротивления нихрома принять равным .

 

Решение

 

Температурный коэффициент сопротивления проволоки:

 

 

Тогда

.

Отсюда

м.

 

2.2.31. При нагревании провода из манганина длиной и диаметром от до его сопротивление уменьшается на , а длина возрастает на Определить температурный коэффициент удельного сопротивления. При расчетах принять, что при комнатной температуре для манганина удельное сопротивление .

2.2.32*. Вычислить удельную теплоемкость меди при температуре . Изобразите (качественно) на графике, как будет изменяться удельная теплоемкость меди при понижении температуры.

 

Решение

 

Удельная теплоемкость металла определяется выражением , где — теплоемкость кристаллической решетки; — теплоемкость электронного газа. При температурах выше температуры Дебая электронная теплоемкость составляет небольшую часть полной теплоемкости кристалла. Для меди , поэтому при электронным вкладом в теплоемкость можно пренебречь.

При согласно закону Дюлонга — Пти, молярная теплоемкость кристаллической решетки равна , где — универсальная газовая постоянная. Тогда .

При понижении температуры от до теплоемкость остается практически постоянной. В области температур ниже наблюдается резкое уменьшение теплоемкости твердых тел.

2.2.33. Пользуясь законом Видемана — Франца, определить отношение удельных теплопроводностей серебра и олова при температуре: а) и б) . Принять, что при температуре удельные сопротивления серебра и олова равны соответственно и мкОм·м, а температурные коэффициенты удельного сопротивления составляют соответственно и .

2.2.34. Определить, во сколько раз изменится удельная теплопроводность меди при изменении температуры от до .

 

Решение

 

Согласно закону Видемана — Франца, , где — удельная проводимость; — число Лоренца. Отсюда следует, что

 

 

2.2.35. Вычислить удельную теплопроводность меди при комнатной температуре по измеренному значению ее удельного сопротивления .

2.2.36. Определить, во сколько раз отличаются удельные теплоемкости серебра и свинца при комнатной температуре. Характеристическая температура Дебая равна для серебра и для свинца.

2.2.37. Для сплавов двух металлов и при температуре получены показанные на рис. 8 зависимости удельного сопротивления и температурного коэффициента удельного сопротивления от состава сплава. Постройте (качественно) на этом же рисунке зависимость удельного сопротивления от состава сплава для температуры считая, что от температуры практически не зависит.

 

Рис.8

 

 

2.2.38*. В металлических сплавах при медленном охлаждении до температур ниже наблюдается образование упорядоченной кристаллической структуры. Изобразите графики зависимости удельного сопротивления от температуры таких сплавов, получаемых путем закалки и при медленном охлаждении, и объясните характерные их различия.

2.2.39. Удельное сопротивление меди, содержащей олова при температуре , составляет . Определить отношение β удельных сопротивлений меди при температурах и : .

 

Решение

Согласно правилу Маттисена, , где — сопротивление, обусловленное рассеянием электронов на тепловых колебаниях решетки; — остаточное сопротивление, связанное с рассеянием электронов на неоднородностях структуры. Для чистой меди . При . Вблизи температуры абсолютного нуля полное сопротивление реального металлического проводника равно остаточному сопротивлению. Отсюда следует, что

 

 

Имеется два проводящих тела, прошедших одинаковую технологическую обработку. Химическим анализом установлено, что состав первого тела ( ), а второго — ( ). Определить, какой материал имеет более высокую удельную проводимость.

 

Решение

 

Согласно правилу Линде, изменение остаточного сопротивления на примеси , где — разность валентностей металла-растворителя (меди) и примесного атома. Константа b одинакова для атомов примесей одного периода периодической системы элементов, например для цинка и мышьяка. Так как медь одновалентна, то при введении цинка , а при введении мышьяка . Следует принять во внимание, что остаточное сопротивление линейно зависит от концентрации х примесных атомов. Таким образом, , откуда

 

 

Таким образом, первый материал обладает меньшим удельным сопротивлением, т. е. более высокой удельной проводимостью.

2.2.41. Определить, в каком из материалов — константане или никеле — влияние примесей сильнее сказывается на относительном изменении удельной проводимости.

2.2.42*. Остаточное удельное сопротивление серебра на примеси золота составляет . Рассчитайте и постройте зависимость удельного сопротивления твердых растворов от концентрации компонентов, предполагая справедливость закона Нордгейма для этой бинарной системы.

2.2.43. Используя условие задачи 2.2.39, вычислить, во сколько раз изменится отношение , если содержание олова в медном проводнике снизить до .

2.2.44. Удельное сопротивление медного проводника, содержащего индия, равно . Определить концентрацию атомов индия в медном сплаве с удельным сопротивлением , полагая, что все остаточное сопротивление обусловлено рассеянием на примесных атомах индия.

2.2.45. Объясните, почему тонкие металлические пленки имеют отрицательный температурный коэффициент удельного сопротивления.

2.2.46. Температура перехода в сверхпроводящее состояние для олова в отсутствие магнитного поля равна , а критическая напряженность магнитного поля Нсв при температуре абсолютного нуля ( ) составляет . Рассчитать максимально допустимое значение тока при температуре для провода диаметром , изготовленного из сверхпроводящего олова. Определить для этой температуры диаметр провода, по которому может протекать ток без разрушения сверхпроводящего состояния.

 

Решение

Для сверхпроводников первого рода справедливо соотношение , для олова . Предельный ток ограничивается критической напряженностью магнитного поля на поверхности образца. Для цилиндрического провода

 

.

 

Диаметр провода, по которому может протекать ток ,

.

 

Таким образом, плотность предельного тока в сверхпроводниках первого рода уменьшается с увеличением диаметра провода; при этом предельный ток пропорционален диаметру провода, а не площади его поперечного сечения.

2.2.47. Определить критическую температуру перехода проводника в состояние сверхпроводимости, если размер энергетической щели . Как изменится эта температура при воздействии внешнего магнитного поля?

2.2.48*. Непрерывные экспериментальные наблюдения за током, наведенным в замкнутом контуре из сверхпроводящего материала, показали, что в течение одного года ток уменьшается в результате релаксации системы к равновесному состоянию всего на . Принимая концентрацию электронов проводимости , оцените удельное сопротивление материала в сверхпроводящем состоянии и сравните его с удельным сопротивлением меди в нормальных условиях.

 

Решение

В соответствии с кинетическим уравнением Больцмана затухание тока определяется выражением , где — время релаксации. Отсюда следует, что

 

Для .

Удельная проводимость материала связана с временем релаксации соотношением

 

См/м.

 

Сравнивая удельные сопротивления сверхпроводника и меди , получаем

 

.

2.2.49*. Критическая температура перехода металла в сверхпроводящее состояние равна . Определить граничную частоту переменного электромагнитного поля, выше которой при происходит разрушение сверхпроводимости.

2.2.50. Оценить удельную теплопроводность магния при температуре , если удельное сопротивление при равно , а температурный коэффициент удельного сопротивления составляет .

stydopedia.ru

Электропроводность металлических сплавов — стр. 2

2.2 Электропроводность металлических сплавов

В металлических сплавах концентрация носителей также не зависит от температуры. Поэтому температурная зависимость электропроводности сплавов целиком определяется зависимостью подвижности носителей от температуры. Рассмотрим этот вопрос более подробно.

Предположим, что в идеальной решетке металла, например меди имеющей строго периодический потенциал U (рис. 2.2.1, а), часть узлов беспорядочно замещена атомами другого элемента, например золота. Так как потенциал поля примесных атомов отличен от потенциала основных атомов, то потенциал решетки не сохранится строго периодическим (рис. 2.2.1, б). Он нарушается беспорядочно распределенными примесными атомами. Такое нарушение приводит, естественно к рассеянию носителей и дополнительному электрическому сопротивлению.

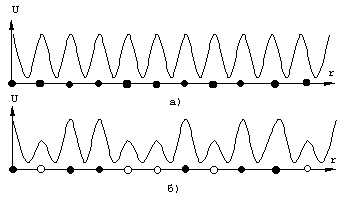
Рис 2.2.1 Потенциальная диаграмма для:

а- идеальной решетки; б-решетки с примесями

Как показал Л. Нордгейм, в простейшем случае бинарных сплавов типа твердых растворов подвижность носителей, обусловленная рассеянием их на нарушениях решетки, определяется следующим приближенным соотношением:

m _спл ~ ω(1 — ω), (2.2.1)

где ω и (1 — ω) — относительные доли металлов, образующих сплав.

Подставив m _спл из (2.2.1) в (2.1.1) и помня, что ρ = 1/ g, получим

следующее выражение для удельного сопротивления бинарного сплава:

ρ_спл=β[ω(1 — ω)], (2.2.2)

где β — коэффициент пропорциональности.

Функция ω (1 — ω)имеет максимум при ω = 1/2, т. е. при равном содержании в сплаве обеих компонент. В качестве примера на рис. 2.2.2, а показана зависимость удельного сопротивления сплавов меди с золотом от содержания золота. Кривая проходит через максимум, отвечающий 50% меди и золота в сплаве.

Рис 2.2.2, а — зависимость удельного сопротивления сплава от примеси;

б-потенциальная диаграмма решетки сплава

Из рис. 2.2.2, а видно далее, что абсолютное значение ρ_спл значительно выше ρ чистых компонент. Так, при комнатной температуре ρ_Cu = 1,710^-8 Омм, ρ_Au = l,5610^-8 Омм, а ρ_{50%Cu. + 50%Au=1510^-8Омм. Это вполне естественно, так как примеси вызывают значительно более сильное нарушение периодичности потенциала решетки, чем тепловые колебания. Если, однако, сплавляемые металлы при определенном соотношении компонент образуют металлическое соединение с упорядоченной внутренней структурой, то периодичность потенциала решетки восстанавливается (рис. 2.2.2, б) и сопротивление, обусловленное рассеянием на примесях, практически почти полностью исчезает. Для сплавов меди с золотом это имеет место при соотношении компонент, отвечающем стехиометрическому составу Cu3Au и CuAu (рис. 2.2.2, а, сплошные кривые). Это является убедительным подтверждением квантовой теории электропроводности, согласно которой основной причиной электрического сопротивления твердых тел является не столкновение свободных электронов с атомами решетки, а рассеяние их на дефектах решетки, вызывающих нарушение периодичности ее потенциала.}

Идеально правильная, бездефектная решетка, имеющая строго периодический потенциал, не способна рассеивать свободные носители заряда и поэтому должна обладать нулевым сопротивлением. Это подтверждается многочисленными опытами с предельно чистыми металлами в области низких температур, в частности данными табл. 2.1.2: по мере повышения степени чистоты металлов их сопротивление вблизи абсолютного нуля непрерывно падает, стремясь к нулю. Подчеркнем, что это не явление сверхпроводимости, о котором будет речь впереди, а естественное поведение всех абсолютно чистых металлов при предельно низких температурах, вытекающее из квантовой природы электрического сопротивления.

При небольшом содержании примеси в (2.2.2) можно положить (1 — ω)1 . Тогда ρ_спл ~ ω. Это удельное сопротивление не зависит от температуры и сохраняется при абсолютном нуле. Его называют остаточным сопротивлением ρ_ост ρ_П (см. рис.2.1.3).

При температуре, отличной от абсолютного нуля, к остаточному сопротивлению присоединяется сопротивление ρ_Т, обусловленное рассеянием на тепловых колебаниях решетки, и общее удельное сопротивление равно

ρ = ρ_П + ρ_Т. (2.2.3)

Это соотношение выражает известное правило Матиссена об аддитивности удельного сопротивления.

Рассмотрим теперь температурный коэффициент сопротивления . Как известно, он выражает относительное изменение удельного сопротивления проводника ρ при нагревании его на 1 К. Так как для чистых металлов ρ= ρ_Т, то

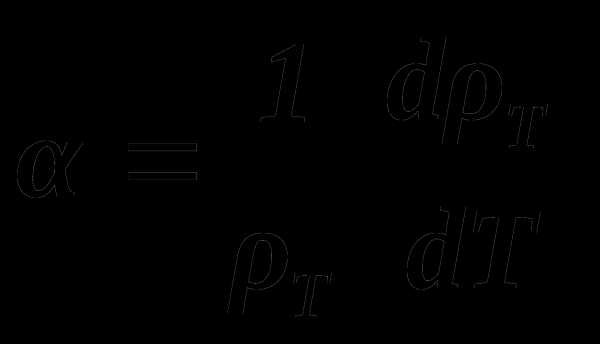(2.2.4)

Как показывает опыт, грубо

[см. табл. (2.2.1)]. Для сплавов ρ = ρ_П + ρ_Т , поэтому

так как ρ_П от температуры не зависит. Это выражение можно преобразовать следующим образом:

, (2.2.5)

где a— температурный коэффициент сопротивления чистых металлов.

Из (2.2.5) видно, что α _спл должен быть меньше α чистого металла, причем тем меньше, чем больше ρ_П по сравнению с ρ_Т . Обычно ρ_{Пна порядок и более выше ρТ , поэтому αспл может быть на порядок и более ниже a чистого металла, что в основном подтверждается опытом (табл. 2.2.1; данные приведены для комнатной температуры).}

Табл.2.2.1

Чистые металлы и сплавы	Медь	Олово	Никель	Бронза (88%Сu, 18% Sn, 1% Pb)	Нихром (80% Ni, 20% Cr)	Константан (54% Cu, 46% Ni)
a 103 ,К	4,1	4,2	6,2	0,5	0,13	-0,004

Однако во многих случаях температурная зависимость сопротивления сплавов является значительно более сложной, чем та, которая вытекает из простой аддитивной закономерности (2.2.3), и температурный коэффициент сопротивления сплавов может быть много меньше, чем можно было бы ожидать согласно (2.2.5). Более того, он не остается постоянным в широком интервале температур, а в ряде случаев является даже отрицательным, как это имеет место, например, у константы (табл. 2.2.1) и у некоторых других сплавов.

Высокое удельное сопротивление и низкий температурный коэффициент сопротивления сплавов открыли для них широкие возможности практического применения для изготовления разнообразных проволочных и пленочных резисторов и переменных сопротивлений (реостатов), используемых в различных областях техники.

2.3 Электропроводность сверхпроводящих сплавов

У многих металлов и сплавов при температурах, близких к абсолютному нулю, наблюдается резкое уменьшение удельного сопротивления. Это явление получило название сверхпроводимости, а температуру Т_св, при которой происходит переход в сверхпроводящее состояние, называют критической температурой перехода. Впервые сверхпроводимость была обнаружена у ртути при Т_СВ = 4,2 К голландским физиком X. Каммерлинг-Оннесом.

Если в кольце из сверхпроводника индуцировать электрический ток (например, с помощью магнитного поля), то он не будет затухать в течение длительного времени. По скорости уменьшения магнитного поля наведенного тока в кольце была произведена оценка удельного сопротивления материалов в сверхпроводящем состоянии. Его значение составило около 10^-25 Омм, что в 10¹⁷ раз меньше сопротивления меди при комнатной температуре.

Физическая природа сверхпроводимости. Явление сверхпроводимости можно понять и обосновать только с помощью квантовых представлений. Почти полвека с момента открытия сверхпроводимости сущность этого явления оставалась неразгаданной из-за того, что методы квантовой механики еще не в полной мере использовались в физике твердого тела. Микроскопическая теория сверхпроводимости, объясняющая все опытные данные, была предложена в 1957 г. американскими учеными Бардиным, Купером и Шриффером (теория БКШ). Значительный вклад в развитие теории сверхпроводимости внесли работы советского академика Н. Н. Боголюбова.

Рис.2. 3.1 Схема образования электронных пар в сверхпроводящем металле

Согласно установившимся представлениям, явление сверхпроводимости возникает в том случае, когда электроны в металле как бы притягиваются друг к другу. Притяжение электронов возможно только в среде, содержащей положительно заряженные ионы, поле которых ослабляет силы кулоновского отталкивания между электронами. Притягиваться могут лишь те электроны, которые принимают участие в электропроводности, т. е. расположенные вблизи уровня Ферми. Если такое притяжение имеет место, то электроны с противоположным направлением импульса и собственного магнитного спина связываются в пары, называемые куперовскими. В образовании куперовских пар решающую роль играют взаимодействие электронов с тепловыми колебаниями решетки — фононами. В твёрдом теле электроны могут как поглощать, так и порождать фононы. Мысленно представим себе следующий процесс: один из электронов, взаимодействуя с решеткой, переводит ее в возбужденное состояние и изменяет свой импульс; другой электрон, также взаимодействуя с решеткой, переводит ее в нормальное состояние и тоже изменяет свой импульс. В результате состояние решетки не изменяется, а электроны обмениваются квантами тепловой энергии — фононами. Обменное фононное взаимодействие и вызывает силы притяжения между электронами, которые превосходят силы кулоновского отталкивания. Обмен фононами при участии решетки происходит непрерывно. В упрощенном виде обменное фононное взаимодействие проиллюстрировано схемой рис.2.3.1. Электрон, движущийся среди положительно заряженных ионов, поляризует решетку, т. е. электростатическими силами притягивает к себе ближайшие ионы. Благодаря такому смещению ионов в окрестности траектории электрона локально возрастает плотность положительного заряда. Второй электрон, движущийся вслед за первым, естественно, может притягиваться областью с избыточным положительным зарядом. В результате косвенным образом, за счет взаимодействия с решеткой между электронами 1 и 2 возникают силы притяжения. Второй электрон становится партнером первого — образуется куперовская пара. Поскольку силы притяжения невелики, спаренные электроны слабо локализованы в пространстве. Эффективный диаметр куперовской пары имеет порядок 10 ^-7 м, т. е. охватывает тысячи элементарных ячеек. Эти парные образования перекрывают друг друга, постоянно распадаются и вновь создаются, но в целом все пары образуют электронный конденсат, энергия которого за счет внутреннего взаимодействия меньше, чем у совокупности разобщенных нормальных электронов. Вследствие этого в энергетическом спектре сверхпроводника появляется энергетическая щель 2 — область запрещенных энергетических состояний (рис. 2.3.2).

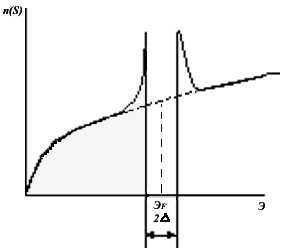
Рис. 2.3.2 Распределение электронов по энергиям в металле в состоянии сверхпроводимости

Спаренные электроны располагаются на дне энергетической щели. Грубая оценка показывает, что количество таких электронов составляет около 10^4 от общего их числа. Размер энергетической щели зависит от температуры, достигая максимального значения при абсолютном нуле и полностью исчезая при Т = Т_СВ. Теория БКШ дает следующую связь ширины щели с критической температурой перехода

(2.3.1)

Формула (2.3.1) достаточно хорошо подтверждается экспериментально. Для большинства сверхпроводников энергетическая щель составляет 10-10 эВ.

Как было показано, электрическое сопротивление металла обусловлено рассеянием электронов на тепловых колебаниях решетки и на примесях. Однако при наличии энергетической щели для перехода электронов из основного состояния в возбужденное требуется достаточная порция тепловой энергии, которую при низких температурах электроны не могут получить от решетки, поскольку энергия тепловых колебаний меньше ширины щели. Именно поэтому спаренные электроны не рассеиваются на дефектах структуры. Особенностью куперовских пар является их импульсная упорядоченность, состоящая в том, что все пары имеют одинаковый импульс и не могут изменять свои состоя­ния независимо друг от друга. Электронные волны, описывающие движение пар, имеют одинаковые длину и фазу. Фактически движение всех электронных пар можно рассматривать как распространение одной электронной волны, которая не рассеивается решеткой, «обтекает» дефекты структуры. Такая согласованность в поведении пар обусловлена высокой мобильностью электронного конденсата: непрерывно меняются наборы пар, происходит постоянная смена партнеров.

Рис.2.3.3 Изменение удельного сопротивления олова вблизи температурных переходов в состоянии сверхпроводимости:

1 – монокристалл; 2 – поликристалл; 3 – поликристалл с примесями

Переход вещества в сверхпроводящее состояние при его охлаждении происходит в очень узком интервале температур (сотые доли градуса). Неоднородности структуры, создаваемые примесями, искажениями решетки, границами зерен, пластической деформацией и т. п., не приводят к уничтожению сверхпроводимости, а вызывают лишь расширение температурного интервала перехода из одного состояния в другое (рис.2.3.3). Электроны, ответственные за создание сверхпроводимости, не обмениваются энергией с решеткой. Поэтому при температуре ниже критической наблюдается существенное уменьшение теплопроводности металлов.

III. ПРИМЕНЕНИЕ МЕТАЛЛИЧЕСКИХ СПЛАВОВ И СОЕДИНЕНИЙ

3.1 Чистые металлы и сплавы, применяемые в радиоэлектронике

Из металлов в радиоэлектронике главным образом применяют медь, алюминий, серебро и золото, а из сплавов — бронзу, латунь и ковар.

Медь — главный материал, обладающий высокой пластичностью, достаточной механической прочностью и высокой электропроводностью. По электропроводности медь стоит на втором месте после серебра. Медь имеет красновато-оранжевый цвет и температуру плавления 1083 °С. Коэффициент температурного расширения меди КТР = 17-10^-6 1/°С.

Проводниковую медь получают из слитков меди после очистки их от примесей в электролитической ванне (с помощью постоянного тока). В нормальной воздушной атмосфере проводниковая медь устойчива к атмосферной коррозии. Этому способствует тонкий слой оксида СuО которым медь покрывается на воздухе. Он препятствует дальнейшему доступу кислорода воздуха к меди.

Для изготовления изделий (обмоточные, радиомонтажные провода и кабели) применяют чистую медь марок М00к, М0ку; М0к; М1к (катодная медь) и М00б; М0б; М1б (бескислородная медь). Содержание меди (с серебром) 99,99 — 99,90%. Наибольшее содержание меди имеют марки М00к и М00б.

Примеси в металлах оказывают неблагоприятное влияние на их электрические и механические свойства. Поэтому для изготовления проводов применяют сорта меди, в которых сумма всех примесей не должна превышать 0,1 %. Для изготовления медной фольги (для печатных плат) и эмалированных обмоточных проводов применяют марки бескислородной меди, отличающейся пластичностью и высокой электропроводностью.

Проволоку для проводов изготовляют 0,01—10 мм в виде мягкого, отожженного изделия (марка ММ) или твердотянутого, неотожженного изделия (марка МТ). У изделий из мягкой меди (при 20 °С) плотность 8900 кг/м³; _р = 200-280 МПа; e_Р = 6-35%; r = 0,0172-0,01724 мкОмм; из твердой меди — плотность 8960 кг/м³; _р = 380 — 450 МПа; e_Р — = 0,6 -2%; r = 0,0178 -0,180 мкОм м.

Проволока меньшего диаметра обладает большими разрушающим напряжением при растяжении и значениями удельного электрического сопротивления, чем проволока большего диаметра. Для проводов очень малого диаметра (0,01 мм), предназначенных для работы при повышенных температурах, применяют проволоку, изготовленную из бескислородной меди (марка МООб), отличающейся высокой чистотой (общее содержание примесей—не более 0,01%). Температурный коэффициент удельного сопротивления для всех марок меди ТКr = 0,004 1°/С.

Бронза представляет собой сплавы меди с оловом (оловянная бронза), алюминием (алюминиевая), бериллием (бериллиевая) и с другими легирующими элементами. Марки бронзы обозначаются буквами Бр (бронза), за которыми следуют буквы и цифры, показывающие, какие легирующие элементы и в каком количестве содержатся в данной бронзе (табл. 3.1.1).

Таблица 3.1.1 Марки и состав некоторых 6poнз и латуней

Марка	Содержание элементов, %
	олово	фосфор	бериллий	алюминий	никель	медь	цинк
БрО10	10					Остальное
БрОФ6,5-0,15	6-7	0,15				Остальное
БрА7				6-8		Остальное
БрБ2			2-2,2		0,2-0,5	Остальное
Л62						60-63	40-37
Л 80						79-81	21-19

gigabaza.ru