Определение упругости, пластичности и прочности материалов
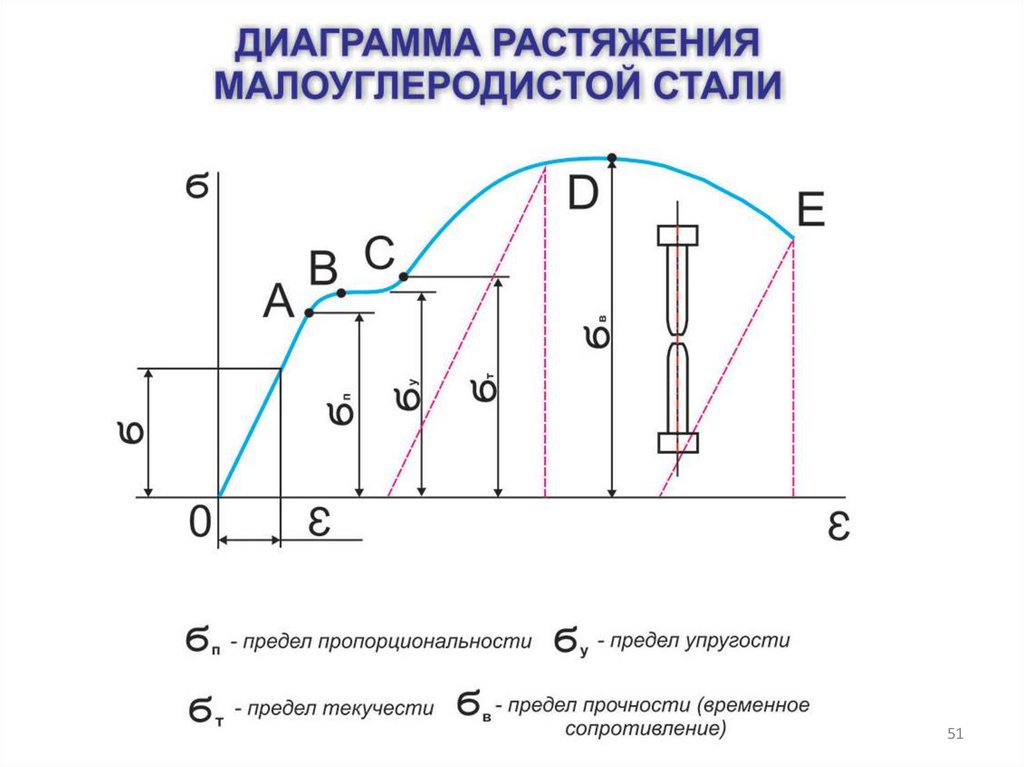
Упругость, пластичность и прочность определяют при испытаниях металлов на растяжение. Для проведения испытаний изготовляют образцы плоской или круглой формы. Испытания проводят на разрывных машинах. В результате получают диаграмму растяжения (рис.5). По оси абсцисс этой диаграммы откладывают значения удлинения (деформации), а по оси ординат – усилие (напряжение), приложенное к образцу.
Рис.5. Диаграмма растяжения образца (L– длина образца; Р – усилие растяжения)
Напряжением называется нагрузка на единицу площади поперечного сечения образца.
Пользуясь
записанной на машине диаграммой
растяжения, можно определить важнейшие
характеристики механических свойств
металлов. Точка А диаграммы показывает
максимальную нагрузку, которую
выдерживает образец, не теряя своих
упругих свойств. Если к образцу приложить
такую или меньшую нагрузку, а затем
снять ее, то остаточного удлинения он
не получит.
.
Выше точки А значение удлинения начинает возрастать быстрее, чем значение усилия, поэтому кривая диаграммы начинает изгибаться, склоняться к горизонтальной линии, образуя площадку текучести (Б-В). Если нагрузку в точке В разделить на площадь поперечного сечения образца, то получим предел текучести :
.
При
дальнейшем увеличении растягивающего
усилия (выше значения предела текучести)
образец будет все больше удлиняться,
а диаметр его – уменьшаться. Когда
усилие достигнет наибольшего значения,
в образце начнет образовываться шейка,
т.е. в каком-то сечении диаметр его
уменьшается больше, чем в других местах.
Если максимальную нагрузку (точка Г), которую выдержал образец до разрыва, разделить на первоначальную площадь его поперечного сечения, то получим предел прочности. Таким образом, предел прочности – это напряжение при максимальной нагрузке, которую выдержал образец во время испытания. Предел прочности обозначается и выражается в килограмм-силах на квадратный миллиметр (кгс/мм2):
.
Кроме
показателей прочности при испытании
на растяжение определяют и показатели
пластичности, характеризующие способность
металла деформироваться не разрушаясь.
Этой характеристикой является
относительное удлинение; для ее получения
обе половинки разорванного образца
складывают вместе и измеряют длину его
рабочей части L
Относительное удлинение обозначается греческой буквой и выражается в процентах. Его определяют по формуле:
,
где –
первоначальная длина образца;
– его длина после испытания.
1. Выберите на свое усмотрение любую деталь машины, механизма, узла или бытового изделия, укажите необходимый материал и способ изготовления этой детали: наименование детали _____, выбранный материал ______, способ (технология) изготовления детали ______.
2. Результат определения ударной вязкости: ширина образца________ мм, толщина в месте надреза____ мм, Fo=_____мм2, АН_____, =__________.
Заключение по материалу ________________________________________
3. Расшифровка твердости материалов
Значения | Твердость материалов для варианта №__ | |||
Метод определения Твердость, единиц Индентор (конус, шарик) Режим определения: Р, кгс D, мм t, с Металл (ориентировочно) | ||||
4. Результаты замера
твердости образцов:
Результаты замера
твердости образцов:
Метод определения твердости ________, нагрузка _____ кгс, индентор (шарик, конус)________.
Метод определения | Образец №___ | Диаметр отпечатка при измерениях, мм | Твердость | |||
первое | второе | третье | среднее | |||
5. Диаграмма испытания образцов на растяжение
Выполнил_____________,
Дата__________.
| Коррозия, упругость и пластичность металлов |
| «Ржа ест железо…» Эта поговорка известна каждому. Все знают, что ржавчина или коррозия металла — первый злейший враг железа. Попав во влажное место, оно начинает быстро разрушаться.
Хотя более медленно, но также неуклонно разрушаются и другие металлы. В наше время придумано множество способов защиты металлов, однако коррозия металла ежегодно съедает одну десятую часть всего производимого металла. Коррозия уничтожает предметы быта, машины, технические сооружения и произведения искусства, особенно расположенные на открытом воздухе.
В первой половине прошлого века архитектором К. Росси был сооружен Александрийский (ныне имени А. С. Пушкина) театр. Его украсила медночеканная скульптура, выполненная по проекту скульптора С. Пименова. Она изображала покровителя муз Аполлона, держащего в руке лиру и управляющего квадригой — колесницей, запряженной четверкой лошадей.
Было установлено, что свойства меди несовместимы не только с железом, но также с алюминием.
Тонкую, как струна, алюминиевую проволоку легко разорвать руками, но не так-то просто сделать это с медной, а тем более стальной. Стальные струны гитары и балалайки при натяжении выдерживают огромные нагрузки. Стальная проволока прочнее, чем медная и алюминиевая.
В технике прочность на растяжение определяется в специальном приборе, на образцах, имеющих определенную форму и размеры. При этом с большой точностью определяется не только прочность, но и упругость металлов, а также прочность пластичность металлов и сплавов. В практике высокую прочность на растяжение должны иметь струны музыкальных инструментов, тросы подъемных устройств, провода линий высоковольтных электропередач.
Кроме прочности на растяжение, различают прочность на сжатие, изгиб, кручение и др. Все эти характеристики прежде всего 19 имеют большое значение в технике.
Если полотно пилы согнуть под небольшим углом, а затем отпустить, оно снова выпрямится. Это свойство называется упругостью металлов. Если бы пила не обладала упругостью металла, то она довольно быстро бы согнулась и помялась настолько, что пилить ею было бы невозможно. Упругость металлов необходима для изготовления всевозможных пружин (для часов, игрушек, механических бритв и т. п.), амортизаторов в автомобилях, пружинящих контактов в электротехнике, булавок и застежек в ювелирном деле.
Прочность и пластичность противоположна упругости металлов. Если при неточном ударе молотка сгибается гвоздь, никто не надеется, что он выпрямится без посторонней помощи. От удара на консервной банке остаются глубокие вмятины. Все это проявления прочности и пластичности металла.
При художественной обработке металла пластичность имеет очень большое значение. Высокую прочность и пластичность должен иметь металл, используемый для выколотки, чеканки, скани, инкрустации, басмы.
Алюминиевую проволоку можно легко строгать ножом, снимая тонкую стружку. Алюминий мягче стали, из которой сделано лезвие ножа. В то же время, проведя алюминиевой проволокой по поверхности свинца, можно оставить на нем глубокую царапину. Свинец мягче алюминия и, разумеется, стали. Говоря иначе, сталь тверже алюминия, а алюминий тверже свинца.
Из металлов и сплавов, имеющих высокую твердость, изготавливают всевозможные инструменты: напильники, пилы, сверла, зубила, фрезы, стамески, рашпили, инструменты гравера и резчика по дереву. Инструменты из инструментальной стали обязательно закаляют, благодаря чему увеличивается твердость их рабочей части.
Прочность, пластичность и твердость металла можно увеличить не только путем термической, но и химико-термической обработки: цементации и азотирования стали, цианирования и др.
Несколько раньше было рассказано о несовместимости некоторых металлов друг с другом, ставшей причиной их разрушения. Но так бывает не всегда.
Найти металл, свойства которого были бы идеальными для какого-то конкретного изделия, не так-то просто. Взять хотя бы обычную кастрюлю. В старину ее делали из меди, так как медь является хорошим проводником тепла, но она быстро окислялась от приготавливаемой в ней пищи. На помощь меди еще в XVIII веке пришел другой металл, стойкий к воздействию слабых кислот,— олово. Медную посуду, в том числе и знаменитые русские самовары, обязательно лудят изнутри. Таким образом, верхний слой посуды был медным, внутренний — оловянным.
Недавно шведские специалисты предложили трехслойный сосуд для приготовления пищи, который они назвали «кастрюлей на всю жизнь». Верхний слой сосуда они сделали из меди, имеющей высокую теплопроводность и теплоемкость. Благодаря этому кастрюля быстро нагревается и долго сохраняет тепло. Средний слой был алюминиевый, способствующий равномерному распределению тепла, а внутренний — из нержавеющей стали, которая, как известно, не окисляется и хорошо чистится.
|
Металлы и сплавы. Модуль упругости Юнга
Упругость материала удобно выражать отношением напряжения к деформации, параметром, также называемым модулем упругости при растяжении или модулем Юнга материала, обычно с символом — Е .
- Модуль Юнга можно использовать для прогнозирования удлинения или сжатия объекта.
Модуль упругости для некоторых распространенных металлов при различных температурах согласно ASME B31.1-1995:
- 1 фунт/кв. дюйм (фунт/дюйм 2 ) = 1 фунт/кв. 2 ) = 6,895×10 -3 N/мм 2
- T ( O C) = 5/9 [T ( O F) — 32]
| Модуль упругости Юнга — E — (10 6 psi) | ||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metal | Temperature ( o C) | |||||||||||||||||||||||||||||
| -200 | -129 | -73 | 21 | 93 | 149 | 204 | 260 | 316 | 371 | 427 | 482 | 538 | 593 | 649 | ||||||||||||||||
| Temperature ( o F) | ||||||||||||||||||||||||||||||
| -325 | -200 | -100 | 70 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | 1200 | ||||||||||||||||
| Чугут | ||||||||||||||||||||||||||||||
| Серый чугун | 13,4 | 13,2 | 12,4 | 13,2 | 12,4 | 13,2 | 12,4 | 13,2 | 12,4 | 13,2 | 12,4 | 13,2 | 12,4 | 13,2 | 12,4 | 0149 | 11. 0 0 | 10.2 | ||||||||||||
| Steel | ||||||||||||||||||||||||||||||
| Carbon steel C <= 0.3% | 31.4 | 30.8 | 30.2 | 29.5 | 28.8 | 28.3 | 27.7 | 27,3 | 26,7 | 25,5 | 24,2 | 22,4 | 20,4 | 18,0 | ||||||||||||||||
| 18,0 | ||||||||||||||||||||||||||||||
| 18,0 | ||||||||||||||||||||||||||||||
| 18,0 | ||||||||||||||||||||||||||||||
| 18,0 | . | 31.2 | 30.6 | 30.0 | 29.3 | 28.6 | 28.1 | 27.5 | 27.1 | 26.5 | 25.3 | 24.0 | 22.2 | 20.2 | 17.9 | 15.4 | ||||||||||||||
| Carbon- molybdenum steels | 31.1 | 30.5 | 29.9 | 29.2 | 28.5 | 28.0 | 27. 4 4 | 27.0 | 26.4 | 25.3 | 23.9 | 22.2 | 20.1 | 17.8 | 15.3 | |||||||||||||||
| Nickel steels Ni 2% — 9% | 29.6 | 29.1 | 28.5 | 27.8 | 27.1 | 26.7 | 26,1 | 25,7 | 25,2 | 24,6 | 23,0 | |||||||||||||||||||
| CR -MO Steels CR 1/2% -2% | ||||||||||||||||||||||||||||||
| CR -MO Steels CR 1/2% -2% | ||||||||||||||||||||||||||||||
| CR -MO CR 1/2% -2% | ||||||||||||||||||||||||||||||
| CR -MO CR 1% -2% | ||||||||||||||||||||||||||||||
| CR -MO CR 1% -2% | ||||||||||||||||||||||||||||||
| CR -MO CR 1% -2% | ||||||||||||||||||||||||||||||
| CR -MO CR 1% -2% | ||||||||||||||||||||||||||||||
| CR -MO Steels. | 30.4 | 29.7 | 29.0 | 28.5 | 27.9 | 27.5 | 26.9 | 26.3 | 25.5 | 24.8 | 23.9 | 23.0 | 21.8 | |||||||||||||||||
| Cr-Mo steels Cr 2 1/ 4% — 3% | 32.6 | 32. 0 0 | 31.4 | 30.6 | 29.8 | 29.4 | 28.8 | 28.3 | 27.7 | 27.1 | 26.3 | 25.6 | 24.6 | 23.7 | 22.5 | |||||||||||||||
| Cr-Mo steels Cr 5% — 9% | 32.9 | 32.3 | 31.7 | 30.9 | 30.1 | 29.7 | 29.0 | 28.6 | 28,0 | 27,3 | 26,1 | 24,7 | 22,7 | 20,4 | 18,2 | |||||||||||||||
| 30.1 | 29.2 | 28.5 | 27.9 | 27.3 | 26.7 | 26.1 | 25.6 | 24.7 | 23.2 | 21.5 | 19.1 | 16.6 | ||||||||||||||||||
| Austenitic steels (TP304, 310, 316, 321, 347) | 30.3 | 29.7 | 29.1 | 28.3 | 27.6 | 27.0 | 26. 5 5 | 25.8 | 25.3 | 24,8 | 24,1 | 23,5 | 22,8 | 22,1 | 21,2 | |||||||||||||||
| и Coppery Allyoy. and leaded-Sn bronze (C83600, C92200) | 14.8 | 14.6 | 14.4 | 14.0 | 13.7 | 13.4 | 13.2 | 12.9 | 12.5 | 12.0 | ||||||||||||||||||||
| Naval brass Si & Al bronze (C46400, C65500, C95200, C95400) | 15.9 | 15.6 | 15.4 | 15.0 | 14.6 | 14.4 | 14.1 | 13.8 | 13.4 | 12.8 | ||||||||||||||||||||
| Copper (C11000) | 16.9 | 16.6 | 16.5 | 16.0 | 15.6 | 15.4 | 15.0 | 14.7 | 14.2 | 13.7 | ||||||||||||||||||||
| Copper red brass Al-bronze (C10200, C12000, C12200, C12500, C14200, C23000, C61400) | 18. 0 0 | 17.7 | 17.5 | 17.0 | 16.6 | 16.3 | 16.0 | 15.6 | 15.1 | 14.5 | ||||||||||||||||||||
| Nickel and Nickel Alloys | ||||||||||||||||||||||||||||||
| Monel 400 (N04400) | 27.8 | 27.3 | 26.8 | 26.0 | 25.4 | 25.0 | 24.7 | 24.3 | 24.1 | 23.7 | 23.1 | 22.6 | 22.1 | 21.7 | 21.2 | |||||||||||||||
| Титан | ||||||||||||||||||||||||||||||
| Нелегированный титан марок 1, 2, 3 и 7 | 15,5 909 15,5 | 14.6 | 14.0 | 13.3 | 12.6 | 11.9 | 11.2 | |||||||||||||||||||||||
| Aluminum and aluminum alloys | ||||||||||||||||||||||||||||||
| Grades 443, 1060, 1100, 3003, 3004, 6063 | 11. 1 1 | 10.8 | 10.5 | 10.0 | 9.6 | 9.2 | 8.7 | |||||||||||||||||||||||
- 1 psi (фунт/дюйм 2 ) = 6 894,8 Н/м 2 (Па)
- T( o C) = 903 8 5/9[T7018 C) ]
Внимание! Вы можете использовать конвертер единиц давления для переключения между единицами модуля упругости.
Эластичность | Определение, примеры и факты
Закон Гука
См. все СМИ
- Ключевые люди:
- Огюстен-Луи Коши Софи Жермен Ктесибий Александрийский 907:45
- Похожие темы:
- Закон Гука предел эластичности пластичность пластичность вязкоупругость
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
эластичность , способность деформированного материального тела возвращаться к своей первоначальной форме и размеру после устранения сил, вызывающих деформацию. Говорят, что тело с этой способностью ведет себя (или реагирует) эластично.
Говорят, что тело с этой способностью ведет себя (или реагирует) эластично.
В большей или меньшей степени большинство твердых материалов проявляют упругие свойства, но существует предел величины силы и сопутствующей деформации, в пределах которой возможно упругое восстановление для любого данного материала. Этот предел, называемый пределом упругости, представляет собой максимальное напряжение или силу на единицу площади внутри твердого материала, которая может возникнуть до начала остаточной деформации. Напряжения, выходящие за предел упругости, вызывают текучесть или текучесть материала. Для таких материалов предел упругости отмечает конец упругого поведения и начало пластического поведения. Для большинства хрупких материалов напряжения, превышающие предел упругости, приводят к разрушению практически без пластической деформации.
Предел упругости заметно зависит от типа рассматриваемого твердого тела; например, стальной стержень или проволока могут быть упруго растянуты только примерно на 1 процент от их первоначальной длины, в то время как для полос из некоторых резиноподобных материалов можно достичь упругого удлинения до 1000 процентов. Однако сталь намного прочнее резины, потому что сила растяжения, необходимая для достижения максимального упругого удлинения в резине, меньше (примерно в 0,01 раза), чем сила, необходимая для стали. Упругие свойства многих твердых тел при растяжении лежат между этими двумя крайностями.
Однако сталь намного прочнее резины, потому что сила растяжения, необходимая для достижения максимального упругого удлинения в резине, меньше (примерно в 0,01 раза), чем сила, необходимая для стали. Упругие свойства многих твердых тел при растяжении лежат между этими двумя крайностями.
Различные макроскопические упругие свойства стали и резины являются результатом их очень разных микроскопических структур. Эластичность стали и других металлов возникает из-за короткодействующих межатомных сил, которые, когда материал не нагружен, удерживают атомы в правильном порядке. Под напряжением атомная связь может быть нарушена при весьма малых деформациях. Напротив, на микроскопическом уровне каучукоподобные материалы и другие полимеры состоят из длинноцепочечных молекул, которые раскручиваются по мере растяжения материала и сжимаются при упругом восстановлении. Математическая теория упругости и ее приложения к инженерной механике связаны с макроскопической реакцией материала, а не с основным механизмом, который ее вызывает.
В простом испытании на растяжение упругая реакция материалов, таких как сталь и кость, характеризуется линейной зависимостью между напряжением растяжения (силой растяжения или растяжения на единицу площади поперечного сечения материала), σ , и коэффициент удлинения (разность между расширенной и начальной длинами, деленная на начальную длину), e . Другими словами, σ пропорционально e; это выражается σ = Ee , где E, константа пропорциональности, называется модулем Юнга. Значение E зависит от материала; отношение его значений для стали и резины составляет около 100 000. Уравнение σ = Ee известно как закон Гука и является примером основного закона. Он выражает в терминах макроскопических величин что-то о природе (или строении) материала. Закон Гука в основном применим к одномерным деформациям, но его можно распространить и на более общие (трехмерные) деформации путем введения линейно связанных напряжений и деформаций (обобщения 9). 0003 σ и e ), которые учитывают сдвиг, скручивание и изменения объема. Полученный в результате обобщенный закон Гука, на котором основана линейная теория упругости, дает хорошее описание упругих свойств всех материалов при условии, что деформации соответствуют растяжениям, не превышающим примерно 5 процентов. Эта теория обычно применяется при анализе инженерных сооружений и сейсмических возмущений.
0003 σ и e ), которые учитывают сдвиг, скручивание и изменения объема. Полученный в результате обобщенный закон Гука, на котором основана линейная теория упругости, дает хорошее описание упругих свойств всех материалов при условии, что деформации соответствуют растяжениям, не превышающим примерно 5 процентов. Эта теория обычно применяется при анализе инженерных сооружений и сейсмических возмущений.
Предел упругости в принципе отличается от предела пропорциональности, который знаменует собой конец упругого поведения, описываемого законом Гука, а именно, при котором напряжение пропорционально деформации (относительная деформация) или, что то же самое, такой, при котором нагрузка пропорциональна перемещению. Предел упругости почти совпадает с пределом пропорциональности для некоторых эластичных материалов, так что иногда их нельзя различить; тогда как для других материалов между ними существует область непропорциональной упругости.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Подпишитесь сейчас
Линейная теория упругости неадекватна для описания больших деформаций, которые могут возникнуть в резине или мягких тканях человека, таких как кожа. Упругий отклик этих материалов является нелинейным, за исключением очень малых деформаций, и для простого растяжения может быть представлен определяющим законом σ = f ( e ), где0003 e ) является математической функцией e , которая зависит от материала и приближается к Ee , когда e очень мало. Термин нелинейный означает, что график σ , построенный против e , не является прямой линией, в отличие от ситуации в линейной теории. Энергия Вт ( e ), запасенная в материале под действием напряжения σ представляет площадь под графиком σ = f ( e ). Она доступна для перевода в другие виды энергии, например, в кинетическую энергию снаряда катапульты.
Функция запасенной энергии Вт ( e ) может быть определена путем сравнения теоретического соотношения между σ и e с результатами экспериментальных испытаний на растяжение, в которых измеряются σ и e . Таким образом, упругая реакция любого твердого тела на растяжение может быть охарактеризована с помощью функции запасенной энергии. Важным аспектом теории упругости является построение конкретных форм функции энергии деформации по результатам экспериментов с трехмерными деформациями, обобщающими описанную выше одномерную ситуацию.
Таким образом, упругая реакция любого твердого тела на растяжение может быть охарактеризована с помощью функции запасенной энергии. Важным аспектом теории упругости является построение конкретных форм функции энергии деформации по результатам экспериментов с трехмерными деформациями, обобщающими описанную выше одномерную ситуацию.
Функции энергии деформации можно использовать для прогнозирования поведения материала в условиях, когда прямое экспериментальное тестирование нецелесообразно. В частности, их можно использовать при проектировании узлов инженерных сооружений. Например, резина используется в подшипниках мостов и опорах двигателей, где ее упругие свойства важны для поглощения вибраций. Стальные балки, пластины и оболочки используются во многих конструкциях; их эластичная гибкость способствует выдерживанию больших нагрузок без повреждения или разрушения материала. Эластичность кожи является важным фактором успешной практики пересадки кожи. В математических рамках теории упругости решаются задачи, связанные с такими приложениями.


 Если железо не уживается с медью и ее сплавами, то оно более покладисто к алюминию, цинку и олову. Олово в свою очередь несовместимо с алюминием. С остальными металлами оно совместимо только при пайке. Цинк совместим со многими распространенными металлами, за исключением меди и ее сплавов. Мало того, он так же, как и олово, активно защищает железо от коррозии металлов.
Если железо не уживается с медью и ее сплавами, то оно более покладисто к алюминию, цинку и олову. Олово в свою очередь несовместимо с алюминием. С остальными металлами оно совместимо только при пайке. Цинк совместим со многими распространенными металлами, за исключением меди и ее сплавов. Мало того, он так же, как и олово, активно защищает железо от коррозии металлов.

 Наиболее дешевым и производительным является упрочнение металлических изделий способом поверхностного наклепа. Сейчас разработаны методы упрочнения поверхности металлических изделий нейтральным потоком, но суть остается прежняя: на поверхности металла образуется плотный твердый слой. Его умели создавать еще в медном веке. Чтобы сделать прочным и твердым лезвие медного топора или ножа, их тщательно проковывали на наковальне. При увеличении прочности и твердости соответственно уменьшались пластичность и вязкость меди. Да и теперь такой способ упрочнения для плотности металла широко применяется в быту. В сенокосную пору по утрам и вечерам в деревнях слышен дробный перестук молотка. Это отбивают косы перед выходом на покос или же впрок, к следующему утру. Выражаясь техническим языком, крестьяне упрочняют жало косы «методом поверхностного наклепа».
Наиболее дешевым и производительным является упрочнение металлических изделий способом поверхностного наклепа. Сейчас разработаны методы упрочнения поверхности металлических изделий нейтральным потоком, но суть остается прежняя: на поверхности металла образуется плотный твердый слой. Его умели создавать еще в медном веке. Чтобы сделать прочным и твердым лезвие медного топора или ножа, их тщательно проковывали на наковальне. При увеличении прочности и твердости соответственно уменьшались пластичность и вязкость меди. Да и теперь такой способ упрочнения для плотности металла широко применяется в быту. В сенокосную пору по утрам и вечерам в деревнях слышен дробный перестук молотка. Это отбивают косы перед выходом на покос или же впрок, к следующему утру. Выражаясь техническим языком, крестьяне упрочняют жало косы «методом поверхностного наклепа».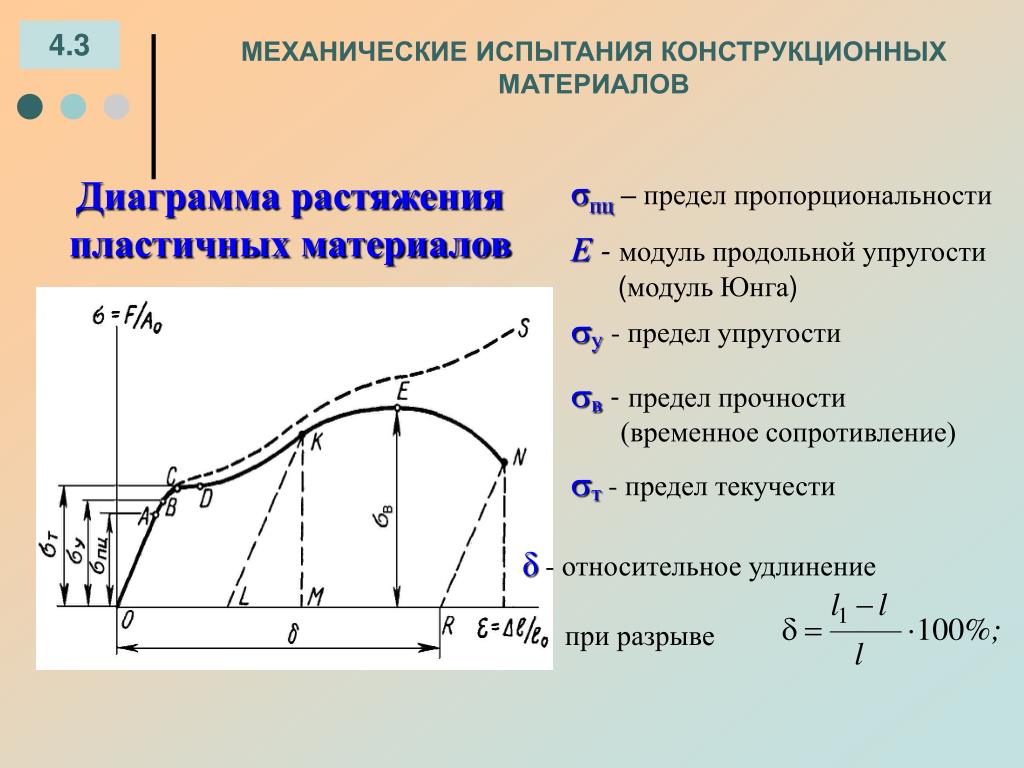 Приведем один из примеров мирного сосуществования некоторых металлов в текущее время.
Приведем один из примеров мирного сосуществования некоторых металлов в текущее время.