Физический класс | Электронная теория проводимости металлов «
В 1900 году немецкий физик П. Друде создал теорию электропроводности металлов. В основе этой теории лежат следующие допущения:
- Свободные электроны в металлах ведут себя подобно молекулам идеального газа. Электронный газ подчиняется законам идеального газа.
- Движение свободных электронов подчиняется законам Ньютона.
- Свободные электроны в процессе хаотического движения сталкиваются только с ионами кристаллической решетки.
- При столкновении электронов с ионами электроны передают ионам свою кинетическую энергию полностью.
Согласно данной модели, на отрезке проводника свободные электроны совершают хаотическое тепловое движение. Действующее в проводнике электрическое поле перемещает электроны с небольшой скоростью (скорость дрейфа электронов ~ 0,1 мм/с) вдоль проводника.
Сила тока в проводнике:
I=en<v>S
где n
<v> – средняя скорость дрейфа электронов
S – поперечное сечение проводника.
С позиции электронной проводимости металлов удалось объяснить причину нагревания проводников при прохождении электрического тока.
Электронная теория проводимости металлов экспериментально подтверждена в 1913 году российскими физиками Л.И. Мандельштамом и Н.Д. Папалекси и в 1916 году американскими физиками Т. Стюартом и Р. Толменом.
Направление электрического тока в проводнике выбрано в сторону движения положительно заряженных частиц.

Отношение заряда, переносимого через поперечное сечение проводника за интервал времени, к этому интервалу времени называется силой тока.

В СИ [I] = 1 А (Ампер)
Для поддержания электрического тока в проводнике необходимо электрическое поле. Его действие характеризуется электрическим напряжением.

В СИ [U] = 1 В (Вольт)
Для поддержания постоянного направленного движения заряженных частиц в проводнике электрическое поле должно совершать работу. Эту работу принято называть работой электрического тока.
Работа сил электрического поля или работа электрического тока на участке цепи сопротивлением R и за время

В СИ [A] = 1 Дж (Джоуль)
При нагревание проводника растет его температура, следовательно, увеличивается внутренняя энергия. С прекращением роста температуры проводника он начинает передавать окружающим телам некоторое количество теплоты, равное работе электрического тока. Таким образом, формула A=IUt определяет количество теплоты, переданное проводником другим телам.
Для последовательного соединения проводников удобнее воспользоваться формулой:
При параллельном соединении удобно использовать формулу:
Для характеристики электрических приборов удобнее пользоваться физической величиной, получившей название мощность тока.
Мощность электрического тока равна:

В СИ [P] = 1 Вт (Ватт)
Назад
fizclass.ru
§ 14.4 Основные свойства полупроводников. Примесная электропроводимость.
Полупроводниками называют вещества, электрическая проводимость которых занимает промежуточное место между проводимостью металлов и диэлектриков. К полупроводникам относятся многие химические элементы (германий, кремний, селен, теллур, мышьяк и др.), огромное количество сплавов и химических соединений (GaAs, PbS, CdS и др.). Почти все неорганические вещества окружающего нас мира – полупроводники. Самым распространенным в природе полупроводником является кремний, составляющий около 30 % земной коры.
Качественное отличие полупроводников от металлов проявляется прежде всего в зависимости удельного сопротивления от температуры. С понижением температуры сопротивление металлов падает. У полупроводников, напротив, с понижением температуры сопротивление возрастает и вблизи абсолютного нуля они практически становятся изоляторами (рис. 14.4).
Такой ход зависимости ρ (T) показывает, что у полупроводников концентрация носителей свободного заряда не остается постоянной, а увеличивается с ростом температуры. Механизм электрического тока в полупроводниках нельзя объяснить в рамках модели газа свободных электронов. Рассмотрим качественно этот механизм на примере германия (Ge). В кристалле кремния (Si) механизм аналогичен.
Атомы германия на внешней оболочке имеют четыре слабо связанных электрона. Их называютвалентными электронами. В кристаллической решетке каждый атом окружен четырьмя ближайшими соседями. Связь между атомами в кристалле германия является ковалентной, т. е. осуществляется парами валентных электронов. Каждый валентный электрон принадлежит двум атомам (рис. 14.5). Валентные электроны в кристалле германия связаны с атомами гораздо сильнее, чем в металлах; поэтому концентрация электронов проводимости при комнатной температуре в полупроводниках на много порядков меньше, чем у металлов. Вблизи абсолютного нуля температуры в кристалле германия все электроны заняты в образовании связей. Такой кристалл электрического тока не проводит.
При повышении температуры некоторая часть валентных электронов может получить энергию, достаточную для разрыва ковалентных связей. Тогда в кристалле возникнут свободные электроны (электроны проводимости). Одновременно в местах разрыва связей образуются вакансии, которые не заняты электронами. Эти вакансии получили название дырок. Вакантное место может быть занято валентным электроном из соседней пары, тогда дырка переместится на новое место в кристалле. При заданной температуре полупроводника в единицу времени образуется определенное количество электронно-дырочных пар. В то же время идет обратный процесс – при встрече свободного электрона с дыркой, восстанавливается электронная связь между атомами германия. Этот процесс называется
Если полупроводник поместить в электрическое поле, то в упорядоченное движение вовлекаются не только свободные электроны, но и дырки, которые ведут себя как положительно заряженные частицы. Поэтому ток I в полупроводнике складывается из электронного In и дырочного Ip токов:
I=In+Ip
Концентрация электронов проводимости в полупроводнике равна концентрации дырок: nn = np. Электронно-дырочный механизм проводимости проявляется только у чистых (т. е. без примесей) полупроводников. Он называется собственной электрической проводимостью полупроводников.
При наличии примесей электрическая проводимость полупроводников сильно изменяется. Например, добавка в кристалл кремния примесей фосфора в количестве 0,001 атомного процента уменьшает удельное сопротивление более чем на пять порядков. Такое сильное влияние примесей может быть объяснено на основе изложенных выше представлений о строении полупроводников.
Необходимым условием резкого уменьшения удельного сопротивления полупроводника при введении примесей является отличие валентности атомов примеси от валентности основных атомов кристалла.
Проводимость полупроводников при наличии примесей называетсяпримесной проводимостью. Различают два типа примесной проводимости – электронную и дырочную.
Электронная проводимость возникает, когда в кристалл германия с четырехвалентными атомами введены пятивалентные атомы (например, атомы мышьяка, As).
На рис. 14.6 показан пятивалентный атом мышьяка, оказавшийся в узле кристаллической решетки германия. Четыре валентных электрона атома мышьяка включены в образование ковалентных связей с четырьмя соседними атомами германия. Пятый валентный электрон оказался излишним; он легко отрывается от атома мышьяка и становится свободным. Атом, потерявший электрон, превращается в положительный ион, расположенный в узле кристаллической решетки.
Примесь из атомов с валентностью, превышающей валентность основных атомов полупроводникового кристалла, называется донорной примесью. В результате ее введения в кристалле появляется значительное число свободных электронов. Это приводит к резкому уменьшению удельного сопротивления полупроводника – в тысячи и даже миллионы раз. Удельное сопротивление проводника с большим содержанием примесей может приближаться к удельному сопротивлению металлического проводника.
Вкристалле германия с примесью мышьяка есть электроны и дырки, ответственные за собственную проводимость кристалла. Но основным типом носителей свободного заряда являются электроны, оторвавшиеся от атомов мышьяка. В таком кристалле n n >> np. Такая проводимость называется электронной, а полупроводник, обладающий электронной проводимостью, называется полупроводником n-типа.
Дырочная проводимость возникает, когда в кристалл германия введены трехвалентные атомы (например, атомы индия, In). На рис. 14.7 показан атом индия, который с помощью своих валентных электронов создал ковалентные связи лишь с тремя соседними атомами германия. На образование связи с четвертым атомом германия у атома индия нет электрона. Этот недостающий электрон может быть захвачен атомом индия из ковалентной связи соседних атомов германия. В этом случае атом индия превращается в отрицательный ион, расположенный в узле кристаллической решетки, а в ковалентной связи соседних атомов образуется вакансия. Примесь атомов, способных захватывать электроны, называется
Наличие акцепторной примеси резко снижает удельное сопротивление полупроводника за счет появления большого числа свободных дырок. Концентрация дырок в полупроводнике с акцепторной примесью значительно превышает концентрацию электронов, которые возникли из-за механизма собственной электропроводности полупроводника: np >> nn. Проводимость такого типа называется дырочной проводимостью. Примесный полупроводник с дырочной проводимостью называется полупроводником p-типа. Основными носителями свободного заряда в полупроводниках p-типа являются дырки.
Следует подчеркнуть, что дырочная проводимость в действительности обусловлена эстафетным перемещением по вакансиям от одного атома германия к другому электронов, которые осуществляют ковалентную связь.
Для полупроводников n- и p-типов закон Ома выполняется в определенных интервалах сил тока и напряжений при условии постоянства концентраций свободных носителей.
studfiles.net
физика — 26
Физика — 2626. Основные положения классической электронной теории. Связь плотности тока со скоростью направленного движения и концентрацией заряженных частиц. Закон Ома в дифференциальной форме.
Исходя из представлений о свободных электронах как основных носителях тока в металлах, Друде разработал классическую теорию электропровод-ности металлов, которая затем была усовершенствована Лоренцем.
Основные положения этой теории сводятся к следующим:
1) Носителями тока в металлах являются электроны, движение которых подчиняется законом классической механики.
2) Поведение электронов подобно поведению молекул идеального газа (электронный газ).
3) При движении электронов в кристаллической решетке можно не учитывать столкновения электронов друг с другом.
4) При упругом столкновении электронов с ионами электроны полностью передают им накопленную в электрическом поле энергию.
Плотность тока — векторная физическая величина , имеющая смысл силы тока , протекающего через единицу площади . Например, при равномерном распределении плотности тока и всюду ортогональности ее плоскости сечения, через которое вычисляется или измеряется ток, величина вектора плотности тока:
где I — сила тока через поперечное сечение проводника площадью S .
В простейшем предположении, что все носители тока (заряженные частицы) двигаются с одинаковым вектором скорости и имеют одинаковые заряды (такое предположение может иногда быть приближенно верным; оно позволяет лучше всего понять физический смысл плотности тока), а концентрация их ,
или
где — плотность заряда этих носителей. (Направление вектора соответствует направлению вектора скорости , с которой движутся заряды , создающие ток, если q положително).
В реальности даже носители одного типа движутся вообще говоря и как правило с различными скоростями. Тогда под следует понимать среднюю скорость.
В сложных системах (с различными типами носителей заряда, например, в плазме или электролитах)
то есть вектор плотности тока есть сумма плотностей тока по всем типам подвижных носителей; где — концентрация частиц каждого типа, — заряд частицы данного типа, — вектор средней скорости частиц этого типа.
Выражение для общего случая может быть записано также через сумму по всем индивидуальным частицам:
(сама формула почти совпадает с формулой, приведенной чуть выше, но теперь индекс суммирования i означает не номер типа частицы, а номер каждой индивидуальной частицы, не важно, имеют они одинаковые заряды или разные, при этом концентрации оказываются уже не нужны).
Закон Ома в дифференциальной форме
где:
- — вектор плотности тока ,
- — удельная проводимость ,
- — вектор напряжённости электрического поля .
malishev.info
§8. Классическая теория электропроводности металлов и ее недостатки.
Изучение природы носителей тока в проводниках (металлах) было начато опытом Рике (1901 г.). Два медных и один алюминиевый цилиндры с тщательно отполированными торцами были взвешены и включены в цепь тока (рис. 8.1.).
В течение года через цилиндры пропускали ток (общий заряд 3,5*106 Кл). Взвешивание показало, что пропускание тока вес цилиндров не изменило. Результат свидетельствовал о том, что перенос заряда осуществлялся не атомами.
Для отожествления носителей тока с электронами, открытыми Д.Д. Томпсоном в 1897 году, Л. Мандельштам и Н. Папалекси (1913 г.), Р. Толмен и Т. Стюарт (1916 г.) поставили опыты. Идея опытов основана на следующих рассуждениях. Если в металлах имеются легко перемещающиеся заряженные частицы, то при торможении проводника они должны некоторое время двигаться по инерции, в результате чего в проводнике будет перенесен некоторый заряд. Цилиндрическая катушка с намотанным проводом раскручивалась и резко тормозилась. Эффект переноса заряда регистрировался приборами. Количественный результат для удельного заряда носителей тока был близок к e/me для электронов.
Исходя из представлений о свободных электронах как носителях тока, П. Друде (1863-1906) разработал классическую теорию проводимости металлов, которую затем усовершенствовал Х. Лоренц (1853-1928). В этой теории электроны уподобляются молекулам идеального газа. Проводимость рассматривается как систематический дрейф под воздействием электрического поля, наложенный на хаотическое тепловое движение.
Методы молекулярно-кинетической теории идеального газа позволяют оценить среднюю скорость теплового движения свободных электронов (Vт)
 , (8.1)
, (8.1)
где k — постоянная Больцмана,
T — абсолютная температура,
me — масса электрона.
При T = 3000К, Vт 105 м/с.
В силу хаотичности, тепловое движение не дает переноса зарядов в отсутствие всякого внешнего поля. Однако, в результате статистических флуктуаций векторная сумма скоростей теплового движения электронов за небольшие промежутки времени может быть отличной от нуля, что приводит к возникновению спонтанно флуктуирующего «шумового» тока. «Шумовой» ток определяет в конечном счете предел чувствительности устройств, регистрирующих слабые электрические сигналы.
При включении электрического поля возникает дрейф электронов проводимости. Среднюю скорость дрейфа легко оценить, воспользовавшись уравнением (7.1):

Для меди, например, предельно допустимая плотность тока jCu= 107 А/м2, а n = 1029 м–3, поэтому
Vдр = 10—3 м/с.
Сравнение величины средней скорости теплового движения и скорости дрейфа позволяет за результирующую скорость электрона проводимости принимать модуль скорости теплового движения.
Рассмотрим проводник как объем, в котором находится идеальный электронный газ. Электроны, находясь в дрейфовом и тепловом движении, испытывают соударения. Обозначим среднее время между соударениями через (время свободного пробега). Под действием электрического поля напряженностью E электрон к концу пробега приобретет максимальную скорость дрейфа
 (8.2)
(8.2)
Так как скорость дрейфа за время пробега меняется линейно, то ее среднее значение равно
 (8.3)
(8.3)
Подставим полученное значение в (7.1), тогда получим
 (8.4)
(8.4)
Таким образом, плотность тока оказалась пропорциональной напряженности электрического поля (закон Ома в дифференциальной форме). Коэффициент пропорциональности равен удельной проводимости
 (8.5)
(8.5)
Среднее время свободного пробега связано со средней длиной свободного пробега следующим образом: =/VT. Подставив это выражение в (8.5), получим
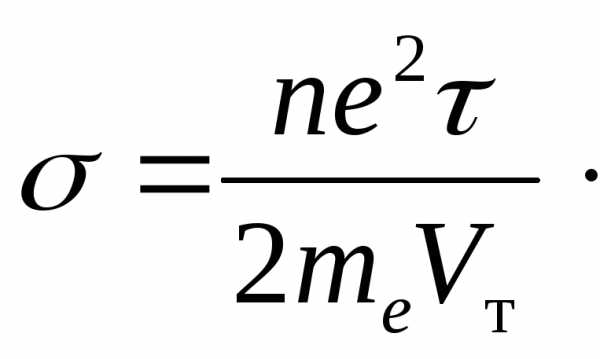 (8.6)
(8.6)
Определяющим в процессе проводимости является взаимодействие свободных электронов с кристаллической решеткой металла.
Интересно физическое подобие механизмов электро- и теплопроводности. Металлы хорошо проводят тепло и электрический ток. Если сравнить значение удельного коэффициента теплопроводности для одноатомного идеального газа, равное
где k — постоянная Больцмана, и выражение (8.6) для удельной электропроводности, то с учетом получим следующее отношение:
 (8.7)
(8.7)
которое называется законом Видемана – Франца и отражает тот факт, что свободные электроны являются основными участниками процессов тепло — и электропроводности. Этот результат довольно хорошо подтвердился на опыте и долгое время считался доказательством правильности исходных положений классической теории электропроводности и теплопроводности металлов, несмотря на то, что в вопросе теплоемкости электронов в металлах эта теория приводила к резкому противоречию с опытом.
Очевидный успех классической теории электропроводности встречается с некоторыми существенными затруднениями также при объяснении температурной зависимости проводимости.
Известно, что удельное сопротивление металлов в определенной области температур изменяется по закону
(8.8)
где 0 — удельное сопротивление при t = 00 C,
— температурный коэффициент сопротивления,
t — температура по шкале Цельсия,
а из формулы (8.6) следует, что
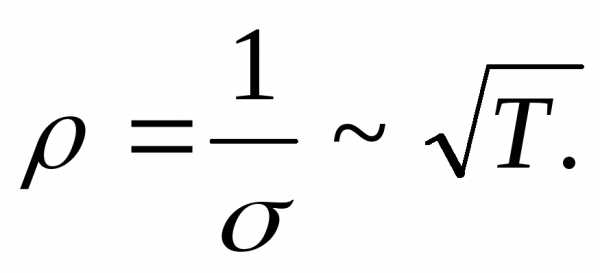
Трудно дать классическое толкование физическому явлению перехода ряда проводников в сверхпроводящее состояние при температурах ниже определенной критической температуры Тк, характерной для данного материала. Впервые исчезновение сопротивления ртути при понижении температуры наблюдал голландский физик Х. Камерлинг-Оннес (1911 г.). Он пришел к выводу, что ртуть при Т = 4,15К переходит в новое состояние, которое было названо сверхпроводящим. Вещества, у которых при охлаждении ниже критической температуры Тк сопротивление падает до нуля называются сверхпроводниками. К сверхпроводникам относятся элементы периодической системы, расположенные в так называемых «островах» сверхпроводимости, в частности: Ti (0,39K), Zr (0,546K), Nb (9,46K), Mo (0,95K), Zn (0,875K), Hg (4,153K), Pb (7,18K), Al (1,19K), Th (1,4K). Переход в сверхпроводящее стояние обнаружен также у целого ряда металлических сплавов и соединений. У ряда сверхпроводящих сплавов отдельные компоненты или даже все компоненты сами по себе не являются сверхпроводниками. Например: PbTl2 , Sb2Sn3 , Bi5Tl3 , Hg5Tl2 , VN, TiN, TiC сплавы сверхпроводника и несверхпроводника сплавы несверхпроводников WC, W2C, MoC, Mo2C.
Недостатки классической теории электропроводности удалось преодолеть А. Зоммерфельду (1868-1951), который для описания состояния электронного газа применил квантовую статистику Ферми-Дирака и тем устранил противоречия теории и эксперимента при объяснении электропроводности, теплопроводности и теплоемкости электронного газа в металлах.
Крепким орешком оказалась проблема объяснения природы сверхпроводимости. Исследуя различные возможности объяснения сверхпроводников, немецкие физики Х. И Ф. Лондоны в 1934 г. пришли к заключению, что сверхпроводящее состояние является макроскопическим квантовым состоянием металла. На основе этого представления они создали феноменологическую теорию, объясняющую отсутствие сопротивления у некоторых проводников. Обобщение теории Лондонов, сделанное советскими физиками В. Гинзбургом и Л. Ландау (1950), позволило рассмотреть поведение сверхпроводников в сильных магнитных полях. При этом было объяснено огромное количество экспериментальных данных и предсказаны новые важные явления.
studfiles.net
Электричество и магнетизм. Часть 2
Страница 11 из 28
2.11. Основные положения классической электронной теории проводимости металлов Друде — Лоренца.
Исходя из представлений о свободных электронах как основных носителях тока в металлах, Друде (Drude P., 1863-1906) разработал классическую теорию электропровод-ности металлов, которая затем была усовершенствована Лоренцем (Lorentz H., 1853-1928).
Основные положения этой теории сводятся к следующим:
1). Носителями тока в металлах являются электроны, движение которых подчиняется законом классической механики.
2). Поведение электронов подобно поведению молекул идеального газа (электронный газ).
3). При движении электронов в кристаллической решетке можно не учитывать столкновения электронов друг с другом.
4). При упругом столкновении электронов с ионами электроны полностью передают им накопленную в электрическом поле энергию.
Средняя тепловая скорость хаотического движения электронов при Т≈300К составляет .
При включении электрического поля на хаотическое движение электронов накладывается упорядоченное движение (называемое иногда «дрейфовым»), происходящее с некоторой средней скоростью ; возникает направленное движение электронов — электрический ток. Плотность тока определяется по формуле.
Оценки показывают, что при максимально допустимой плотности тока в металлах j = 107 А/м2 и концентрации носителей 1028 – 1029м-3, . Таким образом, даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов .
mylect.ru
§ III.7.3. Основы классической электронной теории электропроводности металлов
1°. Высокая электропроводность металлов связана с тем, что в металлах имеется громадное количество носителей тока –электронов проводимости, образовавшихся из валентных электронов атомов металла (VI.2.3.9°), которые не принадлежат определенному атому, а являютсяколлективизированными (обобществленными) электронами. В классической электронной теории Друде-Лоренца эти электроны рассматриваются как электронный газ (III.3.4.1°), обладающий свойствами одноатомного идеального газа (II.1.4.1°).
Число электронов проводимости в единице объема одновалентного металла:
 ,
,
где NА– число Авогадро (IX),A– атомная масса металла,ρ– его плотность. По порядку величиныn0~ (10281029) м-3.
Электроны проводимости в отсутствие электрического поля внутри металла хаотически движутся и сталкиваются с ионами кристаллической решетки металла (VI.1.1.3°). Считается, что средняя длина свободного пробега электрона <λ> (II.3.5.1º) по порядку величины должна быть равна периоду кристаллической решетки металла, т. е. <λ>≈ 10-10м.
Средняя кинетическая энергия теплового движения электронов (II.3.2.4º)
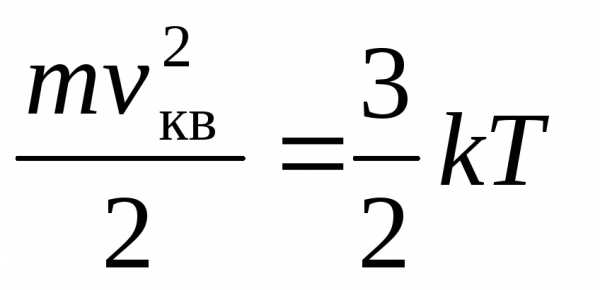 ,
,
где m– масса,vкв– средняя квадратичная скорость электронов (II.3.2.2°). При температуреТ= 273 К скоростьvкв≈ 103м/с.
Средняя арифметическая скорость  теплового движения электронов (II.3.3.6°)
имеет такой же порядок величины.
теплового движения электронов (II.3.3.6°)
имеет такой же порядок величины.
2°. Электрический ток в металле возникает под действием внешнего электрического поля (III.7.1.4°), которое вызывает упорядоченное движение электронов. Плотность токаjравна заряду всех электронов, проходящих за единицу времени через единицу площади поперечного сечения проводника,
 ,
,
где n0– число электронов
проводимости в единице объема,е–
абсолютная величина заряда электрона, – средняя скорость упорядоченного
движения электронов под действием
внешнего электрического поля. При самых
больших плотностях токов
– средняя скорость упорядоченного
движения электронов под действием
внешнего электрического поля. При самых
больших плотностях токов составляет 10-4м/с и ничтожно мало
по сравнению с тепловыми скоростями
электронов (п. 1°).
составляет 10-4м/с и ничтожно мало
по сравнению с тепловыми скоростями
электронов (п. 1°).
3°. Электрический ток в цепи
устанавливается за время ,
гдеL– длина цепи,с– скорость
света в вакууме. Времяtсовпадает
с временем установления вдоль цепи
стационарного электрического поля и
появлением упорядоченного движения
электронов сразу во всей цепи. Поэтому
электрический ток возникает практически
одновременно с замыканием цепи.
,
гдеL– длина цепи,с– скорость
света в вакууме. Времяtсовпадает
с временем установления вдоль цепи
стационарного электрического поля и
появлением упорядоченного движения
электронов сразу во всей цепи. Поэтому
электрический ток возникает практически
одновременно с замыканием цепи.
4°.Закон Ома для плотности тока(закон Ома в дифференциальной форме):
 .
.
Плотность тока в проводнике равна
произведению удельной электрической
проводимости(удельной электропроводности)γна напряженность электрического
поляЕ. Величина называетсяудельным сопротивлением.
называетсяудельным сопротивлением.
Удельная электрическая проводимость в классической электронной теории вычисляется по формуле:
 ,
, ,
,
где n0– число электронов в
единице объема металла, <λ> –
средняя длина свободного пробега
электрона (II.3.5.1°), – средняя арифметическая скорость
теплового движения электронов (II.3.3.6°),еит– абсолютная величина
заряда и масса электрона.
– средняя арифметическая скорость
теплового движения электронов (II.3.3.6°),еит– абсолютная величина
заряда и масса электрона.
5°. На длине свободного пробега электрон приобретает под действием поля скорость упорядоченного движения, равную в конце пробегаvмакс. При соударении с ионом электрон ее теряет и энергия упорядоченного движения электрона преобразуется во внутреннюю энергию проводника, который нагревается при прохождении по нему электрического тока.
Объемной плотностью тепловой мощности тока wназывается энергия, которая выделяется в единице объема проводника за единицу времени.Закон Джоуля-Ленцадля объемной плотности тепловой мощности тока:
.
Закон Джоуля-Ленца в дифференциальной форме: объемная плотность тепловой мощности тока равна скалярному произведению векторов плотности тока и напряжённости электрического поля.
Объемная плотность тепловой мощности
тока не зависит от характера соударения
электронов с узлами кристаллической
решетки (упругий или неупругий удар
(I.3.5.3°)). Из законов сохранения энергии
и импульса следует, что энергия ΔW,
переданная иону при столкновении
электрона с ионом, составляет лишь малую
часть энергииWэлэлектрона.
При неупругом столкновении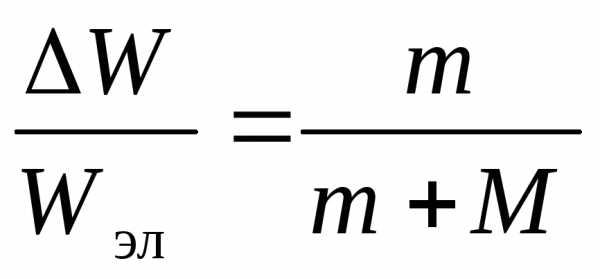 ,
при упругом
,
при упругом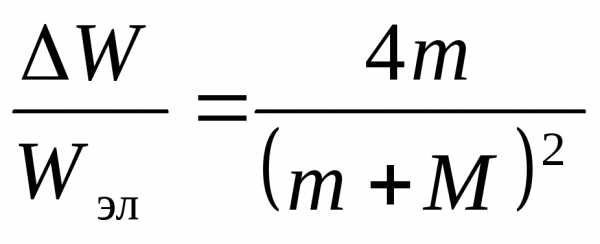 ,
гдеm– масса электрона,M– масса
иона. В обоих случаях практически
,
гдеm– масса электрона,M– масса
иона. В обоих случаях практически .
.
6°.Закон Видемана-Франца: для всех металлов отношение коэффициента теплопроводностиK(II.3.8.5°) к удельной электрической проводимостиγпрямо пропорционально абсолютной температуреТ:
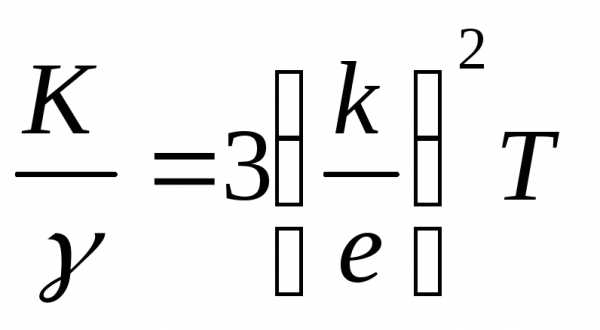 ,
,
где k– постоянная Больцмана (II.1.4.5°),е– заряд электрона.
7°.Недостатки классической электронной теорииэлектропроводности металлов:
а) невозможность объяснить экспериментально наблюдаемую в широком интервале температур линейную зависимость между удельным сопротивлением ρи абсолютной температурой:ρ~Т;
б) неправильное значение молярной
теплоемкости металлов. Она должна быть
равна, согласно этой теории, 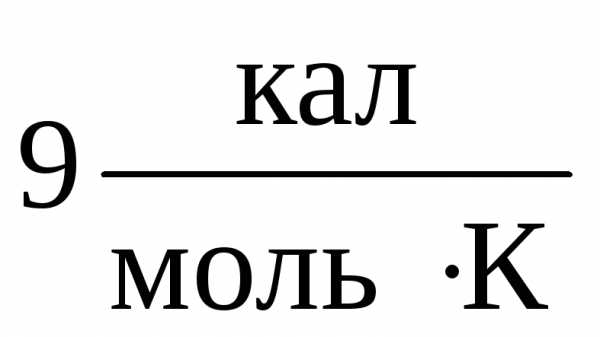 и складываться из теплоемкости ионной
кристаллической решетки
и складываться из теплоемкости ионной
кристаллической решетки и теплоемкости одноатомного электронного
газа
и теплоемкости одноатомного электронного
газа .
Однако, из экспериментально полученного
закона Дюлонга и Пти (VII.2.7.2°) известно,
что молярная теплоемкость металлов
мало отличается от теплоемкости других
твердых тел и составляет приблизительно
.
Однако, из экспериментально полученного
закона Дюлонга и Пти (VII.2.7.2°) известно,
что молярная теплоемкость металлов
мало отличается от теплоемкости других
твердых тел и составляет приблизительно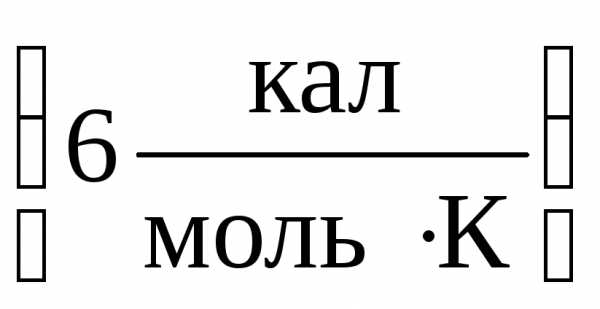 .
Отсутствие электронной составляющей
теплоемкости металлов объяснить
классически невозможно;
.
Отсутствие электронной составляющей
теплоемкости металлов объяснить
классически невозможно;
в) экспериментальные значения удельного
сопротивления ρи теоретические
значения средней арифметической скорости
электронов приводят по формулам п. 4° к величине
средней длины свободного пробега
электрона <λ>, на два порядка превышающей
период кристаллической решетки металла.
Эта противоречит предположениям
классической электронной теории
электропроводности металлов.
приводят по формулам п. 4° к величине
средней длины свободного пробега
электрона <λ>, на два порядка превышающей
период кристаллической решетки металла.
Эта противоречит предположениям
классической электронной теории
электропроводности металлов.
studfiles.net
Лабораторная работа — № 217 изучение зависимости сопротивления металлов и полупроводников от температуры
ЦЕЛЬ РАБОТЫ: Исследование температурной зависимости сопротивления металлов и полупроводников, определение температурного коэффициента сопротивления металла и ширины запрещенной зоны полупроводника.
ПРИНАДЛЕЖНОСТИ: Образцы — медная проволока и полупроводник, электронагреватель, термометр, прибор комбинированный цифровой Щ 4300 или вольтметр электронный цифровой ВК7 — 10А.
1. Основные положения классической теории электропроводности металлов
С
позиций классической электронной теории
высокая электропроводность металлов
обусловлена наличием огромного числа
свободных электронов, движение которых
подчиняется законам классической
механики Ньютона. В этой теории
пренебрегают взаимодействием электронов
между собой, а взаимодействие их с
положительными ионами сводят только к
соударениям. Иными словами, электроны
проводимости рассматриваются как
электронный газ, подобный одноатомному,
идеальному газу. Такой электронный газ
должен подчиняться всем законам
идеального газа. Следовательно, средняя
кинетическая энергия теплового движения
электрона будет равна 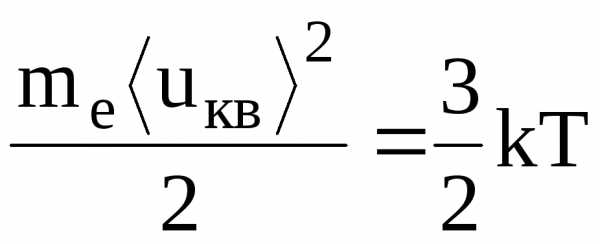 ,
где
,
где — масса электрона,
— масса электрона,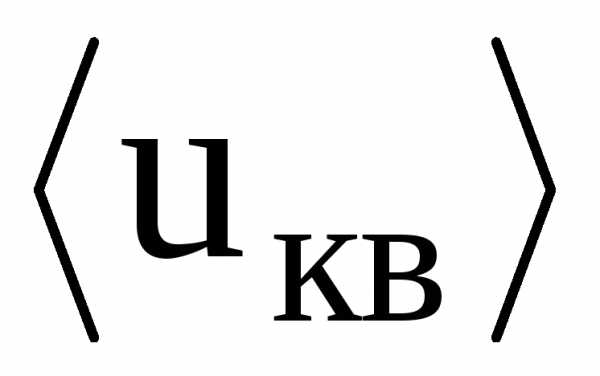 — его среднеквадратичная скорость, k —
постоянная Больцмана, Т — термодинамическая
температура. Отсюда при Т=300 К
среднеквадратичная скорость теплового
движения электронов
— его среднеквадратичная скорость, k —
постоянная Больцмана, Т — термодинамическая
температура. Отсюда при Т=300 К
среднеквадратичная скорость теплового
движения электронов 105
м/с.
105
м/с.
Хаотичное
тепловое движение электронов не может
привести к возникновению электрического
тока, но под действием внешнего
электрического поля в проводнике
возникает упорядоченное движение
электронов со скоростью  .
Оценить величину
.
Оценить величину можно из
соотношения
можно из
соотношения ,
для j — плотности тока, где
,
для j — плотности тока, где — концентрация электронов, e — заряд
электрона. Как показывает расчет,
— концентрация электронов, e — заряд
электрона. Как показывает расчет, 810-4
м/с. Чрезвычайно малое значение величины
по сравнению с величинойобъясняется весьма частыми столкновениями
электронов с ионами решетки. Казалось
бы, полученный результат дляпротиворечит тому факту, что передача
электрического сигнала на очень большие
расстояния происходит практически
мгновенно. Но дело в том, что замыкание
электрической цепи влечет за собой
распространение электрического поля
со скоростью 3108
м/с (скорость света). Поэтому упорядоченное
движение электронов со скоростью
810-4
м/с. Чрезвычайно малое значение величины
по сравнению с величинойобъясняется весьма частыми столкновениями
электронов с ионами решетки. Казалось
бы, полученный результат дляпротиворечит тому факту, что передача
электрического сигнала на очень большие
расстояния происходит практически
мгновенно. Но дело в том, что замыкание
электрической цепи влечет за собой
распространение электрического поля
со скоростью 3108
м/с (скорость света). Поэтому упорядоченное
движение электронов со скоростью  под действием поля возникнет практически
сразу же на всем протяжении цепи, что и
обеспечивает мгновенную передачу
сигнала. На базе классической
электронной теории был выведен закон
электрического тока — закон Ома в
дифференциальной форме,
где-удельная
проводимость, зависящая от природы
металла. Электроны проводимости,
перемещаясь в металле, переносят с собой
не только электрический заряд, но и
кинетическую энергию беспорядочного
теплового движения. Поэтому те металлы,
которые хорошо проводят электрический
ток, являются хорошими проводниками
тепла. Классическая электронная теория
качественно объяснила природу
электрического сопротивления
металлов. Во внешнем поле упорядоченное
движение электронов нарушается их
соударениями с положительными ионами
решетки. Между двумя столкновениями
электрон движется ускоренно и приобретает
энергию, которую при последующем
столкновении отдает иону. Можно считать,
что движение электрона в металле
происходит с трением, подобным внутреннему
трению в газах. Это трение и создает
сопротивление металла.
под действием поля возникнет практически
сразу же на всем протяжении цепи, что и
обеспечивает мгновенную передачу
сигнала. На базе классической
электронной теории был выведен закон
электрического тока — закон Ома в
дифференциальной форме,
где-удельная
проводимость, зависящая от природы
металла. Электроны проводимости,
перемещаясь в металле, переносят с собой
не только электрический заряд, но и
кинетическую энергию беспорядочного
теплового движения. Поэтому те металлы,
которые хорошо проводят электрический
ток, являются хорошими проводниками
тепла. Классическая электронная теория
качественно объяснила природу
электрического сопротивления
металлов. Во внешнем поле упорядоченное
движение электронов нарушается их
соударениями с положительными ионами
решетки. Между двумя столкновениями
электрон движется ускоренно и приобретает
энергию, которую при последующем
столкновении отдает иону. Можно считать,
что движение электрона в металле
происходит с трением, подобным внутреннему
трению в газах. Это трение и создает
сопротивление металла.
Вместе с тем классическая теория встретилась с существенными затруднениями. Перечислим некоторые из них :
1. По расчетам электронной теории, сопротивление R должно быть пропорциональным , где Т — термодинамическая температура. Согласно опытным данным, RТ.
2. Полученные опытным путем значения электропроводности дают для средней длины свободного пробега электронов в металлах величину порядка сотен междоузельных расстояний. Это гораздо больше, чем по классической теории .
Расхождение теории с опытом объясняется тем, что движение электронов в металле подчиняется не законам классической механики, а законам квантовой механики. Достоинством классической электронной теории являются простота, наглядность и правильность многих качественных ее результатов.
studfiles.net
